1 Introduction

One main topic of Diophantine approximation studies the approximation of an irrational number by rational numbers. Given an irrational number x, we call a rational p/q a best approximation of x if

$$\begin{aligned} \left| qx-p\right|< \left| bx-a\right| ~{{\,\mathrm{for}\,}}~{{\,\mathrm{any}\,}}~ \frac{a}{b}\not =\frac{p}{q} ~{{\,\mathrm{such~that}\,}}~ 0<b \le q. \end{aligned}$$

Here, and in the whole paper, by convention, when we write a rational number p/q, we always assume that \(p \in {\mathbb {Z}}\), \(q \in {\mathbb {N}}\) and p and q are coprime. The celebrated Lagrange Theorem (see [17,  Chapter II] and [12,  Section 6]) states that the best approximations of an irrational number x are the convergents, i.e., the finite truncations of the regular continued fraction (RCF) of x:

$$\begin{aligned} x= d_0+\frac{1}{d_1+\frac{1}{{d_2+\frac{1}{\ddots }}}}, \end{aligned}$$
(1)

where \(d_0\in {\mathbb {Z}}\) and \(d_j\in {\mathbb {N}}\), for \(j\ge 1\). More precisely, a rational p/q is a best approximation of an irrational x if and only if it is one of the convergents:

$$\begin{aligned} \frac{p^R_0}{q^R_0}:=d_0, ~ \frac{p^R_1}{q^R_1}:=d_0+\frac{1}{d_1}, ~\frac{p^R_2}{q^R_2}:=d_0+\frac{1}{d_1+\frac{1}{d_2}}, ~\cdots \end{aligned}$$

Let \({\mathbb {H}}= \{z\in {\mathbb {C}}: {{\,\mathrm{Im}\,}}(z)>0\}\) be the upper half-plane. The group \(\text {SL}_2({\mathbb {R}})\) acts on \({\mathbb {H}}\) as isometries defined by

$$\begin{aligned} g = \begin{pmatrix}a&{}b\\ c&{}d\end{pmatrix}: z \mapsto g(z) = \frac{az+b}{cz+d}. \end{aligned}$$

There is a close connection between the geodesics on the modular surface \(\text {SL}_2({\mathbb {Z}})\backslash {\mathbb {H}}\) and the RCF algorithm (e.g. [22]). Especially, the orbit \(\text {SL}_2({\mathbb {Z}})(\infty )={\mathbb {Q}}\) corresponds to a unique cusp of \(\text {SL}_2({\mathbb {Z}})\backslash {\mathbb {H}}\). Let

$$\begin{aligned} \Theta = \left\{ \begin{pmatrix}a&{}b\\ c&{}d\end{pmatrix} \in \text {SL}_2({\mathbb {Z}})\ : \ \begin{pmatrix}a&{}b\\ c&{}d\end{pmatrix}\equiv \begin{pmatrix}1&{}0\\ 0&{}1\end{pmatrix} \text { or } \begin{pmatrix}0&{}-1 \\ 1 &{}0\end{pmatrix} \pmod 2 \right\} . \end{aligned}$$

Then \(\Theta \) is a subgroup of \(\text {SL}_2({\mathbb {Z}})\) of index 3 and the quotient space \(\Theta \backslash {\mathbb {H}}\) is a hyperbolic surface with two cusps corresponding to the orbits \(\Theta (\infty )\) and \(\Theta (1)\) of \(\infty \) and 1. Kraaikamp–Lopes [14] and Boca–Merriman [4] found that the geodesics on \(\Theta \backslash {\mathbb {H}}\) is strongly related to the even integer continued fraction (EICF) introduced by Schweiger [19, 20], which is a continued fraction with even integers such that

$$\begin{aligned} b_0 + \frac{\eta _0}{b_1 + \frac{\eta _1}{b_2 + \ddots } }, \end{aligned}$$
(2)

where \(b_0\in 2{\mathbb {Z}}\), \(b_i \in 2{\mathbb {N}}\) for \(i\ge 1\) and \(\eta _i \in \{ -1, +1\}\).

We classify rational numbers into two classes by the orbits \(\Theta (\infty )\) and \(\Theta (1)\). If \(p/q\in \Theta (\infty )\), then p and q are of different parity. If \(p/q \in \Theta (1)\), then p and q are both odd. We call a rational number in \(\Theta (\infty )\) an \(\infty \)-rational and a rational number in \(\Theta (1)\) a 1-rational. The proportion of odd/even, even/odd and odd/odd in the RCF convergents was investigated by Moeckel [15]. Further, the asymptotic density of the RCF convergents whose denominators and numerators satisfying congruence equations was obtained by Jager-Liadet [10].

Short and Walker [23] defined a best \(\infty \)-rational approximation of x by a rational \(p/q\in \Theta (\infty )\) satisfying

$$\begin{aligned} \left| qx-p\right|< \left| bx-a\right| ~\text {for~any}~ \frac{a}{b}\in \Theta (\infty ) \text { apart from } \frac{p}{q} ~{{\,\mathrm{such~that}\,}}~ 0<b \le q,\nonumber \\ \end{aligned}$$
(3)

and showed that the best \(\infty \)-rational approximations are convergents of EICF.

Our motivation of the paper is to study the best 1-rational approximations of an irrational number defined as follows.

Definition 1.1

For \(x\in {\mathbb {R}}\setminus {\mathbb {Q}}\), \(p/q \in \Theta (1)\) is a best 1-rational approximation of x if

$$\begin{aligned} |qx-p|< |bx-a| ~\text {for~any} \frac{a}{b}\in \Theta (1) \text { apart from } \frac{p}{q} {{\,\mathrm{such~that}\,}}0<b\le q. \end{aligned}$$
(4)

We introduce a new continued fraction, called the odd-odd continued fraction (OOCF, see Sect. 2) of the form

$$\begin{aligned} 1 - \frac{1}{a_1 + \frac{\varepsilon _1}{ 2 - \frac{1}{a_2 + \frac{\varepsilon _2}{ 2 - \frac{1}{\ddots }}}}}, \end{aligned}$$

where \(a_n \in {\mathbb {N}}\), and \(\varepsilon _n \in \{1,-1\}\) for \(a_n \ge 2\) and \(\varepsilon _n = 1\) for \(a_n = 1\). Our first main theorem is the following.

Theorem 1.2

A fraction p/q is a best 1-rational approximation of an irrational number x if and only if it is one of the principal convergents of the odd-odd continued fraction of x.

For RCF, Lagrange and Euler proved that an irrational number has eventually periodic RCF if and only if it is a quadratic irrational. (See [17,  Chapter III-§1] and [12,  Section 10]). For OOCF, we have the following second main theorem.

Theorem 1.3

An eventually periodic OOCF expansion converges to an \(\infty \)-rational or a quadratic irrational. Moreover, a quadratic irrational has an eventually periodic OOCF expansion.

We also investigate the relation between the OOCF and the RCF. We show that for any real number x, the principal convergents of its OOCF are intermediate convergents of its RCF (Theorem 5.2). Further, we can convert RCF expansions into OOCF expansions (Theorem 5.3).

Our paper is organized as follows. In Sect. 2, we introduce the OOCF algorithm and give some basic properties of OOCFs. In Sect. 3 we study the principal convergents of OOCFs, and prove Theorem 1.3. Sect. 4 is devoted to the proof of Theorem 1.2. The relations between the OOCF expansions and the RCF expansions are described in the last section.

2 Odd-odd continued fraction algorithm

It is known that the partial quotients \(d_j=d_j(x)\) of the RCF of an irrational number x as in (1) can be generated by the Gauss map \(G: [0,1] \rightarrow [0,1]\) defined by

$$\begin{aligned} G (x) = \left\{ \frac{1}{x} \right\} \ \text {for }x\in (0,1] \quad \text {and} \quad G(0)=0, \end{aligned}$$

where \(\{ \cdot \}\) is the fractional part. In fact, for an irrational x we have \(d_j(x) = \lfloor 1/G^{j-1}(x) \rfloor \) for \(j\ge 1\) with \(\lfloor \cdot \rfloor \) being the integer part. Further, Gauss map is a jump transformation associated to the Farey map defined by

$$\begin{aligned} F (x) = {\left\{ \begin{array}{ll} \dfrac{x}{1-x} &{}{{\,\mathrm{if}\,}}~ 0 \le x \le \dfrac{1}{2}, \\ \dfrac{1-x}{x} &{}{{\,\mathrm{if}\,}}~ \dfrac{1}{2} \le x \le 1. \\ \end{array}\right. } \end{aligned}$$

In general, let \(U: [0,1]\rightarrow [0,1]\) be a map and E be a subset of [0, 1]. The first hitting time of \(x\in [0,1]\) to E is defined by

$$\begin{aligned} n_E(x):=\min \{j\ge 0: U^j(x)\in E\}. \end{aligned}$$

A map \(J:[0,1]\rightarrow [0,1]\) is called the jump transformation associated to U with respect to E (e.g. [21,  Chapter 19]) if

$$\begin{aligned} J(x) = U^{n_E(x)+1}(x)~{{\,\mathrm{for}\,}}~{{\,\mathrm{all}\,}}~ x\in [0,1]. \end{aligned}$$

We can easily check that G is the jump transformation associated to F with respect to \(E=\{0\}\cup (1/2,1]\). In fact,

$$\begin{aligned} G(x) = F^{n_{E}(x)+1}(x) ~{{\,\mathrm{for}\,}}~ x\in [0,1]. \end{aligned}$$

We also note that \(n_E(x)+1\) is exactly the first partial quotient \(a_1\) of the RCF expansion of x.

Similar to the RCF, the partial quotients of EICF in (2) can be obtained by the EICF map \(T_\mathrm {EICF}:[0,1]\rightarrow [0,1]\) defined by

$$\begin{aligned} T_\mathrm {EICF} (x) = {\left\{ \begin{array}{ll} \dfrac{1}{x} - 2k &{}\text { if } ~\dfrac{1}{2k+1} \le x \le \dfrac{1}{2k}, \\ 2k - \dfrac{1}{x} &{}\text { if } ~\dfrac{1}{2k} \le x \le \dfrac{1}{2k-1}, \end{array}\right. }\quad \text {for all }k \in {\mathbb {N}}, \quad \text {~and~} \quad T_\mathrm {EICF} (0) =0. \end{aligned}$$

The map \(T_\mathrm {EICF}\) turns out to be a jump transformation of the following Romik map

$$\begin{aligned} R(x) = {\left\{ \begin{array}{ll} \dfrac{x}{1-2x} &{}{{\,\mathrm{if}\,}}~ 0 \le x \le \dfrac{1}{3}, \\ \dfrac{1}{x} - 2 &{}{{\,\mathrm{if}\,}}~ \dfrac{1}{3} \le x \le \dfrac{1}{2}, \\ 2 - \dfrac{1}{x} &{}{{\,\mathrm{if}\,}}~ \dfrac{1}{2} \le x \le 1, \\ \end{array}\right. } \end{aligned}$$
(5)

introduced by Romik in [18]. In fact, letting \(E_1:=\{0\}\cup [1/3,1]\), we have

$$\begin{aligned} T_\mathrm {EICF} (x) = R^{n_{E_1}(x)+1} (x) \ ~{{\,\mathrm{for}\,}}~ x \in [0,1]. \end{aligned}$$

The Romik map was used to investigate an algorithm generating the Pythagorean triples by multiplying matrices [1,2,3, 7, 8]. Some number theoretical properties of the Romik map were recently shown in [5, 6]. Panti [16] studied the connection of the Romik map with the billiards in the hyperbolic plane.

Instead of \(E_1\), we choose \(E_2 = [0, 1/2]\cup \{1\}\) and define \(T_\mathrm {OOCF}:[0,1]\rightarrow [0,1]\), called the odd-odd continued fraction (OOCF) map, by the jump transformation associated to the Romik map R with respect to \(E_2\), i.e.,

$$\begin{aligned} T_\mathrm {OOCF} (x) = R^{n_{E_2}(x)+1} (x) \ \text { for }x\in [0,1]. \end{aligned}$$

By simple calculation, we have

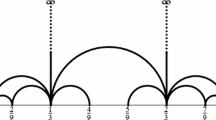
$$\begin{aligned} \quad T_\mathrm {OOCF} (x) = {\left\{ \begin{array}{ll} \dfrac{k x - (k-1) }{k - (k+1) x} &{}{{\,\mathrm{if}\,}}~ \dfrac{k-1}{k} \le x \le \dfrac{2k -1}{2k+1}, \\ \dfrac{k - (k+1) x}{k x - (k-1) } &{}{{\,\mathrm{if}\,}}~ \dfrac{2k -1}{2k+1} \le x \le \dfrac{k}{k+1}, \end{array}\right. } \quad \text {for all }k\ge 1 \quad \text {and} \quad T_\mathrm {OOCF} (1)=1.\nonumber \\ \end{aligned}$$
(6)

The graph of \(T_{\text {OOCF}}\) is shown in Fig.  1.

Fig. 1
figure 1

The graph of R (left) and the graph of \(T_\mathrm {OOCF}\) (right)

Full size image

Using \(T_{\text {OOCF}}\), we can induce an OOCF expansion of \(x\in [0,1]\). For convenience, let \(T:=T_{\text {OOCF}}\). We partition [0, 1] into the subintervals defined by

$$\begin{aligned} B(k+1,-1):=\left[ \frac{k-1}{k},\frac{2k-1}{2k+1}\right] \quad \text { and }\quad B(k,1):=\left[ \frac{2k-1}{2k+1},\frac{k}{k+1}\right] \quad \text { for }k\in {\mathbb {N}}.\nonumber \\ \end{aligned}$$
(7)

By (6), if \(x\ne 1\), then

$$\begin{aligned} \dfrac{1}{1-x}= {\left\{ \begin{array}{ll} {(k+1)+\dfrac{-1}{2-(1-Tx)}} &{} {{\,\mathrm{if}\,}}~x\in B(k+1,-1), \\ {k+\dfrac{1}{2-(1-Tx)}} &{} {{\,\mathrm{if}\,}}~x\in B(k,1), \end{array}\right. } \quad \text {for all }k\ge 1. \end{aligned}$$
(8)

Thus, for all \(x \notin \bigcup _{i =0}^{n-1} T^{-i}( \{ 1 \} )\)

$$\begin{aligned} 1-x = \frac{1}{a_1 + \frac{\varepsilon _1}{ 2 - \frac{1}{{{\ddots \frac{\ddots }{a_n + \frac{\varepsilon _n}{2- (1-T^nx)}}}}}}}, \end{aligned}$$
(9)

where

$$\begin{aligned} (a_n,\varepsilon _n)= {\left\{ \begin{array}{ll} (k+1,-1), ~ \text { if } T^{n-1}(x)\in B(k+1,-1), \\ (k,1) \text {,}~\quad \quad \qquad \text {if } T^{n-1}(x)\in B(k,1). \end{array}\right. } \end{aligned}$$
(10)

In particular, if \(x=0\), then \(T(0)=0\) and we have

$$\begin{aligned} 1-x=\frac{1}{2+\frac{-1}{2-(1-Tx)}}. \end{aligned}$$

Thus, 0 has a unique infinite OOCF expansion: \(0=[\![(2,-1), (2,-1), \cdots ]\!]= [\![(2,-1)^\infty ]\!]\). If \(x = \frac{k}{k+1} \in B(k,1) \cap B(k+2,-1)\) for some \(k \ge 1\). Then \(T(x) = 0\) and we have both choices in (8):

$$\begin{aligned} 1-x= \frac{1}{k+1} = \frac{1}{k+2+\frac{-1}{2-(1-Tx)}}= \frac{1}{k+\frac{1}{2-(1-Tx)}}. \end{aligned}$$

Hence, a rational number \(x={k \over k+1}\) has two infinite OOCF expansions: \(x=[\![(k+2, -1),(2,-1)^\infty ]\!]\) and \(x=[\![(k, 1),(2,-1)^\infty ]\!]\). Furthermore, for any \(x\in T^{-n}(\{0\})\) with some \(n\ge 2\), we can apply the iteration (8) \(n-1\) times, and then write \(1-T^{n-1}(x)\) in two different ways. Therefore, any \(x\in \bigcup _{n\ge 1} T^{-n}(\{0\})\) has two infinite OOCF expansions ending with \((2,-1)^\infty \).

Let \(x={2k-1 \over 2k+1} \in B(k+1,-1) \cap B(k,1)\) for some \(k \ge 1\). Then \(T(x) = 1 \) and

$$\begin{aligned} 1-x= & {} \frac{1}{(k+1)+\frac{-1}{2-(1-Tx)}}=\frac{1}{(k+1)+\frac{-1}{2}}, \quad \text {or} \\ 1-x= & {} \frac{1}{k+\frac{1}{2-(1-Tx)}}=\frac{1}{k+\frac{1}{2}}. \end{aligned}$$

Thus \(x={2k-1 \over 2k+1}\) has two finite OOCF expansions: \(x=[\![(k+1,-1)]\!]\) and \(x=[\![(k,1)]\!]\). Furthermore, for any \(x \in T^{-n} ( \{ 1\})\) with some \(n \ge 1\) and \(x \ne 1 \), we can apply the iteration (8) \(n-1\) times, and then write \(1-T^{n-1}(x)\) in two different ways. Therefore, any \(x\in \bigcup _{n\ge 0} T^{-n} (\{ 1 \} ) \setminus \{ 1\}\) has two finite OOCF expansions which differ at the last partial quotient.

Note that for a rational m/n, the denominator of \(T_{\text {OOCF}}(m/n)\) is strictly less than n. Note also that \(T_{\text {OOCF}}\) sends a 1-rational to a 1-rational and an \(\infty \)-rational to an \(\infty \)-rational. Thus if m/n is a 1-rational, then \(T_{\text {OOCF}}^N(m/n)=1\) for some \(N\ge 1\), while if m/n is a non-zero \(\infty \)-rational, then \(T_{\text {OOCF}}^N(m/n)=0\) for some \(N\ge 1\). Hence any 1-rational and \(\infty \)-rational belongs to \(T_{\text {OOCF}}^{-N}(\{1\})\) and \(T_{\text {OOCF}}^{-N} (\{ 0 \})\) for some \(N\ge 1\) respectively. Finally, we note that

$$\begin{aligned} \bigcup _{n=1}^\infty T_{\text {OOCF}}^{-n}(\{0,1\})={\mathbb {Q}}. \end{aligned}$$

Then for any \(x\in [0,1] \setminus {\mathbb {Q}}\), we can iterated (9) infinitely and uniquely to get its OOCF expansion:

$$\begin{aligned} x = 1 - \frac{1}{a_1 + \frac{\varepsilon _1}{ 2 - \frac{1}{a_2 + \frac{\varepsilon _2}{ 2 - \frac{1}{\ddots }}}}}. \end{aligned}$$

where \(a_n \in {\mathbb {N}}\) and \(\varepsilon _n \in \{1,-1\}\) for \(a_n \ge 2\) and \(\varepsilon _n = 1\) for \(a_n = 1\).

We denote the OOCF expansion of x by

$$\begin{aligned} x=[\![(a_1,\varepsilon _1),(a_2,\varepsilon _2),\cdots ,(a_n,\varepsilon _n),\cdots ]\!], \end{aligned}$$

and call \((a_n,\varepsilon _n)\) the n-th partial quotients of x in its OOCF expansion. By the above discussion, we have the following proposition.

Proposition 2.1

The following properties hold.

  1. (1)

    Any non-zero \(\infty \)-rational has exactly two infinite OOCF expansions ending with \((2,-1)^\infty \).

  2. (2)

    Each 1-rational has exactly two finite OOCF expansions which differ only in the last partial quotient.

  3. (3)

    Every irrational has a unique infinite OOCF expansion.

To end this section, we remark that the two maps \(T_{\text {OOCF}}\) and \(T_{\text {EICF}}\) are conjugate. Define \(f:[0,1]\rightarrow [0,1]\) by \(f(x) := \dfrac{1-x}{1+x}.\) Then the map \(T_{\text {OOCF}}\) is conjugate to \(T_{\text {EICF}}\) via f, i.e.,

$$\begin{aligned} f\circ T_{\text {OOCF}}\circ f^{-1}=T_{\text {EICF}}. \end{aligned}$$

Schweiger [19] proved that \(T_{\text {EICF}}\) admits an ergodic absolutely continuous invariant measure: \(d\mu :=\dfrac{dx}{1-x^2}\). Thus, the measure \(f^{-1}_*\mu \) is an ergodic absolutely continuous invariant measure with respect to \(T_\mathrm {OOCF}\). Denote by \(y = f(x)\). We have

$$\begin{aligned} \frac{dx}{1-x^2} = \frac{(1+x)^2dy}{2(1-x^2)} = \frac{(1+x)dy}{2(1-x)} = \frac{dy}{2y}. \end{aligned}$$

Hence, we have the following conclusion.

Proposition 2.2

The map \(T_\mathrm {OOCF} : [0,1] \rightarrow [0,1]\) preserves an infinite ergodic absolutely continuous invariant measure \(\dfrac{1}{x}dx.\)

We also remark that the infinity of the absolutely continuous invariant measure comes from the fact that the map \(T_\mathrm {OOCF}\) has 0 as an indifferent fixed point.

3 Convergents of the odd-odd continued fraction algorithm

For OOCF, we have three types of convergents by truncating the OOCF in three different places. We will investigate the basic properties of such convergents of OOCF.

Let \(x\in (0,1)\) be a real number such that

$$\begin{aligned} x=[\![(a_1,\varepsilon _1),(a_2,\varepsilon _2),\cdots , (a_n, \varepsilon _n),\cdots ]\!]. \end{aligned}$$

For \(n\ge 1\), the n-th principal convergent of OOCF is defined by

$$\begin{aligned} \frac{p_n}{q_n}=[\![(a_1,\varepsilon _1),(a_2,\varepsilon _2),\cdots ,(a_n,\varepsilon _n)]\!]= 1 -\frac{1}{a_1 + \frac{\varepsilon _1}{ 2 - \frac{1}{\ddots \frac{\varepsilon _{n-1}}{ 2 - \frac{1}{ a_n + \frac{\varepsilon _n}{2}}}}}}. \end{aligned}$$

We denote

$$\begin{aligned} \frac{p'_n}{q'_n}:=1 -\frac{1}{a_1 + \frac{\varepsilon _1}{ 2 - \frac{1}{\ddots \frac{\varepsilon _{n-1}}{ 2 - \frac{1}{ a_n }}}}} \quad \quad \text {and} \quad \quad \frac{p''_n}{q''_n}:=1 -\frac{1}{a_1 + \frac{\varepsilon _1}{ 2 - \frac{1}{\ddots \frac{\varepsilon _{n-1}}{ 2 - \frac{1}{ a_n + \varepsilon _n }}}}}, \end{aligned}$$

and call them the n-th sub-convergent and n-th pseudo-convergent, respectively.

To study the convergents of a continued fraction, we have the following general lemma proved by induction (see [13,  p. 3] for details).

Lemma 3.1

Consider a general infinite continued fraction and its truncated continued fraction of the form

$$\begin{aligned} g_0 + \frac{e_0}{g_1 + \frac{e_1}{ g_2 + \frac{e_2}{g_3 + \ddots }}} \quad \quad \text {and} \quad \frac{r_n}{s_n} := g_0 + \frac{e_0}{g_1 + \frac{e_1}{ g_2 + \frac{e_2}{\ddots + \frac{e_{n-1}}{g_n}}}}, \end{aligned}$$

where \(g_n\in {\mathbb {Z}}\) and \(|e_n|=1\). Then the following matrix relation holds:

$$\begin{aligned} \begin{pmatrix}r_n &{} e_n r_{n-1} \\ s_n &{} e_n s_{n-1} \end{pmatrix}= \begin{pmatrix}g_0 &{} e_0 \\ 1 &{} 0 \end{pmatrix} \begin{pmatrix}g_1 &{} e_1 \\ 1 &{} 0 \end{pmatrix} \cdots \begin{pmatrix}g_n &{} e_n \\ 1 &{} 0 \end{pmatrix}. \end{aligned}$$

Consequently, we have the following recursive formulas:

$$\begin{aligned}\left\{ \begin{array}{l} r_{n}=g_n r_{n-1}+e_{n-1} r_{n-2},\\ s_{n}=g_n s_{n-1}+e_{n-1} s_{n-2}, \end{array}\right. \end{aligned}$$

where \(r_{-1}=1\), \(s_{-1}=0\), \(r_0=g_0\) and \(s_0=1\).

Denote the inverse of \(T_{\text {OOCF}}|_{B(a_n,\varepsilon _n)}\) by \(f_{(a_n,\varepsilon _n)}\). Then by (8), we have

$$\begin{aligned} f_{(a_n,\varepsilon _n)}(t) = 1 - \frac{1}{a_n + \frac{\varepsilon _n}{1+t}}. \end{aligned}$$
(11)

The map \(f_{(a_n,\varepsilon _n)}\) corresponds to a linear fractional map on the upper half-plan \({\mathbb {H}}\) given by the matrix

$$\begin{aligned} A_{(a_n,\varepsilon _n)} := \begin{pmatrix}1 &{}\quad -1 \\ 1 &{}\quad 0 \end{pmatrix} \begin{pmatrix}a_n &{}\quad \varepsilon _n \\ 1 &{}\quad 0 \end{pmatrix} \begin{pmatrix}1 &{}\quad 1 \\ 0 &{} \quad 1 \end{pmatrix}= \begin{pmatrix}a_n-1 &{}\quad a_n+\varepsilon _n-1 \\ a_n &{}\quad a_n+\varepsilon _n \end{pmatrix} \in \Theta \cup \begin{pmatrix} 0 &{}\quad 1 \\ 1 &{}\quad 0 \end{pmatrix} \Theta .\nonumber \\ \end{aligned}$$
(12)

By Lemma 3.1, we have

$$\begin{aligned}&A_{(a_1,\varepsilon _1)}A_{(a_2,\varepsilon _2)}\cdots A_{(a_n,\varepsilon _n)} \begin{pmatrix} 1 &{}\quad -1 \\ 1 &{}\quad 0 \end{pmatrix} =\begin{pmatrix} 1 &{}\quad -1 \\ 1 &{}\quad 0 \end{pmatrix} \begin{pmatrix} a_1 &{}\quad \varepsilon _1 \\ 1 &{}\quad 0 \end{pmatrix} \begin{pmatrix} 2 &{}\quad -1 \\ 1 &{}\quad 0 \end{pmatrix} \begin{pmatrix} a_2 &{}\quad \varepsilon _2 \\ 1 &{}\quad 0 \end{pmatrix}\nonumber \\&\qquad \quad \cdots \begin{pmatrix} 2 &{}\quad -1 \\ 1 &{}\quad 0 \end{pmatrix} \begin{pmatrix} a_n &{} \quad \varepsilon _n \\ 1 &{}\quad 0 \end{pmatrix} \begin{pmatrix} 2 &{}\quad -1 \\ 1 &{} \quad 0 \end{pmatrix} = \begin{pmatrix} p_n &{}\quad -p_n' \\ q_n &{}\quad -q_n' \end{pmatrix}\nonumber \\ \end{aligned}$$
(13)

and

$$\begin{aligned}&A_{(a_1,\varepsilon _1)}A_{(a_2,\varepsilon _2)}\cdots A_{(a_n,\varepsilon _n)}\begin{pmatrix} 0 \\ 1 \end{pmatrix} \nonumber \\&\quad =\begin{pmatrix} 1 &{} -1 \\ 1 &{} 0 \end{pmatrix} \begin{pmatrix} a_1 &{} \varepsilon _1 \\ 1 &{} 0 \end{pmatrix} \begin{pmatrix} 2 &{} -1 \\ 1 &{} 0 \end{pmatrix} \begin{pmatrix} a_2 &{} \varepsilon _2 \\ 1 &{} 0 \end{pmatrix} \cdots \begin{pmatrix} 2 &{} -1 \\ 1 &{} 0 \end{pmatrix} \begin{pmatrix} a_n &{} \varepsilon _n \\ 1 &{} 0 \end{pmatrix} \begin{pmatrix} 1 \\ 1 \end{pmatrix} = \begin{pmatrix} p_n'' \\ q_n'' \end{pmatrix} \nonumber \\ \end{aligned}$$
(14)

These mean that under the linear fractional map of the matrix \(A_{(a_1,\varepsilon _1)}A_{(a_2,\varepsilon _2)}\cdots A_{(a_n,\varepsilon _n)}\), the images of 1, \(\infty \) and 0 are \(p_n/q_n\), \(p_n'/q_n'\) and \(p_n''/q_n''\), respectively.

Since \(A_{(a_1,\varepsilon _1)}A_{(a_2,\varepsilon _2)}\cdots A_{(a_n,\varepsilon _n)}\) is contained in \(\Theta \) or \(\begin{pmatrix}0&{}1\\ 1&{}0\end{pmatrix}\Theta \), we deduce the following proposition.

Proposition 3.2

We have

$$\begin{aligned} \frac{p_n}{q_n} \in \Theta (1) \quad \text { and }\quad \frac{p'_n}{q'_n}, \ \frac{p''_n}{q''_n} \in \Theta (\infty ). \end{aligned}$$

We remark that the name of odd-odd continued fraction comes from the fact that the principal convergents \({p_n}/{q_n}\) are 1-rationals, i.e., of odd denominators and odd numerators. We also remark that by Proposition 3.2, any finite OOCF is a 1-rational.

By (13) and (14), we have the following recursive relations of the three types of convergents.

Lemma 3.3

Let \(p_0'=1\), \(q_0'=0\), \(p_0=1\) and \(q_0=1\). We have the following recursive formulas:

$$\begin{aligned}&{\left\{ \begin{array}{ll} p_{n}'=a_{n}p_{n-1}-p_{n-1}', \\ q_{n}'=a_{n}q_{n-1}-q_{n-1}', \end{array}\right. } \ {\left\{ \begin{array}{ll} p_{n}''=p_{n}'+\varepsilon _{n}p_{n-1}, \\ q_{n}''=q_{n}'+\varepsilon _{n}q_{n-1} \end{array}\right. } \text { and } \nonumber \\&{\left\{ \begin{array}{ll} p_{n}=2p_{n}'+\varepsilon _{n}p_{n-1}, \\ q_{n}=2q_{n}'+\varepsilon _{n}q_{n-1} \end{array}\right. } \quad \text { for }n\ge 1.\end{aligned}$$
(15)

Further,

$$\begin{aligned} {\left\{ \begin{array}{ll} p_n=p_n'+p_n'', \\ q_n=q_n'+q_n'' \end{array}\right. } \text { and }\quad {\left\{ \begin{array}{ll} p_{n-1} = \varepsilon _n(p_n''-p_n'), \\ q_{n-1} = \varepsilon _n(q_n''-q_n') \end{array}\right. } \quad \text { for }n\ge 1. \end{aligned}$$
(16)

Moreover, letting \(p_{-1}=-1, q_{-1}=1\) and \(\varepsilon _0=1\), we have the recursive formulas for the principal convergents

$$\begin{aligned} {\left\{ \begin{array}{ll} p_n=(2a_n+\varepsilon _n-1)p_{n-1}+\varepsilon _{n-1}p_{n-2}, \\ q_n=(2a_n+\varepsilon _n-1)q_{n-1}+\varepsilon _{n-1}q_{n-2} \end{array}\right. } \quad \text { for }n\ge 1. \end{aligned}$$
(17)

Note that \(2a_{n}+\varepsilon _{n}-1\ge 2\) for all \(n\in {\mathbb {N}}\). Since \(q_1\ge 2q_0+\varepsilon _0q_{-1}=3>q_0\), by (17), we have

$$\begin{aligned} q_{n+1}> q_n, \text {~for all~} n\in {\mathbb {N}}. \end{aligned}$$
(18)

By (13) and the second assertion of (16), we have

$$\begin{aligned} A_{(a_1,\varepsilon _1)}A_{(a_2,\varepsilon _2)}\cdots A_{(a_n,\varepsilon _n)} \begin{pmatrix} -1 &{}\quad 1 \\ 1 &{}\quad 1 \end{pmatrix} = \begin{pmatrix} \varepsilon _np_{n-1} &{}\quad p_n \\ \varepsilon _nq_{n-1} &{}\quad q_n \end{pmatrix} \quad \text { for all }n\in {\mathbb {N}}. \end{aligned}$$

Thus, by noting \(\text {det}(A_{(a_i,\varepsilon _i)}) =\varepsilon _i\), we have

$$\begin{aligned} p_{n-1}q_n-p_nq_{n-1}=-2\varepsilon _1\cdots \varepsilon _{n-1} \quad \text { for all }n\in {\mathbb {N}}. \end{aligned}$$
(19)

Denote by

$$\begin{aligned} \zeta _n :=T_{\text {OOCF}}^{n-1}(x)= 1- \frac{1}{a_n+ \frac{\varepsilon _n}{2-\frac{1}{a_{n+1}+\frac{\varepsilon _{n+1}}{\ddots }}}}. \end{aligned}$$

We can show inductively that

$$\begin{aligned} x=\frac{p_{n}''+p_{n}'\zeta _{n+1}}{q_{n}''+q_{n}'\zeta _{n+1}} \quad \text { for all }n\in {\mathbb {N}}.\end{aligned}$$
(20)

By (16), we have

$$\begin{aligned}{\left\{ \begin{array}{ll} p_{n}''=\frac{1}{2}(p_{n}+\varepsilon _{n}p_{n-1}), \\ p_{n}'=\frac{1}{2}(p_{n}-\varepsilon _{n}p_{n-1}), \end{array}\right. } \quad \text {and}\quad \quad {\left\{ \begin{array}{ll} q_{n}''=\frac{1}{2}(q_{n}+\varepsilon _{n}q_{n-1}), \\ q_{n}'=\frac{1}{2}(q_{n}-\varepsilon _{n}q_{n-1}), \end{array}\right. } \quad \text { for all }n\in {\mathbb {N}}. \end{aligned}$$

Thus,

$$\begin{aligned} x=\frac{p_{n}(1+\zeta _{n+1})+\varepsilon _{n}p_{n-1}(1-\zeta _{n+1})}{q_{n}(1+\zeta _{n+1})+\varepsilon _{n}q_{n-1}(1-\zeta _{n+1})}. \end{aligned}$$
(21)

The following theorem gives the convergence of our OOCF.

Theorem 3.4

For all \(x\in [0,1]\), the OOCF expansion of x converges to x.

Proof

Let \(\xi _n = {1-\zeta _n \over 1+ \zeta _n}\). By (21) and (19), we have

$$\begin{aligned} x - \frac{p_n}{q_n} = \frac{\xi _{n+1}\varepsilon _n(p_{n-1}q_n-q_{n-1}p_n)}{q_n(q_{n}+\varepsilon _{n}q_{n-1}\xi _{n+1})} =\frac{-2\xi _{n+1}\varepsilon _1\cdots \varepsilon _n}{q_n(q_{n}+\varepsilon _{n}q_{n-1}\xi _{n+1})}.\end{aligned}$$
(22)

Since \(|\varepsilon _{n}|=1\) and \(|\xi _{n+1}|\le 1\), by (18), we have

$$\begin{aligned} \left| x - \frac{p_n}{q_n}\right| <\frac{2}{q_n}\quad {{\,\mathrm{for}\,}}\ {{\,\mathrm{all}\,}}\ n\in {\mathbb {N}}. \end{aligned}$$

Again by (18), \(q_n\rightarrow \infty \) as \(n\rightarrow \infty \), which concludes \(p_n/q_n\rightarrow x\) as \(n\rightarrow \infty \). \(\square \)

Lemma 3.5

For all \(x\in (0,1)\), x is between \(p_n/q_n\) and \(p''_n/q''_n\).

Proof

The equations (13) and (14) imply that \(p_n'q_n''-p_n''q_n' = \varepsilon _1\cdots \varepsilon _n.\) Thus, by (20),

$$\begin{aligned} x-\frac{p_n''}{q_n''} = \frac{\zeta _{n+1}(p_n'q_n''-p_n''q_n')}{q_n''(q_n''+q_n'\zeta _{n+1})} = \frac{\zeta _{n+1}\varepsilon _1\cdots \varepsilon _n}{q_n''(q_n''+q_n'\zeta _{n+1})}, \end{aligned}$$

which means that \(x-p_n/q_n\) and \(x-p''_n/q''_n\) has opposite signs by comparing with (22). \(\square \)

With the above preparations, we can now show the following lemma.

Lemma 3.6

The following statements hold.

  1. (1)

    The n-th principal convergent \(p_{n}/q_{n}\) is between \(p'_n/q'_n\) and \(p''_n/q''_n\).

  2. (2)

    The \((n-1)\)-th principal convergent \(p_{n-1}/q_{n-1}\) is not between \(p'_{n}/q'_{n}\) and \(p''_{n}/q''_{n}\).

  3. (3)

    The three distinct convergents \(p_n/q_n\), \(p_{n}'/q_{n}'\) and \(p_{n}''/q_{n}''\) are in the half closed interval \(I_{n-1}\) of endpoints \(p_{n-1}/q_{n-1}\) and \(p_{n-1}''/q_{n-1}''\) which contains \(p_{n-1}''/q_{n-1}''\) but does not contain \(p_{n-1}/q_{n-1}\).

Proof

The first two assertions follow from (16) and the fact that for two rationals a/b and c/d such that \(bd>0\), if \(a/b \le c/d\), then

$$\begin{aligned} \frac{a}{b}\le \frac{a+c}{b+d}\le \frac{c}{d}. \end{aligned}$$

For (3), by Lemma 3.3, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} p_{n}'=(a_{n}-1)p_{n-1}+p_{n-1}'',\\ q_{n}'=(a_{n}-1)q_{n-1}+q_{n-1}'', \end{array}\right. } \quad \text {and} \quad {\left\{ \begin{array}{ll} p_{n}''=(a_{n}-1+\varepsilon _{n})p_{n-1}+p_{n-1}'', \\ q_{n}''=(a_{n}-1+\varepsilon _{n})q_{n-1}+q_{n-1}''. \end{array}\right. } \end{aligned}$$

Since \(a_{n}-1\ge 0\) and \(a_{n}+\varepsilon _{n}-1\ge 0\), both \(p_{n}'/q_{n}'\) and \(p_{n}''/q''_{n}\) are in \(I_{n-1}\). By the first assertion, \(p_n/q_n\) is also in \(I_{n-1}\). \(\square \)

Now, we are ready to prove Theorem 1.3.

Proof of Theorem 1.3

If x has an eventually periodic OOCF, then there exist distinct positive integers i and j such that \(T^i(x)=T^j(x)\). Since \(T^i\) and \(T^j\) are linear fractional maps, \(T^i(x)\) is either 0 or a quadratic irrational. In the former case x is an \(\infty \)-rational, while in the latter case x is a quadratic irrational.

For the second assertion, let x be a quadratic irrational between 0 and 1 such that \(\alpha _1x^2+\beta _1x+\gamma _1=0\) where \(\alpha _1\), \(\beta _1\) and \(\gamma _1\) are coprime integers. By (20), we have for all \(i\ge 1\),

$$\begin{aligned} \alpha _1(p_i''+p_i'\zeta _{i+1})^2+\beta _1(p_i''+p_i'\zeta _{i+1})(q_i''+q_i'\zeta _{i+1})+\gamma _1(q_i''+q_i'\zeta _{i+1})^2=0. \end{aligned}$$

For \(i\ge 1\), let

$$\begin{aligned} \begin{aligned}&\alpha _{i+1}=\alpha _1(p_i')^2+\beta _1p_i'q_i'+\gamma _1(q_i')^2,\\&\beta _{i+1}=2\alpha _1p_i''p_i'+\beta _1(p_i''q_i'+p_i'q_i'')+2\gamma _1q_i''q_i',\\&\gamma _{i+1}=\alpha _1(p_i'')^2+\beta _1p_i''q_i''+\gamma _1(q_i'')^2. \end{aligned}\end{aligned}$$
(23)

Then

$$\begin{aligned} \alpha _{i+1}\zeta _{i+1}^2+\beta _{i+1}\zeta _{i+1}+\gamma _{i+1}=0. \end{aligned}$$
(24)

Since \(|q_i'p_i''-q_i''p_i'|=1\), we can check that

$$\begin{aligned} \beta _{i+1}^2-4\alpha _{i+1}\gamma _{i+1}=\beta _1^2-4\alpha _1\gamma _1. \end{aligned}$$
(25)

On the other hand, we also have \(|(x-p_i'/q_i')+(p_i''/q_i''-x)|=1/q_i'q_i''.\) Thus, by Lemma 3.5 and the fact that \(p_i/q_i\) is between \(p_i'/q_i'\) and \(p_i''/q_i''\), we deduce that \(x-p_i'/q_i'\) and \(x-p_i''/q_i''\) have opposite signs. Thus, \(|q_i'x-p_i'|<1/q_i''\) and \(|p_i''-q_i''x|<1/q_i'.\) Hence, there are \(|\delta |<1\) and \(|\lambda |<1\) such that

$$\begin{aligned} p_i' = q_i'x+\delta /q_i'' \ \text { and } \ p_i'' = q_i''x+\lambda /q_i'. \end{aligned}$$
(26)

By plugging (26) in (23), we derive the following expressions

$$\begin{aligned} \alpha _{i+1}= & {} \delta \left( \frac{q_i'}{q_i''}(2\alpha _1x+\beta _1)+\alpha _1\frac{\delta }{(q_i'')^2}\right) , \end{aligned}$$
(27)
$$\begin{aligned} \beta _{i+1}= & {} (2\alpha _1x+\beta _1)(\delta +\lambda )+2\alpha _1\frac{\delta \lambda }{q_i'q_i''} \text { and } \end{aligned}$$
(28)
$$\begin{aligned} \gamma _{i+1}= & {} \lambda \left( \frac{q_i''}{q_i'}(2\alpha _1x+\beta _1)+a_1\frac{\lambda }{(q_i')^2}\right) . \end{aligned}$$
(29)

By (28), we have \(|\beta _{i+1}| \le 2(|2\alpha _1|+|\beta _1|)+|2\alpha _1|\), thus the coefficient \(\beta _{i+1}\) is bounded. If \(q_i''\ge q_i'\), then by (27), we have \(|\alpha _{i+1}|<2|\alpha _1|+|\beta _1|+|\alpha _1|\). Thus, \(\alpha _{i+1}\) is bounded. Further, by (25), \(\gamma _{i+1}\) is bounded. Similarly, if \(q_i''<q_i'\), then by (29), \(\gamma _{i+1}\) is bounded since \(|\gamma _{i+1}|<2|\alpha _1|+|\beta _1|+|\alpha _1|\). Moreover, by (25), \(\alpha _{i+1}\) is also bounded. Thus in all cases, the coefficients of the equation (24) are all bounded. Therefore, \(\{\zeta _i\}_{i\in {\mathbb {N}}}\) has only finitely many values which means that \(\zeta _n=\zeta _m\) for some m and n. Therefore, the OOCF expansion of x is eventually periodic. \(\square \)

Remark 3.7

From the proof of Proposition 2.1-(1), we see that if x is an \(\infty \)-rational, then its OOCF ends with \((2,-1)^\infty \) and thus there exists \(n_0\ge 0\) such that \(\zeta _{n+1}=0\) for all \(n\ge n_0\). Hence, by (20), we have \(x=p''_n/q''_n\) for all \(n\ge n_0\).

At the end of this section, let us discuss the relation between the OOCF convergents of a number x and the EICF convergents of \(1-x\).

We denote the EICF expansion in (2) by a sequence in a double angle bracket:

$$\begin{aligned} {{\,\mathrm{\langle \!\langle }\,}}(b_1,\eta _1),(b_2,\eta _2),\cdots , (b_n,\eta _n),\cdots {{\,\mathrm{\rangle \!\rangle }\,}}={{\,\mathrm{\langle \!\langle }\,}}(b_n,\eta _n)_{n\in {\mathbb {N}}}{{\,\mathrm{\rangle \!\rangle }\,}}. \end{aligned}$$

The n-th EICF convergent is denoted by

$$\begin{aligned} \frac{p^E_n}{q^E_n}={{\,\mathrm{\langle \!\langle }\,}}(b_1,\eta _1),(b_2,\eta _2),\cdots , (b_n,\eta _n){{\,\mathrm{\rangle \!\rangle }\,}}. \end{aligned}$$

By Lemma 3.1, we have the following matrix relation:

$$\begin{aligned} \begin{pmatrix} b_0 &{} \quad \eta _0 \\ 1 &{}\quad 0 \end{pmatrix} \begin{pmatrix} b_1 &{}\quad \eta _1 \\ 1 &{}\quad 0 \end{pmatrix} \cdots \begin{pmatrix} b_n &{}\quad \eta _n \\ 1 &{}\quad 0 \end{pmatrix} = \begin{pmatrix} q^E_n &{}\quad \eta _n q^E_{n-1} \\ p^E_n &{}\quad \eta _n p^E_{n-1} \end{pmatrix}. \end{aligned}$$
(30)

Since each matrix in (30) belongs to \(\Theta \cup \begin{pmatrix}0&{}1\\ 1&{}0\end{pmatrix}\Theta \), each EICF convergent \(p^E_n/q^E_n\) is an \(\infty \)-rational.

Observe that if \(p_n^E(x)/q_n^E(x)\) is of type even/odd, then \(1-p_n^E(x)/q_n^E(x)\) is 1-rational. If \(p_n^E(x)/q_n^E(x)\) is of type odd/even, then \(1-p_n^E(x)/q_n^E(x)\) is still of type odd/even.

Proposition 3.8

Let \(x\in (0,1)\). All rationals of type odd/odd in \(\{1-p_n^E(1-x)/q_n^E(1-x): n\ge 1 \}\) are best 1-rational approximations of x, and hence are OOCF principal convergents of x.

Proof

For each \(n\ge 0\), denote by \(P_n/Q_n:=1-p_n^E(1-x)/q_n^E(1-x)\). We have

$$\begin{aligned} P_n = q_n^E(1-x)-p_n^E(1-x) \ {{\,\mathrm{and}\,}}\ Q_n = q_n^E(1-x). \end{aligned}$$

By the theorem of Short and Walker (see (3); also [23,  Theorem 5]), for any \(a/b\in \Theta (\infty )\) such that \(1\le b\le q_n^E(1-x)\) and \(a/b\not =p_n^E(1-x)/q_n^E(1-x)\),

$$\begin{aligned} |P_n-Q_nx |= |q_n^E(1-x)-p_n^E(1-x)-x \cdot q_n^E(1-x)| < |(1-x)b-a|. \end{aligned}$$

For any \(c/d\in \Theta (1)\) such that \(1\le d\le Q_n\) and \(c/d\not =P_n/Q_n\), we have

$$\begin{aligned} {d-c \over d} = 1-{c \over d}\in \Theta (\infty ) \ {{\,\mathrm{and}\,}}\ {d-c \over d} \not =p_n^E(1-x)/q_n^E(1-x). \end{aligned}$$

Thus \(|P_n-Q_nx|<|(1-x)d-(d-c)|=|c-dx|\), which means that \(P_n/Q_n\) is a best 1-rational approximation of x. \(\square \)

The next proposition describes a connection between the principal convergents of OOCF and EICF. Recall that \(f(x) = \frac{1-x}{1+x}\) is the conjugacy map defined in Sect. 2.

Proposition 3.9

Let \(x\in (0,1)\). There is a 1-1 correspondence between the partial quotients of OOCF of x and that of EICF of f(x). In particular, \(p_n^E(f(x))/q_n^E(f(x))=f(p_n(x)/q_n(x))\) for all \(n \ge 1\).

Proof

Since

$$\begin{aligned} f(B(k+1,-1))=\left[ \frac{1}{2k},\frac{1}{2k-1}\right] ,\quad f(B(k,1))=\left[ \frac{1}{2k+1},\frac{1}{2k}\right] , \end{aligned}$$

there is a 1-1 correspondence \(\phi \) between the partial quotients of OOCF and EICF as follows:

$$\begin{aligned} \phi : (k+1,-1)\mapsto (2k,-1), \quad (k,1)\mapsto (2k,1). \end{aligned}$$

Thus, for \(x=[\![(a_n,\varepsilon _n)_{n\in {\mathbb {N}}}]\!]\), the EICF expansion of f(x) is \({{\,\mathrm{\langle \!\langle }\,}}\phi (a_n,\varepsilon _n)_{n\in {\mathbb {N}}}{{\,\mathrm{\rangle \!\rangle }\,}}\). Considering the finite expansions, we obtain the second assertion. \(\square \)

4 Best 1-rational approximation

Fig. 2
figure 2

Ford circles: white circles are based at \(\infty \)-rationals and gray circles are based at 1-rationals (color figure online)

Full size image

In this section, we prove Theorem 1.2. Recall that \({\mathbb {H}}\) is the upper half-plane. The boundary of \({\mathbb {H}}\) is \({\mathbb {R}}_{\infty }={\mathbb {R}}\cup \{\infty \}\). Denote by \(C_{a/b}\) the horocycle of \({\mathbb {H}}\) based at a/b whose Euclidean radius is \((2b^2)^{-1}\) and \(C_\infty \) the line \(\{z=x+i\in {\mathbb {H}}:x\in {\mathbb {R}}\}\) (see Fig.  2). We call \(C_{a/b}\) a Ford circle. The radius of \(C_{a/b}\) is denoted by \(\text {rad}(C_{a/b})\). We remark that two Ford circles \(C_{a/b}\) and \(C_{c/d}\) are adjacent to each other if and only if \(|ad-bc|=1.\) Let \(R_{a/b}(x)\) be the Euclidean radius of the horocycle based at x tangent to \(C_{a/b}\). Then by Pythagorean theorem,

$$\begin{aligned} R_{a/b}(x)=\frac{1}{2}|bx-a|^2. \end{aligned}$$

Thus

$$\begin{aligned} |qx-p|<|bx-a| \Longleftrightarrow R_{p/q}(x)<R_{a/b}(x). \end{aligned}$$
(31)

Since the Ford circles are not overlapped each other, we have

$$\begin{aligned} \text {rad}(C_{a/b})\le R_{c/d}\left( a/b\right) \text { for all } a/b,\ c/d\in {\mathbb {Q}}.\end{aligned}$$
(32)

With these preparations, we are ready to prove our Theorem 1.2.

Fig. 3
figure 3

Two possible relative locations of x, \(p_n/q_n\), a/b and \(p''_n/q''_n\) in the proof of Theorem 1.2. The dashed circles are the horocycles based at x tangent to \(C_{p_n/q_n}\) and \(C_{a/b}\) (color figure online)

Full size image

Proof of Theorem 1.2

Given \(x\in {\mathbb {R}}\setminus {\mathbb {Q}}\), let us consider its n-th principal convergent \(p_n/q_n\) and its n-th pseudo-convergent \(p''_n/q''_n\). Let \(a/b\in \Theta (1)\) such that \(a/b\not =p_n/q_n\) and \(1\le b\le q_n\). Then

$$\begin{aligned} \text {rad}(C_{p_n/q_n})\le \text {rad}(C_{a/b}).\end{aligned}$$
(33)

By (13) and (14), the Ford circles \(C_{p_n/q_n}\) and \(C_{p''_n/q''_n}\) are tangent to each other. By Lemma 3.5, x is between \(p_n/q_n\) and \(p''_n/q''_n\), then

$$\begin{aligned} R_{p_n/q_n}(x)\le \text {rad}(C_{p''_n/q''_n}).\end{aligned}$$
(34)

Let \(I_n\) be the closed interval of endpoints \(p_n/q_n\) and \(p''_n/q''_n\). Since \(\text {rad}(C_{r/s})\le \text {rad}(C_{p_n/q_n})\) for any \(r/s\in I_n\cap {\mathbb {Q}}\), we deduce from (33) (as shown in Fig. 3) that \(a/b\not \in I_n\). Then we have

$$\begin{aligned} \text {rad}(C_{p''_n/q''_n})<R_{a/b}(x). \end{aligned}$$
(35)

By (34) and (35), we have \(R_{p_n/q_n}(x) < R_{a/b}(x)\). Hence by (31), \(p_n/q_n\) is a best 1-rational approximation of x.

Conversely, assume that \(a/b\in \Theta (1)\) is not a principal convergent of OOCF of x. Then there are consecutive principal convergents \(p_{n-1}/q_{n-1}\) and \(p_{n}/q_{n}\) such that \(q_{n-1} \le b < q_{n}\) and \(a/b\not =p_{n-1}/q_{n-1}.\) Thus,

$$\begin{aligned} \text {rad}(C_{{p_{n}}/{q_{n}}})<\text {rad}(C_{a/b}).\end{aligned}$$
(36)

By (13) and (14), \(C_{{p_{n-1}}/{q_{n-1}}}\) and \(C_{{p_{n}}/{q_{n}}}\) are tangent to both \(C_{{p_{n}'}/{q_{n}'}}\) and \(C_{{p_{n}''}/{q_{n}''}}\). Without loss of generality, we assume that \(p_{n-1}/q_{n-1}<p_{n}'/q_{n}'<p_{n}''/q_{n}''\) (see Fig.  4). By (36), \(a/b\not \in [p'_{n}/q'_{n},p''_{n}/q''_{n}]\). Now we will show that \(R_{p_{n-1}/q_{n-1}}(x)<R_{a/b}(x)\) which by (31), implies that a/b is not a best 1-rational approximation of x. We distinguish three cases.

  1. (1)

    If \(a/b < p_{n-1}/q_{n-1} \), then obviously \(R_{p_{n-1}/q_{n-1}}(x)<R_{a/b}(x)\).

  2. (2)

    Now assume \(a/b > p_{n}''/q_{n}''\). We note that, for \(r/s\in {\mathbb {Q}}\) and t,  \(t'\in {\mathbb {R}}\),

    $$\begin{aligned} |t-r/s|<|t'-r/s| \text { implies that }R_{r/s}(t)<R_{r/s}(t').\end{aligned}$$
    (37)

    Then we have

    $$\begin{aligned} R_{{p_{n-1}}/{q_{n-1}}}(x)<R_{{p_{n-1}}/{q_{n-1}}}(p_{n}''/q_{n}'') =\text {rad}(C_{p_n''/q_n''}) \le R_{a/b}(p_{n}''/q_{n}'') <R_{a/b}(x).\nonumber \\ \end{aligned}$$
    (38)

    The first and last inequalities in (38) follow from (37) and the fact \(p_{n-1}/q_{n-1}<x<p''_{n}/q''_{n}<a/b\). The equality in (38) holds since \(C_{p''_n/q''_n}\) and \(C_{p_{n-1}/q_{n-1}}\) are tangent to each other. The second last inequality in (38) follows from (32).

  3. (3)

    Finally, let \(a/b \in (p_{n-1}/q_{n-1},p_{n}'/q_{n}')\). Denote by C and \(C'\) the horocycles based at x tangent to \(C_{a/b}\) and \(C_{p_{n-1}/q_{n-1}}\), respectively (see Fig. 4). Since the tangent point of C and \(C_{a/b}\) is an interior point of the area bounded by \(C_{p_{n-1}/q_{n-1}}\), \(C_{p_{n}'/q_{n}'}\) and the real line, we conclude that C intersects \(C_{p_{n-1}/q_{n-1}}\). Thus, C is larger than \(C'\), i.e, \(R_{p_{n-1}/q_{n-1}}(x)<R_{a/b}(x)\).

\(\square \)

Fig. 4
figure 4

A possible relative position of x, a/b and the convergents. The dashed circles C and \(C'\) are horocycles based at x tangent to \(C_{a/b}\) and \(C_{p_{n-1}/q_{n-1}}\) (color figure online)

Full size image

5 Relation with the regular continued fraction

For simplicity, we denote a RCF as in (1) by \([d_0;d_1,d_2,\cdots ,d_j,\cdots ]\). For \(1\le j \le d_{n}\) and for \(n\ge 1\), the fractions

$$\begin{aligned} \frac{p^R_{n,j}}{q^R_{n,j}}=\frac{p^R_{n-2}+jp^R_{n-1}}{q^R_{n-2}+jq^R_{n-1}} \end{aligned}$$

are called the intermediate convergents (see [12,  Section 6] and [17,  p.36]). Kraaikamp and Lopes [14] showed that the convergents of EICF are intermediate convergents of RCF. In this section, we show that the OOCF principal convergents are also intermediate convergents of RCF.

The following lemma tells us how the piecewise inverses of OOCF act on RCF expansions.

Lemma 5.1

Let \(x=[0;d_1,d_2,\cdots ]\). Then, the RCF expansion of \(f_{(a,\varepsilon )}(x)\) is as follows:

$$\begin{aligned} f_{(a,\varepsilon )}(x)=\left\{ \begin{array}{ll} {}[0;2,d_1,d_2,\cdots ] &{}{{\,\mathrm{if}\,}}~ \varepsilon =1,~a=1,\\ {}[0;1,(a-1),1,d_1,d_2,\cdots ] &{}{{\,\mathrm{if}\,}}~\varepsilon =1,~a\ge 2,\\ {}[0;(d_1+2),d_2,\cdots ] &{}{{\,\mathrm{if}\,}}~\varepsilon =-1,~a=2,\\ {}[0;1,(a-1),(d_1+1),d_2,\cdots ] &{}{{\,\mathrm{if}\,}}~\varepsilon =-1,~a\ge 3 . \end{array}\right. \end{aligned}$$

Proof

If \(\varepsilon =1\), then

$$\begin{aligned} f_{(a,\varepsilon )}(x)=1-[0;a,1,d_1,d_2,\cdots ]= \left\{ \begin{array}{ll} {}[0;2,d_1,d_2,\cdots ] &{}{{\,\mathrm{if}\,}}~a=1,\\ {}[0;1,a-1,1,d_1,\cdots ] &{}{{\,\mathrm{if}\,}}~a\ge 2. \end{array}\right. \end{aligned}$$

If \(\varepsilon =-1\), then

$$\begin{aligned}\begin{aligned} f_{(a,\varepsilon )}(x)&=1-\frac{1}{a-[0;1,d_1,d_2,\cdots ]}=1-\frac{1}{(a-1)+1-[0;1,d_1,d_2,\cdots ]}\\&=1-[0;a-1,d_1+1,d_2,\cdots ]= \left\{ \begin{array}{ll} {}[0;d_1+2,d_2,\cdots ] &{}{{\,\mathrm{if}\,}}~a=2,\\ {}[0;1,a-1,1,d_1+1,d_2,\cdots ] &{}{{\,\mathrm{if}\,}}~a\ge 3. \end{array}\right. \end{aligned}\end{aligned}$$

\(\square \)

Applying Lemma 5.1, we have the following theorem.

Theorem 5.2

The OOCF principal convergents of x are intermediate convergents of x.

Proof

Let \(x=[0; d_1,d_2,\cdots ]=[\![(a_1,\varepsilon _1),(a_2,\varepsilon _2),\cdots ]\!]\). Note that

$$\begin{aligned} x= & {} f_{(a_1,\varepsilon _1)}\circ f_{(a_2,\varepsilon _2)}\circ \cdots \circ f_{(a_k,\varepsilon _k)}([\![(a_{k+1},\varepsilon _{k+1}),\cdots ]\!]) \quad \text {and}\quad \\ \frac{p_k}{q_k}= & {} f_{(a_1,\varepsilon _1)}\circ f_{(a_2,\varepsilon _2)}\circ \cdots \circ f_{(a_k,\varepsilon _k)} (1). \end{aligned}$$

By Lemma 5.1, x and \(p_k/q_k\) have the same prefix in their RCF expansions, except for the last partial quotient of \(p_k/q_k\). Thus, \(p_k/q_k\) is an intermediate convergent of x. \(\square \)

Next, we show that we can convert RCF expansions into OOCF expansions. Before we state the theorem, let us introduce the following notations:

$$\begin{aligned} \left\{ \begin{array}{ll} x=[0;d_1,\cdots ,d_n,\tau ] &{}\text { if } \ G^n(x)=\tau , \\ x=[\![(a_1,\varepsilon _1),(a_2,\varepsilon _2),\cdots ,(a_n,\varepsilon _n),\gamma ]\!] &{}\text { if } \ T_{\text {OOCF}}^n(x)=\gamma . \end{array}\right. \end{aligned}$$

Theorem 5.3

We can convert RCF expansions into OOCF expansions by the following relations:

$$\begin{aligned} x = [0; d_1, d_2,\tau ]= \left\{ \begin{array}{ll} {}[\![{(2,-1)}^{\frac{d_1-1}{2}},(d_2+1,1),F(\tau )]\!] &{}\text { if } \ d_1 \text { is odd and }\tau \in [\frac{1}{2},1), \\ {[\![}{(2,-1)}^{\frac{d_1-1}{2}},(d_2+2,-1),F(\tau )]\!] &{} \text { if } \ d_1 \text { is odd and } \tau \in [0,\frac{1}{2}), \\ {[\![}{(2,-1)}^{\frac{d_1}{2}-1},(1,1),G(x)]\!] &{} \text { if } \ d_1 \text { is even. } \end{array}\right. \end{aligned}$$

Proof

Noting \(\frac{1}{1+\tau }=1-\frac{1}{1+\frac{1}{\tau }}\), we have

$$\begin{aligned}{}[0;1,d_2,\tau ]=\frac{1}{1+\frac{1}{d_2+\tau }}=1-\frac{1}{(d_2+1)+\tau }. \end{aligned}$$

If \(\tau \in [\frac{1}{2},1)\), then \(\tau =\frac{1}{1+G(\tau )}\). If \(\tau \in [0,\frac{1}{2})\), then

$$\begin{aligned} \tau =1-\frac{1}{1+\frac{1}{[\tau ^{-1}]-1+G(\tau )}}. \end{aligned}$$

Thus \(F(\tau )=\frac{1}{[\tau ^{-1}]-1+G(\tau )}\) if \(\tau \in [0,\frac{1}{2})\) and \(F(\tau )=G(\tau )\) if \(\tau \in (\frac{1}{2},1)\). In the case of \(d_1=1\), we have

$$\begin{aligned} {}[0;1,d_2,\tau ]= \left\{ \begin{array}{ll} {}[\![(d_2+1,1),F(\tau )]\!], &{}\text { if }\tau \in [\frac{1}{2},1),\\ {}[\![(d_2+2,-1),F(\tau )]\!], &{}\text { if }\tau \in [0,\frac{1}{2}).\\ \end{array}\right. \end{aligned}$$
(39)

Similarly, if \(d_1=2\), then

$$\begin{aligned} x= [0;2,G(x)]=\frac{1}{2+G(x)}=1-\frac{1}{1+\frac{1}{1+G(x)}}=[\![(1,1),G(x)]\!]. \end{aligned}$$
(40)

If \(d_1\ge 3\), i.e., \(x\in (0,\frac{1}{3})\), then

$$\begin{aligned} x= & {} [0;d_1,G(x)]=\frac{1}{d_1+G(x)}=1-\frac{1}{1+\frac{1}{1+(d_1-2)+G(x)}}\nonumber \\= & {} 1-\frac{1}{2-\frac{1}{1+\frac{1}{(d_1-2)+G(x)}}}=[\![(2,-1),T_{\text {OOCF}}(x)]\!]. \end{aligned}$$
(41)

Note that there are \(n\in {\mathbb {N}}\) and \(r\in \{0,1\}\) such that \(d_1-1 = 2n+r\). Since \(T_{\text {OOCF}}(x)=[0;d_1-2,G(x)]\), by repeating the process in (41), we have

$$\begin{aligned}{}[0;d_1,G(x)] = [\![(2,-1)^{n}, T_{\text {OOCF}}^{n}(x)]\!]\quad {{\,\mathrm{and}\,}}\quad { T_{\text {OOCF}}^{n}(x) = [0; r+1 ,G(x)]} . \end{aligned}$$

Then we can complete the proof by (39) and (40). \(\square \)

Since \(p^R_n/q^R_n\) is a best approximation, if \(p^R_n/q^R_n\) is a 1-rational, then \(p^R_n/q^R_n\) is a best 1-rational approximation. Thus, by Theorem 1.2, \(p^R_n/q^R_n\) is an OOCF convergent. Now we check when an intermediate convergent is an OOCF convergent. Keita [11] proved the following propostion.

Proposition

(Keita, Proposition 1.2 in [11]) We have

$$\begin{aligned} q^R_{n,0}=q^R_{n-2}<q^R_{n-1}\le q^R_{n,1}<\cdots<q^R_{n,d_n}= & {} q^R_{n}\,and \\ |q^R_{n,d_n}x-p^R_{n,d_n}|= & {} |q^R_{n}x-p^R_{n}|<|q^R_{n-1}x-p^R_{n-1}|\\&\quad \le |q^R_{n,d_n-1}x-p^R_{n,d_n-1}|<\cdots <|q^R_{n,0}x-p^R_{n,0}|=|q^R_{n-2}x-p^R_{n-2}|. \end{aligned}$$

By the above proposition and Theorem 5.2, if \(p^R_{n-1}/q^R_{n-1}\) is a 1-rational, then \(p^R_{n,j}/q^R_{n,j}\) is not an OOCF principal convergent for any \(1\le j < d_n\). If \(p^R_{n-1}/q^R_{n-1}\) is an \(\infty \)-rational and \(p^R_{n,j}/q^R_{n,j}\) is a 1-rational, then \(p^R_{n,j}/q^R_{n,j}\) is an OOCF principal convergent.