1 Introduction

The motions of our atmosphere (and also of our oceans) are extremely complex, particularly when viewed in their totality. However, significant flow patterns can be identified which, when treated as isolated phenomena, are amenable to some level of theoretical analysis. The standard approach is almost exclusively based on modelling the physical processes that are recognised as the main drivers for the motions; this, however, is not the route taken by the mathematical fluid dynamicist. The general governing equations for a fluid, whether that fluid be regarded as viscous, inviscid, compressible, incompressible, laminar or turbulent, have been known for almost two centuries. Thus, although a modelling approach is an excellent initial move, it should be followed by a careful derivation and analysis based on the general governing equations of fluid dynamics. This has a number of important advantages: the assumptions and approximations are evident; equations are derived, not simply written down, so their provenance is clear; error terms in the formulation can be identified and estimated; higher-order corrections are accessible. The foregoing describes the philosophy that underpins what we will present here.

The atmospheric circulation on the Earth is dominated by the latitudinal structure (which varies little in the zonal direction) comprising the Hadley-Ferrel-polar cells. These sit, on each side of the Equator, approximately from the Equator to 30° latitude, from 30° to 60° latitude, and from 60° to the pole, respectively; see, for example, [14]. But in addition, in equatorial regions, the zonal symmetry implied by the existence of the Hadley-Ferrel-polar cells, is disrupted. Here, essentially between the southern edge of the northern Hadley cell, and the northern edge of the southern Hadley cell, we have a line of thin latitudinally-orientated cells around the Earth; see Fig. 1. Controlled mainly by the longitudinal variations in the surface temperature, a number of cells are formed along, and in the neighbourhood of, the Equator. These, locally, are the dominant cell structures; see [8, 11]. Typically, five or six cells appear along the Equator, but the strongest of these (in the sense of size and wind speeds) sits over the Pacific. This is the Walker cell, which drives the westward surface current and, in particular, is the main controller of the weather in this region of the Pacific Ocean. Indeed, this motion of the surface, coupled to the Equatorial Undercurrent, is an important element in the dynamics of the equatorial Pacific Ocean. For a general introduction to atmospheric flows, including a discussion of the Walker circulation, see, for example, [9, 12]; for a mathematical model of this oceanic flow, with associated wave interactions, see [2, 3].

Fig. 1
figure 1

Sketch showing the positions of the Hadley (H), Ferrel (F) and polar (p) cells in the Northern hemisphere, and one complete cell, and two partial cells, in the vertical plane at the Equator

Full size image

The mathematical description that we explore here is based on the system of equations developed in [6], where a compressible, viscous fluid, with suitable thermodynamic properties, is used to represent the atmosphere. The formulation hinges on the thin-shell asymptotic approximation to describe the atmosphere on a (nearly) spherical, rotating Earth. In this presentation, we will briefly outline how these equations are obtained, and then write down the main system of equations that couple the dynamics and the thermodynamics; the full details are given in [6]. The plan is to take these equations and apply them to the Walker circulation; this will then constitute a special reduction of the general asymptotic formulation. The resulting system is readily analysed, the forcing required to generate the flow in the cell being explicit; it takes a simple form which is easily interpreted and can be related directly to the physical structure of the flow field. A few general observations about the flow structure in the Walker cell were given in [6], but the intention here is to provide far more detail. Indeed, we are able to include the adjustments needed to accommodate the changes associated with El Niño and El Niña events (which are described, for example, in [13]).

2 Governing equations

The underlying model that we use for our description of the atmosphere is based on the general equations for a compressible, viscous fluid, coupled to an equation of state and a suitable version of the first law of thermodynamics. In mathematical fluid dynamics, this is what constitutes a model; the development then follows the familiar route of non-dimensionalisation, scaling and the construction of an asymptotic solution. (More details about how the atmosphere is modelled, and the general principles that underpin the analysis, can be found in [6].) For this discussion, we choose to work in rotating, spherical coordinates, assuming a spherical Earth; the ellipsoidal approximation of the Earth’s geoid—not invoked here—is carefully described in [6]. We allow the eddy viscosity to vary with height above the Earth’s surface; indeed, in many models it is taken to be virtually zero beyond about 2 km altitude; see [15].

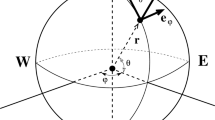
The development rests on one fundamental parameter: \(\varepsilon = {{H^{\prime}} \mathord{\left/ {\vphantom {{H^{\prime}} {R^{\prime}}}} \right. \kern-0pt} {R^{\prime}}}\), the thin-shell parameter, where \(H^{\prime}\) is the maximum thickness of the troposphere (about 16 km) and \(R^{\prime}\) is the average radius of the (spherical) Earth. (We use primes to denote physical (dimensional) variables; we will dispense with these as we move to nondimensional variables.) In the construction of the asymptotic version of this problem, we keep all other parameters fixed, as \(\varepsilon \to 0\), thereby retaining every physical attribute that contributes, at the same order, to both the dynamics and thermodynamics of the atmosphere. The Earth is rotating at the constant angular speed \(\Omega^{\prime} \approx 7 \cdot 29 \times 10^{ - 5} {\text{rad}}\,{\text{s}}^{ - 1}\), and using this we non-dimensionalise according to: \({\mathbf{u^{\prime}}} = H^{\prime}\Omega^{\prime}(u,v,kw)\), the velocity vector in spherical coordinates \((\phi ,\theta ,r^{\prime})\), where k measures the strength (in terms of ε) of the vertical velocity component; \(r^{\prime} = R^{\prime}(1 + \varepsilon z)\); \(p^{\prime} = \overline{\rho }^{\prime}(\Omega^{\prime}R^{\prime})^{2} p\) is the pressure, where \(\overline{\rho }^{\prime}\) is an average density of the atmosphere; \(\rho^{\prime} = \overline{\rho }^{\prime}\rho\) is the density. The coordinates are chosen so that ϕ is the azimuthal angle, and θ the meridional angle, being zero at the Equator and \(\pm {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}\) at the North/South poles, respectively. For a consistent thin-shell approximation, we choose to set \(k = \varepsilon\), and then the governing equations for the steady atmosphere, with error terms indicated, can be written as

$$ - 2\varepsilon \rho v\sin \theta = - \frac{1 - \varepsilon z}{{\cos \theta }}\frac{\partial p}{{\partial \phi }} + \frac{\varepsilon }{{R_{e} }}\frac{\partial \;}{{\partial z}}\left( {m\frac{\partial u}{{\partial z}}} \right) + {\text{O}}\left( {\varepsilon^{2} } \right); $$
(1)
$$ 2\varepsilon \rho u\sin \theta + \rho (1 + \varepsilon z)\sin \theta \cos \theta = - (1 - \varepsilon z)\frac{\partial p}{{\partial \theta }} + \frac{\varepsilon }{{R_{e} }}\frac{\partial \;}{{\partial z}}\left( {m\frac{\partial v}{{\partial z}}} \right) + {\text{O}}\left( {\varepsilon^{2} } \right); $$
(2)
$$ - \varepsilon \rho \cos^{2} \theta = - \frac{\partial p}{{\partial z}} - \rho g(1 - 2\varepsilon z) + {\text{O}}\left( {\varepsilon^{2} } \right), $$
(3)

these being the three components of the Navier–Stokes equation. The parameters that have been introduced here are

$${R_e} = \frac{{\bar \rho '\Omega '{{H'}^2}}}{{\bar \mu '}}\;{\rm{and}}\;g = \frac{{g'H'}}{{{{(\Omega 'R')}^2}}},$$

where the former is a Reynolds number (defined using an average value of the dynamic eddy viscosity, \(\overline{\mu }^{\prime}\)), and the latter (which can be interpreted as the ratio of the square of two speeds) typically takes a value of about \(0 \cdot 72\), for \(H^{\prime} = 16\) km; these are treated as O(1), i.e. fixed, as \(\varepsilon \to 0\). (This choice of parameter definitions ensures that we have a well-defined background state of the atmosphere, together with a dynamic-thermodynamic coupling which describes its motion; an extensive discussion of this formulation is given in [6].) In addition, we have written the dynamic viscosity as \(\mu^{\prime}(r^{\prime}) = \overline{\mu }^{\prime}m(z)\) and the equation of mass conservation becomes

$$ \frac{\partial \;}{{\partial \phi }}(\rho u) + \frac{\partial \;}{{\partial \theta }}(\rho v\cos \theta ) + \frac{\partial \;}{{\partial z}}(\rho w\cos \theta ) = {\text{O}}(\varepsilon ). $$
(4)

The thermodynamic elements of the atmosphere are described, firstly, by

$$ p = \rho T, $$
(5)

the equation of state, where we have defined the temperature as

$$ T^{\prime} = \frac{{(\Omega^{\prime}R^{\prime})^{2} }}{{\Re^{\prime}}}T, $$

with \(\Re^{\prime} \approx 287\;{\text{m}}^{{2}}\,{\text{s}}^{ - 2}\, {\text{K}}^{ - 1}\) the gas constant; secondly, the first law becomes

$$\begin{aligned}& c_{p} \left\{ {(1 - \varepsilon z)\left( {\frac{u}{\cos \theta }\frac{\partial T\;}{{\partial \phi }} + v\frac{\partial T\;}{{\partial \theta }}} \right) + w\frac{\partial T\;}{{\partial z}}} \right\} - \kappa \frac{{\partial^{2} T}}{{\partial z^{2} }} \\ &\quad - \frac{1}{\rho }\left\{ {(1 - \varepsilon z)\left( {\frac{u}{\cos \theta }\frac{\partial p\;}{{\partial \phi }} + v\frac{\partial p\;}{{\partial \theta }}} \right) + w\frac{\partial p\;}{{\partial z}}} \right\} = Q(\phi ,\theta ,z;\varepsilon ) + {\text{O}}(\varepsilon^{2} ), \end{aligned}$$
(6)

where \(c_{p} = \frac{{c^{\prime}_{p} }}{{\Re^{\prime}}} \approx 5 \cdot 25\), \(\kappa = \frac{{\kappa^{\prime}c^{\prime}_{p} }}{{\Re^{\prime}\Omega^{\prime}H^{{\prime}{2}} }}\); \(c^{\prime}_{p}\) is the specific heat of air, \(\kappa^{\prime}\) the thermal diffusivity of predominantly dry air and Q is the (non-dimensional) totality of heat sources/sinks. These final two parameters are also held fixed as \(\varepsilon \to 0\). The normalisation of the temperature, which uses the factor \({{(\Omega^{\prime}R^{\prime})^{2} } \mathord{\left/ {\vphantom {{(\Omega^{\prime}R^{\prime})^{2} } {\Re^{\prime}}}} \right. \kern-0pt} {\Re^{\prime}}}\)(about 800° K), produces a temperature variation of approximately \(T = 0 \cdot 36\) down to \(T = 0 \cdot 27\), from the bottom to the top of the troposphere. Although it transpires that \(R_{e}\) is very large, and κ is very small, there is no necessity to incorporate additional assumptions or approximations: any thin viscous or thermal boundary layers, for example, are automatically included in the solutions. Finally, we observe that the second law of thermodynamics, which sets limits on the transformation between heat energy and mechanical energy, plays no direct rȏle in the calculations that we present here.

3 Asymptotic structure of the solution

To proceed, we seek an asymptotic solution, based on ε, and obtain the first two terms in an asymptotic expansion of the form

$$ q(\phi ,\theta ,z;\varepsilon )\sim q_{0} (\phi ,\theta ,z) + \varepsilon q_{1} (\phi ,\theta ,z),\;{\text{as}}\;\varepsilon \to 0, $$

where q, and correspondingly \(q_{n}\), represent each of u, v, w, p, ρ, T and Q. Further, we assume that the boundary conditions follow this same pattern, so that no terms appear in addition to those in the asymptotic sequence \(\left\{ {\varepsilon^{n} } \right\}\). A general discussion of the nature and validity of this asymptotic expansion is given in [6]. The leading order is then obtained directly from Eqs. (1)–(3), (5) and (6), which gives

$$ 0 =- \frac{{\partial p_{0} }}{\partial \phi };\;\rho_{0} \sin \theta \cos \theta =- \frac{{\partial p_{0} }}{\partial \theta };\;0 = - \frac{{\partial p_{0} }}{\partial z} - \rho_{0} g; $$
(7)
$$ p_{0} = \rho_{0} T_{0} ;\;c_{p} L_{0} (T_{0} ) - \kappa \frac{{\partial^{2} T_{0} }}{{\partial z^{2} }} - \frac{1}{{\rho_{0} }}L_{0} (p_{0} ) = Q_{0} (\phi ,\theta ,z), $$
(8)
$$ {\text{where}}\quad L_{0} \equiv \left( {\frac{{u_{0} }}{\cos \theta }\frac{\partial }{\partial \phi } + v_{0} \frac{\partial }{\partial \theta } + w_{0} \frac{\partial }{\partial z}} \right). $$
(9)

This system has the solution

$$ p_{0} = p_{0} \left( {gz - \frac{1}{2}\cos^{2} \theta } \right),\;\rho_{0} = - \frac{{{\text{d}}p_{0} }}{{{\text{d}}\varsigma }}\;{\text{and}}\;T_{0} (\varsigma ) = \frac{{p_{0} (\varsigma )}}{{\rho_{0} (\varsigma )}} $$
(10)

where \(\varsigma = gz - \frac{1}{2}\cos^{2} \theta\) and \(p_{0}\) is otherwise an arbitrary function at this stage, with

$$ (v_{0} \sin \theta \cos \theta + gw_{0} )\left( {c_{p} \frac{{{\text{d}}T_{0} }}{{{\text{d}}\varsigma }} + 1} \right) - \kappa g^{2} \frac{{{\text{d}}^{2} T_{0} }}{{{\text{d}}\varsigma^{2} }} = Q_{0} $$
(11)

The classical solution which describes the stationary background state of the atmosphere, independent of the velocity field, is given by

$$ \frac{{{\text{d}}T_{0} }}{{{\text{d}}\varsigma }} = - \frac{1}{{c_{p} }} $$
(12)

and then \(Q_{0} \equiv 0\). This choice of model for the atmosphere shows that there are no external heat sources; the only heat supplied is that up from the surface of the Earth into the atmosphere. Further, we note that, although the choice (12) removes any direct coupling to the leading-order velocity field, this velocity field is, in general, a contributor to the solution at leading order (and is determined at the next order, as we now demonstrate).

At the next order, O(ε), we obtain the system of equations which connects all the dynamics and thermodynamics of the motion:

$$ - 2\rho_{0} v_{0} \sin \theta = - \frac{1}{\cos \theta }\frac{{\partial p_{1} }}{\partial \phi } + \frac{1}{{R_{e} }}\frac{\partial \;}{{\partial z}}\left( {m\frac{{\partial u_{0} }}{\partial z}} \right); $$
(13)
$$ 2\rho_{0} u_{0} \sin \theta + (\rho_{1} + 2z\rho_{0} )\sin \theta \cos \theta = - \frac{{\partial p_{1} }}{\partial \theta } + \frac{1}{{R_{e} }}\frac{\partial \;}{{\partial z}}\left( {m\frac{{\partial v_{0} }}{\partial z}} \right); $$
(14)
$$ - \rho_{0} \cos^{2} \theta = - \frac{{\partial p_{1} }}{\partial z} - g(\rho_{1} - 2z\rho_{0} ); $$
(15)
$$ \frac{\partial \;}{{\partial \phi }}\left( {\rho_{0} u_{0} } \right) + \frac{\partial \;}{{\partial \theta }}\left( {\rho_{0} v_{0} \cos \theta } \right) + \frac{\partial \;}{{\partial z}}\left( {\rho_{0} w_{0} \cos \theta } \right) = 0; $$
(16)
$$ p_{1} = \rho_{0} T_{1} + \rho_{1} T_{0} ; $$
(17)
$$ c_{p} L_{0} (T_{1} ) - \kappa \frac{{\partial^{2} T_{1} }}{{\partial z^{2} }} - \frac{1}{{\rho_{0} }}L_{0} (p_{1} ) - \frac{{\rho_{1} }}{{\rho_{0}^{{}} }}\left( {v_{0} \sin \theta \cos \theta + gw_{0} } \right) = Q_{1} + 2\kappa \frac{{\partial T_{0} }}{\partial z}. $$
(18)

At this stage, we have written down the equations that appear, at O(1) and at O(ε), as the relevant descriptions of the general (steady) motion in the atmosphere, invoking only the thin-shell approximation. These equations can be used to describe many different phenomena: the Ekman spiral, geostrophic balance, the thermal wind, the Hadley-Ferrel-polar cell structure, the appearance of jet streams high in the troposphere and the Walker cell; see [6] for a discussion of all the foregoing applications, but where the last example is covered in only the barest outline. We now restrict the application of these equations to a careful and complete analysis of the Walker circulation.

4 The Walker cell: formulation

We start with a few salient features of the Walker cell. Its strength is attributed to the variation of sea-surface temperature across the Pacific along the equator—a difference of about 5 °C, the warmer water to the West and the colder to the East. The cold water is present by virtue of advection northward along the coast of South America by the Humboldt current; see the discussions in [1, 10]. This describes the general situation, but it can be disrupted every few years. In particular, the Walker cell weakens during an El Niño year, but it is strengthened in an El Niña year. So, for example, during an El Niño event, the displacement of the west-Pacific warm-pool to the mid-Pacific triggers the appearance of a double-cell, with an ascending component in the central Pacific (see [13]). In order to provide a mathematical description of these various phenomena, we must introduce some appropriate simplifications, aimed at producing a suitable set of (correctly asymptotic) equations that represent the type of flow field which supports the Walker cell in the neighbourhood of the Equator.

Thus we set \(\theta = 0\) and assume no dependence on θ, together with no motion in the meridional direction, so \(v_{0} \equiv 0\); this describes flow in the \((\phi ,z)\)-plane at the Equator (and we interpret the solution as being appropriate to a neighbourhood of \(\theta = 0\)); see Fig. 2. Equation (13) becomes

$$ \frac{{\partial p_{1} }}{\partial \phi } = \frac{1}{{R_{e} }}\frac{\partial \;}{{\partial z}}\left( {m\frac{{\partial u_{0} }}{\partial z}} \right), $$
(19)
Fig. 2
figure 2

Sketch of the Walker cell (in red), which sits across the Equator between, approximately, 140oE and 140oW; the two adjacent cells are indicated in green

Full size image

Equation (14) is identically satisfied, Eq. (15) is now

$$ \frac{{\partial p_{1} }}{\partial z} = \rho_{0} - g(\rho_{1} - 2z\rho_{0} ) $$
(20)

and (16) simplifies to give

$$ \frac{\partial \;}{{\partial \phi }}\left( {\rho_{0} u_{0} } \right) + \frac{\partial \;}{{\partial z}}\left( {\rho_{0} w_{0} } \right) = 0. $$
(21)

The general approach that we adopt here is that developed in [6]. So, rather than input the heat sources that drive the motion—the obvious manoeuvre based on the physical nature of the problem—we aim to input a suitable temperature profile (as we have already done at O(1); see (12)), deduce the associated velocity field and then we may identify the heat sources required to drive and maintain the motion. This is the best way to proceed, we argue, and on two counts: (1) the precise nature of the heat sources, and how to model them, are notoriously difficult problems (see [7]); (2) the temperature field throughout the atmosphere is well known, using ground-based and satellite measurements (see [8]). So following this philosophy, and the more general development given in [6] (where all the details appear), we write

$$ \rho_{1} = \frac{{\partial r_{1} }}{\partial z}, $$
(22)

which leads to

$$ p_{1} (\phi ,z) = - gr_{1} (\phi ,z) - \left( {\frac{1}{g} + 2z} \right)p_{0} (z) - \frac{{2c_{p} }}{{g(1 + c_{p} )}}p_{0} (z)T_{0} (z), $$
(23)

where \(T_{0} (z) = T_{0E} - \frac{g}{{c_{p} }}z\) and \(p_{0} (z) = p_{0E} \left( {1 - \frac{g}{{c_{p} T_{0E} }}z} \right)^{{c_{p} }}\),

satisfying \(T_{0} = T_{0E}\) and \(p_{0} = p_{0E}\), respectively, on z = 0. We now set

$$ T_{1} (\phi ,z) = T_{0}^{2} \frac{{\partial \tau_{1} }}{\partial z}\;{\text{with}}\;\tau_{1} (\phi ,z) = \int\limits_{0}^{z} {\frac{{T_{1} (\phi ,z^{\prime})}}{{\left[ {T_{0} (z^{\prime})} \right]^{2} }}} \,{\text{d}}z^{\prime} $$
(24)

which allows us to find

$$ r_{1} = \left\{ {G(\phi ) - \tau_{1} } \right\}p_{0} + \frac{{c_{p} }}{{g^{2} }}\left\{ {\frac{{2gc_{p}^{{}} }}{{1 + c_{p} }}zp_{0} + \left[ {1 + 2c_{p} \left( {T_{0} + \frac{g}{{c_{p} }}z} \right)} \right]p_{0} \ln (T_{0} )} \right\}, $$
(25)

where G is an arbitrary function. Using (25) in (23), and evaluating on z = 0, yields

$$ G(\phi ) = - \frac{{p_{1} (\phi ,0)}}{{gp_{0E} }} - \frac{{c_{p} }}{{g^{2} }}(1 + 2c_{p} T_{0E} )\ln T_{0E} - \frac{{2c_{p} }}{{(1 + c_{p} )g^{2} }}T_{0E} - \frac{1}{{g^{2} }}, $$

and so from (19) we obtain

$$ \frac{1}{{R_{e} }}\frac{\partial \;}{{\partial z}}\left( {m\frac{{\partial u_{0} }}{\partial z}} \right) = gp_{0} (z)\int\limits_{0}^{z} {\frac{1}{{[T_{0} (z^{\prime})]^{2} }}} \frac{{\partial T_{1} }}{\partial \phi }(\phi ,z^{\prime})\,{\text{d}}z^{\prime} + \frac{{p_{0} (z)}}{{p_{0E} }}\frac{{\partial p_{1} }}{\partial \phi }(\phi ,0), $$
(26)

with (from (21))

$$ \frac{\partial \;}{{\partial \phi }}\left( {\rho_{0} u_{0} } \right) + \frac{\partial \;}{{\partial z}}\left( {\rho_{0} w_{0} } \right) = 0. $$
(27)

These two equations are our main results, defining the two-dimensional velocity field, given the pressure and temperature gradients; when coupled with (18), which simplifies to

$$ c_{p} \left( {u_{0} \frac{{\partial T_{1} }}{\partial \phi } + w_{0} \frac{{\partial T_{1} }}{\partial z}} \right) - \kappa \frac{{\partial^{2} T_{1} }}{{\partial z^{2} }} - \frac{1}{{\rho_{0} }}\left( {u_{0} \frac{{\partial p_{1} }}{\partial \phi } + w_{0} \frac{{\partial p_{1} }}{\partial z}} \right) - g\frac{{\rho_{1} }}{{\rho_{0} }}w_{0} = Q_{1} + 2\kappa \frac{{\partial T_{0} }}{\partial z}, $$
(28)

we are then able to identify the heat sources associated with this motion. We note, in particular, that Eq. (26) shows that the horizontal component of the velocity field is driven by the pressure gradient in the azimuthal direction evaluated on z = 0, and by the corresponding temperature gradient, but this also possesses a suitable z-structure. These observations are consistent with the accepted mechanism for the maintenance of the Walker cell (see [8, 11]), but our version is quite explicit in providing the details of this forcing. These two gradients which drive the motion are, in our formulation, regarded as given forcing terms, independently assigned. A study of the oceans, however, suggests that the surface wind-stress generates upwelling, bringing colder water to the surface in the East, and so we have cooler water to the East, and warmer to the West, thereby producing the temperature gradient at the surface. A model for this upwelling, in the presence of the westward surface flow and the Equatorial Undercurrent, can be found in [4].

All the above relates to that region of the flow where the eddy viscosity plays a rȏle, most particularly in the lower regions of the troposphere. The upper regions, which are traditionally regarded as inviscid, we treat by using a suitable model for the eddy viscosity. Some of the evidence—see [15, 16] for example—indicates that the eddy viscosity decays rapidly in the upper reaches of the atmosphere, and is virtually zero above about 2 km, although many alternative models for the viscosity appear in the literature; see the overview included in [5]. In our formulation, in conjunction with a variable viscosity, we impose the speed in the azimuthal direction at the bottom of the cell, \(u_{0B} (\phi )\) (which is zero if the no-slip condition is invoked). Thus the two-dimensional velocity field describing the Walker circulation is given by the solution of (26) and (27) which satisfies

$$ u_{0} (\phi ,z) = \left\{ \begin{gathered} u_{0B} (\phi )\quad {\text{on}}\quad z = 0 \hfill \\ u_{0T} (\phi )\quad {\text{on}}\quad z = z_{0} \hfill \\ \end{gathered} \right.,\left. \begin{gathered} w_{0} (\phi ,0) \hfill \\ w_{0} (\phi ,z_{0} ) \hfill \\ \end{gathered} \right\} = 0. $$
(29)

Note that the solution that we seek is bounded below by the ocean’s surface and above by the tropopause (\(z = z_{0} = 1\)) or a boundary close to this (\(z = z_{0} < 1\)), and so we must satisfy \(w_{0} = 0\) on these two boundaries, and satisfying this condition at the top fixes \(u_{0T} (\phi )\).

5 The Walker cell: solution

The construction of a solution of the problem developed in the previous section is, for the most part, a routine exercise and, although we will present the details for a specific example, the main purpose here is to emphasise the choices that are available. This will indicate, in particular, how it is possible to introduce suitable adjustments and additions based on observational data, opening the door to further investigations. As we mentioned earlier, we would, in the best of all possible worlds, aim to input the heat sources, determine the temperature field and then obtain the associated velocity field. This, however, is virtually impossible because neither the background knowledge nor the specific detailed data are available that would enable us to proceed. So we opt for a development based on, in principle, a choice for the temperature field as the starting point. Given this (i.e. \(T_{1} (\phi ,z)\) or \(\tau_{1} (\phi ,z)\)) we obtain the velocity field directly (by integration) and then we may identify the heat sources. But even this sequence is not completely straightforward or useful, because it is far from clear what precise form of perturbation temperature profile, \(T_{1} (\phi ,z)\), will generate the flow associated with a cell. Rather, it is better to guide the choice of \(T_{1} (\phi ,z)\) (or \(\tau_{1} (\phi ,z)\)) by noting the type of velocity field that we need in order to recover a Walker cell. In addition, we must also choose a model for the vertical behaviour of the dynamic eddy viscosity (i.e. m(z)). It is reasonable to adopt this approach since our overall aim is to show that suitable solutions do exist, which provide a description of the Walker cell, and that will also enable us to include the adjustments needed to recover the cell structure that is observed in El Niño years.

Equation (26) describes, in some detail, the vertical structure of the solution and this is to be consistent with the existence of a cell. However, the horizontal structure must be imposed in order to generate cells, the physical property that guides this being the obvious one: the Pacific Ocean is bounded by land masses to the East and to the West. The simplest choice which describes the required property is to set

$$ T_{1} (\phi ,z) = T(z)\cos \left( {\pi \frac{{\phi - \phi_{0} }}{{\phi_{1} - \phi_{0} }}} \right)\;{\text{and}}\;p_{1} (\phi ,0) = \Pi \cos \left( {\pi \frac{{\phi - \phi_{0} }}{{\phi_{1} - \phi_{0} }}} \right), $$
(30)

where Π is a constant and the cell sits in \(\phi_{0} < \phi < \phi_{1}\), expressed in degrees. (Clearly many other choices are possible, but we will limit our discussion here to just this one: we are aiming to confirm the existence of suitable solutions.) The horizontal velocity component then takes the form

$$ u_{0} (\phi ,z) = U(z)\sin \left( {\pi \frac{{\phi - \phi_{0} }}{{\phi_{1} - \phi_{0} }}} \right), $$
(31)

and so Eq. (26) becomes

$$ \left( {\frac{{\phi_{1} - \phi_{0} }}{{\pi gR_{e} }}} \right)\frac{{{\text{d}}\;}}{{{\text{d}}z}}\left( {m\frac{{{\text{d}}U}}{{{\text{d}}z}}} \right) = - p_{0} (z)\left\{ {\int\limits_{0}^{z} {\frac{{T(z^{\prime})}}{{[T_{0} (z^{\prime})]^{2} }}\,{\text{d}}z^{\prime}} + \frac{\Pi }{{gp_{0E} }}} \right\}. $$
(32)

Before we proceed with a more general analysis of Eq. (32), we carry out a simple check to see if this formulation captures some of the important features of the cell structure: we choose \(T(z) = {\rm T}T_{0}^{2} (z)\), with T constant, take \(m = {\text{constant}} = 1\) and \(p_{0} = {\text{constant}} = p_{0E}\), to give

$$ \lambda U^{\prime\prime} = - {\rm T}z - \hat{\Pi }, $$
(33)

where \(\lambda = {{(\phi_{1} - \phi_{0} )} \mathord{\left/ {\vphantom {{(\phi_{1} - \phi_{0} )} {(\pi gp_{0E} R_{e} )}}} \right. \kern-0pt} {(\pi gp_{0E} R_{e} )}}\) and \(\hat{\Pi } = {\Pi \mathord{\left/ {\vphantom {\Pi {(gp_{0E} )}}} \right. \kern-0pt} {(gp_{0E} )}}\). A solution of Eq. (33) is

$$ U(z) = \frac{\rm T}{{6\lambda }}z(z - z_{m} )(\alpha - z) $$
(34)

which satisfies the no-slip condition on z = 0, and also \(U(z_{m} ) = 0\) where we take \(0 < z_{m} < z_{0} \le 1\), and \(\alpha > z_{0}\) with \(\alpha + z_{m} = - 3{{\hat{\Pi }} \mathord{\left/ {\vphantom {{\hat{\Pi }} {\rm T}}} \right. \kern-0pt} {\rm T}}\), the choice of α fixing the speed at the top of the cell; an example of this profile is shown in Fig. 3. Necessarily \(\hat{\Pi } < 0\) for \({\rm T} > 0\), this latter condition ensuring that the flow is westwards low down in the troposphere and eastwards higher up. Thus, from (30), we see that.

$$\frac{{\partial p_{1} }}{\partial \phi } > 0\quad {\rm and} \quad \frac{{\partial T_{1} }}{\partial \phi } < 0,$$
Fig. 3
figure 3

Example of the profile \(z(z - z_{m} )(\alpha - z)\) with \(z_{m} = 0 \cdot 6\), \(\alpha = 1 \cdot 3\) and plotted for \(z_{0} = 0 \cdot 9\)

Full size image

which correspond to the observed properties of the Walker circulation: the pressure at the bottom of the troposphere is higher to the East, and the temperature is higher to the West. However, this simplistic observation ignores many of the detailed ingredients that make up Eq. (32), most notably the rȏle of a variable viscosity. We now take this initial examination a little further.

The perturbation-temperature profile used in the preceding calculation, with T constant, is not likely to be relevant to any realistic description of the Walker circulation, although the general form of the velocity profile is what we expect (when we use the no-slip condition). To proceed, and in order to make more transparent the important properties of this flow, we now use a simplified velocity profile which excludes the no-slip condition at the bottom and therefore admits a wind blowing directly over the surface of the ocean. The simplest such profile is linear:

$$ U(z) = U_{0} (z - z_{m} ), $$
(35)

where \(U_{0} > 0\) and \(0 < z_{m} < z_{0}\) are constants. The viscosity that we work with, and the one for which most of the data is available (as mentioned earlier), is the kinematic eddy viscosity; thus we introduce

$$ n(z) = \frac{m(z)}{{\rho_{0} (z)}} $$

and then we shall make choices for n(z). Equation (32) now becomes

$$ \frac{{U_{0} (\phi_{1} - \phi_{0} )}}{{\pi gR_{e} p_{0E} }}\left\{ {\frac{{{{{\text{d}}n} \mathord{\left/ {\vphantom {{{\text{d}}n} {{\text{d}}z}}} \right. \kern-0pt} {{\text{d}}z}}}}{{1 - \frac{gz}{{c_{p} T_{0E} }}}} - \frac{{g(c_{p} - 1)}}{{c_{p} T_{0E} }}\frac{n(z)}{{\left( {1 - \frac{gz}{{c_{p} T_{0E} }}} \right)^{2} }}} \right\} = - \int\limits_{0}^{z} {\frac{{T(z^{\prime})}}{{\left[ {T_{0} (z^{\prime})} \right]^{2} }}} \,{\text{d}}z^{\prime} - \frac{\Pi }{{gp_{0E} }}, $$
(36)

and an important observation follows directly. Evaluation on z = 0 gives

$$ \frac{{U_{0} (\phi_{1} - \phi_{0} )}}{{\pi R_{e} }}\left\{ {\frac{{{\text{d}}n}}{{{\text{d}}z}}(0) - \frac{{g(c_{p} - 1)}}{{c_{p} T_{0E} }}n(0)} \right\} = - \Pi , $$
(37)

and so a model for the viscosity in which n(0) = 0 and \({{{\text{d}}n} \mathord{\left/ {\vphantom {{{\text{d}}n} {{\text{d}}z}}} \right. \kern-0pt} {{\text{d}}z}}(0) > 0\) (see [15], for example) gives \(\Pi < 0\), which recovers the result \(\frac{{\partial p_{1} }}{\partial \phi } > 0\), consistent with the observations. On the other hand, if n(z) = constant (> 0), then Π > 0; if n(0) > 0 and \({{{\text{d}}n} \mathord{\left/ {\vphantom {{{\text{d}}n} {{\text{d}}z}}} \right. \kern-0pt} {{\text{d}}z}}(0) < 0\), then again \(\Pi > 0\). We conclude that the choice of model for eddy viscosity has a profound effect on the underlying pressure gradient, even though the airflow near the surface of the ocean is always westwards in our formulation. But of course a critical feature of any solution that describes the Walker circulation is the temperature variation and the resulting gradient in the azimuthal direction.

The construction of the temperature perturbation, \(T_{1} (z)\) (see (30)), is obtained directly when we choose the velocity profile, \(U(z)\) (see (31)), together with the model for the kinematic eddy viscosity. In this first stage of the investigation, we have used

$$ n(z) = 1,\quad n(z) = {\text{e}}^{ - \nu z} ,\quad n(z) = \nu z{\text{e}}^{1 - \nu z} , $$

where \(\nu > 0\) is a constant, these describing a constant viscosity, exponentially decreasing viscosity, and a viscosity which increases from zero followed by exponential decrease, respectively. In each model, we have set the maximum value of n to be 1, which is consistent with a suitable choice of the non-dimensionalisation based on \(\overline{\mu }^{\prime}\). We have chosen two velocity profiles for the calculations: the cubic polynomial drawn in Fig. 3 (and see (34)) and the linear model profile in (35). In both cases we have a flow which is westwards in the lower region of the troposphere and eastwards higher up. We tabulate (see the Table 1) the resulting signs of \({{\partial p_{1} } \mathord{\left/ {\vphantom {{\partial p_{1} } {\partial \phi }}} \right. \kern-0pt} {\partial \phi }}\) and \({{\partial T_{1} } \mathord{\left/ {\vphantom {{\partial T_{1} } {\partial \phi }}} \right. \kern-0pt} {\partial \phi }}\) on z = 0 and then, to correspond to the observed properties of the Walker cell, we should expect to use (as mentioned earlier)

$$ \frac{{\partial p_{1} }}{\partial \phi } > 0\;{\text{and}}\;\frac{{\partial T_{1} }}{\partial \phi } < 0\;{\text{both on}}\;z = \, 0. $$
(38)
Table 1 The results of the calculations using the cubic and the linear velocity profiles, and the choice of viscosity model: constant, exponentially decreasing, increasing followed by exponentially decreasing. The signs of the gradients in the azimuthal direction on z = 0 are listed
Full size table

(The properties listed in the Table 1 are the same for all ν > 0.)

If we use the conditions in (38) as the guiding principle for selecting suitable solutions, then the Table shows that we may use either a constant viscosity or a decreasing viscosity, in conjunction with the no-slip condition at the surface of the ocean, or the increasing–decreasing viscosity for the linear profile. In the light of these observations, we now examine in detail a simple profile which accommodates both a linear variation and a no-slip condition (but we produce the results for only one of these).

First, we normalise Eq. (32) by writing

$$U = {\hat U_0}C(z),\;T = \frac{{({\phi _1} - {\phi _0}){{\hat U}_0}}}{{g\pi {p_{0E}}{R_e}}}D(z),\;\Pi = \frac{{({\phi _1} - {\phi _0}){{\hat U}_0}}}{{\pi {R_e}}}P,$$
(39)

with \(\rho_{0} = \left( {1 - \frac{gz}{{c_{p} T_{0E} }}} \right)^{{c_{p} - 1}}\), which takes a maximum value of 1 on z = 0 (consistent with our non-dimensionalisation). Thus we obtain

$$ \frac{{(n\rm{C^{\prime}})^{\prime}}}{{\left( {1 - \frac{gz}{{c_{p} T_{0E} }}} \right)}} - \frac{{g(c_{p} - 1)}}{{c_{p} T_{0E} }}\frac{{n\rm{C^{\prime}}}}{{\left( {1 - \frac{gz}{{c_{p} T_{0E} }}} \right)^{2} }} = - \left( {\int\limits_{0}^{z} {{D}(Z)\;{\text{d}}Z + {P}} } \right), $$
(40)

where the prime denotes the derivative with respect to z. We see directly, by evaluating (40) on z = 0, that

$$ {P} = \frac{{g(c_{p} - 1)}}{{c_{p} T_{0E} }}n(0){C^{\prime}}(0) - (n{C^{\prime}})^{\prime}(0), $$
(41)

which determines \({P}\), and hence the pressure gradient in the azimuthal direction at the surface of the ocean. Here, we choose to work with the simple velocity profile

$$ {{C}}(z) = (z + z_{1} )(z - z_{m} ) + \beta z(1 + \gamma z), $$
(42)

where \(z_{1}\), \(z_{m}\), β and γ are constants. This profile is linear if \(\beta \gamma = - 1\) and it satisfies the no-slip condition at the ocean’s surface if \(z_{1} = 0\); two examples are shown in Fig. 4 where the upper boundary of the flow is fixed at the tropopause (\(z = 1\)). Although we investigated the effects of a number of different profiles based on (42), of all the choices that we might make, we opt for a model which describes a wind that blows (westwards) over the ocean, with a profile which is linear. This choice is the one which, in a direct and natural way, captures the important properties of the wind structure in the atmosphere; other profiles are accessible by suitably choosing the values of \(z_{1}\), \(z_{m}\), β and γ. Further, we invoke the most reasonable model for the kinematic eddy viscosity:

$$ n(z) = \nu z{\text{e}}^{1 - \nu z} , $$

where ν > 0 is a constant. The particular velocity profile that we use for the calculations is shown Fig. 5, and we set \(\nu = 10\) throughout. We find that \({P} \approx - 1 \cdot 568\) associated temperature perturbation, \({D}(z)\), is depicted in Fig. 6 and, because \({D}(0) > 0\), we see that \({{\partial T_{1} } \mathord{\left/ {\vphantom {{\partial T_{1} } {\partial \phi }}} \right. \kern-0pt} {\partial \phi }} < 0\) on z = 0. Furthermore, the temperature profile shows that the perturbation temperature decreases rapidly at higher altitude. This is the type of temperature function that we must use in order to produce the velocity profiles consistent with a Walker cell, given the chosen model for the kinematic eddy viscosity.

Fig. 4
figure 4

Two examples of the profile given in (40); red curve: \(z_{1} = 0 \cdot 4\), \(z_{m} = 0 \cdot 05\), \(\beta = - 0 \cdot 2911\), \(\gamma = 3 \cdot 5\); blue curve: \(z_{1} = 0\), \(z_{m} = 0 \cdot 01\), \(\beta = - 0 \cdot 9094\), \(\gamma = 15\)

Full size image
Fig. 5
figure 5

Thevelocity profile used for the calculations: (42) with \(z_{1} = 0 \cdot 4\), \(z_{m} = 0 \cdot 05\), \(\beta = - 0 \cdot 2923\), \(\beta \gamma = - 1\)

Full size image
Fig. 6
figure 6

The temperature perturbation in the Walker cell

Full size image

From Eq. (27) we may write.

$$\rho_{0} u_{0} = \frac{\partial \psi }{{\partial z}}$$

and

$$\rho_{0} w_{0} = - \frac{\partial \psi }{{\partial \phi }},$$

where \(\psi (\phi ,z)\) is the stream function for the flow; thus we have

$$ \psi (\phi ,z) = \hat{U}_{0} \sin \left( {\pi \frac{{\phi - \phi_{0} }}{{\phi_{1} - \phi_{0} }}} \right)\int\limits_{0}^{z} {\rho_{0} \rm{(}z^{\prime}\rm{)U}(z^{\prime})\,{\text{d}}z^{\prime}} , $$
(43)

which ensures that \(w_{0} = 0\) on z = 0. However, in addition, we must choose the various parameters that describe the velocity profile, (42), so that we also satisfy \(w_{0} = 0\) on \(z = 1\): the flow is bounded below by the surface of the ocean and above by the tropopause. The choices given above (see Fig. 5) satisfy this requirement. We are now able to produce the streamline pattern for this Walker cell, defined by lines \(\psi = {\text{constant}}\), which is shown in Fig. 7 and plotted for

$$0 \le \Phi = \pi \left( {\frac{{\phi - \phi_{0} }}{{\phi_{1} - \phi_{0} }}} \right) \le \pi \; \rm{and} \; 0 \le z \le 1;$$

the flow along the streamlines is in the clockwise direction when viewed northward.

Fig. 7
figure 7

The streamline pattern for the flow in the Walker cell; the flow is clockwise, viewed northward

Full size image

Finally, we may use our solution to provide a representation of the special flow configuration which arises during an El Niño event. This is most easily accomplished by simply adjusting the periodicity in the azimuthal direction, so plotting the streamlines associated with.

$$\psi (\phi ,z) = \hat{U}_{0} \sin \left( {2\pi \frac{{\phi - \phi_{0} }}{{\phi_{1} - \phi_{0} }}} \right)\int\limits_{0}^{z} {\rho_{0} \rm{(}z^{\prime}\rm{)U}(z^{\prime})\,{\text{d}}z^{\prime}} \;\rm{for} \;0 \le \Phi \le \pi, 0 \le z \le 1, $$

gives the streamline pattern shown in Fig. 8 (again, viewed northward). This solution can be analysed to extract the properties associated with this flow, such as the pressure and temperature distributions that are required to maintain this structure.

Fig. 8
figure 8

The streamline pattern that corresponds to the flow during an El Niño event; the flow direction in the right-hand cell is clockwise, and anticlockwise in the left-hand cell. Thus there is an ascending flow in the central Pacific

Full size image

The details of the solution that we have obtained can now be used in the version of the first law of thermodynamics which is appropriate at this order, namely Eq. (28). We have obtained, explicitly, the background temperature, \(T_{0} (z)\), and its perturbation, \(T_{1} (\phi ,z)\), numerically; we can then determine both \(\rho_{1} (\phi ,z)\) and \(p_{1} (\phi ,z)\). All this enables us to find an expression for the heat sources/sinks, \(Q_{1}\), that are required to maintain the Walker cell. In particular we note that there is a contribution to the background (i.e. solar) heating from the terms.

$$ - \kappa \frac{{\partial^{2} T_{1} }}{{\partial z^{2} }} - 2\kappa \frac{{\partial T_{0} }}{\partial z}, $$

and the other terms:

$$ u_{0} \left( {c_{p} \frac{{\partial T_{1} }}{\partial \phi } - \frac{1}{{\rho_{0} }}\frac{{\partial p_{1} }}{\partial \phi }} \right) + w_{0} \left( {c_{p} \frac{{\partial T_{1} }}{\partial z} - \frac{1}{{\rho_{0} }}\frac{{\partial p_{1} }}{\partial z} - g\frac{{\rho_{1} }}{{\rho_{0} }}} \right), $$

are heat sources that move with the fluid and so are associated with latent heat. Although we have not produced the (numerical) details here, they are readily available and, we suggest, are worth exploring if reliable data can be used to produce further properties of the Walker circulation.

6 Discussion

The development presented here is based on the Navier–Stokes equation for a compressible fluid, with variable viscosity, coupled to an equation of state and a suitable version of the first law of thermodynamics. These general governing equations have been non-dimensionalised and then an asymptotic solution is constructed which uses only the thin-shell approximation to describe the atmosphere; all other parameters are held fixed in the limiting process. Although the details are not developed here—they are available in [6]—we have presented the main results to aid the reader. These comprise the equations describing the background state of the atmosphere, together with its perturbation which incorporates all the dynamics and thermodynamics of the steady atmosphere. We have chosen the background state to be that which exists independently of the underlying velocity field; the issue then is to construct suitable solutions which describe the superimposed steady motion.

The particular exercise undertaken here is to find a solution which represents and describes the Walker circulation that sits over the Pacific Ocean and along the Equator. The main drivers for this motion are well known; here, we aim to provide a careful mathematical treatment of this phenomenon. This can then be used to investigate, in detail, various properties of the flow and how it might change according to the ambient conditions. The resulting formulation, Eqs. (26) and (27) with (28), is the main theoretical conclusions of the work. In particular, we can be precise about the mechanisms that drive the motion in the cell: the pressure gradient in the azimuthal direction at the surface and a corresponding temperature gradient. One immediate consequence of our development is the form taken by this temperature-gradient term; this involves a combination of both the background temperature and the gradient of the perturbation temperature, via an integral—possibly not an obvious combination. Furthermore, this element of the forcing vanishes at the ocean’s surface, leaving only the pressure gradient there. The nett result is to produce a simple, very specific differential system which couples the velocity field to the temperature and pressure gradients in the azimuthal direction, together with the opportunity to include any suitable, variable viscosity.

An initial investigation, based on cubic and linear velocity profiles, for various models for the kinematic eddy viscosity, was undertaken. This showed that a realistic azimuthal velocity profile—westward lower down and eastward higher up—could be generated for other than the observed signs of the temperature and pressure gradients. Nevertheless, we used these observations to guide a more comprehensive examination of a solution which used a simple but general velocity profile, which could accommodate both a linear variation and also a quadratic variant, allowing for a no-slip condition at the surface. The choice which most closely accords with the existence of trade winds (crucial to early sailors) is a flow which does not satisfy the (classical and technically correct) no-slip condition at the surface. (Of course, we would certainly allow a non-zero speed at the surface if we are to model wind-driven waves.) Thus we have used parameter values that produce a westward flow down to the surface of the ocean and an eastward flow at higher altitude. In addition, the vertical velocity component, \(w_{0}\), must satisfy the requirement that the flow is bounded by the ocean surface below and the tropopause (or something close to this) above. Although we can always impose \(w_{0} = 0\) on z = 0, for any horizontal velocity profile, we must choose this profile with care so that we also have \(w_{0} = 0\) on z = 1 in order to satisfy mass-flow conservation. This describes the vertical structure of the solution; the horizontal structure required to produce a cell was imposed by invoking a simple trigonometric function that gave \(u_{0} = 0\) at the furthest extremities of the cell. With all these ingredients in place, a solution was computed (using Maple) which produced a vertical perturbation-temperature profile through the depth of the troposphere and a streamline pattern for the flow in the Walker cell.

This temperature profile, shown in Fig. 6, is quite specific for this solution; on the other hand, given this profile and the maximum speeds at the top and bottom of the cell, the solution for U(z) can be recovered. The speed at the top, we note, is fixed by ensuring that \(w_{0} = 0\) along the top of the cell. So the details that we have presented confirm the existence of a suitable solution—and this was the main aim of the work—and, more significantly, the formulation provides an opportunity for further detailed investigation. Thus any number of choices for the variable viscosity, the surface pressure gradient and the temperature profile can be made, and solutions representing the Walker cell constructed; in addition, adjustments to the velocity profile can also be made and the consequences investigated. (We also record that the maximum value attained by the temperature perturbation in our calculations—which always occurs on z = 0—is significantly affected by the choice of ν in the viscosity model.) All this is particularly useful if reliable data are available to guide the choice of viscosity model, the temperature profile and the horizontal structure of the cell. Furthermore, the effects of changes in the ambient conditions (perhaps driven by climate change) can be tested using this system of equations. With this in mind, we introduced a simple modification which models the situation that arises during an El Niño event: we have seen that two cells are easily accommodated, mirroring what happens when the region of warmer water penetrates further to the East.

There is no virtue in including an examination of the El Niña, because this is simply an enhancement—larger gradients and higher wind speeds—of the Walker circulation that we have described. However, there is one final observation that we can make which suggests, albeit in a numerical sense, that we have captured some important attributes of the Walker circulation. Using the values obtained in our numerical example, together with the parameter values and non-dimensionalisation given earlier, taking \(R_{e} = 5 \times 10^{5}\) and assuming that the Walker cell extends over 80° of longitude, we find that a surface wind speed of 5 ms−1 produces a temperature change, \({{\varepsilon T_{1} (\Omega^{\prime}R^{\prime})^{2} } \mathord{\left/ {\vphantom {{\varepsilon T_{1} (\Omega^{\prime}R^{\prime})^{2} } {\Re^{\prime}}}} \right. \kern-0pt} {\Re^{\prime}}}\), along the extent of the cell at the ocean’s surface of about 5 °C. Thus our leading term in the perturbation of the background state produces a result that is altogether reasonable, although there is clearly no certainty about the values that should be used in this rudimentary calculation. The higher-order terms are proportional to \(\varepsilon^{n}\), n = 2, 3, … and, since there is no suggestion of non-uniformities in the asymptotic expansions, we appear to have captured the main contributor to the temperature perturbation which drives the Walker circulation.

In conclusion, we have shown that a careful (asymptotic) approach to the general, governing equations that represent the atmosphere have led to a simplified system of equations. These produce a perturbation of a background state, the perturbation combining all the dynamics and thermodynamics of the steady atmosphere. Furthermore, these equations can be used to give a detailed description of the Walker circulation, providing a simple test-bed for the effects of pressure gradient, temperature profile, velocity profile and variable eddy viscosity to be investigated. Associated with this general flow structure, the disruption caused by El Niño and El Niña events can also be examined. There is much, we submit, that can be explored using the equations presented here, particularly if extensive and reliable data are available.