Skip to main content
SpringerLink
Log in

Criterion for a graph to admit a good orientation in terms of leaf blocks

  • Original Research
  • Published:
Monatshefte für Mathematik Aims and scope Submit manuscript

Abstract

Given a set S of integers, for a directed acyclic pseudograph we say that it has an S-good orientation if all its sources and sinks have degrees in S; in these terms, the existing notion of good orientation is a \(\{\,1\,\}\)-good orientation. We give a criterion for a pseudograph to admit an S-good orientation in terms of the structure of its leaf blocks. This criterion allows to compute whether a pseudograph admits an S-good orientation with optimal (linear) time and space complexity. As an application, we give a simple criterion for a graph to be realized as the Reeb graph of a Morse function in terms of leaf blocks of the graph. Similar conditions can be obtained for other classes of functions, such as (simple) Morse–Bott functions or round functions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Data availability

Data sharing not applicable to this article as no datasets were generated or analysed during the current study.

Code availability

Code availability not applicable to this article as no code was generated or analysed during the current study.

Notes

  1. Recall that by a graph, we understand a graph allowing multiple edges and loop edges, i.e., a pseudograph. For readers who might use individual statements without reading the whole paper, we will refer to this footnote throughout the paper.

  2. The proof (to be given in a future paper) relies on the fact that the (block-cut) tree T can be oriented in such a way that its only sources and sinks be leaves, with a given non-empty set of leaves being sources and non-empty set of leaves being sinks.

  3. We thank an anonymous reviewer for suggesting this example.

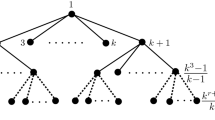
  4. One may consider these estimates as expressing the complexity of the algorithm in terms of its own output. If this is undesirable, one can use (1) instead. However, there are practical situations where \(|E'|\) is known a priori to be much smaller than the bound (1). For example, consider a graph G on the set V of all people in the world, where an edge between persons A and B corresponds to sending an email message, giving a Facebook like, or having a physical contact in the context of epidemiological research. By the very nature of the modeled phenomenon we know a priori that many of multi-edges of such a graph consist of a large number of individual edges, i.e., the set \(E'\) of pairs of people having ever interacted is much smaller than the set E of their individual interactions; the number \(|E'|\) can even be estimated from sociological assumptions without actual calculation on the graph G.

References

  1. Adelson-Velsky, G.M., Kronrod, A.S.: Sur les lignes de niveau des fonctions continues possedant des dérivées partielles. Dokl. Akad. Nauk SSSR 49(4), 235–237 (1945)

    MATH  Google Scholar 

  2. Biasotti, S., Giorgi, D., Spagnuolo, M., Falcidieno, B.: Reeb graphs for shape analysis and applications. Theor. Comput. Sci. 392, 5–22 (2008)

    Article  MathSciNet  Google Scholar 

  3. Conte, A., Grossi, R., Marino, A., Rizzi, R.: Efficient enumeration of graph orientations with sources. Discrete Appl. Math. 246, 22–37 (2018)

    Article  MathSciNet  Google Scholar 

  4. Davey, B.A., Priestley, H.: Introduction to Lattices and Order. Cambridge University Press, Cambridge (2002)

    Book  Google Scholar 

  5. de Fraysseix, H.: Patrice Ossona de Mendez, and Pierre Rosenstiehl, Bipolar orientations revisited. Discrete Appl. Math. 56(2–3), 157–179 (1995)

    Article  MathSciNet  Google Scholar 

  6. Ellis-Monaghan, J.A., Merino, C.: Graph Polynomials and Their Applications I: The Tutte Polynomial, Structural Analysis of Complex Network, pp. 219–255. Birkhäuser, Boston (2011)

    MATH  Google Scholar 

  7. Franks, J.: Nonsingular Smale flows on \({S}^3\). Topology 24(3), 265–282 (1985)

    Article  MathSciNet  Google Scholar 

  8. Gebhard, D.D., Sagan, B.E.: Sinks in acyclic orientations of graphs. J. Comb. Theory 80(1), 130–146 (2000)

    Article  MathSciNet  Google Scholar 

  9. Gelbukh, I.: Loops in Reeb graphs of \(n\)-manifolds. Discrete Comput. Geom. 59(4), 843–863 (2018)

    Article  MathSciNet  Google Scholar 

  10. Gelbukh, I.: Approximation of metric spaces by Reeb graphs: cycle rank of a Reeb graph, the co-rank of the fundamental group, and large components of level sets on Riemannian manifolds. Filomat 33(7), 2031–2049 (2019)

    Article  MathSciNet  Google Scholar 

  11. Gelbukh, I.: A finite graph is homeomorphic to the Reeb graph of a Morse–Bott function. Math. Slovaca 71(3), 757–772 (2021)

    Article  MathSciNet  Google Scholar 

  12. Gelbukh, I.: Morse–Bott functions with two critical values on a surface. Czech Math. J. 71(3), 865–880 (2021)

    Article  MathSciNet  Google Scholar 

  13. Gelbukh, I.: Realization of a graph as the Reeb graph of a Morse–Bott or a round function. Stud. Sci. Math. Hung. 59(1), 1–16 (2022)

  14. Ghosh, R.K., Bhattacharjee, G.P.: A parallel search algorithm for directed acyclic graphs. BIT Numer. Math. 24(2), 133–150 (1984)

    Article  MathSciNet  Google Scholar 

  15. Gioan, E., Vergnas, M.L.: Activity preserving bijections between spanning trees and orientations in graphs. Discrete Math. 298(1), 169–188 (2005)

    Article  MathSciNet  Google Scholar 

  16. Greene, C., Zaslavsky, T.: On the interpretation of Whitney numbers through arrangements of hyperplanes, zonotopes, non-radon partitions, and orientations of graphs. Trans. Am. Math. Soc. 280(1), 97–126 (1983)

    Article  MathSciNet  Google Scholar 

  17. Gutin, G.: Acyclic Digraphs, Classes of Directed Graphs, pp. 125–172. Springer, Berlin (2018)

    Book  Google Scholar 

  18. Hopcroft, J.E., Tarjan, R.E.: Algorithm 447: efficient algorithms for graph manipulation. Commun. ACM 16, 372–378 (1973)

    Article  Google Scholar 

  19. Jonczy, J., Haenni, R.: Network reliability evaluation with propositional directed acyclic graphs. In: Advances in Mathematical Modeling for Reliability, pp. 25–31. IOS Press (2008)

  20. Kaluba, M., Marzantowicz, W., Silva, N.: On representation of the Reeb graph as a sub-complex of manifold. Topol. Methods Nonlinear Anal. 45(1), 287–305 (2015)

    Article  MathSciNet  Google Scholar 

  21. Khohliyk, O., Maksymenko, S.: Diffeomorphisms preserving Morse–Bott functions. Indag. Math. 31(2), 185–203 (2020)

    Article  MathSciNet  Google Scholar 

  22. Kitazawa, N.: Maps on manifolds onto graphs locally regarded as a quotient map onto a Reeb space and construction problem (2019). pre-print, 12 pages, arXiv:1909.10315 [math.GT]

  23. Kitazawa, N.: On Reeb graphs induced from smooth functions on 3-dimensional closed orientable manifolds with finitely many singular values (2019). pre-print, 9 pages, arXiv:1902.08841 [math.GT]

  24. Kitazawa, N.: On Reeb graphs induced from smooth functions on closed or open manifolds (2019). pre-print, 18 pages, arXiv:1908.04340 [math.GT]

  25. Kravchenko, A., Maksymenko, S.: Automorphisms of Kronrod–Reeb graphs of Morse functions on compact surfaces. Eur. J. Math. 6(1), 114–131 (2020)

    Article  MathSciNet  Google Scholar 

  26. Lempel, A., Even, S., Cederbaum., I.: An algorithm for planarity testing of graphs. In: Theory of Graphs (International Symposium, Rome, 1966), pp. 215–232. Gordon and Breach (1967)

  27. Lima, D.V.S., Neto, O.M., de Rezende, K.A.: On handle theory for Morse–Bott critical manifolds. Geom. Dedic. 202, 265–309 (2019)

    Article  MathSciNet  Google Scholar 

  28. Lychak, D.P., Prishlyak, A.O.: Morse functions and flows on nonorientable surfaces. Methods Funct. Anal. Topol. 15(3), 251–258 (2009)

    MathSciNet  MATH  Google Scholar 

  29. Martínez-Alfaro, J., Meza-Sarmiento, I.S., Oliveira, R.: Topological classification of simple Morse Bott functions on surfaces. In: Real and Complex Singularities, Contemporary Mathematics, no. 675, pp. 165–179. AMS (2016)

  30. Marzantowicz, W., Michalak, Ł.P.: Relations between Reeb graphs, systems of hypersurfaces and epimorphisms onto free groups (2020). pre-print, 20 pages, arXiv:2002.02388 [math.GT]

  31. Masumoto, Y., Saeki, O.: Smooth function on a manifold with given Reeb graph. Kyushu J. Math. 65(1), 75–84 (2011)

    Article  MathSciNet  Google Scholar 

  32. Michalak, ŁP.: Realization of a graph as the Reeb graph of a Morse function on a manifold. Topol. Methods Nonlinear Anal. 52(2), 749–762 (2018)

    MathSciNet  MATH  Google Scholar 

  33. Michalak, ŁP.: Combinatorial modifications of Reeb graphs and the realization problem. Discrete Comput. Geom. 65(4), 1038–1060 (2021)

    Article  MathSciNet  Google Scholar 

  34. Pang, C., Junhu Wang, Yu., Cheng, H.Z., Li, T.: Topological sorts on DAGs. Inf. Process. Lett. 115(2), 298–301 (2015)

    Article  MathSciNet  Google Scholar 

  35. Papamanthou, C., Tollis, I.G.: Applications of parameterized \(st\)-orientations. J. Graph Algorithms Appl. 14(2), 337–365 (2010)

    Article  MathSciNet  Google Scholar 

  36. Reeb, G.: Sur les points singuliers d’une forme de Pfaff complétement intégrable ou d’une fonction numérique. C. R. Acad. Ser. Paris 222, 847–849 (1946)

    MATH  Google Scholar 

  37. Saeki, O.: Reeb spaces of smooth functions on manifolds. Int. Math. Res. Not. (2021). https://doi.org/10.1093/imrn/rnaa301

    Article  Google Scholar 

  38. Schmidt, J.M.: A simple test on 2-vertex- and 2-edge-connectivity. Inf. Process. Lett. 113, 241–244 (2013)

    Article  MathSciNet  Google Scholar 

  39. Sharko, V.V.: About Kronrod–Reeb graph of a function on a manifold. Methods Funct. Anal. Topol. 12(4), 389–396 (2006)

    MathSciNet  MATH  Google Scholar 

  40. Stanley, R.P.: Acyclic orientations of graphs. Discrete Math. 306, 905–909 (2006)

    Article  Google Scholar 

  41. Tarjan, R.E.: Two streamlined depth-search algorithms. Fundam. Inform. 9, 85–94 (1986)

    Article  MathSciNet  Google Scholar 

  42. Wu, Q., Wu, Z., Zhuang, Y., Cheng, Y.: Adaptive DAG tasks scheduling with deep reinforcement learning. In: Vaidya, J., Li, J. (eds.) Algorithms and Architectures for Parallel Processing. ICA3PP 2018. Lecture Notes in Computer Science, vol 11335. Springer, Cham (2018)

  43. Yu, B.: Lyapunov graphs of nonsingular Smale flows on \({S}^1\times {S}^2\). Trans. Am. Math. Soc. 365(2), 767–783 (2013)

    Article  Google Scholar 

  44. Yu, Y., Chen, J., Gao, T., Yu, M.: DAG-GNN: DAG structure learning with graph neural networks. In: Proceedings of the 36th International Conference on Machine Learning, Proceedings of Machine Learning Research, vol. 97, pp. 7154–7163. PMLR (2019)

Download references

Funding

Funding statement not applicable to this article as no funding agency sponsored the current study.

Author information

Authors and Affiliations

  1. CIC, Instituto Politécnico Nacional, 07338, Mexico City, Mexico

    Irina Gelbukh

Authors
  1. Irina Gelbukh
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors whose names appear on the paper made substantial contributions to the conception or design of the work; or the acquisition, analysis, or interpretation of data; or the creation of new software used in the work; drafted the work or revised it critically for important intellectual content; approved the version to be published; and agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

Corresponding author

Correspondence to Irina Gelbukh.

Ethics declarations

Conflict of interest

The author declares to have no conflicts of interest.

Additional information

Communicated by Ilse Fischer.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gelbukh, I. Criterion for a graph to admit a good orientation in terms of leaf blocks. Monatsh Math 198, 61–77 (2022). https://doi.org/10.1007/s00605-022-01681-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00605-022-01681-6

Keywords

Mathematics Subject Classification

Search

Navigation