Abstract
This article is the natural continuation of the paper: Mukhammadiev et al. Supremum, infimum and hyperlimits of Colombeau generalized numbers in this journal. Since the ring  of Robinson-Colombeau is non-Archimedean and Cauchy complete, a classical series \(\sum _{n=0}^{+\infty }a_{n}\) of generalized numbers
of Robinson-Colombeau is non-Archimedean and Cauchy complete, a classical series \(\sum _{n=0}^{+\infty }a_{n}\) of generalized numbers  is convergent if and only if \(a_{n}\rightarrow 0\) in the sharp topology. Therefore, this property does not permit us to generalize several classical results, mainly in the study of analytic generalized functions (as well as, e.g., in the study of sigma-additivity in integration of generalized functions). Introducing the notion of hyperseries, we solve this problem recovering classical examples of analytic functions as well as several classical results.
is convergent if and only if \(a_{n}\rightarrow 0\) in the sharp topology. Therefore, this property does not permit us to generalize several classical results, mainly in the study of analytic generalized functions (as well as, e.g., in the study of sigma-additivity in integration of generalized functions). Introducing the notion of hyperseries, we solve this problem recovering classical examples of analytic functions as well as several classical results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this article, the study of supremum, infimum and hyperlimits of Colombeau generalized numbers (CGN) we carried out in [13] is applied to the introduction of a corresponding notion of hyperseries. In [13], we recalled that \((x_{n})_{n\in \mathbb {N}}\in {\widetilde{\mathbb {R}}}^{\mathbb {N}}\) is a Cauchy sequence if and only if \(\lim _{n\rightarrow +\infty }\left| x_{n+1}-x_{n}\right| =0\) (in the sharp topology). As a consequence, a series of CGN
Once again, this is a well-known property of every ultrametric space, cf., e.g., [11]. The point of view of the present work is that in a non-Archimedean ring such as  , the notion of hyperseries
, the notion of hyperseries  , i.e. where we sum over the set of hyperfinite natural numbers
, i.e. where we sum over the set of hyperfinite natural numbers  , yields results which are more closely related to the classical ones, e.g. in studying analytic functions, sigma additivity and limit theorems for integral calculus, or in possible generalization of the Cauchy-Kowalevski theorem to generalized smooth functions (GSF; see e.g. [7]).
, yields results which are more closely related to the classical ones, e.g. in studying analytic functions, sigma additivity and limit theorems for integral calculus, or in possible generalization of the Cauchy-Kowalevski theorem to generalized smooth functions (GSF; see e.g. [7]).
Considering the theory of analytic CGF as developed in [17] for the real case and in [20] for the complex one, it is worth to mention that several properties have been proved in both cases: closure with respect to composition, integration over homotopic paths, Cauchy integral theorem, existence of analytic representatives \(u_{\varepsilon }\), a real analytic CGF is identically zero if it is zero on a set of positive Lebesgue measure, etc. (cf. [14, 17, 20] and references therein). On the other hand, even if in [20] it is also proved that each complex analytic CGF can be written as a Taylor series, necessarily this result holds only in an infinitesimal neighborhood of each point. The impossibility to extend this property to a finite neighborhood is due to (1.1) and is hence closely related to the approach we follow in the present article.
We refer to [13] for notions such as the ring of Robinson-Colombeau, subpoints, hypernatural numbers, supremum, infimum and hyperlimits. See also [12] for a more general approach to asymptotic gauges. In the present paper, we focus only on examples and properties related to hyperseries, postponing those about analytic functions, integral calculus and the Cauchy-Kowalevski theorem to subsequent works. Once again, the ideas presented in the present article, which needs only [13] as prior knowledge, can surely be useful to explore similar ideas in other non-Archimedean Cauchy complete settings, such as [2, 3, 11, 19].
2 Hyperseries and their basic properties
2.1 Definition of hyperfinite sums and hyperseries
In order to define these notions, the main idea, like in the Archimedean case \(\mathbb {R}\), is to reduce the notion of hyperseries to that of hyperlimit. Since to take an hyperlimit we have to consider two gauges \(\rho \), \(\sigma \), it is hence natural to consider the same assumption for hyperseries. However, in a non-Archimedean setting, the aforesaid main idea implies that the main problem is not in defining hyperseries itself, but already in defining what an hyperfinite sum is. In fact, if
 is a family of generalized numbers of
is a family of generalized numbers of
 indexed in
indexed in
 , it is not even clear what
\(\sum _{i=0}^{4}a_{i}\), means because there are infinite
, it is not even clear what
\(\sum _{i=0}^{4}a_{i}\), means because there are infinite
 such that
\(0\le i\le 4\). In general, in a sum of the form
\(\sum _{i=0}^{N}a_{i}\) with
such that
\(0\le i\le 4\). In general, in a sum of the form
\(\sum _{i=0}^{N}a_{i}\) with
 , the number of addends depends on how small is the gauge
\(\sigma \) and hence how large can be
\(N\le \hbox {d}^{-R}\) (for some
\(R\in \mathbb {N}\)). The problem is simplified if we consider only ordinary sequences
\((a_{n})_{n\in \mathbb {N}}\) of CGN in
, the number of addends depends on how small is the gauge
\(\sigma \) and hence how large can be
\(N\le \hbox {d}^{-R}\) (for some
\(R\in \mathbb {N}\)). The problem is simplified if we consider only ordinary sequences
\((a_{n})_{n\in \mathbb {N}}\) of CGN in
 and an
\(\varepsilon \)-wise definition of hyperfinite sum. In order to accomplish this goal, we first need to extend the sequence
and an
\(\varepsilon \)-wise definition of hyperfinite sum. In order to accomplish this goal, we first need to extend the sequence

of partial sums with summands
 ,
\(n\in \mathbb {N}\), to the entire set
,
\(n\in \mathbb {N}\), to the entire set
 of hyperfinite numbers. This problem is not so easy to solve: in fact, the sequence of representatives of zero:
\(a_{n\varepsilon }=0\) if
\(\varepsilon \le \frac{1}{n}\) and
\(a_{n\varepsilon }=(1-\varepsilon )^{-n}\) otherwise, where
\(n\in \mathbb {N}_{>0}\), satisfies
of hyperfinite numbers. This problem is not so easy to solve: in fact, the sequence of representatives of zero:
\(a_{n\varepsilon }=0\) if
\(\varepsilon \le \frac{1}{n}\) and
\(a_{n\varepsilon }=(1-\varepsilon )^{-n}\) otherwise, where
\(n\in \mathbb {N}_{>0}\), satisfies
but if \(N_{\varepsilon }\rightarrow +\infty \) this sum diverges to \(+\infty \) because \(\frac{1}{1-\varepsilon }>1\); moreover, for suitable \(N_{\varepsilon }\), the net in (2.2) is of the order of \(\left( \frac{1}{1-\varepsilon }\right) ^{N_{\varepsilon }}\), which in general is not \(\rho \)-moderate. To solve this first problem, we have at least two possibilities: the first one is to consider a Robinson-Colombeau ring defined by the index set \(\mathbb {N}\times I\) and ordered by \((n,\varepsilon )\le (m,e)\) if and only if \(\varepsilon \le e\). In this solution, moderate representatives are nets \((a_{n\varepsilon })_{n,\varepsilon }\in \mathbb {R}^{\mathbb {N}\times I}\) satisfying the uniformly moderate condition
Negligible nets are \((a_{n\varepsilon })_{n,\varepsilon }\in \mathbb {R}^{\mathbb {N}\times I}\) such that
Note that, with respect to the aforementioned directed order relation, for any property \(\mathcal {P}\), we have
The main problem with this solution is that it works to define hyperfinite sums only if
Assume, indeed, that (2.3) holds for all \(\varepsilon \le \varepsilon _{0}\), so that if  , \(N_{\varepsilon }\in \mathbb {N}\), we have
, \(N_{\varepsilon }\in \mathbb {N}\), we have
where we assumed that \(N_{\varepsilon }\le \sigma _{\varepsilon }^{-R}\) for these \(\varepsilon \le \varepsilon _{0}\). This is intuitively natural since the Robinson-Colombeau ring defined by the aforementioned order relation depends only on the gauge \(\rho \), whereas the moderateness in (2.6) depends on the product \(N_{\varepsilon }\cdot \rho _{\varepsilon }^{-Q}\le \sigma _{\varepsilon }^{-R}\cdot \rho _{\varepsilon }^{-Q}\) between how many addends we are taking (that depends on \(\sigma \)) and the uniform moderateness property (2.3).
This first solution has three drawbacks: The first one, as explained above, is that in this ring we can consider hyperfinite sum only if the relation (2.5) between the two considered gauges holds. The second one is that we cannot consider divergent hyperseries such as e.g.  because \(n\le \rho _{\varepsilon }^{-Q}\) do not hold for \(\varepsilon \) small and uniformly for all \(n\in \mathbb {N}\). The third one is that we would like to apply [13, Thm. 28] to prove the convergence of hyperseries by starting from the corresponding converging series of \(\varepsilon \)-representatives; however, [13, Thm. 28] do not allow us to get the limitation (2.5) (and later, we will see that in general the limitation (2.5) is impossible to achieve: see just after the proof of Theorem 12).
because \(n\le \rho _{\varepsilon }^{-Q}\) do not hold for \(\varepsilon \) small and uniformly for all \(n\in \mathbb {N}\). The third one is that we would like to apply [13, Thm. 28] to prove the convergence of hyperseries by starting from the corresponding converging series of \(\varepsilon \)-representatives; however, [13, Thm. 28] do not allow us to get the limitation (2.5) (and later, we will see that in general the limitation (2.5) is impossible to achieve: see just after the proof of Theorem 12).
The second possibility to extend (2.1) to  , a possibility that depends on two gauges but works for any \(\sigma \) and \(\rho \), is to say that hyperseries can be computed only for representatives \((a_{n\varepsilon })_{n\varepsilon }\) which are moderate over hypersums, i.e. to ask
, a possibility that depends on two gauges but works for any \(\sigma \) and \(\rho \), is to say that hyperseries can be computed only for representatives \((a_{n\varepsilon })_{n\varepsilon }\) which are moderate over hypersums, i.e. to ask

For example, if  , then \(\left( k_{\varepsilon }^{n}\right) _{n,\varepsilon }\) is moderate over hypersums (see also Example 8 below); but also the aforementioned \(a_{n\varepsilon }=n\) for all \(n\in \mathbb {N}\) and \(\varepsilon \in I=(0,1]_{\mathbb {R}}\) is clearly of the same type if \(\mathbb {R}_{\sigma }\subseteq \mathbb {R}_{\rho }\).
, then \(\left( k_{\varepsilon }^{n}\right) _{n,\varepsilon }\) is moderate over hypersums (see also Example 8 below); but also the aforementioned \(a_{n\varepsilon }=n\) for all \(n\in \mathbb {N}\) and \(\varepsilon \in I=(0,1]_{\mathbb {R}}\) is clearly of the same type if \(\mathbb {R}_{\sigma }\subseteq \mathbb {R}_{\rho }\).
However, if \(a_{n}=[a_{n\varepsilon }]=[\bar{a}_{n\varepsilon }]\) for all \(n\in \mathbb {N}\) are two sequences which are moderate over hypersums, does the equality \(\left[ \sum _{n=0}^{\mathrm{ni}{(N)}_{\varepsilon }}a_{n\varepsilon }\right] =\left[ \sum _{n=0}^{\mathrm{ni}{(N)}_{\varepsilon }}\bar{a}_{n\varepsilon }\right] \) hold? The answer is negative: let \(a_{n\varepsilon }{:=}0\) if \(\varepsilon <\frac{1}{n+1}\) and \(a_{n\varepsilon }{:=}1\) otherwise, then \([a_{n\varepsilon }]=0\) are representatives of zero, but the corresponding series is not zero:

Note that both examples (2.2) and (2.8) show that in dealing with hypersums, also the values \(a_{n\varepsilon }\) for “\(\varepsilon \) large” may play a role. We can then proceed like for (2.7) by saying that \((a_{n\varepsilon })_{n,\varepsilon }\sim _{\sigma \rho }(\bar{a}_{n\varepsilon })_{n,\varepsilon }\) if

The idea of this second solution is hence to consider hyperseries only for representatives which are moderate over hypersums modulo the equivalence relation (2.9).
In the following definition, we will consider both solutions:
Definition 1
The quotient set  of the set \(\left( \mathbb {R}^{\mathbb {N}\times I}\right) _{\sigma \rho }\) of nets which are \(\sigma \), \(\rho \)-moderate over hypersums
of the set \(\left( \mathbb {R}^{\mathbb {N}\times I}\right) _{\sigma \rho }\) of nets which are \(\sigma \), \(\rho \)-moderate over hypersums

by \(\sigma \), \(\rho \)-negligible nets

is called the space of sequences for hyperseries. Nets of \(\mathbb {R}^{\mathbb {N}\times I}\) are denoted as \((a_{n\varepsilon })_{n,\varepsilon }\) or simply as \((a_{n\varepsilon })\); equivalence classes of  are denoted as
are denoted as  .
.
The ring of Robinson-Colombeau defined by the index set \(\mathbb {N}\times I\) ordered by
is denoted as  . We recall that
. We recall that  is the quotient space of moderate nets \((a_{n\varepsilon })_{n,\varepsilon }\) (i.e. (2.3) holds) modulo negligible nets (i.e. (2.4) holds) with respect to the directed order relation (2.10).
is the quotient space of moderate nets \((a_{n\varepsilon })_{n,\varepsilon }\) (i.e. (2.3) holds) modulo negligible nets (i.e. (2.4) holds) with respect to the directed order relation (2.10).
The letter ’u’ in  recalls that in this case we are considering uniformly moderate (and uniformly negligible) sequences. The letter ’s’ in
recalls that in this case we are considering uniformly moderate (and uniformly negligible) sequences. The letter ’s’ in  recalls that this is the space of sequences for hyperseries. We recall that
recalls that this is the space of sequences for hyperseries. We recall that  is a ring with respect to pointwise multiplication \((a_{n})_{n}\cdot (b_{n})_{n}=\left[ \left( a_{n\varepsilon }\cdot b_{n\varepsilon }\right) _{n\varepsilon }\right] \). When we want to distinguish equivalence classes in these two quotient sets, we use the notations
is a ring with respect to pointwise multiplication \((a_{n})_{n}\cdot (b_{n})_{n}=\left[ \left( a_{n\varepsilon }\cdot b_{n\varepsilon }\right) _{n\varepsilon }\right] \). When we want to distinguish equivalence classes in these two quotient sets, we use the notations

Note explicitly that, on the contrary with respect to  , the ring
, the ring  depends on only one gauge \(\rho \).
depends on only one gauge \(\rho \).
We already observed the importance to consider suitable relations between the two gauges \(\sigma \) and \(\rho \):
Definition 2
Let \(\sigma \), \(\rho \) be two gauges, then we define
(Note that if \(\sigma \ge \rho ^{*}\), then \(Q_{\sigma ,\rho }>0\) since \(\sigma _{\varepsilon }\rightarrow 0\)).
It is easy to prove that \((-)\le (-)^{*}\) is a reflexive, transitive and antisymmetric relation, in the sense that \(\sigma \le \rho ^{*}\) and \(\rho \le \sigma ^{*}\) imply \(\sigma _{\varepsilon }=\rho _{\varepsilon }\) for \(\varepsilon \) small, whereas \((-)\ge (-)^{*}\) is only a partial order. Clearly, \(\sigma \ge \rho ^{*}\) is equivalent to the inclusion of \(\sigma \)-moderate nets \(\mathbb {R}_{\sigma }\subseteq \mathbb {R}_{\rho }\), whereas \(\sigma \le \rho ^{*}\) is equivalent to \(\mathbb {R}_{\sigma }\supseteq \mathbb {R}_{\rho }\).
It is well-known that there is no natural product between two ordinary series in \(\mathbb {R}\) and involving summations with only one index set in \(\mathbb {N}\) (see e.g. [4] and Sect. 4 below). This is the main motivation to consider only a structure of  -module on
-module on  and, later, the natural Cauchy product between hyperseries:
and, later, the natural Cauchy product between hyperseries:
Theorem 3
 is a quotient
is a quotient  -module.
-module.
Proof
The closure of the set of \(\sigma \), \(\rho \)-moderate nets over hypersums, i.e. with respect to pointwise sum \((a_{n\varepsilon }+b_{n\varepsilon })\) and product \((r_{\varepsilon })\cdot (a_{n,\varepsilon })=(r_{\varepsilon }\cdot a_{n,\varepsilon })\) by \((r_{\varepsilon })\in \mathbb {R}_{\rho }\) follows from similar properties of the ring \(\mathbb {R}_{\rho }\). Similarly to the case of  , we can finally prove that the equivalence relation (2.9) is a congruence with respect to these operations. \(\square \)
, we can finally prove that the equivalence relation (2.9) is a congruence with respect to these operations. \(\square \)
We now prove that if  , then hyperfinite sums are well-defined:
, then hyperfinite sums are well-defined:
Theorem 4
Let  and let \(\sigma \), \(\rho \) be two arbitrary gauges, then the map
and let \(\sigma \), \(\rho \) be two arbitrary gauges, then the map

is well-defined.
Proof
\(\rho \)-moderateness directly follows from  ; in fact:
; in fact:
Now, assume that \((a_{n})_{n}=[\bar{a}_{n\varepsilon }]\) is another representative. For \(q\in \mathbb {N}\), condition (2.9) yields
for \(\varepsilon \) small. \(\square \)
We can finally define hyperfinite sums and hyperseries.
Definition 5
Let  and let \(\sigma \) and \(\rho \) be two arbitrary gauges then the term
and let \(\sigma \) and \(\rho \) be two arbitrary gauges then the term

is called \(\sigma \), \(\rho \)-hypersum of \((a_{n})_{n}\) (hypersum for brevity).
Moreover, we say that s is the \(\rho \)-sum of hyperseries with terms \((a_{n})_{n\in \mathbb {N}}\) as  if s is the hyperlimit of the hypersequence
if s is the hyperlimit of the hypersequence  . In this case, we write
. In this case, we write

In case the use of the gauge \(\rho \) is clear from the context, we simply say that s is the sum of the hyperseries with terms \((a_{n})_{n\in \mathbb {N}}\) as  .
.
As usual, we also say that the hyperseries  is convergent if
is convergent if

Whereas, we say that a hyperseries  does not converge if
does not converge if  does not exist in
does not exist in  . More specifically, if
. More specifically, if  (\(-\infty \)), we say that
(\(-\infty \)), we say that  diverges to \(+\infty \) (\(-\infty \)).
diverges to \(+\infty \) (\(-\infty \)).
For the sake of brevity, when dealing with hyperseries or with hypersums, we always implicitly assume that \(\sigma \), \(\rho \) are two gauges and that  .
.
Remark 6
-
(i)
Note that we are using an abuse of notations, since the term \(\sum _{n=N}^{M}a_{n}\) actually depends on the two considered gauges \(\rho \), \(\sigma \).
-
(ii)
Explicitly,
 means
means  (2.13)
(2.13) -
(iii)
Also note that if N, \(M\in \mathbb {N}\), then
 is the usual finite sum. This is related to our motivating discussion about the definition of hyperfinite series at the beginning of Sect. 2.
is the usual finite sum. This is related to our motivating discussion about the definition of hyperfinite series at the beginning of Sect. 2.
2.2 Relations between  and
and 
A first consequence of the condition \(\sigma \ge \rho ^{*}\) is that if the net \((a_{n\varepsilon })\) is uniformly moderate, then it is also moderate over hypersums. Similarly, we can argue for the equality, so that we have a natural map  :
:
Lemma 7
We have the following properties:
-
(i)
If
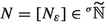 , with \(N_{\varepsilon }\in \mathbb {N}\), and
, with \(N_{\varepsilon }\in \mathbb {N}\), and 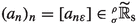 , then
, then  is well defined. That is, any sequence
is well defined. That is, any sequence  can be extended from \(\mathbb {N}\) to the entire set
can be extended from \(\mathbb {N}\) to the entire set  of hyperfinite numbers.
of hyperfinite numbers.Moreover, if we assume that \(\sigma \ge \rho ^{*}\), then we have:
-
(ii)
Both
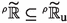 and
and  via the embedding \([x_{\varepsilon }]\mapsto [(x_{\varepsilon })_{n,\varepsilon }]\).
via the embedding \([x_{\varepsilon }]\mapsto [(x_{\varepsilon })_{n,\varepsilon }]\). -
(iii)
The mapping

is a well-defined
 -linear map.
-linear map. -
(iv)
Let us define a hypersum operator

for all M,
 . Then
. Then  . Therefore, the character (convergent or divergent) of the corresponding hyperseries is identical in the two spaces
. Therefore, the character (convergent or divergent) of the corresponding hyperseries is identical in the two spaces  and
and  .
.
Proof
-
(i)
In fact, if \((N_{\varepsilon })\in \mathbb {N}_{\sigma }\), then from
 we get the existence of \(Q_{i}\in \mathbb {N}\) such that $$\begin{aligned} \left| a_{N_{\varepsilon },\varepsilon }\right| =\left| \sum _{n=0}^{N_{\varepsilon }}a_{n\varepsilon }-\sum _{n=0}^{N_{\varepsilon }-1}a_{n\varepsilon }\right| \le \rho _{\varepsilon }^{-Q_{1}}+\rho _{\varepsilon }^{-Q_{2}}. \end{aligned}$$
we get the existence of \(Q_{i}\in \mathbb {N}\) such that $$\begin{aligned} \left| a_{N_{\varepsilon },\varepsilon }\right| =\left| \sum _{n=0}^{N_{\varepsilon }}a_{n\varepsilon }-\sum _{n=0}^{N_{\varepsilon }-1}a_{n\varepsilon }\right| \le \rho _{\varepsilon }^{-Q_{1}}+\rho _{\varepsilon }^{-Q_{2}}. \end{aligned}$$Finally, if
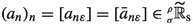 , then directly from (2.9) with \(M=N\) we get \([(a_{\mathrm{ni}{(N)}_{\varepsilon },\varepsilon })_{n,\varepsilon }]=[(\bar{a}_{\mathrm{ni}{(N)}_{\varepsilon },\varepsilon })_{n,\varepsilon }]\) (note that it is to have this result that we defined (2.9) using \(\sum _{\mathrm{ni}{(N)}_{\varepsilon }}^{\mathrm{ni}{(M)}_{\varepsilon }}\) instead of \(\sum _{n=0}^{\mathrm{ni}{(N)}_{\varepsilon }}\) like in (2.7)). Therefore,
, then directly from (2.9) with \(M=N\) we get \([(a_{\mathrm{ni}{(N)}_{\varepsilon },\varepsilon })_{n,\varepsilon }]=[(\bar{a}_{\mathrm{ni}{(N)}_{\varepsilon },\varepsilon })_{n,\varepsilon }]\) (note that it is to have this result that we defined (2.9) using \(\sum _{\mathrm{ni}{(N)}_{\varepsilon }}^{\mathrm{ni}{(M)}_{\varepsilon }}\) instead of \(\sum _{n=0}^{\mathrm{ni}{(N)}_{\varepsilon }}\) like in (2.7)). Therefore, 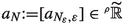 is well-defined. In particular, this applies with \(N=n\in \mathbb {N}\), so that any equivalence class
is well-defined. In particular, this applies with \(N=n\in \mathbb {N}\), so that any equivalence class 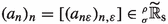 also defines an ordinary sequence \((a_{n})_{n\in \mathbb {N}}=\left( \left[ a_{n\varepsilon }\right] \right) _{n\in \mathbb {N}}\) of
also defines an ordinary sequence \((a_{n})_{n\in \mathbb {N}}=\left( \left[ a_{n\varepsilon }\right] \right) _{n\in \mathbb {N}}\) of  . On the other hand, let us explicitly note that if \((a_{n})_{n\in \mathbb {N}}=(\bar{a}_{n})_{n\in \mathbb {N}}\), i.e. if \(a_{n}=\bar{a}_{n}\) for all \(n\in \mathbb {N}\), then not necessarily (2.9) holds, i.e. we can have \((a_{n})_{n}\ne (\bar{a}_{n})_{n}\) as elements of the quotient module
. On the other hand, let us explicitly note that if \((a_{n})_{n\in \mathbb {N}}=(\bar{a}_{n})_{n\in \mathbb {N}}\), i.e. if \(a_{n}=\bar{a}_{n}\) for all \(n\in \mathbb {N}\), then not necessarily (2.9) holds, i.e. we can have \((a_{n})_{n}\ne (\bar{a}_{n})_{n}\) as elements of the quotient module  .
. -
Claim (ii)
is left to the reader.
-
(iii)
Assume that inequality in (2.3) holds for \(\varepsilon \le \varepsilon _{0}\), i.e.
$$\begin{aligned} \forall \varepsilon \le \varepsilon _{0}\,\forall n\in \mathbb {N}:\ \left| a_{n\varepsilon }\right| \le \rho _{\varepsilon }^{-Q}. \end{aligned}$$(2.14)Without loss of generality, we can also assume that \(\mathrm{ni}{(N)}_{\varepsilon }+1\le \sigma _{\varepsilon }^{-R}\) and \(\sigma _{\varepsilon }\ge \rho _{\varepsilon }^{-Q_{\sigma ,\rho }}\). Then, for each \(\varepsilon \le \varepsilon _{0}\), using (2.14) we have \(\left| \sum _{n=0}^{\mathrm{ni}{(N)}_{\varepsilon }}a_{n\varepsilon }\right| \le \left( \mathrm{ni}{(N)}_{\varepsilon }+1\right) \cdot \rho _{\varepsilon }^{-Q}\le \sigma _{\varepsilon }^{-R}\cdot \rho _{\varepsilon }^{-Q}\le \rho _{\varepsilon }^{-R\cdot Q_{\sigma ,\rho }-Q}\). Moreover, if \(\left[ a_{n\varepsilon }\right] _{\text {u}}=0\) then, for all \(q\in \mathbb {N}\)
$$\begin{aligned} \left| \sum _{n=0}^{\mathrm{ni}{(N)}_{\varepsilon }}a_{n\varepsilon }\right| \le \left( \mathrm{ni}{(N)}_{\varepsilon }+1\right) \cdot \rho _{\varepsilon }^{q} \end{aligned}$$for \(\varepsilon \) small. Since \(\mathrm{ni}{(N)}_{\varepsilon }\) is \(\sigma \)-moderate and \(\sigma \ge \rho ^{*}\), this proves that the linear map \(\lambda \) is well-defined.
-
(iv)
This follows directly from Definition 5. \(\square \)
It remains an open problem the study of injectivity of the map \(\lambda \).
We could say that \(\sigma \ge \rho ^{*}\) and  are sufficient conditions to get
are sufficient conditions to get  and hence to start talking about hyperfinite sums \(\sum _{n=N}^{M}a_{n}\) and hyperseries
and hence to start talking about hyperfinite sums \(\sum _{n=N}^{M}a_{n}\) and hyperseries  . On the other hand, if \(\sigma \ge \rho ^{*}\) is false, we can still consider the space
. On the other hand, if \(\sigma \ge \rho ^{*}\) is false, we can still consider the space  and hence talk about hyperseries, but the corresponding space
and hence talk about hyperseries, but the corresponding space  lacks elements such as \((1)_{n}\) because of the subsequent Lemma 10. As we will see in the following example 8 (3) and (6), the space
lacks elements such as \((1)_{n}\) because of the subsequent Lemma 10. As we will see in the following example 8 (3) and (6), the space  still contains sequences corresponding to interesting converging hyperseries.
still contains sequences corresponding to interesting converging hyperseries.
The following examples of convergent hyperseries justify our definition of hyperseries by recovering classical examples such such geometric and exponential hyperseries. We recall that this is not possible using classical series in a non-Archimedean setting.
Example 8
-
(1)
Let
 , where \(N_{\varepsilon }\in \mathbb {N}\) for all \(\varepsilon \), then
, where \(N_{\varepsilon }\in \mathbb {N}\) for all \(\varepsilon \), then  . We recall that \(a_{N}=\left[ a_{N_{\varepsilon },\varepsilon }\right] \) is the extension of
. We recall that \(a_{N}=\left[ a_{N_{\varepsilon },\varepsilon }\right] \) is the extension of  to
to  (see (i) of Lemma 7).
(see (i) of Lemma 7). -
(2)
For all
 , \(0<k<1\), we have (note that \(\sigma =\rho \))
, \(0<k<1\), we have (note that \(\sigma =\rho \))  (2.15)
(2.15)We first note that \(k^{n}\le 1\), so that
 . Now,
. Now, 
But \(k^{N+1}<\hbox {d}^{q}\) if and only if \((N+1)\log k<q\log \hbox {d}\). Since \(0<k<1\), we have \(\log k<0\) and we obtain \(N>q\frac{\log \hbox {d}}{\log k}-1\). It suffices to take \(M_{\varepsilon }{:=}\text {int}\left( q\frac{\log \rho _{\varepsilon }}{\log k_{\varepsilon }}\right) \) in the definition of hyperseries.
-
(3)
More generally, if
 , \(0<k<1\), we can evaluate
, \(0<k<1\), we can evaluate 
This shows that
 for all gauges \(\sigma \). If we assume \(\sigma \le \rho ^{*}\) then \(M_{\varepsilon }{:=}\text {int}\left( q\frac{\log \rho _{\varepsilon }}{\log k_{\varepsilon }}\right) \in \mathbb {N}_{\sigma }\) and hence, proceeding as above, we can prove that
for all gauges \(\sigma \). If we assume \(\sigma \le \rho ^{*}\) then \(M_{\varepsilon }{:=}\text {int}\left( q\frac{\log \rho _{\varepsilon }}{\log k_{\varepsilon }}\right) \in \mathbb {N}_{\sigma }\) and hence, proceeding as above, we can prove that  .
. -
(4)
Let
 be such that \(k>_{\mathrm{s}}1\) (see [13] for the relations \(>_{\mathrm{s}}\) and \(=_{\mathrm{s}}\) and, more generally, for the language of subpoints), then the hyperseries
be such that \(k>_{\mathrm{s}}1\) (see [13] for the relations \(>_{\mathrm{s}}\) and \(=_{\mathrm{s}}\) and, more generally, for the language of subpoints), then the hyperseries  is not convergent. In fact, by contradiction, in the opposite case we would have \(\sum _{n=0}^{N}k^{n}\in (l-1,l+1)\) for some
is not convergent. In fact, by contradiction, in the opposite case we would have \(\sum _{n=0}^{N}k^{n}\in (l-1,l+1)\) for some  for all N sufficiently large, but this is impossible because for all fixed
for all N sufficiently large, but this is impossible because for all fixed  and for N sufficiently large,
and for N sufficiently large,  because
because  .
. -
(5)
For all
 finite, we have
finite, we have  . We have \(|x|<M\in \mathbb {R}_{>0}\) because x is finite, and hence \(\left| x_{\varepsilon }\right| \le M\) for all \(\varepsilon \le \varepsilon _{0}\). Thereby \(\frac{x_{\varepsilon }^{n}}{n!}\le \frac{\left| x_{\varepsilon }\right| ^{n}}{n!}\le e^{M}\) for all \(n\in \mathbb {N}\) and thus
. We have \(|x|<M\in \mathbb {R}_{>0}\) because x is finite, and hence \(\left| x_{\varepsilon }\right| \le M\) for all \(\varepsilon \le \varepsilon _{0}\). Thereby \(\frac{x_{\varepsilon }^{n}}{n!}\le \frac{\left| x_{\varepsilon }\right| ^{n}}{n!}\le e^{M}\) for all \(n\in \mathbb {N}\) and thus  . For all
. For all  , \(N_{\varepsilon }\in \mathbb {N}\), and all \(\varepsilon \), we have $$\begin{aligned} \sum _{n=0}^{N_{\varepsilon }}\frac{x_{\varepsilon }^{n}}{n!}=e^{x_{\varepsilon }}-\sum _{n=N_{\varepsilon }+1}^{+\infty }\frac{x_{\varepsilon }^{n}}{n!}. \end{aligned}$$(2.16)
, \(N_{\varepsilon }\in \mathbb {N}\), and all \(\varepsilon \), we have $$\begin{aligned} \sum _{n=0}^{N_{\varepsilon }}\frac{x_{\varepsilon }^{n}}{n!}=e^{x_{\varepsilon }}-\sum _{n=N_{\varepsilon }+1}^{+\infty }\frac{x_{\varepsilon }^{n}}{n!}. \end{aligned}$$(2.16)Now, take
 such that \(\frac{M}{N+1}<\frac{1}{2}\), so that we can assume \(N_{\varepsilon }+1>2M\) for all \(\varepsilon \). We have \(\left| \sum _{n=N_{\varepsilon }+1}^{+\infty }\frac{x_{\varepsilon }^{n}}{n!}\right| \le \sum _{n>N_{\varepsilon }}\frac{M^{n}}{n!}\), and for all \(n\ge N_{\varepsilon }\) we have (by induction) $$\begin{aligned} \frac{M^{n+1}}{(n+1)!}<\frac{1}{2^{n+1}}. \end{aligned}$$
such that \(\frac{M}{N+1}<\frac{1}{2}\), so that we can assume \(N_{\varepsilon }+1>2M\) for all \(\varepsilon \). We have \(\left| \sum _{n=N_{\varepsilon }+1}^{+\infty }\frac{x_{\varepsilon }^{n}}{n!}\right| \le \sum _{n>N_{\varepsilon }}\frac{M^{n}}{n!}\), and for all \(n\ge N_{\varepsilon }\) we have (by induction) $$\begin{aligned} \frac{M^{n+1}}{(n+1)!}<\frac{1}{2^{n+1}}. \end{aligned}$$Therefore \(\left| \sum _{n=N_{\varepsilon }+1}^{+\infty }\frac{x_{\varepsilon }^{n}}{n!}\right| \le \sum _{n>N_{\varepsilon }}\frac{1}{2^{n}}\) and hence
 by (2.15). This and (2.16) yields the conclusion.
by (2.15). This and (2.16) yields the conclusion. -
(6)
In the same assumptions of the previous example, we have \(\left[ \left| \sum _{n=0}^{N_{\varepsilon }}\frac{x_{\varepsilon }^{n}}{n!}\right| \right] \le e^{M}\) and hence
 for all gauges \(\sigma \). If \(\sigma \le \rho ^{*}\), proceeding as above, we can prove that
for all gauges \(\sigma \). If \(\sigma \le \rho ^{*}\), proceeding as above, we can prove that  .
.
Finally, the following lemma shows that a sharply bounded sequence of  always defines a sequence for hyperseries, i.e. an element of
always defines a sequence for hyperseries, i.e. an element of  .
.
Lemma 9
Let \((a_{n})_{n\in \mathbb {N}}\) be a sequence of  . If \((a_{n})_{n\in \mathbb {N}}\) is sharply bounded:
. If \((a_{n})_{n\in \mathbb {N}}\) is sharply bounded:

then there exists a sequence \((a_{n\varepsilon })_{n\in \mathbb {N}}\) of \(\mathbb {R}_{\rho }\) such that
-
(i)
 for all \(n\in \mathbb {N}\);
for all \(n\in \mathbb {N}\); -
(ii)
 ;
; -
(iii)
If
 .
.
Proof
Let \(M=[M_{\varepsilon }]\) be any representative of the bound satisfying (2.17), so that \(M_{\varepsilon }\le \rho _{\varepsilon }^{-Q}\) for \(\varepsilon \le \varepsilon _{0}\) and for some \(Q\in \mathbb {N}\). From (2.17), for each \(n\in \mathbb {N}\) we get the existence of a representative \(a_{n}=[\bar{a}_{n\varepsilon }]\) such that \(|\bar{a}_{n\varepsilon }|\le M_{\varepsilon }\) for \(\varepsilon \le \varepsilon _{0n}\le \varepsilon _{0}\). It suffices to define \(a_{n\varepsilon }{:=}\bar{a}_{n\varepsilon }\) if \(\varepsilon \le \varepsilon _{0n}\) and \(a_{n\varepsilon }{:=}M_{\varepsilon }\) otherwise to have \(\forall \varepsilon \le \varepsilon _{0}\,\forall n\in \mathbb {N}:\ \left| a_{n\varepsilon }\right| \le \rho _{\varepsilon }^{-Q}\), so that  . If \(\sigma \ge \rho ^{*}\), we can then apply Lemma 7. \(\square \)
. If \(\sigma \ge \rho ^{*}\), we can then apply Lemma 7. \(\square \)
However, let us note that, generally speaking, changing representatives of \(a_{n}\) as in the previous proof, we also get a different value of the corresponding hyperseries, as proved by example (2.8).
2.3 Divergent hyperseries
By analyzing when the constant net (1) is moderate over hypersums, we discover the relation (2.5) between the gauges \(\sigma \) and \(\rho \):
Lemma 10
The constant net \((1)\in (\mathbb {R}^{\mathbb {N}\times I})_{\sigma \rho }\), i.e. it is \(\sigma \), \(\rho \)-moderate over hypersums, if and only if \(\sigma \ge \rho ^{*}\).
Proof
If \((1)\in (\mathbb {R}^{\mathbb {N}\times I})_{\sigma \rho }\), we set \(N_{\varepsilon }{:=}\text {int}(\sigma _{\varepsilon }^{-1})+1\), so that we get \(\sigma _{\varepsilon }^{-1}\le \sum _{n=0}^{N_{\varepsilon }}1=N_{\varepsilon }\le \rho _{\varepsilon }^{-Q_{\sigma ,\rho }}\) for some \(Q_{\sigma ,\rho }\in \mathbb {N}\), i.e. \(\sigma \ge \rho ^{*}\). Vice versa, if \(\sigma _{\varepsilon }\ge \rho _{\varepsilon }^{Q_{\sigma ,\rho }}\) for all \(\varepsilon \le \varepsilon _{0}\), then for those \(\varepsilon \), we have \(\left| \sum _{n=0}^{\mathrm{ni}{(N)}_{\varepsilon }}1\right| =\mathrm{ni}{(N)}_{\varepsilon }\le \sigma _{\varepsilon }^{-R}\le \rho _{\varepsilon }^{-R\cdot Q_{\sigma ,\rho }}\) for some \(R\in \mathbb {N}\), because  . \(\square \)
. \(\square \)
One could argue that we are mainly interested in converging hyperseries and hence it is not worth considering the constant net (1). On the other hand, we would like to argue in the following way: the hypersums  can be considered, but they do not converge because \(1\not \rightarrow 0\). As we will see in Lemma 15, this argumentation is possible only if \(\sigma \ge \rho ^{*}\) because of the previous Lemma 10.
can be considered, but they do not converge because \(1\not \rightarrow 0\). As we will see in Lemma 15, this argumentation is possible only if \(\sigma \ge \rho ^{*}\) because of the previous Lemma 10.
Let \(\sigma \ge \rho ^{*}\) and  be an infinite number. If
be an infinite number. If  , we can also think at \(\sum _{n=0}^{\omega }a_{n}\) as another way to compute an infinite summation of the numbers \(a_{n}\). In other words, the following examples can be considered as related to calculation of divergent series. They strongly motivate and clarify our definition of hyperfinite sum.
, we can also think at \(\sum _{n=0}^{\omega }a_{n}\) as another way to compute an infinite summation of the numbers \(a_{n}\). In other words, the following examples can be considered as related to calculation of divergent series. They strongly motivate and clarify our definition of hyperfinite sum.
Example 11
Assuming \(\sigma \ge \rho ^{*}\) and working with the module  , we have:
, we have:
-
(5)
 .
. -
(6)
\(\sum _{n=1}^{\omega }n=\left[ \sum _{n=1}^{\mathrm{ni}{(\omega )}_{\varepsilon }}n_{\varepsilon }\right] =\left[ \frac{\mathrm{ni}{(\omega )}_{\varepsilon }(\mathrm{ni}{(\omega )}_{\varepsilon }+1)}{2}\right] =\frac{\omega (\omega +1)}{2}\).
-
(7)
\(\sum _{n=1}^{\omega }(2n-1)=2\sum _{n=1}^{\omega }n-\sum _{n=1}^{\omega }1=\omega ^{2}\) because we know from Theorem 3 that
 is an
is an  -module.
-module. -
(8)
\(\sum _{n=1}^{\omega }\left( a+(n-1)d\right) =\omega a+\frac{\omega ^{2}d}{2}-\frac{\omega d}{2}\).
-
(9)
Using \(\varepsilon \)-wise calculations, we also have \(\sum _{n=0}^{\omega }(-1)^{n}=\frac{1}{2}(-1)^{\omega +1}+\frac{1}{2}\). Note that the final result is a finite generalized number of
 , but it does not converge for \(\omega \rightarrow +\infty \),
, but it does not converge for \(\omega \rightarrow +\infty \),  .
. -
10)
The net \((2^{n})_{n,\varepsilon }\) is not \(\rho \)-moderate over hypersums, in fact if \(\omega =\left[ \text {int}(\rho _{\varepsilon }^{-1})\right] \), then \(\sum _{n=0}^{\omega _{\varepsilon }}2^{n-1}=2^{\omega _{\varepsilon }}-1\), which is not \(\rho \)-moderate. Another possibility to consider the function \(2^{\omega }\) is to take another gauge \(\mu \le \rho \) and the subring of
 defined by
defined by 
where only here we have set
 . If we have $$\begin{aligned} \forall N\in \mathbb {N}\,\exists M\in \mathbb {N}:\ \hbox {d}^{-N}\le -M\log \hbox {d}, \end{aligned}$$(2.18)
. If we have $$\begin{aligned} \forall N\in \mathbb {N}\,\exists M\in \mathbb {N}:\ \hbox {d}^{-N}\le -M\log \hbox {d}, \end{aligned}$$(2.18)then
 is well defined. For example, if \(\mu _{\varepsilon }{:=}\exp \left( -\rho _{\varepsilon }^{1/\varepsilon }\right) \), then \(\mu \le \rho \) and (2.18) holds for \(M=1\). Note that the natural ring morphism
is well defined. For example, if \(\mu _{\varepsilon }{:=}\exp \left( -\rho _{\varepsilon }^{1/\varepsilon }\right) \), then \(\mu \le \rho \) and (2.18) holds for \(M=1\). Note that the natural ring morphism  is surjective but generally not injective. Now, if
is surjective but generally not injective. Now, if  , then
, then  .
. -
(11)
Once again, proceeding by \(\varepsilon \)-wise calculations, we also have the binomial formula: For all a,
 and
and 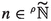 , if
, if 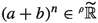 , then $$\begin{aligned} \left( a+b\right) ^{n}=\sum _{k=0}^{n}\left( \begin{array}{c} n\\ k \end{array}\right) a^{k}b^{n-k} \end{aligned}$$
, then $$\begin{aligned} \left( a+b\right) ^{n}=\sum _{k=0}^{n}\left( \begin{array}{c} n\\ k \end{array}\right) a^{k}b^{n-k} \end{aligned}$$where \(n!{:=}\left[ \text {ni }(n)_{\varepsilon }!\right] \) and \(\left( \begin{array}{c} n\\ k \end{array}\right) {:=}\frac{n!}{k!\left( n-k\right) !}\).
2.4 \(\varepsilon \)-wise convergence and hyperseries
The following result allows us to obtain hyperseries by considering \(\varepsilon \)-wise convergence of its summands. Its proof is clearly very similar to that of [13, Theorem 28], but with a special attention to the condition  that we need beforehand to talk about hyperseries.
that we need beforehand to talk about hyperseries.
Theorem 12
Let  and \(a_{n}=[a_{n\varepsilon }]\) for all \(n\in \mathbb {N}\). Let \(q_{\varepsilon }\), \(M_{\varepsilon }\in \mathbb {N}_{>0}\) be such that \((q_{\varepsilon })\rightarrow +\infty \) as \(\varepsilon \rightarrow 0^{+}\), and
and \(a_{n}=[a_{n\varepsilon }]\) for all \(n\in \mathbb {N}\). Let \(q_{\varepsilon }\), \(M_{\varepsilon }\in \mathbb {N}_{>0}\) be such that \((q_{\varepsilon })\rightarrow +\infty \) as \(\varepsilon \rightarrow 0^{+}\), and
(note that this implies that the standard series \(\sum _{n=0}^{+\infty }a_{n\varepsilon }\) converges to \(s_{\varepsilon }\)). Finally, let \(\mu \) be another gauge. If  , then setting \(\sigma _{\varepsilon }{:=}\min (\mu _{\varepsilon },M_{\varepsilon }^{-1})\), we have:
, then setting \(\sigma _{\varepsilon }{:=}\min (\mu _{\varepsilon },M_{\varepsilon }^{-1})\), we have:
-
(i)
\(\sigma \le \mu \) is a gauge (not necessarily a monotonic one);
-
(ii)
 ;
; -
(iii)
 ;
; -
(iv)
 ;
; -
(v)
 .
.
Proof
The net \(\sigma _{\varepsilon }=\min (\mu _{\varepsilon },M_{\varepsilon }^{-1})\rightarrow 0^{+}\) as \(\varepsilon \rightarrow 0^{+}\) because \(\mu _{\varepsilon }\rightarrow 0^{+}\), i.e. it is a gauge (note that not necessarily \(\sigma \) is non-decreasing, e.g. if \(\lim _{\varepsilon \rightarrow \frac{1}{k}}M_{\varepsilon }=+\infty \) for all \(k\in \mathbb {N}_{>0}\) and \(M_{\varepsilon }\ge \mu _{\varepsilon }^{-1}\)). We have  because our definition of \(\sigma \) yields \(M_{\varepsilon }\le \sigma _{\varepsilon }^{-1}\). Moreover, since \((q_{\varepsilon })\rightarrow +\infty \), for all \(\varepsilon \) condition (2.19) yields \(s_{\varepsilon }-1\le s_{\varepsilon }-\rho _{\varepsilon }^{q_{\varepsilon }}<\sum _{n=0}^{N}a_{n\varepsilon }<s_{\varepsilon }+\rho _{\varepsilon }^{q_{\varepsilon }}\le s_{\varepsilon }+1\) for all \(N\ge M_{\varepsilon }\). For \(N=M\) this gives
because our definition of \(\sigma \) yields \(M_{\varepsilon }\le \sigma _{\varepsilon }^{-1}\). Moreover, since \((q_{\varepsilon })\rightarrow +\infty \), for all \(\varepsilon \) condition (2.19) yields \(s_{\varepsilon }-1\le s_{\varepsilon }-\rho _{\varepsilon }^{q_{\varepsilon }}<\sum _{n=0}^{N}a_{n\varepsilon }<s_{\varepsilon }+\rho _{\varepsilon }^{q_{\varepsilon }}\le s_{\varepsilon }+1\) for all \(N\ge M_{\varepsilon }\). For \(N=M\) this gives  , because we assumed that
, because we assumed that  . If
. If  , then \(\mathrm{ni}{(N)}_{\varepsilon }+M_{\varepsilon }\ge M_{\varepsilon }\) for all \(\varepsilon \), and hence \(s_{\varepsilon }-1<\sum _{n=0}^{M_{\varepsilon }-1}a_{n\varepsilon }+\sum _{n=M_{\varepsilon }}^{\mathrm{ni}{(N)}_{\varepsilon }+M_{\varepsilon }}a_{n\varepsilon }=s_{M\varepsilon }+\sum _{n=0}^{\mathrm{ni}{(N)}_{\varepsilon }}a_{n+M_{\varepsilon },\varepsilon }<s_{\varepsilon }+1\). This shows that
, then \(\mathrm{ni}{(N)}_{\varepsilon }+M_{\varepsilon }\ge M_{\varepsilon }\) for all \(\varepsilon \), and hence \(s_{\varepsilon }-1<\sum _{n=0}^{M_{\varepsilon }-1}a_{n\varepsilon }+\sum _{n=M_{\varepsilon }}^{\mathrm{ni}{(N)}_{\varepsilon }+M_{\varepsilon }}a_{n\varepsilon }=s_{M\varepsilon }+\sum _{n=0}^{\mathrm{ni}{(N)}_{\varepsilon }}a_{n+M_{\varepsilon },\varepsilon }<s_{\varepsilon }+1\). This shows that  , because \(s_{M}\),
, because \(s_{M}\),  , i.e.
, i.e.  . Similarly, if \(q\in \mathbb {N}\), then \(q<q_{\varepsilon }\) for \(\varepsilon \) sufficiently small and, proceeding as above, we can prove that \(|\sum _{n=0}^{N}a_{n+M}-s-s_{M}|<\hbox {d}^{q}\). \(\square \)
. Similarly, if \(q\in \mathbb {N}\), then \(q<q_{\varepsilon }\) for \(\varepsilon \) sufficiently small and, proceeding as above, we can prove that \(|\sum _{n=0}^{N}a_{n+M}-s-s_{M}|<\hbox {d}^{q}\). \(\square \)
Note that, if \((M_{\varepsilon })\) is not \(\rho \)-moderate and we set \(\sigma _{\varepsilon }{:=}\min \left( \rho _{\varepsilon },M_{\varepsilon }^{-1}\right) \in (0,1]\), then
and this shows that \(\sigma \ge \rho ^{*}\), i.e. the fundamental condition to have moderateness of hyperfinite sums in the ring  (see (2.6)), always necessarily does not hold. On the other hand, if \((M_{\varepsilon })\) is \(\rho \)-moderate, then \(\mathbb {R}_{\sigma }=\mathbb {R}_{\mu }\); in particular, we can simply take \(\sigma =\mu =\rho \).
(see (2.6)), always necessarily does not hold. On the other hand, if \((M_{\varepsilon })\) is \(\rho \)-moderate, then \(\mathbb {R}_{\sigma }=\mathbb {R}_{\mu }\); in particular, we can simply take \(\sigma =\mu =\rho \).
Assuming absolute convergence, we can obtain a stronger and clearer result:
Theorem 13
Let  and \(a_{n}=[a_{n\varepsilon }]\) for all \(n\in \mathbb {N}\). Assume that the standard series \(\sum _{n=0}^{+\infty }a_{n\varepsilon }\) converges absolutely to \(\bar{s}_{\varepsilon }\) and
and \(a_{n}=[a_{n\varepsilon }]\) for all \(n\in \mathbb {N}\). Assume that the standard series \(\sum _{n=0}^{+\infty }a_{n\varepsilon }\) converges absolutely to \(\bar{s}_{\varepsilon }\) and  . Finally, let \(\mu \) be another gauge and set \(s_{\varepsilon }{:=}\sum _{n=0}^{+\infty }a_{n\varepsilon }\), then there exists a gauge \(\sigma \le \mu \) such that:
. Finally, let \(\mu \) be another gauge and set \(s_{\varepsilon }{:=}\sum _{n=0}^{+\infty }a_{n\varepsilon }\), then there exists a gauge \(\sigma \le \mu \) such that:
-
(i)
 ;
; -
(ii)
 .
.
Proof
Set \(q_{\varepsilon }{:=}\left\lceil \frac{1}{\varepsilon }\right\rceil \), so that the absolute convergence of \(\sum _{n=0}^{+\infty }a_{n\varepsilon }\) yields
and we can thereby apply the previous Theorem 12 obtaining \(\bar{s}_{M}{:=}\left[ \sum _{n=0}^{M_{\varepsilon }-1}|a_{n\varepsilon }|\right] \),  . Therefore, for an arbitrary
. Therefore, for an arbitrary  , we have:
, we have:

and this shows that  . Now, proceeding as above we can prove that
. Now, proceeding as above we can prove that  . \(\square \)
. \(\square \)
2.5 Basic properties of hyperfinite sums and hyperseries
We now study some basic properties of hyperfinite sums (2.12).
Lemma 14
Let \(\sigma \), \(\rho \) be arbitrary gauges,  , and M,
, and M,  , then
, then
Proof
For simplicity, if \(N=[N_{\varepsilon }]\), \(M=[M_{\varepsilon }]\) with \(N_{\varepsilon },M_{\varepsilon }\in \mathbb {N}\) for all \(\varepsilon \), then  and
and
\(\square \)
Lemma 15
If  is convergent and
is convergent and  , then
, then

Therefore, from (2.21), we also have

In particular,  .
.
Proof
Let  . Directly from the definition of convergent hyperseries (2.13), we have
. Directly from the definition of convergent hyperseries (2.13), we have

In particular, if  , then also
, then also  , which is our conclusion. \(\square \)
, which is our conclusion. \(\square \)
Directly from Lemma 14, we also have:
Corollary 16
Let  be a convergent hyperseries. Then adding a hyperfinite number of terms have no effect on the convergence of the hyperseries, that is
be a convergent hyperseries. Then adding a hyperfinite number of terms have no effect on the convergence of the hyperseries, that is

Mimicking the classical theory, we can also say that the hyperseries  is Cesàro hypersummable if
is Cesàro hypersummable if  (this hyperlimit is clearly called Cesàro hypersum). For example, proceeding \(\varepsilon \)-wise, we have that the hyperseries
(this hyperlimit is clearly called Cesàro hypersum). For example, proceeding \(\varepsilon \)-wise, we have that the hyperseries  has Cesàro hypersum equal to \(\frac{1}{2}\). Trivially generalizing the usual proof, we can show that if
has Cesàro hypersum equal to \(\frac{1}{2}\). Trivially generalizing the usual proof, we can show that if  converges to s, then it is also Cesàro hypersummable with the same hypersum s.
converges to s, then it is also Cesàro hypersummable with the same hypersum s.
3 Hyperseries convergence tests
3.1 p-hyperseries
To deal with p-hyperseries, i.e. hyperseries of the form

we always assume that:
-
(i)
 is a finite generalized number such that \(p>0\) or \(p<0\); we recall that if p is an infinite number (at least on a subpoint), the operation \(n^{p}\) is in general not well-defined since it leads to a non \(\rho \)-moderate net (see also Example 11.10)).
is a finite generalized number such that \(p>0\) or \(p<0\); we recall that if p is an infinite number (at least on a subpoint), the operation \(n^{p}\) is in general not well-defined since it leads to a non \(\rho \)-moderate net (see also Example 11.10)). -
(ii)
The gauges \(\sigma \) and \(\rho \) are chosen so that
 . A sufficient condition for this is that \(\sigma \ge \rho ^{*}\), i.e. that \(\mathbb {R}_{\sigma }\subseteq \mathbb {R}_{\rho }\). In fact, since p is finite, we have \(\left( \sum _{n=1}^{N_{\varepsilon }}n^{-p_{\varepsilon }}\right) \le N_{\varepsilon }N_{\varepsilon }^{-p_{\varepsilon }}\in \mathbb {R}_{\sigma }\subseteq \mathbb {R}_{\rho }\) whenever \(N_{\varepsilon }\in \mathbb {N}\), \(\left( N_{\varepsilon }\right) \in \mathbb {N}_{\sigma }\).
. A sufficient condition for this is that \(\sigma \ge \rho ^{*}\), i.e. that \(\mathbb {R}_{\sigma }\subseteq \mathbb {R}_{\rho }\). In fact, since p is finite, we have \(\left( \sum _{n=1}^{N_{\varepsilon }}n^{-p_{\varepsilon }}\right) \le N_{\varepsilon }N_{\varepsilon }^{-p_{\varepsilon }}\in \mathbb {R}_{\sigma }\subseteq \mathbb {R}_{\rho }\) whenever \(N_{\varepsilon }\in \mathbb {N}\), \(\left( N_{\varepsilon }\right) \in \mathbb {N}_{\sigma }\).
Note explicitly that, from the assumption  , we hence have
, we hence have

even if  , and
, and  is a different quotient ring with respect to
is a different quotient ring with respect to  (e.g., in general we do not have
(e.g., in general we do not have  ). In other words, it is not correct to say that the left hand side of (3.1) is the sum for
). In other words, it is not correct to say that the left hand side of (3.1) is the sum for  of terms
of terms  , but instead it is a way to use \((N_{\varepsilon })\in \mathbb {N}_{\sigma }\) to compute a generalized number of
, but instead it is a way to use \((N_{\varepsilon })\in \mathbb {N}_{\sigma }\) to compute a generalized number of  .
.
If \(p<0\), the general term \(\frac{1}{n^{p}}\not \rightarrow 0\) because \(n^{-p}\le \hbox {d}^{q}\) only if \(n<\hbox {d}^{-q/p}\). Therefore, Lemma 15 yields that the p-series diverges. We can hence consider only the case \(p>0\). Let us note that Theorem 4, which is clearly based on our Definition 1 of  , allows us to consider partial hypersums of the form \(\sum _{n=1}^{N}\frac{1}{n^{p}}\) even if \(p<0\). In other words, we can correctly argue that the p-hyperseries does not converge if \(p<0\) not because the partial hypersums cannot be computed, but because the general term does not converge to zero. The situation would be completely different if we restrict our attention only to sequences \((a_{n})_{n}\) satisfying the (more natural) uniformly moderate condition (2.3). Similar remarks can be formulated for the calculus of divergent hyperseries in Example 8, 6)-10).
, allows us to consider partial hypersums of the form \(\sum _{n=1}^{N}\frac{1}{n^{p}}\) even if \(p<0\). In other words, we can correctly argue that the p-hyperseries does not converge if \(p<0\) not because the partial hypersums cannot be computed, but because the general term does not converge to zero. The situation would be completely different if we restrict our attention only to sequences \((a_{n})_{n}\) satisfying the (more natural) uniformly moderate condition (2.3). Similar remarks can be formulated for the calculus of divergent hyperseries in Example 8, 6)-10).
To prove the following results, we will follow some ideas of [10].
Theorem 17
Let  and let \(S_{N}(p)\) be the N-th partial sum of the p-hyperseries, where
and let \(S_{N}(p)\) be the N-th partial sum of the p-hyperseries, where  , then
, then
Proof
Let  , with \(N_{\varepsilon }\in \mathbb {N}_{\ge 1}\) for all \(\varepsilon \), and \(p=[p_{\varepsilon }]\), where \(p_{\varepsilon }>0\) for all \(\varepsilon \). Since
, with \(N_{\varepsilon }\in \mathbb {N}_{\ge 1}\) for all \(\varepsilon \), and \(p=[p_{\varepsilon }]\), where \(p_{\varepsilon }>0\) for all \(\varepsilon \). Since
But
and, since \(p_{\varepsilon }>0\), we also have
Summing (3.3) and (3.4) yields \(S_{2N}(p)>1-\frac{1}{2^{p}}+\frac{2}{2^{p}}S_{N}(p)\). Finally, from (3.3) and
we get \(S_{2N}(p)<1+\frac{1}{2^{p}}S_{N}(p)+\frac{1}{2^{p}}S_{N}(p)\). \(\square \)
Theorem 18
The p-hyperseries is divergent when \(0<p\le _{\mathrm{s}}1\). When \(p>1\), there exist some gauge \(\tau \le \rho \) such that  and the p-series is convergent with respect to the gauges \(\tau \), \(\rho \) (to the usual real value \(\zeta (p)\) if \(p\in \mathbb {R}\)), and in this case
and the p-series is convergent with respect to the gauges \(\tau \), \(\rho \) (to the usual real value \(\zeta (p)\) if \(p\in \mathbb {R}\)), and in this case

Proof
If \(0<p\le _{\mathrm{s}}1\), there exist \(J\subseteq _{0}I\) such that \(p|_{J}\le 1\).Assume that the \(p-\)hyperseries is convergent and set  . Taking \(N\rightarrow \infty \) in the first inequality in (3.2), we have
. Taking \(N\rightarrow \infty \) in the first inequality in (3.2), we have
Since for \(\varepsilon \in J\) sufficiently small we have \(0<p_{\varepsilon }<1\) for some \([p_{\varepsilon }]=p\), we obtain
This shows that the \(p-\)hyperseries is divergent when \(p\le _{\mathrm{s}}1\). Now let \(p>1\), so that we can assume \(p_{\varepsilon }>1\) for all \(\varepsilon \). From (3.2), we have
where \(S_{N_{\varepsilon }}(p_{\varepsilon })=\sum _{n=1}^{N_{\varepsilon }}\frac{1}{n^{p_{\varepsilon }}}\in \mathbb {R}\). Thereby
So \(S_{N_{\varepsilon }}(p)\) is bounded and increasing, and applying Theorem 12, we get the existence of a gauge \(\tau \) such that  and
and  converges to \(\sum _{n=1}^{+\infty }\frac{1}{n^{p}}=\zeta (p)\). \(\square \)
converges to \(\sum _{n=1}^{+\infty }\frac{1}{n^{p}}=\zeta (p)\). \(\square \)
Later, in Corollary 34 and using the integral test Thm. 33, we will prove the convergence of p-hyperseries for arbitrary gauges \(\sigma \), \(\rho \) (even if we will not get the estimates (3.5)).
3.2 Absolute convergence
Theorem 19
If  converges then also
converges then also  converges.
converges.
Proof
Cauchy criterion [13, Thm. 37], yields

The conclusion hence follows from the inequality
and from Cauchy criterion for hypersequences, i.e. [13, Thm. 37]. \(\square \)
3.3 Direct and limit comparison tests
In the direct comparison test, we need to assume a relation of the form \(a_{n}\le b_{n}\) for all \(n\in \mathbb {N}\) between general terms of two hyperseries. If \(a_{n}=[a_{n\varepsilon }]\),  are two representatives, then this inequality would yield
are two representatives, then this inequality would yield

The dependence of \(\varepsilon _{0n}\) from \(n\in \mathbb {N}\) does not allow to prove, e.g., that \(\sum _{n=0}^{N}a_{n}\le \sum _{n=0}^{N}b_{n}\) (e.g. as in (2.8), we can consider \(b_{n\varepsilon }{:=}0\) and \(a_{n\varepsilon }{:=}0\) if \(\varepsilon <\frac{1}{n+1}\) but \(a_{n\varepsilon }{:=}1\) otherwise, then \(a_{n}=[a_{n\varepsilon }]=0=b_{n}\), but \(\sum _{n=0}^{N}a_{n}=N-\left[ \left\lceil \frac{1}{\varepsilon }\right\rceil \right] +2\)).
Moreover, for convergence tests we also need to perform pointwise (in \(n\in \mathbb {N}\)) operations of the form \(\left( \frac{a_{n}}{b_{n}}\right) _{n}\), \(\left( \left| \frac{a_{n+k}}{a_{n}}\right| \right) _{n}\) or \(\left( \left| a_{n}\right| ^{1/n}\right) _{n}\). This kind of pointwise operations can be easily considered if we restrict us to sequences  and we assume that \(\sigma \ge \rho ^{*}\). Anyway, this is a particular sufficient condition, and we can more generally state some convergence tests using the more general space
and we assume that \(\sigma \ge \rho ^{*}\). Anyway, this is a particular sufficient condition, and we can more generally state some convergence tests using the more general space  . For these reasons, we define
. For these reasons, we define
Definition 20
Let \((a_{n})_{n}\),  , then we say that \((a_{n})_{n}\le (b_{n})_{n}\) if
, then we say that \((a_{n})_{n}\le (b_{n})_{n}\) if

Note explicitly that if \(M<_{L}N\) on \(L\subseteq _{0}I\), then \(\sum _{n=N}^{M}a_{n}=_{L}\sum _{n=N}^{M}b_{n}=_{L}0\). Therefore, (3.6) is equivalent to

On the other hand, we recall that the Robinson-Colombeau ring  is already ordered by \(\left\{ a_{n}\right\} _{n}=[a_{n\varepsilon }]_{\text {u}}\le [b_{n\varepsilon }]_{\text {u}}=\left\{ b_{n}\right\} _{n}\) if
is already ordered by \(\left\{ a_{n}\right\} _{n}=[a_{n\varepsilon }]_{\text {u}}\le [b_{n\varepsilon }]_{\text {u}}=\left\{ b_{n}\right\} _{n}\) if

We also recall that  through the embedding \(x\mapsto [(x_{\varepsilon })_{n\varepsilon }]\). Thereby, a relation of the form \(x\le [a_{n\varepsilon }]_{\text {u}}\) yields
through the embedding \(x\mapsto [(x_{\varepsilon })_{n\varepsilon }]\). Thereby, a relation of the form \(x\le [a_{n\varepsilon }]_{\text {u}}\) yields
for some representative \(x=[x_{\varepsilon }]\). Finally, [13, Lem. 2] for the ring  implies that \(\{a_{n}\}_{n}<\{b_{n}\}_{n}\) if and only if
implies that \(\{a_{n}\}_{n}<\{b_{n}\}_{n}\) if and only if
Theorem 21
We have the following properties:
-
(i)
 is an ordered
is an ordered  -module.
-module. -
(ii)
If \((a_{n})_{n}\ge 0\), then
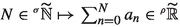 is increasing.
is increasing. -
(iii)
If \(\sigma \ge \rho ^{*}\), and \([a_{n\varepsilon }]_{{u }}\le [b_{n\varepsilon }]_{{u }}\) in
 , then \([a_{n\varepsilon }]_{{s }}\le [b_{n\varepsilon }]_{{s }}\) in
, then \([a_{n\varepsilon }]_{{s }}\le [b_{n\varepsilon }]_{{s }}\) in  .
.
Proof
(i): The relation \(\le \) on  is clearly reflexive and transitive. If \((a_{n})_{n}\le (b_{n})_{n}\le (a_{n})_{n}\), then for all N,
is clearly reflexive and transitive. If \((a_{n})_{n}\le (b_{n})_{n}\le (a_{n})_{n}\), then for all N,  we have \(\sum _{n=N}^{M}a_{n}=\sum _{n=N}^{M}b_{n}\) in
we have \(\sum _{n=N}^{M}a_{n}=\sum _{n=N}^{M}b_{n}\) in  . From Definition 5 of hypersum, this implies (2.9), i.e. that \((a_{n})_{n}=(b_{n})_{n}\) in
. From Definition 5 of hypersum, this implies (2.9), i.e. that \((a_{n})_{n}=(b_{n})_{n}\) in  .
.
(ii): Let N,  with \(N\le M\), then \(\sum _{n=0}^{M}a_{n}=\sum _{n=0}^{N}a_{n}+\sum _{n=N+1}^{M}a_{n}\) by Lemma 14, and \(\sum _{n=N+1}^{M}a_{n}\ge 0\) because \((a_{n})_{n}\ge 0\) in
with \(N\le M\), then \(\sum _{n=0}^{M}a_{n}=\sum _{n=0}^{N}a_{n}+\sum _{n=N+1}^{M}a_{n}\) by Lemma 14, and \(\sum _{n=N+1}^{M}a_{n}\ge 0\) because \((a_{n})_{n}\ge 0\) in  .
.
(iii): Assume that the inequality in (3.7) holds for all \(\varepsilon \le \varepsilon _{0}\) and for all \(n\in \mathbb {N}\). Then, if \(N=[N_{\varepsilon }]\), \(M=[M_{\varepsilon }]\), \(N_{\varepsilon }\), \(M_{\varepsilon }\in \mathbb {N}\), we have \(\sum _{n=N_{\varepsilon }}^{M_{\varepsilon }}a_{n\varepsilon }\le \sum _{n=N_{\varepsilon }}^{M\varepsilon }b_{n\varepsilon }+\sum _{n=N_{\varepsilon }}^{M\varepsilon }z_{n\varepsilon }\) for all \(\varepsilon \le \varepsilon _{0}\). Since  , for each \(q\in \mathbb {N}\), for \(\varepsilon \) small and for all \(n\in \mathbb {N}\), we have \(|z_{n\varepsilon }|\le \rho _{\varepsilon }^{q}\) and hence \(\left| \sum _{n=N_{\varepsilon }}^{M_{\varepsilon }}z_{n\varepsilon }\right| \le \left| M_{\varepsilon }-N_{\varepsilon }\right| \rho _{\varepsilon }^{q}\). Thereby, from the assumption \(\sigma \ge \rho ^{*}\), it follows that \(\left( \sum _{n=N_{\varepsilon }}^{M_{\varepsilon }}z_{n\varepsilon }\right) \sim _{\rho }0\), which proves the conclusion. \(\square \)
, for each \(q\in \mathbb {N}\), for \(\varepsilon \) small and for all \(n\in \mathbb {N}\), we have \(|z_{n\varepsilon }|\le \rho _{\varepsilon }^{q}\) and hence \(\left| \sum _{n=N_{\varepsilon }}^{M_{\varepsilon }}z_{n\varepsilon }\right| \le \left| M_{\varepsilon }-N_{\varepsilon }\right| \rho _{\varepsilon }^{q}\). Thereby, from the assumption \(\sigma \ge \rho ^{*}\), it follows that \(\left( \sum _{n=N_{\varepsilon }}^{M_{\varepsilon }}z_{n\varepsilon }\right) \sim _{\rho }0\), which proves the conclusion. \(\square \)
The direct comparison test for hyperseries can now be stated as follows.
Theorem 22
Let \(\sigma \) and \(\rho \) be arbitrary gauges, let  and
and  be hyperseries with \(\left( a_{n}\right) _{n}\), \(\left( b_{n}\right) _{n}\ge 0\) and such that
be hyperseries with \(\left( a_{n}\right) _{n}\), \(\left( b_{n}\right) _{n}\ge 0\) and such that
Then we have:
-
(i)
If
 is convergent then so is
is convergent then so is  .
. -
(ii)
If
 is divergent to \(+\infty \), then so is
is divergent to \(+\infty \), then so is  .
. -
(iii)
If \(\sigma \ge \rho ^{*}\) and \(\{a_{n}\}_{n}{:=}[a_{n\varepsilon }]_{{u }}\),
 , then we have the same conclusions if we assume that
, then we have the same conclusions if we assume that 
Proof
We first note that (3.8) can be simply written as \((\alpha _{n})_{n}\le (\beta _{n})_{n}\), where \(\alpha _{n}{:=}a_{n+N}\) and \(\beta _{n}{:=}b_{n+N}\). Thereby, Corollary 16 implies that, without loss of generality, we can assume \(N=0\). To prove (i), let us consider the partial sums \(A_{N}{:=}\sum _{i=0}^{N}a_{i}\) and \(B_{N}{:=}\sum _{i=0}^{N}b_{i}\),  . Since
. Since  is convergent, we have
is convergent, we have  . The assumption \(\left( a_{n}\right) _{n}\le \left( b_{n}\right) _{n}\) implies \(A_{N}\le B_{N}\). The hypersequences
. The assumption \(\left( a_{n}\right) _{n}\le \left( b_{n}\right) _{n}\) implies \(A_{N}\le B_{N}\). The hypersequences  ,
,  are increasing because \((a_{n})_{n}\), \((b_{n})_{n}\ge 0\) (Theorem 21.(ii)) and hence
are increasing because \((a_{n})_{n}\), \((b_{n})_{n}\ge 0\) (Theorem 21.(ii)) and hence  decreases to zero because of the convergence assumption. Now, for all N,
decreases to zero because of the convergence assumption. Now, for all N,  , \(M\ge N\), we have
, \(M\ge N\), we have
Thereby, given m, \(n\ge N\), applying (3.9) with m, n instead of M, we get that both \(A_{n}\), \(A_{m}\) belong to the interval \([A_{N},A_{N}+(B-B_{N})]\), whose length \(B-B_{N}\) decreases to zero as  goes to infinity. This shows that
goes to infinity. This shows that  is a Cauchy hypersequence, and therefore
is a Cauchy hypersequence, and therefore  converges.
converges.
The proof of (ii) follows directly from the inequality \(A_{N}\le B_{N}\) for each  . The proof of (iii) follows from Lemma 21.(iii) and from Lemma 7.(iv). \(\square \)
. The proof of (iii) follows from Lemma 21.(iii) and from Lemma 7.(iv). \(\square \)
Note that the two cases (i) and (ii) do not cover the case where the non-decreasing hypersums \(N\mapsto \sum _{n=0}^{N}a_{n}\) are bounded but anyway do not converge because it does not exists the supremum of their values (see [13]).
Example 23
Let  be a finite number so that \(x\le M\in \mathbb {N}_{>0}\) for some M. Assume that \(x_{\varepsilon }\le M\) for all \(\varepsilon \le \varepsilon _{0}\). For these \(\varepsilon \) we have \(\frac{n+x_{\varepsilon }}{n^{3}}\le \frac{2}{n^{2}}\) for all \(n\in \mathbb {N}_{\ge M}\). This shows that \(\left\{ \frac{n+M+x}{(n+M)^{3}}\right\} _{n}\le \left\{ \frac{2}{(n+M)^{2}}\right\} _{n}\) and we can hence apply Theorem 22.
be a finite number so that \(x\le M\in \mathbb {N}_{>0}\) for some M. Assume that \(x_{\varepsilon }\le M\) for all \(\varepsilon \le \varepsilon _{0}\). For these \(\varepsilon \) we have \(\frac{n+x_{\varepsilon }}{n^{3}}\le \frac{2}{n^{2}}\) for all \(n\in \mathbb {N}_{\ge M}\). This shows that \(\left\{ \frac{n+M+x}{(n+M)^{3}}\right\} _{n}\le \left\{ \frac{2}{(n+M)^{2}}\right\} _{n}\) and we can hence apply Theorem 22.
The limit comparison test is the next
Theorem 24
Let \(\sigma \) and \(\rho \) be arbitrary gauges, let  and
and  be hyperseries, with \(\left( a_{n}\right) _{n}\ge 0\). Assume that
be hyperseries, with \(\left( a_{n}\right) _{n}\ge 0\). Assume that

Then we have:
-
(i)
Either both hyperseries
 ,
,  converge or diverge to \(+\infty \).
converge or diverge to \(+\infty \). -
(ii)
If \(\sigma \ge \rho ^{*}\), \(\left\{ a_{n}\right\} _{n}=[a_{n\varepsilon }]_{{u }}\),
 , \([b_{n\varepsilon }]_{{u }}>0\) and
, \([b_{n\varepsilon }]_{{u }}>0\) and 
then the same conclusion as in (i) holds.
Proof
As in the previous proof, without loss of generality, we can assume \(N=0\). Now, if  diverges to \(+\infty \), then so does
diverges to \(+\infty \), then so does  because \(m>0\). Since \(\left( mb_{n}\right) _{n}<\left( a_{n}\right) _{n}\), by the direct comparison test also the hyperseries
because \(m>0\). Since \(\left( mb_{n}\right) _{n}<\left( a_{n}\right) _{n}\), by the direct comparison test also the hyperseries  diverges to \(+\infty \). Likewise, if the hyperseries
diverges to \(+\infty \). Likewise, if the hyperseries  converges then so does
converges then so does  . Since \(\left( a_{n}\right) _{n}<\left( Mb_{n}\right) _{n}\), by the direct comparison test also the hyperseries
. Since \(\left( a_{n}\right) _{n}<\left( Mb_{n}\right) _{n}\), by the direct comparison test also the hyperseries  converges. Property (ii) can be proved as in the previous theorem. \(\square \)
converges. Property (ii) can be proved as in the previous theorem. \(\square \)
Note that if M, \(a_{n}\), \(b_{n}\in \mathbb {R}\), then the condition \(\left\{ \frac{a_{n}}{b_{n}}\right\} _{n}\le M\) is equivalent to \(\limsup _{n\rightarrow +\infty }\frac{a_{n}}{b_{n}}\le M\). Analogously, \(m\le \left\{ \frac{a_{n}}{b_{n}}\right\} _{n}\) is equivalent to \(\liminf _{n\rightarrow +\infty }\frac{a_{n}}{b_{n}}\ge m\). This shows that our formulation of the limit comparison test faithfully generalizes the classical version.
Both the root and the ratio tests are better formulated in  , because their proofs require term-by-term operations (such as e.g. that \(|a_{n}|^{1/n}\le L\) implies \(|a_{n}|\le L^{n}\)), so that the order relation defined in Definition (20) seems too weak for these aims; see also the comment below the proof of the root test.
, because their proofs require term-by-term operations (such as e.g. that \(|a_{n}|^{1/n}\le L\) implies \(|a_{n}|\le L^{n}\)), so that the order relation defined in Definition (20) seems too weak for these aims; see also the comment below the proof of the root test.
3.4 Root test
Theorem 25
Let \(\sigma \ge \rho ^{*}\) and let  (so that also
(so that also  ). Assume that
). Assume that

Then
-
(i)
If \(L<1\), then the hyperseries
 converges absolutely.
converges absolutely. -
(ii)
If \(J\subseteq _{0}I\) and \(L>_{J}1\), then
 and hence the hyperseries
and hence the hyperseries 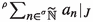 diverges.
diverges. -
(iii)
If \(L\not =_{\mathrm{s}}1\), then the hyperseries
 converges if and only if \(L<1\).
converges if and only if \(L<1\).
Proof
(i): Our assumption \(\left\{ |a_{n}|^{1/n}\right\} _{n}\le L\) entails \(\left\{ |a_{n}|\right\} _{n}<\left( L^{n}\right) _{n}\). Since  is convergent because \(0\le L<1\), by the direct comparison test, the series
is convergent because \(0\le L<1\), by the direct comparison test, the series  is also convergent.
is also convergent.
(ii): Now, assume that \(L_{\varepsilon }>1\) for \(\varepsilon \in J\subseteq _{0}I\) and let us work directly in the ring  . Proceeding as above, we have \(\left\{ |a_{n}|\right\} _{n}\ge _{J}\left( L^{n}\right) _{n}\), and thereby the last claim follows because of \(L>_{J}1\).
. Proceeding as above, we have \(\left\{ |a_{n}|\right\} _{n}\ge _{J}\left( L^{n}\right) _{n}\), and thereby the last claim follows because of \(L>_{J}1\).
(iii): Assume that \(L\not =_{\mathrm{s}}1\), that  converges but \(L>_{\mathrm{s}}1\), then (ii) would yield that
converges but \(L>_{\mathrm{s}}1\), then (ii) would yield that  diverges for some \(J\subseteq _{0}I\) and this contradicts the convergence assumption. Therefore, we have \(L\not =_{\mathrm{s}}1\) and \(L\not >_{\mathrm{s}}1\), and hence [13, Lem. 6.(v)] gives \(L\not \ge _{\mathrm{s}}1\). Thereby, [13, Lem. 5.(ii)] finally implies \(L<1\). \(\square \)
diverges for some \(J\subseteq _{0}I\) and this contradicts the convergence assumption. Therefore, we have \(L\not =_{\mathrm{s}}1\) and \(L\not >_{\mathrm{s}}1\), and hence [13, Lem. 6.(v)] gives \(L\not \ge _{\mathrm{s}}1\). Thereby, [13, Lem. 5.(ii)] finally implies \(L<1\). \(\square \)
Actually, we can also simply reformulate the root test in  by trivially asking that \(\left( \left| a_{n}\right| \right) _{n}\le \left( L^{n}\right) _{n}\), but that would simply recall a non-meaningful consequence of the direct comparison test Theorem 22.
by trivially asking that \(\left( \left| a_{n}\right| \right) _{n}\le \left( L^{n}\right) _{n}\), but that would simply recall a non-meaningful consequence of the direct comparison test Theorem 22.
3.5 Ratio test
Proceeding as in the previous proof, i.e. by generalizing the classical proof for series of real numbers, we also have the following
Theorem 26
Let \(\sigma \ge \rho ^{*}\) and let  , with \(\left\{ |a_{n}|\right\} _{n}>0\). Assume that for some \(k\in \mathbb {N}\) we have
, with \(\left\{ |a_{n}|\right\} _{n}>0\). Assume that for some \(k\in \mathbb {N}\) we have

Then
-
(i)
If \(L<1\), the hyperseries
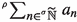 converges.
converges. -
(ii)
If \(J\subseteq _{0}I\), \(L>_{J}1\), then
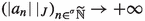 and hence the hyperseries
and hence the hyperseries  diverges.
diverges. -
(iii)
If \(L\not =_{\mathrm{s}}1\), then the hyperseries
 converges if and only if \(L<1\).
converges if and only if \(L<1\).
As in the classical case, the convergent p-hyperseries  and the divergent hyperseries
and the divergent hyperseries  shows that the ratio and the root tests fails if \(L=1\).
shows that the ratio and the root tests fails if \(L=1\).
Example 27
If  is a finite invertible number, then using the ratio test and proceeding as in Example 23, we can prove that
is a finite invertible number, then using the ratio test and proceeding as in Example 23, we can prove that  converges if \(\sigma \ge \rho ^{*}\).
converges if \(\sigma \ge \rho ^{*}\).
3.6 Alternating series test
Also in the proof of this test we need a term-by-term comparison (see (3.14) below).
Theorem 28
Let \(\sigma \ge \rho ^{*}\) and let  . Assume that we have
. Assume that we have

Then the alternating hyperseries  converges.
converges.
Proof
By (3.12), assume that
holds for all \(n\in \mathbb {N}\) and all \(\varepsilon \le \varepsilon _{0}\). Take \(N=[N_{\varepsilon }]\),  , where for \(\varepsilon \le \varepsilon _{0}\) we have \(N_{\varepsilon }\), \(M_{\varepsilon }\in \mathbb {N}\). If \(M_{\varepsilon }\) is odd and \(M_{\varepsilon }\le N_{\varepsilon }\), we can estimate the difference \(S_{N_{\varepsilon }}-S_{M_{\varepsilon }}\) as:
, where for \(\varepsilon \le \varepsilon _{0}\) we have \(N_{\varepsilon }\), \(M_{\varepsilon }\in \mathbb {N}\). If \(M_{\varepsilon }\) is odd and \(M_{\varepsilon }\le N_{\varepsilon }\), we can estimate the difference \(S_{N_{\varepsilon }}-S_{M_{\varepsilon }}\) as:
where we used (3.14). If \(M_{\varepsilon }\) is even and \(M_{\varepsilon }\le N_{\varepsilon }\), a similar argument shows that \(S_{N_{\varepsilon }}-S_{M_{\varepsilon }}\ge -a_{M_{\varepsilon }}\). If \(M_{\varepsilon }>N_{\varepsilon }\), it suffices to revert the role of \(M_{\varepsilon }\) and \(N_{\varepsilon }\) in (3.15). This proves that \(\min (-a_{M},-a_{N})\le S_{N}-S_{M}\le \max (a_{M},a_{N})\). The final claim now follows from (3.13) and Cauchy criterion [13, Thm. 44]. \(\square \)
Example 29
Using the previous Theorem 28, we can prove, e.g., that the hyperseries  is convergent.
is convergent.
3.7 Integral test
The possibility to prove the integral test for hyperseries is constrained by the existence of a notion of generalized function that can be defined on an unbounded interval, e.g. of the form  . This is not possible for an arbitrary Colombeau generalized function, which are defined only on finite (i.e. compactly supported) points, i.e. on domains of the form \(\widetilde{\Omega }_{c}\) (see e.g. [9]). Moreover, we would also need a notion of improper integral extended on \([0,+\infty )\). This notion clearly needs to have good relations with the notion of hyperlimit and with the definite integral over the interval [0, N], where
. This is not possible for an arbitrary Colombeau generalized function, which are defined only on finite (i.e. compactly supported) points, i.e. on domains of the form \(\widetilde{\Omega }_{c}\) (see e.g. [9]). Moreover, we would also need a notion of improper integral extended on \([0,+\infty )\). This notion clearly needs to have good relations with the notion of hyperlimit and with the definite integral over the interval [0, N], where  (see Definition 32 below). This further underscores drawbacks of Colombeau’s theory, where this notion of integral (if N is an infinite number) is not defined, see e.g. [1].
(see Definition 32 below). This further underscores drawbacks of Colombeau’s theory, where this notion of integral (if N is an infinite number) is not defined, see e.g. [1].
The theory of generalized smooth functions overcomes these difficulties, see e.g. [7, 8]. Here, we only recall the equivalent definition. In the following, \(\sigma \), \(\rho \) always denote arbitrary gauges.
Definition 30
Let  and
and  . We say that \(f:X\longrightarrow Y\) is a \(\rho \)-moderate generalized smooth function (GSF), and we write
. We say that \(f:X\longrightarrow Y\) is a \(\rho \)-moderate generalized smooth function (GSF), and we write  , if
, if
-
(i)
\(f:X\longrightarrow Y\) is a set-theoretical function.
-
(ii)
There exists a net \((f_{\varepsilon })\in {\mathcal {C}}^{\infty }(\mathbb {R}^{n},\mathbb {R}^{d})^{(0,1]}\) such that for all \([x_{\varepsilon }]\in X\):
-
(a)
\(f(x)=[f_{\varepsilon }(x_{\varepsilon })]\)
-
(b)
\(\forall \alpha \in \mathbb {N}^{n}:\ (\partial ^{\alpha }f_{\varepsilon }(x_{\varepsilon }))\text { is }\rho -\text {moderate}\).
-
(a)
For generalized smooth functions lots of results hold: closure with respect to composition, embedding of Schwartz’s distributions, differential calculus, one-dimensional integral calculus using primitives, classical theorems (intermediate value, mean value, Taylor, extreme value, inverse and implicit function), multidimensional integration, Banach fixed point theorem, a Picard-Lindelöf theorem for both ODE and PDE, several results of calculus of variations, etc.
In particular, we have the following
Theorem 31
Let a, b,  , with \(a<b\) and \(c\in [a,b]\subseteq U\). Let
, with \(a<b\) and \(c\in [a,b]\subseteq U\). Let  be a generalized smooth function. Then, there exists one and only one generalized smooth function
be a generalized smooth function. Then, there exists one and only one generalized smooth function  such that \(F(c)=0\) and \(F'(x)=f(x)\) for all \(x\in [a,b]\). Moreover, if f is defined by the net \(f_{\varepsilon }\in {\mathcal {C}}^{\infty }(\mathbb {R},\mathbb {R})\) and \(c=[c_{\varepsilon }]\), then
such that \(F(c)=0\) and \(F'(x)=f(x)\) for all \(x\in [a,b]\). Moreover, if f is defined by the net \(f_{\varepsilon }\in {\mathcal {C}}^{\infty }(\mathbb {R},\mathbb {R})\) and \(c=[c_{\varepsilon }]\), then
for all \(x=[x_{\varepsilon }]\in [a,b]\).
We can hence define \(\int _{c}^{x}f(t)\,\hbox {d}{:=}F(x)\) for all \(x\in [a,b]\) (note explicitly that a, b can also be infinite generalized numbers). For this notion of integral we have all the usual elementary property, monotonicity and integration by substitution included.
For the integral test for hyperseries, we finally need the following
Definition 32
Let  , then we say
, then we say

Theorem 33
Let  be a GSF such that
be a GSF such that
then  and
and
-
(i)
The hyperseries
 converges if \(\exists \int _{0}^{+\infty }f(x)\,\hbox {d}\) and
converges if \(\exists \int _{0}^{+\infty }f(x)\,\hbox {d}\) and 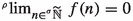 .
. -
(ii)
The hyperseries
 diverges to \(+\infty \) if \(\int _{0}^{+\infty }f(x)\,\hbox {d}=+\infty \).
diverges to \(+\infty \) if \(\int _{0}^{+\infty }f(x)\,\hbox {d}=+\infty \).
Proof
From (3.16), for all N,  we have
we have
Without loss of generality, we can assume \(N_{\varepsilon }\), \(M_{\varepsilon }\in \mathbb {N}\) for all \(\varepsilon \). Thereby
where we used Definition 5 of hypersum and (3.17). On the other hand, since  , using (3.18) we have
, using (3.18) we have
where we used again Definition 5 of hypersum and (3.16). Combining these two inequalities yields
These inequalities show that  . Now, we consider that \(\sum _{n=0}^{M}f(n)-\sum _{n=0}^{N}f(n)=\sum _{n=N}^{M}f(n)\) for \(M\ge N\), and
. Now, we consider that \(\sum _{n=0}^{M}f(n)-\sum _{n=0}^{N}f(n)=\sum _{n=N}^{M}f(n)\) for \(M\ge N\), and
Therefore, if \(\exists \int _{0}^{+\infty }f(x)\,\hbox {d}\) and  , letting N, \(M\rightarrow +\infty \) in (3.19) proves that our hyperseries satisfies the Cauchy criterion. If \(\int _{0}^{+\infty }f(x)\,\hbox {d}=+\infty \), then setting \(N=0\) in the first inequality of (3.19) and \(M\rightarrow +\infty \) we get the second conclusion. \(\square \)
, letting N, \(M\rightarrow +\infty \) in (3.19) proves that our hyperseries satisfies the Cauchy criterion. If \(\int _{0}^{+\infty }f(x)\,\hbox {d}=+\infty \), then setting \(N=0\) in the first inequality of (3.19) and \(M\rightarrow +\infty \) we get the second conclusion. \(\square \)
Note that, generalizing by contradiction the classical proof, we only have

and not \(L=0\) like in classical case.
As usual, from the integral test we can also deduce the p-series test:
Corollary 34
If  , then the p-hyperseries converges.
, then the p-hyperseries converges.
Proof
Since \(p=[p_{\varepsilon }]>1\), we can assume that \(p_{\varepsilon }>1\) for all \(\varepsilon \le \varepsilon _{0}\). For these \(\varepsilon \), if \(x\in [n,n+1)_{\mathbb {R}}\), we also have \(\frac{1}{x^{p_{\varepsilon }}}\le \frac{1}{n^{p_{\varepsilon }}}\), which proves (3.17). Similarly, we can prove (3.18). Note that the function \(f(x)=\frac{1}{x^{p}}\) for all  is \(\rho \)-moderate because \(x\ge 1\) and \(p>1\), so that \(\left| f(x)\right| \le 1\). Finally, like in the classical case, we have
is \(\rho \)-moderate because \(x\ge 1\) and \(p>1\), so that \(\left| f(x)\right| \le 1\). Finally, like in the classical case, we have  because \(p>1\). \(\square \)
because \(p>1\). \(\square \)
Note, however, that our proofs in Sect. 3.1 are independent from the notion of generalized smooth function.
4 Cauchy product of hyperseries
We recall that, on the basis of Theorem 3, the operations of sum and product by a number in  are the sole operations defined in
are the sole operations defined in  . We now consider the classical Cauchy product:
. We now consider the classical Cauchy product:
Definition 35
The Cauchy product of two sequences for hypersums \(\left( a_{n}\right) _{n}\),  is defined as
is defined as
The Cauchy product of two hyperseries is the hyperlimit of the hypersums with general term \(\left( a_{n}\right) _{n}\star \left( b_{n}\right) _{n}\), assuming that it exists:

A similar product of sequences can be defined in  with
with
Theorem 36
The module  is a ring with respect to the Cauchy product of sequences. The ring
is a ring with respect to the Cauchy product of sequences. The ring  is also a ring with respect to the Cauchy product of sequences.
is also a ring with respect to the Cauchy product of sequences.
Proof
Let \(\left( a_{n}\right) _{n}\),  , \((a_{n\varepsilon })_{n,\varepsilon }\sim _{\sigma \rho }(\bar{a}_{n\varepsilon })_{n,\varepsilon }\), \((b_{n\varepsilon })_{n,\varepsilon }\sim _{\sigma \rho }(\bar{b}_{n\varepsilon })_{n,\varepsilon }\). We first prove that the Cauchy product \(\left( a_{n}\right) _{n}\star \left( b_{n}\right) _{n}\) is well-defined in
, \((a_{n\varepsilon })_{n,\varepsilon }\sim _{\sigma \rho }(\bar{a}_{n\varepsilon })_{n,\varepsilon }\), \((b_{n\varepsilon })_{n,\varepsilon }\sim _{\sigma \rho }(\bar{b}_{n\varepsilon })_{n,\varepsilon }\). We first prove that the Cauchy product \(\left( a_{n}\right) _{n}\star \left( b_{n}\right) _{n}\) is well-defined in  . For simplicity, for n,
. For simplicity, for n,  , set \(A_{nm}{:=}\sum _{k=n}^{m}a_{k}\), \(B_{nm}{:=}\sum _{k=n}^{m}b_{k}\) and similar notations \(\bar{A}_{nm}\), \(\bar{B}_{nm}\) using the other representatives. Then
, set \(A_{nm}{:=}\sum _{k=n}^{m}a_{k}\), \(B_{nm}{:=}\sum _{k=n}^{m}b_{k}\) and similar notations \(\bar{A}_{nm}\), \(\bar{B}_{nm}\) using the other representatives. Then
Now, \(A_{nm}-\bar{A}_{nm}\) and \(B_{nm}-\bar{B}_{nm}\) are \(\rho \)-negligible by Definition (2.9) of \(\sim _{\sigma \rho }\), and \(B_{nm}\), \(\bar{A}_{nm}\) are \(\rho \)-moderate because of Lemma 4. This proves that the Cauchy product \(\star \) in  is well-defined. Similarly, we can proceed with
is well-defined. Similarly, we can proceed with  . The ring properties now follow from the same properties of the ring
. The ring properties now follow from the same properties of the ring  . \(\square \)
. \(\square \)
It is well-known that for each \(n\in \mathbb {N}\), we have \(\left( a_{n}\right) _{n}\star \left( b_{n}\right) _{n}=\left( \sum _{i=0}^{n}a_{i}\right) \cdot \left( \sum _{j=0}^{n}b_{j}\right) =\sum _{i=0}^{n}\sum _{j=0}^{n}a_{i}b_{j}=:c_{n}\), so  by Theorem 36. Moreover, if
by Theorem 36. Moreover, if  and
and  converge, taking the hyperlimit of the product of the two partial sums we obtain
converge, taking the hyperlimit of the product of the two partial sums we obtain

but, in general, this is different from

In other words, if the Cauchy product of these hyperseries exists, in general we have

The classical Mertens’ theorem also holds for hyperseries:
Theorem 37
Assume that the hyperseries  converges to A and
converges to A and  converges to B. Assume that the former hyperseries converges absolutely. Then their Cauchy product converges to AB.
converges to B. Assume that the former hyperseries converges absolutely. Then their Cauchy product converges to AB.
We first need the following
Lemma 38
If \((b_{n})_{n}\) converges to B, then

Proof
Set  for all
for all  . The assumption of convergence yields
. The assumption of convergence yields

Set  and let
and let  . We use dichotomy law as in [13, Lem. 7.(ii)], i.e. we consider \(L\subseteq _{0}I\) and two cases \(N\ge _{L}N_{1}\) or \(N\le _{L}N_{1}\). We claim that \(\left| B_{N_{\varepsilon }}-B_{\varepsilon }\right| \le K_{\varepsilon }\) for all \(\varepsilon \in L\) sufficiently small, where \(N_{\varepsilon }{:=}\mathrm{ni}{(N)}_{\varepsilon }\), \(N_{1\varepsilon }{:=}\mathrm{ni}{(N_{1})}_{\varepsilon }\),
. We use dichotomy law as in [13, Lem. 7.(ii)], i.e. we consider \(L\subseteq _{0}I\) and two cases \(N\ge _{L}N_{1}\) or \(N\le _{L}N_{1}\). We claim that \(\left| B_{N_{\varepsilon }}-B_{\varepsilon }\right| \le K_{\varepsilon }\) for all \(\varepsilon \in L\) sufficiently small, where \(N_{\varepsilon }{:=}\mathrm{ni}{(N)}_{\varepsilon }\), \(N_{1\varepsilon }{:=}\mathrm{ni}{(N_{1})}_{\varepsilon }\),  , \(B_{N_{\varepsilon }}{:=}\sum _{k=0}^{N_{\varepsilon }}b_{k\varepsilon }\), \(B=[B_{\varepsilon }]\) and \(K_{\varepsilon }{:=}1+\sum _{k=0}^{N_{1\varepsilon }}\left| b_{k\varepsilon }\right| \) (hence \(K=[K_{\varepsilon }]\)). We also note that, in general, P,
, \(B_{N_{\varepsilon }}{:=}\sum _{k=0}^{N_{\varepsilon }}b_{k\varepsilon }\), \(B=[B_{\varepsilon }]\) and \(K_{\varepsilon }{:=}1+\sum _{k=0}^{N_{1\varepsilon }}\left| b_{k\varepsilon }\right| \) (hence \(K=[K_{\varepsilon }]\)). We also note that, in general, P,  , \(P\le Q\) implies \(\mathrm{ni}{(P)}_{\varepsilon }\le \mathrm{ni}{(Q)}_{\varepsilon }\) for \(\varepsilon \) small. In the first case \(N\ge _{L}N_{1}\), we get \(N_{\varepsilon }\ge N_{1\varepsilon }\) for \(\varepsilon \) small. Set \(M_{\varepsilon }{:=}N_{\varepsilon }\) if \(\varepsilon \in L\) and \(M_{\varepsilon }{:=}N_{1\varepsilon }\) otherwise, so that
, \(P\le Q\) implies \(\mathrm{ni}{(P)}_{\varepsilon }\le \mathrm{ni}{(Q)}_{\varepsilon }\) for \(\varepsilon \) small. In the first case \(N\ge _{L}N_{1}\), we get \(N_{\varepsilon }\ge N_{1\varepsilon }\) for \(\varepsilon \) small. Set \(M_{\varepsilon }{:=}N_{\varepsilon }\) if \(\varepsilon \in L\) and \(M_{\varepsilon }{:=}N_{1\varepsilon }\) otherwise, so that  and from (4.2) we obtain \(\left| B_{M_{\varepsilon }}-B_{\varepsilon }\right| <1\) for \(\varepsilon \) small and, in particular
and from (4.2) we obtain \(\left| B_{M_{\varepsilon }}-B_{\varepsilon }\right| <1\) for \(\varepsilon \) small and, in particular
We claim the same conclusion also in the second case \(N\le _{L}N_{1}\), i.e.
In fact, we have \(B_{N}=B_{N_{1}\vee N}-\sum _{k=N+1}^{N_{1}\vee N}b_{k}\) and hence
Inequalities (4.3) and (4.4) prove the claim also in the second case. Therefore, the dichotomy law yields \(|B_{N}-B|\le K\) and K does not depend on N. \(\square \)
Proof of Theorem 37
Define \(A_{n}{:=}\sum _{i=0}^{n}a_{i}\), \(B_{n}{:=}\sum _{i=0}^{n}b_{i}\) and \(C_{n}{:=}\sum _{i=0}^{n}c_{i}\) for  , and with \(c_{i}{:=}\sum _{k=0}^{i}a_{k}b_{i-k}\) for \(i\in \mathbb {N}\). Then \(C_{n}=\sum _{i=0}^{n}a_{n-i}B_{i}\) because the same equality holds \(\varepsilon \)-wise for any representatives, and hence \(C_{n}=\sum _{i=0}^{n}a_{n-i}(B_{i}-B)+A_{n}B\). The idea is to estimate
, and with \(c_{i}{:=}\sum _{k=0}^{i}a_{k}b_{i-k}\) for \(i\in \mathbb {N}\). Then \(C_{n}=\sum _{i=0}^{n}a_{n-i}B_{i}\) because the same equality holds \(\varepsilon \)-wise for any representatives, and hence \(C_{n}=\sum _{i=0}^{n}a_{n-i}(B_{i}-B)+A_{n}B\). The idea is to estimate
and to use our assumption (4.1) for the first summand. We start from the second summand in (4.5): Since  converges absolutely to some \(\bar{A}\) and \(B_{n}\) converges to B, for all \(q\in \mathbb {N}\) we can find
converges absolutely to some \(\bar{A}\) and \(B_{n}\) converges to B, for all \(q\in \mathbb {N}\) we can find  such that
such that
for all \(n\ge N\). Therefore, for the same \(n\ge N\)
First summand in (4.5): Since  converges,
converges,  must converge to zero. Hence for some
must converge to zero. Hence for some  and for all \(n\ge M\) and because of Lemma 38, we have
and for all \(n\ge M\) and because of Lemma 38, we have
In particular, if \(n\ge M+N\) and \(i\le N-1\), then \(n-i\ge n-N+1>M\) and we can apply (4.6) with \(n-i\) instead of n obtaining
Finally, since \(A_{n}\) converges to A, for some  and for all \(n\ge L\), we have
and for all \(n\ge L\), we have
Then, for all \(n\ge \max \left( L,M+N\right) \) using the aforementioned estimates, (4.5) yields \(\left| C_{n}-AB\right| \le 3\hbox {d}^{q}\). \(\square \)
5 Conclusions
One of the main goals of the present paper is to show that when dealing with non-Archimedean Cauchy complete rings, it can be worth to consider summations over infinite natural numbers instead of classical series indexed by \(n\in \mathbb {N}\). As we proved for the Robinson-Colombeau ring  , this allows us to extend numerous classical results which do not hold using classical series in a non-Archimedean framework. We tried to motivate in a clear way why we have to consider two gauges \(\sigma \) and \(\rho \) and, for each result, what relationships we have to consider among them. To help the reader to summarize the condition on the gauges, we can use the following table
, this allows us to extend numerous classical results which do not hold using classical series in a non-Archimedean framework. We tried to motivate in a clear way why we have to consider two gauges \(\sigma \) and \(\rho \) and, for each result, what relationships we have to consider among them. To help the reader to summarize the condition on the gauges, we can use the following table
| \(\sigma \), \(\rho \) arbitrary |
|---|---|
| \(\sigma \ge \rho ^{*}\) |
Divergent hypersums |
|
Geometric hyperseries | \(\sigma \ge \rho ^{*}\) or \(\sigma \le \rho ^{*}\) |
Taylor series exponential | \(\sigma \ge \rho ^{*}\) or \(\sigma \le \rho ^{*}\) |
\(\varepsilon \)-wise convergence | \(\exists \sigma \le \rho ^{*}\) or \(\sigma =\rho \) |
p-series | \(\sigma \), \(\rho \) arbitrary |
Direct comparison test | \(\sigma \), \(\rho \) arbitrary |
Limit comparison test | \(\sigma \), \(\rho \) arbitrary |
Root test |
|
Ratio test |
|
Alternating series test |
|
Integral test | \(\sigma \), \(\rho \) arbitrary |
Therefore, a possible summary could be: for meaningful examples of convergent series, for all convergence tests, one can assume \(\sigma \ge \rho ^{*}\) and use both  or
or  . For \(\varepsilon \)-wise convergence, to have larger domains (see Example 11.10)), one can assume \(\sigma \le \rho ^{*}\) and hence use
. For \(\varepsilon \)-wise convergence, to have larger domains (see Example 11.10)), one can assume \(\sigma \le \rho ^{*}\) and hence use  . For divergent hypersums, one must assume \(\sigma \ge \rho ^{*}\) and work in
. For divergent hypersums, one must assume \(\sigma \ge \rho ^{*}\) and work in  .
.
Since non-Archimedean rings are not Dedekind-complete, we have been forced to substitute the least-upper-bound property using the weaker Cauchy completeness. We think that several of the proofs we presented here can be generalized to other non-Archimedean Cauchy complete settings.
Clearly, the present work opens the actual possibility to start the study of hyper-power series, (real or complex) hyper-analytic generalized smooth functions and sigma additivity of multidimensional integration of generalized smooth functions (see [8]).
We also finally mention that the embedding of Schwartz’s distributions can be realized by regularization with an entire Colombeau mollifier (see e.g. [9]). We can hence conjecture that this embedding yields a hyper-analytic generalized smooth functions (but note that the hyper-power series of classical non-analytic smooth functions with a flat point would converge to zero under any invertible infinitesimal). This conjecture would open the possibility to extend the Cauchy-Kowalevski theorem to all Schwartz’s distributions.
References
Aragona, J., Fernandez, R., Juriaans, S.O., Oberguggenberger, M.: Differential calculus and integration of generalized functions over membranes. Monatshefte Math. 166(1), 1–18 (2012)
Benci, V., Luperi Baglini, L.: A non-archimedean algebra and the Schwartz impossibility theorem. Monatshefte Math. 176, 503–520 (2015)
Berarducci, A., Mantova, V.: Transseries as germs of surreal functions. Trans. Am. Math. Soc. 371, 3549–3592 (2019)
Bonar, D.D., Khoury, M.J.: Real Infinite Series. The Mathematical Association of America, Washington (2006)
Giordano, P., Kunzinger, M.: New topologies on Colombeau generalized numbers and the Fermat-Reyes theorem. J. Math. Anal. Appl. 399, 229–238 (2013). https://doi.org/10.1016/j.jmaa.2012.10.005
Giordano, P., Kunzinger, M.: A convenient notion of compact sets for generalized functions. Proc. Edinb. Math. Soc. 61(1), 57–92 (2018)
Giordano, P., Kunzinger, M., Vernaeve, H.: Strongly internal sets and generalized smooth functions. J. Math. Anal. Appl. 422(1), 56–71 (2015)
Giordano, P., Kunzinger, M., Vernaeve, H.: The Grothendieck topos of generalized functions I: basic theory. Preprint. See arXiv:2101.04492
Grosser, M., Kunzinger, M., Oberguggenberger, M., Steinbauer, R.: Geometric Theory of Generalized Functions. Kluwer, Dordrecht (2001)
Hansheng, Y.: Another proof for the \(p\)-series test. Coll. Math. J. 36(3), 235–237 (2005)
Koblitz, N.: p-Adic Numbers, p-Adic Analysis and Zeta-functions 2nd end. Graduate Texts in Mathematics, Springer (1996)
Luperi Baglini, L., Giordano, P.: The category of Colombeau algebras. Monatshefte Math. 182(3), 649–674 (2017)
Mukhammadiev, A., Tiwari, D., Apaaboah, G., Giordano, P.: Supremum, Infimum and and hyperlimits of Colombeau generalized numbers. Monatshefte Math. 196, 163–190 (2021)
Oberguggenberger, M., Pilipović, S., Valmorin, V.: Global representatives of Colombeau holomorphic generalized functions. Monatshefte Math. 151(1), 67–74 (2007)
Oberguggenberger, M., Vernaeve, H.: Internal sets and internal functions in Colombeau theory. J. Math. Anal. Appl. 341, 649–659 (2008)
Palmgren, E.: Developments in constructive nonstandard analysis. Bull. Symb. Logic 4, 233–272 (1998)
Pilipović, S., Scarpalezos, D., Valmorin, V.: Real analytic generalized functions. Monatshefte Math. 156, 85 (2009)
Robinson, A.: Function theory on some nonarchimedean fields. Am. Math. Mon. 80(6), 87–109 (1973). (Part II: Papers in the Foundations of Mathematics)
Shamseddine, K.: A brief survey of the study of power series and analyticfunctions on the Levi-Civita fields. Contemp. Math. 596, 269–280 (2013)
Vernaeve, H.: Generalized analytic functions on generalized domains. arXiv:0811.1521v1 (2008)
Colombeau, J.F.: New Generalized Functions and Multiplication of Distributions. North-Holland, Amsterdam (1984)
Acknowledgements
The authors would like to thank the referee for several suggestions that have led to considerable improvements of the paper.
Funding
Open access funding provided by University of Vienna.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Michael Kunzinger.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
D. Tiwari has been supported by Grant P 30407 of the Austrian Science Fund FWF.
P. Giordano has been supported by Grants P30407, P34113, P33538 of the Austrian Science Fund FWF.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tiwari, D., Giordano, P. Hyperseries in the non-Archimedean ring of Colombeau generalized numbers. Monatsh Math 197, 193–223 (2022). https://doi.org/10.1007/s00605-021-01647-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00605-021-01647-0



 means
means 
 is the usual finite sum. This is related to our motivating discussion about the definition of hyperfinite series at the beginning of Sect.
is the usual finite sum. This is related to our motivating discussion about the definition of hyperfinite series at the beginning of Sect.  and
and 
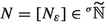 , with
, with 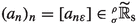 , then
, then  is well defined. That is, any sequence
is well defined. That is, any sequence  can be extended from
can be extended from  of hyperfinite numbers.
of hyperfinite numbers.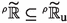 and
and  via the embedding
via the embedding 
 -linear map.
-linear map.
 . Then
. Then  . Therefore, the character (convergent or divergent) of the corresponding hyperseries is identical in the two spaces
. Therefore, the character (convergent or divergent) of the corresponding hyperseries is identical in the two spaces  and
and  .
. we get the existence of
we get the existence of 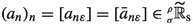 , then directly from (
, then directly from (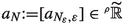 is well-defined. In particular, this applies with
is well-defined. In particular, this applies with 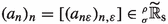 also defines an ordinary sequence
also defines an ordinary sequence  . On the other hand, let us explicitly note that if
. On the other hand, let us explicitly note that if  .
. , where
, where  . We recall that
. We recall that  to
to  (see (i) of Lemma
(see (i) of Lemma  ,
, 
 . Now,
. Now, 
 ,
, 
 for all gauges
for all gauges  .
. be such that
be such that  is not convergent. In fact, by contradiction, in the opposite case we would have
is not convergent. In fact, by contradiction, in the opposite case we would have  for all N sufficiently large, but this is impossible because for all fixed
for all N sufficiently large, but this is impossible because for all fixed  and for N sufficiently large,
and for N sufficiently large,  because
because  .
. finite, we have
finite, we have  . We have
. We have  . For all
. For all  ,
,  such that
such that  by (
by ( for all gauges
for all gauges  .
. for all
for all  ;
; .
. .
. is an
is an  -module.
-module. , but it does not converge for
, but it does not converge for  .
. defined by
defined by 
 . If we have
. If we have  is well defined. For example, if
is well defined. For example, if  is surjective but generally not injective. Now, if
is surjective but generally not injective. Now, if  , then
, then  .
. and
and  , if
, if 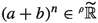 , then
, then  ;
; ;
; ;
; .
. ;
; .
. is a finite generalized number such that
is a finite generalized number such that  . A sufficient condition for this is that
. A sufficient condition for this is that  is an ordered
is an ordered  -module.
-module.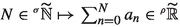 is increasing.
is increasing. , then
, then  .
. is convergent then so is
is convergent then so is  .
. is divergent to
is divergent to  .
. , then we have the same conclusions if we assume that
, then we have the same conclusions if we assume that 
 ,
,  converge or diverge to
converge or diverge to  ,
, 
 converges absolutely.
converges absolutely. and hence the hyperseries
and hence the hyperseries 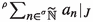 diverges.
diverges. converges if and only if
converges if and only if 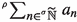 converges.
converges.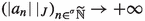 and hence the hyperseries
and hence the hyperseries  diverges.
diverges. converges if and only if
converges if and only if  converges if
converges if 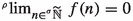 .
. diverges to
diverges to 

 and
and  and
and  and
and  and
and