Abstract
It is proved that the class of c-closed distribution spaces contains extremal domains and codomains to make convolution of distributions a well-defined bilinear mapping. The distribution spaces are systematically endowed with topologies and bornologies that make convolution hypocontinuous whenever defined. Largest modules and smallest algebras for convolution semigroups are constructed along the same lines. The fact that extremal domains and codomains for convolution exist within this class of spaces is fundamentally related to quantale theory. The quantale theoretic residual formed from two c-closed spaces is characterized as the largest c-closed subspace of the corresponding space of convolutors. The theory is applied to obtain maximal distributional domains for fractional integrals and derivatives, for fractional Laplacians, Riesz potentials and for the Hilbert transform. Further, maximal joint domains for families of these operators are obtained such that their composition laws are preserved.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A recurring problem in applications of distribution theory is to find an optimal domain for a given convolution operator or semigroups of such [1, 20, 34, 56]. Here, “optimal” means as large as admissible for convolution of distributions [45, 50, 52, 55]. In other words, optimal spaces are defined as the convolution duals (originally called “c-duals” [24, 58]) of a given set of distributions.
The main goal of this work is to develop a systematic method to construct optimal domains and codomains of distributions. Our method applies to general sets or semigroups of convolution operators.
Different from most investigations on this topic we study sets of function spaces endowed with a composition of spaces that is naturally induced by convolution. The emerging algebraic and order theoretic structures are investigated in detail, and they reveal interesting links to quantale theory [47, 17, p. 114-116]. Subsequently, the distribution spaces are endowed with topologies and bornologies in a uniform way, which ensures continuity and boundedness properties of convolutions between these spaces. The application of our general theory is exemplified for convolution operators used in fractional calculus and for the Hilbert transform.
To explain the crosslinks with quantale theory recall first the general order theoretic concept of Galois connections on power sets (also called “polarities”) [3, p. 122], [17, p. 116-120]. According to [3, Thm. 19 & Cor., p. 123] any symmetric binary relation \(R \subseteq X \times X \) on a set X induces a “symmetric Galois connection”
and an associated closure operator \(H_R := G_R \circ G_R \). Taking the set \(X := {\mathscr {D}}' \) of distributions and the relation \(y R z := ``\)y \( \text {and}\,\,\)z \( \text {are convolvable''} \) furnishes convolution duals \(G_R = ( - )^{\mathbin {*}}_{{\mathscr {D}}'} \) and perfections \(H_R = ( - )^{\mathbin {*}\mathbin {*}}_{\mathscr { D}'} \) [58, p. 20]. The elements of \(( {{\mathfrak {P}}}( {\mathscr {D}}' ) )^{\mathbin {*}\mathbin {*}}_{{\mathscr {D}}'} = \{ U \subseteq {\mathscr {D}}' \,;\, ( U )^{\mathbin {*}\mathbin {*}}_{\mathscr { D}'} = U \} \), the closure system associated to \(( - )^{\mathbin {*}\mathbin {*}}_{{\mathscr {D}}'} \), are called convolution perfect spaces. These spaces are linear by the definition of convolvability and \(( {{\mathfrak {P}}}( {\mathscr {D}}' ) )^{\mathbin {*}\mathbin {*}}_{{\mathscr {D}}'} \) constitutes a complete lattice [3].
The link between convolution perfect spaces and quantales emerges when studying extremality of inclusions \(U \mathbin {*} V \subseteq W \), where \(U, V, W \subseteq {\mathscr {D}}' \) are convolution perfect. This becomes clear from our extremality Theorem 1.
Theorem 1
Let U, V and W be convolution perfect spaces such that convolution of distributions is well-defined as a bilinear mapping \( \mathbin {*} :U \times V \rightarrow W \). Then, there exists a largest convolution perfect space \( U' \) containing U and a smallest convolution perfect space \( W' \) contained in W such that \( \mathbin {*} :U' \times V \rightarrow W \) and \( \mathbin {*} :U \times V \rightarrow W' \) are well-defined bilinear mappings in the same sense.
The second part of our extremality theorem is immediate from linearity properties of convolution and the fact that convolution perfect spaces constitute a closure system. Let \( \mathbin {\mathop {\widetilde{\mathbin {*}}}} \) denote the partially defined composition
of convolution perfect spaces U and V that is defined if and only if U und V are convolvable elementwise. Clearly, the space \( U \mathbin {\mathop {\widetilde{\mathbin {*}}}} V \) is the unique solution for \( W' \) in Theorem 1. This applies to convolution operators in the following way: Any set of distributions \( U \subseteq {\mathscr {D}}' \) induces a bilinear mapping
The space \( ( U )^{\mathbin {*}}_{{\mathscr {D}}'} \) serves as the largest joint domain for convolution operators with kernels from U and \( ( U )^{\mathbin {*}\mathbin {*}}_{{\mathscr {D}}'} \) is the smallest convolution perfect space containing the kernels. Note, that when all convolution operators K with kernel \( u \in U \) are represented by \( K( v ) = u \mathbin {*} v = B( u, v ) \) for all \( v \in ( U )^{\mathbin {*}}_{{\mathscr {D}}'} \) with some fixed bilinear convolution mapping B between convolution perfect spaces, then \( U \mathbin {\mathop {\widetilde{\mathbin {*}}}} V \) is the smallest possible codomain for this mapping B.
The partially defined operation (1.2) furnishes an algebraic and order theoretic structure \( \smash { \left( ( {{\mathfrak {P}}}( {\mathscr {D}}' ) )^{\mathbin {*}\mathbin {*}}_{{\mathscr {D}}'}, \subseteq , \mathbin {\mathop {\widetilde{\mathbin {*}}}} \right) } \). This triple is identified as a “commutative quantale with partially defined operation”, as explained in the following.
Up to formalities a commutative quantale [47, 48] is a triple \( ( Q, \le , \mathbin {\bullet } ) \) with \( ( Q, \le ) \) a complete lattice and \( ( Q, \mathbin {\bullet } ) \) a commutative semigroup such that
Now, consider for \( ( Q, \le ) \) the set of convolution perfect distribution spaces, ordered by inclusion, enriched with the null vector space \( \{ 0 \} \) and an artificially adjoined largest element “\( \infty \)”. Define \( \mathbin {\bullet } \) as the extension of \( \mathbin {\mathop {\widetilde{\mathbin {*}}}} \) to Q by \( \{ 0 \} \mathbin {\bullet } U = \{ 0 \} \) for \( U \in Q \), by \( U \mathbin {\bullet } V = \infty \) for non-convolvable \( U, V \in Q \setminus \{ \infty \} \) and by \( U \mathbin {\bullet } \infty = \infty \) for \( U \in Q \setminus \{ \{ 0 \} \} \). It will be proved that this defines a quantale \( ( Q, \le , \mathbin {\bullet } ) \) and we will call it the quantale associated to \( \left( ( {{\mathfrak {P}}}( {\mathscr {D}}' ) )^{\mathbin {*}\mathbin {*}}_{{\mathscr {D}}'}, \subseteq , \mathbin {\mathop {\widetilde{\mathbin {*}}}} \right) \).
Commutative quantales \( ( Q, \le , \mathbin {\bullet } ) \) possess residuals (using the nomenclature from [48, p. 922]) [47, p. 15]. The residual called “c by b” is defined as

The property (1.4) and the definition (1.5) result in the equivalence

see [47, p. 15], [17, Def. 3]. Because the quantale associated to \( \left( ( {{\mathfrak {P}}}( {\mathscr {D}}' ) )^{\mathbin {*}\mathbin {*}}_{{\mathscr {D}}'}, \subseteq , \mathbin {\mathop {\widetilde{\mathbin {*}}}} \right) \) possesses residuals it follows that the residual “W by V”, given by the set
is a well-defined convolution perfect space if \( V \subseteq W \) and is empty otherwise. Here \( V \subseteq W \) is equivalent to \( {\mathscr {E}}' \mathbin {\mathop {\widetilde{\mathbin {*}}}} V \subseteq W \), because \( {\mathscr {E}}' \) is identified as the neutral element for \( \mathbin {\mathop {\widetilde{\mathbin {*}}}} \). By construction, the space defined by (1.7) is the unique solution for \( U' \) in Theorem 1. Wrapping up, Theorem 1 reflects the closure system property of convolution perfect spaces and the quantale property (1.4) of the composition \( \mathbin {\mathop {\widetilde{\mathbin {*}}}} \) (more precisely, of its extension \( \bullet \) from above).
Let us now outline the paper section by section, thereby introducing notations and highlighting some important results. Beginning in Sect. 2 we introduce and study the so called \( {\varPhi } \)-absolute value
where \( {{\mathfrak {B}}}( {\mathscr {D}} ) := \left\{ B \subseteq {\mathscr {D}} \,;\, B ~ \text {bounded} \right\} \). Note, that \( |- |_{ \varPhi } \) is absolutely homogeneous and subadditive, just like a seminorm. In Theorems 2 and 3, these functionals are used to characterize mapping properties of convolution of distributions via convolution on \( {\mathscr {I}}_+ := \{ f:{\mathbb {R}}^d \rightarrow \overline{{\mathbb {R}}}_+ ~\text {lower semicontinuous}\} \).
The first part of Sect. 3 studies the quantale structure induced by convolution on the set system \( {\mathfrak {I}}_{\text {T}} \), which consist of the cone ideals, i.e. non-empty additively closed downsets \( I \subseteq {\mathscr {I}}_+ \), that are moderated, i.e.
Here \( \overline{\text {T}}_{ K } f := \sup \{ \text {T}_{ y } f \,;\, y \in K \} \) is the translation shell of \( f :{\mathbb {R}}^d \rightarrow \overline{{\mathbb {R}}}_+ \) with \( \text {T}_{ y } \) denoting translation by \( y \in {\mathbb {R}}^d \). A composition  is introduced on \( {\mathfrak {I}}_{\text {T}} \) via
is introduced on \( {\mathfrak {I}}_{\text {T}} \) via

where \( I \mathbin {*} J = \{ f \mathbin {*} g \,;\, f \in I, g \in J \}\) with \( f \mathbin {*} g \) declared pointwise by upper integrals and where \( \left( H \right) ^\curlyvee \) denotes the smallest cone ideal containing \( H \subseteq {\mathscr {I}}_+ \). Proposition 4 establishes that  is a commutative quantale.
is a commutative quantale.
The second part of Sect. 3 transports the quantale structure to a class of distribution spaces: To \( U \subseteq {\mathscr {D}}' \) one associates the moderated cone ideal
The regularization-solid closure of U is defined as the set \( V \subseteq {\mathscr {D}}' \) adjoint to the cone ideal \( I = |U |^{\curlyvee }_{{{\mathfrak {B}}}} \) with respect to the mapping \( |- |^{\curlyvee }_{{{\mathfrak {B}}}} \), in other words
Proposition 6 establishes a bijection between regularization-solid spaces and moderated cone ideals \( I \subseteq {\mathscr {I}}^+_{\text {lb}} := \left\{ f \in {\mathscr {I}}_+ \,;\, f ~ \text {locally bounded} \right\} \), that is interpreted via order theoretic adjoints. Further, Theorem 5 states that any convolution inclusion of regularization-solid spaces is equivalent to the convolution inclusion of the corresponding moderated cone ideals.
Section 4 is devoted to algebraic and order theoretic properties of convolution duals by studying the quantale  . Proposition 9 yields a correspondence between the convolution dual \( ( - )^{\mathbin {*}}_{{\mathscr {D}}'} \) and the duality operation
. Proposition 9 yields a correspondence between the convolution dual \( ( - )^{\mathbin {*}}_{{\mathscr {D}}'} \) and the duality operation

where denotes residuals (1.5) formed in  . The correspondence is induced by the bijection from Proposition 6, mentioned above. Defining
. The correspondence is induced by the bijection from Proposition 6, mentioned above. Defining
the convolution perfect distribution spaces are found to map bijectively to the non-degenerate \( J \in {\mathfrak {I}}^{\mathbin {*} \mathbin {*}}_{\text {T}} \) (this means \( J \in {\mathfrak {I}}^{\mathbin {*} \mathbin {*}}_{\text {T}} \) with \( \{ 0 \} \ne J \subseteq {\mathscr {I}}^+_{\text {lb}} \)). With the composition \( I \mathbin {\mathop {\widetilde{\mathbin {*}}}} J := ( I \mathbin {*} J )^{\mathbin {*}\mathbin {*}}_{\text {T}} \) for \( I, J \in {\mathfrak {I}}^{\mathbin {*} \mathbin {*}}_{\text {T}} \) this gives rise to a Girard-quantale \( ( {\mathfrak {I}}^{\mathbin {*} \mathbin {*}}_{\text {T}}, \subseteq , \mathbin {\mathop {\widetilde{\mathbin {*}}}} ) \) with dualizing element \( {\mathscr {I}}^+_{\text {lb}} \) [47, Sec. 6]. Identifying the space \( {\mathscr {I}}_+ \) with \( \infty \), it follows that \( ( {\mathfrak {I}}^{\mathbin {*} \mathbin {*}}_{\text {T}}, \subseteq , \mathbin {\mathop {\widetilde{\mathbin {*}}}} ) \) is isomorphic to the quantale associated to \( \left( ( {{\mathfrak {P}}}( {\mathscr {D}}' ) )^{\mathbin {*}\mathbin {*}}_{{\mathscr {D}}'}, \subseteq , \mathbin {\mathop {\widetilde{\mathbin {*}}}} \right) \), defined below Equation (1.4). These results are applied to maximal domains for composites of convolution operators in Theorem 6.
The construction (1.2) by itself does not yield optimal modules and algebras associated to semigroups of convolution operators, as has been observed for the Hilbert transform in [20, p. 301]. Therefore, Sect. 5 studies universal constructions of maximal modules and associated algebras. Let \( A \subseteq {\mathscr {D}}' \) be totally convolvable, that is, every p-tuple from A is convolvable. The space
and related constructions are studied in Sect. 5. This construction was introduced and applied to the mathematical modeling of fractional relaxation as linear translation invariant systems involving fractional derivatives on distributional domains in [31]. Theorem 7 establishes, that \( ( A )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \) defines a convolution module over \( ( A )^{\mathbin {*} \text {A}}_{{\mathscr {D}}'} := ( ( A )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} )^{\mathbin {*}}_{{\mathscr {D}}'} \), improving an earlier result by the authors [31, Thm. 8]. The latter constitutes a perfect convolution algebra: A convolution perfect space A that is totally convolvable and closed with respect to convolution. With Proposition 13 it is obtained that perfect convolution algebras correspond to idempotent elements [47, Def. 2.1.3] of \( ( {\mathfrak {I}}^{\mathbin {*} \mathbin {*}}_{\text {T}}, \subseteq , \mathbin {\mathop {\widetilde{\mathbin {*}}}} ) \). The construction (1.15) is applied to the Hilbert transform in Example 9.
In Sect. 6 topological structures are introduced and investigated. Inspired by Köthes’ “normale Topologie” on perfect sequence spaces [33, §30] convolution perfect spaces U will be endowed systematically with a weighted \( L^1 \)-type topology \( {\mathfrak {T}}^{\mathbin {*}}( U ) \) and a bornology \( {\mathfrak {B}}^{\mathbin {*}}( U ) \). For these definitions we obtain two functional analytic results. Theorem 8: Convolution between convolution perfect spaces is hypocontinuous whenever well-defined in the algebraic sense. Theorem 9: For given convolution perfect spaces \( V \subseteq W \), the quantale theoretic residual “W by V” from Equation (1.7) is equal to the largest regularization-solid space contained in the space of convolutors \( {\mathscr {O}}'{}_C( V, W ) \) [2, Def. 12]. The space \( {\mathscr {O}}'{}_C( V, W ) \) corresponds to the continuous convolution operators \( V \rightarrow W \).
Section 7 treats applications to causal fractional integrals and derivatives considered as translation invariant convolution operators. Their domains are significantly extended and the index laws are generalized to larger classes of distributions. Special cases of these results were recently discussed in [31] and in [22] with reference to desiderata for fractional integrals and derivatives. The negative fractional Laplacian \( (-\varDelta )^{ \alpha / 2 } \), \( \alpha > 0 \) is discussed in Sect. 8. We prove that the operator \( (-\varDelta )^{ \alpha / 2 } \), \( \alpha > 0 \) defines a continuous linear endomorphism of \( {\mathscr {D}}'_{ \alpha } \) by applying the maximal domain operator. This result was also stated in the recent “Handbook of Fractional Calculus with Applications” [34], but the characterization of the distributional domain, which is provided therein, is not accurate due to a subtle error in its functional analytic construction.
Some remarks on notation: We always treat distributions on \( {\mathbb {R}}^d \) and suppress the attribute \( ( {\mathbb {R}}^d ) \) with the exception of Sect. 7 and the space of causal distributions \( {\mathscr {D}}'_+ = {\mathscr {D}}'_+( {\mathbb {R}} ) \). The reader’s familiarity with notations for function spaces from [51], such as \( {\mathscr {E}}' \), \( {\mathscr {D}} \), \( {\mathscr {B}} \) etc. is assumed. The compact and bounded subsets of a locally convex space E are denoted as \( {{\mathfrak {K}}}( E ) \) and \( {{\mathfrak {B}}}( E ) \). The abbreviation \( {{\mathfrak {K}}} := {{\mathfrak {K}}}( {\mathbb {R}}^d ) \) is used and we write \( {\mathscr {D}} _K := \{ \phi \in {\mathscr {D}} \,;\, {\text {supp}}\phi \subseteq K \} \) for \( K \subseteq {\mathbb {R}}^d \). Translation, reflection and the support of a distribution u are denoted as \( \text {T}_{ x } u \), \( {\check{u}} \) and \( {\text {supp}} u \) respectively. The absolute convex closure of a subset B of a linear space is denoted by \( {\text {acx}} B \). Dual pairings are denoted by \( \langle - , - \rangle \). The shorthand \( \{ f = g \} \) stands for \( \{ x \in {\mathbb {R}}^d \,;\, f( x ) = g( x ) \} \). Because many uncommon or new notations are used in this work, we included Table 1 for convenient reference.
2 Generalized absolute values and convolution of distributions
This Section summarizes properties of generalized absolute values and translation shells and then describes their application to convolution.
2.1 Basic properties of generalized absolute values and translation shells
Definition 1
Let \( u \in {\mathscr {D}}' \) and \( \varPhi \in {{\mathfrak {B}}}( {\mathscr {D}} ) \). Define the \( \varPhi \)-absolute value of u as
Let \( f \in {\mathscr {I}}_+ \) and \( K \subseteq {\mathbb {R}}^d \). The K-translation shell of f is defined as
The \( \varPhi \)-absolute value \( |u |_{ \varPhi } \) of a distribution u is a locally Lipschitz continuous function \( {\mathbb {R}}^d \rightarrow {\mathbb {R}}_+ \). In particular \( |u |_{ \varPhi } \in {\mathscr {I}}^+_{\text {lb}} \) and \( |u |_{ \varPhi } \) is a regular distribution. Note, that the mapping \( {\mathscr {D}}' \ni u \mapsto |u |_{ \varPhi } \in {\mathscr {I}}_+ \) is absolutely homogeneous and subadditive, just like a seminorm. Similar to the definition of the spaces \( {\mathscr {D}}'{}_{L^{ p }} \) the definition of generalized absolute values depends on the Lie group structure of \( {\mathbb {R}}^d \). The fact that
makes generalized absolute values more convenient to use in connection with translation shell operators as compared to absolute values of regularizations. The latter could be called “weak generalized absolute values”.
Formation of K-translation shells equals supremal convolution with the indicator function \( 1_{ K } \). Supremal convolution arises in the context of convolution operators of measures on weighted spaces of continuous functions [30]. By virtue of [30, Prop. 3] \( \overline{\text {T}}_{ K } {\mathscr {I}}_+ \subseteq {\mathscr {I}}_+ \) and \( \overline{\text {T}}_{ K } {\mathscr {I}}^+_{\text {lb}} \subseteq {\mathscr {I}}^+_{\text {lb}} \) for all \( K \in {{\mathfrak {K}}} \).
Let us summarize some readily verified relations. Generalized absolute values and compact translation shells are connected by the relations
and
Moreover, for all \( K \in {{\mathfrak {K}}} \) with non-empty interior one finds \( \phi \in {\mathscr {D}} _K \) such that
Generalized absolute values preserve supports up to compact sets, that is
Further, if \( f \in {\mathscr {E}} \) is such that \( \{ f = 1 \} \supseteq {\text {supp}} u + ( K \cup \{ 0 \} ) \), then
For \(1 \le p \le +\infty \) and \( u \in {\mathscr {D}}' \) one readily derives from [51, Thm. XXV] that
Proposition 1
Let \( ( \theta _n ) \) be an approximate unit and \( \varPhi \in {{\mathfrak {B}}}( {\mathscr {D}} ) \). Then
and there exists \( \varPsi \in {{\mathfrak {B}}}( {\mathscr {D}} ) \) such that
Proof
Let \( x \in {\mathbb {R}}^d \) and \( u \in {\mathscr {D}}' \). Then the functions from the set \( ( 1 - \theta _n ) \mathrm {T}_{ x } \check{ \varPhi } \) converge to zero uniformly within \( {\mathscr {D}} \) for \( n \rightarrow \infty \) and \( |( 1 - \theta _n ) u |_{ \varPhi }( x ) \) is equal to \( \sup \{ |\langle u , ( 1 - \theta _n ) \text {T}_{ x } {\check{\phi }} \rangle |\,;\, \phi \in \varPhi \} \) by transposition. It follows \( |( 1 - \theta _n ) u |_{ \varPhi }( x ) \rightarrow 0 \) for \( n \rightarrow \infty \). Further, \(|\theta _n u |_{ \varPhi } \rightarrow |u |_{ \varPhi }\) point-wise for \( n \rightarrow \infty \), because \( |- |_{ \varPhi } \) satisfies the inverse triangle inequality. Replacing \( \varPhi \) by \( \text {T}_{ K } \varPhi \) and using (2.4a) yields (2.7a). Because the set of functions \( B := \{ 1 - \text {T}_{ x } {\check{\theta }}_n , \text {T}_{ x } {\check{\theta }}_n \,;\, x \in {\mathbb {R}}^d, n \in {\mathbb {N}} \} \) belongs to \( {{\mathfrak {B}}}( {\mathscr {B}} ) \), the set of test functions \( \varPsi := B \cdot \varPhi \) belongs to \( {{\mathfrak {B}}}( {\mathscr {D}} ) \). Now, Equation (2.7b) follows by construction of \( \varPsi \). \(\square \)
Proposition 2
The following three sets of functions \( {\mathscr {D}}' \rightarrow {\mathscr {I}}_+ \)
generate the same cone ideal of functions \( {\mathscr {D}}' \rightarrow {\mathscr {I}}_+ \).
Proof
It is known that every finite \( \varPhi \subseteq {\mathscr {D}} \) is contained in \( {\text {acx}}( \varPsi \mathbin {*} \varPsi ) \) for some other finite \( \varPsi \subseteq {\mathscr {D}} \) [14]. An examination of the proof in [14] reveals, that every \( \varPhi \in {{\mathfrak {B}}}( {\mathscr {D}} ) \) is contained in \( {\text {acx}} ( \varPsi \mathbin {*} \varTheta ) \) for some \( \varPsi \in {{\mathfrak {B}}}( {\mathscr {D}} ) \) and some finite \( \varTheta \subseteq {\mathscr {D}} \) (see also [12], where this is further generalized). Using this, one estimates
for some \( C < \infty \) and \( K \in {{\mathfrak {K}}} \) with a finite sum on the right-hand side. For the converse, note that \( C \cdot \text {T}_{ K } \theta \in {{\mathfrak {B}}}( {\mathscr {D}} ) \) and apply the relation (2.4a). \(\square \)
Proposition 3
Let \( \varPhi , \varPsi , \varTheta \in {{\mathfrak {B}}}( {\mathscr {D}} ) \). There exist \( {\tilde{\varPhi }}, {\tilde{\varPsi }}, {\tilde{\varTheta }} \in {{\mathfrak {B}}}( {\mathscr {D}} ) \) such that
Proof
Let \( u \in {\mathscr {D}}' \). Let \( L \in {{\mathfrak {K}}} \) and \( \psi \in {\mathscr {D}} _L \) with \( \int \psi ( x ) \,\text {d}{ x } = 1 \). Using (2.4c) and (2.4a) one obtains
Define K and \( \lambda \) as in (2.4b). By virtue of (2.4b) and (2.4a) one obtains
Thus \( {\tilde{\varPhi }} := \text {T}_{ L } \varTheta \), \( {\tilde{\varPsi }} := \{ \psi \} \) and \( {\tilde{\varTheta }} := \lambda \cdot \text {T}_{ K } \varPhi \) satisfy (2.10). \(\square \)
2.2 Characterization of convolution in terms of generalized absolute values
In the following we recall some properties of convolution \( \mathbin {*} \) on the set \( {\mathscr {I}}_+ \) of lower semicontinuous functions \( {\mathbb {R}}^d \rightarrow \overline{{\mathbb {R}}}_+ \). For definitions and properties of convolution of distributions we refer to [13, 27, 39, 42, 43, 46, 52, 59, 60]. In particular, for convolution of p-tuples see [27, 43, 46, 52, 60]. The most common definition for convolvability of p-tuples seems to be condition (a) in Theorem 2 below.
The convolution \( f \mathbin {*} g \) of \( f, g \in {\mathscr {I}}_+ \) is defined by the formula
via an upper integral [5]. By virtue of Fubini’s Theorem for lower semicontinuous functions [19, p. 55 (a)], one obtains that \( ( {\mathscr {I}}_+, \mathbin {*} ) \) is a semigroup. Further, \( \mathbin {*} \) is homogeneous with respect to \( \overline{{\mathbb {R}}}_+ \)-scalar multiplication, additive, isotone, reflection invariant and commutes argumentwise with translations. Conveniently, convolution on \( {\mathscr {I}}_+ \) does not require a convolvability condition for well behavedness. Isotony implies the inequality
where \( \overline{\text {T}}_{ K } f := \sup \{ \text {T}_{ x } f \,;\, x \in K \} \) as in Definition 1. The inequality (2.12) with compact K, L is fundamental for the quantale structures studied in Sect. 3.
Theorem 2
Let \( u_1, \dots , u_p \in {\mathscr {D}}' \), \( p \in {\mathbb {N}} \). The following are equivalent:
-
(a)
The inclusion \( { \theta }^{\varDelta p }( u_1 \otimes \cdots \otimes u_p ) \in {\mathscr {D}}'_{ L^1 }( {\mathbb {R}}^{dp} ) \) holds for all \( \theta \in {\mathscr {D}} \).
-
(b)
The inclusion \( |u_1 |_{ \varPhi } \mathbin {*} \cdots \mathbin {*} |u_p |_{ \varPhi } \in {\mathscr {I}}^+_{\text {lb}} \) holds for all \( \varPhi \in {{\mathfrak {B}}}( {\mathscr {D}} ) \).
-
(c)
The convolution \( |u_1 |_{ \{ \phi _1 \} } \mathbin {*} \cdots \mathbin {*} |u_p |_{ \{ \phi _p \} } \) is finite-valued for all \( \phi _1, \dots , \phi _p \in {\mathscr {D}} \).
Proof
It suffices to give a proof for \( p = 2 \), the generalization to \( p \in {\mathbb {N}} \) is straightforward. Denote \( u = u_1 \) and \( v = u_2 \). Due to (2.6) condition (a) implies
Using Equations (2.5a) and (2.5b), and the fact that \( { \theta }^{\varDelta } \) has uniformly bounded derivatives for \( \theta \in {\mathscr {D}} \), this is found to be equivalent to
According to [54, Theorem 51.7], \( \varPhi \in {{\mathfrak {B}}}( {\mathscr {D}} ( {\mathbb {R}}^{2d} ) ) \) can be replaced by \( \varPsi \otimes \varPsi \) with \( \varPsi \in {{\mathfrak {B}}}( {\mathscr {D}} ) \) in (2.14). Using \( |u \otimes v |_{ \varPsi \otimes \varPsi } = |u |_{ \varPsi } \otimes |v |_{ \varPsi } \) it follows that
is equivalent to (2.14). The integral in (2.15) is rewritten as
and therefore (2.15) is equivalent to \( |u |_{ \varPsi } \mathbin {*} |v |_{ \varPsi } \in L^{ 1 }_{\text {loc}} \) for all \( \varPsi \in {{\mathfrak {B}}}( {\mathscr {D}} ) \). Due to Equations (2.4a) and (2.12), this entails \( |u |_{ \varPsi } \mathbin {*} |v |_{ \varPsi } \in L^{ \infty }_{\text {loc}} \) for all \( \varPsi \in {{\mathfrak {B}}}( {\mathscr {D}} ) \), which is Condition (b). For trivial reasons “(b) \( \Rightarrow \) (c)”.
Note, that (c) is equivalent to \( (\psi \mathbin {*} u) \cdot (\phi \mathbin {*} {\check{v}}) \in L^1 \) for \( \psi , \phi \in {\mathscr {D}} \) when \( p = 2 \). Therefore “(c) \( \Rightarrow \) (a)” is a corollary of [52, Thm. 2]. \(\square \)
Theorem 3
Let \( \varPhi \in {{\mathfrak {B}}}( {\mathscr {D}} ) \) and \( p \in {\mathbb {N}} \). There exists \( \varPsi \in {{\mathfrak {B}}}( {\mathscr {D}} ) \) such that
for all convolvable tuples \( ( u_1, \dots , u_p ) \) with \( u_1, \dots , u_p \in {\mathscr {D}}' \).
Proof
Assume \( p = 2 \). Let \( u, v \in {\mathscr {D}}' \) convolvable and \( \varPsi \in {{\mathfrak {B}}}( {\mathscr {D}} ) \) such that \( \varPhi \subseteq {\text {acx}}( \varPsi \mathbin {*} \varPsi ) \) (see proof of Proposition 2). Using [46, Prop. 1] one estimates
\(\square \)
In the remaining part of this section we demonstrate a possible utilization of generalized absolute values by giving another proof for the associativity properties of convolution that were obtained in [27, 52, 60].
Lemma 1
Let \( u_1, \dots , u_p \in {\mathscr {D}}' \), \( p \in {\mathbb {N}} \) with \( ( u_1, \dots , u_p ) \) convolvable and \( ( \phi _n ) \) an approximate unit. Let \( \varPhi \in {{\mathfrak {B}}}( {\mathscr {D}} ) \). There exists \( \varTheta \in {{\mathfrak {B}}}( {\mathscr {D}} ) \) such that
for all \( n \in {\mathbb {N}} \). Moreover,
uniformly on compact sets.
Proof
Assume \( p = 2 \). Let \( \varPsi \in {{\mathfrak {B}}}( {\mathscr {D}} ) \) such that (2.17) holds and set
Clearly, \( \varTheta \in {{\mathfrak {B}}}( {\mathscr {D}} ) \). Using Equation (2.17) one estimates
Lebesgue’s Theorem of dominated convergence and Proposition 1 yield (2.19b). The generalization to general \( p \in {\mathbb {N}} \) is straightforward. \(\square \)
Corollary 1
Under the assumptions of Lemma 1 the sequence \( \phi _nu_1 \mathbin {*} \cdots \mathbin {*} \phi _nu_p \) converges to \( u_1 \mathbin {*} \cdots \mathbin {*} u_p \) for \( n \rightarrow \infty \) with respect to the strong topology of \( {\mathscr {D}}' \).
Theorem 4
Let \( u_0, u_1, \dots , u_p \in {\mathscr {D}}' \), \( p \in {\mathbb {N}} \). Convolvability of all the three tuples \( ( u_0, u_1, \dots , u_p ) \), \( ( u_1, \dots , u_p ) \) and \( ( u_0, u_1 \mathbin {*} \cdots \mathbin {*} u_p ) \) implies
In addition, if the tuple \( ( u_0, u_1, \dots , u_p ) \) is convolvable and \( u_0 \ne 0 \), then the tuples \( ( u_1, \dots , u_p ) \) and \( ( u_0, u_1 \mathbin {*} \cdots \mathbin {*} u_p ) \) are convolvable as well.
Proof
It holds by associativity of \( ( {\mathscr {E}}', \mathbin {*} ) \) [54, Thm. 27.7]. Using Lemma 1 multiple times, and then Corollary 1, yields that this equation holds in the limit. Now, assume \( u_0 \ne 0 \) and let \( \varPhi \in {{\mathfrak {B}}}( {\mathscr {D}} ) \) with \( |u_0 |_{ \varPhi } \ne 0 \). If at least one of the tuples \( ( u_1, \dots , u_p ) \) and \( ( u_0, u_1 \mathbin {*} \cdots \mathbin {*} u_p ) \) is non-convolvable then Theorem 3, Theorem 2 and the associative law for \( ( {\mathscr {I}}_+, \mathbin {*} ) \) imply that \( ( u_0, u_1, \dots , u_p ) \) is non-convolvable as well. \(\square \)
Corollary 2
Convolvable p-tuples of non-zero distributions can be arbitrarily rewritten by introducing parentheses without changing the result.
Corollary 3
Let \( u_1, \dots , u_p \in {\mathscr {D}}' \), \( v_1, \dots , v_p \in {\mathscr {E}}' \), \( p \in {\mathbb {N}} \). If \( ( u_1, \dots , u_p ) \) is convolvable then \( ( v_1 \mathbin {*} u_1, \dots , v_p \mathbin {*} u_p ) \) is convolvable and
Proof
Use “(a) \( \Leftrightarrow \) (c)” from Theorem 2, \( f \mathbin {*} {\mathscr {I}}^+_{\text {lb}} \subseteq {\mathscr {I}}^+_{\text {lb}} \) for all \( f \in {\mathscr {I}}^+_{\text {lb}} \) with compact support and Corollary 2. \(\square \)
3 Regularization-solid spaces and moderated cone ideals
This section first describes the convolution quantale structure on the set system of moderated cone ideals \( {\mathfrak {I}}_{\text {T}} \). Then regularization-solid distribution spaces are introduced using generalized absolute values. Convolution inclusions between such spaces are then characterized by the convolution inclusions of the corresponding moderated cone ideals via Proposition 6 and Theorem 5.
3.1 The convolution quantale of moderated cone ideals
Definition 2
A non-empty subset \( I \subseteq {\mathscr {I}}_+ \) will be called cone ideal if
A cone ideal \( I \subseteq {\mathscr {I}}_+ \) is called moderated if
The set system of (moderated) cone ideals and the corresponding closure operator are denoted by \( {\mathfrak {I}} \) (\( {\mathfrak {I}}_{\text {T}} \)) and \( \left( - \right) ^\curlyvee \) (\( \left( - \right) ^\curlyvee _{\text {T}} \)). One defines the binary operation

The residual operator of  and
and  is denoted by
is denoted by  and
and  , respectively. Equations (3.6) below extend
, respectively. Equations (3.6) below extend  and
and  to arbitrary subsets of \( {\mathscr {I}}_+ \). Ideals \( I \in {\mathfrak {I}}_{\text {T}} \) are called non-degenerate if \( {\mathscr {I}}^+_{\text {c}} \subseteq I \subseteq {\mathscr {I}}^+_{\text {lb}} \), where
to arbitrary subsets of \( {\mathscr {I}}_+ \). Ideals \( I \in {\mathfrak {I}}_{\text {T}} \) are called non-degenerate if \( {\mathscr {I}}^+_{\text {c}} \subseteq I \subseteq {\mathscr {I}}^+_{\text {lb}} \), where
Remark 1
-
1.
Cone ideals are precisely the non-empty additively closed down sets of \( {\mathscr {I}}_+ \). The set systems \( {\mathfrak {I}} \) and \( {\mathfrak {I}}_{\text {T}} \) are closure systems over \( {\mathscr {I}}_+ \). The set system \( {\mathfrak {I}}_{\text {T}} \) is a complete sublattice of \( {\mathfrak {I}} \).
-
2.
The closure operators \( \left( - \right) ^\curlyvee \) and \( \left( - \right) ^\curlyvee _{\text {T}} \) can be described explicitly as
$$\begin{aligned} \left( I \right) ^\curlyvee&= \left\{ f \in {\mathscr {I}}_+ \,;\, { \exists G \subseteq I~\text {finite},\, \lambda \in {\mathbb {R}}_+ : f \le \lambda \cdot \sup G } \right\} , \end{aligned}$$(3.5a)$$\begin{aligned}&= \left\{ f \in {\mathscr {I}}_+ \,;\, { \exists g_1, \dots , g_n \in I,\,n\in {\mathbb {N}}_0 : f \le \textstyle \sum ^n_{k=1} g_k } \right\} , \end{aligned}$$(3.5b)$$\begin{aligned} \left( I \right) ^\curlyvee _{\text {T}}&= \left( \left\{ \overline{\text {T}}_{ K } f \,;\, { f \in I, K \in {{\mathfrak {K}}} } \right\} \right) ^\curlyvee , \end{aligned}$$(3.5c)for \( I \subseteq {\mathscr {I}}^+_{\text {lb}} \). Here “\( \sup \)” denotes the pointwise supremum of sets of functions in \( {\mathscr {I}}_+ \). Note, that \( \overline{\text {T}}_{ K } ( \sup F ) = \sup \{ \overline{\text {T}}_{ K } f : f \in F \} \) for \( F \subseteq {\mathscr {I}}_+ \) and \( K \in {{\mathfrak {K}}} \), because suprema over two independent variables commute.
-
3.
Equation (3.2) is a typical mild assumption for weight function systems to obtain well behaved weighted (ultra-)distibution spaces and relates to the condition [wM] for weight function systems from [11].
Proposition 4
The triple  is a commutative quantale. The triple
is a commutative quantale. The triple  is a subquantale of
is a subquantale of  in the sense of [47, Def. 3.1.3]. The residuals formed in
in the sense of [47, Def. 3.1.3]. The residuals formed in  can be described by the formula
can be described by the formula

Residuals formed in  can be described by the formula
can be described by the formula

The quantale  is unitary with unit \( {\mathscr {I}}^+_{\text {c}} \), that is
is unitary with unit \( {\mathscr {I}}^+_{\text {c}} \), that is

Further, it holds

Proof
Using isotony and additivity of convolution one obtains the inclusion
Equation (3.9) and the fact that \( \mathbin {*} \) is associative and respects unions as an operation on \( {{\mathfrak {P}}}({\mathscr {I}}_+ ) \) [47, Exa. (10), p. 18] imply the quantale property (1.4), by virtue of [47, Thm. 3.3.1]. Equation (2.12) and Remark 1 entail that \( {\mathfrak {I}}_{\text {T}} \) is a subquantale. The Equations (3.6) are immediate from the definitions.
For unitarity of  , let \( 0 \ne f \in {\mathscr {I}}^+_{\text {c}} \), \( I \in {\mathfrak {I}}_{\text {T}} \), \( K := {\text {supp}} f \) and \(\lambda := \int f(x) \,\text {d}{ x }\). Using the inequalities (2.4) one estimates
, let \( 0 \ne f \in {\mathscr {I}}^+_{\text {c}} \), \( I \in {\mathfrak {I}}_{\text {T}} \), \( K := {\text {supp}} f \) and \(\lambda := \int f(x) \,\text {d}{ x }\). Using the inequalities (2.4) one estimates
which implies \( \left( {\mathscr {I}}^+_{\text {c}} \mathbin {*} I \right) ^\curlyvee = I \). Now, for \( I, J \in {\mathfrak {I}}_{\text {T}} \) with \( I, J \supseteq {\mathscr {I}}^+_{\text {c}} \) the inclusion (3.8) follows from (3.7), because  is monotone and because \( I + J \) is equal to the supremum of I and J formed in \( {\mathfrak {I}}_{\text {T}} \). \(\square \)
is monotone and because \( I + J \) is equal to the supremum of I and J formed in \( {\mathfrak {I}}_{\text {T}} \). \(\square \)
3.2 Regularization-solid distribution spaces and convolution inclusions
Definition 3
The moderated cone ideal associated to \( U \subseteq {\mathscr {D}}' \) is defined as
and the regularization-solid set of distributions associated to \( I \subseteq {\mathscr {I}}_+ \) is
The regularization-solid closure is the composite operator

and its fixed points are called regularization-solid distribution spaces.
Remark 2
Due to Proposition 2 one has
for every cone ideal \( I \subseteq {\mathscr {I}}_+ \) that satisfies \( 1_{ K } \mathbin {*} I \subseteq I \) for all \( K \in {{\mathfrak {K}}} \), which holds for all \( I \in {\mathfrak {I}}_{\text {T}} \) in particular. This yields another proof for Equation (2.6).
Proposition 5
It holds \( ||U |^{\curlyvee }_{{{\mathfrak {B}}}} |^{\curlyvee }_{{{\mathfrak {B}}}} = |U |^{\curlyvee }_{{{\mathfrak {B}}}} \) and  for all \( U \subseteq {\mathscr {D}}' \).
for all \( U \subseteq {\mathscr {D}}' \).
Proof
These are direct consequences of Proposition 3. \(\square \)
By an adjoint pair we will refer to a tuple (f, g) of isotone mappings \( f :X \rightarrow Y \) and \( g :Y \rightarrow X \) between to ordered sets X and Y such that \( f( x ) \le y \) if and only if \( x \le g( y ) \) for all \( x \in X \) and \( y \in Y \) (this is called “Galois connection” in [10, 7.23], [17]). The range of f is the associated kernel system (also called “interior system”) in Y and the range of g is the associated closure system in X. Kernel systems are the closure systems with respect to the reversed order.
Proposition 6
One has an adjoint pair
The associated kernel system in \( {\mathfrak {I}} \) is equal to \( {\mathfrak {I}}_{\text {T}} \cap {{\mathfrak {P}}}( {\mathscr {I}}^+_{\text {lb}} ) \).
Proof
Clearly, the criteria (Gal1) and (Gal2) from [10, 7.26] are satisfied, implying adjointness. Equation (2.4a) implies \( |U |^{\curlyvee }_{{{\mathfrak {B}}}} \in {\mathfrak {I}}_{\text {T}} \) for all \( U \subseteq {\mathscr {D}}' \) and it remains to prove \( I = |( I )^{\preceq }_{{\mathscr {D}}'} |^{\curlyvee }_{{{\mathfrak {B}}}} \) for \( I \in {\mathfrak {I}}_{\text {T}} \) with \( I \subseteq {\mathscr {I}}^+_{\text {lb}} \). Here, adjointness implies “\( \subseteq \)” and the reverse inclusion follows from (2.4b). \(\square \)
Corollary 4
The assignment defines a closure operator on \( {{\mathfrak {P}}}( {\mathscr {D}}' ) \) and \( U \mapsto |U |^{\curlyvee }_{{{\mathfrak {B}}}} \) defines an order isomorphism from the set system of regularization-solid distribution spaces to the set system \( {\mathfrak {I}}_{\text {T}} \cap {{\mathfrak {P}}}( {\mathscr {I}}^+_{\text {lb}} ) \), which constitutes a kernel system in \( {\mathfrak {I}}{} \) with kernel operator \( I \mapsto |( I )^{\preceq }_{{\mathscr {D}}'} |^{\curlyvee }_{{{\mathfrak {B}}}} \).
Proof
These are standard order theoretic conclusions found in [10, 7.27]. \(\square \)
Corollary 5
It holds \( |I |^{\curlyvee }_{{{\mathfrak {B}}}} = I \) for all \( I \in {\mathfrak {I}}_{\text {T}} \) with \( I \subseteq {\mathscr {I}}^+_{\text {lb}} \).
Lemma 2
Let \( p \in {\mathbb {N}} \). Convolution, regularization-solid closures and associated moderated cone ideals satisfy the compatibility relations


Proof
Assume \( p = 2 \), let \( I, J \in {\mathfrak {I}}_{\text {T}} \) and \( U, V \subseteq {\mathscr {D}}' \). The inequalities (2.4c) and (2.12) yield \( |I \mathbin {*} J |^{\curlyvee }_{{{\mathfrak {B}}}} \supseteq I \mathbin {*} J \). Conversely, Theorem 3 and Corollary 5 yield  and that
and that  . The proof is completed by using the inclusions \( |I \mathbin {*} J |^{\curlyvee }_{{{\mathfrak {B}}}} \in {\mathfrak {I}}_{\text {T}} \),
. The proof is completed by using the inclusions \( |I \mathbin {*} J |^{\curlyvee }_{{{\mathfrak {B}}}} \in {\mathfrak {I}}_{\text {T}} \),  ,
,  and applying the definition of
and applying the definition of  . \(\square \)
. \(\square \)
Theorem 5
Let U, V, W be regularization-solid distribution spaces with corresponding moderated cone ideals I, J, K (in the sense of Proposition 6). Then
Proof
Theorem 2 and Theorem 3 imply “\( \Leftarrow \)”. In order to prove “\( \Rightarrow \)”, assume \( U \mathbin {*} V \subseteq W \) with the left-hand side well defined. Proposition 5 yields \( I \subseteq U \) and \( J \subseteq V \) and thus \( I \mathbin {*} J \subseteq W \). Applying \( |- |^{\curlyvee }_{{{\mathfrak {B}}}} \) on both sides of the inclusion \( I \mathbin {*} J \subseteq W \) and using Lemma 2 yields  . \(\square \)
. \(\square \)
Example 1
Consider the moderated cone ideals
Clearly, \( {\mathscr {D}}' = ( {\mathscr {I}}^+_{\text {lb}} )^{\preceq }_{{\mathscr {D}}'} \). Using (2.5a) it is readily seen that \( {\mathscr {E}}' = ( {\mathscr {I}}^+_{\text {c}} )^{\preceq }_{{\mathscr {D}}'} \) and \( {\mathscr {D}}'_+ = ( {\mathscr {I}}^+_{+} )^{\preceq }_{{\mathscr {D}}'} \). Conversely, Proposition 6 implies \( |{\mathscr {E}}' |^{\curlyvee }_{{{\mathfrak {B}}}} = {\mathscr {I}}^+_{\text {c}} \), \( |{\mathscr {D}}' |^{\curlyvee }_{{{\mathfrak {B}}}} = {\mathscr {I}}^+_{\text {lb}} \) and \( |{\mathscr {D}}'_+ |^{\curlyvee }_{{{\mathfrak {B}}}} = {\mathscr {I}}^+_{+} \). Equation (2.6) implies \( {\mathscr {D}}'{}_{L^{ p }} = ( L^p \cap {\mathscr {I}}^+_{\text {lb}} )^{\preceq }_{{\mathscr {D}}'} \) for \( p \in [ 1, +\infty ] \). Conversely, however, \( |{\mathscr {D}}'{}_{L^{ p }} |^{\curlyvee }_{{{\mathfrak {B}}}} = {\mathscr {I}}^+_{\text {i}, p } \subsetneq L^p \cap {\mathscr {I}}^+_{\text {lb}} \). Using Theorem 5 the well known inclusions \( {\mathscr {E}}' \mathbin {*} {\mathscr {E}}' \subseteq {\mathscr {E}}' \), \( {\mathscr {E}}' \mathbin {*} {\mathscr {D}}' \subseteq {\mathscr {D}}' \), \( {\mathscr {D}}'_+ \mathbin {*} {\mathscr {D}}'_+ \subseteq {\mathscr {D}}'_+ \) and \( {\mathscr {D}}'{}_{L^{ p }} \mathbin {*} {\mathscr {D}}'{}_{L^{ q }} \subseteq {\mathscr {D}}'{}_{L^{ r }} \) for \( 1 / p + 1 / q = 1 + 1 / r \) can be derived from those for the corresponding ideals. For example, \( {\mathscr {I}}^+_{\text {i}, p } \mathbin {*} {\mathscr {I}}^+_{\text {i}, q } \subseteq {\mathscr {I}}^+_{\text {i}, r } \) follows from Youngs’ inequality and Equation (2.12).
Example 2
With the notations from Example 1 it holds

This is clear for \( p = \infty \) because constant functions belong to \( {\mathscr {I}}^+_{\text {i}, \infty } \). For \( p < \infty \) one uses [36, Thm. 3.6.1] with \( G = {\mathbb {Z}}^d \), the inequality \( \overline{\text {T}}_{ Q } f \mathbin {*} \overline{\text {T}}_{ Q } g \ge \overline{\text {T}}_{ 2Q } ( f \mathbin {*} g ) \) and the equivalence \( f \in \ell ^{p,+}( {\mathbb {Z}}^d ) \Leftrightarrow \overline{\text {T}}_{ Q } f \in {\mathscr {I}}^+_{\text {i}, p }( {\mathbb {R}}^d ) \). Here \( Q = [ -1, 1 ]^d \) and f is extended to a function \( {\mathbb {R}}^d \rightarrow \overline{{\mathbb {R}}}_+ \) by zero.
Example 3
The slowly increasing and rapidly decreasing lower semicontinuous functions P and \( P^* \) are moderated cone ideals. The corresponding regularization-solid spaces are the tempered distributions \( {\mathscr {S}}' = ( P )^{\preceq }_{{\mathscr {D}}'} \) and the convolutors \( {\mathscr {O}}'{}_C = ( P^* )^{\preceq }_{{\mathscr {D}}'} \). The space of very rapidly decreasing distributions \( {\mathscr {O}}'_M \) is not regularization-solid, because \( P^* \subseteq {\mathscr {O}}'_M \), but \( {\mathscr {O}}'_M \subsetneq {\mathscr {O}}'{}_C \).
Example 4
Let \( A \subseteq {\mathbb {R}}^{ d \times d } \) be positive definite and \( p \in {\mathbb {R}}_+ \). Consider the function \( g_{A,p}( x ) := \exp ( ( x^t A x )^p ) \). It holds \( \left( \{ g_{ A, p } \} \right) ^\curlyvee \in {\mathfrak {I}}_{\text {T}} \) if only if \( p \le 1 / 2 \). For \( p = 1 \) one calculates \( \left( \{ g_{ A, 1 } \} \right) ^\curlyvee _{\text {T}} = \left( \{ g_{ A, 1 } \cdot g_{ \lambda \text { I }, 1 / 2 } \,;\, \lambda \in {\mathbb {R}}_+ \} \right) ^\curlyvee \) where \( \text { I } \in {\mathbb {R}}^{ d \times d } \) denotes the unit matrix. Note, that adjoining infinitesimal translates of \( g_{ A, 1 }\) does not suffice to turn \( \left( \{ g_{ A, p } \} \right) ^\curlyvee \) into a moderated cone ideal because \( \left( g_{ A, 1 } \cdot P \right) ^\curlyvee \subsetneq \left( \{ g_{ A, 1 } \} \right) ^\curlyvee _{\text {T}} \).
4 Duals and perfections with respect to convolution
Convolution duals and perfections are investigated and interpreted with reference to quantale theory. Theorem 6 provides a systematic method to define the domain of composed convolution operators \( A \circ B \) such that the composition law \( A( B ( x ) ) = ( A \circ B )( x ) \) holds for all x from the domain of \( A \circ B \). Here, the convolution kernel of \( A \circ B \) is the convolution of the kernels of A and B.
4.1 Convolution perfect moderated cone ideals as a Girard quantale
Definition 4
Let \( I \subseteq {\mathscr {I}}_+ \). Define the operators
and denote the set \( {\mathfrak {I}}^{\mathbin {*} \mathbin {*}}_{\text {T}} := \{ I \in {\mathfrak {I}}_{\text {T}} \,;\, ( I )^{\mathbin {*}\mathbin {*}}_{\text {T}} = I \} \).
Remark 3
Convolution duals can be interpreted as residuals formed in the quantale  . Comparing Equations (4.1a) and (3.6) one notices
. Comparing Equations (4.1a) and (3.6) one notices

Proposition 7
Let \( I, J \in {\mathfrak {I}}_{\text {T}} \) and \( K \subseteq {\mathscr {I}}_+ \). Then
Proof
Let \(f\in I\), \(h^\prime \in ( K )^{\mathbin {*}}_{\text {T}}\) and \(g\in J\). It suffices to prove \((f\mathbin {*} h^\prime )\mathbin {*} g\in {\mathscr {I}}^+_{\text {lb}}\) because \(( K )^{\mathbin {*}}_{\text {T}}\in {\mathfrak {I}}_{\text {T}} \). Associativity and commutativity imply \((f\mathbin {*} h^\prime )\mathbin {*} g=(f\mathbin {*} g)\mathbin {*} h^\prime \). By assumption \(f\mathbin {*} g\in K\) and thus \((f\mathbin {*} g)\mathbin {*} h^\prime \in {\mathscr {I}}^+_{\text {lb}}\). \(\square \)
Corollary 6
For moderated cone ideals I, J, K such that \(I\mathbin {*} J\subseteq K\) it follows
Inserting \(K=\left( I\mathbin {*} J \right) ^\curlyvee \) one obtains
Remark 4
Corollary 6 implies that \( \big ( ( {\mathfrak {I}}_{\text {T}} )^{\mathbin {*}\mathbin {*}}_{\text {T}}, \subseteq , \mathbin {\mathop {\widetilde{\mathbin {*}}}} \big ) \) with

is a quotient quantale of  [47, Def. 3.1.1 & p. 32] and a Girard quantale with dualizing element \( {\mathscr {I}}^+_{\text {lb}} \) [47, Sec. 6]. See also [15, Thm. 2.6.13].
[47, Def. 3.1.1 & p. 32] and a Girard quantale with dualizing element \( {\mathscr {I}}^+_{\text {lb}} \) [47, Sec. 6]. See also [15, Thm. 2.6.13].
Proposition 8
It holds  for all \( K \in {\mathfrak {I}}^{ \mathbin {*} \mathbin {*} }_{ \text { T } } \) and \( J \in {\mathfrak {I}}_{\text {T}} \).
for all \( K \in {\mathfrak {I}}^{ \mathbin {*} \mathbin {*} }_{ \text { T } } \) and \( J \in {\mathfrak {I}}_{\text {T}} \).
Proof
First note, that  holds due to Equation (4.4b). The proposition then follows by calculating, for all \( I \in {\mathfrak {I}}_{\text {T}} \), that
holds due to Equation (4.4b). The proposition then follows by calculating, for all \( I \in {\mathfrak {I}}_{\text {T}} \), that

Here it was used that \(( - )^{\mathbin {*}\mathbin {*}}_{\text {T}}\) is a closure operator, Equations (1.6) and (4.4a) and that \(( - )^{\mathbin {*}}_{\text {T}}\) is a Galois connection. \(\square \)
4.2 Implications for convolution duals and perfections of distributions
Definition 5
The convolution dual and perfection of \( U \subseteq {\mathscr {D}}' \) are defined as
Spaces U such that \( ( U )^{\mathbin {*}\mathbin {*}}_{{\mathscr {D}}'} = U \) are called convolution perfect.
The mapping \( {{\mathfrak {P}}}( {\mathscr {D}}' ) \ni U \mapsto ( U )^{\mathbin {*}}_{{\mathscr {D}}'} \) reverses inclusions and \( U \subseteq ( ( U )^{\mathbin {*}}_{{\mathscr {D}}'} )^{\mathbin {*}}_{{\mathscr {D}}'} \) holds. Thus \( ( - )^{\mathbin {*}}_{{\mathscr {D}}'} \) is a Galois connection on \( {{\mathfrak {P}}}( {\mathscr {D}}' ) \) with \( ( - )^{\mathbin {*}\mathbin {*}}_{{\mathscr {D}}'} \) the associated closure [58, p. 20]. The same holds for \( ( - )^{\mathbin {*}}_{\text {T}} \) and \( ( - )^{\mathbin {*}\mathbin {*}}_{\text {T}} \). Convolution duals of classical distribution spaces were calculated in [58, Thm. 5].
Lemma 3
The convolution dual satisfies
Proof
Let \( v \in {\mathscr {D}}' \). One derives the chain of equivalences
by using Definitions 3 and 5 , and (i) Theorem 2; (ii) additivity and monotonicity of convolution; (iii) Equation (2.4a) and \( |U |^{\curlyvee }_{{{\mathfrak {B}}}} \in {\mathfrak {I}}_{\text {T}} \). \(\square \)
Proposition 9
The convolution dual operators \( ( - )^{\mathbin {*}}_{\text {T}} \) and \( ( - )^{\mathbin {*}}_{{\mathscr {D}}'} \) correspond to each other in the sense that
The space \( ( U )^{\mathbin {*}}_{{\mathscr {D}}'} \) is regularization-solid for all \( U \subseteq {\mathscr {D}}' \) and

Proof
Equation (4.8a) follows from Equation (4.7) by inserting \( U = ( I )^{\preceq }_{{\mathscr {D}}'} \) and using \( I = |( I )^{\preceq }_{{\mathscr {D}}'} |^{\curlyvee }_{{{\mathfrak {B}}}} \) for \( I \in {\mathfrak {I}}_{\text {T}} \), which holds by Corollary 4. Equation (4.8b) follows by applying \( |- |^{\curlyvee }_{{{\mathfrak {B}}}} \) on both sides of Equation (4.7) and using \(( |U |^{\curlyvee }_{{{\mathfrak {B}}}} )^{\mathbin {*}}_{\text {T}} = |( ( |U |^{\curlyvee }_{{{\mathfrak {B}}}} )^{\mathbin {*}}_{\text {T}} )^{\preceq }_{{\mathscr {D}}'} |^{\curlyvee }_{{{\mathfrak {B}}}}\) for \( U \subseteq {\mathscr {D}}' \), \( U \nsubseteq \{ 0 \} \), which holds by Corollary 4.
Equation (4.7) implies that \( ( U )^{\mathbin {*}}_{{\mathscr {D}}'} \) is regularization-solid for any \( U \subseteq {\mathscr {D}}' \). Using this fact and Equations (4.8) yields

\(\square \)
Proposition 10
Let \( U, V, W \subseteq {\mathscr {D}}' \) be regularization-solid and \( V \ne \{ 0 \} \). Then:
Proof
Let I, J, K be the moderated cone ideals corresponding to U, V, W. By Theorem 5, the left-hand side of (4.11) is equivalent to the left-hand side of (4.3) and the right-hand side of (4.3) follows from Proposition 7. It holds \( J \ne \{ 0 \} \) and thus \( ( J )^{\mathbin {*}}_{\text {T}} \subseteq {\mathscr {I}}^+_{\text {lb}} \). Theorem 5, Theorem 2 and Proposition 9 imply the right-hand side of (4.11). \(\square \)
Theorem 6
Let \( U, V \subseteq {\mathscr {D}}' \) be regularization-solid and non-zero with (U, V) convolvable. Then \( ( ( U \mathbin {*} V )^{\mathbin {*}}_{{\mathscr {D}}'}, U ) \) and \( ( ( U \mathbin {*} V )^{\mathbin {*}}_{{\mathscr {D}}'}, V ) \) are convolvable and
Moreover, for \( u \in U \), \( v \in V \) and \( w \in ( U \mathbin {*} V )^{\mathbin {*}}_{{\mathscr {D}}'} \), one has the associative law
Proof
Equation (4.12a) follows from Corollary 6 and Proposition 4 applied in the light of Theorem 5 and Proposition 9. The inclusions (4.12a) imply that triples (u, v, w) in (4.12b) are convolvable. Thus, Theorem 4 implies (4.12b). \(\square \)
Example 5
The most illustrative example of a non-perfect regularization-solid distribution space is the space \( \dot{{\mathscr {B}}}' = ( {\mathscr {I}}^+_{\text {v}} )^{\preceq }_{{\mathscr {D}}'} \) of distributions vanishing at infinity. The convolution perfection of \( \dot{{\mathscr {B}}}' \) is the space \( {\mathscr {B}}' = ( {\mathscr {I}}^+_{\text {b}} )^{\preceq }_{{\mathscr {D}}'} \) of uniformly bounded distributions [58, Theorem 5].
Example 6
An important example of weighted distribution spaces are spaces of power-logarithmic growth in dimension \( d \in {\mathbb {N}} \). Define the sets
and the functions of \( \mu \)-power growth \( P^\mu := P^{ \mu ; 0 } \). As sets, the associated distribution spaces and their convolution duals coincide with the spaces

that were studied in [1, 20, 44, 57]. For \( \mu \in ( -\infty , \infty ] \) we define further
When \( d = 1 \) the notation
will be used. All the defined sets belong to \( {\mathfrak {I}}_{\text {T}} \). It can be calculated that



whenever \( \mu + \nu < -d \) and \( P^{ \mu ; k } \mathbin {*} P^{ \nu ; l } = \left( \{ +\infty \} \right) ^\curlyvee \) otherwise. The relations (4.17) hold for all \( \mu , \nu \in {\mathbb {R}} \) with \( d = 1 \) when \( P^{ \mu ; k } \) is replaced by \( P^{ \mu ; k }_+ \). As many of the relations (4.17) were proved previously in [4, 8, 41, 9, Lemma 2.2] [1, Lemma 2.8] and [18, VIII.8] we omit the calculations.
5 Largest distributional modules for convolution semigroups
Operators that generate algebras and modules of distributions,  , \( ( - )^{\mathbin {*} \text {A}}_{{\mathscr {D}}'} \) and \( ( - )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \), are introduced and investigated parallel to their counterparts \( ( - )^{\mathbin {*} \text {a}}_{{\mathscr {I}}_+} \), \( ( - )^{\mathbin {*} \text {A}}_{\text {T}} \) and \(( - )^{\mathbin {*} \text {M}}_{\text {T}} \). Theorem 7 characterizes \( ( A )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \) as convolution module over the associative algebra \( ( A )^{\mathbin {*} \text {A}}_{{\mathscr {D}}'} \) for given totally convolvable \( A \subseteq {\mathscr {D}}' \).
, \( ( - )^{\mathbin {*} \text {A}}_{{\mathscr {D}}'} \) and \( ( - )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \), are introduced and investigated parallel to their counterparts \( ( - )^{\mathbin {*} \text {a}}_{{\mathscr {I}}_+} \), \( ( - )^{\mathbin {*} \text {A}}_{\text {T}} \) and \(( - )^{\mathbin {*} \text {M}}_{\text {T}} \). Theorem 7 characterizes \( ( A )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \) as convolution module over the associative algebra \( ( A )^{\mathbin {*} \text {A}}_{{\mathscr {D}}'} \) for given totally convolvable \( A \subseteq {\mathscr {D}}' \).
5.1 Regularization-solid algebras and modules
Definition 6
-
1.
Let \( I \subseteq {\mathscr {I}}_+ \). The smallest cone ideal J that satisfies the inclusions \( J \mathbin {*} J \subseteq J \) and \( I \subseteq J \) is denoted by \( ( I )^{\mathbin {*} \text {a}}_{{\mathscr {I}}_+} \).
-
2.
Let \( A \subseteq {\mathscr {D}}' \). The set A is called totally convolvable if for all \( p \in {\mathbb {N}} \) all tuples \( ( a_1, \dots , a_p ) \) with \( a_1, \dots , a_p \in A \) are convolvable. If, in addition, \( A \mathbin {*} A \subseteq A \) (and \( \delta \in A \)) then A is called a convolution semigroup (monoid). Linear convolution monoids are called convolution algebras. The smallest convolution semigroup and regularization-solid convolution algebra containing A are denoted \( ( A )^{\mathbin {*} \text {s}}_{{\mathscr {D}}'} \) and
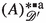 , respectively.
, respectively.
Proposition 11
-
1.
For \( I \in {\mathfrak {I}}_{\text {T}} \) it holds \( ( I )^{\mathbin {*} \text {a}}_{{\mathscr {I}}_+} \in {\mathfrak {I}}_{\text {T}} \).
-
2.
A set \( A \subseteq {\mathscr {D}}' \) is totally convolvable iff \( ( |A |^{\curlyvee }_{{{\mathfrak {B}}}} )^{\mathbin {*} \text {a}}_{{\mathscr {I}}_+} \subseteq {\mathscr {I}}^+_{\text {lb}} \).
-
3.
If \( A \subseteq {\mathscr {D}}' \) is totally convolvable then the same holds for
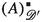 . Moreover, \( ( A )^{\mathbin {*} \text {s}}_{{\mathscr {D}}'} \),
. Moreover, \( ( A )^{\mathbin {*} \text {s}}_{{\mathscr {D}}'} \), 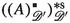 and
and 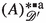 exist and
exist and 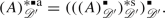 (5.1)
(5.1) -
4.
The operators
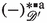 and \( ( - )^{\mathbin {*} \text {a}}_{{\mathscr {I}}_+} \) correspond to each other via
and \( ( - )^{\mathbin {*} \text {a}}_{{\mathscr {I}}_+} \) correspond to each other via 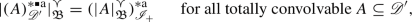 (5.2a)
(5.2a)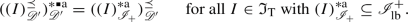 (5.2b)
(5.2b)
Proof
Part 1 follows from Equation (2.12) and Part 2 from Theorem 2.
Part 3: Part 2 and the equation  , furnished by Proposition 6, imply that
, furnished by Proposition 6, imply that  is totally convolvable. Now, the existence of \( ( A )^{\mathbin {*} \text {s}}_{{\mathscr {D}}'} \) and
is totally convolvable. Now, the existence of \( ( A )^{\mathbin {*} \text {s}}_{{\mathscr {D}}'} \) and  is clear. Once it is proved that
is clear. Once it is proved that  is a regularization-solid convolution algebra containing A it is clear that this is the smallest such set of distributions, proving Equation (5.1). Now, Lemma 2 implies
is a regularization-solid convolution algebra containing A it is clear that this is the smallest such set of distributions, proving Equation (5.1). Now, Lemma 2 implies

Forming the supremum over \( p \in {\mathbb {N}} \) within the complete lattice \( {\mathfrak {I}}_{\text {T}} \) results in \( ( |A |^{\curlyvee }_{{{\mathfrak {B}}}} )^{\mathbin {*} \text {a}}_{{\mathscr {I}}_+} \) on the right-hand side. The supremum on the left-hand side can be moved inside of \( |- |^{\curlyvee }_{{{\mathfrak {B}}}} \) turning into a union of sets, due to Proposition 6 and [10, Prop. 7.31]. Thus, the left-hand side becomes  . Further,
. Further,

follows from Proposition 6. Finally, Theorem 5 applied to (5.4) yields that the left-hand side is a convolution algebra.
Part 4: Inserting (5.1) in (5.4), applying \(|- |^{\curlyvee }_{{{\mathfrak {B}}}}\), and using Corollary 4 yields Equation (5.2a). Let \( I \in {\mathfrak {I}}_{\text {T}} \) with \( ( I )^{\mathbin {*} \text {a}}_{{\mathscr {I}}_+} \in {\mathscr {I}}^+_{\text {lb}} \) and \( A := ( I )^{\preceq }_{{\mathscr {D}}'} \). By Part 2 A is totally convolvable. Now insert \( A = ( I )^{\preceq }_{{\mathscr {D}}'} \) into (5.2a) and apply the operator \( ( - )^{\preceq }_{{\mathscr {D}}'} \) on both sides. Because  is regularization-solid and \( ( I )^{\mathbin {*} \text {a}}_{{\mathscr {I}}_+} \in {\mathfrak {I}}_{\text {T}}\), another application of Corollary 4 yields (5.2b). \(\square \)
is regularization-solid and \( ( I )^{\mathbin {*} \text {a}}_{{\mathscr {I}}_+} \in {\mathfrak {I}}_{\text {T}}\), another application of Corollary 4 yields (5.2b). \(\square \)
5.2 Convolution perfect algebras and modules
Definition 7
Let \( I \subseteq {\mathscr {I}}_+ \). Define the operators
The maximal convolution module for totally convolvable \( A \subseteq {\mathscr {D}}' \) is defined as
The convolution perfect algebra generated by A is defined as
Proposition 12
Let \( A \subseteq {\mathscr {D}}' \) be totally convolvable. Then:

Proof
Let  and \( 0 \ne m \in {\mathscr {D}}' \). Using the inclusion \( |B |^{\curlyvee }_{{{\mathfrak {B}}}} \mathbin {*} \cdots \mathbin {*} |B |^{\curlyvee }_{{{\mathfrak {B}}}} \subseteq B \) and Theorem 2 the statement “\( ( b_1, \dots , b_p, m ) \) is convolvable for all \( b_1, \dots , b_p \in B \), \( p \in {\mathbb {N}} \)” is seen to be equivalent to “ (b, m) is convolvable for all \( b \in B \)”. This equivalence means just that \( ( B )^{\mathbin {*}}_{{\mathscr {D}}'} = ( B )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \). Using the latter equation, one obtains
and \( 0 \ne m \in {\mathscr {D}}' \). Using the inclusion \( |B |^{\curlyvee }_{{{\mathfrak {B}}}} \mathbin {*} \cdots \mathbin {*} |B |^{\curlyvee }_{{{\mathfrak {B}}}} \subseteq B \) and Theorem 2 the statement “\( ( b_1, \dots , b_p, m ) \) is convolvable for all \( b_1, \dots , b_p \in B \), \( p \in {\mathbb {N}} \)” is seen to be equivalent to “ (b, m) is convolvable for all \( b \in B \)”. This equivalence means just that \( ( B )^{\mathbin {*}}_{{\mathscr {D}}'} = ( B )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \). Using the latter equation, one obtains
which completes the proof. \(\square \)
Proposition 13
The operators \( ( - )^{\mathbin {*} \text {M}}_{\text {T}} \) and \( ( - )^{\mathbin {*} \text {A}}_{\text {T}} \) are related to \( ( - )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \) and \( ( - )^{\mathbin {*} \text {A}}_{{\mathscr {D}}'} \), respectively, analogously to Equations (4.8) and (5.2).
Proof
This follows from Propositions 9 and 11 . \(\square \)
Theorem 7
Let \( A \subseteq {\mathscr {D}}' \) be totally convolvable. Then \( ( A )^{\mathbin {*} \text {A}}_{{\mathscr {D}}'} \) is totally convolvable as well and convolution defines bilinear operations
that are associative. That is, for all \( a, b, c \in ( A )^{\mathbin {*} \text {A}}_{{\mathscr {D}}'} \) and \( m \in ( A )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \) we have
Proof
Let  . By Theorem 2, the pair \( ( B, ( A )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} ) \) is convolvable and \( ( A )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} = ( B )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \). Therefore B instead of A can be considered. Let \( b_1, \dots , b_p, b \in B \), \( p \in {\mathbb {N}} \), \( b_1 \ne 0 \) and let \( m \in ( B )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \). By definition of \( ( - )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \) the tuple \( ( b_1, \dots , b_p, b, m ) \) is convolvable. Using Theorem 4 one concludes that the tuple \( ( b_1, \dots , b_p, b \mathbin {*} m ) \) is convolvable as well. This proves \( B \mathbin {*} ( B )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \subseteq ( B )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \). Using Proposition 10 with \( U, W = ( B )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \), \( V = B \) and Proposition 11 one obtains
. By Theorem 2, the pair \( ( B, ( A )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} ) \) is convolvable and \( ( A )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} = ( B )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \). Therefore B instead of A can be considered. Let \( b_1, \dots , b_p, b \in B \), \( p \in {\mathbb {N}} \), \( b_1 \ne 0 \) and let \( m \in ( B )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \). By definition of \( ( - )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \) the tuple \( ( b_1, \dots , b_p, b, m ) \) is convolvable. Using Theorem 4 one concludes that the tuple \( ( b_1, \dots , b_p, b \mathbin {*} m ) \) is convolvable as well. This proves \( B \mathbin {*} ( B )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \subseteq ( B )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \). Using Proposition 10 with \( U, W = ( B )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \), \( V = B \) and Proposition 11 one obtains
Applying Proposition 10 to (5.10) one obtains \(( B )^{\mathbin {*} \text {A}}_{{\mathscr {D}}'}\mathbin {*}( B )^{\mathbin {*} \text {A}}_{{\mathscr {D}}'}\subseteq ( B )^{\mathbin {*} \text {A}}_{{\mathscr {D}}'}\).
Having proved well definedness of (5.8), the associative laws (5.9) are immediate from Theorem 4 and the definitions of \( ( A )^{\mathbin {*} \text {A}}_{{\mathscr {D}}'} \) and \( ( A )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \). \(\square \)
Example 7
The pairs \( ( {\mathscr {E}}', {\mathscr {D}}' ) \), \( ( {\mathscr {D}}'_{L^1}, {\mathscr {B}}' ) \), \( ( {\mathscr {O}}'{}_C, {\mathscr {S}}' ) \), \( ( {\mathscr {D}}'_+, {\mathscr {D}}'_+ ) \) and \( ( {\mathscr {D}}'_-, {\mathscr {D}}'_- ) \) are classical examples of the form \( ( ( U )^{\mathbin {*} \text {A}}_{{\mathscr {D}}'}, ( U )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} ) \). The spaces \( {\mathscr {S}}'_+ \) and \( ( {\mathscr {S}}'_+ )^{\mathbin {*}}_{{\mathscr {D}}'} \) arise naturally in causal fractional calculus on the real line, see Sect. 7. It is well known that \( {\mathscr {S}}'_+ \) is a convolution algebra of distributions [55]. The space \( ( {\mathscr {S}}'_+ )^{\mathbin {*}}_{{\mathscr {D}}'} \) consists of distributions vanishing rapidly for \( t \rightarrow -\infty \).
Example 8
Continuing Example 6 consider an arbitrary sum (supremum of ideals) \( \sum {\mathcal {P}} \) formed from a subset \( {\mathcal {P}} \) of \( \{ P^{\nu ;l}_+ \,;\, \nu \in {\mathbb {R}}, l \in {\mathbb {N}}_0 \} \). Equations (4.17) imply that of such sums precisely the sets \( P^{ -\mu }_+ \), \( P^{ < -\mu }_+ \), \( P^{ -\mu ; k }_+ \), \( P^{ -\mu ; \infty }_+ \), \( P_+ \), \( Q_+ \) and \( R_+ \), where \( \mu \in ( 1, +\infty ) \) and \( k \in {\mathbb {N}}_0 \), are closed with respect to convolution. Similar statements are true for the sets \( P^{ \mu , k } \). Due to Proposition 11, the corresponding regularization-solid distribution spaces are regularization-solid convolution algebras.
6 Hypocontinuity with respect to a weighted \( L^1 \)-type topology
Topologies and bornologies are now introduced on every convolution perfect distribution space using generalized absolute values and convolution. Hypocontinuity [26, Ch. 4, §7] and boundedness [25, 1:2] of convolution are established in Theorem 8 for these topologies and bornologies. A residual formed in \( ( {\mathfrak {I}}^{\mathbin {*} \mathbin {*}}_{\text {T}}, \subseteq , \mathbin {\mathop {\widetilde{\mathbin {*}}}} ) \) is characterized as the largest regularization-solid space contained in the corresponding space of convolutors in Theorem 9. The Hilbert transform on \( {\mathscr {D}}'{}_{L^{ p }} \) is a convolutor not contained in this subspace, see Example 9.
Recall, that the space of convolutors \( {\mathscr {O}}'{}_C( V, W ) \) from V to W consists of the distributions u with the property that the mapping \( {\mathscr {D}} \ni \phi \mapsto u \mathbin {*} \phi \) extends to a continuous linear mapping \( V \rightarrow W \), see [2, Def. 12]. Here V and W are normal distribution spaces in the sense of [26, p. 319].
Definition 8
Let U be a convolution perfect distribution space. The locally convex topology \( {\mathfrak {T}}^{\mathbin {*}}( U ) \) is generated by the seminorms
The bornology \( {\mathfrak {B}}^{\mathbin {*}}( U ) \) is defined as the set of subsets \( B \subseteq U \) such that
Remark 5
The inclusion \( ( U, {\mathfrak {T}}^{\mathbin {*}}( U ), {\mathfrak {B}}^{\mathbin {*}}( U ) ) \rightarrow ( V, {\mathfrak {T}}^{\mathbin {*}}( V ), {\mathfrak {B}}^{\mathbin {*}}( V ) ) \) is continuous and bounded for convolution perfect \( U \subseteq V \) due to \( ( U )^{\mathbin {*}}_{{\mathscr {D}}'} \supseteq ( V )^{\mathbin {*}}_{{\mathscr {D}}'} \).
Remark 6
The topology \( {\mathfrak {T}}^{\mathbin {*}}( {\mathscr {D}}' ) \) coincides with the strong topology on \( {\mathscr {D}}' \) due to \( {\mathscr {I}}^+_{\text {c}} = |( {\mathscr {D}}' )^{\mathbin {*}}_{{\mathscr {D}}'} |^{\curlyvee }_{{{\mathfrak {B}}}} \) and Proposition 2.
Remark 7
Any convolution perfect space \( U \subseteq {\mathscr {D}}' \) defines a normal space of distributions \( U = ( U, {\mathfrak {T}}^{\mathbin {*}}( U ) ) \): Clearly, the space \( {\mathscr {E}}'_K \) is continuously included in U for any compact \( K \subseteq {\mathbb {R}}^d \), and thus, \( {\mathscr {E}}' \) is continuously included in U by [26, Thm. 1, p. 321]. Proposition 1 and Lebesgue’s theorem of dominated convergence yield that \( {\mathscr {E}}' \), and thus \( {\mathscr {D}} \), is dense in U. Remarks 5 and 6 yield that U is continuously included in \( {\mathscr {D}}' \).
Remark 8
The seminorm in (6.1a) is equal to \( \sup _{K\in {{\mathfrak {K}}}} \int _K |u |_{ \varPhi }( x ) |v |_{ \varPhi }( -x ) \,\text {d}{ x } \) and therefore Remark 6 implies that any \( {\mathfrak {T}}^{\mathbin {*}}( U ) \)-neighborhood is \( {\mathscr {D}}' \)-closed. By virtue of [28, Thm. 3.2.4] it follows, that any \( {\mathfrak {T}}^{\mathbin {*}}( U ) \)-Cauchy-filter that has a \( {\mathscr {D}}' \)-limit, has the same \( {\mathfrak {T}}^{\mathbin {*}}( U ) \)-limit.
Theorem 8
Let U, V and W be convolution perfect distribution spaces and assume that (U, V) is convolvable and \( U \mathbin {*} V \subseteq W \). Then, convolution defines a hypocontinuous and bounded bilinear mapping
Proof
Let \( I := |U |^{\curlyvee }_{{{\mathfrak {B}}}} \), \( J := |V |^{\curlyvee }_{{{\mathfrak {B}}}} \) and \( K := |W |^{\curlyvee }_{{{\mathfrak {B}}}} \). Theorem 5 and Corollary 6 yield the inclusion \( ( I )^{\mathbin {*}\mathbin {*}}_{\text {T}} \mathbin {*} ( J )^{\mathbin {*}\mathbin {*}}_{\text {T}} \subseteq ( K )^{\mathbin {*}\mathbin {*}}_{\text {T}} \). Then, an application of Theorem 3 yields the inclusion \( {\mathfrak {B}}^{\mathbin {*}}( U ) \mathbin {*} {\mathfrak {B}}^{\mathbin {*}}( V ) \subseteq {\mathfrak {B}}^{\mathbin {*}}( W ) \), that is, (6.2) is bounded.
Let \( B \in {\mathfrak {B}}^{\mathbin {*}}( U ) \), \( v \in V \), \( w^\prime \in ( W )^{\mathbin {*}}_{{\mathscr {D}}'} \) and \( \varPhi \in {{\mathfrak {B}}}( {\mathscr {D}} ) \). Theorem 3 yields
with \(\varPsi \in {{\mathfrak {B}}}( {\mathscr {D}} )\) independent of B, v and \(w^\prime \). Corollary 6 implies
Thus (6.3) implies hypocontinuity. \(\square \)
In the following, when a particular bornology [25, 1:1] is specified on the spaces V, W then \( {\mathscr {O}}'{}_C( V, W ) \) is endowed with the topology of uniform convergence with respect to the bornology on V [28, Sec. 8.4]. The bornology on \( {\mathscr {O}}'{}_C( V, W ) \) is defined as the sets of mappings \( L \subseteq {\mathscr {O}}'{}_C( V, W ) \) such that L(B) is bounded in W for any bounded \( B \subseteq V \). In the following we will occassionally write U instead of \( ( U, {\mathfrak {T}}^{\mathbin {*}}( U ), {\mathfrak {B}}^{\mathbin {*}}( U ) ) \), when the meaning is clear.
Lemma 4
Let \( u, v \in {\mathscr {D}}' \) be convolvable and \( \varPhi \in {{\mathfrak {B}}}( {\mathscr {D}} ) \). There exist \( {\tilde{u}} \in |\{ u \} |^{\curlyvee }_{{{\mathfrak {B}}}} \), \( {\tilde{v}} \in |\{ v \} |^{\curlyvee }_{{{\mathfrak {B}}}} \) and \( \varPsi \in {{\mathfrak {B}}}( {\mathscr {D}} ) \) such that \( |u |_{ \varPhi } \mathbin {*} |v |_{ \varPhi } \le |{\tilde{u}} \mathbin {*} {\tilde{v}} |_{ \varPsi } \).
Proof
Using (2.4c), (2.12) and (2.4a) one obtains
for \( {\tilde{u}} := |u |_{ \text {T}_{ Q } \varPhi } \) and \( {\tilde{v}} := |v |_{ \text {T}_{ Q } \varPhi } \) with \( Q = [ -1, 1 ]^d \) and \( \varPsi := \{ \psi \} \) with \( \psi \in {\mathscr {D}} _{ Q } \) such that \( \int \psi ( x ) \,\text {d}{ x } = 1 \). \(\square \)
Lemma 5
Let V, W be convolution perfect distribution spaces with \( V \subseteq W \) and let \( u \in {\mathscr {O}}'{}_C( V, W ) \), where V, W are endowed with the topologies from (6.1a). The continuous extension \( C_u :V \rightarrow W \) of the mapping \( {\mathscr {D}} \ni \phi \mapsto u \mathbin {*} \phi \in W \) is given by convolution of distributions \( C_u( v ) = u \mathbin {*} v \).
Proof
Let \( u \in {\mathscr {D}}' \) such that \( {\mathscr {D}} \ni \phi \mapsto u \mathbin {*} \phi \in W \) is \( {\mathfrak {T}}^{\mathbin {*}}( V ) \)-\( {\mathfrak {T}}^{\mathbin {*}}( W ) \)-continuous. Then \( v \mapsto C_u( v ) \) is continuous as a mapping \( \mathscr {E}' \rightarrow \mathscr {D}' \) by Remarks 5, 6 and 7. Because \(\mathscr {D}\) is dense in \( \mathscr {E}' \) and convolution of distributions is hypocontinuous as a mapping \( \mathscr {D}' \times \mathscr {E}' \rightarrow \mathscr {D}' \) it follows that \( C_u( v ) = u \mathbin {*} v \) for all \( v \in \mathscr {E}' \).
Now, let \( ( \phi _n ) \) be an approximate unit and \( v \in V \). Proposition 1 and Lebesgue’s theorem of dominated convergence imply that \( ( \phi _n v ) \) converges in V. Thus, \( C_u( \phi _n v ) = u \mathbin {*} ( \phi _n v ) \) is a \( {\mathfrak {T}}^{\mathbin {*}}( W ) \)-Cauchy-filter that converges in \( {\mathscr {D}}' \) by continuity, completeness and Remarks 5 and 6. Then [39, Thm. 7.1] implies that (u, v) is convolvable and that \( \lim _{n\rightarrow \infty } C_u(\phi _n v) = u \mathbin {*} v \) within \( {\mathscr {D}}' \). According to Remark 8, this implies \( C_u( v ) = u \mathbin {*} v \) for all \( v \in V \). \(\square \)
Theorem 9
Let \( V, W \subseteq {\mathscr {D}}' \) be convolution perfect with \( V \subseteq W \). Then
with the arrow “\( \rightarrow \)” indicating a bounded and continuous inclusion and with the convolution perfect distribution space U specified as

The space U is characterized as the largest regularization-solid space of distributions that is contained in \( {\mathscr {O}}'{}_C( V, W ) \).
Proof
Proposition 4 and Corollary 4 allow to apply Equation (1.6) to Equation (6.6b) to obtain \( |U |^{\curlyvee }_{{{\mathfrak {B}}}} \mathbin {*} |V |^{\curlyvee }_{{{\mathfrak {B}}}} \subseteq |W |^{\curlyvee }_{{{\mathfrak {B}}}} \). Then Theorem 5 yields that (U, V) is convolvable with \( U \mathbin {*} V \subseteq W \) and Theorem 8 yields the continuous and bounded inclusion \( U \rightarrow {\mathscr {O}}'{}_C( V, W ) \) from (6.6a).
Now, let \( v \in V \), \( \varPhi \in {{\mathfrak {B}}}( {\mathscr {D}} ) \) and \( u \in {\mathscr {D}}' \) with \( |\{ u \} |^{\curlyvee }_{{{\mathfrak {B}}}} \subseteq {\mathscr {O}}'{}_C( V, W ) \). Lemma 4 yields \( {\tilde{u}} \in |\{ u \} |^{\curlyvee }_{{{\mathfrak {B}}}} \), \( {\tilde{v}} \in V \) and \( \varPsi \in {{\mathfrak {B}}}( {\mathscr {D}} ) \) with \( \varPhi \subseteq \varPsi \) and \( |{\tilde{u}} \mathbin {*} {\tilde{v}} |_{ \varPsi } \ge |u |_{ \varPhi } \mathbin {*} |v |_{ \varPhi } \). By Lemma 5\( ( {\tilde{u}}, {\tilde{v}} ) \) is convolvable and \( {\tilde{u}} \mathbin {*} {\tilde{v}} \in W \). Thus, Theorem 2 yields
Finally, Equation (6.7) and Proposition 8 imply

\(\square \)
Example 9
The Hilbert transform \( H :u \mapsto \text {PV}( 1 / x ) \mathbin {*} u \) is a convolutor of \( {\mathscr {D}}'{}_{L^{ p }}( {\mathbb {R}} ) \) for all \( 1< p < \infty \) [42, p. 356], [29]. One calculates that
with the weights \( w_p \) and \( w_{ p; k } \) as defined in Example 6. Using Proposition 11, Proposition 13 and Equations (4.17) one obtains
Note, that \( ( \text {PV}(1/x) )^{\mathbin {*}}_{{\mathscr {D}}'} \supsetneq ( \text {PV}(1/x) )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \), as observed in [20, Remark (3)].
According to Equations (6.9) and (3.18) the distribution \(\text {PV}( 1 / x )\) is not contained in the largest regularization-solid subspace of the space of convolutors \( {\mathscr {O}}'{}_C( {\mathscr {D}}'{}_{L^{ p }} ) \), compare Theorem 9. On the other hand, (6.10) entails
Theorem 7 guarantees that \( H( H f ) = -\pi ^2 f \) holds for all \( f \in ( \text {PV}( 1 / x ) )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \).
7 Distributional causal fractional calculus on the real line
The machinery developed so far is now applied to the causal fractional integration and differentiation operators. We determine their largest natural domains, generalize the index laws and determine spaces on which semigroups of these operators operate continuously and linearly. Following Schwartz [51] the fractional integrals \( {\text {I}}^{ \alpha }_+ \) and derivatives \( {\text {D}}^{ \alpha }_+ \) with \( \alpha \in {\mathbb {C}} \) are defined as convolution operators [21, Sec.9]
with kernel
for \( \Re \alpha > -m \) and \( m \in {\mathbb {N}}_0 \). The distributions \( \{ Y_{ \alpha } \,;\, \alpha \in {\mathbb {C}} \} \) form a convolution group, more precisely
The operators \( {\text {I}}^{ \alpha }_+ \) and \( {\text {D}}^{ \alpha }_+ \) are continuous and linear on the space of causal distributions \( {\mathscr {D}}'_+ \). Equation (7.3) entails the index law \( {\text {I}}^{ \alpha }_+( {\text {I}}^{ \beta }_+ u ) = {\text {I}}^{ \alpha + \beta }_+ u \) for all \( u \in {\mathscr {D}}'_+ \) and \( \alpha , \beta \in {\mathbb {C}} \). Enlarged domains to be obtained now are described using the spaces \( P^{ \mu ; k }_+ \) from Example 6 on page 18.
7.1 Largest distributional domains and index laws
Calculating the generalized absolute values of the distributions \( Y_{ \alpha } \) one obtains
Using the convolution dual operator \(( - )^{\mathbin {*}}_{{\mathscr {D}}'}\) we specify the domain of \({\text {I}}^{\alpha }_+\) as
Using Remark 2 the domain of \( {\text {I}}^{ \alpha }_+ \) with \( \alpha \in {\mathbb {C}} \setminus {-{\mathbb {N}}_0} \) can also be written as
Remark 7 and Theorem 8 guarantee that \( {\text {I}}^{ \alpha }_+ \) coincides with the unique continuous extension from \( {\mathscr {D}} \) to \( {\text {Dom}} {\text {I}}^{ \alpha }_+ \).
Remark 9
Equation (7.4) clearly extends Schwartz’ definition of \( {\text {I}}^{ \alpha }_+ \). Further, its extension contains exponentially weighted spaces of distributions [35] and the test function space \({\mathfrak {G}}_+\) from [49, p. 146-147]. For \( \Re \alpha < 0 \) the domain (7.4) contains the distributional analogues for differentiable functions suitable for Marchaud’s approach of fractional differentiation [49, p. 109].
Theorem 10
Let \( \alpha , \beta \in {\mathbb {H}} := \{ z \in {\mathbb {C}} \,;\, \Re z > 0 \} \). The following equations hold true with all expressions well defined in the sense of (7.4)
This includes the special case
Proof
The proof is an application of Theorem 6. Equation (7.6a) follows using \( U := ( P^{ \Re \alpha - 1 }_+ )^{\preceq }_{{\mathscr {D}}'} \) and \( V := ( P^{ \Re \beta - 1 }_+ )^{\preceq }_{{\mathscr {D}}'} \) which results in \( ( U )^{\mathbin {*}}_{{\mathscr {D}}'} = {\text {Dom}}{\text {I}}^{ \alpha }_+ \), \( ( V )^{\mathbin {*}}_{{\mathscr {D}}'} = {\text {Dom}}{\text {I}}^{ \beta }_+ \) and \( ( U \mathbin {*} V )^{\mathbin {*}}_{{\mathscr {D}}'} = {\text {Dom}}{\text {I}}^{ \alpha + \beta }_+ \) according to equations (7.4), (4.17a) and Theorem 5. The proofs for the remaining equations are similar. \(\square \)
Remark 10
The conditions on u in Theorem 10 have a similar form as the index laws for fractional powers of generators of semigroups [16, Thm. 5.32], [32, Prop. 5.2]. See [7, 21, 38] for more references on this topic. Using the theory developed in the present work has the advantage that one obtains simple and explicit formulas for the domains.
Remark 11
Interpreting \( {\text {I}}^{ \alpha }_+ \) as an improper integral leads to different sufficient conditions for the index law, see Theorem 1.3 and Remark 1.4 in [37].
7.2 Largest distributional domains for endomorphic operation
In order to realize the operators \( {\text {I}}^{ \alpha }_+ \) as convolution endomorphisms of distribution spaces we apply the operator \( ( - )^{\mathbin {*} \text {M}}_{{\mathscr {D}}'} \). Using Equations (4.17) one obtains
One observes, that \( {\text {Dom}}{\text {D}}^{ \alpha }_+ = {\text {Endom}}{ {\text {D}}^{ \alpha }_+ } \) iff \( \alpha \in \{ 0 \} \cup {\mathbb {H}} \). Applying the operator \( ( - )^{\mathbin {*} \text {A}}_{{\mathscr {D}}'} \) induces natural semigroups of operators \( {\text {D}}^{ \alpha }_+ \) as described in the following: Let \( \text { I } \) denote the closure operator associated to the closure system
Using Equations (4.17) we calculate that
for all \( A \subseteq {\mathbb {C}} \). This means that the closure operator \( \text {I} \) on \( {\mathbb {C}} \) generates those subsemigroups of \( \{ Y_{ \alpha } \,;\, \alpha \in {\mathbb {C}} \} \), that are maximal with respect to total convolvability on some joint domain space from the class of convolution perfect distribution spaces.
Theorem 11
Let \( p > 0 \). The convolution semigroup \( {\mathsf {X}} \) operates continuously and linearly on the distribution space \( {\mathsf {Y}} \) by convolution of distributions for
The convolution group \( {\mathsf {X}} \) operates bijectively and continuously on \( {\mathsf {Y}} \) for
In all cases compact sets of indices \( \alpha \) map to equicontinuous sets of operators.
Proof
This is proved similar to Theorem 10 using (7.8), Theorems 7 and 8 . \(\square \)
Example 10
The convolution dual \( ( \{ \exp ( \text {i} x^2 ) \} )^{\mathbin {*}}_{{\mathscr {D}}'} = {\mathscr {S}}' \) was calculated in [56, Satz 4]. Due to \( Y_{ \alpha } \in {\mathscr {S}}' \) this implies the existence of \( {\text {I}}^{ \alpha }_+ \exp ( \text {i} x^2 ) \) for all \( \alpha \in {\mathbb {C}} \). Theorem 11 yields in addition, that \( {\text {I}}^{ \alpha }_+ \exp ( \text {i} x^2 ) \in {\text {Dom}}{\text {I}}^{ \beta }_+ \) and \( {\text {I}}^{ \alpha + \beta }_+ \exp ( \text {i} x^2 ) = {\text {I}}^{ \beta }_+( {\text {I}}^{ \alpha }_+ \exp ( \text {i} x^2 ) ) \) for all \( \alpha , \beta \in {\mathbb {C}} \) because \( \exp ( \text {i} x^2 ) \in {\mathscr {O}}'{}_C \subseteq ( P_+ )^{\mathbin {*}}_{{\mathscr {D}}'} \).
Remark 12
The above results can be placed into the context of the desiderata for fractional calculus proposed in [23].
-
a)
For the group \( \{ Y_{ \alpha } \,;\, \alpha \in {\mathbb {C}} \} \) the domain \( ( P_+ )^{\mathbin {*}}_{{\mathscr {D}}'} = {\mathsf {G}}_{ \text { (b) } } = {\mathsf {G}}_{ \text { (c) } } \) satisfies the desiderata (a)-(c) by virtue of Theorem 11. Theorem 8 yields that the desiderata (d)-(f) are satisfied as well with \( {\mathsf {G}}_{ \text { (d) } } = ( P_+ )^{\mathbin {*}}_{{\mathscr {D}}'} \).
-
b)
For the semigroup cases (7.9a)-(7.9d) Theorem 11 shows that desideratum (b) in [23] is satisfied for fractional derivatives instead of integrals. However, apart from desideratum (c) also desideratum (d) can never hold for the semigroup case \(( Q_+ )^{\mathbin {*}}_{{\mathscr {D}}'}\) in (7.9d), not even if \({\mathbb {H}}\) were replaced with \( {\mathbb {H}} \cup \{ 0 \} \). The reason is, that \(1\in ( Q_+ )^{\mathbin {*}}_{{\mathscr {D}}'}\) and Remark (3) in [43, p. 327] implies \(Y_{- \alpha }\mathbin {*} 1=0\) for all \(\Re \alpha >0\).
-
c)
The case (7.9f) in Theorem 11 establishes a kind of (purely imaginary) “fractional calculus of order zero” in the sense that \(\Re \alpha =0\) for all operators in the desiderata of [23].
8 Distributional domains for fractional laplacians
In the following we consider the fractional (negative) Laplacian \( (-\varDelta )^{ \alpha / 2 } \) on \( {\mathbb {R}}^d \) with general \( \alpha \in {\mathbb {C}} \). The operator \( (-\varDelta )^{ \alpha / 2 } \) can be defined as
with the domain \( {\text {Dom}} (-\varDelta )^{ \alpha / 2 } := ( R_{ -\alpha } )^{\mathbin {*}}_{{\mathscr {D}}'} \) and the Riesz kernel \( R_\alpha \) [42, p. 369], [34], which is given by the density
The mapping \( \alpha \mapsto R_\alpha \) is extended to all of \( {\mathbb {C}} \) by taking the finite part of the meromorphic extension of (8.2). Using [42, p. 369] the generalized absolute values of \( R_{ \alpha } \) are calculated as
with the notations from Equation (4.13a). Because \( R_\alpha \) and \( R_\beta \) are convolvable if and only if \( \Re ( \alpha + \beta ) < d \), the convolution kernel \( R_\alpha \) gives rise to an endomorphism on a regularization-solid distribution space if and only if \( \Re \alpha \le 0 \). For such \( \alpha \), Equations (4.17b) and (4.17c) furnish
Remark 13
Consider the special case \(d=1\).
-
a)
Then, if \( \Re \alpha > - 1 \), the operator \( (-\varDelta )^{ \alpha / 2 } \) can be factorized into causal and anticausal fractional derivatives
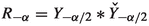 due to the differentiation rule from [43] and Equation (1.5.7) from [45] (see also [49, §12]). Further, using Theorem 6 and the relation
due to the differentiation rule from [43] and Equation (1.5.7) from [45] (see also [49, §12]). Further, using Theorem 6 and the relation 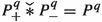 for \( q < -1 \) one finds, for \( \Re \alpha > 0 \), the factorization theorem $$\begin{aligned} (-\varDelta )^{ 2 \alpha } u&= {\text {D}}^{ \alpha }_+( {\text {D}}^{ \alpha }_- u ) = {\text {D}}^{ \alpha }_-( {\text {D}}^{ \alpha }_+ u ) \end{aligned}$$(8.5)
for \( q < -1 \) one finds, for \( \Re \alpha > 0 \), the factorization theorem $$\begin{aligned} (-\varDelta )^{ 2 \alpha } u&= {\text {D}}^{ \alpha }_+( {\text {D}}^{ \alpha }_- u ) = {\text {D}}^{ \alpha }_-( {\text {D}}^{ \alpha }_+ u ) \end{aligned}$$(8.5)for all \( u \in {\text {Dom}} {\text {D}}^{ \alpha }_+ \cap {\text {Dom}} {\text {D}}^{ \alpha }_- \), where \( {\text {Dom}} {\text {D}}^{ \alpha }_+ \cap {\text {Dom}} {\text {D}}^{ \alpha }_- = {\text {Dom}} (-\varDelta )^{ \alpha } \) if \( \alpha \notin {\mathbb {Z}} \). Thus, the factorization (8.5) is valid only on a strict subdomain of the fractional Laplacian. This domain contains the joint domain \( \bigcap \{ {\mathscr {D}}'_\alpha \,;\, \Re \alpha > 0 \} = ( Q )^{\mathbin {*}}_{{\mathscr {D}}'} \) of all fractional Laplacians with \( \Re \alpha > 0 \). In particular \( ( Q )^{\mathbin {*}}_{{\mathscr {D}}'} \supsetneq {\mathscr {B}}' = {\mathscr {D}}'{}_{L^{\infty }} \).
-
b)
The set of distributions \( F := \{ Y_{ \alpha },\, {\check{Y}}_{ \alpha },\, R_{ \alpha },\, \text {PV}(1/x) \,;\, { \Re \alpha \le 0 } \} \) is totally convolvable according to Example 2, Equations (7.4a), (8.3), (4.17b) and (4.17c). The algebra of convolution operators \( ( F )^{\mathbin {*} \text {a}}_{{\mathscr {D}}'} \) generated by this set contains Riesz-Feller derivatives and generalized Hilbert transforms [6, 40]. According to Theorem 7 and eqs. (7.7), (6.10) and (8.4) this algebra operates on \( ( R )^{\mathbin {*}}_{{\mathscr {D}}'} \) by convolution. In contrast to the above \( ( R )^{\mathbin {*}}_{{\mathscr {D}}'} \subsetneq {\mathscr {B}}' \).
Remark 14
For \( \alpha > 0\), \( \alpha \notin 2{\mathbb {N}} \) the endomorphic domain of \( (-\varDelta )^{ \alpha / 2 } \) reads
with the weight
Note, that \( {\mathscr {D}}'_\alpha = {\mathscr {D}}'_{ L^1, \alpha } \). Thus, \((-\varDelta )^{\alpha /2}\) is a continuous linear endomorphism of \(({\mathscr {D}}'_\alpha ,{\mathfrak {T}}^{\mathbin {*}}( {\mathscr {D}}'_\alpha ))\). The space \({\mathscr {D}}'_\alpha \) was envisaged in [34, 53] as the dual space of
endowed with the seminorms \( f \mapsto \Vert ( \partial ^\beta f ) \cdot w_{ d + \alpha } \Vert _\infty \) and \( \beta \in {\mathbb {N}}^d_0 \). The dual of \( {\mathscr {D}} _\alpha \) is not contained in \({\mathscr {D}}'\), contrary to the statements in [34] and [53, Sect. 2.1], because \( {\mathscr {D}} \) is not dense in \( {\mathscr {D}} _\alpha \). However, the oversight can be repaired by using the set of seminorms \( f \mapsto \Vert ( \partial ^\beta f ) \cdot w_{ d + \alpha } \cdot g \Vert _\infty \) with \(g\in {\mathscr {C}}_{0}\) and \(\beta \in {\mathbb {N}}^d_0\) instead, similar to [44, Prop. 1.3.1.]. With this topology the dual space of \( {\mathscr {D}} _\alpha \) is indeed given by \({\mathscr {D}}'_\alpha \) as defined in (8.6a). For \( \alpha \in ( 0, 2 ) \) the same argument as in [34] proves that \( (-\varDelta )^{ \alpha / 2 }\) defines a continuous linear endomorphism of \( {\mathscr {D}} _\alpha \) with respect to the modified topology.
Remark 15
Using Theorem 6 and (4.17c), as in the proof of Theorem 10, it follows that the convolution operators \( (-\varDelta )^{ \alpha / 2 } \) and \( (-\varDelta )^{ -\alpha / 2 } \), \(\Re \alpha \ge 0\), can be composed both ways when restricted to \(u\in {\text {Dom}}(-\varDelta )^{ -\alpha / 2 } \), and then obey
Thus, one obtains an inversion theorem for Riesz potentials free from the restriction \( \alpha < d \) that applies for \(L^p\)-spaces, compare [49, Thm. 26.3].
Remark 16
The Riesz potentials \(R_\alpha \) with \(\alpha \in {\mathbb {H}} \setminus ( d + 2{\mathbb {N}}_0 )\) can be turned into a group with \(\alpha \in {\mathbb {C}}\), if they are defined as operators on the dual space \( \varPhi ' \) of the Lizorkin space [49, (25.16)]
where \({\mathscr {F}}\) denotes the Fourier transform on the Schwartz space. However, the elements of \( \varPhi ' \) can not be interpreted as distributions because \( \varPhi \cap {\mathscr {D}} = \{ 0 \} \). This follows from the Wiener-Paley Theorem and the Taylor formula for multivariate power series.
Remarks 15 and 16 combined with \({\mathscr {D}}'_\alpha \subseteq {\mathscr {S}}^\prime \) lead us to conjecture that there exist random variables \(w\in {\mathscr {D}}'_\alpha \) and a measure on \({\mathscr {D}}'_\alpha \) such that for all \(g\in {\mathscr {S}}\) the dual pairing \(\langle (-\varDelta )^{-\alpha /2}w , g \rangle \) is a centered Gaussian with variance \( \Vert g \Vert ^2_{ L^2({\mathbb {R}}^d) } \). If true, the conjecture would render the traditional construction of multidimensional fractional Brownian fields more direct.
References
Alvarez, J., Guzman-Partida, M., Perez-Esteva, S.: Harmonic extensions of distributions. Mathematische Nachrichten 280, 1443–1466 (2007)
Bargetz, C., Nigsch, E., Ortner, N.: Convolvability and regularization of distributions. Annali di Matematica Pura ed Applicata 196, 2239–2251 (2017)
Birkhoff, G.: Lattice Theory. American Mathematical Society, Providence. Rhode Island, 3rd edition (1973)
Biswas, A., Swanson, D.: Navier-Stokes equations and weighted convolution inequalities in groups. Comm. Partial Differ. Equ. 35, 559–589 (2010)
Bourbaki, N.: Elements of Mathematics: Integration I. Springer, Berlin (2004)
Butzer, P., Trebels, W.: Hilberttransformationen, gebrochene integration und differentiation. In Brandt, L. (ed) Forschungsberichte des Landes Nordrhein-Westfalen, Nr. 1889, pp. 1–81, Köln, Opladen. Westdeutscher Verlag (1968)
Butzer, P.L., Westphal, U.: Introduction to fractional calculus. In: Hilfer, R. (ed.) Applications of Fractional Calculus in Physics, pp. 1–86. World Scientific, Singapore (2000)
Cui, Z., Omey, E., Wang, W., Wang, Y.: Asymptotics of convolution with the semi-regular-variation tail and its application to risk. Extremes 21, 509–532 (2018)
Damek, E., Dziubanski, J., Jaming, P., Perez-Esteva, S.: Distributions that are convolvable with generalized Poisson kernel of solvable extensions of homogeneous Lie groups. Math. Scand. 105, 31–65 (2009)
Davey, B., Priestley, H.: Introduction to Lattices and Order, 2nd edn. Cambridge University Press, Cambridge (2002)
Debrouwere, A., Neyt, L., Vindas, J.: The nuclearity of Gelfand-Shilov spaces and kernel theorems. Collect. Math. 72, 203–227 (2021)
Debrouwere, A., Prangoski, B., Vindas, J.: Factorization in Denjoy-Carleman classes associated to representations of \( ( {\mathbb{R}}^d, + ) \). J. Funct. Anal. 280, 108831 (2021)
Dierolf, P., Voigt, J.: Convolution and S-convolution of distributions. Collect. Math. 29, 185–196 (1978)
Dixmier, J., Malliavin, P.: Factorisation de Fonctions et de Vecteurs Indefiniment Differentiables. Bull. Sci. Math. 102, 305–330 (1978)
Eklund, P., Gutierrez-Garcia, J., Höhle, U., Kortelainen, J.: Semigroups in Complete Lattices. Springer, Berlin (2018)
Engel, K., Nagel, R.: One-Parameter Semigroups for Linear Evolution Equations. Springer, Berlin (2000)
Erné, M., Koslowski, J., Melton, A., Strecker, G.E.: A Primer on Galois Connections. Ann. N. Y. Acad. Sci. 704, 103–125 (1993)
Feller, W.: An Introduction to Probability Theory and Its Applications, vol. II. Wiley, New York (1971)
Godement, R.: Analysis IV: Integration and Spectral Theory. Springer, Berlin (2015)
Guzman-Partida, M., Ortner N., Wagner P.: M. Riesz’ kernels as boundary values of conjugate Poisson kernels. Bull. Sci. Math. 135, 291–302 (2011)
Hilfer, R.: Mathematical and physical interpretations of fractional derivatives and integrals. In Kochubei, A. and Luchko, Y. (eds.) Handbook of Fractional Calculus with Applications: Basic Theory, Vol. 1, pp. 47–86, Berlin. Walter de Gruyter GmbH (2019)
Hilfer, R., Kleiner, T.: Maximal domains for fractional derivatives and integrals. Mathematics 8, 1107 (2020)
Hilfer, R., Luchko, Yu.: Desiderata for fractional derivatives and integrals. Mathematics 7, 149 (2019)
Hirata, Y.: On Convolutions in the Theory of Distributions. J. Sci. Hiroshima Univ. Ser. A 22, 89–98 (1958)
Hogbe-Nlend, H.: Bornologies and Functional Analysis. North-Holland Publ.Co, Amsterdam (1977)
Horvath, J.: Topological Vector Spaces and Distributions. Addison-Wesley, Reading (1966)
Horvath, J.: Sur la Convolution des Distributions. Bull. Sci. Math. 98, 183–192 (1974)
Jarchow, H.: Locally Convex Spaces. Teubner, Stuttgart (1981)
King, F.: Hilbert Transforms, vol. 1. Cambridge University Press, Cambridge (2009)
Kleiner, T., Hilfer, R.: Convolution operators on weighted spaces of continuous functions and supremal convolution. Ann. Matematica 199, 1547–1569 (2020)
Kleiner, T., Hilfer, R.: Fractional glassy relaxation and convolution modules of distributions. Anal. Math. Phys. 11, 130 (2021)
Komatsu, H.: Fractional powers of operators. Pac. J. Math. 19, 285–346 (1966)
Köthe, G.: Topologische Lineare Räume. Springer, Berlin (1966)
Kwasnicki, M.: Fractional Laplace operator and its properties. In: Kochubei, A., Luchko, Y. (eds.) Handbook of Fractional Calculus with Applications: Basic Theory, vol. 1, pp. 159–193. Berlin. Walter de Gruyter GmbH (2019)
Lamb, W.: A distributional theory of fractional calculus. Proc. R. Soc. Edinb. 99A, 347–357 (1985)
Larsen, R.: An Introduction to the Theory of Multipliers. Springer, Berlin (1971)
Martinez, C., Redondo, A., Sanz, M.: Suitable domains to define fractional integrals of Weyl via fractional powers of operators. Stud. Math. 202, 145–164 (2011)
Martinez Carracedo, C., Sanz Alix, M.: The Theory of Fractional Powers of Operators. Elsevier, Amsterdam (2001)
Mincheva-Kaminska, S.: Convolution of distributions in sequential approach. Filomat 28, 1543–1557 (2014)
Okikiolu, G.: A generalisation of the Hilbert transform. J. Lond. Math. Soc. 40, 27–30 (1965)
Omey, E., van Gulck, S., Vesilo, R.: Semi-heavy tails. Lith. Math. J. 58, 480–499 (2018)
Ortner, N.: On some contributions of John Horvath to the theory of distributions. J. Math. Anal. Appl. 297, 353–383 (2004)
Ortner, N.: On convolvability conditions for distributions. Monatshefte für Mathematik 160, 313–335 (2010)
Ortner, N., Wagner, P.: Distribution-Valued Analytic Functions - Theory and Applications. Tredition GmbH, Hamburg (2013)
Ortner, N., Wagner, P.: Fundamental Solutions of Linear Partial Differential Operators. Springer, Cham (2015)
Roider, B.: Sur la Convolution des Distributions. Bull. Sci. Math. 100, 193–199 (1976)
Rosenthal, K.I.: Quantales and Their Applications. Longman Group, London (1990)
Russo, C.: Quantale modules and their operators, with applications. J. Log. Comput. 20, 917–946 (2010)
Samko, S., Kilbas, A., Marichev, O.: Fractional Integrals and Derivatives. Gordon and Breach, Berlin (1993)
Schwartz, L.: Definition integrale de la convolution de deux distributions. Seminaire Schwartz 1, 1–7 (1954)
Schwartz, L.: Theorie des Distributions. Hermann, Paris (1966)
Shiraishi, R.: On the definition of convolutions for distributions. J. Sci. Hiroshima Univ. Ser. A 23, 19–32 (1959)
Silvestre, L.: Regularity of the obstacle problem for a fractional power of the Laplace operator. Commun. Pure Appl. Math. LX 0067–0112,(2007)
Treves, F.: Topological Vector Spaces. Distributions and Kernels. Academic Press, New York (1967)
Vladimirov, V.: Methods of the Theory of Generalized Functions. Taylor and Francis, London (2002)
Wagner, P.: Zur Faltung von Distributionen. Math. Ann. 276, 467–485 (1987)
Wagner, P.: On convolution in weighted \({\cal{D}}^{\prime }_{L^p}\)-spaces. Math. Nachr. 287, 472–477 (2014)
Yoshinaga, K., Ogata, H.: On convolutions. J. Sci. Hiroshima Univ. Ser. A 22, 15–24 (1958)
Youn, H., Richards, I.: On the general definition of convolution for distributions. J. Korean Math. Soc. 17, 13–37 (1980)
Youn, H., Richards, I.: On the general definition of convolution for several distributions. J. Korean Math. Soc. 17, 161–168 (1981)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Adrian Constantin.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kleiner, T., Hilfer, R. On extremal domains and codomains for convolution of distributions and fractional calculus. Monatsh Math 198, 121–152 (2022). https://doi.org/10.1007/s00605-021-01646-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00605-021-01646-1



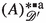 , respectively.
, respectively.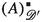 . Moreover,
. Moreover, 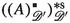 and
and 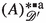 exist and
exist and 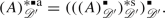
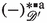 and
and 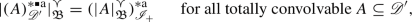
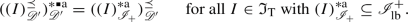
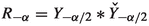 due to the differentiation rule from [
due to the differentiation rule from [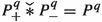 for
for