Abstract
The notion of rigid commutators is introduced to determine the sequence of the logarithms of the indices of a certain normalizer chain in the Sylow 2-subgroup of the symmetric group on \(2^n\) letters. The terms of this sequence are proved to be those of the partial sums of the partitions of an integer into at least two distinct parts, that relates to a famous Euler’s partition theorem.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In a recent paper [5], the authors observed a rather surprising coincidence between the sequence of integers
representing the partial sums of the famous sequence \(\{b_j\}\) of the number of partitions of the integer j into at least two distinct parts, already studied by Euler [15], and a sequence of group-theoretical invariants. Our sequence arises in connection with a problem in algebraic cryptography, namely the study of the conjugacy classes of affine elementary abelian regular subgroups of the symmetric group on \(2^n\) letters [4, 9, 10]. This is relevant in the cryptanalysis of block ciphers, since it may trigger a variation of the well-known differential attack [7]: a statistical attack which allows us to recover information on the secret unknown key by detecting a bias in the distribution of the differences on a given set of ciphertexts when the corresponding plaintext difference is known. In particular, if \(\mathbb F_2^n\) serves as the message space of a block cipher (see e.g. [12]) which has been proven secure with respect to differential cryptanalysis [22] and if T represents the translation group on \(\mathbb F_2^n\), any conjugate of T can be potentially used to define new alternative operations on \(\mathbb F_2^n\) for a successful differential attack [11]. In [5], on the basis of the aforementioned motivation, the authors studied a chain of normalizers, which begins with the normalizer \(N_n^0\) of T in a suitable Sylow 2-subgroup \(\varSigma _n\) of \({{\,\mathrm{Sym}\,}}(2^n)\) and whose ith term \(N_n^i\) is defined as the normalizer in \(\varSigma _n\) of the previous one. After providing some experimental as well as theoretical evidence, the authors conjectured [5, Conjecture 1] that the number \(\log _{2}\left|N^{i}_n : N^{i-1}_n \right|\) is independent of n for \(1\le i\le n-2\), and indeed is equal to the \((i+2)\)th term of the sequence of the partial sums of the sequenceFootnote 1\(\{b_j\}\) mentioned above [1, https://oeis.org/A317910]. In this paper we completely settle this conjecture. The first attempts to solve this problem were based on theoretical techniques which clashed with their own growing computational complexity. For this reason, we develop here a framework to approach the problem from a different point of view. In this new approach, indeed, we take into account both the imprimitivity and the nilpotence of the Sylow 2-subgroup \(\varSigma _n\) to represent its elements in terms of a special family of left-normed commutators, that we call rigid commutators, in a fixed set of generators. Any such commutator [X] can be identified with a subset X of \(\{1, \ldots ,n\}\). The subgroups of \(\varSigma _n\) that can be generated by rigid commutators are called here saturated subgroups. A careful inspection led us to prove that the normalizers \(N^i_n\) are saturated subgroups. In particular, a set of generators of \(N^i_n\) can be obtained from a set of generators of \(N^{i-1}_n\) by adding the rigid commutators of the form [X] for all X such that the elements of the complementary set of X in \(\{1, \ldots ,k\}\), where \(k=\max X \le n\), yield a partition of \(i+2-n+k\) into at least two distinct parts. This is the key to prove the conjecture.
The advantage of adopting rigid commutators is twofold. In the first place, they prove to be handy in calculations with the use of the rigid commutator machinery, a dedicated set of rules which we develop in this paper. Secondly, rigid commutators can be seen as factors in a unique factorization formula for the elements of any given saturated subgroup. This representation is crucial in showing that the normalizers \(N^i_n\) are saturated. By means of this result and of the machinery, we derive an algorithm which efficiently computes the normalizer chain.
The paper is organized as follows: in Sect. 2 some basic facts on the Sylow 2-subgroup \(\varSigma _n\) of \({{\,\mathrm{Sym}\,}}(2^n)\) are recalled. Section 3 is totally devoted to the introduction and the study of rigid commutators and to the construction of the rigid commutator machinery. In Sect. 4 the rigid commutator machinery is used to prove the conjecture on the normalizer chain previously mentioned [5, Conjecture 1]. In Sect. 5 it is shown that each term of the normalizer chain is a saturated group and an efficient procedure to determine the rigid generators of the normalizers is derived. An explicit construction of the normalizer chain in a specific case is provided in Section 6, and some open problems arising from computational evidence are discussed. Finally, some hints for future investigations are presented in Sect. 7.
2 The Sylow 2-subgroup of \({{\,\mathrm{Sym}\,}}(2^n)\)
Let n be a non-negative integer. We start recalling some well-known facts about the Sylow 2-subgroup \(\varSigma _n\) of the symmetric group on \(2^n\) letters.
Let us consider the set
of binary words of length n, where \(\mathcal {T}_0\) contains only the empty word. The infinite rooted binary tree \(\mathcal {T}\) is defined as the graph whose vertices are \(\bigcup _{j\ge 0} \mathcal {T}_j\) and where two vertices, say \(w_1\dots w_{n}\) and \(v_1\dots v_{m}\), are connected by an edge if \(|m-n|=1\) and \(w_i=v_i\) for \(1 \le i \le \min (m,n)\). The empty word is the root of the tree and it is connected with both the two words of length 1.
We can define a sequence \(\left\{ s_i \right\} _{i \ge 1}\) of automorphisms of this tree. Each \(s_i\) necessarily fixes the root, which is the only vertex of degree 2. The automorphism \(s_1\) changes the value \(w_1\) of the first letter of every non-empty word into  and leaves the other letters unchanged. If \(i\ge 2\), we define
and leaves the other letters unchanged. If \(i\ge 2\), we define

In general, \(s_i\) leaves a word unchanged unless the word has length at least i and the letters preceding the ith one are all zero, in which case the ith letter is increased by 1 modulo 2. If \(i \le n\) and the word \(w_1\dots w_n\in \mathcal {T}_n\) is identified with the integer \(1+\sum _{i=1}^{n}2^{n-i} w_{i}\in \left\{ 1, \ldots , 2^n \right\} \), then \(s_i\) acts on \( \mathcal {T}_n\) as the the permutation whose cyclic decomposition is
which has order 2. In particular, the group \(\left\langle \,s_1, \ldots ,s_n\,\right\rangle \) acts faithfully on the set \(\mathcal {T}_n\), whose cardinality is \(2^n\), as a Sylow 2-subgroup \(\varSigma _n\) of the symmetric group \({{\,\mathrm{Sym}\,}}(2^n)\) (see also Fig. 1).
It is also well known that
is the iterated wreath product of n copies of the cyclic group \(C_2\) of order 2.
The support of a permutation is the set of the letters which are moved by the permutation. We say that two permutations \(\sigma \) and \(\tau \) are disjoint if they have disjoint supports; two disjoint permutations always commute.
The closure

is generated by disjoint conjugates of \(s_i\), hence \(S_i\) is an elementary abelian 2-group which is normalized by \(S_j\) if \(j\le i\). Moreover, \(\varSigma _n=S_1 < imes \dots < imes S_n\cong \varSigma _{n-1} < imes S_n\).
3 Rigid commutators
The commutator of two elements h and k in a group G is defined as  . The left-normed commutator of the m elements \(g_1, \ldots ,g_m\in G\) is the usual commutator if \(m=2\) and is recursively defined by
. The left-normed commutator of the m elements \(g_1, \ldots ,g_m\in G\) is the usual commutator if \(m=2\) and is recursively defined by

if \(m\ge 3\). It is well known that the commutator subgroup \(G'\) of a finitely generated nilpotent group G can be generated by left-normed commutators involving only generators of G [19, III.1.11]. From now on, we will focus on left-normed commutators in \(s_1, \ldots , s_n\). For the sake of simplicity, we write \([i_1, \ldots ,i_k]\) to denote the left-normed commutator \([s_{i_1}, \ldots , s_{i_k}]\), when \(k\ge 2\), and we also write [i] to denote the element \(s_i\).
Definition 1
A left-normed commutator \([i_1, \ldots ,i_k]\) is called rigid, based at \(i_1\) and hanging from \(i_k\), if \(i_1>i_2>\dots >i_k\). Given a subset \(X=\left\{ i_1, \ldots , i_k \right\} \subseteq \left\{ 1, \ldots ,n \right\} \) such that \(i_1>i_2>\dots > i_k\), the rigid commutator indexed by X, denoted by [X], is the left-normed commutator \([i_1, \ldots ,i_k]\). We set  when \(X=\emptyset \). The set of all the rigid commutators of \(\varSigma _n\) is denoted by \(\mathcal {R}\) and we let
when \(X=\emptyset \). The set of all the rigid commutators of \(\varSigma _n\) is denoted by \(\mathcal {R}\) and we let  .
.
At the end of this section we prove that every permutation in the Sylow 2-subgroup \(\varSigma _n\) can be expressed, in a unique way, as a product of the objects previously defined. To this purpose, we develop below a set of rules to perform computations with (rigid) commutators.
3.1 Rigid commutator machinery
Let \(1 \le i_1, i_2, \ldots , i_k \le n\) be integers and let us consider the commutator \([i_1, \ldots ,i_k]\). The following facts are easily checked.
Fact 1
Denoting by \(i = \max \left\{ i_1, \ldots ,i_k \right\} \), the commutator \([i_1, \ldots ,i_k]\) is a product of conjugates of \(s_{i}\) by way of elements in \(\left\langle \,s_{i_1}, \ldots ,s_{i_k}\,\right\rangle \) and thus it belongs to \(S_i\). Any two such conjugates commute, since they belong to the same \(S_i\).
Fact 2
As a direct consequence of Fact 1, if \(\max \left\{ i_1, \ldots ,i_k \right\} = \max \left\{ j_1, \ldots ,j_l \right\} \) then \([i_1, \ldots ,i_k]\) and \([j_1, \ldots ,j_l]\) commute.
Note that if \(g\in S_i\) and \(h\in S_j\), then \([g,h]\in S_k\), where \(k=\max \left\{ i,j \right\} \), so \([g,h]^2=1\) since \(S_k\) is elementary abelian. It follows that \([g,h,h]=[g,h]^2[g,h,h]=[g,h^2]=[g,1]=1\). As a consequence we have:
Fact 3
If \(k \ge 2\) and \(i_j = i_{j+1}\) for some \(1 \le j \le k-1\), then \([i_1, \ldots , i_k]=1\).
The following result is crucial since it allows us to rewrite every commutator as a rigid commutator.
Lemma 1
Let \(k\ge 2\) and \(l\ge 1\) be integers. If

is the commutator of the two rigid commutators \([i_1, \ldots ,i_k]\) and \([j_1, \ldots ,j_l]\), then
-
1.
the order of c divides 2, so \( c=[[j_1, \ldots ,j_l],[i_1, \ldots ,i_k]]\);
-
2.
if \(i_1=j_1\), then \(c=1\);
-
3.
if \(l\ge 2\) and \(i_k >j_l \), then \(j_l\) can be dropped, i.e.
$$\begin{aligned} c= [[i_1, \ldots ,i_k],[j_1, \ldots ,j_{l-1}]]; \end{aligned}$$ -
4.
if \(i_1>j_1\), \(\left\{ i_1, \ldots ,i_k \right\} \cap \left\{ j_1, \ldots ,j_l \right\} =\emptyset \), and
 , then $$\begin{aligned} c=[i_1, \ldots , i_s, j_1]; \end{aligned}$$
, then $$\begin{aligned} c=[i_1, \ldots , i_s, j_1]; \end{aligned}$$ -
5.
if \(l\ge 2\) and \(i_k=j_l\), then
$$\begin{aligned} c= [[i_1, \ldots ,i_{k-1}],[j_1, \ldots ,j_{l-1}], j_l ]; \end{aligned}$$ -
6.
if \(i_s >j_1 \ge i_{s+1}\), then
$$\begin{aligned} c=[i_1, \ldots , i_s, j_1, h_1, \ldots , h_t], \end{aligned}$$where \(h_1> \dots > h_t\) and
 . Moreover, \(c=1\) if \(j_1\in {\left\{ i_1, \ldots , i_k \right\} }\).
. Moreover, \(c=1\) if \(j_1\in {\left\{ i_1, \ldots , i_k \right\} }\).
Proof
Let us prove each claim separately.
-
1.
The claim \(c^2 = 1\) depends on the fact that \(c\in S_i\), where the index i is defined as
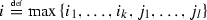 .
. -
2.
If \(i_1=j_1\), then both of \([i_1, \ldots ,i_k]\) and \([j_1, \ldots ,j_l]\) belong to \(S_{i_1}\) which is abelian, thus the claim follows.
-
3.
Assume that \(l\ge 2\) and \(j_l < i_k\). In this case
$$\begin{aligned} c&=[i_1, \ldots ,i_k][i_1, \ldots ,i_k]^{[j_1, \ldots ,j_{l-1}]s_{j_l}[j_1, \ldots ,j_{l-1}]s_{j_l}} \\&= [i_1, \ldots ,i_k]\bigl ([i_1, \ldots ,i_k]^{[j_1, \ldots ,j_{l-1}]}\bigr )^{s_{j_l}[j_1, \ldots ,j_{l-1}]s_{j_l}}. \end{aligned}$$The permutations \(s_{j_l}[j_1, \ldots ,j_{l-1}]s_{j_l}\) and \([i_1, \ldots ,i_k]^{[j_1, \ldots ,j_{l-1}]}\) are disjoint: the first one has support contained in \(\left\{ 2^{n-j_l}+1, \ldots , 2^{n-j_l+1} \right\} \) and the support of the second one is contained in
$$\begin{aligned} \left\{ 1, \ldots , 2^{n-\min (i_k,j_{l-1})+1} \right\} \subseteq \left\{ 1, \ldots , 2^{n-j_l} \right\} . \end{aligned}$$Hence
$$\begin{aligned} c=[i_1, \ldots ,i_k][i_1, \ldots ,i_k]^{[j_1, \ldots ,j_{l-1}]}=[[i_1, \ldots ,i_k],[j_1, \ldots ,j_{l-1}]], \end{aligned}$$which proves the claim.
-
4.
The claim follows by a repeated applications of items (3) and (1).
-
5.
For every
 the permutations x and \(y^{s_{j_l}}\) are disjoint and so they commute. In particular, if \(x^2=1\), then \([x,s_{j_l}]^2= (xx^{s_{j_l}})^2= x^2(x^2)^{s_{j_l}}=1\). If \(a,b\in G \) are such that \(a^2=b^2=1\), then $$\begin{aligned}{}[[a,b],s_{j_l}]&= [abab, s_{j_l}]\\&= ababa^{s_{j_l}} b^{s_{j_l}}a^{s_{j_l}}b^{s_{j_l}} = aa^{s_{j_l}}bb^{s_{j_l}}aa^{s_{j_l}} b b^{s_{j_l}} \\&= [a,s_{j_l}] [b,s_{j_l}] [a,s_{j_l}] [b,s_{j_l}] \\&= [a,s_{j_l}]^{-1} [b,s_{j_l}]^{-1} [a,s_{j_l}] [b,s_{j_l}] =[[a,s_{j_l}],[b,s_{j_l}]]. \end{aligned}$$
the permutations x and \(y^{s_{j_l}}\) are disjoint and so they commute. In particular, if \(x^2=1\), then \([x,s_{j_l}]^2= (xx^{s_{j_l}})^2= x^2(x^2)^{s_{j_l}}=1\). If \(a,b\in G \) are such that \(a^2=b^2=1\), then $$\begin{aligned}{}[[a,b],s_{j_l}]&= [abab, s_{j_l}]\\&= ababa^{s_{j_l}} b^{s_{j_l}}a^{s_{j_l}}b^{s_{j_l}} = aa^{s_{j_l}}bb^{s_{j_l}}aa^{s_{j_l}} b b^{s_{j_l}} \\&= [a,s_{j_l}] [b,s_{j_l}] [a,s_{j_l}] [b,s_{j_l}] \\&= [a,s_{j_l}]^{-1} [b,s_{j_l}]^{-1} [a,s_{j_l}] [b,s_{j_l}] =[[a,s_{j_l}],[b,s_{j_l}]]. \end{aligned}$$For
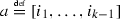 and
and  , we have $$\begin{aligned} {[}[i_1, \ldots ,i_{k-1},j_l],[j_1, \ldots ,j_{l-1}, j_l ]]= [[i_1, \ldots ,i_{k-1}],[j_1, \ldots ,j_{l-1}], j_l ], \end{aligned}$$
, we have $$\begin{aligned} {[}[i_1, \ldots ,i_{k-1},j_l],[j_1, \ldots ,j_{l-1}, j_l ]]= [[i_1, \ldots ,i_{k-1}],[j_1, \ldots ,j_{l-1}], j_l ], \end{aligned}$$as required.
-
6.
An iterated use of items (1), (3) and (5) yields
$$\begin{aligned} c=[[i_1, \ldots , i_s], [j_1, \dots , j_v], h_1, \ldots , h_t] \end{aligned}$$if \(j_1 > i_{s+1} \ge h_1\), where the intersection \(\left\{ i_1, \ldots , i_s \right\} \cap \left\{ j_1, \ldots , j_v \right\} =\emptyset \) is trivial, while, if \(j_1=h_1=i_{s+1}\), then \(c=[[[i_1, \ldots , i_s,h_1], h_1], \ldots , h_t]\). By Fact 3, the commutator \([[i_1, \ldots , i_s,h_1], h_1]\) is trivial, and so \(c=1\). We may then assume that \(j_1 > i_{s+1} \ge h_1\). By (4), we obtain the equality \([[i_1, \ldots , i_s], [j_1, \ldots , j_v]]=[i_1, \ldots , i_s, j_1]\), therefore
$$\begin{aligned} c=[i_1, \ldots , i_s, j_1, h_1, \ldots , h_t] \end{aligned}$$as claimed. \(\square \)
A repeated application of Lemma 1 shows that every left-normed commutator \([i_1, \ldots ,i_k]\) can be written as a commutator \([j_1, \ldots ,j_l]\), where \(\left\{ j_1, \ldots ,j_l \right\} \subseteq \left\{ i_1, \ldots ,i_k \right\} \) and \(j_h \ge j_{h+1}\) for all \(1\le h \le l-1\). If \(j_h=j_{h+1}\) for some h, then Fact 3 shows that \([j_1, \ldots ,j_h,j_{h+1}]=1\), which in turn implies \([j_1, \ldots ,j_l]=1\). This fact is summarized in the following result.
Proposition 1
Any left-normed commutator \([i_1, \ldots ,i_k]\) can be written as a rigid commutator \([j_1, \ldots ,j_l]\), for a suitable subset \(\left\{ j_1, \ldots ,j_l \right\} \subseteq \left\{ i_1, \ldots ,i_k \right\} \).
It is worth noticing here that rigid commutators are the images of P. Hall’s basic commutators [18] under the presentation of the group \(\varSigma _n\) as a factor of the n-generated free group, once the order of the generators is reversed.
3.2 Saturated subgroups
In this section we give a representation of the elements of \(\varSigma _n\) in terms of rigid commutators.
Lemma 2
The set of all the rigid commutators \([X]\in \mathcal {R}\), where X varies among the subsets of \(\left\{ 1, \ldots ,n \right\} \) such that \(\max (X)=i\), is a basis for \(S_i\).
Proof
Let \(1 \le i \le n\). To prove the claim, we look at \(S_i\) as a \(2^{i-1}\)-dimensional vector space over \({{\,\mathrm{\mathbb {F}}\,}}_2\). Proceeding by backward induction on j, for \(i \ge j \ge 1\), we show that the set of all the rigid commutators based at i and hanging from h, for some \(h\ge j\), is linearly independent. When \(j=i\) there is nothing to prove. Assume
where the exponents are in \({{\,\mathrm{\mathbb {F}}\,}}_2\). We aim at proving that all the exponents are 0. From Eq. (2) we have
and so
Note that if the permutation on the right-hand side of Eq. (3) is non-trivial, then it moves some x with \(x>2^{n-j}\), which is fixed by the one on the left-hand side. Hence the permutations on both sides are trivial. By induction, the exponents in the left-hand side of Eq. (3) are all 0. Now, the commutator map
is injective, hence the equality
implies
Again, by the inductive hypothesis, we find \(e_{i,i_1, \ldots ,i_{t-1}, j}=0\) for every choice of \( i_1>\dots >i_{t-1}\). As the number of rigid commutators based at i equals the dimension of \(S_i\), the proof is complete. \(\square \)
We can now state our first main result as a straightforward consequence of Lemma 2. Let us call a proper order \(\prec \) on \(\mathcal {R}^*\) any total order refining the partial order defined by \([i_1, \ldots ,i_t] \prec [j_1, \ldots ,j_l]\) if \(i_1 < j_1\). Here we denote by \(\mathcal {P}_{n}\) the power set of \(\left\{ 1, \ldots ,n \right\} \).
Theorem 1
Given a proper order \(\prec \) in \(\mathcal R^*\), every element \(g\in \varSigma _n\) can be uniquely represented in the form
where the factors are ordered with respect to \(\prec \) and \(e_{g} :\mathcal {P}_{n}{\setminus }\left\{ \emptyset \right\} \rightarrow \left\{ 0,1 \right\} \) is a function depending on g.
Proof
Since \(\varSigma _n = S_1 < imes \dots < imes S_n\), the claim is a straightforward consequence of Lemma 2. \(\square \)
Some of the following corollaries are straightforward and their proof will be omitted.
Corollary 1
If G is a subgroup of \(\varSigma _n\) containing k distinct rigid commutators, then \(\left|G \right|\ge 2^k\).
We now need a new concept which plays a key role in the remainder of this work.
Definition 2
A subset \(\mathcal {G}\) of \(\mathcal {R}\) is called saturated if \(\mathcal {G}\cup \left\{ [\emptyset ] \right\} \) is closed under taking commutators and the subgroup  is called a saturated subgroup.
is called a saturated subgroup.
Remark 1
A subgroup \(G\le \varSigma _n\) is saturated if and only if it can be generated by some subset \(\mathcal {X}\) of \(\mathcal {R}\): indeed G is also generated by the smallest saturated subset of \(\mathcal {G}\cap \mathcal {R}\) containing \(\mathcal {X}\).
Corollary 2
Let \(G\le \varSigma _n\) be a saturated subgroup generated by a saturated set \(\mathcal {G}\subseteq \mathcal {R}^*\) and let \(\prec \) be any given proper order on \(\mathcal {G}\). Every element \(g\in G\) has a unique representation
where the commutators in the product are ordered with respect to \(\prec \) and \(e_c(g)\in \left\{ 0,1 \right\} \). In particular \(\left|G \right|=2^{\left|\mathcal {G} \right|}\).
Corollary 3
Let \(G\le \varSigma _n\) be a saturated subgroup generated by a saturated set \(\mathcal {G}\subseteq \mathcal {R}^*\) and let \(\prec \) any given proper order on \(\mathcal {G}\). If the product \(c_1\cdots c_k\in G\), where \(c_i\in \mathcal {R}^*\), and \(c_1\precneqq c_{2} \precneqq \dots \precneqq c_k\), then \(c_i\in \mathcal {G}\) for all \(1 \le i \le k\).
Proof
Note that since every rigid commutator belongs to some \(S_i\), the group G has the semidirect product decomposition \(G=(G\cap S_1) < imes \dots < imes (G\cap S_n)\). In particular every element of G can be written as an ordered product of elements of \(\mathcal {G}\). Write \(c_1\cdots c_k=g_1\cdots g_t\) where \(g_i\in \mathcal {G}\) and \(g_1\precneqq \dots \precneqq g_t\). By Theorem 1, we have \(k=t\) and \(c_i=g_i\in \mathcal {G}\). \(\square \)
The next statement follows immediately from Corollary 3.
Corollary 4
Let \(G\le \varSigma _n\) be a saturated subgroup. If \(g=g_1\cdots g_n\), where \(g_i\in S_i\) for \(1\le i \le n\), then \(g\in G\) if and only if \(g_i\in G\cap S_i\) for \(1 \le i \le n\). Moreover if \(g=h_1\cdots h_n\), where \(h_i\in S_i\) for \(1 \le i \le n\), then \(h_i=g_i\) for \(1 \le i \le n\).
4 Elementary abelian regular 2-groups and their chain of normalizers
A vector space T of dimension n over \({{\,\mathrm{\mathbb {F}}\,}}_2\) acts regularly over itself as a group of translations. By way of this action, T can be seen as a regular elementary abelian subgroup of \({{\,\mathrm{Sym}\,}}(2^n)\), and any other regular elementary abelian subgroup of \({{\,\mathrm{Sym}\,}}(2^n)\) is conjugate to T in \({{\,\mathrm{Sym}\,}}(2^n)\) [13]. The normalizer of T in \({{\,\mathrm{Sym}\,}}(2^n)\) is the affine group \({{\,\mathrm{AGL}\,}}(T)\), where T embeds as the normal subgroup of translations. For this reason, we refer to any of the conjugates of T as a translation subgroup of \({{\,\mathrm{Sym}\,}}(2^n)\). Every chief series \(\mathfrak {F}=\left\{ T_i \right\} _{i=0}^n\) of T, where \(1=T_0< T_1< \dots < T_n=T\), is normalized by exactly one Sylow 2-subgroup \(U_{\mathfrak {F}}\) of \({{\,\mathrm{AGL}\,}}(T)\). In [21, Theorem p. 226] it is proved that every chief series \(\mathfrak {F}\) of T corresponds to a Sylow 2-subgroup \(\varSigma _{\mathfrak {F}}\) of \({{\,\mathrm{Sym}\,}}(2^n)\) containing T and having a chief series that intersects T in \(\mathfrak {F}\). The correspondence \(\mathfrak {F}\mapsto \varSigma _\mathfrak {F}\) is a bijection between the sets of the chief series of T and the set of Sylow 2-subgroups of \({{\,\mathrm{Sym}\,}}(2^n)\) containing T. In [5] it is also pointed out that \(U_{\mathfrak {F}}=N_{\varSigma _{\mathfrak {F}}}(T)=\varSigma _{\mathfrak {F}}\cap {{\,\mathrm{AGL}\,}}(T)\). From now on the chief series \(\mathfrak {F}\) will be fixed, and so, without ambiguity, we will write \(\varSigma _n\) and \(U_n\) to denote respectively \(\varSigma _{\mathfrak {F}}\) and \(U_{\mathfrak {F}}\). In [4] it is proved that \(U_n\) contains, as normal subgroups, exactly two conjugates of T, namely T and \(T_{U_n}=T^{g}\), for some \(g \in {{\,\mathrm{Sym}\,}}(2^n)\). It is also shown that the normalizer \(N_n^1=N_{{{\,\mathrm{Sym}\,}}(2^n)}(U_n)\) interchanges by conjugation these two subgroups and that \(N_n^1\) contains \(U_n\) as a subgroup of index 2. In particular, \(N_n^1\le \varSigma _n\). In the following section we will extend these results on \(T, U_n, N_n^1\) to the entire chain of normalizers, which is defined below.
4.1 The normalizer chain
The normalizer chain starting at T is defined as

In [5] the authors proved that \(N_{\varSigma _n}(N_{n}^i)=N_{{{\,\mathrm{Sym}\,}}(2^n)}(N_{n}^i)\), for all \(i\ge 0\), computed the normalizer chain for \(n \le 11\) by way of the computer algebra package GAP [17], and conjectured that the index \(\left|N^{i+1}_n : N_n^{i} \right|\) does not depend on n for \(n\ge i+3\) [5, Conjecture 1]. In this section we prove this conjecture arguing by induction, by means of the rigid commutator machinery developed in Sect. 3.1. We start by defining

where

Lemma 3
T is an elementary abelian regular subgroup of \(\varSigma _n\). In particular, T is a translation subgroup of \({{\,\mathrm{Sym}\,}}(2^n)\).
Proof
T is a subgroup of \(\varSigma _n\) as it is generated by elements belonging to \(\varSigma _n\). By item 6 of Lemma 1 it follows that \([t_i,t_j]=1\), so that T is abelian. Note that \(t_i^2=1\) as \(t_i\in S_i\), and so T is elementary abelian of order at most \(2^n\). Let us now prove that T is transitive. Let \(1 \le x \le 2^n\) be an integer represented as \(x= 1+\sum _{i=1}^{n}2^{n-i} w_{i}\) in binary form and let \(t=\prod _{i=1}^nt_i^{w_i}\). A direct check shows that t moves 1 to x. Since T has an orbit with \(2^n\) elements and it has order at most \(2^n\), it follows that \(\left|T \right|=2^n\) and that every point stabilizer is trivial, therefore T is a regular permutation group on \(\left\{ 1, \ldots , 2^n \right\} \). \(\square \)
Let us now determine the permutations in \(\varSigma _n\) normalizing T. For \(1 \le j<i\le n\) let us define  and
and

From now on we will set

Proposition 2
The group \(\left\langle \,\mathcal {U}_n\,\right\rangle \) is the normalizer of T in \(\varSigma _n\), i.e.
Proof
Let us set  and let us prove that \(U = U_n = N_{\varSigma _n}(T)\). By Lemma 1 we have
and let us prove that \(U = U_n = N_{\varSigma _n}(T)\). By Lemma 1 we have
This shows that \(U\le N_{\varSigma _n}(T) = U_n\) and that \(\mathcal U_n\) is a saturated set. Therefore, from Corollary 2, \(\left|U \right|= 2^{\left|\mathcal U_n \right|} = 2^{\frac{n(n+1)}{2}} = \left|U_n \right|\), which proves the claim. \(\square \)
We aim at proving our second main result, providing the generators of the normalizer \(N_n^i\) in terms of rigid commutators. The result is proved by induction on \(i\ge 1\).
4.2 Induction basis
Let us denote by \(\eta _n\) the rigid commutator based at n and hanging from 3 such that no intermediate integer is missing, i.e.

We now prove that we can generate \(N_n^1\) by appending \(\eta _n\) to the list \(\mathcal {U}_n\) of the rigid commutators generating \(U_n\).
Proposition 3
If \(n\ge 3\), then the group \(\left\langle \,\mathcal {U}_n,\eta _n\,\right\rangle \) is the normalizer \(N_n^1\) of \(U_n\) in \(\varSigma _n\), i.e.
Moreover, \(\left|N_n^1:U_n \right|=2\).
Proof
By Lemma 1,
Thus the rigid commutator \(\eta _n\) belongs to \(N_{\varSigma _n}(U_n)\), hence \(\left\langle \,U_n,\eta _n\,\right\rangle \le N_{\varSigma _n}(U_n)\). Moreover \(U_n \cap S_n=\left\langle \,t_n,u_{n,1}, \ldots ,u_{n,n-1}\,\right\rangle \) and so \(\eta _n\), which is based at n, is such that \(\eta _n \notin U_n\). The claim now follows from \(\left|N_{\varSigma _n}(U_n):U_n \right|=2\) [4, Theorem 7]. \(\square \)
4.3 Inductive step
Let \(1\le b \le n\) and let I be a (possibly empty) subset of \(\left\{ 1,2, \ldots ,b-1 \right\} \). We define the rigid commutator based at b and punctured at I as

and, if \(I = \left\{ i_1,i_2, \ldots ,i_k \right\} \) we also denote \(\mathop {\vee }\!\left[ b;I \right] \) by \(\mathop {\vee }\!\left[ b;i_1,i_2, \ldots ,i_k \right] \).
For example, the permutation \(\eta _n\) defined in Eq. (5) is equal to \(\mathop {\vee }\!\left[ n;2,1 \right] \).
We also define

for each \(1 \le i \le n\) and j, and

Note that, if \(j \le i-2\), then \(\left| \mathcal {W}_{i,j} \right|=b_j\), i.e. the number of partitions of j into at least two distinct parts. Our next goal is to prove that \(N_n^i=\left\langle \,\mathcal {N}_n^i\,\right\rangle \) for each \(0\le i \le n-2\), where \(N_n^i\) is defined as in Eq. (4). Propositions 2 and 3 show that this is actually the case when \(i\in \{0,1\}\).
In order to prove the general result, we need the following reformulation of item 6 of Lemma 1 to compute commutators of rigid commutators written in punctured form.
Proposition 4
Let \(1 \le a,b \le n\) and let I and J subsets of \(\left\{ 1,2, \ldots ,a-1 \right\} \) and \(\left\{ 1,2, \ldots ,b-1 \right\} \) respectively. Then
Proof
Let  . If \(a=b\), then \(c=1\). Without loss of generality, we can assume that \(a> b\). By Lemma 1, if \(b \notin I\), then \(c=1\). If \(b\in I\), the claim follows from item 6 of Lemma 1. \(\square \)
. If \(a=b\), then \(c=1\). Without loss of generality, we can assume that \(a> b\). By Lemma 1, if \(b \notin I\), then \(c=1\). If \(b\in I\), the claim follows from item 6 of Lemma 1. \(\square \)
In the following facts, we summarize some properties that will be useful in the proof of the conjecture.
Fact 4
A commutator \(\mathop {\vee }\!\left[ a;J \right] \) such that \(1 \le a \le n\) and \(J \subseteq \left\{ 1,2, \ldots ,a-1 \right\} \) belongs to \(\mathcal {N}_n^{i}\) if and only if one of the following conditions is satisfied:
-
1.
\(J=\emptyset \), and so \(\mathop {\vee }\!\left[ a;J \right] =t_a\);
-
2.
\(\left|J \right|=1\), and so \(\mathop {\vee }\!\left[ a;J \right] =u_{aj}\) where \(J=\left\{ j \right\} \);
-
3.
\(\left|J \right|\ge 2\), and \(\sum _{j\in J} j \le i+2-(n-a)\).
Fact 5
Note that for \(2\le i\le n-2\) the set \(\mathcal {N}_n^i\cap (S_1 < imes \dots < imes S_{n-1})\) is equal to \(\mathcal {N}_{n-1}^{i-1}\). Indeed, at the ith iteration, the newly generated elements of \(\mathcal {N}_n^i\), which are those in \(\mathcal {N}_n^i{\setminus } \mathcal {N}_n^{i-1}\), are constructed by lifting the elements of \(\mathcal {N}_n^{i-1}{\setminus } \mathcal {N}_n^{i-2}\), i.e. by replacing a rigid commutator based at j with the rigid commutator obtained by removing its left-most element, for \(j \le n\), and by adding some new rigid commutators based at n, in accordance with Eq. (8). Proceeding in this way it is easy to check that, disregarding all the commutators based at n in \(\mathcal {N}_n^{i}\), the lifted elements are exactly the elements of \(\mathcal {N}_{n-1}^{i-1}\). The reader is referred to Sect. 6 for explicit examples.
Fact 6
In the proof of Proposition 3 we showed that \( [\,\mathcal {N}_n^{1} , \mathcal {N}_n^{0} ] \subseteq \mathcal {N}_n^{0} \cup \left\{ [\emptyset ] \right\} \). Assuming by induction on \(2\le i\le n-2\) that \([\,\mathcal {N}_{n-1}^{i-1},\mathcal {N}_{n-1}^{i-2}] \subseteq \mathcal {N}_{n-1}^{i-2} {\cup \left\{ [\emptyset ] \right\} }\) and using Fact 5, we can conclude that
Similarly,
From the previous fact we have that, in order to prove by induction on i that \([\,\mathcal {N}_n^{i}, \mathcal {N}_n^{i-1}]\subseteq \mathcal {N}_n^{i-1} \cup \left\{ [\emptyset ] \right\} \) and that \([\,\mathcal {N}_n^{i}, \mathcal {N}_n^{i}]\subseteq \mathcal {N}_n^{i} \cup \left\{ [\emptyset ] \right\} \), it suffices to show that \([\,\mathcal {W}_{n,\,i+2}\, ,\, \mathcal {N}_n^{i-1}] \subseteq \mathcal {N}_n^{i-1}\cup \left\{ [\emptyset ] \right\} \) and that \([\,\mathcal {W}_{n,\,i+2}\, ,\, \mathcal {N}_n^{i}] \subseteq \mathcal {N}_n^{i}\cup \left\{ [\emptyset ] \right\} \). This is accomplished in the following result.
Lemma 4
If \(i\le n-2\), then \([\mathcal {N}_n^i,\mathcal {N}_n^{i-1}]\subseteq \mathcal {N}_n^{i-1} \cup \left\{ [\emptyset ] \right\} \) and \([\mathcal {N}_n^i,\mathcal {N}_n^i]\subseteq \mathcal {N}_n^i \cup \left\{ [\emptyset ] \right\} \).
Proof
If \(\mathop {\vee }\!\left[ n;I \right] \in \mathcal {W}_{n,\,i+2}\subseteq \mathcal {N}_n^i{\setminus } \mathcal {N}_n^{i-1}\) and \(\mathop {\vee }\!\left[ a;J \right] \in \mathcal {N}_n^{i-1}\) then, by Proposition 4,

We may assume \(a\in I\). From Fact 4, if \(\mathop {\vee }\!\left[ a;J \right] \) is as in case (3), we have
and so \(c \in \mathcal {N}_n^{i-1}\). If \(\mathop {\vee }\!\left[ a;J \right] \) is as in case (1), i.e. \(\mathop {\vee }\!\left[ a;J \right] =t_a\), then we have
and so, also in this case, \(c\in \mathcal {N}_n^{i-1}\). Finally, if \(\mathop {\vee }\!\left[ a;J \right] \) is as in case (2), i.e. \(\mathop {\vee }\!\left[ a;J \right] =u_{a,j}\), we have
and again \(c\in \mathcal {N}_n^{i-1}\). Similar computations prove that, if \(\mathop {\vee }\!\left[ a;J \right] \in \mathcal {N}_n^{i}\), then also \(c \in \mathcal {N}_n^{i}\). \(\square \)
The following result is now straightforward.
Proposition 5
The set \(\mathcal {N}_n^i\) is a saturated set of rigid commutators and \(\left\langle \,\mathcal {N}_n^{i}\,\right\rangle \le N_{\varSigma _n}\bigl (\left\langle \,\mathcal {N}_n^{i-1}\,\right\rangle \bigr )\). Moreover, \(\left|\left\langle \,\mathcal {N}_n^{i}\,\right\rangle \right|=2^{\left|\mathcal {N}_n^i \right|}\).
Proof
The claim follows from Lemma 4, Fact 6 and Corollary 2. \(\square \)
We conclude this section with our main result showing that the ith term of the normalizer chain is actually generated by the set \(\mathcal {N}_n^i\) of rigid commutators defined in Eq. (8). We prove, indeed, that the inclusion \(\left\langle \,\mathcal {N}^i_{n}\,\right\rangle \le N_{\varSigma _n}\bigl (\left\langle \,\mathcal {N}_n^{i-1}\,\right\rangle \bigr )\) shown in the previous proposition is actually an equality.
Theorem 2
For \(i \le n-2\), the group \(\left\langle \,\mathcal {N}_n^i\,\right\rangle \) is the ith term \(N_n^{i}\) of the normalizer chain.
Proof
The cases \(i=0\) and \(i=1\) has been addressed respectively in Propositions 2 and 3. We assume by induction on \(i\ge 2\) that \(N_m^{j}=\left\langle \,\mathcal {N}_m^j\,\right\rangle \) for all \(m\le n\) whenever \(j<i \le m-2\). In particular
Notice that
where the first equality in the last line holds since the following inclusions
imply that \(N_{\varSigma _{n-1}}(N_{n}^{i-1}\cap \varSigma _{n-1}) \subseteq N_{\varSigma _{n-1}}(N_{n}^{i-1}\cap S_n)\). As \(S_n\) is abelian, we have
We are then left to determine \(N_{S_n}(N_{n}^{i-1})= \left\{ x\in S_n \mid [x,\mathcal {N}_{n-1}^{i-1}]\subseteq N_{n}^{i-1}\cap S_n \right\} \). Let us point out that, by Eqs. (7) and (8), the groups

have trivial intersection and that \(S_n=A\times B\). By Lemma 4 we have that A is a subgroup of \(N_{n}^{i}\cap S_n\), for \(1 \le j \le i\), so that \(N_{n}^{i}=A\times H\) where

We denote a generic element of H by

where the product is taken over the set \(\mathcal {I}\) of all the subsets \(I\subseteq \left\{ 1, \ldots ,n-1 \right\} \) such that \(\sum _{y\in I}y \ge i+3\). For \(1 \le l \le n\) let \(\mathcal {I}_l=\left\{ I\in \mathcal {I} \mid \min (I)=l \right\} \). Let \(u= u_{l,\, l-1}\) if \(l> 1\), or \(u=t_1=[1]\) if \(l=1\). Since \(x\in H\), we have that
belongs to \( \mathcal {N}_{n}^{i-1},\) and in particular \(e_I\ne 0\) implies
If \(I\in \mathcal {I}_l\) then
so that \(e_I=0\) for \(I\in \mathcal {I}_l\). As \(\mathcal {I}=\bigcup _{l=1}^n\mathcal {I}_l\), we have \(H=\left\{ 1 \right\} \). This finally shows that \(N_{S_n}(N^{n}_{i-1})=A=N^n_{i}\cap S_n = \left\langle \,\mathcal {N}_n^i\cap S_n\,\right\rangle \) and, by Eq. (9), that
as claimed. \(\square \)
4.4 Partitions into at least two distinct parts
This work was motivated by the computational evidence that the number  does not depend on n, if \(3\le i \le n\) [5]. The first terms of the sequence \(\left\{ c_i \right\} \) coincide with those of the sequence \(\{a_i\}\) defined in [1, https://oeis.org/A317910], where \(a_i\) is the ith partial sum of the sequence \(\{b_i\}\), where \(b_i\) is the number of partitions of i into at least two distinct parts. Some values of the aforementioned sequences are displayed in Table 1.
does not depend on n, if \(3\le i \le n\) [5]. The first terms of the sequence \(\left\{ c_i \right\} \) coincide with those of the sequence \(\{a_i\}\) defined in [1, https://oeis.org/A317910], where \(a_i\) is the ith partial sum of the sequence \(\{b_i\}\), where \(b_i\) is the number of partitions of i into at least two distinct parts. Some values of the aforementioned sequences are displayed in Table 1.
We have developed the rigid commutator machinery as a theoretical tool of investigation. It is no longer surprising that the equality \(b_i=\left|\mathcal {W}_{n,i} \right|\), where \(\mathcal {W}_{n,i}\) is defined by Eq. (7), is the link with the mentioned sequence. This combinatorial identity, Eq. (1), Proposition 5 and Theorem 2 give at last a positive answer to Conjecture 1 in [5].
Corollary 5
For \(1\le i\le n-2\), the number \(\log _{2}\left|N^{i}_n : N^{i-1}_n \right|\) is independent of n. It equals the \((i+2)\)th term of the sequence \(\left\{ a_j \right\} \) of the partial sums of the sequence \(\left\{ b_j \right\} \) counting the number of partitions of j into at least two distinct parts.
5 Normalizers of saturated subgroups
In this section we will prove that the normalizer  of a saturated subgroup G of \(\varSigma _n\) is also saturated, provided that \(T\le N\), and thus we can use our rigid commutator machinery in the computation of N. In particular, for \(i\le n-2\), the machinery could be used as an alternative tool to derive the theoretical description of \(N_n^i\) as in Theorem 2. Even if we do not have such a description when \(i>n-2\), the machinery can be anyway used to efficiently compute via \(\mathsf {GAP}\) the complete normalizer chain.
of a saturated subgroup G of \(\varSigma _n\) is also saturated, provided that \(T\le N\), and thus we can use our rigid commutator machinery in the computation of N. In particular, for \(i\le n-2\), the machinery could be used as an alternative tool to derive the theoretical description of \(N_n^i\) as in Theorem 2. Even if we do not have such a description when \(i>n-2\), the machinery can be anyway used to efficiently compute via \(\mathsf {GAP}\) the complete normalizer chain.
We denote below by \(N_i\) the intersection \(N\cap S_i\).
Proposition 6
If G is a saturated subgroup of \(\varSigma _n\), and \(N=N_{\varSigma _n}(G)\) is its normalizer in \(\varSigma _n\), then
In particular if \(x\in N\) and \(x=x_1\cdots x_n\), with \(x_i\in S_i\) for all \(1 \le i \le n\), then \(x_i\in N_i\) for all \(1 \le i \le n\).
Proof
Let \(x\in N\) and write \(x=x_{i_1}\dots x_{i_k}\) where  and \(x_ {i_j}\in S_{i_j}\), for \(1 \le j \le k\). In order to prove our claim we first show that \([x_{i_1},c]\in G\) for every non-trivial rigid commutator c of G. Since G is generated by its own non-trivial rigid commutators, it will follow that \(x_{i_1}\in N\). As a consequence, also \(x_{i_2}\dots x_{i_k} \in N\). Thus, we may argue by induction on k to obtain that \(x_{i_j}\in N\) for all \(1\le j \le k\).
and \(x_ {i_j}\in S_{i_j}\), for \(1 \le j \le k\). In order to prove our claim we first show that \([x_{i_1},c]\in G\) for every non-trivial rigid commutator c of G. Since G is generated by its own non-trivial rigid commutators, it will follow that \(x_{i_1}\in N\). As a consequence, also \(x_{i_2}\dots x_{i_k} \in N\). Thus, we may argue by induction on k to obtain that \(x_{i_j}\in N\) for all \(1\le j \le k\).
Let i be such that \(c\in G\cap S_i\). Suppose first that \(i < i_1\). If \([c,x_{i_1}]= 1\), then \([c,x_{i_1}]\in G\). If \([c,x_{i_1}]\ne 1\), then \([c,x]=[c,x_{i_1}]h\in G\), where \([c,x_{i_1}]\in S_{i_1}\) and \(h\in \prod _{t>i_1}S_t\). By Corollary 4 we obtain that \([c,x_{i_1}]\in G\cap S_{i_1}\le G\). If \(i=i_1\), then trivially \([c,x_{i_1}]=1\in G\). The last possibility is \(i_1<\dots< i_m < i\le i_{m+1}\) for some \(m\le k\). Suppose that \([x_{i_1},c]\ne 1\). In this case
Let us consider the commutators
written as ordered product of distinct rigid commutators
and
Notice that \(\left\{ d_1, \ldots , d_t \right\} \cap \left\{ f_1, \ldots , f_s \right\} =\emptyset \) since the commutators \(d_i\) are of the form [X] for some set X with \(i_1\in X\), whereas the commutators \(f_j\) are of the form [Y] for some set Y with \(i_1\notin Y\). This yields \([x_ {i_1},c]^{x_ {i_2}\cdots x_ {i_m}} \in G\cap S_i\) and so \([x_ {i_1},c] \in G\cap S_i \le G\). \(\square \)
Lemma 5
Suppose that G is a saturated subgroup of \(\varSigma _n\) normalized by T. If \(x_1, \ldots , x_k\in S_j\) are distinct rigid commutators such that \(x=x_1\cdots x_k\in N\), then \(x_i\in N\) for all \(1\le i \le k\).
Proof
Let \(c_1,\ldots , c_h\in \mathcal R^*\) such that \(G=\left\langle \,c_1,\ldots , c_h\,\right\rangle \) and let us write every \(c_s\) and \(x_t\) in punctured form: \(c_s=\mathop {\vee }\!\left[ m_s;C_s \right] \) and \(x_t=\mathop {\vee }\!\left[ j;X_t \right] \).
Suppose first that \(m_s <j\), so that
where  . Notice that if the commutator \(d_{s,t}\) appears only once in the product, then, by Corollary 3, \(d_{s,t}\in G\). If \(C_s\cap X_t=\emptyset \) for all \(1\le t \le k\), then all the non-trivial \(d_{s,t}\) appearing in the product are distinct and hence they appear only once in the product, so that \(d_{s,t}\in G\) for all \(1 \le t \le k\). If \(C_s\cap X_t\ne \emptyset \), then the commutator \(d_{s,t}\) may appear more than once in the product displayed in Eq. (10). Let \(l\in C_s\cap X_t\) and consider the commutator \(c_{s,l}=[c_s, t_l] = \mathop {\vee }\!\left[ m_s;C_s{\setminus }\left\{ l \right\} \right] \in G\) as \(t_l=[l, \ldots ,1]\in T\le N_{\varSigma _n}(G)\). Notice that
. Notice that if the commutator \(d_{s,t}\) appears only once in the product, then, by Corollary 3, \(d_{s,t}\in G\). If \(C_s\cap X_t=\emptyset \) for all \(1\le t \le k\), then all the non-trivial \(d_{s,t}\) appearing in the product are distinct and hence they appear only once in the product, so that \(d_{s,t}\in G\) for all \(1 \le t \le k\). If \(C_s\cap X_t\ne \emptyset \), then the commutator \(d_{s,t}\) may appear more than once in the product displayed in Eq. (10). Let \(l\in C_s\cap X_t\) and consider the commutator \(c_{s,l}=[c_s, t_l] = \mathop {\vee }\!\left[ m_s;C_s{\setminus }\left\{ l \right\} \right] \in G\) as \(t_l=[l, \ldots ,1]\in T\le N_{\varSigma _n}(G)\). Notice that
Let \(C=C_s{\setminus }\left\{ l \right\} \). We have determined a new rigid commutator \(c=c_{s,l}=\mathop {\vee }\!\left[ m_s;C \right] \in G\) such that \(\left|C\cap X_t \right| < \left|C_s\cap X_t \right|\), that \(\left|C \right| < \left|C_s \right|\) and that \( d_{s,t}=[c,x_t]\) appears in the expansion of [c, x]. Using the same strategy, after a finite number of steps, we obtain \(c=\mathop {\vee }\!\left[ m_s;C \right] \in G\) such that \(C\cap X_t=\emptyset \). If \( d_{s,t}=[c,x_t]=[c,x_{t_1}]=d_{s,t_1}\), for some \(t_1\ne t\), then \(C\cap X_{t_1}\ne \emptyset \), since otherwise \(X_t=X_{t_1}\) and consequently \(x_t=x_{t_1}\) with \(t\ne t_1\), contrary to the hypotheses. Thus we may proceed in the same way with \(d_{s,t_1}\). Since at each step the cardinality of C is strictly decreasing, after a finite number of steps we find a \(c\in G\) and \(x_{t_r}\) such that \(d_{s,t}=d_{s,t_1}=\dots = d_{s,t_r}\) appears only once in [c, x] giving \(d_{s,t}\in G\). This finally shows that \(d_{s,t}\in G\) for all \(1\le t \le k\).
If \(j=m_s\) then \(x_i\) and \(c_s\) commute for all i and there is nothing to prove.
We are left with the case when \(m_s>j\). As above, we have
where  . Reasoning as we did for \(m_s<j\), we obtain that \(d_{s,t}\in G\) for all \(1\le t \le k\).
. Reasoning as we did for \(m_s<j\), we obtain that \(d_{s,t}\in G\) for all \(1\le t \le k\).
In all the cases we have proved that \(x_i\in N\) for all \(1\le i \le k\), which is our claim. \(\square \)
As an easy consequence of Proposition 6 and Lemma 5 we find the following result.
Theorem 3
The normalizer N in \(\varSigma _n\) of a saturated subgroup of \(\varSigma _n\) is also saturated, provided that N contains T.
Remark 2
Let \(\mathcal {A}\) and \(\mathcal {B}\) be two subsets of \(\mathcal {R}\) such that \(\left\{ t_1, \ldots , t_n \right\} \subseteq \mathcal {A} \subseteq \mathcal {B}\), let \(A=\left\langle \,\mathcal {A}\,\right\rangle \) and \(B=\left\langle \,\mathcal {B}\,\right\rangle \) be the corresponding saturated subgroups. It is easy to recognize that \(N_B(A)=\left\langle \,b\in \mathcal {B} \mid [b,\mathcal {A}]\subseteq \mathcal {A}\cup \left\{ [\emptyset ] \right\} \,\right\rangle \). Similarly, the normal closure \(A^B\) of A in B is the subgroup generated by the intersection of all the subsets \(\mathcal {C}\) of \(\mathcal {R}\) such that \(\mathcal {A} \subseteq \mathcal {C} \subseteq \mathcal {B}\) and \([\mathcal {C} ,\mathcal {B} ] \subseteq \mathcal {C} \cup \left\{ [\emptyset ] \right\} \). In particular, both the normalizer \(N_B(A)\) and the normal closure \(A^B\) are saturated.
Remark 3
The condition that T is contained in the normalizer \(N=N_{\varSigma _n}(G)\) of a saturated subgroup G cannot be removed from the hypotheses of Theorem 3. Indeed, if \(G=\left\langle \,[n,\ldots ,3]\,\right\rangle \), then the product \([2]\cdot [2,1]\) is contained in the centralizer of A, and hence also in the normalizer N of A, but none of the two rigid commutators [2] or \([2,1] \in T\) normalizes G. In particular, by Corollary 4, the subgroup N cannot be saturated.
Remark 4
Another proof of Theorem 2 can be obtained from Theorem 3. Indeed, it is not difficult, but rather tedious, to check that
for \(0\le i \le n-2\). The result then follows by Proposition 5.
From Theorems 2 and 3 and from Remark 4 we derive a straightforward corollary resulting in an algorithm whose \(\mathsf {GAP}\) implementation is publicly available at GitHub (see https://github.com/ngunivaq/normalizer-chain). This script produces a significant speed-up in the computation of the normalizer N of a saturated subgroup provided that N contains T. We could easily apply this script to compute our normalizer chain up to the dimension \(n=22\). For example, whereas the standard libraries required one month on a cluster to compute the terms of the normalizer chain in \({{\,\mathrm{Sym}\,}}(2^{10})\), our implementation of the rigid commutator machinery gives the result in a few minutes, even on a standalone PC. With a similar approach, we can also use rigid commutators to compute the normal closure of a saturated subgroup. Some explicit calculations are shown below in Sect. 6. Let \(\mathcal {M}_n^i\) be the set of all the rigid commutators belonging to \(N_n^i\). From Theorem 3, the subgroups \(N_n^i\) are saturated, hence \(N_n^i = \left\langle \,\mathcal {M}_n^i\,\right\rangle \) for all \(i \ge 1\).
Corollary 6
The set \(\mathcal {M}_n^i\) is the largest subset of \(\mathcal {R}\) that normalizes \(\mathcal {M}_n^{i-1}\), i.e.
Moreover, \(\mathcal {N}_n^i =\mathcal {M}_n^i {\setminus } \left\{ [\emptyset ] \right\} \) for \(1\le i\le n-2\).
The construction of the terms of the normalizer chain is then reduced to the determination of the sets \(\mathcal {M}_n^i\), a task which turns out to be way faster than computing the terms of the normalizer chains as subgroups of \(\varSigma _n\) via the Normalizer command provided by GAP.
6 A computational supplement
In this section we show an explicit construction of the first four groups in the normalizer chain when \(n=6\), i.e. in \({{\,\mathrm{Sym}\,}}(64)\). Let us start by determining the generators of T in terms of rigid commutators:
We have that \(T = \left\langle \,t_1, t_2, \ldots , t_6\,\right\rangle \) and, from Proposition 2, its normalizer in \(\varSigma _n\) is \(N_6^0 = U_6=\left\langle \,\mathcal U_6\,\right\rangle = \left\langle \,T,u_{ij} \mid 1 \le j < i \le 6\,\right\rangle \). Thus the generators of \(N^0_6\), besides those of T, are
consequently \(|N_6^0| = 2^{21}\). Now, in accordance with Eq. (8) and Theorem 2, the normalizer \(N_6^1\) is generated by the rigid commutators previously listed and by \(\eta _6\), the only element of \(\mathcal {W}_{6,3}\) (see Eq. (7)). The commutator \(\eta _6\) is the punctured rigid commutator based at 6 and missing the integers 1 and 2, i.e.
where 1 and 2 indeed represent the sole partition of 3 into at least two distinct parts. From this, \(\log _2\left|N^{1}_6 : N^{0}_6 \right|= 1 = a_3\). Again from Eq. (8) and Theorem 2, the normalizer \(N_6^2\) is generated, along with the elements already mentioned, by the rigid commutators in \(\mathcal {W}_{5,3}\) and \(\mathcal {W}_{6,4}\), i.e.
The commutator of Eq. (12), which belongs to \(\mathcal {W}_{5,3}\), is the punctured rigid commutator based at 5 and missing the integers 1 and 2. The commutator of Eq. (13) instead, which belongs to \(\mathcal {W}_{6,4}\), is based at 6 and misses the integers 1 and 3, composing the sole partition of 4 into at least two distinct parts. Notice that  . Indeed, as discussed in Fact. 5, the commutator of Eq. (12) is obtained by lifting the one of Eq. (11), i.e. by removing 6, the left-most element of \(\eta _6\). We have \(\log _2\left|N^{2}_6 : N^{1}_6 \right|= 2 = a_4\). Similarly, \(N_6^3\) is generated by adding the new rigid commutators
. Indeed, as discussed in Fact. 5, the commutator of Eq. (12) is obtained by lifting the one of Eq. (11), i.e. by removing 6, the left-most element of \(\eta _6\). We have \(\log _2\left|N^{2}_6 : N^{1}_6 \right|= 2 = a_4\). Similarly, \(N_6^3\) is generated by adding the new rigid commutators


where the commutators of Eqs. (14) and (15) are respectively obtained by lifting those of Eqs. (12) and (13), and the commutators of Eqs. (16) and (17) belong to \(\mathcal {W}_{6,5}\), respectively corresponding to the partitions \(4+1\) and \(3+2\) of 5. At this stage, we have that \(\log _2\left|N^{3}_6 : N^{2}_6 \right|= 4 = a_5\). Ultimately, the commutators

complete the set of rigid generators of \(N_6^4\), and \(\log _2\left|N^{4}_6 : N^{3}_6 \right|= 7 = a_6\).
Using Corollary 6, we can find a saturated set of rigid generators for all the elements of the chain. Notice that for \(i > 5\), the sequence \(\log _2\left|N^{i}_6 : N^{i-1}_6 \right|\) does not fit the pattern of the sequence \(\{a_j\}\). Although we do not have a general formula to calculate the values of the relative indices between two consecutive terms in the normalizer chain, they can be explicitly determined by the algorithm in GitHub. Computational results are summarized in Table 2, where we list all the relative indices of the normalizer chain. In the second column, the logarithms of the sizes of the intersections of each term with each of the subgroups \(S_6, \ldots , S_1\) are displayed.
7 Problems for future research
We conclude this work by highlighting some suggestions for further properties and structures of the set \(\mathcal R\) of rigid commutators and providing some hints for future research.
7.1 Algebras of rigid commutators
The operation of commutation in \(\mathcal {R}\) is commutative and \([\emptyset ]\) represents the zero element. Moreover, for every \(x,y \in \mathcal {R}\) the following identity is satisfied
Let \({{\,\mathrm{\mathbb {F}}\,}}\) be any field of characteristic 2 and let \(\mathfrak {r}\) be the vector space over \({{\,\mathrm{\mathbb {F}}\,}}\) having the set \(\mathcal {R}^*\) of the non-trivial rigid commutators as a basis. The space \(\mathfrak {r}\) is endowed with a natural structure of an algebra. The product \(x\star y\) of two rigid commutators \(x,y \in \mathcal R\) is defined as

This operation is then extended to the whole \(\mathfrak {r}\) by bilinearity and turns \(\mathfrak {r}\) into a Jordan algebra, since it is commutative and \(x\star x=0\) for all \(x \in \mathfrak {r}\). Moreover, if \(\mathcal {H}\) is a saturated subset of \(\mathcal {R}^*\), then, on the one hand the group \(H=\left\langle \,\mathcal {H}\,\right\rangle \) is a saturated subgroup of \(\varSigma _n\) and, on the other hand, the \({{\,\mathrm{\mathbb {F}}\,}}\)-linear span \(\mathfrak {h}\) of \(\mathcal {H}\) is a subalgebra of \(\mathfrak {r}\). The property \([\mathcal {R},\mathcal {H}] \subseteq \mathcal {H}\cup \left\{ [\emptyset ] \right\} \) is a necessary and sufficient condition for H to be a normal subgroup of \(\varSigma _n\) and for \(\mathfrak {h}\) to be an ideal of \(\mathfrak {r}\). We point out that the fact that \(\mathcal {R}\) is closed under commutation is crucial to check the previous statement. If c is the nilpotency class of \(\varSigma _n\), then the product of \(c+1\) elements of \(\mathfrak {r}\) is always zero, so that \(\mathfrak {r}\) is nilpotent. The study of the properties and the representations of this algebra seems to be a problem of independent interest, in connection with the study of the saturated subgroups of \(\varSigma _n\).
7.2 Again on the normalizer chain
We have obtained from Theorem 2 an explicit description of the non-trivial rigid generators of the ith term of the normalizer chain when \(1 \le i \le n-2\), i.e. the set \( \mathcal {N}_n^i\). We have seen that \(\mathcal {N}_n^i\) has a nice description by way of Eqs. (7) and (8), i.e. it is generated by some rigid commutators either belonging to \(\mathcal {U}_n\) or having a punctured form corresponding to suitable partitions into at least two distinct parts. Although we can efficiently compute all the normalizers in the chain, as described in the lines following Corollary 6, it is an interesting problem to find a similar combinatorial formula for the generating set \(\mathcal {M}_n^i\) of \(N^i_n\) when \(i>n-2\). Moreover, as already mentioned in Sect. 6, the values of the sequence \(\log _2|N_n^i : N_n^{i-1}|\) do not seem to conform to any special known pattern when \(i > n-2\). Table 3 contains the values of \(\log _2|N_n^i : N_n^{i-1}|\) for \(1\le i\le 14\) and \(3 \le n \le 15\). The determination of the general behavior of the sequence is an open problem.
7.3 An odd generalization
It appears natural to ask whether a similar rigid commutator machinery can be developed in a Sylow p-subgroup of the symmetric group \({{\,\mathrm{Sym}\,}}(p^n)\) when p is an odd prime. This seems to be an entirely different problem in terms of techniques and results. For example, a rigid commutator could contain repetitions. It may turn out interesting on a computational point of view, although such a machinery might have a weaker cryptographic application.
Notes
The sequence \(b_j+1\) appears in several others areas of mathematics, from number theory to commutative algebra [14]. In particular, it was already known to Euler that \(b_j+1\) corresponds to the number of partitions of j into odd parts (see [15, Chapter 16] and [3, §3]). Several proofs of this Euler’s partition theorem have been offered ever since [2, 20, 24], and several important refinements have been obtained [6, 8, 16, 23, 24].
References
The On-Line Encyclopedia of Integer Sequences. Published electronically at https://oeis.org. Accessed 2020-03-01
Andrews, G.E.: Number Theory. Dover Publications Inc, New York (1994). (Corrected reprint of the 1971 original)
Andrews, G.E.: Euler’s De Partitio numerorum. Bull. Am. Math. Soc. N.S. 44(4), 561–573 (2007)
Aragona, R., Civino, R., Gavioli, N., Scoppola, C.M.: Regular subgroups with large intersection. Ann. Mat. Pura Appl. (4) 198(6), 2043–2057 (2019)
Aragona, R., Civino, R., Gavioli, N., Scoppola, C.M.: A chain of normalizers in the sylow \(2\)-subgroups of the symmetric group on \(2^n\) letters. Preprint published electronically at arxiv:2008.13423: to appear in Indian J. Pure Appl. Math. (2020)
Bessenrodt, C.: A bijection for Lebesgue’s partition identity in the spirit of Sylvester. Discrete Math. 132(1–3), 1–10 (1994)
Biham, E., Shamir, A.: Differential cryptanalysis of DES-like cryptosystems. J. Cryptol. 4(1), 3–72 (1991)
Bousquet-Mélou, M., Eriksson, K.: Lecture hall partitions. Ramanujan J. 1(1), 101–111 (1997)
Calderini, M., Civino, R., Sala, M.: On properties of translation groups in the affine general linear group with applications to cryptography. J. Algebra 569, 658–680 (2021)
Caranti, A., Dalla Volta, F., Sala, M.: Abelian regular subgroups of the affine group and radical rings. Publ. Math. Debrecen 69(3), 297–308 (2006)
Civino, R., Blondeau, C., Sala, M.: Differential attacks: using alternative operations. Des. Codes Cryptogr. 87(2–3), 225–247 (2019)
Daemen, J., Rijmen, V.: The Design of Rijndael: AES-The Advanced Encryption Standard. Springer, Berlin (2013)
Dixon, J.D.: Maximal abelian subgroups of the symmetric groups. Can. J. Math. 23, 426–438 (1971)
Enkosky, T., Stone, B.: A sequence defined by \(M\)-sequences. Discrete Math. 333, 35–38 (2014)
Euler, L.: Introductio in Analysin Infinitorum, vol 1. MM Bousquet, Lausanne (1748)
Fine, N.J.: Basic hypergeometric series and applications, vol. 27 of Mathematical Surveys and Monographs. American Mathematical Society, Providence (1988). With a foreword by George E. Andrews
The GAP Group. GAP—Groups, Algorithms, and Programming, Version 4.11.0 (2020)
Hall, P.: A contribution to the theory of groups of prime-power order. Proc. Lond. Math. Soc. 2(36), 29–95 (1934)
Huppert, B.: Endliche Gruppen. I. Die Grundlehren der Mathematischen Wissenschaften, Band 134. Springer, Berlin (1967)
Kim, D., Yee, A.J.: A note on partitions into distinct parts and odd parts. Ramanujan J. 3(2), 227–231 (1999)
Leinen, F.: Chief series and right regular representations of finite \(p\)-groups. J. Aust. Math. Soc. Ser. A 44(2), 225–232 (1988)
Nyberg, K., Knudsen, L.R.: Provable security against a differential attack. J. Cryptol. 8(1), 27–37 (1995)
Straub, A.: Core partitions into distinct parts and an analog of Euler’s theorem. Eur. J. Combin. 57, 40–49 (2016)
Sylvester, J.J., Franklin, F.: A constructive theory of partitions, arranged in three acts, an interact and an exodion. Am. J. Math. 5(1–4), 251–330 (1882)
Acknowledgements
We thank the staff of the Department of Information Engineering, Computer Science and Mathematics at the University of L’Aquila for helping us in managing the HPC cluster CALIBAN, which we extensively used to run our simulations (caliband.disim.univaq.it). We are also grateful to the Istituto Nazionale d’Alta Matematica - F. Severi for regularly hosting our research seminar Gruppi al Centro in which this paper was conceived.
Funding
Open Access funding provided by Universitá degli Studi dell’Aquila
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by John S. Wilson.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
All the authors are members of INdAM-GNSAGA (Italy) and of the group “Crittografia e Codici” of the Italian Mathematical Union. R. Civino is partially funded by the Centre of Excellence EX-EMERGE at University of L’Aquila. N. Gavioli is a member of the Centre of Excellence EX-EMERGE at University of L’Aquila.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Aragona, R., Civino, R., Gavioli, N. et al. Rigid commutators and a normalizer chain. Monatsh Math 196, 431–455 (2021). https://doi.org/10.1007/s00605-021-01514-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00605-021-01514-y
Keywords
- Symmetric group on \(2^n\) elements
- Elementary abelian regular subgroups
- Sylow 2-subgroups
- Normalizers
- Euler’s partition theorem




 , then
, then  . Moreover,
. Moreover, 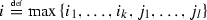 .
. the permutations x and
the permutations x and 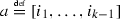 and
and  , we have
, we have