Explicit two-dimensional solutions for the ocean flow in arctic gyres

Abstract

We investigate the ocean flow in an arctic gyre. For given linear or constant oceanic vorticites, we prove explicit solutions which depend on both the polar and the azimuthal angles in the spherical coordinates associated with a rotating Earth. This enables us to identify resonant modes.

Introduction

In an overly-simplified model of our planet, the major ocean currents would be solely driven by the winds. In reality however, the Coriolis force, due to the rotation of the Earth, deflects these practically steady currents so that they produce in the Northern Hemisphere a clockwise circular motion and in the Southern Hemisphere counter-clockwise circular paths. Furthermore, continental boundaries interrupt and divert their flow as well. These large-scale linked-up ocean currents rimmed by land masses are known as “gyres” [2]. There are three types of gyres: tropical, which form near the Equator (confined to either the Northern or the Southern hemisphere since gyres do not cross the Equator, which acts like a wave-guide due to the vanishing of the meridional component of the Coriolis force, thereby facilitating east-west flow propagation—see the discussion in [7, 8]), subtropical (between polar and equatorial regions) and subpolar (in the polar regions). In this paper we will focus on the Arctic basin. It is worth mentioning that the Arctic is very different from the Antarctic: whereas the Arctic is a semi-enclosed ocean almost completely surrounded by landmasses, the Antarctic is almost its complete geographical opposite, a single landmass encircled by a very powerful current known as the Antarctic Circumpolar Current (ACC) [20]; we refer to [9, 18, 19, 22] for studies of the gyre-like flow of the ACC.

To study gyres, one can reduce their complexity by using some of their properties: as their vertical velocity is negligeable with respect to their horizontal one, they can be considered as being two-dimensional flows. This feature was exploited recently in [10] to derive a model for ocean gyres in spherical coordinates. In [3], the author uses the stereographical projection to transform this model into a planar elliptic boundary-value problem which he then reduces to a one-dimensional ODE by neglecting azimuthal variations. This permits him to provide explicit solutions for given oceanic vorticities.

In this paper we replace the stereographic projection by the Mercator projection, which reduces the model in [10] to a semilinear elliptic PDE that is simpler than the equation obtained recently in [3]. The advantage of this new transformation is that for linear oceanic vorticity functions, thanks to the periodicity of the azimuthal velocity, we can use Fourier series to separate our x and y variables (in a planar geometry context, as we can take advantage of the Mercator projection). This in turn provides us with explicit solutions which take into account possible azimuthal variations. The availability of explicit linear solutions opens up possibilities for the investigation of weakly nonlinear effects by means of perturbation theory, along the lines of the developments in [4, 5] of the considerations made in [3].

The Mercator projection

We begin by recalling the recently derived model for gyres in spherical coordinates. [10] Let $\theta \in [0,\pi )$ be the polar angle, where $\theta =0$ corresponds to the South Pole. Our latitude angle is therefore $\theta -\frac{\pi }{2}$. Let $\varphi \in [0,2\pi )$ be the azimuthal (or longitude) angle. The polar and azimuthal velocity components of the horizontal flow on the Earth are given by

$$\begin{aligned} \frac{1}{\sin (\theta )}\psi _{\varphi },\quad -\psi _{\theta }, \end{aligned}$$

respectively, where $\psi (\theta ,\varphi )$ represents the stream function in spherical coordinates.

The governing equation for gyres is given by

$$\begin{aligned} \frac{1}{\sin ^2(\theta )}\Psi _{\varphi \varphi }+\Psi _{\theta }\cot (\theta )+\Psi _{\theta \theta }=F(\Psi -\omega \cos (\theta )) \end{aligned}$$

where $\Psi (\theta ,\varphi )=\psi (\theta ,\varphi )+\omega \cos (\theta )$ is associated with the vorticity of motion of the ocean relative to the Earth’s surface, $2\omega \cos (\theta )$ is the spin vorticity due to the rotation of the Earth and $F(\Psi -\omega \cos (\theta ))$ is the oceanic vorticity, due to the motion of the ocean and specific to a particular gyre. Given $\omega$ and F, we have to solve the governing equation in a given spherical region whose boundary is $\psi _0(\varphi )$. For this, we turn to the Mercator projection.

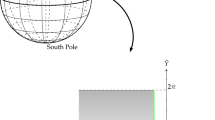
The Mercator projection maps the sphere onto the plane such that the north-south direction is the horizontal direction, the east-west direction is the vertical direction with the length of the Equator preserved, and all paths of equal compass bearing on the sphere are straight lines. It is conformal but distorts areas [12]. The change of variables

$$\begin{aligned} x=-\ln \left[ \tan \left( \frac{\theta }{2}\right) \right] ,\quad y=\varphi \end{aligned}$$

satisfies the above mentioned properties. With this change of variables, the North Pole $(\theta =\pi )$ corresponds to $x=-\infty$ and the Equator $(\theta =\frac{\pi }{2})$ to $x=0$. Therefore, $x<0$ in the Northern Hemisphere with

$$\begin{aligned} \cos (\theta )=\tanh (x),\quad \sin (\theta )=\cosh ^{-1}(x) \end{aligned}$$

Let us set

$$\begin{aligned} u(x,y)=\psi (\theta ,\varphi ). \end{aligned}$$

We can then rewrite the governing equation as the following semilinear elliptic PDE

$$\begin{aligned} \triangle u(x,y)=\frac{F(u(x,y))}{\cosh ^2(x)}+2\omega \frac{\sinh (x)}{\cosh ^3(x)} \end{aligned}$$

(1)

with boundary condition

$$\begin{aligned} u(x_0,y)=u_0(y), \quad x=x_0<0 \end{aligned}$$

if the boundary of our spherical region corresponds to the parallel $\theta _0=2\arctan (e^{-x_0})\in \left( \frac{\pi }{2},\pi \right)$, situated in the Northern Hemisphere (Fig. 1).

Since u(x, y) is periodic in the y-variable, we can reformulate u as the Fourier series

$$\begin{aligned} u(x,y)=\sum _{k\in {\mathbb {Z}}}u_k(x)e^{iky},\quad x\le x_0<0. \end{aligned}$$

and therefore, if F is linear, the linear elliptic PDE reduces to an infinite number of boundary-value problems for second-order ODEs:

$$\begin{aligned} u''_k(x)-k^2u_k= & {} \frac{F(u_k)}{\cosh ^2(x)}\nonumber \\ u_k(x_0)= & {} \alpha _k \end{aligned}$$

(2)

when $k\in {\mathbb {Z}}$ and $k\ne 0$, and

$$\begin{aligned} u''_{0}(x)= & {} \frac{F(u_{0})}{\cosh ^2(x)}+2\omega \frac{\sinh (x)}{\cosh ^3(x)}\nonumber \\ u_0(x_0)= & {} \alpha _0 \end{aligned}$$

(3)

where

$$\begin{aligned} u(x_0,y)=\sum _{k\in {\mathbb {Z}}}\alpha _ke^{iky}. \end{aligned}$$

(4)

When $u(x_0,y)$ is a constant the boundary is defined as a streamline (i.e. a level set of $\psi$).

Fig. 1

The Mercator Projection: We project the polar angle onto the y-axis and the azimuthal angle onto the x-axis. The North Pole is situated at $x=-\infty$

For our general solution to be physically admissible, we require that our stream function be equal to some constant at the North Pole, and that the North Pole be a stagnation point. Therefore, u(x, y) needs to satisfy the following asymptotic conditions:

$$\begin{aligned} \lim _{x\rightarrow -\infty }\{u(x,y)\}=0,\quad \lim _{x\rightarrow -\infty }\{\left( u_x(x,y),u_y(x,y)\right) \cosh (x)\}=(0,0) \end{aligned}$$

(5)

uniformly in $y\in {\mathbb {R}}$ since the horizontal velocity is $\left( \frac{1}{\sin (\theta )}\psi _\varphi ,-\psi _\theta \right) =(u_y,u_x)\cosh (x)$.

Constant oceanic vorticity

Let us consider the case when the oceanic vorticity is constant, $F\equiv \gamma$ with $\gamma \in \mathbb {R}$. Therefore, (2)–(3) takes the form:

$$\begin{aligned} u''_k(x)= & {} k^2u_k,\quad k\ne 0 \end{aligned}$$

(6)

$$\begin{aligned} u''_{0}(x)= & {} \frac{\gamma }{\cosh ^2(x)}+2\omega \frac{\sinh (x)}{\cosh ^3(x)} \end{aligned}$$

(7)

with boundary conditions

$$\begin{aligned} u_k(x_0)= & {} \alpha _{k},\quad k\ne 0\nonumber \\ u_0(x_0)= & {} \alpha _0,\quad k=0 \end{aligned}$$

(8)

The general solution to (6) is

$$\begin{aligned} u_k(x)=c_1(k)e^{kx}+c_2(k) e^{-kx},\quad k\ne 0. \end{aligned}$$

(9)

Since (5) yields

$$\begin{aligned} \lim _{x\rightarrow -\infty }u_k(x)=\frac{1}{2\pi }\int _{0}^{2\pi }\lim _{x\rightarrow -\infty }u(x,y)e^{-iky}dy=0, \end{aligned}$$

(10)

we must have

$$\begin{aligned} u_k(x)= & {} c_1(k)e^{kx},\quad k>0,\nonumber \\ u_k(x)= & {} c_2(k)e^{kx},\quad k<0. \end{aligned}$$

(11)

Theorem 1

If $u(x_0,y)=\psi _0$ for all $y\in [0,2\pi )$, then $u_k\equiv 0$ for $k\ne 0$.

Proof

We note that $u(x_0,y)=\sum _{k\in {\mathbb {Z}}}u_k(x_0)e^{iky}$ for $k\ne 0$ is only equal to some constant for all $y\in [0,2\pi )$ when $u_k(x_0)=0$ for all $k\ne 0$. Because of (11), this means $u_k\equiv 0$ for all $k\ne 0$. $\square$

We are now ready to state and prove our main result.

Theorem 2

Assume the boundary is not a streamline, i.e. $u_0(y)$ is not a constant. If $\alpha _1=\alpha _{-1}=0$, then for a given $\gamma \in {\mathbb {R}}$,

$$\begin{aligned} u(x,y)&=\sum _{k\in {\mathbb {Z}},k\le -2}\alpha _k e^{iky}e^{k(x_0-x)}+\sum _{k\in {\mathbb {Z}},k\ge 2} \alpha _k e^{iky}e^{k(x-x_0)}\\ \\&\quad +\gamma [x+\ln (2\cosh (x))] -\omega [1+\tanh (x)] \end{aligned}$$

is the general solution of (2)–(3) with $F=\gamma$, satisfying the asymptotic conditions (5) and the boundary condition (4), provided $\alpha _0=\gamma [x_0+\ln (2\cosh (x_0))] -\omega [1+\tanh (x_0)]$. There are no solutions for $\alpha _1\ne 0$ or for $\alpha _{-1}\ne 0$, the modes $k=\pm 1$ being resonant.

Proof

We begin by looking at the case ${k=0}$. We have:

$$\begin{aligned} u_0''(x)=\frac{\gamma }{\cosh ^2(x)}+2\omega \frac{\sinh (x)}{\cosh ^3(x)},\quad x\le x_o \end{aligned}$$

(12)

It can be easily verified that

$$\begin{aligned} u_P(x)=\gamma \ln (\cosh (x))-\omega \tanh (x)\quad x\le x_0 \end{aligned}$$

is a particular solution of (12) and therefore, the general solution can be written in the form:

$$\begin{aligned} u(x)=\delta x+\beta +\gamma \ln (\cosh (x))-\omega \tanh (x),\quad x\le x_0,\quad \delta ,\beta \in \mathbb {R} \end{aligned}$$

(13)

We claim that for $\delta =\gamma$ and $\beta =-\omega +\gamma \ln (2)$, (13) satisfies the asymptotic conditions (5). Indeed, setting $\delta =\gamma$, we get:

$$\begin{aligned} \lim _{x\rightarrow -\infty }\{u'(x)\cosh (x)\}=\lim _{x\rightarrow -\infty }\left\{ \gamma e^x-\frac{\omega }{\cosh (x)}\right\} =0 \end{aligned}$$

For the first condition in (5), we have

$$\begin{aligned} \lim _{x\rightarrow -\infty }\{u(x)\}&=\lim _{x\rightarrow -\infty }\{\gamma [\ln (1+e^x)-\ln (2)]+\beta -\omega \tanh (x)\}\\&=-\gamma \ln (2)+\beta +\omega \end{aligned}$$

which vanishes when $\beta =\gamma \ln (2)-\omega$. Note that these values of $\delta$ and $\beta$ are the only ones that come in question.

From the boundary condition (4), we get that

$$\begin{aligned} \alpha _0=\gamma [x_0+\ln (2\cosh (x_0))] -\omega [1+\tanh (x_0)] \end{aligned}$$

We now look at the case $k=1$ and $k=-1$. In order for $u_1(x)=c_1e^x+c_2e^{-x}$ to satisfy (5), we need to set $c_1=c_2=0$. Therefore, for $k=\pm 1$, $u_k\equiv 0$. Consequently, from the boundary condition (4) we can deduce that for $\alpha _1\ne 0$ or $\alpha _{-1}\ne 0$, we have no physically relevant solution.

From (11), we can see that (5) is satisfied for all $|k|\ge 2$. In addition, using the boundary condition (4), we have

$$\begin{aligned} u(x_0,y)=\sum _{k\in {\mathbb {Z}}}\alpha _ke^{iky} \end{aligned}$$

from which we get

$$\begin{aligned} \begin{array}{ll} c_1(k)=\alpha _ke^{-kx_0},&{}\quad k\ge 2\\ c_2(k)=\alpha _ke^{kx_0},&{}\quad k\le -2. \end{array} \end{aligned}$$

$\square$

Remark 1

The problem with no y-dependence was considered in [3]. The result in [3] corresponds to the setting $u_k\equiv 0$ for $k\ne 0$.

Concerning the physical relevance of the above considerations, the basic sources of oceanic vorticity are wind force and the gravitational forces due to the relative motions of the Moon, the Sun and the Earth in the form of the flood and ebb tidal currents (see the discussions in [6, 16]). Both oceanic vorticities can be realisticallly regarded as non-zero constants (see [11, 14]), with the sign depending on the prevalent wind direction, and, respectively, on whether the flow is of ebb or flood type. Let us note that wave-current interactions in flows with vorticity are a topic of great current interest (see the discussions in [6, 11, 13, 15]), at the large scales that are relevant for gyre flows the presence of surface waves is not relevant.

Some special linear oceanic vorticities

Let us now consider the case of linear vorticity, setting $F(u_k)=au_k$. (2) then takes the form:

$$\begin{aligned} u''_k(x)=\left( \frac{a}{\cosh ^2(x)}+k^2\right) u_k(x) \end{aligned}$$

(14)

for $k\ne 0$ and

$$\begin{aligned} u''_0(x)=\left( \frac{a}{\cosh ^2(x)}\right) u_0(x)+2\omega \frac{\sinh (x)}{\cosh ^3(x)} \end{aligned}$$

(15)

for $k=0$. The case for $k=0$ has been shown in [3].

To begin with, we make the change of variable

$$\begin{aligned} z=\tanh (x) \end{aligned}$$

and thus, using the fact that $1-z^2=\cosh ^{-2}(x)$, (14) becomes

$$\begin{aligned} (1-z^2)u_k''(z)-2zu_k'(z)+\left( -a-\frac{k^2}{1-z^2}\right) u_k(z)=0. \end{aligned}$$

(16)

We rewrite

$$\begin{aligned} -a=\frac{1-4a}{4}-\frac{1}{4}=\left( \frac{-1+\sqrt{1-4a}}{2}\right) \left( \frac{1+\sqrt{1-4a}}{2}\right) =l(l+1). \end{aligned}$$

(17)

Setting (17) into (16) yields

$$\begin{aligned} (1-z^2)u_k''(z)-2zu_k'(z)+\left( l(l+1)-\frac{k^2}{1-z^2}\right) u_k(z)=0 \end{aligned}$$

(18)

which, if l is a positive integer, is known as the associated Legendre Differential equation, see [1, 17]. Therefore, the general solution to (18) is

$$\begin{aligned} u_k(x)=c_1P_l^k(\tanh (x))+c_2P_l^k(\tanh (x))\int _{-\infty }^x\frac{\cosh ^2(t)}{[P_l^k(\tanh (t))]^2}\,dt \end{aligned}$$

(19)

where $P_l^k(z)$ denotes the associated Legendre function.

Theorem 3

For $a=\frac{1-(2l+1)^2}{4}$, where l is any positive integer, and for any $b\in {\mathbb {R}}$,

$$\begin{aligned} u(x,y)&=\sum _{k\in {\mathbb {Z}}^*,\,|k|\le l}\alpha _k[P_l^k(\tanh (x_0))]^{-1}P_l^k(\tanh (x))e^{iky}\\ \\&\quad +b[x+\ln (2\cosh (x))] -\omega [1+\tanh (x)] \end{aligned}$$

with

$$\begin{aligned} l=\frac{-1+\sqrt{1-4a}}{2} \end{aligned}$$

is the general solution to (2) with $F(u)=au+b$ satisfying the asymptotic conditions (5) and the boundary condition (4), provided $\alpha _0=b[x_0+\ln (2\cosh (x_0))] -\omega [1+\tanh (x_0)]$.

Proof

To begin with, the associated Legendre polynomial for $0\le k\le l$ is defined as:

$$\begin{aligned} P_l^k(\tanh (x))=\frac{(-1)^k}{2^l l!}\left( \frac{1}{\cosh ^2(x)}\right) ^{\frac{k}{2}}\frac{d^{k+l}}{dx^{k+l}}\left( -\frac{1}{\cosh ^2(x)}\right) ^l \end{aligned}$$

(20)

and we can therefore write

$$\begin{aligned} \lim _{x\rightarrow -\infty }{P_l^k(\tanh (x))}=\lim _{x\rightarrow -\infty }\left\{ \frac{1}{\cosh ^n(x)}\right\} \end{aligned}$$

(21)

where $n\ge 2$, $n\in \mathbb {N}$.

Therefore, for (20) to satisfy the asymptotic conditions (5), we need to set $c_2=0$.

From the boundary condition (4), we have

$$\begin{aligned} c_1=\frac{\alpha _k}{P_l^k(\tanh (x_0))} \end{aligned}$$

thus concluding the proof for $k>0$.

For negative k, the associated Legendre polynomial $P_l^k(z)$ is defined as

$$\begin{aligned} P_l^{-k}(z)=(-1)^k\frac{(l-k)!}{(l+k)!}P_l^k(z) \end{aligned}$$

and therefore the proof follows directly from the one for $k>0$.

Finally, from the previous section, we know that the asymptotic conditions are satisfied for

$$\begin{aligned} u''_0(x)=\frac{b}{\cosh ^2(x)}+2\omega \frac{\sinh (x)}{\cosh ^3(x)} \end{aligned}$$

if and only if $u_0(x)=b[x+\ln (2\cosh (x))] -\omega [1+\tanh (x)]$. From the boundary condition (4), we have

$$\begin{aligned} \alpha _0=b[x_0+\ln (2\cosh (x_0))] -\omega [1+\tanh (x_0)]. \end{aligned}$$

$\square$

Some considerations about general linear oceanic vorticity

It is interesting to observe that (14) can be reduced to a Riccati’s equation, which in turn is equivalent to solving an Ermakov equation.

Indeed, assuming that the solution to (14) is of the form $u_k(x)=e^{f(x)}$, where f is an arbitrary function, solving (14) is equivalent to solving the following Riccati equation (see [17])

$$\begin{aligned} g'(x)=-g^2(x)+\frac{a}{\cosh ^2(x)}+k^2 \end{aligned}$$

(22)

with $g(x)=f'(x)$.

Using the following substitution

$$\begin{aligned} g(x)=s(x)v(x) \end{aligned}$$

(23)

and choosing s(x) such that

$$\begin{aligned} \frac{s''(x)}{2s(x)}-\frac{3(s'(x))^2}{4s^2(x)}+s^2(x)=\frac{a}{\cosh ^2(x)}+k^2. \end{aligned}$$

(24)

we can write (22) as

$$\begin{aligned} v'(x)=-s(x)v^2(x)-2s(x)h(x)v(x)-s(x)h^2(x)+s(x)-h'(x) \end{aligned}$$

(25)

where

$$\begin{aligned} h(x)=\frac{s'(x)}{2s^2(x)} \end{aligned}$$

(26)

We assume for now that such an s exists. A condition for its existence will be given later on.

We can now rewrite (25) as

$$\begin{aligned} v'(x)=-s(x)[(v(x)+h(x))^2-1]-h'(x) \end{aligned}$$

(27)

and using the substitution

$$\begin{aligned} w(x)=v(x)+h(x) \end{aligned}$$

we get

$$\begin{aligned} w'(x)=-s(x)[w^2(x)-1]. \end{aligned}$$

(28)

The solution to (28) is

$$\begin{aligned} w(x)=\tanh \left( \int _{-\infty }^{x}s(t)\,dt\right) \end{aligned}$$

and therefore a particular solution to (14) is

$$\begin{aligned} u_{k_0}=\frac{\cosh \left( \int _{-\infty }^{x}s(t)\,dt\right) }{\sqrt{s(x)}}. \end{aligned}$$

(29)

It remains to find s(x). From (24), we get the following second-order ODE

$$\begin{aligned} s''(x)s(x)-\frac{3}{2}[s'(x)]^2+2s^4(x)=2s^2(x)\left[ \frac{a}{\cosh ^2(x)}+k^2\right] \end{aligned}$$

(30)

and using the substitution

$$\begin{aligned} \gamma (x)=s^{-1/2}(x) \end{aligned}$$

we can reduce (30) to the following Ermakov equation ( see [21])

$$\begin{aligned} \gamma ''(x)=\gamma ^{-3}(x)+\gamma (x)\left[ \frac{a}{\cosh ^2(x)}+k^2\right] \end{aligned}$$

(31)

The general solution to an Ermakov equation (see [21]) is of the form

$$\begin{aligned} k_1\gamma ^2(x)=p_0^2(x)+p_0^2(x)\left[ k_2+k_1\int _{-\infty }^{x}\frac{dt}{p_0^2(t)\,dt}\right] ^2 \end{aligned}$$

(32)

where $p_0(x)$ is a particular solution to

$$\begin{aligned} \tilde{\gamma }''(x)=\tilde{\gamma }(x)\left[ \frac{a}{\cosh ^2(x)}+k^2\right] . \end{aligned}$$

(33)

Remark 2

If $a=-l(l+1)$, for some integer $l\ge 1$, then from (19) we already know that a particular solution to (33) is the associated Legendre polynomial $P_l^k(z)$ with $z=\tanh (x)$ and $l=\frac{-1+\sqrt{1-4a}}{2}$. We can therefore conclude that

$$\begin{aligned} s(x)=\frac{k_1}{[P_l^k(z)]^2\left[ 1+\left( k_2+k_1\int _{-\infty }^{x}\frac{1}{[P_l^k(z)]^2}\right) ^2\right] }. \end{aligned}$$