1 Introduction

Owing to long-term geological activities, rock masses in nature commonly exhibit anisotropy, i.e., foliations, fabrics and bedding planes (Chong and Boresi 1990; Liang et al. 2019; Chen et al. 2022; Yu et al. 2022; Feng et al. 2022a). Anisotropy has a substantial influence on rock mechanical behaviors, including the deformability, strength, fracture toughness, and failure patterns, and plays an important role in governing the safety of rock structures when rocks are subject to various loadings (Debecker and Vervoort 2009; Liang et al. 2014; Cho et al. 2012; Gong et al. 2019a; Wang et al. 2022a). In addition, dynamic loadings, i.e., blasting, impacts and earthquakes, widely occur in infrastructure construction and mining activities, and the dynamic responses of rock masses (Tavallali and Vervoort 2010; Zhu et al. 2021, 2022), in particular, rock masses with transverse isotropy, can be largely governed by rock structural features.

In recent years, many experimental and theoretical studies have been conducted on the mechanical anisotropic behavior of bedded shale (Chao et al. 2023; Dong et al. 2019; Yang et al. 2019; Raef et al. 2018). Experimental investigations have mainly focused on conventional dynamic uniaxial compression and direct shear tests (Heng et al. 2015). Mahanta et al. (2018) analyzed the bearing, deformation and fracture attributes and fracture mechanisms at various strain rates by uniaxial compressive testing. Yang et al. (2020) discussed the effect of bedding on the mechanical parameters of shales via confining pressure tests. Liu et al. (2015) suggested that the strengths of coal rocks with varying bedding directions show significant differences, i.e., significant anisotropy under static and dynamic uniaxial compression. To achieve sufficient theoretical advances and practical applications, research on the loading rate of bedding rock fragmentation should not be limited to the macroscopic scale (Zhang et al. 2000). Thus, it becomes necessary to further understand the static and dynamic fracturing of rocks at the microscopic scale (Ma et al. 2018; Zhao et al. 2021). Zhang et al. (2000) monitored crack propagation close to the broken surfaces of dynamically fractured rock samples. Niu et al. (2021) discussed the evolution of microscopic damage and the dynamic response of sandstones subjected to freeze‒thaw cycles. However, the dynamic failure mechanisms of transversely isotropic shales subject to varying impact loading are not fully understood, and the effect of the loading rate on the bearing features of transversely isotropic shales at the microscale remains unclear.

In the field of experimental rock mechanics, two-dimensional (2D) digital image correlation (DIC) has increasingly become a powerful tool in studying crack propagation in rocks (Feng et al. 2022b; Gong et al. 2022; Wang et al. 2022b, c). Many studies have suggested that the formation of bedding surfaces and microcracks significantly affects the mechanical behaviors and crack growth in rocks (Szwedzicki 2006; Gong et al. 2019b; Jing 2003). Pan et al. (2021) investigated the effect of the inner bedding planes in front of artificial crack tips on the crack evolution related to the bedding planes. Nath and Mokhtari (2018) applied optical techniques to measure the strain on the surfaces of shale samples with various angles of animation through indirect tensile experiments. Zhou et al. (2021) used central-straight notched Brazilian discs composed of shales to study crack creation and development subjected to various load angles via the DIC method. Cho et al. (2012) analyzed the strong deformational and bearing anisotropy of rocks, including Asan gneiss, Boryeong shale and Yeoncheon schist. Identifying different fracture types is critical for analyzing the mechanism of anisotropic rock strength (Debecker and Vervoort 2009; Ramamurthy 1993). Wu et al. (2021) demonstrated that fractures propagate increasingly less along bedding interfaces with increasing strain rate. Liu et al. (2023) found that the dynamic strength and Young’s modulus of shales increase first and then decrease with increasing the pre-static load. However, the effects of loading rate, bedding angle and crack development on indirect dynamic tensile strengths and final failure modes are still unclear.

Characterizing the tensile strengths of shales is significant for many geotechnical and geophysical projects (Gholami and Rasouli 2013; Pufahl et al. 2014). Due to the difficulty of direct tension, the Brazilian disc test has been proposed as a convenient alternative approach for obtaining the tensile strengths of rocks (Perras and Diederichs 2014). The tensile strengths of shales are related to loading rate (Wu et al. 2021), anisotropic degree (Cho et al. 2012), etc. Many theoretical analyses have also been performed for predicting the strength anisotropy of shales either from an experimental or a theoretical standpoint, e.g., by Nova and Zaninetti (1990), Hobbs (1967), Lee and Pietruszczak (2015) and Jaeger (2009). Hobbs (1967) predicted the tensile strengths of rocks by the Griffith crack theory. Jaeger (2009) proposed the single weakness plane theory. However, additional dynamic loading may cause potential adverse consequences (Yang et al. 2020; Wu et al. 2021; Zhao 2000). Moreover, predicting the excavation-induced damage by drill-and-blasting operations is important for assessing the long-term stability and functionality of tunnels, caves, repositories, etc. (Wang et al. 2023; Zhang et al. 2022) With the aim of achieving this goal, it becomes necessary to understand the dynamic mechanical behaviors of rock masses, such as shales. However, the determination of the constitutive model and strength index of rock materials for this purpose must take the effect of strain rate into account.

In the present study, Brazilian splitting tests were carried out using shale specimens with seven bedding angles to ascertain crack propagation and investigate the fracture mechanisms under impact loads by a split Hopkinson pressure bar (SHPB) testing instrument. The progressive fracture process was captured by DIC technology, depending on the complete deformation field of each sample disc. Then, scanning electron microscopy (SEM) technology was used to detect the microscopic morphology of rock fractures. Through a systematic experimental study, the strength characteristics and failure mechanisms of shales subjected to various strain rates were discussed at the microscale and macroscale. Furthermore, based on the Nova‒Zaninetti model, a new strength criterion that considers the strain rate effect was proposed and verified by Brazilian splitting tests. The established strength criterion can effectively show the law of dynamic strength and provide valuable insights for understanding the effect of strain rate on shales.

2 Experimental Setup and Method

2.1 Sample Preparation

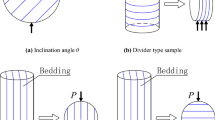
A shale block with low-grade metamorphism was drilled from fresh outcrops in Lushan city, Jiangxi Province, China. The initial orientation of the predominant bedding planes was nearly horizontal. To investigate the influence of the anisotropic features on the mechanical responses of shale rocks, seven groups of samples with bedding angles θ of 0°, 15°, 30°, 45°, 60°, 75° and 90° were acquired from the same shale block. The bedding angle θ is defined as the angle of the predominant bedding plane counterclockwise from the loading direction, as shown in Fig. 1. The diameter and thickness of the samples were 75 mm and 30 mm, respectively. Simultaneously, the sample surfaces were well-polished by following the recommendation of the International Society for Rock Mechanics and Rock Engineering (Aminzadeh et al. 2019) and the German Geotechnical Society (Lepique 2008).

Fig. 1
figure 1

Configuration of the dynamic Brazilian splitting test

Full size image

To understand the mineralogical components and bedding surfaces of the tested shale specimens, as shown in Fig. 2a, the mineral composition and structure were analyzed using X-ray diffraction (XRD) and scanning electron microscopy (SEM). The lithostratigraphic protolith of the Lushan copper ore deposit is primarily composed of acidic igneous rocks, exhibiting poor rock structure maturity and compositional maturity. It contains numerous unstable clasts, such as rock fragments, feldspar, and iron–magnesium minerals, indicating limited transport and a low degree of weathering, as well as weak alteration. The predominant cementation type is matrix cementation, providing particle support. The rock bed was formed during the syndepositional sedimentary period and experienced relatively weak compaction. Under the influence of tectonic forces, localized stress variations were induced, resulting in oblique symmetrical pressure shadows in the rocks. Mild fracturing, alteration, and mineralization processes are observable within the rocks.

Fig. 2
figure 2

Microscopic structure of the shale sample

Full size image

The shale samples behave as transversely isotropic materials, with alternating light and dark layers, and the boundaries along those layers are almost parallel. Furthermore, dark-colored beddings are related to fine-grained textures, while light-colored beddings are related to coarse-grained textures, as shown in Fig. 2b. The mineral grains are displayed in Fig. 2c, and the related bulk fractions are clay (60–65%), silt (30–35%), iron (5%), and carbonaceous matter (1–3%). The dark layers are directionally distributed in the shape of fine scales and composed of clay minerals with particle sizes of less than 0.002 mm. Simultaneously, the light layers are disordered, as shown in Fig. 2d, and are mainly composed of silts, with particle sizes from 0.01 to 0.03 mm.

2.2 Testing Apparatus and Methodology

The SHPB testing system, which has increasingly become a useful laboratory tool to determine the dynamic mechanical behaviors of rocks, was applied in the current study. Figure 3 displays the configuration of the SHPB testing instrument. The bar system consisted of a gas gun, a striker, an incident bar and a transmitted bar. Meanwhile, the striker, incident bar and transmitted bar were 200 mm, 3000 mm and 1800 mm in length and had the same diameter of 75 mm. The tested shale samples were clamped between the incident bar and the transmitted bar. Two strain gauges were glued onto the incident bar and the transmitted bar to monitor the signals of the incident waves, the reflected waves and the transmitted waves. Moreover, an 8-channel DL750 Scope Corder digital oscilloscope and a 6-channel dynamic strain amplifier were utilized to acquire data. In addition, the Photron SA-Z high-speed digital camera, whose capture rate can reach 100,000 frames/second and resolution ratio can be as high as 640 × 280 pixels, was selected for capturing the shale failure process during impacting. Note that the striker and bars were made of hardened 60 Si2Mn, and the corresponding Young’s modulus, density and P-wave velocity were 211 GPa, 7850 kg/m3 and 5102 m/s, respectively.

Fig. 3
figure 3

The split Hopkinson pressure bar (SHPB) testing system

Full size image

To quantitatively determine the deformation behaviors of the tested shale specimens, the DIC technique was utilized in this study. DIC provides an optical numerical full-field measurement and can capture the complicated inhomogeneous deformation fields of the tested samples. By comparing the photographs taken by the digital camera at different loading moments, the variation in the deformation characteristics on the surface of the tested shale samples could be determined. Figure 4 illustrates the representative speckled DIC pattern. The surfaces of the tested shale samples were cleaned before spraying the speckled pattern. The background color was white matte paint, and the speckled pattern was randomly distributed black spots.

Fig. 4
figure 4

The high-speed digital image correlation (DIC) technology

Full size image

The processed SHPB data included the incident, reflected and transmitted historical strain waves monitored by the strain gauges glued on the incident and transmitted bars. In addition, the three-wave analysis approach (Lifshitz and Leber 1994; Sharafisafa et al. 2020) was utilized to calculate the strain and stress characteristics of the tested shale sample. According to one-dimensional elastic wave theory, the relationship between the load and time at the 1 and 2 contact ends can be obtained using:

$$P_{1} (t) = {\rm E}{\rm A}_{{\text{e}}} \left[ {\varepsilon_{I} (t) + \varepsilon_{R} (t)} \right]$$
(1)
$$P_{2} (t) = {\rm E}{\rm A}_{e} \varepsilon_{T} (t)$$
(2)

The average load P(t) at both ends of the sample is

$$P\left( t \right) = \frac{{P_{1} \left( t \right) + P_{2} \left( t \right)}}{2} = {\rm E}{\rm A}_{e} \frac{{\varepsilon_{I} (t) + \varepsilon_{R} (t) + \varepsilon_{T} (t)}}{2}$$
(3)

According to the assumption of stress uniformity, the stress balance at both ends of the sample can be reached as follows:

$$\varepsilon_{I} (t) + \varepsilon_{R} (t) = \varepsilon_{T} (t)$$
(4)

If Eq. (3) is substituted into Eqs. (1) and (2), we can obtain

$$u_{s} = \int_{0}^{t} {C_{0} \left( {\varepsilon_{I} - \varepsilon_{R} } \right)dt} = - 2\int_{0}^{t} {C_{0} } \varepsilon_{R} dt$$
(5)
$$P\left( t \right) = {\rm E}{\rm A}_{e} \varepsilon_{T} (t)$$
(6)

where P1 and P2 stand for the loading forces at the interfaces between the rock samples and the incident and transmitted bars, respectively; εI, εR and εT denote the incident, reflected and transmitted strain waves, respectively, which are monitored by the strain gauges glued on the incident and transmitted bars; Eb and C0 represent the Young’s modulus and P-wave velocity of the bar material, respectively; L refers to the rock sample length; and Ab corresponds to the bar cross-sectional area.

Equations (5) and (6) can be used to calculate the strain and force of the sample during the dynamic SHPB tensile test. According to the static Brazilian disc splitting principle, the tensile strength of the sample is expressed as follows:

$$\sigma_{t} = \frac{2P}{{\pi Dt}}$$
(7)

where P is the failure load, D is the specimen diameter, and t is the specimen thickness.

Because the fractures do not generally initiate at the center of a shale disc, Eq. (7) can be used to calculate only the nominal dynamic tensile strength in this study. By combining Eqs. (6) and (7), the nominal tensile strength of a shale disc under dynamic Brazilian splitting conditions can be obtained as follows:

$$\sigma_{t} = \frac{{2P(t)_{\max } }}{\pi DL}{ = }\frac{{2EA_{{\text{e}}} \varepsilon_{T} (t)_{\max } }}{\pi DL}$$
(8)

where L and D are the thickness and diameter of the disc, respectively; Ae is the cross-sectional area of the incident and transmitted bars; and E is the elastic modulus of the incident and transmitted bars.

3 Experimental Results

3.1 Stress Equilibrium Characteristics

To clarify the effect of anisotropy on the mechanical resistance of shale rocks, seven groups of shale samples with varying bedding angles θ of 0°, 15°, 30°, 45°, 60°, 75° and 90° were tested in this study. Moreover, the effect of strain rate was also considered. Figure 5a illustrates the incident, reflected, transmitted and superposed incident waves measured in the laboratory when the bedding angle is θ = 0°. The slow rising incident wave was derived, and the superposed incident and reflected waves agreed well with the transmitted wave, indicating that the balance of force on the two sides of the tested shale specimen was achieved. Figure 5b depicts the variation in the stress equilibrium factor during the test. Notably, the state of stress equilibrium was achieved when the stress equilibrium factor equaled zero. In addition, the shale sample was under the stress-equilibrium state after a few iterations of wave propagation across the shale specimen. However, in the later stage of the impact, the state of the stress equilibrium was broken because of the serious failure of the shale sample.

Fig. 5
figure 5

The measured curves during the SHPB Brazilian splitting test

Full size image

3.2 Force‒Time Curves

Although there were some differences in the force‒time curves of shale samples under different strain rates, the trend was basically the same. Figure 6 shows that the changes in the force‒time curves at the various stain rates were divided into three different stages, i.e., compaction stage I (I, Iʹ), linear elastic stage II (II, IIʹ) and failure stage III (III, IIIʹ). Furthermore, in the compaction stage, many microcracks closed, and the grains were compacted. However, microcrack propagation or polymerization did not occur. In the linear stage, the microscopic cracks propagated through the hard grains. Simultaneously, the shales displayed obvious resistance behavior. In the failure stage, microscopic cracks continued to develop and penetrate, and macroscopic cracks gradually formed, leading to the final instability of the sample (Gong and Zhao 2014; Li et al. 2017; Gong et al. 2019c). As the strain rate increased, the brittleness at failure and instability of shale samples became increasingly prominent, and the tensile strength also showed an increasing trend.

Fig. 6
figure 6

Force–time curve of the specimen θ = 75° during SHPB Brazilian splitting test when the strain rate \(\dot{\varepsilon }\) = 40.77 s−1

Full size image

3.3 Effect of Bedding Angle

To understand the influence of bedding angle on the rock fracture patterns, seven groups of bedding angles ranging from 0° to 90° were selected for this study. Figure 7 illustrates the corresponding cracking processes of the shale samples, where the strain rate remained approximately constant at approximately 40 s−1. To better represent the crack initiation and propagation characteristics, the photographs shot by the high-speed camera were binarized, implying that the bedding features were not shown. The failure process of the bedded shales under impact were classified into three representative stages, including the crack initiation stage, the crack propagation stage and the complete failure stage, regardless of the variation in the bedding angles.

Fig. 7
figure 7

Failure characteristics of the shale samples with different bedding angles at three representative stages (Note: Paths 1 and 2 refer to the initial and dominant cracks, respectively)

Full size image

In the first stage, the crack initiation stage started at 120–140 μs after impact. Cracks did not initiate at the center of the disc. Indeed, obvious microcracks were first observed at both ends of the disc, particularly when θ = 90°. Moreover, the orientation of the initial cracks highly depended on the bedding angle of the shale samples, except when θ = 90°.

In the crack propagation stage (from 160 to 190 µs after impact), the initial cracks continuously propagated, and secondary cracks were generated. Clearly, the orientation of the secondary cracks changed with the bedding angle. In the case of θ = 0°, 15° and 30°, the bedding plane dominated the propagation of the secondary cracks, i.e., the secondary cracks propagated along the bedding interfaces. When θ = 45°, 60° and 75°, the secondary cracks had a cambered shape and depended on both the axial force and the bedding plane, i.e., the secondary cracks propagated within the angle between the bedding plane and the axial loading direction. For θ = 90°, the bedding interface showed a negligible effect on the failure mode, and the disc was split into two semicircles along the loading direction.

In the complete failure stage, the initial and secondary cracks further propagated and coalesced. Simultaneously, a large number of microcracks emerged, leading to the overall splitting failure of the shale samples.

3.4 Effect of Strain Rate

This section systematically investigates the effect of the strain rate on the failure patterns of shale samples with different bedding angles. Clearly, the strain rate ranging from 30 to 320 s−1 was taken into consideration by controlling the velocity of the striker, and the corresponding results are shown in Fig. 8. The stain rate showed a great influence on the failure patterns of the shale specimens with different bedding angles. On one hand, the failure of the shale samples became more severe with increasing strain rate, regardless of the bedding angle variation. On the other hand, with increasing strain rate, the effect of bedding planes on the rock fracture patterns significantly increased. At a relatively low strain rate, i.e., \(\dot{\varepsilon }\) = 30 s−1, splitting failure phenomena were observed. However, at a relatively high strain rate, particularly \(\dot{\varepsilon }\) = 200 s−1 and \(\dot{\varepsilon }\) = 300 s−1, the bedding plane dominated the failure of the shale samples, and the cracks propagated along the rock stratification plane. Notably, for θ = 90°, splitting failure could always occur regardless of the variation in the strain rate.

Fig. 8
figure 8

Failure patterns of the specimens with different bedding angles under impact shock

Full size image

3.5 Dynamic Nominal Tensile Strength and Energy Absorption

Figure 9a shows the nominal tensile strengths of the layered slates with different bedding angles. The measured dynamic nominal tensile strengths displayed various patterns of changes for different bedding angles and increased rapidly as the strain rate increased from 30 to 320 s−1.

Fig. 9
figure 9

The obtained strength and consumed energy of the specimens by experiment

Full size image

During the continuous process of rock deformation and failure, the storage and consumption of energy is accompanied by loading. It is more consistent with the nature of rock deformation and failure to study rock mechanics from the perspective of energy. To further quantify the effect of bedding angle and strain rate on the dynamic fracturing of the shales, the energy absorption characteristics were systematically analyzed. The energy absorption Wc in the process of the rock dynamic fracture can be calculated as

$${W}_{c}={W}_{i}-{W}_{r}-{W}_{t}$$
(9)

where Wi, Wr and Wt refer to the energy of the incident wave, the reflected wave and the transmitted wave, respectively, which can be determined by

$$W={A}_{b}{E}_{b}C\int \varepsilon {\left(t\right)}^{2}dt$$
(10)

where Ab, Eb and C stand for the cross-sectional area, Young’s modulus and wave velocity of the bars, respectively. ε(t) denotes the variation in the strain measured by strain gauges during the SHPB tests, which could be the incident strain wave, the reflected strain wave or the transmitted strain wave.

Figure 9b shows the energy consumption of shales subjected to various strain rates, from which it is apparent that under different strain rates, the energy consumed by shale samples generally decreased at the beginning but then increased as the bedding angle increased. The consumed energy reached a minimum at a bedding angle of 30° or 60° and a maximum at a bedding angle of 0° or 90°. A comparison of the energy consumption amounts with the dynamic strength characteristics in Fig. 9b reveals that the energy consumed by samples with different bedding angles also had a rate correlation effect, and the energy consumption increased as the strain rate level increased. In addition, the energy absorbed by the rock sample was divided into the fracture energy, the kinetic energy, the rotational energy of the resulting debris or energy in other forms.

4 Discussion

4.1 Effects of Bedding Angle on Deformation Characteristics

Figures 7 and 8 demonstrate that the bedding angle has a great influence on the failure patterns of shales. In summary, the failure patterns of shales with different bedding angles can be classified into five typical types, namely, (a) central fracture I, (b) central fracture II, (c) single layer crack, (d) Z-type crack and (e) parallel-double cracks, as shown in Fig. 10.

Fig. 10
figure 10

Classification of the fracture types: a central fracture I, b central fracture II, c single layer crack, d Z-type crack and e parallel-double cracks

Full size image

The results demonstrate that as the bedding angle increases, the fracture pattern varies from central fractures to layer-activated mixed mode, and the shear failure is gradually replaced by tensile failure. The central fracture mode of the 0° or 90° samples basically cannot be influenced by the bedding plane angle; a main crack appears in the loading direction. From 15° to 75°, the anisotropy of the model specimen becomes more obvious as the bedding angle increases. The 90° specimen shows the typical central fracture II whose paths are not influenced by the inclination of the bedding interfaces. To determine the physical mechanisms of the five typical fracture types, cross-sectional fracture morphology analysis was conducted using SEM.

According to the micrographs of the representative rock fragments at different magnifications, the rock fracture characteristics at the microscale were analyzed. Two categories (Zhang and Zhao 2013a), i.e., cleavage surfaces and fractured surfaces, can be clearly observed, as shown in Fig. 11a, b. Cleavage fractures are a kind of transgranular fracture and mostly form in extensional and tension–shear fractures (Li et al. 2021). The 0° specimen is a typical central fracture I that the loading direction coincides with the bedding direction, and the cleavage fracture occurs in a crystallographic plane. Moreover, the fracture surface is visible based on the fracture morphologies in Fig. 11c. Simultaneously, the fractured surface of the shale corresponds to the performance of the fragility failure of the clay mineral (Fig. 11d). Figure 11e shows a typical cleavage fracture morphology with cleavage steps and river patterns.

Fig. 11
figure 11

Two typical fracture modes captured by SEM: a cleavage surface and b fractured surface

Full size image

In addition, full-field strain analysis was conducted using the DIC technique to determine the variation in the strain distribution on the surface of the shale specimens with different bedding angles. The lateral strain contours of the disk surfaces in which the positive and negative values represent the tensile and compressive strains are shown in Fig. 12, respectively. Simultaneously, the high tensile strain that can form a tensile crack is shown in red. The strain contours show the strain localization and the initiation of cracks. Figure 12a shows that the deformation field is dispersively distributed at the beginning of loading, implying that the stress inside the specimen gradually satisfies the stress equilibrium state based on the multiple reflections of incident waves in the specimen (Li et al. 2020). Figure 12b exhibits the localized strains covering the adjacent areas to the load point. Local high strains of up to 3.8% develop in these locations, indicating the appearance of plastic deformations inside the bar. Furthermore, the formation of plastic zones causes local stretches near the load point, leading to high local positive strains. Clearly, local strain can accumulate quickly in the area near the impacted side of the sample, as shown in Fig. 12c. Then, the highly concentrated strains continue to grow across the entire observation area. The total concentrated strain is 7.4%.

Fig. 12
figure 12

Strain fields of the specimens with different bedding angles when the strain rate \(\dot{\varepsilon }\) = 40.77 s-1

Full size image

4.2 Effects of Strain Rate on Deformation Features

To obtain the fracture characteristics of shales subjected to various strain rate conditions, samples with a bedding angle of θ = 30° were selected to conduct SEM tests on rock fractures, and the high-speed photography and DIC results were combined to analyze the correlation of the rate of rock failure on these bases. The fracture modes of the 30° samples display mixed features, i.e., sliding along the bedding interface and shearing across the bedding interface. The main cracking direction is parallel to the impact axial. Moreover, the axial fracture separates the disc into two main large blocks. The extent of damage in two shear zones near the load points is closely related to the loading rate. The magnitude of local strains gradually increases, and the strain concentration can be accelerated as the strain rate increases at the initial loading state, as shown in Fig. 13. For a higher strain rate, the stress concentrations at the two ends of the specimen and the fracture speed of the sample increase faster, the propagation path is shorter, and the number of cracks is larger.

Fig. 13
figure 13

Strain fields of the specimen θ = 30° under increasing strain rates

Full size image

4.3 Effects of Strain Rate on Strength

Dynamic tensile failure is a significant characteristic of anisotropic rock. To develop a strength criterion for predicting the dynamic bearing capacity of transversely isotropic shales, we examined three typical strength criteria, including the Hobbs–Barron criterion (Hobbs 1967), the Nova‒Zaninetti criterion (Nova and Zaninetti 1990; Jyh Jong et al. 1997) and the single plane of weakness (SPW) criterion (Lee and Pietruszczak 2008, 2015). To evaluate the strength criteria for predicting the nominal tensile strength of layered shales, we selected the corresponding experimental data from three groups of tests, as shown in Table 1.

Table 1 Comparison of test results and calculated strengths with different tensile failure criteria
Full size table

The experimental values were compared with the predicted results according to the different criteria, as shown in Fig. 14. Table 1 denotes the absolute relative error (ARE), and the formula for calculating ARE can be expressed as follows:

$$ARE = \frac{{\left| {T_{P} \left( \theta \right) - T_{E} \left( \theta \right)} \right|}}{{T_{E} \left( \theta \right)}} \times 100\%$$
(11)

where TP (θ) is the predicted tensile strength by the various criteria, and TE (θ) is the mean experimental tensile strength.

Fig. 14
figure 14

Comparison of the nominal tensile strengths determined by three classical predicted criteria

Full size image

Table 1 shows that the predictions of the Nova‒Zaninetti criterion are much closer to the experimental data than the values calculated by the Hobbs–Barron criterion and SPW criterion. Thus, the Nova‒Zaninetti criterion is chosen for further modification to better characterize the tensile strength of anisotropic layered shales under the dynamic Brazilian splitting test in this study. The curve of the strength of the criterion given by Nova and Zaninetti (1990) can be calculated as follows:

$$T(\theta ) = \frac{{T_{{\text{b}}} T_{m} }}{{T_{{\text{b}}} \sin^{2} (\theta ) + T_{m} \cos^{2} (\theta )}}$$
(12)

where θ represents the angle of the applied force direction inclining to the plane of transverse isotropy; Tb represents the tensile strength parallel to the bedding planes; and Tm represents the tensile strength of the intact rock matrix.

Indeed, the rock strengths are not physical constants (Qian et al. 2009). Previous studies have shown that the tensile strength and fracture toughness of rocks increase as the loading rate increases. However, the static fracture toughness of the rock is nearly a constant (Zhang et al. 2000). The response markedly changes when the strain rate exceeds the critical threshold (Zhang 2016; Yao et al. 2015). In the present study, a new strength criterion that can consider the strain rate effect is proposed by collating Brazilian splitting test data and establishing a dynamic coordinate system.

To capture the variation in the dynamic strength subject to different strain rates, the dynamic increase factor (DIF) is represented as the characteristic quantity of strengths. The DIF can be defined as the ratio of dynamic strength to quasistatic strength. For the strain rate, a dimensionless quantity \(\dot{\varepsilon }/\dot{{\varepsilon }_{0}}\) is constructed to characterize the relative strain rate. This ratio can be represented as the logarithmic relation of the strain rate, as follows:

$$DIF = \frac{{\sigma_{d} }}{{\sigma_{0} }}{ = }K_{{\text{a}}} ln(m\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }} + 1) + b$$
(13)
$$y=a-b{c}^{x}$$
(14)

Sorting the test data with dimensionless quantities shows that the DIF in the semilogarithmic coordinate system is associated with the strain rate. σ0 represents the average quasistatic tensile strength when θ = 0°, and σd represents the dynamic tensile strength of the specimen under different strain rates. Simultaneously,\(\dot{\varepsilon }\) represents the strain rate (s−1). In this study,\({\dot{\varepsilon }}_{0}\) = 3 × 10–6 s−1. m and b are the fitting coefficients, which are 1 × 10–7 and 0.27, respectively.

The relationship between Ka and the change in the bedding angle can be obtained by fitting the experimental data, as follows:

$$K_{a} = 2.71 + 0.81sin\frac{{\pi \times \left( {\theta - \theta_{0} } \right)}}{167}$$
(15)

where the critical angle constant θ0 is 92°.

Therefore, a unified equation can be proposed to describe the dynamic strength characteristics of shales subject to a given strain rate range, as follows:

$$DIF = (2.71 + 0.81sin\pi (\theta - \theta_{0} )/167) \times ln(\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }} + 1) + 0.27$$
(16)

Figure 15 shows the DIF curve changing with the strain rate for the shale samples with different bedding directions.

Fig. 15
figure 15

Variation of DIF with the strain rate increasing under different bedding directions

Full size image

The tensile strength characteristics of anisotropic layered rocks have been discussed by Nova and Zaninetti (1990). By substituting Eq. (13) into Eq. (12), the model of the dynamic fracture pressure under the Nova‒Zaninetti criterion can be expressed as follows:

$$T(\theta ) = \frac{{T_{b} T_{m} \left[ {K_{a} ln\left( {m\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }} + 1} \right) + b} \right]}}{{T_{b} sin^{2} \theta + T_{m} cos^{2} \theta }}$$
(17)

Equation (17) indicates the modified Nova‒Zaninetti criterion established in this study. With the aim of verifying the correctness of the proposed dynamic strength criterion, the predicted values were compared with the experimental data. First, the criterion coefficients under different strain rates and bedding angles were determined. Then, the theoretical curves calculated by the modified Nova‒Zaninetti criterion were compared with the test data, as shown in Fig. 16. To quantitatively describe the fitting effect of the dynamic strength criterion on shales with different bedding angles within a certain range of strain rates, the standard deviation and the correlation coefficient R2 were used for evaluation.

Fig. 16
figure 16

Comparison of the dynamic tensile strengths obtained by theory and test: a θ = 0°, b θ = 15°, c θ = 30°, d θ = 45°, e θ = 60°, f θ = 75° and g θ = 90°

Full size image

The results demonstrated that the strength criterion established in this study is in good agreement with the test data. Moreover, the correlation coefficient between the theoretical curve and the experimental curve is greater than 0.86. By comparing the fitting curve with the research results of other researchers, it is clear that the trend of tensile strength at different angles with increasing strain rate corresponds to the general changing pattern of the dynamic strength of shales (Zhang 2016; Zhang and Zhao 2013b).

According to the above analysis, the dynamic tensile strength and the anisotropy of failure patterns increase as the strain rate increases. The predictive model shows high accuracy for samples with significant anisotropy, which implies that the proposed model has a sound physical base and is applicable to a wide range of strain rates (30–320 s−1). The fitting formula fully considers the dynamic strength law, provides a new understanding of the effect of rate, and can be utilized to effectively calculate the dynamic strength of layered shales. However, the effectiveness and accuracy of the proposed model can be affected by rock heterogeneity and preexisting secondary microcracks and fissures, and it is applicable only when the strain rate values are between 30 and 320 s−1.

5 Conclusion

The deformation and failure behaviors of anisotropic shale specimens subjected to various impact loads were investigated by SHPB testing equipment and high-speed DIC technology. Systematic experimental studies were carried out to reveal the failure process, fracture mode and mechanical mechanism of shales under dynamic impacts at the macroscopic and microscopic scales. The failure patterns and strength features were comprehensively discussed, and the main conclusions are as follows:

  1. (1)

    The crack initiation position of the disc specimens is greatly influenced by the bedding angle and the strain rate. Moreover, five classic failure patterns are measurable: (a) central fracture I, (b) central fracture II, (c) single layer crack, (d) Z-type crack and (e) parallel-double cracks.

  2. (2)

    Cracks are mainly generated along the direction of loading, and the fracture patterns are only slightly affected by the strain rate when θ = 0° and θ = 90°. Namely, the effect of strain rate shows anisotropic characteristics and becomes more significant when the layer orientation changes from 15° to 75°.

  3. (3)

    For low strain rates, central fractures are prone to occur, and the orientation of the bedding planes has only a slight influence on the failure pattern. Two parallel cracks are apparently generated along the bedding planes from both ends of the samples with increasing strain rate. For moderate bedding plane angles, a relatively complicated failure pattern is induced by the strain rate effect. For high strain rates, cracks generally develop along different directions inclined to the bedding planes.

  4. (4)

    For a higher strain rate, the energy release becomes quicker and larger, leading to the appearance of transgranular cracks. Moreover, with increasing strain rate, the high stresses concentrate more significantly at both ends of the specimens, the fracture speed of the specimens becomes faster, and the propagation path and number of cracks become shorter and larger, respectively.

  5. (5)

    In a semilogarithmic coordinate system, the dynamic strength shows a linear relationship with the growth of the dimensionless quantity \(\dot{\varepsilon }/\dot{{\varepsilon }_{0}}+1\). Simultaneously, the proposed modified Nova‒Zaninetti criterion contains two parameters with clear physical meaning that are easy to determine, i.e., the critical strain rate and bedding angle. It has proven to be reliable and effective for predicting the strength of shales under impact loading within a certain range.