Calibration Method and Material Constants of an Anisotropic, Linearly Elastic and Perfectly Plastic Mohr–Coulomb Constitutive Model for Opalinus Clay

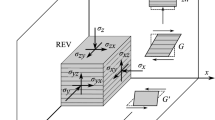
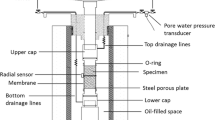
Abstract

Nagra, the cooperative for developing and implementing a long-term radioactive waste depository in Switzerland, identified Opalinus Clay as the most suitable host rock for deep geological containment. This paper deals with those features of Opalinus Clay that are important for the design and construction of the underground structures. Consolidated drained (CD) and consolidated undrained (CU) triaxial compression tests on specimens from deep boreholes revealed that Opalinus Clay exhibits pronounced stiffness and strength anisotropy, dependency of stiffness on the initial confining pressure, slightly non-linear pre-failure stress–strain behaviour, and a drop in axial resistance after a certain amount of shearing. Within the scope of establishing a rigorous—yet practical—design approach for the repository tunnels and caverns, the simplest possible constitutive model capable of reproducing the main aspects of the Opalinus Clay behaviour is adopted. The non-associated linear elastic and perfectly plastic MC model is chosen as a starting point, on account of its wide use in tunnel engineering practice, its simplicity, and the clear physical meaning of its parameters. This paper presents a systematic and robust calibration method for an extended version of this model, which considers the pronounced strength and stiffness anisotropy of Opalinus Clay. The paper additionally provides the full suite of the equations that describe the model behaviour under triaxial CU or CD testing conditions and for any bedding orientation relative to the specimen axis. The equations are employed to determine ranges of material constants for two varieties of Opalinus Clay, based upon the results of 73 CU and CD tests. A thorough comparison between the model predictions and the experimental response is conducted, to demonstrate the versatility and limitations of the constitutive model and of the proposed calibration approach.

Highlights

• A large number of CD and CU triaxial compression tests was evaluated.

• The adequacy of a simplified non-linear anisotropic material model was assessed.

• The prediction and calibration equations for the model were provided.

• The strength and stiffness constants of Opalinus Clay were determined based on the large experimental database.

1 Introduction

Argillaceous formations have been identified as the most suitable host rocks for the Central European repositories, due to their favourable properties for long-term nuclear waste containment that enable them to act as natural barriers (ANDRA 2005; Bundesamt für Energie 2018; Nagra 2021; Bock et al. 2010; Boisson 2005; Bernier et al. 2011). The properties and behaviour of such rocks have been extensively investigated over the past years, inter alia in underground research laboratories (URLs) conducting in situ investigations in the candidate repository regions. Figure 1 shows the locations of the most prominent host rock formations in Central Europe and the corresponding URLs: Callovo Oxfordian Clay (East of Parisian basin)—Meuse/Haute-Marne URL, Bure, France (ANDRA 2005); Domerian and Toarcian Marls and Argillites (Causses basin)—Tournemire URL, France (Abdi et al. 2015); Boom Clay—Mol URL, Belgium (Bernier et al. 2011); and Opalinus Clay—Mont Terri URL, Switzerland (Bundesamt für Energie 2018; Nagra 2021; Bossart 2008). Table 1 provides an overview of the key geological, mineralogical, and geotechnical properties of these claystones, along with the calibration results of the present paper for Opalinus Clay in the last two columns.

Fig. 1

Locations of Central European underground research laboratories (Mol, Tournemire, Bure, Mont Terri), boreholes in Opalinus Clay (candidate sites, Mont Terri) and candidate siting regions for the Swiss underground repository (dark grey)

Table 1 Key geological, mineralogical and hydromechanical properties of argillaceous formations considered as candidate host rocks for European radioactive waste repositories

Opalinus Clay was identified by the National Cooperative for the Disposal of Radioactive Waste in Switzerland (Nagra) as the most promising host rock for a deep geological repository (Bundesamt für Energie 2018; Nagra 2021), on account of its (i), extremely low permeability (10^–12–10^–14 m/s), (ii), swelling behaviour, which enables resealing of fissures generated by tunnel excavation and effectively prevents radionuclide transfer into the ground, (iii), ability to permanently bind positively charged waste radionuclides on its negatively charged clay platelets (sorption) and, (iv), homogeneous macroscopic structure, which remained unchanged over large areas for centuries, thus enabling its properties to be reliably predicted. Over the past decades, substantial research has been conducted into Opalinus Clay’s geo-mechanical (e.g., Zhang et al. 2004; Minardi et al. 2021; Bossart 2008; Favero et al. 2018, 2016; Giger et al. 2015a; Crisci et al. 2019; Wild and Amann 2018; Nitsch et al. 2023), thermal (e.g., Zhang et al. 2004; Monfared et al. 2011) and mineralogical (e.g., Mazurek and Aschwanden 2020) properties. Opalinus Clay formations exist in the northern part of Switzerland, where three candidate repository siting regions have been identified at the end of Stage 2 of the site selection process (marked dark grey in Fig. 1; Bundesamt für Energie 2008), offering an optimal combination of layer thickness (ca. 110 m) and depth (ca. 400–900 m) for geological disposal.

Within the scope of designing the envisioned repository tunnels, a constitutive model capable of reproducing the main aspects of the mechanical behaviour of Opalinus Clay must be adopted and calibrated based on experimental data to establish representative material constants. A vast variety of constitutive models for geomaterials exists in the literature, such as coupled elastoplastic damage models (e.g.,Chazallon and Hicher 1998; Jia et al. 2007; Salari et al. 2004), plasticity-based models (e.g.,Kavvadas and Amorosi 2000; Suebsuk et al. 2010) phenomenological models (e.g., Souley et al. 2011) and models based on micro-mechanical considerations (e.g.,Cariou et al. 2013; Guéry et al. 2008). Many amongst them accurately capture particular intricate aspects of the behaviour of claystones and argillites, such as stiffness and strength anisotropy and strain hardening and softening (e.g., Parisio and Laloui 2017; Zhao et al. 2018; Chen et al. 2012; Mánica et al. 2017; Ismael et al. 2019; Bertrand and Collin 2017; Nguyen and Le 2015).

Notwithstanding the above, the employment of sophisticated models poses several limitations: (i) their formulation encompasses numerous parameters (particularly in the case of anisotropy; e.g., Pietruszczak and Haghighat 2015) very often lacking clear physical meaning (Suebsuk et al. 2010), which renders the model calibration cumbersome; (ii) their systematic application in large 3D tunnel design computations (as the ones required in the design of underground repositories) can be prohibitive in terms of computational resources and time; and (iii) models considering softening and involving strain localisation suffer from the inherent limitation of non-uniqueness of the numerical solution, as well as the computational cost of regularisation techniques and the fine spatial discretisation required, which is prohibitive particularly for real life field problems. Simpler constitutive models are thus favoured from a practical engineering viewpoint, as they ensure computational stability, well-posedness and solution uniqueness, and offer the considerable benefit of fewer material constants that are universally interpreted, have a clear physical meaning, and can be calibrated with a simpler procedure.

The most widely employed model, that is the isotropic linearly elastic and perfectly plastic model with a Mohr–Coulomb (MC) yield criterion, evidently falls short of capturing the strain hardening or softening typically exhibited by claystones. However, hardening can be considered in the tunnel calculations via an appropriate secant stiffness modulus (see Sect. 5 point (i) and Vrakas et al. 2018), while softening can be considered via two limit cases (peak strength and residual strength) which overall bound the actual response of softening ground. Depending on the problem parameters, the perfectly plastic model predictions may be very close to those of a softening model. For the candidate repository sites, comparative plane strain tunnel calculations showed that the predictions of a perfectly plastic model with residual parameters are very close to those of a model with brittle softening (Nordas and Anagnostou 2021; Nordas et al. 2023). Nonetheless, the most important limitation of isotropic models is their inability to capture stiffness and strength anisotropy with a single set of material constants. Hence, existing calibration approaches consider different sets of model parameters for different orientations of the bedding plane. (cf., e.g., Favero et al. 2018). While isotropic models might be adequate for considering different scenarios in a preliminary design stage, detailed design computations call for a more complex, yet practical, modelling strategy which enables capturing the phenomena manifested in the tunnel vicinity in cases of pronouncedly anisotropic rock behaviour (e.g., pore pressure redistributions around the tunnel during consolidation; anisotropic convergences, interaction of matrix and bedding plasticity, etc.) with a unique material parameter set.

Motivated by this insufficiency, the authors present in this paper a simple and practical calibration approach for an anisotropic, linearly elastic and perfectly plastic constitutive model with a non-associated MC yield criterion. The novel, full suite of calibration equations for various initial and hydraulic conditions is presented. Finally, the proposed calibration strategy is employed to determine representative engineering material constants for Opalinus Clay.

The adopted model assumes cross-anisotropic linear elasticity (which is suitable considering the relatively uniform bedding layering of Opalinus Clay; cf., e.g., Giger et al. 2015b) as well as the validity of Coulomb’s failure hypothesis both for the matrix and the bedding. The latter implies that the strength is lower in certain loading directions, depending on the bedding orientation relative to the principal stress axes. The model extends the widely applied in engineering practice elastoplastic model to anisotropic problems while still preserving its main benefits of simplicity, clear physical meaning of the embedded parameters and experience in its use; in addition, it offers the considerable advantage of capturing stiffness, strength and stress path anisotropies with a single set of material constants. It can thus be widely employed as a simple model in practical engineering design. The constitutive model was originally implemented in Abaqus/Standard (Dassault Systèmes 2019) by ETH Zurich as a user-defined material subroutine (UMAT) for in-house activities, and was recently incorporated into the commercial FE suite FLAC (Itasca 2019).

In the following, the principal features of the observed behaviour of Opalinus Clay is examined first in Sect. 2. Subsequently, the constitutive model is formulated and its behaviour under triaxial testing conditions is discussed in Sects. 3 and 4. Section 5 presents a comparison between the experimental results and the model predictions, and discusses the achieved prediction accuracy and the adopted calibration assumptions for treating the inherent model limitations. Section 6 presents the general calibration method for the elasticity, strength and dilatancy parameters of the model. Finally, Sect. 7 presents the determined ranges of material constants for two Opalinus Clay varieties from the candidate sites and the Mont Terri URL, and discusses their differences, followed by concluding remarks in Sect. 8.

2 Observed Behaviour

Most recent knowledge about the mechanical behaviour of Opalinus Clay is based upon 73 consolidated undrained (CU) and consolidated drained (CD) triaxial compression tests described in Crisci et al. (2023), Minardi et al. (2021) and Favero et al. (2018). The specimens were obtained from the Mont Terri rock laboratory and from deep boreholes in Bülach, Trüllikon and Bözberg, which are located in the three candidate repository sites (Fig. 1, Table 2). The specimens from the candidate sites are treated as a single variety; its distinction form the Mont Terri variety is justified by their different geological background (Sect. 7).

Table 2 Overview of available triaxial compression tests

Depending on the angle between the bedding plane and the specimen axis, the tests are referred to as S-, P- and Z-tests (major principal stress oriented perpendicularly, parallel, and obliquely to the bedding, respectively; see sketches at the top of Figs. 2, 3). The red curves in Figs. 2 and 3 show for CU and CD tests, respectively, the typical behaviour of Opalinus Clay in terms of: deviatoric stress q (= σ_a− σ_r = σ′_a− σ′_r) versus axial strain ε_a, excess pore pressure p_w (CU tests) or volumetric strain ε_vol (CD tests) versus axial strain ε_a, and deviatoric stress q versus mean effective stress p′ = (σ′_a + 2 σ′_r)/3. The samples have been obtained from the candidate sites and the tests shown in each of Figs. 2 and 3 have been performed with an approximately equal initial effective confining pressure (ca. σ′_r,0 = 13 MPa and 5 MPa, respectively). (No CD Z-tests have been performed.) The black and blue lines in the diagrams of Figs. 2 and 3 show the theoretical behaviour after the adopted constitutive model and will be discussed later.

Fig. 2

Observed behaviour (red lines) and model behaviour (black and blue lines) in CU tests: a–c deviatoric stress q versus axial strain ε_α, d–f excess pore pressure p_w versus axial strain ε_α, g–i deviatoric stress q versus mean effective stress p′ (candidate sites variety; S-test ID: A9_TRU1_1; P-test ID: B8_TRU1_1; Z-test (θ = 60°) ID: C13T_BUL1-1; Crisci et al. 22023)

Fig. 3

Observed behaviour (red lines) and model behaviour (black and blue lines) in CD tests: a, b deviatoric stress q versus axial strain ε_α, c, d volumetric strain ε_vol versus axial strain ε_α, e, f deviatoric stress q versus mean effective stress p′ (candidate sites variety; S-test ID: B2_MAR1_1; P-test ID: A12_TRU1_1; Crisci et al. 2023)

Main aspects of the observed behaviour of Opalinus Clay are:

• (i) Slightly nonlinear stress–strain behaviour right from the start of deviatoric loading (Figs. 2a–c, 3a, b; cf., e.g., Minardi et al. 2021; Favero et al. 2018). Specimens of the Mont Terri variety exhibit a slightly more non-linear pre-failure stress–strain behaviour. The non-linearity can be modelled as plastic hardening, because, according to Favero et al. (2018), irreversible strains develop almost right from the start of deviatoric loading.

• (ii) Moderate stiffness dependency on the initial confining pressure (cf., e.g., Giger et al. 2015b; Favero et al. 2018). This only becomes evident via comparison of the pre-peak response of samples with different σ′_r,0, and is thus not visible in Figs. 2 and 3. It is mentioned here for completeness and will be demonstrated later in Sect. 6.1.

• (iii) Stiffness anisotropy (cf., e.g., Giger et al. 2015b; Minardi et al. 2021; Favero et al. 2018). The highest axial stiffness is observed in P-tests, the lowest in S-tests, and an intermediate in Z-tests (Figs. 2a–c, 3a, b). The stiffness anisotropy appears to be less pronounced in CU tests (Fig. 2a–c) than in CD tests (Fig. 3a, b), since the pore water (which cannot flow out of or into the specimen) stiffens the specimens, particularly in the softer direction (S), and leads to a less anisotropic overall response.

• (iv) Pre-peak stress path anisotropy in CU tests (cf., e.g., Minardi et al. 2021). According to the pre-peak stress path in the p′–q space (Fig. 2g–i) p′ decreases with increasing q in the S-tests and increases with q in the P-tests. This can be explained as a consequence of stiffness anisotropy (cf. Anagnostou and Vrakas 2019 and Sect. 4).

• (v) Strength anisotropy (cf., e.g., Giger et al. 2015b; Minardi et al 2021; Martin et al. 2016). Shearing through the rock matrix prevails in S-tests and P-tests, whereas Z-tests are governed by shearing in the bedding plane and exhibit a substantially lower peak strength (Fig. 2a–c, g–i).

• (vi) Decrease in axial stress after a certain shearing ("strain softening"), both in the S-tests and P-tests (where failure occurs through the matrix) and in the Z-tests (where failure occurs in the bedding plane) (cf., e.g., Giger et al. 2015b; Minardi et al. 2021; Favero et al 2018). The behaviour is generally more brittle (sudden decrease in stress) in CD tests (Fig. 3a, b) and in CU P-tests (Fig. 2b) and more ductile in CU S-tests and Z-tests (Fig. 2a, c). The apparently ductile behaviour may be due to the stabilising effect of the monotonically decreasing pore pressure after the peak (Fig. 2d, f).

3 Constitutive Model

The components of the model formulation are largely standard. The main equations are given in “Elasticity Equations” and “Plasticity Equations” sections of the “Appendix” and the underlying assumptions are outlined below.

The elastic behaviour is taken as linear cross-anisotropic, which is fully defined by five parameters (Eqs. 7–9): the Young’s modulus E_o orthogonal to the bedding; the anisotropy ratio n (that is the ratio of the Young’s modulus E_p parallel to the bedding plane to the modulus E_o orthogonal to the bedding); the Poisson’s ratio ν_pp for stress and strain components parallel to the bedding; the Poisson’s ratio ν_op for stress components orthogonal and strain components parallel to the bedding; and the shear modulus G_op on planes orthogonal to the bedding.

The model assumes perfectly plastic behaviour with lower shear strength parameters in the bedding plane, MC yield condition (Eqs. 12–17) and a non-associated plastic flow rule (Eqs. 24–26). This is fully defined by six parameters c, φ, ψ and c_b, φ_b, ψ_b, where the former and the latter triplets, respectively, denote the cohesion, friction angle and dilatancy angle of the rock matrix and the bedding plane. The consideration of both yield conditions makes it possible to take into account the strength reduction occurring within a range of bedding orientations (Fig. 4) in a physically founded manner; that is Coulomb's failure hypothesis, according to which failure occurs when the shear stress in an arbitrary section reaches the shear resistance of the material.

Fig. 4

Assumed yield condition

Alternative to the above, the dilatancy factor κ, as well as the slopes and the intercepts of the MC yield envelopes for the matrix (M, d₀) and the bedding (M_β, d_0β) in the triaxial stress space (p′, q), can be considered as independent plasticity parameters (Eqs. 18–23, 25). bearing in mind that M_β and d_0β are not material constants, because they depend on the angle β between the maximum principal stress and the bedding plane. (β = π/2 − θ, where θ denotes the dip angle of the bedding planes in the testing device.)

4 Model Behaviour

The derivation of the equations describing the model behaviour in CD and CU triaxial compression tests considers: (i), the MC yield conditions of the matrix and bedding (Eqs. 18–23); (ii), the consistency condition (effective stresses remain on the yield envelopes post-yielding); (iii), the usual strain decomposition of elastoplastic constitutive laws, where elastic components fulfil the cross-anisotropic relationship (Eq. 7) and plastic components the flow rules (Eqs. 24–26); (iv), the initial and boundary conditions of triaxial tests (initial effective confining pressure, constant total radial stresses), as well as their known characteristics (constant effective stress during yielding in CD tests, constant water content in CU tests).

The derivation is straightforward for the limit cases of S-tests and P-tests, where the bedding is oriented parallel to the axes of the specimen coordinate system and only yielding in the matrix is relevant. However, it becomes mathematically cumbersome in the general case of inclined bedding, which necessitates lengthy transformations (from the bedding to the specimen co-ordinate system and vice versa), and which must consider two possibilities for yielding in the matrix or along the bedding (cf. Fig. 4). The full suite of the general equations for both CU and CD conditions and arbitrary bedding inclinations is novel and is given in “Prediction Equations for Behaviour Before Yielding”–“Coefficients” sections of the “Appendix” (Eqs. 27–41). These equations are used to calibrate the anisotropic model and to determine the material constants of the Opalinus Clay in the present case. Furthermore, they are valuable as analytical benchmarks for the validation of the numerical implementation of the constitutive model in finite-element codes.

Figure 5 shows the predicted relationships between deviatoric stress (q), volumetric strain (ε_vol), excess pore pressure (p_w) and axial strain (ε_a), as well as the effective stress paths (p′–q), for CD and CU S- and P-tests with the same initial effective confining pressure of 10 MPa. (The predictions for Z0tests are similar; the elastic branches of the relationships mentioned are between the limit cases of P-tests and S-tests, and cease earlier due to the lower strength of the bedding.)

Fig. 5

Model behaviour in the CD and CU S-tests and P-tests: a deviatoric stress q versus axial strain ε_α, b volumetric strain ε_vol (CD tests) or excess pore pressure p_w (CU tests) versus axial strain ε_α, c deviatoric stress q versus mean effective stress p′ (σ′_r,0 = 10 MPa; other parameters: last column of Table 3)

Under CD conditions the stresses remain constant during yielding (perfectly plastic material) and are equal for P- and S-tests, because matrix yielding is relevant in both cases, but CD P-tests yield earlier (at a lower axial strain) because of the higher stiffness parallel to the bedding (blue lines in Fig. 5a). The volumetric strain (expansion) developing during yielding is equal in both cases (equal slopes of blue lines in Fig. 5b), because it is purely plastic (the effective stresses are constant during yielding, and hence the elastic strain increments are zero) and consequently the elastic anisotropy does not play a role. The elastic stress paths coincide in both cases and follow the familiar line of isotropic materials with a slope of 3 (blue lines in Fig. 5c).

Under CU conditions the expansion observed in the CD tests during yielding cannot occur. Instead, the pore pressure drops (red lines in Fig. 5b), which in combination with the constant radial total stress results in a higher effective radial stress and an increase in the frictional component of the resistance to shearing; this translates into the observed increase in the deviatoric stress during yielding (so-called "dilatancy hardening"; Rice 1975; red lines in Fig. 5a). P-tests reach yielding at a higher deviatoric stress than S-tests (see kinks in the red lines in Fig. 5a).

The apparently higher strength of P-tests is due to the elastic anisotropy, which under undrained conditions results in a different pre-peak stress path compared to S-tests (red lines in Fig. 5c). This can be directly inferred considering the general expression of the pre-peak stress path slope in CU tests (Eq. 32 using Eqs. 46 and 47):

$$\frac{\Delta q}{{\Delta p^{\prime}}} = \frac{{3\left( {2 + n - 2\nu_{{\text{pp}}} - 4n\nu_{{\text{op}}} } \right)}}{{\left( { - 2 + 3\sin^2 \theta } \right)\left( {n - 1 + \nu_{{\text{pp}}} - n\nu_{{\text{op}}} } \right)}},$$

(1)

which reads as follows for S-tests (θ = 0°):

$$\frac{\Delta q}{{\Delta p^{\prime}}} = - \frac{{3\left( {2 + n - 2\nu_{{\text{pp}}} - 4n\nu_{{\text{op}}} } \right)}}{{2\left( {n - 1 + \nu_{{\text{pp}}} - n\nu_{{\text{op}}} } \right)}}$$

(2)

and as follows for P-tests (θ = 90°):

$$\frac{\Delta q}{{\Delta p^{\prime}}} = \frac{{3\left( {2 + n - 2\nu_{{\text{pp}}} - 4n\nu_{{\text{op}}} } \right)}}{{\left( {n - 1 + \nu_{{\text{pp}}} - n\nu_{{\text{op}}} } \right)}}.$$

(3)

The above expressions evidently deviate from the familiar vertical line of isotropic materials and indicate that the mean effective stress decreases in S-tests and increases in P-tests. Consequently, for the same initial effective confining pressure, the stress path of P-tests intersects the yield condition at a higher deviatoric stress compared to S-tests. It is interesting to note, and can be readily verified from Eqs. 2 and 3, that the P-test stress path is not only in the opposite direction, but also twice as steep compared to the stress path of S-tests, regardless of the values of the material constants. This intrinsic limitation of the model and its effects are discussed in the next section.

5 Comparison with Observed Behaviour and Consequences for Calibration

The black and blue lines in Figs. 2 and 3 show the model behaviour for CU and CD tests, respectively, which allows a direct comparison with the observed behaviour discussed in Sect. 2. Six sets of material constants are considered, as given in Table 3: the first five sets were determined through model calibrations that considered the results of a single test from each of the test types considered (model behaviour: black lines in Figs. 2, and 3); the sixth was determined through a model calibration that considered all 50 (Table 2) Opalinus Clay samples from the candidate sites (model behaviour: blue lines in Figs. 2, and 3). The first five sets enable assessing the model prediction accuracy in the best case, that is if the rock was homogeneous and only test of one type was considered. The sixth set enables a comparative evaluation of the model prediction accuracy for one single test of a specific type and for multiple tests of variable types, which better showcases the model limitations arising in the latter case.

Table 3 Material constants determined from each of the five tests of Figs. 2 and 3 separately (columns CU-S, -P, -Z- and CD -S, -P) and from the entirety of experimental data from the boreholes in the candidate sites (last column)

The model behaviour is discussed below with reference to aspects (i)–(vi) discussed in Sect. 2:

• (i) Slightly non-linear stress–strain behaviour: The model assumes linearly elastic behaviour (Figs. 2a–c, 3a, b). The non-linearity of the actual behaviour can be considered via secant Young’s moduli E_o, E_p evaluated at 50% of the peak deviatoric stress q_peak. This is sufficiently accurate for tunnel calculations (Vrakas et al. 2018). For consistency with this assumption, all other elasticity parameters are determined at 50% of q_peak.

• (ii) Moderate stiffness dependency on the initial confining pressure: The model considers constant values for all elasticity parameters, irrespective of σ′_r,0. However, tunnelling calculations shall be performed for adequate values of E_o and E_p, based upon the expected in situ stress σ′_r,0 (Vrakas et al. 2018). E_o and E_p are thus expressed as linear functions of σ′_r,0 via linear regression of the available experimental data, while n, ν_op, ν_pp and ν_po are assumed constant and independent of σ′_r,0.

• (iii) Stiffness anisotropy: The cross-anisotropic elasticity formulation readily captures stiffness anisotropy with a single set of material constants, by considering different stiffnesses orthogonal (E_o) and parallel (E_p) to the bedding, and distinct Poisson’s ratios ν_op, ν_pp, ν_po that better approximate the relationship between axial and horizontal strain components. The black lines (which hold for the parameters obtained through calibration of individual tests separately) are very close to the blue lines (which consider the entirety of tests), which underscores that the model achieves a good stiffness correlation amongst the different test types with a single parameter set (Figs. 2a–c, 3a, b).

• (iv) Pre-peak stress path anisotropy in CU tests: The cross-anisotropy of the elastic behaviour results in a decreasing p′ over q function in the S-tests and an increasing function in the P-tests (blue lines in Fig. 2g–i) and—for high dip angles—also in the Z-tests. This agrees with the experimental evidence (black lines in Fig. 2g–i). Accordingly, the differences in the apparent peak strength of S-tests and P-tests due to pre-peak stress path anisotropy can potentially be captured. However, when considering the entirety of the tests, the model predictions deviate from the experimental results. This is due to the intrinsic limitation discussed in Sect. 4 and shown in Fig. 5: the ratio of the elastic stress path slope of P-tests over that of S-tests is always equal to − 2, independently of the elasticity parameters. The corresponding ratio is − 0.3 and − 0.8 for samples from the candidate sites and Mont Terri, respectively, and hence the model is incapable of reproducing the stress paths of both test types from these geological sites with the same set of material constants.

  The predicted stress path slope depends on the anisotropy ratio n for given values of ν_op and ν_pp (cf. Eq. 1). Figure 6 shows a comparison between the experimental stress paths of the CU S-tests and P-tests shown in Fig. 2 and the model predictions for n = 1.7–2.2, which is the range determined from calibration considering all samples from the candidate sites. Evidently, the low values of the anisotropy ratio n are more suitable for capturing the stress path and peak strength of S-tests, whereas the opposite holds for P-tests. The adoption of an intermediate value of 2, therefore, leads to deviations in both test types.

• (v) Strength anisotropy: The plasticity formulation readily captures strength anisotropy for the various bedding orientations, by considering two independent sets of plasticity parameters and MC yield conditions for the matrix and bedding (Eqs. 18–23; Fig. 4). Peak strength differences among CD S-tests and P-tests cannot be captured by the model, which predicts the same strength in both test types (blue lines in Fig. 3a, b, e, f). In CU S-tests and P-tests, only differences attributed to the pre-peak stress path anisotropy may be captured, as discussed in (iv) (blue lines, Fig. 2).

• (vi) Softening: The model cannot reproduce a decrease in strength and predicts constant stresses during yielding for CD tests (Fig. 3a, b, e, f) and dilatancy hardening for CU tests (Fig. 2a–c, g–i); therefore, two distinct sets of plasticity parameters for the matrix and bedding are established at the peak and residual states. The model predictions with peak (solid lines) and residual (dashed lines) parameters define the upper and lower bounds of the actual response in respect of softening (Figs. 2, 3). The adoption of residual strength parameters is a plausible and reasonably conservative assumption in the context of tunnel computations for the envisioned repository (Nordas and Anagnostou 2021).

Fig. 6

Observed and predicted stress paths (p′–q) in CU tests for the minimum (a), average (b) and maximum (c) value of the anisotropy ratio n determined through calibration (tests: after Crisci et al. 2023)

6 Detailed Calibration Procedure

6.1 Determination of Elasticity Parameters

The determination of elasticity parameters is based upon the prediction equations for the behaviour before yielding. From a mathematical viewpoint, independent variables are the four experimentally measured slopes Δq/Δε_a, Δp_w/Δε_a, Δε_r,p/Δε_a and Δε_r,2/Δε_a. These are related to the material constants using Eqs. 27–32 given in the “Appendix”. All slopes are determined at 50% of q_peak, on account of the model’s pre-failure linearity [cf. Sect. 5, Point (i)]. In CD tests Δp_w/Δε_a = 0 and in CU tests Δε_vol/Δε_a = 0 (Δε_r,p/Δε_a and Δε_r,2/Δε_a are linearly dependent), and hence the test evaluation is in the general case a mathematically under-determinate problem of 3 independent equations with 5 unknowns (E_o, n, v_op, v_pp, G_op). This necessitates the adoption of appropriate assumptions for the determination of all 5 elasticity parameters.

Under CD testing conditions, the prediction equations simplify substantially for S-tests (θ = 0°) and P-tests (θ = 90°) and enable one parameter to be directly determined from one equation. In CD S-tests E_o is directly determined from the slope Δq/Δε_a = E_o, and v_op from the slope Δε_r,p/Δε_a = − v_op (or equivalently Δε_r,2/Δε_a = − v_op). In CD P-tests E_p (= n E_o) is directly determined from the slope Δq/Δε_a = E_p and v_pp, v_po (= n v_op) from the slopes Δε_r,p/Δε_a = − v_pp, and Δε_r,2/Δε_a = − v_po, respectively. The evaluation of CD Z-tests is a mathematically under-determinate problem, which can be tackled analogously to the evaluation of CU tests discussed hereafter.

Under CU testing conditions, the test evaluation is an under-determinate problem for all test types. The proposed calibration method assumes a priori the values of v_op and v_pp, and uses them to determine n directly from the slope Δq/Δp′ (Eq. 1) and subsequently E_o directly from the slope Δq/Δε_a (Eq. 27). The equations of S-tests and P-tests are considerably simpler than those of Z-tests. For S-tests, n is determined after Eq. 2 and then E_o from the following expression (Eq. 27, using 43 and 46 with θ = 0°):

$$\frac{\Delta q}{{\Delta \varepsilon_{\text{a}} }} = E_{\text{o}} \cdot \frac{{2 + n - 2\nu_{{\text{pp}}} - 4n\nu_{{\text{op}}} }}{{2 - 2\nu_{{\text{pp}}} - 4n\nu_{{\text{op}}}^2 }},$$

(4)

while for CU P-tests, n is determined after Eq. 3 and E_o from the following expression (Eq. 27, using 43 and 46 with θ = 90°):

$$\frac{\Delta q}{{\Delta \varepsilon_{\text{a}} }} = E_{\text{o}} \cdot n \cdot \frac{{2 + n - 2\nu_{{\text{pp}}} - 4n\nu_{{\text{op}}} }}{{1 + n - n^2 \nu_{{\text{op}}}^2 - \nu_{{\text{pp}}}^2 - 2n\nu_{{\text{op}}} - 2n\nu_{{\text{pp}}} \nu_{{\text{op}}} }}.$$

(5)

The above expressions evidently differ from the classic relationships between undrained and drained moduli in isotropic materials. The adopted values of v_op and v_pp can be those determined from CD tests; in the absence of reliable data, values common for isotropic materials can be adopted (e.g., 0.25).

G_op can only be determined from the evaluation of CD and CU Z-tests, based on stress and strain tensor transformations from the specimen to the bedding co-ordinate system. Even so, these are generally under-determinate problems, and thus embed the assumptions for the values of v_op and v_pp. Taking this into consideration, the following simpler assumption is adopted (Wittke 1990):

$$G_{{\text{op}}} = \frac{{E_{\text{o}} }}{{2\left( {1 + v_{{\text{op}}} } \right)}}.$$

(6)

CD Z-tests are not available for the Opalinus Clay variety of the candidate sites, while the number of CU Z-tests is small in comparison with that of CD and CU S-tests and P-tests (Table 2) and is thus expected to have a small influence on the results. Therefore, for the sake of simplicity, consideration is given solely to CD and CU S-tests and P-tests in the calibration.

Two distinct calibration methods A and B are adopted. Method A considers the average values of the Poisson’s ratios v_op and v_pp determined directly from CD tests as constant throughout the entire data set, and uses them to determine the remaining elasticity parameters via linear regression. Method B uses as a starting point the results of Method A and employs a nonlinear optimisation algorithm that varies the values of v_op and v_pp to obtain the best possible correlation of elasticity parameters throughout the data set. The steps common in both methods are outlined hereafter:

• 1. Determination of E_o, v_op for CD S-tests and E_p (= n E_o), v_pp, v_po (= n v_op) for CD P-tests (Eqs. 27, 29, 30). The average values of v_op and v_pp are adopted for the entire data set, assuming they are independent of the initial effective confining pressure σ′_r,0 (cf. Point (ii), Sect. 5).

• 2. Determination of n, E_o, E_p (= n E_o) for the CU S-tests and CU P-tests (Eqs. 27 and 32, respectively), using the average v_op and v_pp-values determined from CD S-tests and P-tests.

• 3. Evaluation from the CU tests of the average anisotropy ratio ${\bar{n}}$, which is assumed to be constant and independent of σ′_r,0 for the entire data set, and subsequently of E_p =${\bar{n}}$  E_o for CD S-tests and E_o = E_p/${\bar{n}}$ for CD P-tests. (This achieves data homogenisation, in the sense of each test having individual E_o, E_p values, since CU tests have data points for both E_o, E_p, but CD tests only for one of the E_o, E_p.)

• 4. Establishment of linear functions ${\bar{E}_\text{o}}$ (σ′_r,0) and ${\bar{E}_\text{p}}$ (σ′_r,0) via linear regression.

  Method B considers the following additional step:

• 5. Minimisation of the objective SRSS (Square-Root-of-Sum-of-Squares) error function

  $$e = \sqrt {{\sum {\left[ {\left( {\overline{E}_{\text{o}} \left( {\sigma ^{\prime}_{{\mathrm{r}},0} } \right) - E_{\text{o}} \left( {\sigma ^{\prime}_{{\mathrm{r}},0} } \right)} \right)^2 + \left( {\overline{E}_{\text{p}} \left( {\sigma ^{\prime}_{{\mathrm{r}},0} } \right) - E_{\text{p}} \left( {\sigma ^{\prime}_{{\mathrm{r}},0} } \right)} \right)^2 } \right]} }}$$

  with respect to the control variables v_op and v_pp, using a nonlinear optimisation algorithm. The algorithm considers thermodynamic constraints (Eqs. 10, 11), along with 0.05 ≤ v_op < 0.5 and 0.05 ≤ v_pp < 0.5, to ensure consistency with the physical problem. This optimisation achieves the best possible correlation of E_o and E_p over the entire data set.

For both methods the ranges of the elastic stiffness parameters are determined as follows:

• Range of E_o values: The maximum and minimum E_o values are determined from the upper and lower envelopes of the respective data points. These are established visually, considering for the sake of simplicity constant slopes dE_o/dσ′_ro (envelopes parallel to regression line) and only variable intercepts E_o (σ′_ro = 0) (see Fig. 7b).

• Ranges of n, E_p and Δp′/Δq values: For Method A, the range of n values is determined, such that the resulting envelope of E_p = n E_o contains all E_p data points. For Method B, the range of n corresponds to that determined from CU tests in step 2 (see Fig. 7a), and n is assumed constant for the entire data set (cf. Point (ii), Sect. 5). The range of E_p = n E_o (see Fig. 7c) is based on the minimum and maximum values of both n and E_o. The range of the stress paths inclinations Δp′/Δq in CU tests (see Fig. 8a, b; the inverse of Δq/Δp′ is used to limit the values between − 1 and 1) is calculated after Eq. 1, using the minimum and maximum values of n, respectively. (For drained tests Δp′/Δq is always equal to 1/3.)

• Range of G_op values: Determined after Eq. 6 using minimum and maximum E_o values.

Fig. 7

Values resulting from the individual tests on the samples from the candidate sites (marked points) and model calibration results after Method B (straight lines) for, (a), anisotropy ratio n, (b), Young’s Modulus orthogonal to the bedding plane E_o and, (c), Young’s Modulus parallel to the bedding plane E_p

Fig. 8

Stress paths inclination Δp′/Δq after Method B, a in CU S-tests and, b in CU P-tests: values resulting from the individual tests on samples from the candidate sites (marked points) and model predictions based upon the calibration results

The calibration results after Method B are shown in Figs. 7 and 8 and the elasticity parameters obtained with both methods are given in Table 4. E_o, G_op and their dependence on σ′_r,0 are higher, whereas n is smaller, in Method B compared to Method A. The exact opposite holds for the Mont Terri variety, as will be later shown in Sect. 7. Both methods have benefits and shortcomings, as discussed below.

Table 4 Material constants of Opalinus Clay

Method A is simpler, more practical, and based directly on the experimental results. However, considering the natural material heterogeneity and the small number of available CD tests (see Table 2), the average v_op and v_pp values determined solely from CD tests can scarcely be considered representative for the entire data set, which consists mainly of CU tests. Hence, their adoption results in a worse correlation over the data set in E_o, E_p, as well as n and Δp′/Δq.

The purely mathematical Method B alleviates this insufficiency of Method A, by employing optimisation to achieve the best possible correlation of E_o and E_p throughout the data set. E_o and E_p are chosen, since the model behaviour is far more sensitive to these in comparison with v_op and v_pp, and additionally these are more critical parameters for estimating deformations in tunnel boundary value problems. Nevertheless, Method B completely disregards the experimental evidence for the values of v_op and v_pp from CD tests, since the number of CD tests is not sufficient to establish a reliable range of v_op and v_pp values that can be used as constraints during optimisation. The optimisation produces a value of v_pp = 0.05 for both varieties (candidate sites and Mont Terri) and a value of v_op = 0.40 for the candidate sites variety. These may appear extreme at first glance but result from the mathematical formulation of the optimisation problem, which is in turn governed by the model formulation.

Specifically, in CU tests n depends on v_op and v_pp (Eq. 1) and becomes identical for all CU S-tests and P-tests when v_pp = 0 and v_pp = 0.5 (Eqs. 2, 3 become constant, and hence n does not depend on Δq/Δp′, i.e., on the test type). For an identical n, the best correlation of E_o and E_p is achieved among all CU tests. Since the optimisation algorithm mostly considers CU tests and very few CD tests, it is governed by the former; therefore, it tends monotonically to the minimum possible v_pp and the maximum possible v_op values, aiming to achieve the best correlation of E_o and E_p amongst the CU tests. As a result, the determined range of n values (1.7–2.2; see Table 4) deviates substantially from the average n that would be calculated from CD tests alone (i.e., the ratio of the average E_p and E_o determined solely from these tests), which is ca. 4.5 for the variety of the candidate sites. The same applies to the value of v_op = 0.4, which is much higher than the average value of 0.10 of CD tests alone.

Taking due account of the above, it cannot be clearly stated that any of the two methods is better than the other. In general, Method B achieves a smaller overall difference between predictions and observations. The Authors’ recommendation for engineering design is to conduct tunnel calculations with the sets of parameters of both methods and critically evaluate the results.

6.2 Determination of Strength Parameters

The determination of the strength parameters for the rock matrix (c, φ) and the bedding plane (c_b, φ_b) is based upon the equation of the respective MC yield criteria. Due to the model's inability to capture softening [cf. Point (vi), Sect. 5] distinct sets of strength parameters are determined for the peak and residual states.

The strength parameters c and φ are determined from the evaluation of CD and CU S- and P-tests, where yielding in the matrix prevails. The equations for the average peak and residual MC yield envelopes of the matrix in the triaxial stress space (p′, q) are established in the form of Eq. 18 via linear regression, using the data points of CD and CU S-tests and P-tests at different initial confining pressures σ′_r,0. The average peak and residual c and φ are then obtained from Eqs. 20 and 21.

The strength parameters c_b and φ_b are determined from the Z-tests by means of linear regression in the (σ′, τ) space, where σ′ and τ, respectively, denote the effective normal stress and the shear stress in the bedding plane. This approach avoids the need to consider the different bedding orientations of the various Z-tests, which would be necessary if the calibration was performed in the triaxial stress space (p′, q), as for the case of the rock matrix (see Eqs. 22, 23).

Figure 9 illustrates the calibration approach for the example of the variety of Opalinus Clay from the candidate sites and Table 4 summarizes the parameter ranges. The latter have been established analogously to the approach adopted for the elasticity parameters, that is graphically for the peak and residual strength parameters of the matrix and bedding as the envelopes of the respective experimental data points. It must be noted that the range of the mean effective stress p′ at failure for the experiments considered in the calibration is approximately 5–30 MPa, or approximately 10–60 MPa in terms of maximum principal effective stress σ₁'.

Fig. 9

Stress states at failure from the individual tests on samples from the candidate sites (marked points) and Mohr–Coulomb strength envelopes: a matrix strength at the peak state, b matrix strength at the residual state, c bedding strength at the peak state and d bedding strength at the residual state

6.3 Determination of Dilatancy Parameters

The determination of dilatancy parameters for the rock matrix (ψ) and the bedding plane (ψ_b) is based upon the model prediction equations for the behaviour during yielding (Eqs. 36–41). Analogously to strength parameters, ψ is determined from the evaluation of S-tests and P-tests, and ψ_b from the evaluation of Z-tests, considering distinct values at the peak and residual states [cf. Point (vi), Sect. 5].

In CD tests perfectly plastic flow at the peak state is assumed to occur between the points of peak volumetric strain (ε_vol) and deviatoric stress (q) (points P₁ and P₂ in Fig. 10a, b), while for the residual state, two points on the residual branch are considered, where Δε_vol/Δε_a is constant (points P₃ and P₄ in Fig. 10a, b). Along these branches, ψ and ψ_b can be directly determined from the slope Δε_vol/Δε_a, using Eq. 40.

Fig. 10

Points considered for the determination of the dilatancy angle in the deviatoric stress q and volumetric strain ε_vol versus axial strain ε_a diagrams of CD tests (test after Crisci et al. 2023)

In CU tests perfectly plastic flow at the peak state is assumed to occur between the points of peak excess pore pressure (p_w) and deviatoric stress (q) (points P₁ and P₂ in Fig. 11a, b), while two points are considered for the residual state on a part of the residual branch, where Δp_w/Δε_a is constant (points P₃ and P₄ in Fig. 11a, b). Along these branches, ψ and ψ_b can be directly determined from the slope Δp_w/Δε_a, using Eq. 41. Evidently, ψ and ψ_b also depend on elasticity and strength parameters (since elastic strain increments are non-zero under CU testing conditions; cf. Sect. 4), which vary within the ranges determined from the calibration of elasticity and strength parameters (Sects. 6.1 and 6.2). For the sake of simplicity, average values are adopted for the elasticity and strength parameters. For the elasticity parameters, both Methods A and B must be considered.

Fig. 11

Points considered for the determination of the dilatancy angle in the deviatoric stress q and excess pore pressure p_w versus axial strain ε_a diagrams of CU tests (test after Crisci et al. 2023)

Figure 12 shows the detailed results after Method B for the example of the variety of Opalinus Clay from the candidate sites; the final range of values is given in Table 4, considering the results of the elasticity calibration after both Methods A and B. In CD tests the strain measurements over the residual response range are unreliable, due to the manifestation of strain localisation; for this purpose, only CU tests were considered, where ψ and ψ_b depend solely on the measurements of p_w at the top and bottom surfaces of the sample, where the influence of localisation is limited. Analogously to the approach adopted for elasticity and strength parameters, a range of values is graphically established for the peak and residual dilatancy parameters of the matrix and bedding as the envelope of the respective experimental data points. The maximum values of matrix residual dilatancy and bedding peak dilatancy are probably outliers and not representative of the actual dilatancy range.

Fig. 12

Values resulting from the individual tests on the samples from the candidate sites (marked points) and model calibration results after Method B (straight lines) for dilatancy angles: a matrix dilatancy angle at the peak state, b matrix dilatancy angle at the residual state, c bedding dilatancy angle at the peak state and d bedding dilatancy angle at the residual state

7 Comparison Between the Variety of Opalinus Clay from the Candidate Sites and the Mont Terri Variety

Table 4 summarizes the material constants determined for the two Opalinus Clay varieties. A distinction is made between Methods A and B in the elasticity and dilatancy parameters (cf. Sects. 6.1 and 6.3). Compared to the variety of the candidate sites, the Mont Terri variety is associated with a considerably lower stiffness and strength (both for the matrix and the bedding, and both at peak and residual states; cf., e.g., Giger et al. 2015b). The differences in the parameters of the two varieties are probably due to differences in the maximum past burial depth and tectonic effects, which are discussed hereafter.

The maximum past burial depth in Mont Terri is lower (1100–1300 m) than in the repository candidate regions (1700 m) (Marschall and Giger 2016; Giger et al. 2015b). This affects the porosity and strength evolution of the two varieties through the mechanisms of compaction and diagenesis, and results in a lower overconsolidation ratio.

The tectonic effects experienced by Opalinus Clay during uplift have been more pronounced in Mont Terri than in the candidate regions. Specifically, Mont Terri can be assigned to the Folded Jura of the detached Alpine foreland, which experienced the most intense deformation of the Jura fold-and-thrust belt during late Miocene N–S shortening. On the other hand, the candidate regions are located within the Tabular Jura and the Subjurassic Zone, which experienced much less internal deformation during Miocene shortening (Giger et al. 2015b; Marschall and Giger 2016). A more pronounced tectonisation results in "loss of memory of previous consolidation states and diagenetic modifications" which "increase porosity and reduce strength and stiffness" of the rock (Marschall and Giger 2016).

8 Conclusions

Within the scope of the design of a deep geological nuclear waste repository in Opalinus Clay, this paper: (i) introduces a simple and systematic calibration method for an anisotropic elastoplastic constitutive model, based upon CD and CU triaxial compression tests with variable bedding plane orientations; (ii) presents the novel suite of equations describing the constitutive model behaviour for any bedding orientation, which are employed in the calibration and are also useful for validating the numerical implementation of the model in FE codes; and (iii) provides representative engineering material constants for the Opalinus Clay varieties of the candidate sites and of Mont Terri, based upon the established calibration approach.

The constitutive model considers linear, cross-anisotropic elasticity and perfect plasticity according to the MC yield criterion, with a non-associated plastic flow rule and an embedded strength reduction depending on the bedding plane orientation (Sect. 3); it is thus capable of capturing with a single set of material constants the stiffness, strength, and pre-peak stress path anisotropies (only in CU tests) observed in experiments on Opalinus Clay samples (Sect. 4). Other aspects including hardening, softening and stiffness dependence on initial confining pressure are accounted for via adequate, plausible, and sufficiently accurate assumptions for practical engineering applications (Sect. 5).

An inherent limitation of the constitutive model is that it predicts a fixed ratio for the pre-peak stress path inclinations of the CU P-tests and S-tests, which affects the respective strength predictions and, in addition to the natural material heterogeneity, impacts the model performance (Sect. 4). Notwithstanding this, the overall prediction accuracy is deemed sufficiently accurate for engineering practice. The adopted constitutive model achieves a fine balance between the classic isotropic elastoplastic model, which cannot reproduce anisotropies, and more sophisticated models with hardening, softening and pressure-dependent stiffness capabilities, which introduce difficulties related to computational cost, non-uniqueness of solution and calibration. More importantly, it offers the considerable advantage of its parameters having a clear physical meaning capable of being universally interpreted, which renders it suitable for systematic employment in engineering design practice.

Appendix: Constitutive Model Formulation and Prediction Equations

1.1 Elasticity Equations

The elastic model behaviour is defined by the cross-anisotropic constitutive relationship (Puzrin 2012):

$$\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\varepsilon_{zz} } \\ {\gamma_{xy} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {{1 / {E_{\text{p}} }}} & { - {{\nu_{{\text{pp}}} } / {E_{\text{p}} }}} & { - {{\nu_{{\text{op}}} } / {E_{\text{o}} }}} & 0 & 0 & 0 \\ { - {{\nu_{{\text{pp}}} } / {E_{\text{p}} }}} & {{1 / {E_{\text{p}} }}} & { - {{\nu_{{\text{op}}} } / {E_{\text{o}} }}} & 0 & 0 & 0 \\ { - {{\nu_{{\text{po}}} } / {E_{\text{p}} }}} & { - {{\nu_{{\text{po}}} } / {E_{\text{p}} }}} & {{1 / {E_{\text{o}} }}} & 0 & 0 & 0 \\ 0 & 0 & 0 & {{1 / {G_{{\text{pp}}} }}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {{1 / {G_{{\text{op}}} }}} & 0 \\ 0 & 0 & 0 & 0 & 0 & {{1 / {G_{{\text{op}}} }}} \\ \end{array} } \right]\,\,\left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{zz} } \\ {\sigma_{xy} } \\ {\sigma_{xz} } \\ {\sigma_{yz} } \\ \end{array} } \right\},$$

(7)

where z is directed orthogonal to the bedding plane; E_o and E_p are the Young’s moduli orthogonal and parallel to the bedding, respectively; ν_op is the Poisson’s ratio for the stress components orthogonal and strain components parallel to the bedding; ν_pp is the Poisson’s ratio for the stress and strain components parallel to the bedding; ν_po is the Poisson’s ratio for the stress components parallel to the bedding and the strain components orthogonal to the bedding; G_op is the shear modulus on the planes orthogonal to the bedding; and G_pp is the shear modulus in the bedding plane:

$$G_{{\text{pp}}} = \frac{{E_{\text{p}} }}{{2\left( {1 + v_{{\text{pp}}} } \right)}}.$$

(8)

The first law of thermodynamics (energy conservation) dictates symmetry of the constitutive matrix in Eq. 7, which yields the following equality (Puzrin 2012):

$$\frac{{v_{{\text{po}}} }}{{v_{{\text{op}}} }} = \frac{{E_{\text{p}} }}{{E_{\text{o}} }} = n,$$

(9)

where n will be referred to hereafter as anisotropy ratio. Thermodynamic considerations additionally require the strain energy of an elastic material to be strictly positive-definite, which results in the following constraints for cross-anisotropic materials (Amadei et al. 1987):

$$\left| {\nu_{{\text{pp}}} } \right| < 1,$$

(10)

$$\left| {\nu_{{\text{op}}} } \right| < \sqrt {{\frac{{1 - \nu_{{\text{pp}}} }}{2n}.}}$$

(11)

Due to Eqs. 8 and 9, the elastic model behaviour can be fully defined by 5 independent parameters (E_o, n, ν_pp, ν_op, G_op).

1.2 Plasticity Equations

The model obeys the MC yield criterion both for the matrix and the bedding. In the special case of triaxial compression testing conditions, where the two minor principal stresses are equal, the MC yield condition for the rock matrix can be expressed as

$$\sigma_{\text{a}}^{\prime} = m\sigma_{{\mathrm{r}}}^{\prime} + f_{\text{c}} ,$$

(12)

where σ′_a, σ′_r, m and f_c denote the effective axial and radial stresses, the slope of the MC yield envelope and the uniaxial compressive strength, respectively, with

$$m = \frac{1 + \sin \varphi }{{1 - \sin \varphi }},$$

(13)

$$f_{\text{c}} = \frac{2c\cos \varphi }{{1 - \sin \varphi }}.$$

(14)

The corresponding expression for shearing along the bedding plane is

$$\sigma_{\text{a}}^{\prime} = m_\beta \;\sigma_{{\mathrm{r}}}^{\prime} + f_{{\text{c}}\beta } ,$$

(15)

where

$$m_\beta = \frac{{\tan \left( {\beta + \varphi_{\text{b}} } \right)}}{\tan \beta },$$

(16)

$$f_{{\text{c}}\beta } = \frac{{2c_{\text{b}} }}{{\sin 2\beta \left( {1 - \tan \varphi_{\text{b}} \tan \beta } \right)}}$$

(17)

and β is the angle between the maximum principal stress and the bedding plane (Fig. 4). The parameters m_β and f_cβ are not material constants, because they depend on the bedding orientation β.

The MC yield criteria for the matrix and the bedding are expressed in the (p′–q) space as follows:

$$q = M \cdot p^{\prime} + d_0 ,$$

(18)

$$q = M_\beta \cdot p^{\prime} + d_{0\beta } ,$$

(19)

where

$$M = \frac{6\sin \varphi }{{3 - \sin \varphi }},$$

(20)

$$d_0 = \frac{6\,c\cos \varphi }{{3 - \sin \varphi }},$$

(21)

$$M_\beta = \frac{{6\sin \varphi_{\text{b}} }}{{3\sin \left( {2\beta + \varphi_{\text{b}} } \right) - \sin \varphi_{\text{b}} }},$$

(22)

$$d_{0\beta } = \frac{{2\,c_{\text{b}} }}{{\sin 2\beta \cdot \left( {1 - \tan \varphi_{\text{b}} \cdot \tan \beta } \right)}}\left( {1 - \frac{{M_{\text{b}} }}{3}} \right).$$

(23)

The ratios of the plastic strain rates of the rock matrix read as follows in the special case of triaxial compression testing conditions:

$$\frac{{\dot{\varepsilon }_2^{PL} }}{{\dot{\varepsilon }_1^{PL} }} = \frac{{\dot{\varepsilon }_3^{PL} }}{{\dot{\varepsilon }_1^{PL} }} = - \frac{\kappa }{2},$$

(24)

where κ is the dilatancy constant:

$$\kappa = \frac{1 + \sin \psi }{{1 - \sin \psi }}.$$

(25)

For the bedding, the plastic flow rule reads as follows:

$$\dot{\varepsilon }_{\text{o}}^{PL} = - \dot{\gamma }_{{\text{op}}}^{PL} \,\tan \psi_{\text{b}} ,$$

(26)

where ε̇_o^PL denotes the normal plastic strain rate along the direction orthogonal to the bedding and γ̇_o^PL the shear plastic strain rate over the bedding plane surface.

1.3 Prediction Equations for Behaviour Before Yielding

The slope of the elastic branch of the deviatoric stress (q) versus axial strain (ε_a) line reads as follows:

$$\frac{\Delta q}{{\Delta \varepsilon_{\text{a}} }} = nE_{\text{o}} \cdot \left\{ {\begin{array}{*{20}l} {\frac{1}{{\alpha_{\text{d}} }}} \hfill & {\left( {\text{CD}} \right),} \hfill \\ {\frac{B_1 }{{\alpha_{\text{u}} }}} \hfill & {\left( {\text{CU}} \right),} \hfill \\ \end{array} } \right.$$

(27)

where the coefficients α_d, α_u and B₁ (as well as all other coefficients A_k, B_k, C_k and D_k appearing in the next equations) are given in “Coefficients” section of the “Appendix” at the end of this “Appendix”. (These coefficients are functions of the material constants and/or the bedding inclination.)

The relationships between the imposed axial strain (ε_a) and the excess pore pressure (p_w), the horizontal strains (ε_r,p, ε_r,2) and the volumetric strain (ε_vol) in the CD and CU tests read as follows:

$$\frac{{\Delta p_{\text{w}} }}{{\Delta \varepsilon_{\text{a}} }} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\left( {\text{CD}} \right),} \hfill \\ {nE_{\text{o}} \frac{B_2 }{{\alpha_{\text{u}} }}} \hfill & {\left( {\text{CU}} \right),} \hfill \\ \end{array} } \right.$$

(28)

$$\frac{{\Delta \varepsilon_{\text{r,p}} }}{{\Delta \varepsilon_{\text{a}} }} = \left\{ {\begin{array}{*{20}l} { - \frac{A_2 }{{\alpha_{\text{d}} }}} \hfill & {\left( {\text{CD}} \right),} \hfill \\ { - \frac{0.5\,C_1 + C_2 \sin^2 \theta }{{\alpha_{\text{u}} }}} \hfill & {\left( {\text{CU}} \right),} \hfill \\ \end{array} } \right.$$

(29)

$$ \frac{{\Delta \varepsilon_{{\mathrm{r}},2} }}{{\Delta \varepsilon_{\text{a}} }} = \left\{ {\begin{array}{*{20}l} { - \frac{A_1 }{{\alpha_{\text{d}} }}} \hfill {(\text{CD}),} \hfill \\ { - \frac{{\Delta \varepsilon_{{\mathrm{r}},p} }}{{\Delta \varepsilon_{\text{a}} }} - 1} \hfill {(\text{CU}),} \hfill \\ \end{array} } \right.$$

(30)

$$\frac{{\Delta \varepsilon_{{\text{vol}}} }}{{\Delta \varepsilon_{\text{a}} }} = \left\{ {\begin{array}{*{20}l} {\frac{{\alpha_{\text{d}} - A_1 - A_2 }}{{\alpha_{\text{d}} }}} \hfill & {\left( {\text{CD}} \right),} \hfill \\ 0 \hfill & {\left( {\text{CU}} \right).} \hfill \\ \end{array} } \right.$$

(31)

The slope of the elastic branch of the effective stress path in the (p′, q) space is

$$\frac{\Delta q}{{\Delta p^{\prime}}} = \left\{ {\begin{array}{*{20}c} 3 {\left( {{\text{CD}}} \right),} \\ {\frac{3}{{1 - 3\frac{B_2 }{{B_1 }}}}} {\left( {{\text{CU}}} \right).} \\ \end{array} } \right.$$

(32)

The equations given above hold as long as the stress state does not violate the isotropic or the anisotropic yield condition (Eqs. 18 and 19). The stress state will reach the two conditions in general at different axial strains. Considering that shearing along the bedding plane cannot occur if it is not steeper than the friction angle (i.e., when θ = 90° − β ≤ φ_b; see Fig. 4), the critical axial strain can be written as follows:

$$\varepsilon_y = \left\{ {\begin{array}{*{20}l} {\varepsilon_{ym} ,} \hfill & {{\text{if}}\quad \theta \le \varphi_{\text{b}} ,} \hfill \\ {\min \left( {\varepsilon_{ym} ,\;\varepsilon_{yb} } \right),} \hfill & {{\text{if}}\quad \theta > \varphi_{\text{b}} ,} \hfill \\ \end{array} } \right.$$

(33)

where

$$\varepsilon_{ym} = \frac{{\left( {m - 1} \right)\sigma^{\prime}_{{\mathrm{r}},0} + f_{\text{c}} }}{{nE_{\text{o}} }}\left\{ {\begin{array}{*{20}l} {\alpha_{\text{d}} } \hfill {\left( {\text{CD}} \right),} \hfill \\ {\frac{{\alpha_{\text{u}} }}{{B_1 + \left( {m - 1} \right)B_2 }}} \hfill {\left( {\text{CU}} \right),} \hfill \\ \end{array} } \right.$$

(34)

and

$$\varepsilon_{y{\text{b}}} = \frac{{\sigma^{\prime}_{{\mathrm{r}},0} \tan \varphi_{\text{b}} + c_{\text{b}} }}{{nE_{\text{o}} }}\left\{ {\begin{array}{*{20}l} {\frac{\alpha_d }{{\cos^2 \theta \left( {\tan \theta - \tan \varphi_{\text{b}} } \right)}}} \hfill & {\left( {\text{CD}} \right),} \hfill \\ {\frac{{\alpha_{\text{u}} }}{{B_1 \cos^2 \theta \left( {\tan \theta - \tan \varphi_b } \right) + B_2 \tan \varphi_{\text{b}} }}} \hfill & {\left( {\text{CU}} \right).} \hfill \\ \end{array} } \right.$$

(35)

1.4 Prediction Equations for Behaviour During Yielding

The following equations give the relationships between the imposed axial strain (ε_a) and the deviatoric stress (q), excess pore pressure (p_w), horizontal strains (ε_r,p, ε_r,2) and volumetric strain (ε_vol) in the CD tests and in CU tests during yielding:

$$\frac{\Delta q}{{\Delta \varepsilon_{\text{a}} }} = \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}c} 0 & {\left( {\text{CD}} \right),} \\ \end{array} } \hfill \\ { - \frac{{\Delta p_{\text{w}} }}{{\Delta \varepsilon_{\text{a}} }} \cdot \left\{ {\begin{array}{*{20}l} {\frac{3M}{{3 - M}}} \hfill & {\text{(CU, yielding in the matrix),}} \hfill \\ {\frac{3M_\beta }{{3 - M_\beta }}} \hfill & {\text{(CU, yielding in the bedding),}} \hfill \\ \end{array} } \right.} \hfill \\ \end{array} } \right.$$

(36)

$$\frac{{\Delta p_{\text{w}} }}{{\Delta \varepsilon_{\text{a}} }} = \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}c} 0 & {(CD)} \\ \end{array} ,} \hfill \\ {\begin{array}{*{20}l} { - nE_{\text{o}} \frac{\kappa - 1}{{\left( {\kappa - 1} \right)D_1 + D_2 }}} \hfill & {\text{(CU, yielding in the matrix),}} \hfill \\ {nE_{\text{o}} \frac{{D_3 \tan \psi_{\text{b}} }}{{D_4 - D_5 \tan \psi_{\text{b}} }}} \hfill & {\text{(CU, yielding in the bedding),}} \hfill \\ \end{array} } \hfill \\ \end{array} } \right.$$

(37)

$$\frac{{\Delta \varepsilon_{{\mathrm{r}},p} }}{{\Delta \varepsilon_{\text{a}} }} = \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} { - \frac{\kappa }{2}} \hfill & {\text{(CD, yielding in the matrix),}} \hfill \\ 0 \hfill & {\text{(CD, yielding in the bedding),}} \hfill \\ \end{array} } \hfill \\ {\begin{array}{*{20}l} { - \frac{\kappa }{2} + \frac{1}{{nE_{\text{o}} }}\frac{{\Delta p_{\text{w}} }}{{\Delta \varepsilon_{\text{a}} }}\left( {E_1 + \frac{\kappa }{2}D_1 } \right)} \hfill & {\text{(CU, yielding in the matrix),}} \hfill \\ {\frac{1}{{nE_{\text{o}} }}\frac{{\Delta p_{\text{w}} }}{{\Delta \varepsilon_{\text{a}} }}\left( {\frac{E_2 }{{E_3 }} + 1} \right)} \hfill & {\text{(CU, yielding in the bedding),}} \hfill \\ \end{array} } \hfill \\ \end{array} } \right.$$

(38)

$$\frac{{\Delta \varepsilon_{{\mathrm{r}},2} }}{{\Delta \varepsilon_{\text{a}} }} = \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} { - \frac{\kappa }{2}} \hfill {\text{(CD, yielding in the matrix),}} \hfill \\ { - \frac{{\sin 2\theta + \left( {1 - \cos 2\theta } \right)\tan \psi_{\text{b}} }}{{\sin 2\theta - \left( {1 + \cos 2\theta } \right)\tan \psi_{\text{b}} }}} \hfill {\text{(CD, yielding in the bedding),}} \hfill \\ \end{array} } \hfill \\ {\begin{array}{*{20}c} { - \frac{{\Delta \varepsilon_{{\mathrm{r}},{\text{p}}} }}{{\Delta \varepsilon_{\text{a}} }} - 1} {\left( {\text{CU}} \right),} \\ \end{array} } \hfill \\ \end{array} } \right.$$

(39)

$$\frac{{\Delta \varepsilon_{{\text{vol}}} }}{{\Delta \varepsilon_{\text{a}} }} = \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {1 - \kappa } \hfill {\text{(CD, yielding in the matrix),}} \hfill \\ { - \frac{{\tan \psi_{\text{b}} }}{{\cos^2 \theta \left( {\tan \theta - \tan \psi_{\text{b}} } \right)}}} \hfill {{\text{(CD, yielding in the bedding)}}{,}} \hfill \\ \end{array} } \hfill \\ {\begin{array}{*{20}c} 0 {\left( {{\text{CU}}} \right)} \\ \end{array} .} \hfill \\ \end{array} } \right.$$

(40)

The slope of the effective stress path in the (p′, q) space is given by the yield condition:

$$\frac{\Delta q}{{\Delta p^{\prime}}} = \left\{ {\begin{array}{*{20}l} M \hfill & {\left( {\text{yielding in the matrix}} \right),} \hfill \\ {M_\beta } \hfill & {\left( {\text{yielding in the bedding}} \right).} \hfill \\ \end{array} } \right.$$

(41)

1.5 Coefficients

The coefficients α_d, α_u, A_k, B_k, C_k, D_k and E_k in the prediction equations read as follows:

$$\alpha_{\text{d}} = n - \left( {n - 1} \right)\sin^4 \theta ,$$

(42)

$$\alpha_{\text{u}} = C_1 + C_2 \sin^2 \theta + C_3 \sin^2 \theta \cos^2 \theta ,$$

(43)

$$A_1 = n\nu_{{\text{op}}} + \left( {n - 1} \right)\sin^2 \theta \cos^2 \theta ,$$

(44)

$$A_2 = n\nu_{{\text{op}}} + \left( {\nu_{{\text{pp}}} - n\nu_{{\text{op}}} } \right)\sin^2 \theta ,$$

(45)

$$B_1 = 2 + n - 2\nu_{{\text{pp}}} - 4n\nu_{{\text{op}}} ,$$

(46)

$$B_2 = n - 2n\nu_{{\text{op}}} - \left( {n - 1 + \nu_{{\text{pp}}} - n\nu_{{\text{op}}} } \right)\sin^2 \theta ,$$

(47)

$$C_1 = 2n\left( {1 - \;\nu_{{\text{pp}}} - 2n\nu_{{\text{op}}}^2 } \right),$$

(48)

$$C_2 = 1 - n + 2n\nu_{{\text{pp}}} - \nu_{{\text{pp}}}^2 - 2n\nu_{{\text{op}}} - 2n\nu_{{\text{pp}}} \nu_{{\text{op}}} + 3n^2 \nu_{{\text{op}}}^2 ,$$

(49)

$$C_3 = 2n^2 - 1 - n + \nu_{{\text{pp}}}^2 + 6n\nu_{{\text{op}}} (1 - n) - 2\,\nu_{{\text{pp}}} n\nu_{{\text{op}}} + n^2 \nu_{{\text{op}}}^2,$$

(50)

$$\begin{aligned} D_1 & = m - \nu_{{\text{pp}}} - n\nu_{{\text{op}}} + \left( {mn - m + \nu_{{\text{pp}}} - n\nu_{{\text{op}}} } \right)\cos^2 \theta \\ & \quad + \left( {\frac{{nE_{\text{o}} }}{{G_{{\text{op}}} }} - 1 - n - 2nv_{{\text{op}}} } \right)\left( {m - 1} \right)\sin^2 \theta \cos^2 \theta , \\ \end{aligned}$$

(51)

$$D_2 = 2\left( {1 - \nu_{{\text{pp}}} - mn\nu_{{\text{op}}} - n\nu_{{\text{op}}} } \right) + nm - \left( {n - 1 + \nu_{{\text{pp}}} - n\nu_{{\text{op}}} } \right)\left( {m - 1} \right)\sin^2 \theta ,$$

(52)

$$D_3 = 4\left( {\tan \theta - \tan \varphi_{\text{b}} } \right)\cos^2 \theta ,$$

(53)

$$D_4 = \sin 2\theta \left( {\left( {1 + 3\cos 2\theta } \right)\left( {1 - \nu_{{\text{pp}}} - n\nu_{{\text{op}}} } \right)\tan \varphi_{\text{b}} - \left( {n + 2 - 2\nu_{{\text{pp}}} - 4n\nu_{{\text{op}}} } \right)\sin 2\theta } \right),$$

(54)

$$\begin{aligned} D_5 = \left( {\left( {6 - 4\nu_{{\text{pp}}} } \right)\cos^2 2\theta + \left( {1 + \frac{{nE_{\text{o}} }}{{G_{{\text{op}}} }}} \right)\sin^2 2\theta + 2\left( {1 - 2\nu_{{\text{pp}}} } \right)\cos 2\theta } \right)\tan \varphi_{\text{b}} \\ \quad - \left( {1 - \nu_{{\text{pp}}} - n\nu_{{\text{op}}} } \right)\left( {1 + 3\cos 2\theta } \right)\sin 2\theta , \\ \end{aligned}$$

(55)

$$E_1 = 1 - \nu_{{\text{pp}}} - mn\nu_{{\text{op}}} + \left( {n\nu_{{\text{op}}} - \nu_{{\text{pp}}} } \right)\left( {m - 1} \right)\sin^2 \theta,$$

(56)

$$E_2 = - \nu_{{\text{pp}}} \left( {\sin 2\theta - 2\cos 2\theta \tan \varphi_{\text{b}} } \right) - n\nu_{{\text{op}}} \sin 2\theta,$$

(57)

$$E_3 = \sin 2\theta - \left( {1 + \cos 2\theta } \right)\tan \varphi_{\text{b}} .$$

(58)