1 Introduction

Capturing the true strength properties of rock materials has been a long-standing challenge in rock engineering, particularly in rocks with high brittleness where a complex mixed mode of shear and tensile cracking is expected. The word “brittle” is explained as hard but likely to break easily (Stevenson 2010) and a brittle failure in rock is referred to a case where the failure can happen at less than 3–5% deformation (Bates and Jackson 1984; Neuendorf 2005). Brittleness can be described as a lack of ductility and the ductility is referred to the ability of a material to endure a large plastic deformation without fracturing (Hetenyi 1950). Considerable endeavors have been undertaken to develop a quantitative Brittleness Index (BI) based on various approaches and rock properties. Early attempts were performed by Protodyakonov (1962) and Bishop (1967) who quantified the brittleness mainly based on the uniaxial compressive strength (UCS) as well as peak and residual strengths. Later, more BIs were developed based on strength parameters which were highly dependent on the UCS and tensile strength (TS) (Hucka and Das 1974; Altindag 2003; Yagiz 2009; Dursun and Gokay 2016). Some rock mechanical properties, such as Poisson’s ratio and elastic modulus, have been frequently used in BIs formulas (Andreev 1995; Rickman et al. 2008; Sun et al. 2013; Luan et al. 2014; Guo et al. 2015). A number of BIs have been proposed based on the weight of the minerals in rock materials (Jarvie et al. 2007; Wang and Gale 2009; Jin et al. 2015; Shi et al. 2017). Also, various ratios of energy segments in stress–strain curves, including elastic strain and fracture energies, have been deployed to introduce energy-based BIs (Hucka and Das 1974; Tarasov and Potvin 2013; Munoz et al. 2016b; Li et al. 2019). Some other BIs were developed based on other rock properties which can be obtained through particular testing methods, such as hardness (Hucka and Das 1974) and punch penetration (Yagiz 2009) tests. Yet, nothing has been introduced with universal versatility based on point load testing.

Many rock engineering projects are tightly bounded with the accurate estimation of rock brittleness including evaluating the rock burst proneness (Wang and Park 2001; Hajiabdolmajid and Kaiser 2003; Gong et al. 2020), hydraulic fracturing and well logging (Wang and Gale 2009; Jin et al. 2015; Rybacki et al. 2016; Zhang et al. 2016; Feng et al. 2020), ground control (Hajiabdolmajid and Kaiser 2003; Tarasov and Potvin 2013), and rock cutability and drillability (Altindag 2002, 2003; Kahraman 2002; Gong and Zhao 2007; Yagiz 2008). Among these cases, assessing the brittle fracturing mechanism of rocks under burst conditions has been a long-standing challenge in underground hard rock and coal mining (Singh 1989; Feng et al. 2015; Zhang et al. 2017; Zhou et al. 2018; Wang et al. 2020). Therefore, rock burst has attracted considerable attention leading to the development of several so-called Bursting Liability Indices (BLIs) to assess the coal burst proneness. The BLIs particularly focus on measuring the UCS (or Rc), strain energy storage index (WET), bursting energy index (KE), and duration of dynamic fracture (DT) (Kidybiński 1981; Gong et al. 2019, 2022).

Despite large efforts that have been undertaken to estimate/quantify the brittleness, there is still a lack of universal agreement among scholars and practitioners on both the definition and measurement of brittleness or brittleness index. Consequently, so far, over 90 different BIs have been proposed to be used in assessing the brittleness of different rocks within various applications. As discussed earlier, the UCS plays an important role in the suggested brittleness and burst indices and acts as a key parameter in a broad range of rock engineering design methodologies. The testing procedure for the UCS measurement has been standardized by the International Society for Rock Mechanics (ISRM 1979) and the American Society for Testing and Materials (ASTM 1992). The triaxial (Tarasov and Potvin 2013), indentation (Hucka and Das 1974), and punch penetration (Yagiz 2009) tests have been used in brittleness assessment. They require customized and expensive equipment, precise conditions for sample preparation and test execution, and highly dependent on lab conditions. To overcome such challenges, a practical rock testing method known as point load testing (PLT) can be potentially deployed to provide an accurate and timely estimation of brittleness. Such a testing approach has gained a fairly widespread recognition as a convenient way for indexing strength of rocks owing to ease of testing, being inexpensive, flexibility in samples’ size and shapes, as well as portability of the testing equipment (Broch and Franklin 1972; Bieniawski 1975; Kahraman and Gunaydin 2009). The PLT has been utilized in practical engineering applications, such as rock strength classification (Deere and Miller 1966; Bieniawski 1973) borehole logging (Bieniawski 1975), rock mass rating (RMR) (Bieniawski 1988), and geological site investigation (AS 1726 1993).

In view of the noticeable PLT advantages, in this study, first, the fundamental principles of Brittleness Index (BI) and Bursting Liability Index (BLI) are discussed followed by introduction of a Burst–Brittleness Ratio (BBR) governed through a convenient PLT method. The BBR is aimed to overcome the shortcomings associated with assessing the relative burst–brittleness level of different rock types irrespective of their engineering applications. Although characterization of cracking processes during the rock failure provides useful information in assessing the burst–brittleness level of brittle rock and rock-like materials, little attention has been given to such a characterization particularly through high-speed imaging techniques. Hence, to verify the suitability of the proposed BBR, a set of systematic analyses was conducted through a combined Acoustic Emission (AE) and high-speed imaging technique. Such analyses aimed to study the cracking types (e.g., failure under shear or tension) and fracture process of three different rock types, including coal, granite, and sandstone during the point load testing. The newly established BBR ranked coal with the highest burst–brittleness ratio followed by granite and sandstone, which was ultimately endorsed by the high-speed imaging technique particularly under uniaxial compression.

2 Brittleness Index and Bursting Liability Index

Lack of universal agreement on brittleness definition and a standardized analytical formula led to the development of quite a large number of Brittleness Indices (BIs) for various applications. The existing BIs can be categorized into six groups based on energy, mineral composition, strength, strain, and elastic parameters as well as miscellaneous testing. Each BI has its own limitations particularly in regards to ignoring some important influential factors which then make them not suitable for all rock types or different rock engineering applications.

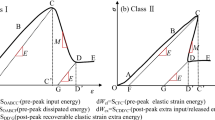
Bursting Liability Indices (BLIs), on the other hand, consider the ability of rock in absorbing and releasing energy which can be conventionally classified into four types that are commonly used in assessing the coal burst proneness. All four types of BLIs can be quantified from the stress–strain curve resulted from a uniaxial compressive test as demonstrated in Fig. 1. The first type is the strain energy storage index (WET) which was originally proposed by Szecowka et al. (1973) as a ratio of elastic strain energy over the dissipated energy obtained from an elastic hysteresis loop under uniaxial compression. The second type is known as bursting energy index (KE) which includes the ratio of post-peak failure strain energy over the pre-peak accumulated elastic energy. In the third type, UCS (or Rc) has been solely utilized as a BLI, and in the last type, the duration of dynamic fracture (DT) exhibits the severity of energy release and, subsequently, strength loss. Some of the concepts used for the proposal of BLIs were utilized in the development of BIs. For instance, a reverse ratio of strain energy storage (WET) was introduced as an energy-based BI by Munoz et al. (2016b). Similar to bursting energy index (KE), a combination of different energy-related components, such as elastic, dissipated, and fracture energies, was used in energy-based BIs where a complete stress–strain response is required (Tarasov and Potvin 2013; Ai et al. 2016; Munoz et al. 2016b, 2016a; Zhang et al. 2021b; Gong and Wang 2022; Wang et al. 2022). The UCS (or Rc) was widely used in strength parameter-based BIs and the duration of dynamic fracture (DT) has been broadly utilized in the energy-based BIs to define the type of failure, ranging from absolute brittle to ductile behavior (Tarasov and Potvin 2013; Ai et al. 2016; Zhang et al. 2018).

Fig. 1
figure 1

Schematic representation of the four widely used BLIs including; a strain energy storage index (1) and b bursting energy index (2), UCS or Rc (3) and duration of dynamic fracture (4)

Full size image

From an extensive review of the literature, it has been found that the concepts of BI and BLI have been introduced to the scientific community at around the same time, but are being utilized in two different domains. Their primary objective has been to evaluate the level of “burst–brittleness” of rocks in various engineering applications, typically determined through laboratory testing methods. Conventionally, the term “burst” has been associated with a “violent brittle failure” that involves the release of significant strain energy storage. Similar to many established BIs, tailored to specific rock types and/or applications, the BLIs have been specifically developed for coal, in particular, to assess the bursting level in underground coal mining (Kidybiński 1981). Therefore, despite their distinct names, it is true to state that the genesis of both BI and BLI originated from the same school of thought, whereby BLI serving as a distinct BI primarily designed for coal burst/brittleness assessment. As a result, when the failure of coal is assessed beside other rock types, it is logical to include both BI and BLI for any universal assessment of brittle failure of various rock types.

3 A Novel Approach to Estimate Burst–Brittleness Level

3.1 Brittleness Index Versus Index-to-Strength Conversion Factor

The determination of brittleness or so-called “Brittleness Index” is largely empirical, which measures the relative susceptibility of materials to deformation and fracture responses (Altindag 2003). In an early attempt to quantify the rock brittleness, the BI1 was introduced as the ratio of UCS to tensile strength (TS) (Hucka and Das 1974). It is generally accepted that the difference between compressive and tensile strengths increases with an increase in brittleness (Hucka and Das 1974). The UCS is widely used for classification and design purposes in rock engineering practice. In general, unavoidable challenges associated with expensive testing equipment and recovery of core samples with the desired geometry from highly jointed brittle rocks are yet to be considered as major limitations in implementing different rocks testing techniques for brittleness assessment. Under point load testing (PLT), these challenges to high extent have been addressed in which the flexibility in sample size and shape, little preparation time, and ease of operation can be ensured and thus making it a popular strength indexing approach (Masoumi et al. 2012, 2018; Forbes et al. 2015). The index-to-strength conversion factor (k) that is relating UCS to the point load index (PLI) was proposed to estimate the UCS from the PLI indirectly (ISRM 1985). Numerous studies have been conducted on a wide range of rock types with different sizes, shapes, and point loading directions to establish reliable empirical conversion factors (ISRM 1985; Li and Wong 2013).

Broch and Franklin (1972) argued that the UCS is approximately 24 times (k) higher than the PLI of a standard core sample size (50 mm). A size correction chart was also developed for determining the cores’ UCS with various diameters (Broch and Franklin 1972). Bieniawski (1975) suggested a value of 23 as a universal conversion factor (k). Greminger (1982) and Forster (1983) showed that the conversion factor of 24 could not be adequately applied to anisotropic rocks. The International Society for Rock Mechanics (ISRM) stated that, on average, UCS is 20–25 times greater than PLI, although it has been highlighted that for different rock types, especially anisotropic rocks, k can range between 15 and 50 (ISRM 1985). Chau and Wong (1996) argued that k depends on the UCS/TS ratio, Poisson’s ratio, and length and diameter of rock samples. Hawkins (1998) indicated that the k varies from 7 to 68 for rocks originated from different lithologies. Kahraman (2001) found two separate trends for k values using the testing data obtained from 48 different rock types.

From various experimental and theoretical investigations, it has been noted that k is dependent on a range of physical and intrinsic rock properties, including origin and fabric (Fener et al. 2005; Kahraman et al. 2005; Kahraman and Gunaydin 2009), degree of anisotropy (Greminger 1982; Forster 1983), size and shape (Chau and Wong 1996; Masoumi et al. 2012, 2018), Poisson’s ratio (Chau and Wong 1996), water content (Broch and Franklin 1972; Hawkins 1998), porosity (Palchik and Hatzor 2004), and degree of weathering (Chau and Wong 1996). Although several forms of regression analysis have been used to correlate such parameters, the relationships between UCS and PLI were mainly established through linear regressions with a zero intercept (Broch and Franklin 1972; Bieniawski 1975; Hassani et al. 1980; ISRM 1985; Smith 1997; Sabatakakis et al. 2008; Singh et al. 2012; Li and Wong 2013).

In the same vein as that elaborated regarding the correlations between UCS and PLI, the so-called “Brittleness Index”, including BI1 (UCS/TS), can be examined where the brittleness depends on a variety of rock physical and intrinsic characteristics, including mechanical properties (Hucka and Das 1974), size and geometry (Hajiabdolmajid and Kaiser 2003), water content (Kodama et al. 2013), temperature (Kodama et al. 2013), stress–strain responses (Tarasov and Potvin 2013; Kuang et al. 2021), energy transformation (Munoz et al. 2016b), mineral composition (Wang and Gale 2009), elastic parameters (Rickman et al. 2008), porosity (Heidari et al. 2014), and strain rate (Kodama et al. 2013). Thus, it can be hypothesized that in principle, k and BI1 are dependent on the physical and intrinsic properties of rock materials given that both are functions of UCS and the dominant failure mode under point load and indirect tensile Brazilian tests is indeed tensile failure (Russell and Wood 2009). However, the indirect tensile Brazilian loading on strong rocks with potentially high brittleness has been proven to be unreliable due to the limitations associated with shearing at the contact platens and the disk sample that can lead to multiple cracking failure and overestimation of tensile strength (Erarslan et al. 2012; Masoumi et al. 2018; Khadivi Boroujeni et al. 2021; Khadivi et al. 2023). Such limitations can be avoided under point loading and, thus, making the PLI a suitable alternative to TS for burst–brittleness characterization of various rocks, particularly those with high brittleness.

3.2 Burst–Brittleness Ratio (BBR) Based on PLI

The PLT involves compressing of a brittle sample between two conical steel platens (pointers) until failure to evaluate its point load index (PLI or \({I}_{\mathrm{s}}\)). In this study, for standard classification of such an index, the reference sample diameter of approximately 50 mm was used, and to obtain the optimum outcome, the rock samples were loaded under diametral and axial directions as suggested by ISRM (1985). The diametral \({I}_{\mathrm{s}}\) is defined according to

$${I}_{\mathrm{S}}=\frac{P}{{D}^{2}},$$
(1)

where P is the maximum applied load and D is the diameter of a sample which equals to the distance between the two pointers. Under axial point loading, the force is applied at the center of the end surfaces and the \({I}_{\mathrm{s}}\) is estimated using the following equation:

$${I}_{\mathrm{S}}=\frac{P}{4LD/\pi },$$
(2)

where L is the length of a sample and LD represents the minimum cross-sectional area of a plane through the pointers. Equations (1) and (2) were developed by Franklin (1985) where the effect of contact surface area between the pointers and sample were not considered. Masoumi et al. (2016) argued that the radius of the conical platens under point loading is important for estimation of PLI inspiring by the work conducted by Russell and Wood (2009) who demonstrated that the contact area controls the stress intensity immediately below the contact points where the failure initiates. Thus, Masoumi et al. (2016) included the contact area based on Timoshenko and Goodier’s (1951) theory to introduce a more reliable estimation of point load index. The radius of contact area between two elastic spheres with different radii and mechanical properties can be calculated as follows:

$$r=\sqrt[3]{\frac{3\pi P({K}_{1}+{K}_{2}){R}_{1}{R}_{2}}{4 ({R}_{1}+{R}_{2})},}$$
(3)

where R1 and R2 are radii of two spheres; and K1 and K2 are calculated by the following equations:

$${K}_{1}=\frac{1-{v}_{1}^{2}}{\pi {E}_{1}}$$
(4)
$${K}_{2}=\frac{1-{v}_{2}^{2}}{\pi {E}_{2}},$$
(5)

where \({v}_{1}\) and \({v}_{2}\) represent Poisson’s ratios and E1 and E2 are Young’s moduli of two spheres. For simplicity, the surface roughness between the pointer and sample can be ignored as explained by Russell and Wood (2009). The pointers are usually made of tungsten carbide or hardened steel, with a smooth and spherically curved tip of 5 mm as suggested by ISRM (Franklin 1985). The elastic modulus and Poisson’s ratio of tungsten carbide are about 700 GPa and 0.25, respectively (Russell and Wood 2009). Under diametral point loading, the contact area is elliptical shape as a pointer with a spherical tip pushes on a cylindrical surface. For typical elastic properties, the major and minor diameters in the ellipse have a ratio of one; therefore, the contact area can be assumed as a circle for simplicity.

Under axial point loading, since the pointer pushes on a flat surface, the contact area is circular leading to R2 \(\gg\) R1 where Eq. (3) can be simplified as follows:

$$r=\sqrt[3]{\frac{3\pi P({K}_{1}+{K}_{2}){R}_{1}}{4}.}$$
(6)

As a result, the new PLI was proposed by Masoumi et al. (2016) including the influence of contact area according to

$${I}_{\mathrm{s}(\mathrm{n})}=\frac{P}{A},$$
(7)

where \({I}_{\mathrm{s}(\mathrm{n})}\) denotes the new PLI; A is the contact area that can be estimated based on the radii obtained from Eqs. (3) and (6), for point loadings under diametral and axial directions, respectively. As explained earlier, a conventional regression to correlate UCS with PLI is

$$\mathrm{UCS}=k{I}_{\mathrm{s}},$$
(8)

where k denotes index-to-strength conversion factor. The new correlations for relating UCS and PLI are derived through re-arranging Eq. (8) and incorporating Eqs. (1), (2) and (7) as follows:

$${\text{UCS}} = k\frac{A}{{D^{2} }}I_{{{\text{s}}({\text{nd}})}} \quad {\text{for}}\,{\text{diametral}}$$
(9)
$${\text{UCS}} = k\frac{A}{4LD/\pi }I_{{{\text{s}}({\text{na}})}} \quad {\text{for}}\,{\text{axial,}}$$
(10)

where \({I}_{\mathrm{s}(\mathrm{nd})}\) and \({I}_{\mathrm{s}(\mathrm{na})}\) represent new diametral and axial point load indices, respectively. As a result, the burst–brittleness ratio (BBR) is defined as follows;

$$\mathrm{BBR}=\frac{\mathrm{Compression\;conponent}}{\mathrm{Tensile\;component}}.$$
(11)

The compression component is estimated through UCS, while the \({I}_{\mathrm{s}(\mathrm{na})}\) and \({I}_{\mathrm{s}(\mathrm{nd})}\) derived from Eqs. (9) and (10) are substituted to tensile component leading to BBR for two different point loading directions as follows:

$${\text{BBR}}_{d} = \frac{{{\text{UCS}}}}{{I_{{s({\text{nd}})}} }} = k\frac{A}{{D^{2} }}\quad {\text{for}}\,{\text{diametral}}$$
(12)
$${\text{BBR}}_{a} = \frac{{{\text{UCS}}}}{{I_{{s({\text{na}})}} }} = k\frac{A}{4LD/\pi }\quad {\text{for}}\,{\text{axial,}}$$
(13)

where BBRd and BBRa represent the Burst–Brittleness Ratio for diametral and axial loading conditions, respectively. In principle, the BBR has the same characteristics as BI1, but its tensile component is replaced by the new PLI proposed by Masoumi et al. (2016). It is believed that incorporation of contact area in the proposed BBR can improve the accuracy of burst–brittleness assessment and can assist to make it more versatile for various rocks and different applications. Also, flexibility in performing point load testing is another major advantage of BBR over conventional BIs where PLI can be estimated very rapidly as opposed to other experiments, such as triaxial, direct/indirect tensile, and punch penetration tests. To assess the performance of the proposed BBR, three different rock types from various geological origins, including coal, granite, and sandstone, were selected for a comprehensive examination and their BBR, BI1, and k are compared. Also, the failure processes of tested rocks under uniaxial compression and point loading are visualized through high-speed imaging technique to then analyze their level of violent failure with the estimated BBR and BI1.

4 Experimental Study

4.1 Sample Preparation

Gosford sandstone was sourced from Gosford quarry in Somersby, New South Wales (NSW) (Roshan et al. 2018), Coal blocks were obtained from Ulan seam in NSW and granite was sourced from Mount Martha Quarry, Victoria in Australia (Khadivi et al. 2022). All samples were cored at standard NX (54 mm) size followed by cutting into cylinders with three different slenderness (length-to-diameter) ratios of 0.5, 1, and 2 to be utilized for testing under uniaxial compressive, Brazilian and point loadings as shown in Fig. 2. The ends of the samples were cut parallel in accordance with the ASTM (2001) to reduce the end surface effects with an accuracy of ± 0.02 mm. A minimum of five repetitions were executed for each testing scenario at room temperature (21–25 °C) condition.

Fig. 2
figure 2

Examples of the prepared coal, granite, and sandstone samples for uniaxial compressive, indirect tensile Brazilian, and point load tests

Full size image

4.2 Uniaxial Compressive Testing

The uniaxial compressive tests were performed on the samples with a slenderness ratio of two at the displacement rate of 5 × 10–3 mm/s to obtain the sample failure within the suggested period by ASTM (1992). A servo-controlled Instron 600DX testing frame with a maximum loading capacity of 60 tons was used to perform the experiments (see Fig. 3) and the results are presented in Table 1. To measure the Poisson’s ratios, necessary instrumentations including circumferential linear variable differential transducer (LVDT) were attached to the samples where the radial strains were computed according to Masoumi et al. (2015).

Fig. 3
figure 3

Uniaxial compressive testing setup (600 kN Instron frame); a loading frame control system, b emergency stop, c control console, d movable platform, e LVDT, and f rock sample

Full size image
Table 1 Mean physical and mechanical properties of the samples tested under uniaxial compressive loading
Full size table

The stress–strain curves obtained from uniaxial compressive tests representing the strength and deformation characteristics of rocks in the pre- and post-failure stages are shown in Fig. 4.

Fig. 4
figure 4

Examples of stress–strain responses of samples under uniaxial compression

Full size image

4.3 Indirect Tensile Brazilian Testing

The Brazilian tests were performed using an Instron 33R-4204 loading frame with a maximum loading capacity of 50 kN (see Fig. 5) on the cylindrical samples with a slenderness ratio of 0.5 according to the suggested method by the ASTM (2016). The same displacement rate as that used for uniaxial compressive tests was utilized here to obtain the suggested testing period as per the ASTM (2016). The maximum recorded load is used to determine the tensile strength according to (ISRM 1978; ASTM 2016)

$${\sigma }_{\mathrm{t}}=\frac{2P}{\pi Dt},$$
(14)

where P denotes the peak load at the failure, D is the disc’s diameter, and t represents the thickness of sample measured at the center. Table 2 lists the resulting data from the Brazilian tests. Also, the examples of load–displacement curves obtained from the Brazilian tests are shown in Fig. 6.

Fig. 5
figure 5

Indirect tensile Brazilian testing setup (50 kN Instron frame); a loading frame control system, b control console, c rock sample, and d movable platform

Full size image
Table 2 Physical and mechanical properties of the samples tested under indirect tensile Brazilian loading
Full size table
Fig. 6
figure 6

Examples of force–displacement responses of different rock samples tested under Brazilian loading

Full size image

4.4 Point Load Testing (PLT)

The NX size cylindrical samples with a slenderness ratio of one were tested according to the ISRM suggested method under axial and diametral loadings (ISRM 1985). The tests were conducted using a GCTS PLT-2W point loading apparatus (see Fig. 7) equipped with a high-precision load sensor with an accuracy of ± 0.05%. The PLT results are tabulated in Table 3 using Eqs. (1) and (2) to estimate PLI (IS(50)) from diametral and axial loadings, respectively. Figure 8 demonstrates the examples of load–displacement curves obtained from point load tests on coal, granite, and sandstone samples under axial and diametral loading conditions.

Fig. 7
figure 7

Point load testing setup; a PLT apparatus, b DAQ device, c electronic balance, and d coal samples

Full size image
Table 3 Mean physical and mechanical properties of the samples tested under point loading
Full size table
Fig. 8
figure 8

Load–displacement curves obtained from point load tests on various rock types under axial and diametral conditions

Full size image

4.5 High-Speed Imaging

Real-time study of the macro-fracturing process of brittle materials can help to identify and classify their failure mechanism. The high-speed imaging is an advanced laboratory technique that enables the real-time visualization of rock deformation and fragmentation at high resolution (Xing et al. 2017; Khadivi Boroujeni et al. 2021; Khadivi et al. 2023). In this study, a high-speed CMOS camera (Phantom V2511) was adopted with a resolution of 512 × 512 pixels at the frame rate of 200,000 fps with the lens of Nikon AF-S DX Nikkor 18–105 mm F/3.5–5.6 G ED to track the full fracturing behavior of tested rock types under uniaxial compressive and point loadings. The setup of high-speed imaging camera for uniaxial compressive testing is shown in Fig. 9.

Fig. 9
figure 9

600kN Instron uniaxial testing setup equipped with high-speed imaging system; a Phantom V2511 camera, b camera control system, c loading frame control system, d safety shield, e LED lights, and f movable platform

Full size image

4.6 Acoustic Emission (AE)

Acoustic emission (AE) is a technique for monitoring of microcracks’ development in rock materials (Lockner et al. 1991; Chang and Lee 2004). In this study, such a technique was adopted to further investigate the brakeage process of samples under point loading.

4.6.1 Methodology

AE parameters (e.g., counts, amplitude, rise time, and duration) can be seen as valuable information to mainly characterize the microcracking process of rocks (Liu et al. 2020; Li et al. 2021). Such parameters are utilized to assist in identifying the failure mechanism of rocks (Eberhardt et al. 1998; Rudajev et al. 2000). The AE count is the number of oscillations of signal that crosses the threshold. The AE amplitude is the highest peak of the measured voltage signal waveform. Rise time is the time interval between the first time that an event signal exceeds the threshold and the maximum amplitude history. Duration is the time interval between the first and the last AE counts which crosses the threshold. Here, a parametric-based analysis of AE signals was utilized to classify the types of microcracks. Such an approach has been accredited based on the generalized theory of AE through the simplified Green’s functions for moment tensor analysis (SiGMA) procedure (Ohno and Ohtsu 2010).

Two AE parameters including AF (counts over duration) and RA (rise time over maximum amplitude) are the key factors for characterizing the microcracks into two categories, namely, tensile and shear, as shown in Fig. 10. Low AF and high RA values generally indicate the occurrence and development of shear cracks, while high AF and low RA values represent tensile cracks (Ohno and Ohtsu 2010; Du et al. 2020; Ge and Sun 2021). Tensile cracks typically exhibit higher extension speeds and lower extension scales compared to shear cracks, which consequently result in acoustic emission (AE) signals with higher peak frequencies (Du et al. 2020).

Fig. 10
figure 10

Schematic view of classification of AE data into micro-tensile and shear cracks

Full size image

A classification benchmark line (AF/RA = 70) differentiates the crack types (Hu et al. 2019). This is not a strict dividing line between tensile and shear cracks, but rather a baseline to determine the ratio of tensile and shear microcracks (Aggelis 2011). Also, it is generally believed that with an increase in brittleness level of rocks, tensile cracking dominates the failure process (Tang and Kou 1998; Hajiabdolmajid et al. 2002; Zhang and Zhang 2017; Zhang et al. 2021a; Xu et al. 2022). In other words, with an increase in brittleness of rocks, the distribution ratio of AE parameters with high AF and low RA increases (see Fig. 10).

4.6.2 AE Setup

Two piezoelectric transducers were glued on each sample for effective data acquisition during the rock failure under point loading. The acoustic waves emitted from samples were recorded using the system manufactured by Physical Acoustics Pty Ltd (Corporation 2007) and its hardware is called the Peripheral Component Interconnect (PCI) 2-channel data acquisition system, as shown in Fig. 11. This AE system has a broadband transducer (ULTRAN SWC37-0.5) with an operating frequency ranges from 1 kHz to 2 MHz and a nominal resonant frequency of 500 kHz. The software component of the system is AEwin, for data acquisition and analysis. To enable the detection and amplification of low-frequency acoustic waves generated during the cracking process while minimizing interference from other laboratory activities, the external amplifiers were adjusted to 40 dB. This setting facilitated accurate reading and amplification of the cracking signals while effectively eliminating any unwanted noise.

Fig. 11
figure 11

Point load testing setup paired with acoustic emission device and high-speed camera; a AE DAQ system, b camera control system, c PLT apparatus, d rock samples, and e high-speed camera

Full size image

5 Data Analysis

In this section, the experimental results are presented followed by examining the suitability of the proposed BBR based on the recorded fracturing process of tested samples using high-speed imaging technique and AE data. Cracks may grow through several mechanisms, such as pore crushing, sliding along pre-existing cracks, elastic mismatch between grains, dislocation movement, and Hertzian contacts (Kemeny and Cook 1991; Eberhardt et al. 1999; Gatelier et al. 2002). Considering various rock structures, one or more of the above-mentioned mechanisms can predominantly contribute to the rock failure process. For instance, pore crushing can be the main failure mechanism in sandstone due to the relatively high porosity percentage, whereas cleat network associated with bedding planes plays a crucial role in coal fracturing. Despite having different failure processes, the BBR can characterize the brittleness of materials based on the severity of strength loss and subsequent violent failure. Table 4 compares the resulting ratios from the experimental study including k, BI1, and BBR.

Table 4 Mean values of mechanical properties along with the calculated ratios
Full size table

From Table 4, it is clear that coal has the highest burst–brittleness ratio followed by granite and sandstone under both diametral and axial loadings. Such a trend was not captured through either BI1 or k, as shown in Fig. 12. Generally, diametrically loaded samples were found to possess the highest burst–brittle levels compared to the axially loaded ones for all rock types. Under axial loading, coal demonstrates nearly two-to-three times greater burst–brittleness levels compared to granite and sandstone, respectively, and about the same folds or higher under diametral loading.

Fig. 12
figure 12

Burst–brittleness ratio, brittleness, and k rankings of various rock types

Full size image

For testing coal diametrally, the direction of load was parallel to the beddings, while under axial loading, the load was normal to the beddings. Therefore, under diametral loading, the samples failed at lower forces due to the sliding along the bedding plane and not failure of intact component. Such a failure mechanism cannot be counted under brittleness assessment as the loading was concentrated on the sample discontinuity. To further examine the validity of the newly established BBR, the high-speed imaging technique was deployed to visualize the real-time deformation, fracturing process, and failure patterns of tested rocks at macroscale under uniaxial compressive and point loadings. Also, AE technique was used during the point loading to further assess the microcracking development in the tested rocks.

5.1 High-Speed Imaging Data

The resulting high-speed imaging frames under axial and diametral point loadings are presented in Figs. 13, 14, 15, 16, 17 and 18 along with their cracking velocities written in the last frames. Such velocities were calculated by tracking the cracks’ development under pointers, from the initiation of the crack to complete propagation using high-speed frames. Single tensile failure on the loaded line is the dominant failure mechanism in almost all tested rock types. However, failure time, cracking velocity, and the subsequent failure intensity were different under each condition. For coal sample under axial loading, a tensile crack was instantly developed under loaded line and at the peak load (see Fig. 13) resulting in a tensile failure through splitting the sample into two halves. Such splitting was also observed under diametral loading on coal sample; however, the controlling failure mechanism was shearing or sliding along the pre-existing bedding plane, as shown in Fig. 14. Granite was considered isotropic and intact given that there were no observable defects in the tested samples. A similar failure mechanism as that reported for coal under axial loading is observable for granite under both axial and diametral loadings with relatively high cracking velocities (see Figs. 15, 16). Sandstone samples were also intact under both axial and diametral loadings which exhibited a progressive failure rather than an instant failure, as demonstrated in Figs. 17 and 18.

Fig. 13
figure 13

Real-time fracturing behavior of a coal sample under axial PLT and its cracking velocities

Full size image
Fig. 14
figure 14

Real-time fracturing behavior of a coal sample under diametral PLT and its cracking velocities

Full size image
Fig. 15
figure 15

Real-time fracturing behavior of a granite sample under axial PLT and its cracking velocities

Full size image
Fig. 16
figure 16

Real-time fracturing behavior of a granite sample under diametral PLT and its cracking velocities

Full size image
Fig. 17
figure 17

Real-time fracturing behavior of a sandstone sample under axial PLT and its cracking velocities

Full size image
Fig. 18
figure 18

Real-time fracturing behavior of a sandstone sample under diametral PLT and its cracking velocities

Full size image

Under point loading, the load is applied through pointers on small local areas where a sample is failed in tension with less energy dissipation, whereas failure in compression due to a significant shearing mechanism can exhibit a high level of energy dissipation. Therefore, to further investigate such behavior, fracturing responses of all three rock types were tracked under uniaxial compression as one of the important experiments to assess the credibility of the proposed BBR. The chains of real-time fracturing processes under uniaxial compressive loading are shown in Figs. 19, 20 and 21.

Fig. 19
figure 19

Real-time fracturing behavior of a coal sample under compressive loading exhibiting macroscale cracks’ initiation, stable and unstable growth, propagation, coalescence, and dominant violent failure under mixed mode of shear and tension

Full size image
Fig. 20
figure 20

Real-time fracturing behavior of a granite sample under compressive loading exhibiting macroscale cracks’ initiation, stable and unstable growth, propagation, coalescence, and dominant violent failure under mixed mode of shear and tension

Full size image
Fig. 21
figure 21

Real-time fracturing behavior of a sandstone sample under compressive loading exhibiting cracks’ initiation, stable and unstable growth, propagation, coalescence, and dominant shear failure with a single tensile crack

Full size image

Figure 19 demonstrates various stages of coal failure under uniaxial compression where a localized vertical crack initially formed within the sample (see Fig. 19b) and then propagated with an increase in the load. During a very short segment of time, intensive localized cracks were activated at various scales and orientations (see Fig. 19d, e). Such cracks were not necessarily correspondent to the initially formed cracks which could be due to the activation of the pre-existing fractures or so-called “cleat network”. Despite such an extensive crack network development, the sample was still under the cylindrical shape and took further load (see Fig. 19f). After just 2 ms, it failed in a strongly violent manner through a mixed mode of shear and tension with dominant tensile fractures. Fragmentation ranged from powder to two course conical-shaped fragments (see Fig. 19h, i). It is evident that the stable and unstable cracking occurred simultaneously in the coal sample where the complete failure process happened within 2 ms.

A similar failure process as that observed for coal sample was recorded for the granite sample (see Fig. 20) but with less severity. Cracking was started through a number of localized vertical tensile cracks which then propagated toward the end surfaces as load increased (see Fig. 20b, c). The multiple tensile cracks at different scales and orientations were generated within the sample and propagated (see Fig. 20d–f) leading to the strong violent failure (see Fig. 20g, h). In this case, unlike coal, the propagated cracks were mainly the continuation of the generated ones leading to a violent mixed mode of shear and tensile failure.

For the sandstone sample which was subjected to compressive loading (see Fig. 21), a vertical crack was initiated near the end surfaces of the sample (see Fig. 21b) and then propagated and coalesced (see Fig. 21c–e) to form a shear band (see Fig. 21f) as load increased. The sample failed through a single shear band into two approximately equal halves (see Fig. 21h) with a single tensile crack.

Coal demonstrated the highest level of cracking density during the failure process followed by granite and then sandstone, respectively. Stable and unstable cracking stages can be differentiated in sandstone during its progressive failure, while in coal and granite samples due to the sudden activation of intensive localized cracks, stable and unstable cracking happened at nearly the same time. The other major distinction between sandstone and the other two rock types is related to the failure mechanism where the former was primarily shearing and the latter was a mixed mode of shear and tension. The complete failure process of coal from the initial crack formation to complete failure happened at about 10 and 100 times faster than those in granite and sandstone, respectively, indicating high brittle failure in coal compared to granite and sandstone and endorsing the validity of the proposed BBR. The coal sample also exhibited the least duration of dynamic fracturing and the highest rate of strength loss, while the sandstone sample resulted in the greatest dynamic fracturing and lowest rate of strength loss. It is noteworthy that tested coal has the lowest compressive and tensile strengths among the examined rock types while possessing the highest relative burst-brittle level. Therefore, it is important to highlight that the burst–brittleness characteristic cannot be described by the UCS alone, and indeed, other strength factors like PLI with precise estimation are required.

5.2 Acoustic Emission Analysis

The AE events obtained from point load tests were parametrized to characterize the microcracking process in the tested rocks. The cumulative scatter AF-RA data as well as the cumulative probability density maps for coal, granite, and sandstone samples are presented in Figs. 22 and 23. The data distribution changes from sparse to dense with the color changing from red to purple in the density maps. The associated scatter plots are provided next to each of the density maps showing the AE parameters’ distribution in blue dots. The AE parameters are split into two regions by the red benchmark line, differentiating tensile and shear microcracks with associated cracking percentages in pie charts. The AF ranged from 0 to 2000 kHz and RA varied between 0 and 20 ms/V. For consistency and making the results comparable, the area where the largest proportion of AE parameters concentrated (e.g., in the range of 0–250 kHz for AF and 0–1 ms/V for RA) was selected to be further investigated. The dense areas located above the diagonal benchmark line indicate that the tensile microcracks in all rock types are the dominant ones. Under both axial and diametral loadings, the AF values are mainly concentrated in the range of 0–100 kHz for the granite samples, which is larger than that for coal and sandstone samples with the interval of 0–50 kHz. These results confirm the failure of rocks in tension under point loading as highlighted by Russell and Wood (2009). The percentage of tensile microcracks can also be associated with the level of brittleness in the rocks where higher tensile cracks can lead to violent rock failure as has been indicated under compressive failure (Zhou et al. 2019; Zhang et al. 2021a; Peng et al. 2022).

Fig. 22
figure 22

The cumulative RA–AF density maps (left) and their corresponding scatter data plots (right) for a coal, b granite, and c sandstone samples under axial point loading

Full size image
Fig. 23
figure 23

The cumulative RA–AF density maps (left) and their corresponding scatter data plots (right) for a granite and b sandstone samples under diametral point loading

Full size image

Table 5 summarizes the distribution of tensile and shear microcracks obtained from this analysis along with the computed BBR and BI1 for the tested samples. Coal samples revealed the maximum tensile microcracks’ portion among the tested rock types followed by granite and sandstone, respectively, endorsing the validity of the proposed BBR based on AE analysis. Furthermore, this effort aimed to unify the concepts of burst and brittleness by introducing a versatile ratio that can be utilized for the burst (coal and rock bursts) and brittleness assessments of a broad range of rocks in rock engineering projects. It is also suggested to investigate the applicability of BBR across a wide range of brittle rocks and rock-like martials in future studies.

Table 5 Percentage of microcracking types along with BBR and BI1 values
Full size table

6 Conclusions

In this paper, the challenges and efforts undertaken to estimate/quantify the Brittleness Index (BI) and Bursting Liability Index (BLI) were discussed. It was noticed that the development of BI and BLI emerged at the relatively same time and originated from similar concepts but aimed at evaluating the burst–brittle failure of various rocks in different engineering applications. Therefore, a universal so-called Burst–Brittleness Ratio (BBR) governed by point load testing (PLT) was proposed to address the existing limitations for both BIs and BLIs as well as for being a practical measure in the relative burst–brittleness assessment of different rock types irrespective of their applications. In principle, the proposed BBR has two strength components under compression (UCS) and tension (\({I}_{\mathrm{s}(\mathrm{nd})}\) or \({I}_{\mathrm{s}(\mathrm{na})}\)). The former has been standardized by ISRM and ASTM, while in here, the latter was calculated through incorporating the contact area to improve the accuracy of the point load index estimation and, subsequently, the proposed BBR.

Coal, sandstone, and granite were selected for a comprehensive examination of the BBR. It was found that coal possessed the highest BBR followed by granite and sandstone where such a trend was not captured through other deployed measures, such as BI1 and k factor. Also, with the aid of high-speed imaging visualization under different loading conditions, it was demonstrated that a rock with a higher BBR value failed more violently. From high-speed and AE analyses under point loadings, a progressive failure of sandstone was depicted, while coal and granite failed instantly. The parametric analysis of AE data revealed strong consistency in generated tensile microcrack percentages with model predictions, endorsed the suitability of BBR. Under uniaxial compression, the complete failure process of coal from initial crack formation to complete failure happened at around 10 and 100 times faster than those in granite and sandstone, respectively. The AE and high-speed imaging data altogether ranked coal as the highest brittle failure/rock followed by granite and sandstone which were in good agreement with the computed BBR. Above all, it was found that although coal had the lowest compressive and tensile strengths among the examined rock types, it possessed the highest relative burst–brittle level. Such a finding highlights the fact that a strong rock may not necessarily fail in a more brittle manner and for a universal burst–brittleness assessment, other strength factors such as PLI with more accurate estimation are also required.