Characterizing Anisotropic Swelling Strains of Coal Using Combined Rosette Strain Gauge and CT-Scans

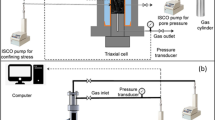
Abstract

Matrix shrinkage/swelling induced by gas sorption can be a major geomechanical driver for coalbed methane reservoir stress depletion and gas transport enhancement under in situ reservoir conditions. The pressure-dependent three-dimensional (3-D) coal matrix shrinkage/swelling is of obvious interest for investigating the mechanical failures and gas transport behaviors of coal. An integrated sorption and matrix shrinkage system was employed for simultaneously measuring the gas sorption capacity and 3-D anisotropic swelling/shrinkage strains. The sorbing methane gas and non-sorbing helium gas were used as the flooding fluids on two coals. The high heterogeneity and anisotropy features in micro- to macro- scale of coals were confirmed using FESEM-EDS imaging and elemental analysis. To quantify the 3-D anisotropic characteristics in directional swelling strains, rosette strain gauges were employed. The 3-D principal strains for the two coals were computed through combining the proposed strain transformation model and the visualized cleat coordinate system established via the reconstructed 3-D coal structure using the X-ray CT images. For helium injection, coals were in compression and the maximum compression strain in the newly established cleat system can be up to ~  – 0.11% and ~  – 0.10% for samples S1 and S2 at pressure of 1664.35 psi, respectively. The maximum principal strain in dilation for coals S1 and S2 due to methane injection can be up to ~ 0.21% and ~ 0.149%, respectively, at pressure of 2279.37 psi. The pressure- or methane content- dependent anisotropic degree based on the actual three-dimensional principal strains in the cleat coordinate system was calculated and discussed. The results will provide a comprehensive modeling framework to evaluate sorption-induced swelling effects under in situ complex boundary conditions.

Highlights

• 3D swelling strains of coal induced by gas sorption are determined.

• Micro- to macro- scale heterogeneity and anisotropy of coals are confirmed.

• 3D principle swelling strains are modeled in the cleat coordinate system.

Appendices

Appendix A: Experimental Procedure for Synchronous Gas Sorption and Matrix Swelling Measurements

Approximately 150 g coal powders were loaded into the powder sample cell and the cubic coal sample was placed into the cubic sample cell prior to gas injections (Fig. 

Fig. 19

Experimental apparatus for synchronous gas sorption and matrix swelling measurements

19). Pressure-dependent gas sorption and sorption-induced directional swelling strains can be monitored and estimated using the recorded pressures and strains. For the matrix swelling test, we initially opened all the valves and vacuumed the whole experimental system for residual air removal. Then, the reference cell was pressurized through opening valve 3 and shutting off valve 1, valve 2, and valve 4. When the pressure in reference cell reached p1 indicated by pressure transducer 3, we shut off valve 3 and waited for the pressure stabilization. Then, we opened valve 1, the gas was dosed to cubic sample cell from reference cell with its pressure decreases from p1 to p2, which was recorded by pressure transducer 3. At this stage, both the reference cell and cubic sample cell stabilized at the same pressure p2, which can be indicated by pressure transducers 1 and 3. Subsequently, valve 1 was closed and the cubic sample cell was isolated as a closed system with testing pressure of p2 (pressure transducer 1). The stabilized pressure p2 at different stages was defined as the stage-based equilibrium pressures for matrix swelling tests. Till then, the pressure in reference cell was still p2. Then, we started to operate the adsorption test. After closing valves 1, the reference cell and powder sample cell separated by valve 2 were established as a traditional volumetric-based sorption measurement system. Since the reference cell was stabilized at pressure p2, the total amount of gas molecules in reference cell was known. We opened valve 2, a portion of gas molecules in reference cell was dosed into powder samples cell. We kept valve 2 open till the pressure stabilized at p3 in both reference cell and powder sample cell, which are indicated by pressure transducers 2 and 3. The final stabilized pressure p3 was used as the gas pressure for this stage. The stabilized pressures p3 at different stages were defined as the stage-based equilibrium pressures for adsorption tests. Because gas sorption in power coal sample is quicker than the strain equilibrium on cubic sample in cubic sample cell, we waited for at least 3 days for each pressure step. To complete all the testing program, we repeated all the steps for each pressure until the final pressure was achieved. The recorded pressures and strains were used for data analyses.

Appendix B: Modeling Analysis

2.1 Determination of Principal Strains on Coal from Strain Rosettes

Various techniques have been implemented to measure the state of strain on a plane for rocks under both unconstrained and constrained conditions. These techniques, primarily involving strain gauges or displacement extensometers, depend on measured normal strains in various directions. In this study, the ${45}^{^\circ }$-rectangular strain rosette was employed to determine the state of strain at any given coal surficial plane. The question then arises to use the measured three angular normal strains to identify the principal strains and the directions. As illustrated in Fig. 

Fig. 20

Strain transformation diagram: (a) on a test surface, the grid of a rectangular rosette was installed at the arbitrary angle $\varphi$ from the major principal axis; (b) axes of the rectangular rosette superimposed on Mohr’s circle for strain. Determined from the directional strains on the plane at the directions of $\varphi$, $\varphi +{45}^{^\circ }$, and $\varphi +{90}^{^\circ }$, the maximum and minimum normal strains (i.e., ${\varepsilon }_{P}$ and ${\varepsilon }_{Q}$) can be determined based on Eqs. (1) to (3). Except in the case in which $x$ or $y$ is a principal direction, these two subsidiary principal strains will not correspond to two of the actual three-dimensional principal strains. In other words, the angle $\gamma$ from the $x$-axis defines the rotation degree of principal strain/stress from the coordinate system showing the actual three-dimensional principal strains. If $\gamma =\varphi$, the calculated principal strain directions are coaxial with the actual principal directions

20, the strain transformation from principal strains can be determined using rectangular strain gage rosette (Fig. 20a) and then recalling strain-transformation relationship with the aid of strain Mohr’s circle (Fig. 20b).

At any angle $\varphi$ from the major principal axis, the angles in Mohr’s circle double the normal strains, and thus, the normal strains at three arbitrary directions measured from three grids in rectangular rosette can be expressed as

$${\varepsilon }_{\varphi }=\frac{1}{2}\left({\varepsilon }_{P}+{\varepsilon }_{Q}\right)+\frac{1}{2}({\varepsilon }_{P}-{\varepsilon }_{Q})\mathrm{cos}2\varphi$$

(1)

$${\varepsilon }_{\varphi +{45}^{^\circ }}=\frac{1}{2}\left({\varepsilon }_{P}+{\varepsilon }_{Q}\right)+\frac{1}{2}({\varepsilon }_{P}-{\varepsilon }_{Q})\mathrm{cos}2(\varphi +{45}^{^\circ })$$

(2)

$${\varepsilon }_{\varphi +{90}^{^\circ }}=\frac{1}{2}\left({\varepsilon }_{P}+{\varepsilon }_{Q}\right)+\frac{1}{2}({\varepsilon }_{P}-{\varepsilon }_{Q})\mathrm{cos}2\left(\varphi +{90}^{^\circ }\right),$$

(3)

where ${\varepsilon }_{\varphi }$, ${\varepsilon }_{\varphi +{45}^{^\circ }}$, and ${\varepsilon }_{\varphi +{90}^{^\circ }}$ are the measured directional strains, dimensionless; ${\varepsilon }_{P}$ and ${\varepsilon }_{Q}$ are the maximum and minimum normal strains, dimensionless; $\varphi$ is the acute angle from the principal axis to the Grid 1, as shown in Fig. 20a.

In terms of the three measured strains (i.e.,${\varepsilon }_{\varphi }$, ${\varepsilon }_{\varphi +{45}^{^\circ }}$ and ${\varepsilon }_{\varphi +{90}^{^\circ }}$), the unknown quantities ${\varepsilon }_{P}$, ${\varepsilon }_{Q}$, and $\varphi$, can be obtained by solving the Eqs. (1)–(3) simultaneously, which can be expressed as

$${\varepsilon }_{P,Q}=\frac{{\varepsilon }_{\varphi }+{\varepsilon }_{\varphi +{90}^{^\circ }}}{2}\pm \frac{\sqrt{2}}{2}\sqrt{{\left({\varepsilon }_{\varphi }-{\varepsilon }_{\varphi +{45}^{^\circ }}\right)}^{2}+{\left({\varepsilon }_{\varphi +{45}^{^\circ }}-{\varepsilon }_{\varphi +{90}^{^\circ }}\right)}^{2}}$$

(4)

$$\varphi _{{P,Q}} = \frac{1}{2}\tan ^{{ - 1}} \left( {\frac{{2\varepsilon _{{\varphi + 45^\circ }} - \varepsilon _{\varphi } - \varepsilon _{{\varphi + 90^\circ }} }}{{\varepsilon _{\varphi } - \varepsilon _{{\varphi + 90^\circ }} }}} \right).$$

(5)

If positive, the physical direction of the angle $\varphi$ given by Eq. (5) is counterclockwise. If negative, it is clockwise. Since $\mathrm{tan}2\varphi =\mathrm{tan}(2\varphi +{90}^{^\circ })$, the calculated angle $\varphi$ can refer to either principal axis, and hence, the identification in Eq. (5) was represented as ${\varphi }_{P,Q}$. This ambiguity can readily be solved by application of the following criteria: (a) if ${\varepsilon }_{\varphi }>{\varepsilon }_{\varphi +{90}^{^\circ }}$, then ${\varphi }_{P,Q}={\varphi }_{P}$; (b) if ${\varepsilon }_{\varphi }<{\varepsilon }_{\varphi +{90}^{^\circ }}$, then ${\varphi }_{P,Q}={\varphi }_{Q}$; (c) if ${\varepsilon }_{\varphi }={\varepsilon }_{\varphi +{90}^{^\circ }}$ and ${\varepsilon }_{\varphi }<{\varepsilon }_{\varphi +{45}^{^\circ }}$, then ${\varphi }_{P,Q}={\varphi }_{P}=-{45}^{^\circ }$; (d) if ${\varepsilon }_{\varphi }={\varepsilon }_{\varphi +{90}^{^\circ }}$ and ${\varepsilon }_{\varphi }>{\varepsilon }_{\varphi +{45}^{^\circ }}$, then ${\varphi }_{P,Q}={\varphi }_{Q}={45}^{^\circ }$; (e) if ${\varepsilon }_{\varphi }={\varepsilon }_{\varphi +{45}^{^\circ }}={\varepsilon }_{\varphi +{90}^{^\circ }}$, then ${\varphi }_{P,Q}$ is indeterminate (equal biaxial strain).

Under hydrostatic pressure condition, there is no shear stress and the directions exhibiting the maximum and minimum normal strains ${\varepsilon }_{P}$ and ${\varepsilon }_{Q}$ are regarded as coaxial to two of the actual three-dimensional principal directions. Using the strain transformation relation, the directional strains at any arbitrary directions can be expressed as

$${\varepsilon }_{{P}^{^{\prime}}}=\frac{{\varepsilon }_{P}+{\varepsilon }_{Q}}{2}+\frac{{\varepsilon }_{P}-{\varepsilon }_{Q}}{2}\mathrm{cos}2\theta$$

(6)

$${\varepsilon }_{{Q}^{^{\prime}}}=\frac{{\varepsilon }_{P}+{\varepsilon }_{Q}}{2}+\frac{{\varepsilon }_{P}-{\varepsilon }_{Q}}{2}\mathrm{cos}2\theta$$

(7)

$${\varepsilon }_{{{P}^{^{\prime}}Q}^{^{\prime}}}=-\frac{{\varepsilon }_{P}-{\varepsilon }_{Q}}{2}\mathrm{sin}2\theta ,$$

(8)

where ${\varepsilon }_{{P}^{^{\prime}}}$, ${\varepsilon }_{{Q}^{^{\prime}}}$ and ${\varepsilon }_{{{P}^{^{\prime}}Q}^{^{\prime}}}$ are the plane strains at arbitrary directions;$\theta$ is the angle between the targeted plane and the principal directions, which is defined as positive in the counterclockwise direction.

Based on Eqs. (6)–(8), the directional strains on each of the orthogonal surfaces at arbitrary directions can be computed and quantified.

2.2 Determination of Principal Strains at the Matrix Coordinate System Using Strain Gage Rosettes

Based on the tensors of Young’s moduli and Poisson’s ratios, the anisotropic elastic properties of bulk coal can be depicted. By applying Hooke’s law (Jaeger 1969; Pan and Connell 2011), the isothermal anisotropy strains induced by mechanical compression can be written as

$${\varepsilon }_{c\_i}=\frac{{\sigma }_{i}-{\sigma }_{i0}}{{E}_{i}}-\sum_{j=x, j\ne i}^{z}{v}_{ji}\frac{{\sigma }_{j}-{\sigma }_{j0}}{{E}_{j}},$$

(9)

where ${\varepsilon }_{c\_i}$ is the apparent strain solely attributed to the mechanical compression with the subscript $i$ represents the $i$ -component stress; ${\sigma }_{i}$(${\sigma }_{j}$) ($i,j=x,y,z$) represents the i-component effective stress; ${E}_{i}$ (${E}_{j}$) ($i,j=x,y,z$) and ${v}_{ji}$ ($i=x,y,z$) are the directional Young’s moduli and Poisson’s ratios, respectively.

In an orthorhombic symmetry system, the relationships between the principal stresses and strains can be derived as (Liu et al. 2020a)

$$\left[ {\begin{array}{*{20}c} {\varepsilon _{{c\_x}} } \\ {\varepsilon _{{c\_y}} } \\ {\varepsilon _{{c\_z}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{1}{{E_{x} }}} & { - \frac{{\upsilon _{{yx}} }}{{E_{y} }}} & { - \frac{{\upsilon _{{zx}} }}{{E_{z} }}} \\ { - \frac{{\upsilon _{{xy}} }}{{E_{x} }}} & {\frac{1}{{E_{y} }}} & { - \frac{{\upsilon _{{zy}} }}{{E_{z} }}} \\ { - \frac{{\upsilon _{{xz}} }}{{E_{z} }}} & { - \frac{{\upsilon _{{yz}} }}{{E_{y} }}} & {\frac{1}{{E_{z} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\sigma _{x} } \\ {\sigma _{y} } \\ {\sigma _{z} } \\ \end{array} } \right].$$

(10)

Taking the derivative of Eq. (10) with respect to gas pressure, it gives the directional matrix compressibility

$$\left[ {\begin{array}{*{20}c} {\frac{{d\varepsilon _{{c\_x}} }}{{dp}}} \\ {\frac{{d\varepsilon _{{c\_y}} }}{{dp}}} \\ {\frac{{d\varepsilon _{{c\_z}} }}{{dp}}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{1}{{E_{x} }}} & { - \frac{{\upsilon _{{yx}} }}{{E_{y} }}} & { - \frac{{\upsilon _{{zx}} }}{{E_{z} }}} \\ { - \frac{{\upsilon _{{xy}} }}{{E_{x} }}} & {\frac{1}{{E_{y} }}} & { - \frac{{\upsilon _{{zy}} }}{{E_{z} }}} \\ { - \frac{{\upsilon _{{xz}} }}{{E_{z} }}} & { - \frac{{\upsilon _{{yz}} }}{{E_{y} }}} & {\frac{1}{{E_{z} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} { - 1} \\ { - 1} \\ { - 1} \\ \end{array} } \right].$$

(11)

From Eq. (11), it shows that the difference in directional swelling/shrinkage strain with gas injection/depletion under unconstrained condition is controlled by the intrinsic elastic properties, such as Young’s modulus and Poisson’s ratio.