1 Introduction

Clay-sulfate rocks can exhibit excessive swelling upon contact with water. The volume increase can threat the foundation of buildings, roads, and underground structures (Anagnostou et al. 2010; Taherdangkoo et al. 2022b; Alonso et al. 2022). In cases where the expansion is constrained, a high pressure is exerted on layers and structures above the swelling zone, leading to damage of structures through ground heave. An example of case histories from tunnels include the ingress of water into clay-sulfate rocks of the Gipskeuper formation during construction of the Hauenstein tunnel in the Jura Mountains in Switzerland, which led to heave of the invert and loading of the lining, eventually damaging the tunnel crown (Steiner 1993). Similarly, swelling of clay-sulfate rocks of the Gipskeuper formation exerted large pressures on the lining of other tunnels, e.g., Engelberg and Freudenstein tunnels, excavated in the Stuttgart metropolitan area in southern Germany, which resulted in rapid heave of the tunnel floor (Butscher et al. 2018; Wittke-Gattermann 2003).

Swelling of pure argillaceous rocks (clay without anhydrite) is mainly caused by osmotic water uptake and hydration of clay minerals. In clay-sulfate rocks, the initial volume increase due to clay swelling is followed by a slow swelling, attributed to the chemical transformation of anhydrite into gypsum, i.e. anhydrite dissolves in pore water and gypsum precipitates from the solution (Madsen and Müller-Vonmoos 1989; Narmandakh et al. 2023). The molar volume of gypsum is 61% higher than that of anhydrite (Butscher et al. 2016). Because pure clay swelling involves much lower swelling deformation and pressure than the swelling typically observed in clay-sulfate rocks, the gypsification of anhydrite is considered the main mechanism contributing to the swelling of clay-sulfate rocks (Wanninger 2020; Jarzyna et al. 2021).

The swelling of argillaceous rock is well understood in contrast to clay-sulfate rocks where considerable knowledge gaps still exist. A swelling law to quantify the swelling in terms of developing strain or stress as a function of time does not yet exist (Butscher et al. 2016). The strain–stress–time relation is unknown because limited swelling experiments have been performed on clay-sulfate rocks, and none of the experiments conducted under constant load conditions reached an equilibrium state. This is due to the fact that the gypsification of anhydrite is a slow process and the self-sealing of anhydrite, i.e., formation of gypsum coating on the anhydrite surface, can impede hydration of the rock. Therefore, swelling experiments are usually interrupted prematurely (Wanninger 2020; Butscher et al. 2016; Serafeimidis and Anagnostou 2013).

Grob (1992) established a semi-logarithmic relation between the swelling strain and stress, widely known as the “Grob’s law”, to describe the swelling behaviour of clay and clay-sulfate rocks. Kirschke (1987, 1996) suggested that the swelling cannot be described by a general swelling law. He observed the developing swelling strains of rock specimens from the Freudenstein tunnel using a free swelling test and an oedometer test. Kirschke (1996) proposed a time development of the stress–strain relation, where different curves of stress–strain in a diagram are adopted for each consecutive time period. Pimentel (2007a, 2007b) postulated that Grob’s law is not adequate for clay-sulfate rocks. He suggested a “tri-linear” relation to describe three different phases observed during swelling tests of rock specimens from the Freudenstein tunnel. The uncertainties of his analysis lie, however, in the fact that none of the tests reached an equilibrium state, and final stress and strain values of a single specimen were calculated via an extrapolation technique. Note that Kirschke (1996) and Pimentel (2007a) presented their swelling laws through graphical illustrations without providing a constitutive equation. Butscher et al. (2018) suggested that none of the swelling laws can be generally confirmed or rejected based on available test data. They rather questioned the existence of a universal swelling law that describes the swelling behaviour of clay-sulfate rocks.

Since clay-sulfate rock swelling is controlled by coupled thermal, hydraulic, mechanical and chemical processes, an understanding of the underlying coupled processes is essential to determine stress and strain development during the gypsification of anhydrite (Butscher et al. 2018, 2016). Few authors presented numerical models that considered chemical processes by relating the swelling strains to the mass change of gypsum through a so-called “bulking parameter”, which is unknown so far (Ramon and Alonso 2013; Ramon et al. 2017; Schweizer et al. 2018). The main deficiency of these chemo-mechanical models is their dependencies on many indeterminate factors, which makes the model’s establishment and calibration difficult. Furthermore, a knowledge gap exists with respect to the coupling between the hydraulic, mechanical, and chemical processes due to (1) a lack of long-term swelling tests that would deliver a database for the development of a coupled model, and (2) the fact that previous tests were terminated before reaching an equilibrium state (Butscher et al. 2018; Taherdangkoo et al. 2022a).

In this work, we developed a coupled hydro-mechanical model to reproduce the strain–time relation obtained from oedometer testing of a clay-sulfate rock specimen. The model presented here is the first model built to reproduce the outcomes of a swelling test on clay-sulfate rock specimens. We implemented a modified version of Grob’s law, which relates the swelling strain to changes of the volumetric water content of rock. Swelling stress and strain obtained from the laboratory testing (Pimentel 2003) were used for model calibration. We then performed a sensitivity analysis by changing values of important parameters, namely the maximum swelling pressure \({\sigma }_{max}^{sw}\), swelling parameter \(k\), and diffusion coefficient \(D\) to understand their influence on the long-term swelling behaviour of clay-sulfate rocks under oedometer testing conditions.

2 Laboratory Testing

The Freudenstein railway tunnel in Southwest Germany was constructed in the Triassic Grabfeld Formation (formerly Gipskeuper = “Gypsum Keuper”) between 1987 and 1991. Systematic multistage swelling tests on specimens from the tunnel were performed at the Karlsruhe Institute of Technology (formerly “University of Karlsruhe”) and the Technical University of Darmstadt. The campaign preformed arguably the longest and most elaborate experimental studies on swelling of clay-sulfate rocks. The self-designed oedometer apparatus used for performing the experiments on the specimens is shown in Fig. 1. The procedure of the experimental testing is briefly discussed here, and the detailed description can be found in Pimentel (2007a, 2003). Different researchers analysed the outcomes of these experiments, and published their respective interpretations (Kirschke 1987; Pimentel 2007a, 2003; Wittke 2003).

Fig. 1
figure 1

Apparatus used for swelling experiments on specimens collected from the Freudenstein tunnel (modified after Pimentel 2003)

Full size image

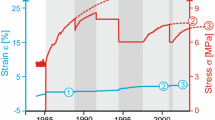
The testing apparatus was designed to tolerate a maximum load of 4 MPa, because it was expected that the specimens develop maximum swelling pressures of 2–3 MPa. The swelling process was initiated by watering the specimen under an expansion-constrained condition (no strain). The swelling stress reached around 4 MPa during this period “A”, which lasted for 3.3 years, and made several unloading cycles necessary to avoid damaging the apparatus. Thereafter, in the test period B, a constant load of 0.5 MPa was applied over a period of 5.1 years, leading to the development of approximately 30% swelling strain. Then, within period C, the expansion was constrained over 6 years. After this, a constant load of 2.6 MPa was applied over the specimen in the period D and a relatively slow swelling rate was observed. In the following period E, the expansion was again constrained (Pimentel 2003). However, a sharp drop in the recorded swelling stress can be seen at the beginning of the test period E (Fig. 2), which is be related to the technical problems. The total duration of the swelling test was around 20 years. The stress–time and strain–time values, plotted in Fig. 2, were extracted from Pimentel (2003) using WebPlotDigitizer (Drevon et al. 2017).

Fig. 2
figure 2

Measured stress and strain values from a swelling test on a clay-sulfate rock specimen (Pimentel 2003)

Full size image

Depending on the test period, a monotonic increase of either swelling stress or strain was observed over time. Since the gypsification of anhydrite is a relatively slow process and the complete transformation of anhydrite to gypsum may take years, neither loading nor constrained steps of the swelling experiment did reach an equilibrium state. Pimentel (2007a) used the indirect least square method to estimate swelling strain values at the equilibrium state. The extrapolation of the first loading step (period B) with the constant load of 0.5 MPa led to about 50% swelling strain at the equilibrium state (Pimentel 2007a).

3 Coupled Hydro-mechanical Model

3.1 General Approach

Firstly, we extracted experimental swelling data of an oedometer test performed on a clay-sulfate rock specimen (Fig. 2). We then developed a finite element HM model to reproduce the test outcomes, i.e. stress–time and strain–time relations. The HM model is developed based on a modified version of Grob’s law, which relates the swelling strain to changes in the volumetric water content of the rock (Eqs. 4 and 5). We calibrated the HM model using the total experimental data provided in Fig. 2. We then used the model to describe the long-term swelling behaviour of clay-sulfate rock specimen and determine the swelling strain value at the equilibrium state. Since long-term experimental swelling data are scarce, we also calibrated the HM model using limited experimental data, i.e., 12, 24, 36, and 48 months, to understand how much data is required for the calibration process. We finally ran a sensitivity analysis on influential parameters, namely, maximum swelling pressure, diffusivity coefficient, and swelling parameter to reveal their importance on the swelling phenomena (Fig. 3).

Fig. 3
figure 3

A general workflow for numerical modelling of the swelling behaviour of a clay-sulfate rock specimen under oedometer conditions

Full size image

3.2 Summary of Mathematical Background

The water uptake of clay-sulfate rocks is controlled by water consumption of clay and gypsification of the anhydrite fraction embedded within the clay. The latter is governed by transport processes such as convection of ions within pore water and diffusion driven by ionic concentration gradients in the water (Anagnostou et al. 2010; Wittke 2003; Gattermann et al. 2001). Therefore, the water uptake of clay-sulfate rocks can be described by a diffusion equation (Gattermann et al. 2001; Wittke 2014). We introduced a concentration term “numerical tracer” into the mass balance equation, which accounts for the volumetric water uptake of the rock. The use of a numerical tracer as a proxy for inflowing water that triggers swelling enables us to account for the circumstance that swelling does not occur prior to the ingress of water into the specimen (Schweizer et al. 2018). By doing so, we assume that the entire volume of inflowing water into the specimen is used for the gypsification of anhydrite and, thus, the consumption of water, in our model "the magnitude of the tracer concentration", is linearly related to the amount of gypsum in the specimen. The following set of equations describe the transport of the tracer in a porous media (Bear and Bachmat 2012):

$$\frac{{\partial_{c} }}{{\partial_{t} }} + \nabla \cdot \left( { - D^{eff} \nabla c} \right) = 0$$
(1)
$${D}^{eff}=D\frac{\phi }{\tau },$$
(2)

where \({D}^{eff}\) and \(D\) [m2 s−1] are the effective and free diffusion coefficients of the solute, respectively, and \(c\) [mol m−3] is the numerical tracer concentration acting as a proxy for the volumetric water uptake of the rock. ϕ [–] is the average porosity, and τ [–] is the tortuosity factor, estimated by the Bruggeman correlation (Bruggeman 1936). The diffusion coefficient is an important transport parameter that relates the diffusive flux to the gradient of concentration. The time delay caused by the gypsification of anhydrite can be taken into account in a HM model by using a low diffusion coefficient, which in turn reduces the transport of the tracer within the specimen. Note that a low diffusion coefficient is employed to account for the chemical processes and, thus, its value depends on the anhydrite and swellable clay content of the rock (Wittke 2014), and it is independent of the water content (Gattermann et al. 2001). Previously, Wittke (2014) employed a low diffusion coefficient, called the water uptake coefficient, equal to 1.5 × 10−12 m2 s−1 in his HM model to describe the water uptake of the unleached Gypsum Keuper.

The mechanical behaviour of the specimen was represented using a linear elastic model based on Hooke’s law complemented with swelling-induced strains (Wittke 2014):

$$\sigma ={\sigma }^{ex}+C:\left(\varepsilon -{\varepsilon }^{sw}\right),$$
(3)

where \(\sigma\) is the effective stress tensor, \({\sigma }^{ex}\) is an extra stress with contributions from initial stresses, \(C\) is the 4th order stiffness tensor of material properties, \(\varepsilon\) is the total strain tensor, and \({\varepsilon }^{sw}\) is the swelling strain tensor.

Grob (1992) proposed a semi-logarithmic relation between the swelling strain and stress for clay and clay-sulfate rocks developed based on the oedometric swelling experiments of Huder and Amberg (1970). Grob’s law assumes the swelling has reached an equilibrium state, i.e., the swelling stress and strain remain constant over time. The semi-logarithmic swelling law reads as (Grob 1992)

$${\varepsilon }^{sw}=k\left(1-log{\sigma }^{sw}/log{\sigma }_{max}^{sw}\right),$$
(4)

where \({\varepsilon }^{sw}\) is the swelling strain, k is the swelling constant independent of the water supply, \({\sigma }^{sw}\) is the swelling stress, and \({\sigma }_{max}^{sw}\) is the maximum swelling stress at the prevented strain. We used this often-applied semi-logarithmic relation but calculated the swelling stress using a swelling model (Eq. 5) often employed for clay and clay-sulfate rocks (Wittke 2014; Graupner et al. 2018; Schäfers et al. 2019). By doing so, we are able to include the time dependent swelling behaviour based on the water ingress, expressed as the “tracer concentration” in our model. Water inflow is a basic requirement for clay-sulfate rock swelling to occur and can be regarded as the trigger of the swelling process (Schweizer et al. 2018). Herein, the swelling stress is related to the maximum swelling pressure \({\sigma }_{max}^{sw}\) by changes in the tracer concentration as follows (Taherdangkoo et al. 2022b):

$${\sigma }^{sw}={\sigma }_{max}^{sw}\left(c-{c}_{i}\right),$$
(5)

where \(c\) and \({c}_{i}\) are the current and initial tracer concentrations, respectively. The initial water content of the specimen was assumed to be zero, thus the initial tracer concentration \({c}_{i}\) was set to zero in all of the simulations.

3.3 Modelling Workflow

The above equations were solved numerically using COMSOL Multiphysics 6.0, which is a finite element based software. We used “Transport of Diluted Species in Porous Media” and “Solid Mechanics” modules to model the transport of the numerical tracer in a deformable porous media. Equations 1–3 are available in COMSOL, and we further implemented Eqs. 4 and 5 into the “Solid Mechanics” module to take into account the additional strain caused by the swelling. The transport and mechanical equations were coupled through the concentration term “c”.

We built an axial symmetric 2.5D domain with a radius of 4 cm and a vertical extent of 4 cm (Fig. 4), being representative of cylindrical clay-sulfate rock specimens from the Freudenstein tunnel (the actual specimens have a radius of 4.055 cm and a height of 3.885 cm). The domain was assumed to be homogeneous and isotropic. The specimen was initially dry and the ingress of water into the specimen initiated the swelling. We used unstructured triangular mesh to discritize the model domain. The maximum and minimum element size were equal to 0.54 and 0.00263 mm, respectively. The resulting mesh consisted of 6042 domain elements and 204 boundary elements. Doubling the mesh refinement showed that results were not sensitive to mesh resolution.

Fig. 4
figure 4

General setup of the numerical model showing the model domain, including the mesh as well as boundary conditions

Full size image

The base-case simulation used to reproduce the stress and strain data obtained from Pimentel (2003) consists of five consecutive runs representing the test history described in Sect. 2. An initial 3.3 year run was used to simulate the constrained condition in the test period A, i.e., the top of the model domain was set to a constrained boundary condition (zero displacement). The output of this run was used as the initial condition of period B, where a constant load of 0.5 MPa was applied over the top boundary for 5.1 years. The top boundary was then switched to a constrained boundary again to simulate the subsequent 6 years (period C). To model the next test period (period D), 2.6 MPa load was applied on the top boundary and rock deformations were observed over 4 years. Thereafter, the top boundary was set to a constrained boundary condition and the development of swelling pressure was monitored for around 2.3 years. Note that the HM model does not take into account the errors occurred during the swelling test at the end of period A, i.e., fluctuations in the recorded swelling stresses, and beginning of period E, i.e., a sharp drop in the recorded swelling stresses (Fig. 2). The entire simulation period was 20.7 years.

3.4 Boundary Conditions and Parameter Values

The boundary conditions applied in the numerical modelling are similar to those of oedometer testing of clay-sulfate rocks. Pimentel (2007a) reported that the cylindrical specimen was cut on a lathe, fitted into a stiff metal ring, and mounted in the testing frame, which was then immersed in a water tank to trigger the swelling. The water inflow into the specimen occurred at the top and bottom boundaries, which was realized by the numerical tracer, and was expressed as a “concentration” term. Therefore, the top and bottom of the model domain were set to a fixed concentration equal to 1 mol m−3. The metal ring around the specimen did not allow water infiltration and, thus, the right side of the domain was set to a no flux boundary to prescribe zero flux across the boundary. The left side of the domain was set to an axial symmetry, resulting in a cylindrical 3D model based on a rectangular 2D section (“2.5D”). The stiff metal ring around the specimen prevented lateral (in 3D: radial) displacement of the rock, but allowed axial swelling in response to increase in water content. Therefore, the right and bottom sides were fixed in their normal direction (roller). The top boundary was set to either constrained or contraction free with a prescribed load (c.f., Sect. 2).

The base-case value of each parameter used for the numerical simulation and its range of variation in the sensitivity analysis are listed in Table 1. The maximum swelling pressure was set to 9.6 MPa, which is the value obtained by Pimentel (2003) and Wittke (2014) through extrapolating the outcomes of the swelling test. Since the specimen was immersed in pure water, the density of the tracer \(c\) infiltrating the specimen was set to 1000 kg m−3. The initial value of the diffusion coefficient \(D\) was set to 1.5 × 10−12 m2 s−1 (Wittke 2014), and it was then updated during the calibration process. Additionally, the swelling parameter \(k\) was selected as calibrated parameter.

Table 1 Parameter values and ranges of variation used for the parametric study. The values of the diffusion coefficient and the swelling parameter were obtained by the calibration process
Full size table

We used the base-case model to (1) reproduce the stress–time and strain–time behaviour of the specimen obtained during the experimental testing, and (2) observe the long-term swelling behaviour of the specimen under the test period B. We then designed a sensitivity analysis by varying the values of swelling parameters. We applied the one-at-a-time (OAT) method to analyse the influence of each chosen parameter separately, and reveal its independent effect on our model.

The values of \({\sigma }_{max}^{sw}\), D, and k were changed in the sensitivity analysis as listed in Table 1; and the evolution of the strain with time was recorded as the parameter of interest. The ranges of values of \({\sigma }_{max}^{sw}\) and k are not limited to samples taken from the Freudenstein tunnel (Alonso and Ramon 2013; Butscher et al. 2018, 2011; Schädlich et al. 2013; Wittke 2003). The water diffusion coefficients are typically in the range of 10–10 to 10–9 m2 s−1. Wittke (2014) suggested a low diffusion coefficient of 1.5 × 10−12 m2 s−1 to describe the water uptake of the unleached Gypsum Keuper. Herein, the value of D was varied between 10−12 and 10–9 m2 s−1. The findings of the sensitivity analysis provide insights into the importance of a wide range of possible field conditions on the swelling behaviour of clay-sulfate rocks under oedometer testing.

4 Results and Discussion

4.1 Hydro-mechanical Modelling

The swelling of clay-sulfate rocks is delayed by the gypsification of anhydrite mineral embedded within the rock. We took into account this time delay by choosing a relatively low diffusion coefficient in the mass balance equation, which in turn reduced the infiltration of the numerical tracer within the specimen. We ran several numerical simulations to obtain the optimal values of the diffusion coefficient \(D\) and swelling parameter k. The HM model was calibrated using strain–time data obtained from the swelling test of Pimentel (2003). Accordingly, the diffusion coefficient was set to 3 × 10−12 m2 s−1 and the swelling parameter was set to 0.6.

The testing periods depicted in Fig. 2 were based on either constrained or load conditions. The deformation was constrained in the test period A leading to the development of swelling pressure within the rock specimen. The HM model captures the rock behaviour under the constrained condition generally well, with simulated swelling pressures being only slightly higher than measured (Fig. 5).

Fig. 5
figure 5

Comparing the simulated (blue lines) values with the measured values (red lines) obtained from Pimentel (2003). The top figure depicts the changes of swelling strains with time during the oedometer testing, while the bottom figure shows the changes of stress with time

Full size image

The strain–time behaviour observed in period B shows a systematic overestimation of strain by the model. The deviations, i.e. difference between experimental and modelling values, are higher at early simulation times, which is due to the strong dependency of the swelling on changes in the tracer concentration, i.e., volumetric water content. The modelling deviations decrease when the strain–time curve approaches a plateau. The same trend was observed under subsequent testing periods. Overall, the HM model captures the swelling behaviour, i.e. development of swelling stress and strain with time, of clay-sulfate rocks under oedometer testing conditions with an accuracy that would be sufficient for the planning of geotechnical projects.

Figures 6 and 7 display the spatial distributions of the tracer within the specimen and the swelling deformations at the end of period B. As discussed, the concentration of the numerical tracer in our HM model corresponds to the degree of swelling consisting of chemical (transformation of anhydrite into gypsum) and mechanical swellings (water uptake of clay minerals). In the upper/lowermost sections of the specimen, the tracer concentration is higher, implicating that the swelling proceeds faster at these locations comparing to the centre of the specimen. The swelling is completed once the tracer concentration reaches the threshold value of 1 mol m−3. Noted that the complete gypsification of anhydrite is only possible should clay and anhydrite fractions be adequately distributed within the rock mass (Butscher et al. 2018). Figure 7 shows that the modelled swelling deformation at the end of period B equals to 12 mm, i.e., 30% of the initial specimen’s thickness (4 cm), which is close to the value obtained from the experimental testing (XY %).

Fig. 6
figure 6

The concentration distribution of the numerical tracer representing the volumetric water inflow within the specimen (left), and along the Z axis (right) at the end of simulation period B

Full size image
Fig. 7
figure 7

Displacement profile of the specimen (left), and along the Z axis (right) at the end of simulation period B

Full size image

A vertical load of 2.6 MPa was applied over the specimen during the test period D, which led to the development of much lower strains (2.15%) compared to period B (30%), where the load was 0.5 MPa. The small swelling strains observed during period D were also due to the fact that this period was started around 15 years after watering the specimen, thus most of anhydrite embedded in the specimen has already been transformed into gypsum. The comparison of loading periods shows that the HM model can effectively capture the influence of a vertical load on the swelling behaviour of the specimen.

The analysis shows that it is possible to account for the swelling processes in the presented HM model by adjusting the diffusion coefficient in the transport equation, which controls infiltration of the tracer in the rock matrix. Although the modelling approach is sufficiently accurate from a practical point of view, there are also shortcomings, attributed to two main reasons: (1) the swelling is governed by coupled hydraulic, chemical and mechanical processes that hardly can be reflected by a general constitutive law, such as Grob’s law used in the model. The results of Figure 5, in particular the comparison of loading periods, suggest that a more complex constitutive law is needed to describe the swelling behaviour of clay-sulfate rocks. However, the relationship between the swelling pressure (stress) and strain remains unknown (Butscher et al. 2018; Wanninger 2020). (2) The swelling potential and swelling rate of clay-sulfate rocks also depends on other factors including temperature, petrographic features (mineralogical composition, sedimentary and tectonic structures), advective flow, and chemical composition of the groundwater (Butscher et al. 2018; Rauh 2007). Therefore, a coupled thermo-hydro-mechanical-chemical (HMC) model that considers the underlying processes and factors is needed to better describe the swelling phenomena. Although other researchers, e.g., Ramon et al. (2017), have already developed complex HMC models, their models failed to accurately reproduce the observed deformations caused by the swelling because knowledge about the coupling of hydro-mechanical processes to the chemical processes is still limited (Wanninger 2020; Butscher et al. 2016).

Both the constrained and loading periods in Pimentel (2003) experiments were terminated before reaching an equilibrium state due to technical limitations and the long duration of the experiments. Therefore, Pimentel (2007a) extrapolated the strain values of the loading period B to obtain the strain value at the equilibrium. Herein, we used our HM model to describe the long-term behaviour of the specimen under the same loading condition, i.e. test period B. The concentration of the tracer within the specimen after 30 years (Fig. 8) equals 1 mol/m3 indicating that the swelling is completed within the model domain, and watering the specimen would no longer contribute to swelling deformations. The swelling deformation at the equilibrium state is 18 mm (Fig. 9). Using the calibrated model, the development of the swelling strain after the termination of the experiment until reaching equilibrium conditions can be simulated based on hydro-mechanical processes, which may lead to better estimate of the final swelling deformation compared to a purely mathematical interpolation.

Fig. 8
figure 8

The concentration distribution of the numerical tracer (corresponding to volumetric water inflow) within the specimen (left), and along the Z axis (right) after 30 years of simulation, based on the loading condition of period B of Pimentel (2003) experiments

Full size image
Fig. 9
figure 9

The displacement profile of the specimen (left), and along the Z axis (right), after 30 years of simulation, based on the loading condition of period B of Pimentel (2003) experiments

Full size image

The modelled strain–time values fit to Pimentel (2007a) extrapolations (Fig. 10). The strain–time curve approached a plateau after 15 years of simulations. The swelling strain increased only 1.26% in the final 10 years of simulations. The swelling strain reached 44.53% after 30 years. Pimentel (2007a) reported approximately 50% swelling strain at the equilibrium, which he obtained based on his own swelling law. Note that Pimentel (2007a) proposed his swelling law through a graph, and did not provide a constitutive equation. The difference between our modelled swelling strain at equilibrium (44.53%) and the suggested value (50%) is 5.47%, which is close and may be due to the different employed swelling laws.

Fig. 10
figure 10

Comparing the simulated swelling strain (blue lines) with the measured values (red circles) obtained from the loading period B from Pimentel (2003), and extrapolated values (yellow circles) from Pimentel (2007a)

Full size image

The HM model presented here was calibrated against the long-term swelling experimental data. However, such long-term data are rather unique and swelling tests are usually terminated much earlier due to various reasons. For example, research projects are usually funded for around 3 years making it difficult or in some cases impossible to continue the experiments; or time constraints of an ongoing geotechnical project make earlier results necessary. In this context, one might wonder whether it is possible to predict the long-term swelling behaviour of clay-sulfate rocks based on a HM model that was calibrated using only short-term experimental data (e.g., several months to few years). To answer the question, which could be interesting for scientists and engineers in the field of geotechnics, we used limited strain–time data, i.e. only the data from the first year of the loading period B, to calibrate the HM model. The results provide insights about the efficiency of the modelling approach and the minimum experimental data required to properly calibrate the model and make predictions about the final equilibrium stage.

Figure 11 shows that the HM model, calibrated with swelling data from only 1 year, is well fitted to the experimental strain data during this period. However, since only the first 12 months of the strain–time experimental data were used for calibrating the model, it was not possible to accurately reproduce the long-term strain–time relation observed during the experimental testing. The swelling strain value obtained at the end of the simulation (30 years) is 28.75%, around 36.85% lower than the value of the calibrated HM model (XY %), depicted in Fig. 10. Although short-term swelling tests cannot be used to accurately determine the long-term behaviour of the clay-sulfate rocks, the presented HM model can at least provide an understanding of the initial swelling behaviour needed for the development of meaningful countermeasures to the swelling problem.

Fig. 11
figure 11

The simulated swelling strain (blue line) with the experimental values (red line) obtained from the loading period B from Pimentel (2003). Only the first twelve months strain–time data (red circles) were used to calibrate the HM model

Full size image

Figure 12 shows that the accuracy of the model to estimate the swelling strain–time relation increases by using more experimental data for the calibration process. The swelling strain at the equilibrium equals 39.51% when the HM model is calibrated using 24 months experimental data. The final strain value (39.51%) is 13.22% lower than the HM model prediction with the complete 5.1 years data employed for the calibration process. The analysis shows that a minimum of 24 months strain–time data is needed to calibrate the presented HM model, and predict the long-term swelling behaviour of clay-sulfate rocks under oedometer conditions. The difference between final strain values obtained from the HM model calibrated using 36 and 48 months experimental data is minor, i.e. only 2.56%. From the results presented in Figs. 11 and 12, we can conclude that at least 24 months strain–time experimental data is required for the model calibration, and the HM model can provide even more accurate predictions when calibrated with 36 months experimental data.

Fig. 12
figure 12

The simulated swelling strain (solid lines) with the experimental values (red circles) obtained from the loading period B from Pimentel (2003). Different sets of strain–time experimental data (i.e. data from the first 2, 3 and 4 years of the long-term experiment) were used to calibrate the HM model

Full size image

4.2 Sensitivity Analysis

We used the calibrated HM model as the base case, and altered the value of the parameter of interest over a wide range to expose its influence on the swelling. The sensitivity analysis indicates that swelling strains are notably sensitive to all swelling parameters having different effects on the induced strains (Fig. 13). Results indicate an increase of swelling strains with the maximum swelling pressure. As shown in Eq. 4, a semi-logarithmic relation exists between the swelling strain and stress. Our analysis shows that even a low maximum swelling pressure (\({\sigma }_{max}^{sw}\)=3 MPa) leads to around 20% swelling strain at the equilibrium, showing the amount of damage that swelling can potentially impose to infrastructures.

Fig. 13
figure 13

Sensitivity analysis of swelling parameters, in which the calibrated HM model was used as the base case. The strain versus time is plotted, varying the maximum swelling pressure, diffusivity coefficient, and swelling parameter. Gray areas represent possible variations in the strain–time relation by changing values of swelling parameters

Full size image

The swelling parameter k in the base model was calibrated according to the measured strain–time curve (Fig. 2). We varied k over the range of 0.1–1.2 to provide a deeper understanding on the influence of this parameter. The swelling increased monotonically with increasing the value of k, indicating its significance on the calculated swelling strains (c.f., Eq. 4). The diffusion coefficient directly influences the diffusive transport of the tracer within the specimen and, thus, it controls the time needed to complete the swelling process. The value of the diffusion coefficient does not influence the magnitude of swelling. For the case of a high diffusion coefficient (10–9 m2 s−1), the fast transport of the tracer within the specimen resulted in the swelling to be completed in only 30 days. In contrast, the swelling process took nearly 80 years for D = 10–12 m2 s−1. This shows that the diffusion coefficient is an important parameter, which needs to be properly adjusted during the calibration process.

5 Conclusions

The following conclusions can be drawn from the study:

  1. 1.

    The swelling process is delayed by gypsification of anhydrite embedded within the rock. This time delay was taken into account in our HM model by adjusting the value of the diffusion coefficient in the transport equation, which in turn reduced the tracer infiltration within the specimen. The effectiveness of the modelling approach employed here is proved here to be adequate enough, as the modelled stress and strain values are close to the measured ones. Therefore, the modelling approach can be applied in future studies to describe the swelling behaviour of unleached clay-sulfate rock specimens.

  2. 2.

    Comparing the modelled and experimental swelling data of Pimentel (2003) showed that the modelling approach is sufficiently accurate. However, the HM approach is associated with minor deficiencies leading to slight overestimations of swelling strain values during loading periods. The strain-time behaviour cannot be accurately reproduced due to (1) strong dependency of the swelling model on the supply of water and (2) employing a semi-logarithmic constitutive model, which cannot describe the complex stress–strain–time behaviour occurring during the swelling.

  3. 3.

    The HM model can capture the swelling behaviour of the specimen should sufficient experimental data be employed for the calibration process. Although employing 12 months strain–time experimental data to calibrate the model led to 36.85% error, the results can still provide valuable insights into the initial swelling deformation, which can be a major help in designing geotechnical counter measures to the problem.

  4. 4.

    The findings show that at least 24 months experimental data is needed to properly calibrate the HM model. In this case, the swelling strain at the equilibrium is 13.22% lower than the case with the complete 5.1 years data used for the calibration process.