Stability Evaluation of Rock Slopes with Cracks Using Limit Analysis

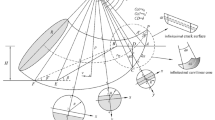
Abstract

Cracks are commonplace on slope crests. It has been found that cracks have a significant influence on the stability of slopes in soil with strength governed by a linear criterion; rock slopes with cracks are analyzed in this study using a nonlinear rock model. The kinematic approach of limit analysis is utilized because it straightforwardly considers open cracks and provides rigorous bounds to limit loads. The depth range of a vertical crack in the Hoek–Brown rock mass is derived for dry and wet crack boundary conditions. The stability number and factor of safety are provided by assuming the most adverse crack location, and the presence of water is considered as pore-water pressure acting on the boundaries of the crack and failure surface. When the inclination angle of the rock slope is less than 60°, the influence of cracks on the slope stability is negligible (< 5%). However, it increases to 33.9% when the slope angle is increased to 85°. Based on the critical collapse mechanism, the most adverse vertical cracks appear to be deeper in steeper slopes. Examinations of stress vectors on rupture surfaces and principal stresses indicate that the tensile stress components are eliminated by the presence of cracks, whereas the compressive stresses are maintained as they are. Cracks introduced in rock slopes cause the removal of tension in slopes without adjusting the strength envelope to eliminate the tensile strength of rock.

Highlights

• Stability analysis of rock slopes with cracks are performed by means of parametric form of Hoek–Brown failure criterion.

• The range of vertical crack depth in rock mass is investigated based on dry and wet crack boundary conditions.

• Most adverse crack depths and locations are identified for various slope geometry and rock properties.

• Introduced cracks in rock slopes eliminate tensile stress on failure surfaces.

Appendices

Appendix A

See Eqs. (34–44).

The normal and shear stress components on the Hoek–Brown strength envelope can be written as a function of σ₃ (Balmer 1952; Kumar 1998):

$$\sigma_{n} (\sigma_{3} ) = \sigma_{3} + \frac{{\sigma_{ci} \left( {m_{b} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{a} }}{{2 + am_{b} \left( {m_{b} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{a - 1} }},$$

(34)

$$\tau (\sigma_{3} ) = \frac{{\sigma_{ci} \left( {m_{b} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{a} }}{{2 + am_{b} \left( {m_{b} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{a - 1} }}\sqrt {1 + am_{b} \left( {m_{b} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{a - 1} } .$$

(35)

Appendix B

From the geometric relations in Fig. 3, the angle θ_d in Eq. (17) can be calculated as

$$\theta_{d} = \arctan \frac{{r_{a} \sin \theta_{a} - H}}{{r_{a} \cos \theta_{a} + H\cot \beta }},$$

(36)

where θ_a = θ_n and r_a = r_n for toe mechanisms (point B_n = A). For below-toe failure mechanisms, r_a is calculated by

$$r_{a} = r_{n} \frac{{\sin \theta_{n} }}{{\sin \theta_{a} }},$$

(37)

with θ_a being an additional variable in the optimization procedure (in this case, the total number of total variables is 2n + 2). The relationship between the height of the slope H and radius r₀ is given by

$$H = r_{\textit0} {\kern 1pt} \left( {e^{{\sum\limits_{j = 1}^{n} {\eta_{j} \tan \delta_{j} } }} \sin \theta_{n} - \sin \theta_{\textit0} } \right).$$

(38)

This indicates that one of the two parameters needs to be predefined as a scale parameter of the problem at the beginning of computation. Distance z in Fig. 4a can be calculated from the following expressions:

$$z = \left\{ \begin{gathered} r\sin \theta - r_{w} \sin \theta_{w} ,\;\;\;\;\;\;\,\,\,\;\,\,\,\,\,\,\,\,\;\;\;\;\;{\kern 1pt} {\kern 1pt} \theta_{w} < \theta \le \theta_{1} \hfill \\ \left( {r - r_{s} } \right)\sin \theta ,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,\,\,\,\,\,\,\,\;\;\;\;\;{\kern 1pt} {\kern 1pt} \theta_{1} < \theta \le \theta_{D*} \hfill \\ \left( {r - r_{s} } \right)\left( {\sin \theta + \cos \theta \tan \beta } \right)\;,\;\;\;\;\theta_{D*} < \theta \le \,\,\theta_{A*} \, \hfill \\ \left( {r - r_{s} } \right)\sin \theta \;,\;\;\;\;\;\;\;\;\;\;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\;\;\theta_{A*} < \theta \le \,\,\theta_{n} \,\,\,({{\rm below toe only}}) \hfill \\ \end{gathered} \right.,$$

(39)

where θ_D* and θ_A* are angular coordinates of points D^* and A^*, respectively.

Appendix C

Hoek et al. (2002) derived the following strength parameters of substituted linear criterion, the so-called equivalent Mohr–Coulomb parameters ϕ_b and c_b, from the Hoek–Brown criterion, by balancing the areas between the linear and Hoek–Brown fittings in the principal stress plane in the range from − σ_t to σ_3max.

$$\phi_{b} = \sin^{ - 1} \left[ {\frac{{6am_{b} \left( {s + m_{b} \sigma_{3n} } \right)^{a - 1} }}{{2\left( {1 + a} \right)\left( {2 + a} \right) + 6am_{b} \left( {s + m_{b} \sigma_{3n} } \right)^{a - 1} }}} \right],$$

(40)

$$c_{b} = \frac{{\sigma_{ci} \left[ {\left( {1 + 2a} \right)s + \left( {1 - a} \right)m_{b} \sigma_{3n} } \right]\left( {s + m_{b} \sigma_{3n} } \right)^{a - 1} }}{{\left( {1 + a} \right)\left( {2 + a} \right)\sqrt {1 + \frac{{6am_{b} \left( {s + m_{b} \sigma_{3n} } \right)^{a - 1} }}{{\left( {1 + a} \right)\left( {2 + a} \right)}}} }},$$

(41)

where

$$\sigma_{3n} = \frac{{\sigma_{3 max } }}{{\sigma_{ci} }},$$

(42)

in which σ_3max is the maximum stress used in the fitting process. The determination of this upper limit is crucial because different structures are subjected to different stress ranges. Considering a wide range of slope geometries and rock properties, the following guideline was suggested for slope stability problems (Hoek et al. 2002).

$$\frac{{\sigma_{3max } }}{{\sigma_{{{{ cm}}}} }} = 0.72\left( {\frac{{\sigma_{{{{ cm}}}} }}{\gamma H}} \right)^{ - 0.91} ,$$

(43)

where σ_cm is the rock mass strength. In the stress range of − σ_t < σ₃ < σ_ci /4, σ_cm is found to be

$$\sigma_{{{{ cm}}}} = \sigma_{{{{ ci}}}} \frac{{\left[ {m_{b} + 4s - a\left( {m_{b} - 8s} \right)} \right]\left( {m_{b} /4 + s} \right)^{a - 1} }}{{2\left( {1 + a} \right)\left( {2 + a} \right)}}.$$

(44)