1 Introduction and Background

Tunnels excavated in anhydritic formations are known to experience high swelling stresses against the lining. Case histories of tunnels built in Triassic Keuper rocks of Central Europe, mainly in Switzerland and Southern Germany have been reported by Einstein (1996), Kovári et al. (1988), Kovári and Vogelhuber (2014), Steiner and Schwalt (2019), Steiner (1993, 2020), Wittke-Gatterman and Wittke (2004), Wittke (2006, 2014), Wittke et al. (2017), Anagnostou (2007), Alonso et al. (2013), Serafeimidis and Anagnostou (2014), Anagnostou et al. (2015) and Serafeimidis et al. (2014). Severe heaving and swelling pressures are found also in tunnelling Tertiary Eocene anhydrite claystones (Alonso et al. 2013). Other types of infrastructures built in the same geological formations are severely impaired due to the development of volumetric swelling of the anhydritic rock in depth, under the position of their foundations. This is the case of the uplifts of the historic centres of the villages of Staufen in Germany (Sass and Burbaum 2010; Ruch and Wirsing 2013; Schweizer et al. 2019) and Lochviller in France, a building near Barcelona in Spain (Ramon and Alonso 2018) and the heave of Pont de Candí bridge, a large railway viaduct founded, by deep piles, on anhydritic clayey rocks (Alonso and Ramon 2013; Ramon and Alonso 2013; Alonso et al. 2015).

A simple procedure to introduce swelling phenomena into the calculation of design pressures against linings relies in the determination of a “swelling law”, which relates swelling pressure and deformation under one-dimensional conditions and lateral confinement. Then, under certain assumptions of the expected radial deformations of the rock induced by the tunnel excavation, a “swelling characteristic curve” may be found (Kovári et al. 1988) which serves to determine the equilibrium stress against a lining of given radial stiffness. Because swelling develops over time, characteristic lines can be thought as time dependent, and therefore the equilibrium swelling pressure against linings increases with time. In this procedure, the swelling pressure is assumed to act against the invert lining. The swelling pressure is often assumed to be radial but Amstad and Kovári (2001) indicate that it may be also vertical, rather than radial, depending on the lining-rock interface. Anagnostou and Pimentel (2020) and Pimentel et al (2020) mention two cases of swelling pressures acting against sidewalls.

Rock expansions, expressed in terms of stress state and time by a suitable constitutive model, may be introduced as imposed external deformations in numerical analysis, typically based on a Finite Element model. Several authors (Gysel 1987; Fröhlich 1986; Anagnostou 1992; Heidkamp and Katz 2002, 2004; Barla 2008; Kramer and Moore 2005) followed this approach to calculate contact swelling stresses as well as the structural response of lining. Kovári and Vogelhuber (2014), in a back-calculation of the invert design loads of five tunnels, by means of an elastic finite element model, assumed plane strain conditions and uniform radial swelling pressures. Some of the mentioned authors included procedures considering coupled flow-deformation, time and anisotropic characteristics of the rock mass.

A further step in the development of swelling calculation procedures is the addition of water flow effects, which depend on rock permeability that is, in turn, controlled by the aperture of discontinuities (Anagnostou 1993, 1995; Wittke-Gattermann 1998; Wittke 2003, 2014; Wahlen and Wittke 2009; Schädlich et al. 2013). Butscher et al. (2011) analysed the hydrogeological effects of the change in flow regimes around the tunnels.

Time and stress-dependent “point” swelling strains, described by a direct interpretation of laboratory tests, may be substituted by a representation of the fundamental mechanisms explaining the heave of anhydritic formations. In fact, the observed swelling is a direct consequence of the precipitations of gypsum from supersaturated solutions of calcium sulphate in water (Alonso et al. 2013; Ramon and Alonso 2014). The presence of anhydrite explains the supersaturation conditions. Gypsum precipitation may be expressed in terms of solute concentration, pressure, temperature and other rock physical characteristics, such as the specific surface of gypsum and anhydrite. Then, a transport balance equation of dissolved sulphate provides the time development of dissolution/precipitation and the associated volumetric strains, which take place in fractures (Ramon and Alonso 2018; Ramon et al. 2017).

It is reasonable to expect that the increased attention to the fundamental phenomena leads to more accurate predictions of field observations. However, this is not, in general, the case. Swelling contact pressures between lining and rock, registered by load cells, exhibit wide ranges even when comparing results for closely spaced measuring points. All the calculation procedures outlined adopt homogeneity assumptions, which do not match field data. The method based on a “characteristic” displacement–pressure curve is an extreme case of homogeneity. In addition, working with average parameters in plain strain finite element analysis disregards variability in the direction of the tunnel axis. Even in a cross section, a reasonable homogeneity is seldom observed in practice. The implications for the structural design of linings are large, as shown below.

Field heterogeneity is explained by a number of aspects directly linked with the spatial distribution of anhydrite and gypsum within the involved rock and with structural features such as the pattern of discontinuities, either original or induced by the tunnel excavation unloading. Tectonic events and the associated pre-shearing of the rock-mass modify to a large extent regular sedimentary structures. Since the precipitation of gypsum requires the “space” offered by open fissures, the geometry of shear and tensile cracks determines the direction of swelling pressures. Overall, the heterogeneity of swelling deformations and stresses becomes a complex problem difficult to define “a priori”, at the design stage.

This paper is a contribution to interpret this complexity and its relevance in the design of tunnel linings. The discussion relies on the data provided by the comprehensive field instrumentations installed in the lining of the 2 km long Lilla tunnel and the observations available in a period extending from 2005 to 2011. This tunnel (AVE Lilla Tunnel) belongs to the high-speed railway line connecting Madrid and Barcelona. The observations include swelling pressures at the lining-rock interface, strains measured in the lining reinforcement bars and circumferential stresses in the vicinity of the neutral position of the lining invert and vault (Alonso et al. 2013).

The next two sections present observations and monitoring data concerning the heterogeneity of the Lilla anhydritic claystone. Maximum swelling pressures, already stabilized, against the rigid lining of Lilla tunnel ranged from a small fraction of MPa to 7 MPa. However, the stresses in the reinforcement exhibited a small variability. The idea to investigate the heterogeneity of swelling pressure, both its intensity and spatial distribution, was to interpret the large set of lining structural data as a gigantic transducer capable of giving information on the rock-lining interaction by back-analysis techniques. The results are compared with the original design hypotheses.

2 Heterogeneity of Anhydritic Claystones

Table 1, taken from Alonso et al (2013), provides the main mineralogical and geotechnical indices of the undisturbed Lilla claystone. The table shows the range of parameters measured in cores recovered in borings 15 m long drilled from the initially built flat slab of the tunnel. The tunnel cover was 80–100 m for most of its length.

Table 1 Mineralogy and geotechnical indices of undisturbed Lilla claystone
Full size table

Non-expansive clay minerals dominate the composition of the claystone. Anhydrite content is relatively small compared with other central Alps tunnels excavated in the Triassic-Keuper rocks. The Gypsum content was also particularly low. The claystone has high unconfined strength, a low porosity and a low water content (1–2%) when undisturbed. Plasticity of the clay matrix is low: wL = 23–25%; PI = 8%.

Figure 1 shows a long crack infilled with precipitated gypsum and additional cracks as a result of desiccation. The scattered whitish spots are gypsum nodules. Anhydrite is more difficult to distinguish visually.

Fig. 1
figure 1

Core of Lilla claystone recovered from a borehole drilled from tunnel floor. (Pineda 2014)

Full size image

Gypsum crystals precipitate in cracks. This is shown in Fig. 2. A small monoclinic crystal seems to grow in a direction parallel to the plane of the crack opened in the claystone. Often the gypsum crystals grow in a direction perpendicular to fissures. This is shown in Fig. 3, which shows a polished cross section of a core (Oldecop and Alonso 2012) that experienced a water flow, for just 2 days, from saturated conditions at one end to the relative humidity conditions prevailing in the Laboratory, at the opposite face. The photograph illustrates the complex structure of the Lilla claystone, the development of fibrous gypsum in discontinuities and the damage (opening) progressing in a diagonal fissure, almost unnoticed at the start of the test.

Fig. 2
figure 2

Needles of gypsum crystals growing in a discontinuity of Lilla claystone

Full size image
Fig. 3
figure 3

Polished cross section of a core of Lilla claystone after two days of testing under a flow-evaporation test (Oldecop and Alonso 2012)

Full size image

Lilla claystone experienced an intense Alpine tectonic activity because of its proximity to a Mesozoic mountain range (Alonso et al. 2013). Figure 4 shows a polished and irregular tectonic shearing surface which is a candidate to receive gypsum precipitates if it becomes open (because of the excavation-induced unloading of a tunnel construction), water flow is available and the presence of anhydrite leads to supersaturation conditions.

Fig. 4
figure 4

Surface of a slickenside found in a sample recovered from a borehole drilled from Lilla tunnel floor

Full size image

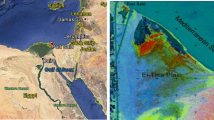
Four to five families o discontinuities were identified in Lilla claystone. Joints are generally smooth or moderately rough (JCR = 2–6). Their spacing ranges from 30 to 60 cm. The observed length of discontinuities, observed in exposed front faces is usually close to 1 m. Maximum observed lengths are around 3 m. At the scale of the tunnel diameter the rock mass is reasonably homogeneous. Lilla Eocene claystone suffered a high tectonic activity. This is shown in Fig. 5 that indicates the position of Lilla tunnel and its proximity to the folded Triassic strata.

Fig. 5
figure 5

Geological profiles in transversal and longitudinal direction of Lilla tunnel

Full size image

The initial tunnel excavation (horseshoe section) was completed in February 2002. The drainage system and the concrete flat slab were built in May–September 2002. First swelling symptoms were observed in September 2002. The additional excavation and a new circular highly reinforced lining were performed during the period July 2004–August 2005. The tunnel experienced scattered entrance of dripping water during excavation. A water level close to the tunnel floor was observed in boreholes located in a 600 m stretch immediate to the North Portal. This length coincides with the fastest heave rate. Alonso et al (2013) provide additional details.

Soon after the construction of the original design of the Lilla tunnel, the flat slab looked as shown in Fig. 6. Heave spots deform the slab in a chaotic pattern, which is far from a regular geometry. The heave reflects the heterogeneous nature of the rock as well as the complexity of the swelling mechanism.

Fig. 6
figure 6

Photograph of Lilla flat slab a few months after construction showing heave spots

Full size image

Under low confining stress, anhydrite is absent and gypsum crystallizes in a variety of facies. Figures 7, 8 and 9 show three examples from the Iberian Peninsula (Salvany 1989). Figure 7 shows fibrous gypsum filling discontinuities from a Tertiary Miocene claystone formation in Navarra province. The pattern suggests an advanced stage of gypsum precipitation and rock degradation, which reminds some of the structures described for Lilla claystone. Figure 8 is structurally similar to Fig. 7 but this time the rock is Keuper marl from the Pyrenees. Figure 9 shows a different structure. Gypsum has grown in nodules, which probably occupy a previous arrangement of anhydrite nodules. The rock in this case belongs also to a Keuper substratum (Serra de Prades, Tarragona) not far from the location of Lilla tunnel. One may expect different swelling deformations from the original anhydritic formations of Figs. 7, 8 or 9 if a swelling mechanism is triggered.

Fig. 7
figure 7

Veins of Miocene fibrous gypsum, Ablitas, Navarra, Spain (Salvany 1989)

Full size image
Fig. 8
figure 8

Triassic (Keuper) fibrous gypsum from the Spanish Pyrenees Courtesy of Dr J. M. Salvany

Full size image
Fig. 9
figure 9

Nodular gypsum, Keuper, Serra de Prades, Tarragona, Spain. Courtesy of Dr J. M. Salvany

Full size image

A flat parallel and uniform series of alternating layers of anhydrite-laden rock and other lithologies may lead to relatively uniform expansion of a horizontal tunnel excavated in such a structure. This was the case described by Wittke-Gatterman and Wittke (2004). However, in the case of Lilla and other anhydritic claystones characterized by a different original “fabric” of the anhydrite distribution and a subsequent tectonic activity, the strong heterogeneity of expected swelling is probably the rule.

3 Variability of Recorded Stresses in AVE Lilla Tunnel

The serious heave of the flat slab detected in the original design of Lilla tunnel led to select a 300 m long stretch of the tunnel to excavate and build a curved invert to install several monitoring sections at the concrete-rock interface to measure the magnitude of swelling pressures. Figure 10 shows the invert design, the load cell measurements and the recorded displacements in a limited time interval (January–December 2003). Despite this short interval, the recorded swelling pressure reached high pressures (4–5 MPa) in a few load cells at the end of the measuring period. However, most of the 45 pressure cells recorded relatively low pressures in the range 0–2 MPa. Errors in load cell measurements are explained by uneven excavation contours and the presence of joints and cracks. Nevertheless, it is believed that the long-term swelling stresses analysed here are representative because the strong swelling mechanism is capable of compensating gaps and irregularities. In a given cross section, the three cells were located at a 4 m interval. In a longitudinal direction, the measuring sections were spaced 18–20 m. Figure 10 indicates that the variability of pressures in two directions (tunnel axis and the perpendicular plane) is approximately the same. This preliminary testing effort provided the first information on the expected swelling pressures against the finally adopted stiff circular lining, described below.

Fig. 10
figure 10

Recorded total radial pressures and heave at tunnel floor of Lilla tunnel along a testing portion of the tunnel, which was modified by building a curved invert with the purpose of investigating the intensity of swelling phenomena. December 2003 (Alonso et al. 2013)

Full size image

The design criteria for the circular lining was to specify a uniform high pressure (4.50 MPa) acting on a given length of the invert and a significantly lower value (1.5 MPa) against vault and abutments.

It is interesting to find the response of a circular lining, embedded in a rock mass, when loaded in a finite length of the concrete-rock interface. Figure 11 is an example of the response of a circular lining, 11 m in diameter, embedded in a Mohr–Coulomb elastoplastic clayey rock (E = 500 MPa; ν = 0.3; cʹ = 100 kPa; φʹ = 35º) when a 3 m long arc of the invert receives a uniform pressure of 1 MPa under plane strain conditions. The lining is an elastic material (Ec = 30,000 MPa; νc = 0.25) characterized by a constant thickness of 50 cm. The result depends moderately on the mobilized friction at the rock-lining interface. The bending moment (Fig. 11a) reaches a maximum at the centre of the application of the uniformly distributed pressure. It decreases and changes sign towards the tunnel abutments. The moment distribution reminds the case of a fully clamped beam loaded in its central part. Shear forces concentrate in positions where gradients of bending moments are high (Fig. 11b). Compression hoop forces, however, reach a significant intensity along the entire circular lining (Fig. 11c). Therefore, if swelling forces essentially develop at the invert, the lining steel reinforcements and increased lining thickness, if necessary, should concentrate at the tunnel invert.

Fig. 11
figure 11

Response of a circular elastic lining under plain strain conditions when under a uniform pressure along a 3 m long arc of the invert. The loading arc is indicated in the figures

Full size image

In the new design of Lilla tunnel lining (Fig. 12a, b) the lining thickness and reinforcement was determined for a uniform swelling pressure of 4.5 MPa acting on an invert perimeter length of 5.8 m. This loading led to the maximum steel reinforcement of the lining (Marí and Pérez 2003; Marí and Molins 2007; Alonso et al. 2013).

Fig. 12
figure 12

a Rigid support adopted for the reinforced Lilla tunnel (Marí and Pérez 2003, with permission); b details of reinforcement and lining of Lilla tunnel (ADIF 2006); c distribution of instruments in a typical cross section with instrumented invert and vault

Full size image

Figure 12c shows the type and position of monitoring devices installed in cross-sections of the tunnel, especially at the invert. Out of the two kilometres length of the tunnel, significant maximum swelling pressures were recorded in a length of 1.5 km immediate to the North portal. In the remaining 0.5 km long, tunnel maximum swelling pressures were lower (< 1 MPa) because of the lower anhydrite content and the reduced intensity of slickensides observed in the rock.

In addition to contact lining-rock radial stresses, the strain of the main reinforcement bars, placed on both sides of the resisting cross-section, was also measured. Cells oriented radially in central positions of the lining cross-section recorded hoop stresses. The set of recording instruments was organized in the manner shown in Fig. 12c. Numbers 1–6 refer to a monitoring section. They cover the width of the invert.

Figure 13a shows the evolution of recorded swelling stresses for a given section (Chainage 411 + 348). Most of the readings stabilize within the first 1.5 years. Note the variability of recorded stresses against the invert, from a minimum value of a fraction of one MPa to 5.5 MPa. This high spatial variability of swelling stresses across the invert was present in all monitoring sections.

Fig. 13
figure 13

a Recorded swelling pressures; b recorded stresses in upper reinforcement bars; c recorded stresses in lower reinforcement bars (Alonso et al. 2013). Chainage 411 + 348

Full size image

Figure 13b, c show the measured steel stresses in the upper and lower reinforcement bars. In all cases, they recorded compressive stresses. In addition, if compatibility of stresses and strains are accepted, the compressive concrete stresses in the lining is obtained by multiplying the steel stresses by the ratio of concrete to steel elastic moduli, which is close to 6 in our case. Therefore, the compression stresses in the concrete remain in the range 0.5–3 MPa, which are a small fraction of the concrete characteristic strength (80 MPa). In three tunnel cross sections, the six cells embedded in a mid-position of the invert lining, which measure hoop stresses in the concrete, reported always small compressive stresses in the range of 0.5–2 MPa. This is consistent with the interpretation given in terms of stresses in steel bar reinforcement.

Consider now the overall variability of stabilized swelling pressure. Figure 14 shows a histogram of recorded contact swelling pressures in cells covering a length of 1.3 km (Chainages 411 + 348 to 412 + 680). The histogram reflects the heterogeneity of the rock mass. The word heterogeneity includes aspects such as the content of anhydrite and gypsum, the internal “damage” of the rock and the availability of water. The histogram may be interpreted in terms of a “probability” or “frequency” of getting a given point swelling pressure against the lining. With this interpretation, Fig. 14 suggests that the probability of recording a point swelling pressure decreases in an exponential manner as the swelling pressure increases. Low swelling pressures are more likely than high swelling pressures. The cumulative frequency distribution, F(σ), is shown in Fig. 15. The relationship:

$$F(\sigma ) = 1 - \exp ( - 0.7\sigma /p_{{{\text{atm}}}} ),$$
(1)

is an analytic expression that reproduces approximately the field monitoring data. The atmospheric pressure, patm, is a reference stress to normalize σ. The equation predicts a slightly higher frequency of swelling pressures in the mid-pressure range (say, from 1 to 3 MPa) than the actual set of data. It is believed that a more extensive data set could favour this interpretation. In any case, the very precise representation of the frequency distribution of the intensity of swelling forces has a minor relevance for the approach described below.

Fig. 14
figure 14

Histogram of observed radial swelling pressures recorded in December 2011

Full size image
Fig. 15
figure 15

Cumulative frequency distribution of recorded swelling pressures and the adopted analytic expression to generate simulations

Full size image

4 A Plane Strain 2D Interpretation of Monitoring Results

The described rock heterogeneity and variability of measured swelling pressures suggest that the recorded internal stresses in the lining may be explained if the hypothesis of uniform swelling pressure against the invert is abandoned. The difficulty now is to estimate the spatial distribution of swelling pressures. The available data are “point” values of stress on measuring cells, 25 cm in diameter, spaced 2.50 m in the instrumented cross sections.

However, the internal strains, available in several locations of the bar reinforcement, offer the possibility of investigating the variability of external loads through an “inverse analysis” operating with the structural model “connecting” internal strains and externally applied forces.

Strains in the lining depend on the concrete structure, applied loads and the stiffness of the rock mass. The model used in the inverse analysis is a finite element representation of the construction of the tunnel and the installation of the lining (Fig. 16). The model represents the average cross-section geometry between Chainages 411 + 348 and 411 + 707 (360 m long stretch). Three cross sections located at Chainages 411 + 348, 411 + 468 and 411 + 707 will be analysed.

Fig. 16
figure 16

The plain strain model of Lilla tunnel to perform the inverse analysis

Full size image

The tunnel axis is 84 m below the surface. The position of the mesh boundaries (lower boundary is 40 m below the tunnel axis and the overall width of the model is 100 m) was selected to minimize boundary effects. Applied swelling pressure loads will be non-symmetric as described later.

The Mohr–Coulomb parameters of the Lilla claystone are given in Table 2. No water pressures are considered in the analysis. The selected parameters derive from previous information given in Alonso et al. (2013) and Ramon et al. (2017): average unconfined compression strength of intact claystone 92 MPa; porosity 6%; water content 2%. The Mohr–Coulomb strength parameters are an approximation, which follow available correlations with rock mass classifications.

Table 2 Mohr–Coulomb parameters
Full size table

The lining has a variable thickness (Fig. 17). The figure shows the plate elements used to characterize the geometry. The calculated bending moments, shear and normal forces in the plates help to calculate stresses in the position of monitored steel reinforcements. Table 3 shows the parameters defining the plates in Fig. 17.

Fig. 17
figure 17

Length and thickness (d) of plate elements considered in the geometry of the tunnel lining

Full size image
Table 3 Structural definition of lining plates
Full size table

Tunnel construction was simplified into three phases:

  1. a)

    Initial conditions. Weight applied to the rock and stresses calculated for K0 = 2 because of the known alpine tectonic activity of the area.

  2. b)

    Excavation. Applied in one phase. The initial tunnel (flat slab, Fig. 6) was initially stabilized by a shotcrete support. Later, further excavation was necessary to reach the circular geometry. The hypothesis made is that at this stage the tunnel was in equilibrium before the concreting of the final reinforced lining represented in Fig. 12.

  3. c)

    Lining simulated by the set of connected plates described. Interphase elements were introduced at the lining-rock contact.

4.1 Swelling Loads Applied Against the Invert

Consider (Fig. 13a) the pressures measured in load cells in Chainage 411 + 348. This cross section is selected to illustrate the consequences of plane strain modelling of lining behaviour. Three cases of loading against the lining have been analysed according to three different loading hypotheses. A first hypothesis concerning the actual distribution of maximum stabilized swelling loads (Fig. 13a) is to assume a continuous loading against the entire invert. The magnitude of the load is defined by linear interpolation between measured values. This is “Case A” shown in Fig. 18a.

Fig. 18
figure 18

Hypotheses of swelling pressure loading against lining considered for Chainage 411 + 348

Full size image

With the purpose of reducing the magnitude of applied loads, for the definition of the two additional loading hypotheses, the magnitude of the measured stresses at the location of load cells is maintained but the area of the stress application is changed and no swelling stresses are considered in intervals between load cells of the same cross-section. A loading arc length of 40 cm and 20 cm, respectively (Fig. 18b, c) characterizes “Case B” and “Case C”. The total magnitude of the swelling load reduces significantly from Case A to Case C.

The three loading cases defined were applied to the three monitored cross sections mentioned before. In all cases, a comparison is made between measured steel bar stresses and calculated ones.

4.2 Stresses in Reinforcement Bars of Lining Invert

  1. a)

    Case A. Continuous interpolated distribution of swelling loads

Figure 19a–c show a comparison of measured and calculated stresses in reinforcement bars for the three cross sections selected for the comparison. The figure includes a diagram of measured lining-rock contact stresses. The comparison is made at the six locations (1–6) where transducers were located (Fig. 12c). “Upper” and “lower” positions refer to the reinforcement, away or close, to the invert-rock contact.

Fig. 19
figure 19

Comparison of measured and calculated stresses in reinforcement bars. Loading case A “Continuous”. a Chainage 411 + 348; b Chainage 411 + 468; c Chainage 411 + 707. C compressive stress, T tensile stress

Full size image

Unlike measurements, calculations show significant tensile and compression stresses in the central zone of the invert. In absolute terms the discrepancy is very large. Calculated maximum stresses in bars reach 200–350 MPa against very small measurements (2–15 MPa), always in compression.

Similar conclusions are found in Chainages 411 + 468 (Fig. 19b) and 411 + 707 (Fig. 19c). In these two sections, the swelling pressures are characterized by a very high value measured in one cell (5.64 MPa and 6.71 MPa) and much-reduced values in the remaining cells. The “continuous” pressure distribution applied in the transversal and longitudinal direction due to the plain strain hypothesis leads to high bending moments in the lining near the application of the maximum recorded swelling pressure. The resulting steel reinforcement stresses are also much higher than the measured ones.

  1. b)

    Case B. Swelling pressure applied in a 40 cm wide segment centred in the position of load cells.

Figure 20a–c show the comparison between calculated and measured reinforcement steel stresses. Because of the reduction of the magnitude of applied swelling loads, the calculated maximum values of compression and tensile stresses in reinforcement reduce significantly but they remain, in absolute values, well above the measured compressions.

  1. iii)

    Case C. Swelling pressure applied in a 20 m wide segment centred in the position of load cells.

Fig. 20
figure 20

Comparison of measured and calculated stresses in reinforcement bars. Loading case B: “40 cm” (isolated swelling forces). a Chainage 411 + 348; b Chainage 411 + 468; c Chainage 411 + 707. C compressive stress, T tensile stress

Full size image

Figure 21a–c show the comparison between calculated and measured steel stresses.

Fig. 21
figure 21

Comparison of measured and calculated stresses in reinforcement bars. Loading case C: “20 cm” (Isolated swelling forces). a Chainage 411 + 348; b Chainage 411 + 468; c Chainage 411 + 707

Full size image

A further reduction in the intensity of applied load to half of the values of case B brings the calculated stresses close, in absolute values, to the measured compressive stresses in reinforcement bars. However, important discrepancies are still present specially in the proximity of high swelling stress (Fig. 21c). More significant is that the model predicts compressive and tensile stresses at both sides of the lining-resisting section. In other words, the structural response of the model is dominated by bending moments, something not supported by “in situ” measurements.

The answer to the persistent inconsistency of 2D modelling is to generalize the model to three dimensions with the purpose of capturing the expected “in situ” heterogeneity.

5 Three-Dimensional Analysis

It will be accepted that the histogram and cumulative frequency distribution in Figs. 14 and 15, which collect the observed swelling pressures against a long stretch of Lilla tunnel, are a reasonable description of the expected intensity of invert swelling forces against a resisting support rigid lining. The cumulative frequency distribution (frequencies in the range of 0–1) allows an easy generation of random swelling forces. Equation (1) was truncated at a maximum swelling pressure of 7 MPa according to the magnitude of the maximum recorded swelling pressure.

However, the spatial distribution of pressures is unknown. This vital information may be approximated by matching with a model calculation the compressive set of stresses measured in the reinforcements.

The main condition to be satisfied by the distribution of swelling forces is to reproduce stresses in reinforcement. This is a powerful requirement, which will not be satisfied by “extreme” hypothesis of swelling pressure (for instance long stretches without loading and a few concentrated loads). Most probably, the distribution of pressures against the invert is a continuous function of space, impossible to measure and to reproduce. Substitution of this “real” behaviour by a set of radial forces regularly spaced, whose intensity would reproduce the cumulative distribution following Fig. 15 is a simple procedure that interprets the real continuous swelling forces. It will not modify (if compared with the continuous approach) the internal forces (bending moments, shear and compression forces) because of the rigid lining structure and the structural model of the lining easily handles point swelling forces.

Swelling forces will follow the cumulative frequencies of Fig. 14. To transform pressures into forces a local area of application of a given pressure should be selected. If swelling stresses are multiplied by a constant area the result is a change in the scale of the histogram and the cumulative probability distribution will follow a curve similar to Fig. 14, changing the stress scale by a force scale.

This is not a particularly limiting hypothesis because the fundamental target condition i.e.: matching the measured reinforcement stresses may be reached by alternative values of force spacing and force intensity. Of course, there are experimental observations (the variability of swelling stresses measured in cells at distances in the range of 2–3 m) which set upper limits to the distance between the set of loading forces.

Figure 22 illustrates the situation. The tunnel lining is represented by an elastic structure made of plates as discussed before (Fig. 17 and Table 3). The calculation effort was reduced by simulating the rock mass with a Winkler model. It looks like a reasonable assumption because the stresses in the lining essentially depend on the rock stiffness.

Fig. 22
figure 22

Spatial distribution of point swelling loads against the tunnel lining

Full size image

The spring constant was approximated from available information on the rock elastic modulus as follows:

The radial displacement, δr, of a cylindrical excavation of radius R in an infinite elastic space (E, ν) loaded radially by an internal pressure p is:

$$\delta_{{\text{r}}} = \frac{Rp}{{2G}},$$
(2)

where \(G = \frac{E}{{2\left( {1 + \nu } \right)}}\) is the shear modulus.

If the supporting rock is represented by unconnected springs of constant K

$$\delta_{{\text{r}}} = p{/}K.$$
(3)

Therefore,

$$K = \frac{2G}{R} = \frac{E}{{\left( {1 + \nu } \right)R}}.$$
(4)

Figure 23 shows a comparison between the calculated reinforcement stresses (Section 411 + 348 and a loading arc length of 40 cm, 2D) for two calculation procedures: M-C, finite elements, described above, and a 2D structural calculation of lining supported by springs. The first case is solved for to E = 1000 MPa; ν = 0.2 and the second for a spring constant K = 0.14·106 kN/m3 (Eq. 4). The differences are not significant having in mind the uncertainties in rock stiffness, the approximate nature of the correspondence between spring and continuum models. Both models lead to a similar distribution of stresses across the invert.

Fig. 23
figure 23

Cross section 411 + 348, loaded arc length 40 cm. Comparison of FE and spring approaches for lining support

Full size image

Modulus E reduces fast with deviatoric strains. In the range E = 500–3000 MPa and ν = 0.35, K varies in the range 0.6·105 to 0.36·106 kN/m3. In all the analyses reported below the effect of changing K between these two extreme values was examined.

Point loads represented in Fig. 22 were obtained by multiplying the swelling pressure by the area of a circle 25 cm in diameter, which is very close to the actual diameter of the measuring load cells installed in the Lilla tunnel.

5.1 Solved Cases

Figure 24 shows the first solved case: 36 concentrated forces spaced 2.50 m in longitudinal and circumferential directions. The cross section of interest is the vertical “calculation plane” shown in the figure. The calculation plane is any cross section of the tunnel. The extension of the loaded areas on both sides is limited to a distance beyond which swelling forces do not affect results in the calculation plane. The length of the simulated tunnel is 52.5 m. Calculated stresses in bar reinforcements are compared with the results measured in seven available instrumented cross sections at the particular location of the vibrating wire extensometer selected for the comparison. The position of the twelve extensometers is shown in Fig. 25 (ECV-1 to ECV-12). Odd numbers in Figs. 25, 26, 2728 correspond to bar extensometers located near the lining-rock interface (“lower” in Figs. 19, 20, 21). Even numbers designate extensometers on the inner side of the lining (“upper” in Figs. 19, 20, 21). Figure 25 indicates the average and the standard deviation of measured stresses for the seven tunnel cross sections. Also represented are the calculated values for the three spring constants representing the rock stiffness.

Fig. 24
figure 24

Grid model of 36 (6 × 6) concentrated forces distributed with 2.50 m × 2.50 m spacing

Full size image
Fig. 25
figure 25

Measured and calculated stresses in reinforcement considering 36 point loads

Full size image
Fig. 26
figure 26

a Spatial distribution of the reference “calculation plane” and the point loads in grid models of 36 (6 × 6) and 108 (6 × 18) concentrated forces. b Calculated reinforcement stresses in both grid models for different values of spring coefficient

Full size image
Fig. 27
figure 27

Spatial distribution of the reference “calculation plane” and the 26 × 26 punctual forces (spacing of 0.5 m) in plain view

Full size image
Fig. 28
figure 28

Average stress measurements and calculated stresses in the twelve locations of the bar extensometers in the grid model of 26 × 26 punctual forces

Full size image

The measured compression stresses are larger in the lower bars (1, 3, 5, 7, 9, 11) than the stresses measured in the upper locations (2, 4, 6, 8, 10, 12). Average compression stresses are 9–12 MPa for the lower reinforcement and 4–8 MPa for the upper one. This is consistent with the expected distribution of bending moments when a swelling load is applied against the invert (Fig. 11a). Standard deviations range between 2 and 5 MPa.

The calculated values are very small compared with the measurements. The effect of rock stiffness, K, is not particularly relevant. However, the model always predicts compression stresses, unlike the previous 2D analysis. This preliminary analysis indicates that the spacing between swelling forces should be reduced. Before this is done, it was checked that the overall area selected for the application of the 36 forces (12.5 m in the longitudinal direction by 11.5 m in the transverse direction) ensured that swelling forces located beyond the far away forces, in the longitudinal direction, did not have any significant effect on results at the “calculation plane”.

Figure 26 represents a new calculation case. Spacing of concentrated loads is maintained but the grid of forces is now expanded to 6 × 18 loading points. Results of calculations are also given in Fig. 26. The comparison between the two cases does not show a systematic effect on the calculated reinforcement stresses. Some differences are always expected, other than the effect of the overall extension of the loading zone, because each one of the computed cases represents a “realization” (in probabilistic terms) of the set of forces obeying the underlying frequency distribution of swelling pressures. On the other hand, the effect of the spring coefficient indicates that stresses increase when the rock stiffness decreases. In all cases, the calculated compression stresses are a small fraction of the measured ones.

The next step was to reduce the spacing among swelling forces until a good match between measured and calculated bar stresses is achieved. A good match was reached for a mean force spacing of 0.50 m. Figure 27 shows the position of the swelling forces in plain view and the reference “calculation plane”. 676 swelling forces were applied in a mesh of 26 × 26 loading points. The number of loads and extension of the loaded area provide structural and statistical reliability to the three-dimensional calculation.

Figure 28 compares average stress measurements with model predictions for the twelve locations of the bar extensometers. The best agreement is found for a spring constant in the range 0.167–0.334·106 kN/m3 which corresponds to a rock elastic modulus in the range 1350–2700 MPa (if ν = 0.35). If the rock spring coefficient reduces to 0.337·105 kN/m3 (E = 270 MPa) the calculated stresses overestimate measurements in reinforcement bars close to the lining-rock contact.

An interesting modelling result, which reproduces the field measurements, is that the 3D model and the distribution of swelling pressures leads always to compressive and low stress in the lining actually built. The 3D case, compared with the plane strain hypothesis (Figs. 19, 20, 21), reduces drastically the magnitude of the applied load to the invert because of the spatial heterogeneity in longitudinal direction of swelling stresses, especially when low swelling pressures dominate (Figs. 14 and 15). In case of concentrated swelling pressure, bending moments remain near the applied load whereas the axial forces develop in the entire lining (Fig. 11). These trends explain the absence of tensile stresses in the lining.

6 Application to the Lining Design of Two New Tunnels

Two parallel tunnels for a motorway connecting the cities of Tarragona and Lleida, currently under construction, cross the Lilla anhydritic claystone under a cover of 160 m. The tunnels are subparallel to the AVE Lilla tunnel, analysed in this paper, at an average distance, in plain view, of approximately 1.5 km. Figure 29 shows the lining geometry. In the initial design, the reinforcement was calculated following the criteria selected for the AVE Lilla tunnel (a uniform pressure of 4.5 MPa against the invert; details in Alonso et al. 2013).

Fig. 29
figure 29

Lining geometry of the motorway tunnels

Full size image

The measured performance of AVE Lilla tunnel and the analysis described here motivated a revision of the design methodology. The geological investigations, direct observation of the claystone during the initial phases of tunnel excavation and the measured mineral content revealed a rock mass essentially similar to the claystone found in AVE Lilla tunnel. The decision was to adopt the variability of swelling pressures described in Figs. 14 and 15 and to perform a series of 3D calculations applying the spatial criteria of swelling forces against the invert shown in Fig. 27. This time, calculations were repeated, following a Montecarlo approach, to investigate the effect of random loading schemes.

The calculation procedure to define the lining reinforcement followed several steps:

  • Definition of a 3D calculation procedure. The results given below correspond to a finite element 3D representation of a 30 m long stretch of the tunnel loaded in a central section 10 m long. Figure 30 is a representation of the point loads of one realization. The adopted elastoplastic M–C parameters of the rock mass were E = 3000 MPa, cʹ = 0.33 MPa, ϕʹ = 32.5° and no dilatancy. A 10 cm thick shotcrete layer and a grid of 4 m long passive bolts at 2.35 m intervals were simulated at vault and abutments, in addition to the lining.

  • The swelling pressures were increased by a safety factor of 1.5 to comply with the applied structural code.

  • The lining was described by shell elements to find bending moments, axial and shear forces induced by the swelling forces.

  • A selected reinforcement design, described by a Moment-Axial force interaction diagram, served to judge the suitability of the design. This is given in Fig. 29. It corresponds to a fiber-concrete solution (no bar reinforcements) and an invert thickness of 0.95 m. The diagram is symmetrical with respect to the horizontal axis. Also plotted are the calculated maximum moments (positive and negative) and axial forces from the Montecarlo exercise.

Fig. 30
figure 30

Example of applied swelling forces in one of the 20 calculations for the A-27 tunnel linings. Courtesy of Túnel y Asistencia Técnica, Madrid. Maximum point force applied: 2.28 × 106 N

Full size image

Figure 31 shows the heterogeneity-related scatter of calculated invert forces. The 20 cases solved (one point represents a calculated case) remain inside the interaction diagram are acceptable and they are grouped in reduced areas of the diagram. This is an indication of the consistency of the calculation approach in the sense that no “anomalous” high lining internal forces were found.

Fig. 31
figure 31

Motorway tunnels. Moment-Axial force interaction diagram (absolute values for bending moments) for a representative section of the invert. The plot shows the results of calculated values for the 20 realizations of swelling forces

Full size image

Lining design, synthesized in Fig. 29, implies a major reduction in the cost of the tunnel lining if compared with the approaches relying on plane strain calculations and uniform distribution of swelling stresses against the invert.

7 Conclusions

The comprehensive swelling pressure data against the invert of AVE Lilla tunnel was described by an exponential probability density function in the range of 0–7 MPa. No long-term swelling pressures above a maximum of 6.7 MPa were recorded.

A back-analysis of measured stresses in lining reinforcement bars provided information on the spatial distribution of swelling pressures against the invert. The loading system was defined by a set of point swelling forces, which incorporate the distribution of measured swelling pressures, at intervals of 0.5 m. Within limits, this loading definition may be modified but the condition of reproducing the lining internal stresses should be fulfilled.

These findings led to a computational 3D procedure to design tunnel lining in anhydritic claystones. The proposal was applied to two motorway tunnels, currently under construction, crossing the Lilla claystone. The resulting lining design results in major savings if compared with a previous design approach, namely a plane strain analysis of the cross section under a uniform swelling pressure applied against the invert.