1 Introduction

The effect of dilation and compression on hydro-mechanical behaviour of rock discontinuities are of significant importance in various geotechnical applications such as hydraulic fracturing design, earthquake and seismic analysis, dams and slope stability analysis, CO2 geo-sequestration operations, contaminant transport modelling, and disposal of nuclear wastes, amongst others (Pirzada et al. 2020; Rutqvist and Stephansson 2003; Tsang 1991). A great number of studies have been conducted to understand the hydro-mechanical behaviour of rock joints (Berkowitz 2002; Pirzada et al. 2018; Pyrak-Nolte et al. 1987; Zimmerman and Bodvarsson 1996). Rock joints provide the conduit for fluid flow in rock mass where flow characteristics are highly influenced by joint aperture, joint roughness, and joint contact area. While the effect of joint aperture and roughness on joint fluid flow have been investigated (Barton 1982), the effect of contact area with varying joint aperture and roughness on joint hydro-mechanical behaviour remains unexplored mainly due to experimental difficulties to track the evolution of contact area during shearing experiments (Brown 1987; Zimmerman and Bodvarsson 1996).

On the other hand, several theoretical foundations have been developed to model the fluid flow in rock joints (Chen et al. 2015). The cubic law, initially developed for incompressible fluids, is one of the most basic models of flow through a rock joint (Lomize 1951; Snow 1965; Witherspoon et al. 1980). To drive cubic law, the fracture is assumed to be contained by two smooth, parallel walls separated by an opening E. To extend the cubic law to compressible fluids, Zhang et al. (2020) and Ranjith et al. (2011) integrated the fluid compressibility term into cubic law:

$$Q=\frac{w{E}^{3}}{12\mu L}\frac{{{\mathrm{P}}_{in}}^{2 }- {{\mathrm{P}}_{o}}^{2 }}{2{\mathrm{P}}_{o}},$$
(1)

where Q is the volumetric flow rate, E is the aperture between two parallel idealised smooth plates, μ is dynamic viscosity of the fluid, Po is the downstream pressure, Pin is the injection pressure and w and L are the joint width and length, respectively. On the other hand, the role of asperities in contact across the joint on the fluid flow was investigated by Witherspoon et al. (1980). They discussed that the roughness and contact area account for some of the pressure loss of the fluid in the joint because the void space geometry forces the fluid to take a tortuous path around the asperities. Using this understanding, cubic law was further used in many data sets of rough joints where the total aperture is replaced by a hydraulic aperture (i.e. the effective flow path for the fluid flow) (Brush and Thomson 2003; Hussain et al. 2021; Li et al. 2016; Ranjith and Darlington 2007).

Despite the integration of fluid compressibility to cubic law equation, its use for gases has been rather limited partly due to gases showing turbulent flow in many instances which violates the laminar flow assumption used to drive the cubic law. The most commonly used correlation for the flow of gases in fractures/bedding planes is suggested by Forchheimer (1901) where a relationship between the hydraulic gradient and the flow rate of the gas was formulated. The simplest form of Forchheimer equation referred by Chen et al. (2015) is defined:

$$- \triangle P=AQ+B{Q}^{2},$$
(2)

where \(\triangle P\) is the pressure gradient, A is the coefficient of viscous loss and B is the coefficient of inertial loss. As Forchheimer’s equation considers both viscous and inertial forces (linear and non-linear flow terms), it can be used to predict flow behaviour in joints with various flow rates (fluid velocities) within laminar to turbulent flow ranges (Moutsopoulos et al. 2009; Ranjith and Darlington 2007; Tzelepis et al. 2015). The determination of the coefficients of Forchheimer’s equation, however, remains a challenge in various applications (Chen et al. 2015). Some works have been carried out to determine these viscous and inertial loss coefficients (Bear 1988; Sidiropoulou et al. 2007). The most widely used empirical correlations for estimation of these coefficients are (Chen et al. 2015):

$$A=\frac{\mu }{k{we}_{h}},$$
(3)
$$B=\frac{\beta \rho }{{w}^{2}{{e}_{h}}^{2}},$$
(4)

where eh is the hydraulic aperture, ρ is the fluid density, β (beta) is the non-Darcy flow coefficient and k is considered as intrinsic permeability and is given as eh2/12. Different correlations have been proposed for the determination of non-Darcy flow coefficient (β); however, the experimentally driven correlation proposed by Geertsma (1974) is considered to be one of the most suitable correlations according to Thauvin and Mohanty (1998):

$$\beta =\frac{0.005}{{\varphi }^{5.5}.{k}^{0.5}},$$
(5)

where \(\varphi\) is the porosity and can be assumed 1 in the case of joints. The hydraulic properties of joints during the shearing process are more complicated due to the significant effect of asperities dilation and later production of gouge material, which results from the interlocking and subsequent destruction of the asperities. Makurat et al. (1985) initially observed that the presence of irregularities on the joint surface can lead to an initial opening of the joint during the shearing process by dilation, thus increasing the fluid conductivity. This phenomenon was later examined by many researchers including Brown (1987), Teufel (1987), Yeo et al. (1998), and Esaki et al. (1999). In addition, the interlocking of the joints asperities and their gouge production was first pointed out by Ladanyi and Archambault (1969). The production of gouge can intuitively lead to reduction of fluid conductivity.

While the roughness induces the change in mechanical aperture (e.g. dilation, interlocking and gouge production), it also affects the fluid flow regime in the joint demanding the estimation of the hydraulic aperture. One of the significant challenges in Forchheimer’s equation is the determination of the hydraulic aperture. Barton (1982) is amongst the first who developed an empirical equation to estimate the hydraulic aperture by considering the effect of joint roughness coefficient (JRC):

$${e}_{h}=\frac{{E}^{2}}{{JRC}^{2.5}}.$$
(6)

Roughness, however, is not always representative of the real contact area; the property that controls the fluid flow in both shearing and normal loading conditions. The joint conductivity reduces with increase in joint contact area as the flow becomes repressed by increasingly tortuous pathways thus hindering fluid flow (Zimmerman et al. 1992). The elliptical contact areas is used in some studies to consider the effect of contact area in the estimation of hydraulic aperture (Obdam and Veling 1987). The application of elliptical contact area model is, however, limited due to the presence of irregular surface shapes and complicated spatial distribution in real rocks. Gale et al. (1990) suggested the use of contact area for hydraulic aperture estimation along with a factor that can be represented as the ratio of the standard deviation of mechanical aperture to its mean value. Zimmerman and Bodvarsson (1996), based on the original work of Walsh (1981), applied an effective medium assumption to derive an analytical solution for the effective permeability of a joint with consistently dispersed circular contact areas:

$${{e}_{h}}^{3}={E}^{3}\frac{(1-{R}_{c})}{(1+{R}_{c})},$$
(7)

where Rc is the contact area ratio (contact area per total joint area). The measurement of contact area of rock joints during normal and shear loadings, however, has been an experimental challenge for decades. Several experimental methods have been employed to measure the contact area, including inserting materials such as sensitive papers (Choi et al. 2019; Duncan and Hancock 1966), pressure-sensitive films (Nemoto et al. 2009; Selvadurai 2015), epoxy or molten metals (Hakami and Larsson 1996; Stesky and Hannan 1987); (Pyrak-Nolte et al. 1987), indirect electrical resistance measurement (Power and Hencher 1996), optical techniques (Dieterich and Kilgore 1996), visual inspection (Bahaaddini et al. 2016; Fathi et al. 2016; Pirzada et al. 2021, 2020), numerical modelling (Bahaaddini et al. 2013a, 2013b, 2012; Park and Song 2013) and X-ray tomography technique. A detailed review of these techniques can be found in Pirzada et al. (2021).

In the X-ray computed tomography technique, the X-ray beam is passed through the sample, and the density contrast between the sample matrix and the joint space filled by fluid with a different density is used to calculate the joint aperture (Pirzada et al. 2021). The application of this technique has been problematic in the past mainly due to the requirements of special X-ray transparent equipment and the low resolution of X-ray computed tomography (CT) images to differentiate the joint zone from rock materials in contact. Recently, Roshan et al. (2019) developed an X-ray transparent apparatus to enable scanning the internal structure of rock in triaxial and direct shear experiments. This apparatus has been successfully employed for the detection of contact area evolution during the shearing process of natural rock joints and porous rocks with high resolution (Chen et al. 2020a, 2020b; Pirzada et al. 2021) and is therefore used in this study.

Despite the research conducted to date, the micro-scale evolution of contact area leading to macro-scale experimental observations during normal deformability and shear loading on joints with varying roughness and its effect on joint fluid flow remain unexplored. This study therefore aims to investigate the effect of time evolution of contact area, joint aperture and roughness on joint flow behaviour under normal and shearing loading using gas (helium) as a working fluid. X-ray micro-computed tomography (XRCT) is used to accurately detect the contact area and the void volume/joint aperture in the loading processes. Two natural joints having different roughness profiles are reproduced in the laboratory and subjected to normal deformability and direct shear experiments while measuring gas flow continually. These samples are XRCT scanned at several stages during the experiments to track the evolution of joint aperture and contact area, along with recording the hydro-mechanical responses. Based on these experiments, a new model is developed to predict the hydraulic aperture from joint contact area, roughness and average mechanical aperture.

2 Experimental Methodology

2.1 Sample Preparation

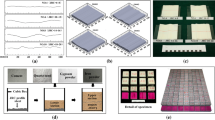
As the geometrical characteristics of joint surfaces can significantly affect their hydro-mechanical behaviour, synthetic samples are prepared from induced fractures/joints to ensure that the geometry of joint surfaces is identical in the experiments. Two different joints are made from shale and sandstone core specimens having 10 mm diameter. To replicate the joint surfaces, araldite was poured on both the joint surfaces. The araldite resin is a 5 to 1 ratio mixture of Huntsman CW 177 CL and HY 177 CL hardener, which solidifies in a few minutes making well-mated joint surfaces as natural samples. Hydro-stone TB, a gypsum cement, is used as a synthetic material in this study (Bahaaddini 2017; Bahaaddini et al. 2016). Hydro-stone is a mixture of Plaster of Paris, crystalline silica, and Portland cement. Hydro-stone is first mixed with water in a ratio of 1:0.35 (hydro-stone to water). The mixture is poured on the araldite mould and the synthetic sample is removed after solidification. The sample is kept in the oven for 28 days at 40 °C (Bahaaddini 2014). The procedure of sample preparation is illustrated in Fig. 1. The mechanical testing of the hydro-stone sample is also explained in the appendix.

Fig. 1
figure 1

a 10 mm cylindrical core specimens are drilled from a bulk material. b A tensile crack is induced in the specimen along its length axis using a hydraulic press; the samples are broken into two halves. c 3D printed moulds are prepared to fix one-half. d Replica of sides of the joint are prepared using araldite on the sample. e The synthetic samples are made using the moulds of the previous step. f For direct shear tests, 3 mm from the top and bottom, synthetic samples are cut and the aluminium spacers are placed on both sides of the specimen

Full size image

2.2 Measurement of Surface Roughness of Joints

To quantify the surface roughness of joints, both surfaces are scanned using a high-resolution 3D GOM scanner (core 80) with optical radiation. This optical radiation scanner can digitise the surface by collecting several measurements at various angles, axes, and courses of movement. The joint surfaces are measured with a resolution of 30 μm as shown in Fig. 2. These surfaces are digitised along the shearing direction with a point spacing of 0.5 mm to import the prepared profiles into MATLAB to calculate the joint surface roughness (JRC) using the root mean square of the profile first derivative Z2 (Tse and Cruden 1979):

$${Z}_{2}={\left[\frac{1}{{m\left(\Delta x\right)}^{2}} \sum_{i=1}^{m}\left({y}_{i+1}- {y}_{i}\right)\right]}^\frac{1}{2},$$
(8)
$$JRC=32.2+32.47{\mathit{log}}_{10}{Z}_{2,}$$
(9)

where Δx is the sampling interval and \(\left({y}_{i+1}- {y}_{i}\right)\) is the height difference between two adjacent sampling points. The measured JRC profile for the shale (will be referred to as profile 1) and sandstone (will be referred to as profile 2) are 8.7 and 15.0, respectively.

Fig. 2
figure 2

3D view of the joint surfaces for a sandstone and b shale replicas

Full size image

2.3 Experimental Procedure

Experiments are carried out using the newly developed X-ray transparent triaxial-direct shear test apparatus (Roshan et al. 2019). This system consists of an ISCO pump (D500) for applying normal stress on the joint, an aluminium cell, a Viton rubber sleeve placed inside the cell to hold the normal stress, a burette tube to measure the gas flow rate and a platen on the top to provide axial movement on the sample during the direct shear test. A schematic view of the system is shown in Fig. 3.

Fig. 3
figure 3

Schematic representation of the direct shear system setup

Full size image

In this study, two types of experiments are conducted, namely normal deformability and direct shear tests, during which the fluid flow is measured.

2.3.1 Normal Deformability Test with Fluid Flow Measurement

To perform the normal deformability test, joints of the synthetic samples are subjected to increasing normal stresses. Here, a constant inlet helium gas flow pressure of 6.1 psi is applied, and the flow rate is measured with the burette tube for five different normal stresses of 0.5, 1.0, 3.0, 5.0 and 10.0 MPa. The sample is scanned using XRCT system for the applied normal stresses at different stages.

2.3.2 Direct Shear Test with Fluid Flow Measurement

As mentioned earlier, to perform the direct shear test, each side of the upper and lower blocks is cut by 3 mm and aluminium-made half-cylindrical spacers are placed in the gaps. The sample is covered with tape and grease is applied between half-cylindrical spacers and the rubber sleeve to reduce possible friction. After applying the specified normal stress, the sample is initially scanned using the XRCT system. Then, a constant displacement rate of 0.003 mm/s is applied to the upper platen to provide shear displacement. Here, the shearing process is paused following specified shear displacement increments by holding the load where XRCT imaging is performed. The shear load and shear displacement are continuously recorded using the LabView software. The joint gas flow rate is also measured during the shearing process as shown in Fig. 3. As mentioned, the shearing process is paused at several specific displacement positions for the scanning purposes, where returning to the exact same inlet pressure after each scan is not feasible. Due to slight variation in inlet pressure after each scan, the measured continuous flow rate is divided per inlet pressure (Q/ΔP), the ratio of which is a representative of permeability × aperture through Darcy’s law (\(\frac{Q}{\mathrm{\Delta P}}=\frac{k}{\upmu }\frac{A}{L}\)), where L and µ are constant during the tests. It is noted that the differential pressure is equal to inlet pressure, as the outlet pressure is atmospheric.

2.4 X-Ray Micro-Computed Tomography

X-ray micro-computed tomography is used to scan the specimens during the normal deformability test and at intermediate stages during the direct shear test. The specimens are scanned in a helical trajectory and a voxel size of 24.6 µm is obtained. In this technique, the polychromatic beam from an X-ray source is attenuated as it is being transmitted across the specimen. A 2D projection image is obtained as the attenuated beam is encountered by the detectors positioned on the other side of the specimen. Different positions of the sample rotating on a rotational stage give an array of 2D X-ray projections which are then used for the mathematical reconstruction of 3D tomograms. Each voxel is a function of atomic number and the material density where the grey value indicates effective progression of the X-ray. The image analysis of the reconstructed 3D datasets is carried out using Avizo software. Different zones are differentiated using the CAC (converging active contours) technique to segment the XRCT images (Sheppard et al. 2004). This technique involves the selection of two greyscale threshold values gleaned from layer-by-layer examination of the obtained 3D tomogram. These values are categorised into the void and solid depending upon their status as less than the lower threshold (air at a known location) and greater than the upper threshold (solid at a known location), respectively. Consequently, CAC keeps growing the boundaries towards each other until all boundaries are converged (Pirzada et al. 2018; Schlüter et al. 2014). To ensure the accurate segmentation of joint zones, slide-by-slide examination of XRCT images is also carried out. By identifying the 3D shape of the void in the upper and lower blocks of the specimen as shown in Fig. 4b, the contact area can be evaluated. To calculate the joint aperture of each 2D tomograph (image slide), the pixels representing the aperture area on each segmented 2D image are first identified and the obtained surface is then divided per width of the joint (constant throughout) to obtain the average aperture. The geometry of the joint sample used for a direct shear test is shown in Fig. 4a, the segmented image for the rock joint is shown in Fig. 4b and the schematic diagram for the calculation of average mechanical aperture is shown in Fig. 4c.

Fig. 4
figure 4

a XRCT image of the sample with joint and aluminium spacer, prepared for the direct shear test. b Segmented image of the joint; here white represents the area in contact and blue represents the gap between the two parts. c Schematic diagram for the calculation of the average mechanical aperture

Full size image

3 Experimental Results

3.1 Normal Deformability Experiments

The variation of gas flow rate, the average mechanical aperture (Ē) and contact area for both specimens having profiles of different roughness under normal deformation are shown in Fig. 5. For profile 1 (relatively lower roughness), a significant decrease in the flow rate is observed specially from 0.5 MPa to 3.0 MPa due to a reduction in the joint conductivity (Fig. 5a). However, a more gradual decline in flow rate up to the normal stress of 10 MPa is seen for the profile 2 (relatively higher roughness). It is attributed to stronger engagement of asperities in profile 2 due to its higher roughness leading to more gradual reduction in aperture thus flow rates. Figure 5b additionally shows the average mechanical aperture of profile 1 and profile 2 which follow the flow rate trend presented in Fig. 5a closely. The difference between average mechanical aperture of profile 1 and 2 deceases with normal stress as expected. Interestingly though, while the flow rate measured for profile 1 and 2 almost overlap at 10 MPa normal stress (Fig. 5a), there are still differences between the average mechanical apertures of profile 1 and 2 (Fig. 5b) showing that other factors contribute to fluid flow than a sole mechanical aperture.

Fig. 5
figure 5

Change in a flow rate, b average mechanical aperture and c contact area with increase in normal stresses and d average mechanical aperture change with flow rate

Full size image

In addition, Fig. 5c shows that for the profile 2 with relatively higher roughness, there is only 3% contact area between blocks under 0.5 MPa normal stress and it increases to a maximum of 34% at 10.0 MPa. The contact area increases from 14% (0.5 MPa normal stress) to 43% (for 10.0 MPa normal stress) for profile 1 with relatively lower roughness. As the normal stress increases, the contact area of both samples increases. This is intuitive as a greater normal stress pushes the asperities of the joint closer to each other, thus increasing the contact area. It is noted that for relatively low roughness (profile 1), significant stresses are required to make new contact. Also while the relative contact area increases as the normal stress increases, it is not physically possible to reach full contact even for these artificially made samples at a high normal stress of 10 MPa, which contrasts with the general understanding of full contact for synthetic and well-mated specimens (Pirzada et al. 2020; Sharifzadeh et al. 2008).

Figure 5d also indicates that the flow rate is almost linearly correlated to the average mechanical aperture, although slight deviation occurs at relatively higher normal stresses.

3.2 Direct Shear Experiments

Figure 6 shows the change in shear stress versus shear displacement (top) along with the normalised flow rate. The direct shear experiments are complemented by measuring the gas flow rate evolution during shearing process for both profile 1 and profile 2 at different normal stresses of 0.5 MPa, 1.0 MPa and 1.5 MPa. The normalisation of flow rate is performed by dividing each value of the flow rate over pressure with the maximum value of obtained Q/ΔP.

Fig. 6
figure 6

The behaviour of joints during the shearing process coupled with fluid flow measurement for a profile 1 and b profile 2

Full size image

The results show that the shearing process could significantly alter the normalised flow rate at different normal stresses. It can be seen from Fig. 6 that the initial normalised flow rate of profile 2 with relatively higher roughness is significantly greater than that of profile 1 with relatively lower roughness. The flow rate evolution of profile 2 under lower normal stress is found to be different from that of higher normal stress due to a change in the shearing mechanism. Under the low normal stress, the normalised flow rate remains constant initially during the shear process before reaching the peak shear stress. It then increases at peak shear stress, the increment of which is dependent on the applied normal stress. As the shear process continues toward the residual stage, the normalised flow rate also stays unchanged. For higher normal stress, the normalised flow rate stays constant until reaching the peak shear stress. However, a slight decrease in the normalised flow rate is observed due to the asperities shearing off around the peak stress point and likely the production of gouge materials. The normalised flow rate remains constant after this point toward the residual stage. For profile 1, however, the evolution of normalised flow rate closely follows the normal stress before reaching peak stress owing to predominant elastic deformation of the asperities. The increase in normal stress slightly alters the normalised flow rate at peak shear stress toward residual.

To understand the underlying hydro-mechanical mechanisms of joints under the shearing process, XRCT scanning is carried out at several steps during the shearing process to measure the joint contact area and joint aperture as previously explained; the results are presented in Figs. 7 and 8.

Fig. 7
figure 7

Change in the contact area, average mechanical aperture and normalised flow rate in the shearing process for profile 2, at a 0.5 MPa normal stress and b 1.0 MPa normal stress

Full size image
Fig. 8
figure 8

Change in the contact area, average mechanical aperture and normalised flow rate in the shearing process for Profile 1, at a 0.5 MPa normal stress and b 1.0 MPa normal stress

Full size image

For profile 2 (relatively higher roughness), at low normal stress (0.5 MPa), there is only 1.1% contact between the upper and lower blocks at the initial stage, as shown in Fig. 7a. The shearing displacement before reaching the peak shear stress results in almost no change in contact area (a trivial increase of 1.1% to 1.3% is observed that sits within the resolution of the images). On the other hand, the average mechanical aperture very slightly increases from 118 µm to 127 µm before reaching peak indicating a relatively minor effect of asperities on the fluid flow. After the peak shear stress, the contact area slightly decreases due to dilation occurring across the asperities followed by a slight damage of the asperities. The dilation results in an increase in the average joint aperture and, as a result, an increase in the normalised flow rate takes place, see Fig. 7a.

At higher normal stress of 1.0 MPa, the initial relative contact area is around 11.1% and more asperities are engaged in the shearing process, as can be seen in Fig. 7b. At the initial stage of shearing, no significant change is observed in the contact area and a slight decrease of aperture only relates to a minor contraction of the joint in the shearing process with no significant influence on the normalised flow rate. The contact area, however, increases to 20.5% towards peak stress and the average aperture is reduced from 102 to 74 μm, which corresponds to a decrease in the normalised flow rate, as shown in Fig. 7b. This decrease in contact area is driven by the engagement of the asperities, a process governed by the normal stress, i.e. the greater the normal stress, the greater is the contact area and asperities engagement. With a further increase in the shearing displacement, a slight damage occurs on the asperities, although it is not enough to fully break the asperities. Therefore, the joint dilation results in the reduction of contact area to 16.2%, and an increase in the average aperture and a corresponding increase in the normalised flow rate.

For profile 1 (relatively lower roughness) at the normal stress of 0.5 MPa, there is an initial 9.2% contact area between the two blocks (Fig. 8), considerably greater than that for profile 2 (Fig. 8). The contact area decreases to 6.5% when the shearing displacement is applied due to engagement of asperities before reaching the peak shear stress. This results in a slight reduction of the average aperture from 45 to 34 μm. However, this average aperture reduction is not enough to noticeably alter the normalised flow rate. After peak shear stress, a very small decrease in the contact area is observed (i.e. 6.2%), while the average mechanical aperture stays constant. Despite the trend in the average mechanical aperture not following the trends in the normalised flow rate precisely, the trend in the contact area follows the normalised flow rate very closely throughout the shearing process. Furthermore, based on the contact area and aperture evolution, it is seen that the sliding is the main controlling mechanism in this case, and the joint simply experiences new sites of contact.

At the normal stress of 1.0 MPa, the initial contact area decreases from 10.3% to 9.1% and the average mechanical aperture decreases from 31 to 26 μm, showing a change in the contact points due to the engagement of asperities. However, fluctuation in normalised flow rate can be seen in Fig. 8b. Right after the peak shear stress, the average mechanical aperture increases again to 30 μm, and the contact area decreases to 8.2%, which clearly shows the dilation trend, as can be seen in Fig. 8b. At the last point in the test, although the average mechanical aperture does not change significantly, the contact area increases substantially to 11.2%, which indicates that the asperity destruction continues throughout the test. In this case, evidently, none of the measured variables (average mechanical aperture or contact area) can explain or predict the changes in the normalised flow rate due to the extent of the damage to asperities.

3.2.1 Gas Flow Analysis

As noted earlier, the joint aperture is considered to be the most effective parameter controlling the joint fluid flow. Looking at Fig. 5a, b, it is noted that the flow rates of both profiles 1 and 2 become approximately identical and close to zero at high normal stresses, while at the same normal stress (10 MPa), the average mechanical aperture of the two profiles is relatively different. This behaviour presents a challenge for the conventional models to predict the joint conductivity evolution by varying normal stresses and roughness and indicates that other factors contribute to flow rather than sole mechanical aperture.

To gain insight into the observed flow rates variation, the Forchheimer equation (i.e. Eq. 2) and modified cubic law (i.e. Eq. 1) are used to back calculate the hydraulic aperture from the experimental flow rate data of normal deformability tests (Table 1). The back calculation of hydraulic aperture is performed using the measured pressures and flow rates from the experiments, as well as the density (ρ) of the helium gas (0.1786 kg/m3), width of the joint (10 mm), and helium viscosity (µ) of 1.87 × 10–5 PaS, the values that are used in Eq. 2 along with Eqs. 3, 4 and 5. It is nted that during the normal deformabaility tests, the inlet pressure is kept constant at 6.1 psi.

Table 1 Hydraulic apertures back calculated from experimental data using Forchheimer equation and modified cubic law
Full size table

The results presented in Table 1 evidently indicate that the value of hydraulic aperture calculated by the Forchheimer’s equation for all the cases is only slightly higher than those obtained from the modified cubic law. While both equations consider the compressible fluid behaviour, Forchheimer’s equation additionally considers the non-linearity by turbulent flow. We thus next assess the flow regime in each test condition by calculating the Reynolds number (Re) (Brush and Thomson, 2003; Zimmerman et al. 2004):

$${R}_{e}=\frac{\rho Q}{\mu w},$$
(10)

where, ρ is density of the fluid, w is the joint width, Q is the flow rate and μ is the fluid viscosity. The calculated Reynolds numbers are plotted versus the normal stress representing the flow rate variation by aperture changes (Fig. 9). The previous experimental investigations using natural fracture samples have shown that inertial forces can be important at Re numbers exceeding 7–15. (Hansen and Gudmundsson 1999; Oron and Berkowitz 1998; Zimmerman and Yeo 2000). The calculated Reynolds numbers are all below these values indicating the existence of rather overall laminar flow, although a week inertial regime may still be experienced for the values of Reynold’s number between 1 and 10 (Zimmerman et al. 2004). This implies that the non-linear term of Forchheimer’s equation returns negligible values for the obtained experimental data.

Fig. 9
figure 9

Reynolds numbers calculated for flow at each normal stress (representing different apertures)

Full size image

What makes the data interesting is that the values of hydraulic aperture (calculated by Forchheimer’s and modified cubic law equations) are significantly different from the average mechanical aperture calculated from the XRCT images as shown in Fig. 10. The hydraulic aperture calculated from modified cubic law is additionally plotted in Fig. 10. The above analysis indicates that irrespective of the model used (Forchheimer’s or modified cubic law), joint roughness and contact area significantly influence the hydraulic aperture deviating it from average mechanical aperture. Thus, a model to convert the mechanical to hydraulic aperture is required to make the flow model applicable in real experimental scenarios.

Fig. 10
figure 10

Comparison of average mechanical apertures extracted from XRCT images and hydraulic aperture calculated by Forchheimer's equation and modified cubic law

Full size image

We thus calculated the hydraulic aperture from some of the most common correlations developed to date and plotted them versus actual hydraulic aperture (Table 2). The results presented in Table 2 show that none of the proposed correlations to estimate the hydraulic aperture can fit the experimental data obtained in this study. This calls for a new model that can fit our obtained experimental data.

Table 2 Experimental hydraulic aperture versus the calculated hydraulic aperture by some of the common correlations existing in the literature
Full size table

To develop this new correlation for calculating eh, the hydraulic aperture obtained from Forchheimer’s equation is used as a reference (will be referred to as experimental eh herein). This correlation should essentially relate the main parameters influencing the hydraulic aperture including average mechanical aperture, joint contact area and joint roughness to hydraulic aperture. Normal deformability test data is used to calculate the values of experimental eh at every confinement for both profile 1 and profile 2 using the known parameters including (i) contact area calculated from the XRCT images, (ii) roughness using JRC profiling from surface scans and (iii) average mechanical apertures calculated from XRCT images (Fig. 11).

Fig. 11
figure 11

Relationship between hydraulic aperture and average mechanical aperture, roughness (JRC) and contact area

Full size image

To develop the correlation, we first consider that the contact area is inversely and JRC and average mechanical aperture are directly correlated to hydraulic aperture and that they have exponential relation (following fractal behaviour). Different functions are then fitted to the experimental eh data with average mechanical aperture, roughness (JRC) and contact area relation and the best fit with the least square error is selected (Eq. 11). The aperture calculated by this equation is referred to as calculated eh. The units of both mechanical and hydraulic aperture are in μm.

$${e}_{h}=42.1{e}^{-1.97\mathrm{ln}(JRC\times E)\times {{R}_{c}}^{2}}.$$
(11)

The newly developed correlation is now used to calculate the hydraulic aperture and are then used in Forchheimer’s equation and modified cubic law to estimate the experimental flow rates. The flow rate calculated by both equations is in close agreement with the measured flow rate as shown in Fig. 12. This clearly shows that the developed correlation for estimating the hydraulic aperture has captured main influencing factors in joint gas flow (roughness and contact area) and can be used to predict the joint flow rates in both Forchheimer’s equation and modified cubic within a wide range of Reynolds numbers (laminar/transient flow).

Fig. 12
figure 12

Comparison between flow rate calculated by modified cubic law and Forchheimer's equation using hydraulic aperture estimated by the proposed correlation

Full size image

4 Discussion

The developed correlation not only predicts the experimental flow rate data, but also captures several different flow rate phenomena, e.g. the flow rate dropping significantly at very low normal stresses (0.5 to 3.0 MPa) or flow rate remaining relatively stable in the joints of profile 1 (calculated eh as shown in Fig. 13). This figure shows that the eh decreases significantly till 3.0 MPa, but later becomes constant from 3.0 to 10.0 MPa, which is well in line with what has been observed for the changes in flow rate of profile 1, see Fig. 5. For profile 2, a gradual decrease in flow rate is observed in Fig. 5, and the same is seen for the newly derived hydraulic aperture using the developed model, which continuously decreases with the increase in normal stress explaining the behaviour of the flow rate accurately.

Fig. 13
figure 13

Evolution of the hydraulic aperture with normal stress calculated using Eq. (11) and the experimental data for a profile 1 and b profile 2

Full size image

Furthermore, to assess the validity of Eq. (11) in the direct shear test experimental data, the calculated flow rates based on Forchheimer’s equation are plotted versus the measured flow rate in Fig. 14. A very good agreement is seen between the calculated and measured flow rates. It is, however, observed that two of the measured flow rates stay higher than the calculated flow rate at higher normal stresses on the joints of profile 2 around peak shear stress and during the residual stage. We hypothesise that these deviations occur due to the inability to accurately detect the joint contact area due to damage and degradation of the asperities and production of the gouge at high normal stresses. We recommend a future study to explore the phenomenon of gouge production during shearing process to gain further insight into this process.

Fig. 14
figure 14

Calculated flow rate versus measured flow rate for direct shear test experiments

Full size image

Moreover, for the direct shear test results, where both average mechanical aperture and contact area cannot predict the changes in normalised flow rate (e.g. Figs. 7 and 8), the newly developed model has been successful in explaining the experimental observations. For profile 2 in Fig. 15a, at 0.5 MPa normal stress, a good correlation is found between normalised flow rate and hydraulic aperture. At this stage of the test, the normalised flow rate does not change significantly until the peak shear stress is reached. The normalised flow rate suddenly increases at the peak shear stress but remains constant afterward. The same trend is observed for hydraulic aperture which does not change considerably for the first three measurement points, but an increase is observed for the measurement point after the peak shear stress.

Fig. 15
figure 15

Change in the hydraulic aperture and normalised flow rate with shearing for a profile 1 and b profile 2

Full size image

Likewise, for 1.0 MPa normal stress, the hydraulic aperture is constant initially but later starts decreasing till peak shear stress and a rise is seen after peak shear stress. The normalised flow rate in this case follows the same trend. More importantly, for profile 1 at 0.5 MPa normal stress (where the contact area and average mechanical aperture cannot explain the changes in normalised flow rate), it is seen from Fig. 15b that the hydraulic aperture increases initially and later in the test becomes constant. The normalised flow rate follows the same behaviour, which indicates that the developed model can adequately capture the physical processes involved. The measured normalised flow rate in the case of 1.0 MPa normal stress, again follows the same trend to that of hydraulic aperture.

5 Conclusion

A series of normal deformability and direct shear experiments are performed on non-reactive rock joints with two different roughness profiles. The tests are visualised with time-lapse 3D X-ray micro-computed tomography along with recording the joint gas flow rate in normal deformability and direct shear tests. The results of this study show that the decrease in joint flow rate, with normal stress, in both profile 1 (relatively low roughness) and profile 2 (relatively high roughness) can be correlated to the mean hydraulic aperture changes. Under shearing, however, the sliding of asperities and their degradation causes significant changes in joint normalised flow rate and joint hydraulic aperture. At low normal stresses, the normalised flow rate in the shearing process increases for profile 1, then becomes constant at higher normal stresses. For profile 2, the joint conductivity only increases with shearing at low normal stresses. Contrarily, at higher normal stress, the conductivity decreases with shearing. The changes in average mechanical aperture are unable to explain the changes in normalised flow rate in some cases, demanding a more rigorous insight. The normal deformability test is thus used to develop a new model to predict accurate values of hydraulic aperture based on joint average mechanical aperture, contact area and roughness. The newly developed model accurately predicts the change in flow rate with increase in normal stress and also provides a better understanding of changes in normalised flow rate during direct shear experiments. The developed model is also able to capture the major physical processes involved showing its robustness for practical applications.