1 Introduction

Rockbursting, including strainbursting, as well as spalling, has long been recognised as a crucial failure mechanism in deep underground mines and tunnels (e.g. Cai and Kaiser 2018, Diederichs 2007, Diederichs et al. 2004, Ortlepp 2001, Martin 1997, Kaiser et al. 1995, Ortlepp and Stacey 1994). As tunnelling and mining projects are at greater overburden depths than ever before, the likelihood of strainburst events has increased significantly. This extremely dangerous hazard occurs very suddenly and can release enormous amounts of energy, posing a high risk to worker’s lives and equipment. Hence, there is a need to understand the failure mechanism as completely as possible. This is the only way to effectively anticipate failure and reduce or even avoid the consequences of strainburst.

Cai and Kaiser (2018) define strainburst as a sudden and violent failure of rock near an excavation boundary caused by excessive straining of an un-fractured or partially fractured volume of stiff and strong rock. The primary source of seismicity is the rock mass around the tunnel itself, and not a remote seismic event (Diederichs 2018). Strainbursts are, therefore, a specific kind of rockburst. Rockbursts are mostly associated with hard brittle rock types that are ‘intrinsically’ brittle, i.e. rocks that can store substantial amounts of strain energy before failure and release this energy during a rapid post-peak strength loss. If these rocks fail suddenly in an unstable and violent manner, most of the stored strain energy will be released (Cai and Kaiser 2018). Therefore, the stored strain energy is, besides the loading system stiffness and the in situ stress field, a dominant factor. The potential for energy storage and rapid release must be accounted for in order to understand the burst potential early in the basic design stage. Considerations of rock petrology, fabric, mechanical parameters, and structure allow an estimate of brittle response (Diederichs 2018).

The microstructure of rock is known to influence its strength and deformation characteristics (Eberhardt 1999). Research (e.g. Klammer et al. 2021, Wang and Cai 2018, Peng et al. 2017, Lan et al. 2010, Tang and Hudson 2010, Tang 2000, Dyskin 1999, Wawersik and Fairhurst 1970) indicates that rocks’ heterogeneity at the grain-scale plays an important role in the failure process. Defects (e.g. cracks) as well as mechanical and structural characteristics, depending on their variety, induce local stress concentrations. At locations with increased tensile and compressive stresses, the stress state may reach the critical value and initiate local fracture—even if the overall stress is lower than the rock strength. Simmons and Richter (1976) and Kranz (1983) divide micro-cracks in rock in four types: grain boundary-, intragranular-, intergranular- and multigranular cracks. The initiation, propagation and coalescence of these cracks result in the degradation of material strength which eventually leads to failure (Eberhardt 1999). As each cracking process consumes strain energy, each pre-failure cracking process reduces the available energy at failure. The probability of an intense strainburst event is thus reduced.

As outlined, it has been recognised that rocks’ intrinsic proneness to strainburst (potential to energy storage and rapid release) is an important factor in hazard evaluation. Moreover, it is acknowledged that rock petrology, fabric, mechanical and structural characteristics, and in specific its heterogeneity, should be considered to understand the burst potential. The effects of grain size and porosity, on the initiation and propagation thresholds of stress-induced brittle fractures have also been studied extensively (Eberhardt et al. 1999, Hatzor and Palchik 1997, Hatzor et al. 1997, Wong et al. 1996, Fredrich et al. 1990, Olsson 1974, Brace 1961). Yet, there are still some open questions regarding the quantitative influence of heterogeneity aspects at grain scale, e.g. influence of mineral stiffness. Furthermore, there are still no robust recommendations on how to incorporate that knowledge, e.g. through the inclusion of petrographic information, in strainburst risk assessment.

To improve the understanding of the failure process and its relationship to rocks’ heterogeneity at the grain-scale, a laboratory program on rock-like samples was carried out. Several sample sets were prepared, consisting of a very fine-grained fibreless ultra-high-performance concrete (UHPC) and a constant volumetric fraction of coarse rock grains. Thereby, the heterogeneity aspect was introduced by the different properties of the aggregates. The main focus was placed on the stiffness component. One sample set, consisting of pure UHPC, acted as reference for the ‘rock matrix’. Different rock types were selected for the added coarse grains, based on their mechanical characteristics. Distinct stiff grains in the UHPC simulated the effect of various stiff minerals in real rock samples. The use of artificial samples ensured the reproducibility of tests under controlled conditions.

Within the study, acoustic emission testing (AET) was used. AET is already highly developed and has been used extensively to study fracture behaviour of rock (Zhang et al. 2014, Rao 2012, Amann et al. 2011, He et al. 2010, Stanchits and Dresen 2010, Cai et al. 2007, Moriya et al. 2006, Cai et al. 2004, Eberhardt et al. 1999). Acoustic emission testing can detect small-scale damage prior to failure, and cracks in surrounding rock masses may produce elastic waveforms with frequencies that range from a few Hz to kHz (Cai et al. 2007); these waveforms are derived from acoustic emission sources and contain valuable information about rock mass damage and failure process. AE activities can, therefore, be investigated to assess the levels of damage within rock masses.

This paper summarises the first part of a research project funded by the Austrian Research Promotion Agency (FFG), which investigates the influence of rocks’ (micro-) structure on the failure mechanism ‘strainburst’ within a multidisciplinary study. In the course of the research analysis methods such as Object-Based Image Analysis (OBIA), µCT-scans and AET were used and combined with state-of-the-art rock mechanical laboratory tests. Overall, the paper at hand emphasises the usefulness of petrographic information and AET within strainburst hazard analysis, contributes to a better understanding of the failure mechanism, and sets the basis for investigations on real rock (e.g. Klammer et al. (2021)).

The paper is organised as follows: after a description of the investigated material including its production (Sect. 2), the laboratory test program and its main mechanical results are presented in Sect. 3 and Sect. 4. Section 5 focuses on the acoustic emission testing. Section 6 links the presented results and discusses the relation between strainburst proneness and the structure at grain-scale. Section 7 deals with empirical strainburst parameters, which were determined based on the executed laboratory tests. The results are discussed and recommendations regarding their application are given. The paper concludes with a section summarising the conclusions (Sect. 8) and a section giving an outlook (Sect. 9).

2 Investigated Material

The samples consist mainly of a very fine-grained fibreless ultra-high-performance concrete (UHPC) with a maximum grain size of 0.2 mm, acting as ‘rock matrix’. UHPC was chosen due to its similar mechanical characteristics to rocks prone to strainburst. Those characteristics are a high uniaxial compressive strength in combination with brittle failure tendency. The exact amounts of all ingredients may not be published due to contractual obligations.

Five sample sets were produced for the study. As the first production series featured a high degree of porosity (Klammer et al. 2017), a second production series was produced. This paper deals exclusively with this second series.

One sample set consisting of pure UHPC acted as reference for the ‘rock matrix’. The other four sample sets consisted of UHPC and a constant volumetric fraction (33%) of coarse rock grains. Using different stiff grains heterogeneity was introduced. The different rock types were, therefore, primarily chosen based on the ratio of the Modulus of Elasticity of the original rocks (based on samples taken before grinding them up to the desired grain size) to those of the UHPC-matrix. Table 1 shows the mechanical properties of the chosen rock types and the shape parameters of the admixed rock grains. The values given are mean values of rocks tested in the laboratory. The crushed and sieved rock grains were all washed to remove dust and dried in an oven. Grain shape varied, as outlined in Table 1, due to the different breaking characteristics of the used rock types, e.g. talc breaks completely differently than marble. Due to the different characteristics of the rock types, for an optimal workability, slight modifications (see Table 2) of the basic UHPC-mixture were necessary. For example, the mixture containing talc needed more water as the included talc grains absorbed some of it—leaving less for the matrix. The mixture was deaerated by vibration and cured for two days in the casing. Afterwards the stripped blocks cured for 7 days under water. They were then removed and placed in a drying oven at a constant ambient temperature of 80 °C.

Table 1 Characteristics of the rock aggregates
Full size table
Table 2 Required modifications compared to the basic UHPC-mixture for a total of 7 L of mixture
Full size table

Comparing the stiffness of the aggregates to the matrix, the quartzite containing sample, ‘UHPC-Quartzite’, as well as ‘UHPC-Limestone’ represent the most homogeneous ones besides the pure UHPC sample. The sample containing marble aggregates exhibits a matrix with stiff inclusions as the marble is significantly stiffer than the matrix. Conversely, the sample containing talc aggregates presents a matrix with soft inclusions.

In addition, the degree of porosity of the produced samples was determined. Table 3 shows the total pore volume in percent as well as values for the visible pores on the surface. The total pore volume was obtained based on pycnometer tests (OENORM EN 1936). The visible surface pores (diameter greater than one millimetre) were captured by an alternative pore determination method, which transfers the pores from the surface to a digital picture and evaluates them with the help of a Matlab-routine. The results show that although ‘UHPC-Talc’ features the greatest total pore volume, it exhibits also the smallest pores. The samples with the lowest pore volume were the ‘UHPC-Marble’ and ‘UHPC-Quartzite’ at about 8.5%.

Table 3 Degree of porosity of produced rock-like samples
Full size table

3 Laboratory Test Program

3.1 Overview

The test program consisted of various laboratory tests to describe the mechanical behaviour of the samples. In addition to uniaxial compression tests, ultrasonic P-wave velocity measurements and splitting tensile tests were carried out. The uniaxial compression tests were combined with Acoustic Emission Testing to capture the failure process more accurately. The AE-data and results are discussed in Sect. 5.

3.2 Laboratory Tests

The uniaxial compression tests were carried out in a standard servo-controlled testing machine (MTS 815) and comply with ASTM-standards ‘D7012’ and ‘4543’. Strain gauges measured the longitudinal and lateral deformation during loading. Unloading/ reloading loops were performed to determine the Modulus of Elasticity and some of the most common strainburst parameters. The Modulus of Elasticity was determined according to the Austrian standard ‘OENORM B 3124—9’. Hence, it is a tangent modulus of the unloading part of the first loop within the test procedure. After the last loop, a constant circumferential displacement rate was used to control the loading. In that way, post-failure behaviour could also be obtained for the more brittle samples (Fairhurst and Hudson 1999; Mutschler 2004) and various energy values determined. It is recognised that a Class II post-peak stress–strain curve obtained under lateral-strain-controlled loading is not a pure property of brittle rock. It is influenced by the unloading of the actuator in response to the servo-control system to keep the lateral strain rate constant (Hou et. al. 2021). As the same test machine and the same control method were used for all samples, the determined post-peak stress–strain curves contain relative values regarding the brittleness and failure behaviour of the material. ‘The more brittle a rock is, the more obvious the characteristic of the Class II curve is’ (Hou et. al. 2021). Figure 1 shows the samples prior to and directly after the test execution.

Fig. 1
figure 1

Specimen prior to (top) and directly after the loading (bottom)

Full size image

Ultrasonic P-wave velocity measurements were performed on all samples prepared for the uniaxial compression tests. The ultrasonic unit ‘Ultrasonic-Tester BP5’ from the company Steinkamp was used. To capture also differences within a sample, measurements were done in axial as well as in two radial directions. The Dynamic Young’s Modulus Edyn in axial direction was then calculated after ASTM Standard E1876-15.

To estimate the uniaxial tensile strength, splitting tensile tests (ASTM Standard D3967-16) were carried out. By definition, the uniaxial tensile strength is obtained by the direct uniaxial tensile test. The values obtained by splitting tensile tests are generally higher than the true tensile strength (Perras and Diederichs 2014). As the tensile test is difficult and expensive for routine applications, the Splitting Tensile Test is widely used in practice.

4 Mechanical Properties and Results of Ultrasonic P-Wave Velocity Measurement

Table 4 summarises the results of the laboratory tests. For each rock-like material, a minimum of three samples was tested. As the individual test results within one material match well with each other, one representative sample was chosen to depict the material behaviour. The number below the material designation is the internal laboratory test number of the presented sample. Figures 2 and 3 show the stress–strain curves for the pre-peak and post-peak range.

Table 4 Mechanical properties of produced rock-like samples
Full size table
Fig. 2
figure 2

Stress–strain curves for the pre-peak range

Full size image
Fig. 3
figure 3

Stress–strain curves for the post-peak range. The ‘pure UHPC’ serves as reference curve

Full size image

The samples containing limestone, quartzite and the pure UHPC sample reach uniaxial compressive strengths of about 200 MPa. ‘UHPC-Talc’ with 72 MPa exhibits by far the lowest strength. The tensile strength is quite low with about 3 to 7% of the uniaxial compressive strength. ‘UHPC-Quartzite’ possesses the highest tensile strength with about 10 MPa. ‘UHPC-Talc’ and ‘UHPC-Limestone’ show the lowest with about 5.5 MPa.

The ability to store strain energy strongly depends on the uniaxial compressive strength. The pure UHPC sample shows the highest peak energy (= Energy 100% in Table 4) with 840 kJ/m3. ‘UHPC-Quartzite’ and ‘UHPC-Limestone’ follow with values of about 600 kJ/m3. The sample containing talc possesses the lowest one, not even reaching 200 kJ/m3. The energy, more specifically the strain energy density, was determined as the area under the axial stress—axial strain curve.

Comparing the determined post-peak stress–strain curves, ‘UHPC-Quartzite’ and ‘pure UHPC’ can be characterised as particularly brittle compared to the others. The samples containing talc and marble aggregates show a less brittle behaviour (see Fig. 3). Figure 1 shows the samples after the conducted post-failure compression tests. The samples containing marble and talc aggregates reveal mainly vertical cracks whereas the other samples show areas of intense chipping, which is in good accordance to the obtained test data.

The similarity of the p-wave velocities in axial and diametric directions indicate that the samples are fairly isotropic.

5 Acoustic Emission Testing

5.1 Introduction

Acoustic emission testing (AET) is a passive, non-destructive testing method. The term acoustic emission refers to the generation of transient elastic waves due to a sudden redistribution of stress in a material. The acoustic emissions of a solid material provide information about initiation and propagation of (micro-) cracks and deformation behaviour in general, which gives an idea about the rock behaviour under certain stress conditions (Beattie 2013; Grosse and Ohtsu 2008). The phenomenon that causes such an acoustic emission is called an ‘event’. The detections of signals by the sensors are defined as ‘hits’.

5.2 Test Setup and Execution

An eight-channel system (Micro-II Digital AE System) and six piezoelectric acoustic sensors (PAC Nano30) developed by Physical Acoustics Corporation were used to monitor the cracking process during the uniaxial compression tests. These sensors have good frequency response in the range of 125–750 kHz, and the natural frequency is 300 kHz. They were attached to the sample in an isosceles triangular arrangement and mounted with a silicon adhesive. Coupling tests (Hsu-Nielsen test and automatic pulsing test) according to OENORM EN 13477-2 were conducted before and after the test procedure. The signals were preamplified by 40 decibels. In the used ‘PAC-2/4/6’-preamplifiers, customised filters (300–1200 kHz) were installed to minimise noise. Figure 4a shows the general setup.

Fig. 4
figure 4

a) Testing setup (A = Load Frame; B = AE sensors; C = axial strain gauge; D = circumferential strain gauge) and b) cumulative display of 3D-location of AE events at about 100% of uniaxial compressive strength (in this case, very uniform distribution)

Full size image

The real-time data acquisition and replay software AEwin software from MISTRAS Group Inc. was used to capture AE signals as well as to obtain AE-parameters and locate AE sources. The system timing parameters for calculation of the AE-parameters, PDT (Peak Definition Time), HDT (Hit Definition Time), and HLT (Hit Lockout Time), were set to 50, 100, and 100 μs, respectively. A proper setting of the PDT ensures correct identification of the signal peak for risetime and peak amplitude measurements. Proper setting of the HDT ensures that each AE signal from the structure is reported as one and only one hit. With proper setting of the HLT, spurious measurements during the signal decay are avoided and data acquisition speed can be increased (Mistras Group Inc. 2011). The maximal duration of the AE signals was adjusted to 100 ms and the waveform sample rate was set to 10 Msps (= 10 MHz). To exclude electronic noise and background noise, the level of sensitivity of the system (amplitude threshold) was set to 30 dB.

Three-dimensional localisation (Fig. 4b) was performed by applying the Time of Arrival method. This requires the coordinates of each sensor, the P-wave velocity of the material and the relative arrival time of the P-wave at each sensor. The P-wave velocity used was based on the initial state of the material. An average of those reported in Table 4 and results from AE pre-tests (e.g. pulsing from one AE-sensor to the others) were taken. Velocity changes with increasing micro-fracture damage, especially as peak strength is approached, and the velocity anisotropy increases (Turichshev 2016). The location of each AE source is calculated in the course of a multiple regression analysis by applying the simplex algorithm for minimisation of the travel time residual mean square of the P-waves. Although three-dimensional localisation of the AE sources can be performed using only four sensors, six sensors were used in this study to increase the accuracy and compensate for potential signal losses or dubious data. As no updated 3D-velocity model during loading was used in this study, 3D-location of AE events was mainly used to underline the cracking homogeneity within the samples (as seen in Fig. 4b). AE-analysis focussed more on general AE-parameters (e.g. hit, event, and energy).

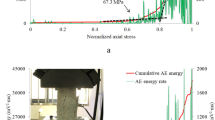
In addition to the AE-data, the stress values were imported from the testing machine. Figure 5 shows typical plots of the real-time data. Figure 5 (top) displays the performed loading loops together with the cumulative number of hits over the time of the pre-failure range of the compression test. The hit values of the six sensors depict well the Kaiser effect, which states that AE activity is only produced when the former maximum stress is exceeded (Lavrov 2003). In other words, discontinuities created in a material do not expand or move before that. However, when the applied load is high enough, significant emissions can occur even though the previous maximum load was not reached. This phenomenon is known as the Felicity Effect (Anastasopoulos et al. 2008). Knowledge on those two effects can be used to determine if major structural defects are present. For this study, the knowledge of those effects was important for a correct post-processing of the AE-data. Otherwise, the AE-results might have been biased by the loading loops.

Fig. 5
figure 5

Real-time data acquisition by the AEwin software: ‘Number of hits vs. time’ diagram (top) and ‘Energy vs. time’ diagram (bottom). Exemplarily for the UHPC-Quartzite sample ‘268.36’

Full size image

The bottom graph of Fig. 5 shows the loading loops together with the energy over the time for the same range as the top diagram. The energy values depict well that for this sample major cracking only takes place above about 95% of the uniaxial compressive strength.

5.3 Post-processing of Data

The software Noesis (Mistras Group Hellas) was also used for post-processing. Both software packages, AEwin and Noesis, are signal based analysis tools.

In the post-processing phase, initially the raw data were cleaned with regard to detached sensors or external ambient noise. In the process, doubtful data for the intervals in question were removed. An example can be seen in Fig. 5. Here, sensor 6 was excluded after t = 960 s because of a strong drop of received signals, potentially due to an off shadowing by a crack. The high amount of released energy at this point also indicates the occurrence of a major crack. Based on the adjusted data, several evaluations were done and summarised in a clear form in an AE-post-processing data-sheet for each sample.

In addition to the typical parametrical analysis, the 3D-location of AE events was assessed (Fig. 4).

The AE-energy is calculated from the time integral of the square of the absolute signal voltage before amplification divided by the impedance and is expressed in attojoule (aJ).

The AE-parameters were calculated for each sensor and then averaged. In addition, the individual AE-parameters were also assigned to the different deformation phases (crack closure phase, elastic deformation phase, steady crack growth phase and unsteady crack growth phase) (Lehtonen et al. 2012, Eberhardt 1999, Martin 1993, Bieniawski 1967, Brace 1964). Crack closure occurs during the initial stages of loading when pre-existing cracks orientated at an angle to the applied load close (Eberhardt et al., 1998). Since this study discusses artificially manufactured samples, most of the observed cracks at low stress levels are not the classical crack closures. They are rather micro-cracks that arise due to the great stiffness difference of matrix and aggregate at first loading. Following the terminology in the literature, this phase was nevertheless referred to as crack closure phase. In general, once the majority of pre-existing cracks have closed, linear elastic deformation takes place. Crack initiation σci represents the stress level where micro-fracturing begins—leading into the steady crack growth phase. In this phase crack growth is stable, which means that it can be stopped by controlling the applied load. At the point of critical energy release or crack damage stress threshold σcd crack growth becomes unstable. In this phase, the relationship between the applied stress and the crack length ceases to exist. Under such conditions, crack growth would continue even if the applied load was kept constant. Precisely establishing these thresholds through laboratory testing can prove difficult (Eberhardt 1998 & 1999). Therefore, the phases were determined using three different methods to identify the key stresses σcc (crack closure stress; beginning of elastic deformation phase), σci (crack initiation stress; beginning of steady crack growth phase), and σcd (crack damage stress; beginning of unsteady crack growth phase).

For the identification via deformation strain analysis, σcc is set as the point where the axial strain reaches linearity for the first time, σci as the point at which the lateral deformation strain deviates from linearity and σcd as the point where the volumetric deformation reaches its inflection point (Eberhardt 1999, Martin and Chandler, 1994, Martin 1993). Eberhardt (1998) found that the thresholds could be more accurately determined by also using acoustic emission measurements. The following two determination methods of deformation phases were based on acoustic emission measurements.

Considering the analysis of the cumulative AE-energy release, σcc refers to the point where the cumulative energy reaches a state of linearity, σci to the deviation of linearity and σcd to the transition to an irregular and exponentially rising energy release.

Another method for the separation of the deformation process into different phases is the unsupervised pattern recognition via Noesis (Kattis 2013). Therefore, five signal characteristics (Sigma 1, Energy, Absolute Energy, Amplitude, and Frequency Centroid) were combined to split the deformation process into clusters with different patterns using the k-means method. However, frequently only three clusters could be detected, whereby the crack closure phase remained undetected. A combination with the other two methods is, therefore, indispensable.

It is important to keep in mind that the obtained AE waveforms and AE waveform parameters are not only a product of the generating mechanism, but also of the material itself, the travel paths and the detection systems.

5.4 AE Results

Regarding the relative limits of the deformation phases (Lehtonen et al. 2012), the transition between the crack closure phase and the elastic deformation phase is about 10% of the UCS. With an average of 6%, the samples containing limestone show the lowest transition value. The marble-containing samples and those without additive show the highest transition values at about 11% of the UCS. The steady crack growth phase starts at about 35% considering the samples with talc or limestone and about 49% for the samples containing quartzite and those without additives. The unsteady crack growth phase begins at about 77% of the UCS for the talc bearing samples and about 85% for the others.

Accordingly, the samples without additives and those containing quartzite show the widest phase of elastic deformation in relation to their UCS, whereas the phases of crack growth (steady and unsteady crack growth phase) are significantly larger in the other samples, especially regarding those containing talc.

In general, the highest amount of released energy takes place in the unsteady crack growth phase. The talc bearing samples, which show also the lowest amount of total released energy, are an exception (Figs. 6 and 7). This is based on an overall more continuous cracking process. The high stiffness difference between the UHPC-matrix and the talc aggregates cause a more distinct crack formation during the early deformation process.

Fig. 6
figure 6

Normalised released energy grouped after the different deformation phases and total released energy

Full size image
Fig. 7
figure 7

Released absolute energy per hit grouped after the different deformation phases

Full size image

To observe the intensity of the acoustic signals, the released energy is divided by the number of hits (Fig. 7). As the total energy release, the strongest hits occur in the unsteady crack growth phase, except for the samples with talc. The samples without additive and those with quartzite show the most intense hits.

The combination of the two diagrams, shown in Figs. 6 and 7, display the failure mechanism and potential strain energy release very well. Typical for strainburst prone samples is a high total amount of released energy, which primarily occurs within the last deformation phase. Another characteristic is a high absolute energy per hit rate within this phase. Hence, such AE-analysis could be used to capture the materials intrinsic susceptibility to strainbursting.

6 Discussion

This section discusses the relation between intrinsic strainburst proneness of the investigated rock-like material and its structure at grain-scale. Special attention is paid to heterogeneity aspects.

In the laboratory, rocks’ intrinsic proneness to strainburst can be assessed by examining the general failure mode in connection to the energy at failure. In terms of hazard assessment, the general failure mode stands for the probability of a brittle failure occurrence, whereas the energy is a value for the magnitude.

In this study, strainburst proneness of the investigated rock-like material is assessed on behalf of the following elements:

  • Stress–strain curves in pre- and post-peak-range,

  • Mechanical properties such as UCS, Modulus of Elasticity and peak energy,

  • Fracture characteristics (see Fig. 1), and

  • AE evaluation results.

To discuss the influence of the grain structure in an organised way, each sample set is compared to the set consisting of pure UHPC indicating the ‘homogeneous’ reference sample. It is assumed that no continuous grain skeleton develops within the artificial samples containing rock grains.

  1. 1)

    UHPC-Talc vs. pure UHPC

The stiffness of the rock-like sample containing talc is close to the stiffness of the pure talc sample. Hence, one can assume that the soft grains govern the stiffness. The high porosity as well as the great stiffness difference between the ‘rock matrix’ and the talc aggregates generate a highly non-uniform stress distribution within the sample. The elongated, flaky shape of the talc grains support the non-uniform stress distribution. Compared to the pure UHPC sample, this leads to an earlier crack formation at stress concentrations. It is supposed that new cracks initiate due to the mentioned characteristics (stiffness contrast, high porosity, grain shape) at grain and pore boundaries, as well as within grains as the talc aggregates possess a relatively low strength. The high stiffness contrast between the matrix and the aggregates, the relatively great pore volume, as well as the flaky grain shape, also lead to the observed earlier crack propagation along boundaries. In addition, the low strength of the talc grains facilitates intra- and intergranular crack propagation. Therefore, the UHPC-Talc exhibits a relatively low crack initiation stress σci and crack damage stress σcd. Hence, it has a less brittle failure behaviour (compare stress–strain curves, fracture characteristics and AE evaluation results) and the lowest overall compressive strength. The AE evaluation clearly shows that the energy release is a distributed over the whole test. The energy per hit is also considerably lower in the crack growth phases (see Fig. 7). This failure behaviour also accounts for less stored energy (compare peak energy and AE evaluation results). Hence, a potential strainburst event is not only less probable, but would also be significantly less violent than in the case of the pure UHPC sample.

  1. 2)

    UHPC-Marble vs. pure UHPC

The stiffness of the UHPC-Marble sample is only slightly higher than that of the pure UHPC sample, although the original marble is considerably stiffer. Therefore, it can be assumed that due to a missing continuous grain skeleton the stiffness is primarily influenced by the ‘rock matrix’. The difference in stiffness within the UHPC-Marble as well as the round yet sharp-edged marble grains lead to a heterogeneous stress pattern. Hence, similar to the UHPC-Talc sample, grain boundary cracks form earlier at stress concentrations. In addition, intragranular cracks form at an early stage as the marble aggregates possess a considerably lower strength than the matrix. It is assumed that due to those mentioned characteristics (stiffness contrast, sharp-edged grains, and low aggregate strength) cracks also propagate earlier at grain boundaries, within grains and through grains. Therefore, the UHPC-Marble sample possesses a relatively low absolute crack initiation stress σci and crack damage stress σcd. This leads to a less brittle failure behaviour and to a low UCS compared to the pure UHPC sample (see stress–strain curves, fracture characteristics and AE evaluation results). This failure behaviour also accounts for less stored energy (compare peak energy and AE evaluation results). The UHPC-Marble sample has a lower susceptibility to strainbursting.

  1. 3)

    UHPC-Limestone vs. pure UHPC

The UHPC-Limestone sample shows more or less the same failure behaviour at a 10% lower stress level than the pure UHPC sample (compare stress–strain curves, fracture characteristics, mechanical parameters and AE evaluation results). Failure occurs in the form of shell-shaped spalling, which is typical for brittle failure. These samples, as well as the pure limestone sample, possess fairly the same stiffness. The degree of porosity of the artificially produced samples is also identical. The lower crack initiation stress σci, 75 MPa compared to 108 MPa, is most likely connected to grain boundary cracks. They presumably result from stress concentrations at elongated, sharp-edged grains. At those grain boundaries, crack propagation starts earlier. Besides a lower UCS, the UHPC-Limestone samples also exhibit an about 20% lower splitting tensile strength than the one of pure UHPC. In terms of strainburst, the failure of the UHPC-Limestone material would lead to an event of lower magnitude (compare peak energy and AE evaluation results) compared to the pure UHPC sample.

  1. 4)

    UHPC-Quartzite vs. pure UHPC

During the conduction of the tests, a similar behaviour was observed. The crack initiation stress σci and crack damage stress σcd are very similar. The slightly lower uniaxial strength might be explained by the relatively low clast strength, which most likely leads to more intra- and intergranular cracks. The lower volume porosity and smaller pore size of the UHPC-Quartzite sample compensates for this to a certain extent. Especially, the more uniform distribution of the small pores leads to a more homogeneous stress field than within the pure UHPC sample. It has to be noted that the splitting tensile strength of the UHPC-Quartzite sample is considerably higher than the one of the pure UHPC. The stiffness of the samples is only deviating slightly. Both, ‘rock matrix’ and admixed grains, determine the stiffness of the artificial quartzite sample. Both samples show very brittle behaviour and high strengths in the conducted tests. In terms of strainburst, those two sample sets and the limestone samples show the highest intrinsic strainburst proneness.

The evaluation underlines the influence of mechanical and structural characteristics at grain scale on rocks intrinsic susceptibility to strainbursting. The potential for high energy storage and rapid release is highly determined by it, especially by its heterogeneity. For example, the comparison between the UHPC-Talc sample and the pure UHPC sample shows this quite clearly. For the determination of strainburst the crack initiation stress σci and crack damage stress σcd are meaningful parameters. Low parameters contradict high energy storage rates, as each cracking process consumes strain energy. Local fractures initiate at locations with increased tensile and compressive stresses, when the stress state reaches the critical value. At the investigated samples, early crack initiation at the grain boundaries is assumedly to be mainly influenced by grain shape (e.g. elongated vs. round) and grain boundary characteristics (e.g. sharp-edged vs. smooth), as well as by a high stiffness contrast within the sample (e.g. mineral stiffness). Crack initiation within grains depends mainly on the strength of the grain. Eberhardt (1999) showed that grain size has a minor effect on crack initiation in crystalline rocks, but plays a bigger role once cracks start to propagate. Larger grains, and thus longer grain boundaries and larger intergranular cracks, provide longer paths of weakness for growing cracks to propagate along. For this study the added grains were all sieved and, therefore, their sizes differed only slightly. A major effect on the failure behaviour was, therefore, excluded. A lower grain strength facilitates intra- and intergranular crack propagation. In this study boundary crack propagation is probably mainly influenced by stiffness contrasts and boundary characteristics. This is reflected well in the results. Porosity seemed to play a minor role in the failure behaviour of the samples. An initial series of samples, that had similar pore volumes, but bigger pores, showed a comparable failure behaviour. The samples possessed only minimal lower values regarding the uniaxial compressive strength and the Modulus of Elasticity. Hatzor and Palchik (1997) outlined a connection between the degree of porosity and the effect of grain size. Obviously, the direction of flaws and structure at grain scale in relation to the loading have also a great influence. Specifically, the evaluations show that a high matrix-clast stiffness contrast, elongated, sharp-edged grains as well as a low clast strength reduce the materials susceptibility to strainbursting and the magnitude potential. Overall, the test results point to the major role of the heterogeneity of the mentioned structural and mechanical characteristics in the failure process and on the materials intrinsic proneness to strainbursting.

7 Empirical Rockburst Parameters

On the basis of the discussed tests, several parameters concerning rocks’ proneness to strainburst can be determined. The following subsections describe the most commonly used parameters briefly, depict the results (Fig. 8 – 12), and comment on their expressiveness.

Fig. 8
figure 8

Results for the Brittleness Index

Full size image

8 Evaluation and Results

The Brittleness Index (B) is a commonly used parameter, which describes the ratio between the uniaxial compressive strength and the tensile strength. Qiao and Tian (1998) and Zhang et al. (2012) propose two conflicting classifications regarding strainburst. The results for the Brittleness Index and the corresponding classifications are shown in Fig. 8.

The Dynamic Rupture Potential (DRP) (Diederichs 2018) expands the approach of Zhang et al. (2012). Thereby it is possible to rank rock types based on their brittle character and the capacity for energy storage, represented by unconfined compressive strength. Figure 9 shows the corresponding diagram, which also includes the results for the presented samples.

Fig. 9
figure 9

Results for the dynamic rupture potential

Full size image

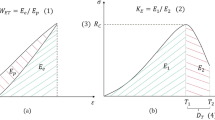
The Potential Energy of Elastic Strain (PES) (Kwaśniewski et al. 1994; Wang and Park 2001) pursues the approach that the elastic strain energy prior to peak strength stored in a volume of rock is directly related to strainburst. The parameter is determined by the following equation. Figure 10 depicts the results for the tested samples:

Fig. 10
figure 10

Results for the potential energy of elastic strain (PES)

Full size image
$$PES= \frac{{\sigma }_{c}^{2}}{2*{E}_{S}} $$
(1)

with σc being the uniaxial compressive strength [MPa] and ES being the unloading tangential modulus at the beginning of the unloading/reloading loop at about 70% of σc [MPa].

The Strain Energy Storage Index (WET) (Kidybinski 1981), also called index F (Wang and Park 2001), describes the rocks’ capacity to dissipate and release energy at failure (see also Eq. (2)). To determine the parameter, an unloading step at about 70–90% of σc is required. The classification, shown in the diagram (Fig. 11), was proposed by Kwaśniewski et al. (1994):

Fig. 11
figure 11

Results for the Strain Energy Storage Index (WET)

Full size image
$${W}_{ET}=\frac{{\Phi }_{sp}}{{\Phi }_{st}} $$
(2)

with Φsp being the retained elastic energy and Φst being the dissipated energy.

Aubertin et al. (1988) (as reported in Tang 2000) propose an index similar to the Strain Energy Storage Index called Brittleness Index Modified (BIM). The index has the advantage that no estimation of σc prior to the test is necessary to set the test procedure. The parameter is determined by Eq. (3) and the results of the tested materials are shown in Fig. 12:

Fig. 12
figure 12

Results for the Brittleness Index Modified (BIM)

Full size image
$$BIM=\frac{{A}_{2}}{{A}_{1}}$$
(3)

with A2 being the total area under the stress–strain curve up to σc. A1 being the triangular area under the linear slope corresponding to the deformation modulus taken at 50% of σc and starting at the peak strength point.

9 Classification and Discussion of the Evaluated Criteria

Table 5 summarises the results of the evaluated empirical strainburst parameters. It can be seen that the assessments of the material vary substantially. In this context, it is also important to address the purposeful distinction between hazard (probability of a strainburst occurrence) and magnitude (magnitude of the shock). While the present study shows a general tendency of highly hazardous materials also having an inclination for strong strainburst, there may be instances where a high hazard coincides with a weaker shock or the reverse.

Table 5 Evaluated empirical rockburst parameters (according to Sect. 6.1)
Full size table

The Brittleness Index (B) according to (Zhang et al. 2012) states that a high compressive strength in proportion to the tensile strength constitutes a brittle behaviour and, therefore, is an indicator of a ‘heavy’ rockburst. The classification seen in the Table 5 shows general accordance with the observed failure mechanism. The only outlier in this case is the UHPC-Quartzite sample. The low value is due to its relatively high tensile strength in comparison to the UHPC-Marble and the pure UHPC sample.

Qiao and Tian (1998) on the other hand suggest the exact opposite: the closer compressive and tensile strength are, the more violent the rockburst. It is supposed that (Qian and Tian 1998) give tensile cracking, and therefore, the tensile strength, high relevance in the rockburst process. A high tensile strength in relation to the compressive strength might, therefore, increase the rockburst proneness of a rock. This classification contradicts the observed failure behaviour.

Regardless of the results, it has to be kept in mind that the Brittleness Index merely reflects the ratio of the two strength parameters. A high compressive strength in combination with a high tensile strength gives the same result as a low compressive strength combined with a low tensile strength. Hence, it does not give any information about the potential energy available. The parameter also does not adequately capture the failure mode. Regardless of the classification method the usefulness of this parameter within strainburst proneness assessment has to be questioned. Nevertheless, it does make sense to have a look at the uniaxial compressive strength and the tensile strength. For rocks with low strength values, strainburst can be excluded.

The Dynamic Rupture Potential (DRP) includes, besides the brittle character of a rock, its capacity for energy storage, represented by the compressive strength. Combined with other indicators, as described in (Diederichs 2018), it is suitable for a first hazard assessment. The classification seen in Table 5 shows general accordance with the observed failure mechanism.

The Potential Energy of Elastic Strain (PES) is basically an estimate of the elastic strain energy prior to peak strength stored in a volume of rock. The estimation is thereby done via an unloading tangential modulus and the uniaxial compressive strength. Hence, this parameter describes the potential magnitude rather than the failure mode. The results, therefore, correlate well with the energy values from the AE evaluation. As a first indicator for rocks’ strainburst proneness, PES is certainly suitable. However, a supplementation by a description of the failure mode would be beneficial.

The Strain Energy Storage Index (WET) reflects the ratio between the elastic strain energy and the energy lost due to plastic deformation. Therefore, it is a good parameter to assess the failure mode. The results correlate well with the stress–strain curves for the post-peak range and the absolute results for the crack initiation and crack damage stresses. Only the WET value of the UHPC-Limestone is relatively high compared to the key stresses σci and σcd. As a first indicator for strainburst proneness, WET is certainly suitable. However, based on the study’s results, the addition of an absolute value regarding potential magnitude is recommended.

The Brittleness Index Modified (BIM) is in its general idea similar to the WET. It reflects the relationship between the total energy and the elastic strain energy. In contrast to the PES, the estimation of the elastic strain energy prior to peak strength is done via an initial loading tangential modulus. This very simplified estimation makes the parameter less expressive. In addition, like WET, the parameter lacks information regarding potential magnitude. Its great advantage compared to PES and WET is that no special test procedure is required for its estimation. This also eliminates the often difficult estimation of the uniaxial compressive strength prior to laboratory testing. However, the results do neither reflect the observed failure mode nor the potential shock magnitude of the tested samples. The BIM results for UHPC-Talc and UHPC-Quartz are even the same. Hence, the application of BIM cannot be recommended.

10 Conclusions

Rocks intrinsic proneness regarding strainburst is a key factor to a robust strainburst risk assessment in the field. Main factors are the potential to energy storage and rapid release. This depends highly on rocks mechanical and structural characteristics at grain scale, especially on its heterogeneity. This study substantiates former research and demonstrates the potential of including rocks structure at grain-scale in estimating rocks intrinsic proneness regarding strainburst well. Five artificially produced sample sets were produced and tested. It could be shown that both stiffness and shape aspects at grain-scale have a great influence on the intrinsic proneness to strainburst of rocks. Elongated grain shape, specific grain boundary characteristics (e.g. sharp-edged), as well as a high stiffness contrast within the sample (e.g. mineral stiffness) promote early crack initiation and propagation. Hence, all those mentioned factors reduce rocks susceptibility to strainbursting and the magnitude potential. Porosity as well as grain size aspects were not investigated specifically in this study.

Within this study, experience in using AET for strainburst risk assessment could be gathered. Typical for strainburst prone samples is a high total amount of released energy, which primarily occurs within the last deformation phase—the unsteady crack growth phase. Another characteristic is a high absolute energy per hit rate within this phase. A further indication is a large elastic deformation phase in relation to the UCS. AE-analysis, as presented in Figs. 6 and 7, are, therefore, well suited for capturing the materials intrinsic proneness to strainbursting.

Furthermore, the study showed that commonly used empirical parameters based on laboratory tests, which evaluate rocks intrinsic proneness regarding strainburst, have to be applied with caution. At best, they provide a rough estimation on either the failure mode or the potential magnitude. DRP, PES and WET are suitable for a first hazard assessment. B and BIM are not recommended. At any rate, any of these parameters should be used at most in combination with other parameters or numerical calculations.

As in many practical cases, analyses at grain-scale (e.g. thin section analyses) are already available and do not incur further costs, including them in modern strainburst risk assessment systems holds quite some potential. The results of this study provide a basis for knowing on which mechanical and structural characteristics at grain scale further research needs to focus. Hence, they set a base for future investigation on real rock, like Klammer et al. (2021), which will hopefully lead to more specific recommendations for practitioners.

Last but not least, it is important to keep in mind that this study deals with the proneness of a rock to violent, brittle failure (e.g. strainburst). For a robust strainburst risk assessment at a specific area, a single parameter can never be sufficient and in situ conditions (e.g. geological features, overburden, and excavation method) have to be taken into account.

11 Outlook

In order to predict, reduce or avoid the consequences of strainburst, it is essential to have a good understanding of the failure mechanism and to put the knowledge gained into practice. Hence, an expansion and further development of the running laboratory program is in process. The focus is on intrinsic properties of rock that promote its tendency to strainburst, as well as on extending the knowledge in AE-Testing and transferring it to on-site monitoring.

Klammer et al. (2021) emphasise the usefulness of petrographic information within strainburst risk analysis. In the study an extensive laboratory program on various rock types has been performed, including uniaxial compression tests (incl. post-failure tests to evaluate the failure energy), acoustic emission testing (to monitor the cracking activity) and Object-Based Image Analysis (to analyse rock’s structure at grain scale). The results show that the hazard mode is highly influenced by the grain-level structure of rock.

Currently, the newly developed testing routine is applied to strainburst prone rock samples from Chile, where major strainbursts have occurred. To verify and refine the results, cooperation with further sites around the world is in planning.

In addition, the aim for future research is to implement the knowledge gained in AE-Testing into in situ monitoring. For this, an installation routine for in situ testing has to be developed. This could be tested in mines or quarries. For testing, the different installation routines in the field and construction sites have to be selected where strainburst events occur regularly. For an optimal preparation, rock samples from these sites should be sent to the rock mechanics laboratory, so that the previously developed testing routine for laboratory samples can be carried out on the specific rock types. Based on this, acoustic emission sensors can be customised and the on-site geological conditions better understood. Here, the goal is to improve the installation of optimised sensors for collecting acoustic emission data and evaluate these data by sophisticated methods.

By implementing this knowledge to up-to-date risk management systems, strainburst predictions are likely to become more accurate so that countermeasures can be implemented more precisely. Overall, this research will hopefully contribute to reduce the safety risk to workers and equipment in tunnelling and mining.