Abstract
Hydraulic fracture in deep rock masses is used across a variety of disciplines, from unconventional oil and gas to geothermal exploration. The overall efficiency of this process requires not only knowledge of the fracture mechanics of the rocks, but also how the newly generated fractures influence macro-scale pore connectivity. We here use cylindrical samples of Crab Orchard sandstone (90 mm length and 36 mm diameter), drilled with a central conduit of 9.6 mm diameter, to simulate hydraulic fracture. Results show that the anisotropy (mm-scale crossbedding orientation) affects breakdown pressure, and subsequent fluid flow. In experiments with samples cored parallel to bedding, breakdown pressures of 11.3 MPa, 27.7 MPa and 40.5 MPa are recorded at initial confining pressures at injection of 5 MPa, 11 MPa and 16 MPa, respectively. For samples cored perpendicular to bedding, breakdown pressure of 15.4 MPa, 27.4 MPa and 34.2 MPa were recorded at initial confining pressure at injection of 5 MPa, 11 MPa and 16 MPa, respectively. An increase in confining pressure after the initial fracture event often results in a significant decrease in flow rate through the newly generated fracture. We note that fluid flow recovers during a confining pressure “re-set” and that the ability of flow to recover is strongly dependent on sample anisotropy and initial confining pressure at injection.
Highlights
-
A new laboratory method designed to measure in situ fluid flow rate through a tensile fracture in a tight anisotropic sandstone at variable confining pressures was reported.
-
Results show an irreversible effect of cycling effective pressure on fluid flow in samples with fracture networks.
-
Tomography data show that variations in fluid flow depends on both fracture thickness and anisotropy.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Global energy consumption is dominated by fossil fuels (Chedid et al. 2007; Aydin 2015), whose demand continues to increase (Aydin 2014a, b; Chang et al. 2012). Conventional hydrocarbon resources have traditionally focused on reservoirs characterized by structural traps and featuring a porous, high permeability reservoir. In contrast, unconventional reservoirs (characterized by low permeability) (e.g. Lee and Hopkins 1994) are often developed and produced by hydraulic fracturing. Whilst in this context, hydraulic fracturing is used to intentionally fracture host rock, it is also an important natural phenomenon in the earth subsurface, exhibited across a range of processes including magma intrusion (Rubin 1993; Tuffen and Dingwell 2005) and mineral emplacement (Richards 2003). However, in the engineered environment, the method has become a standard technique, used in the petroleum industry since the mid-1950’s (Tuefel 1981), to enhance oil and gas production from tight reservoirs (characterized by low permeabilities in the microDarcy range of 10–100’s × 10–18 mD). Hydraulic fracturing is now a common method to improve oil and gas recovery (Gillard et al. 2010; Kennedy et al. 2012; Wang et al. 2014). These new technologies have led some nations (for example the USA) to become significant producers of natural gas (Wang et al. 2014) as previously low permeable formations were fractured. However, the process is not without controversy, and additionally has been developed over years in a somewhat ‘ad-hoc’ or trial-and-error manner (Golden and Wiseman 2014). This has resulted in varying degrees of overall success due to the complexities of reservoirs that contain significant structural, sedimentological and mechanical heterogeneities. Together, these features alter the relationship between the tensile fracture mechanics needed to generate new fractures for fluid movement, as balanced against the fundamental rock physical properties and local stress field (Martin and Chandler 1993; Sone 2013; Gehne and Benson 2017, 2019).
The objective of hydraulic fracture is to increase the rock permeability through inducing new tensile fracture in the rock mass. This is achieved by pumping a pore fluid (with or without additional propping agents to keep new fractures mechanically open) into a wellbore at a sufficiently high pressure to fracture the surrounding rock mass in tension. This, in turn, requires a sufficiently high fluid flow rate to overcome the background permeability and radial fluid flow, which is a function of the permeability of the unfractured rock mass (Fazio et al. 2021). If the fluid injection is higher that the natural fluid dispersion rate, pressure builds up inside the borehole which leads to fracture, including reopening and further propagation of existing fractures when the in-situ tensile rock strength is exceeded. The resultant hydraulic fracture extends until the formation loss is greater than the pumping rate (Reinicke et al. 2010).
Different approaches have been applied to study the pressure (Pb ) at which the rock first yields (fractures), known as the breakdown pressure. The simple linear elastic approach considers a defect-free, impermeable and non-porous rock matrix around the borehole (Hubbert and Willis 1972; Jaeger et al. 2009) via
where σT is the tensile strength (an inherent property of the rock), and Sh and SH are the minimum and maximum horizontal stresses, respectively.
However, the above approach represents an ‘end-member’ case as no rock is truly impermeable: all rocks contain pores and fractures, and when saturated with pore fluid exerting a fluid pressure P0, (Eq. 1) above is modified to:
The expression above (Eq. 2) may be further modified by adding poroelastic effects which account for the rock being both porous and permeable (e.g. Haimson and Fairhurst 1969; Jaeger et al. 2009):
where (α) is the Biot poroelastic coefficient and ν is the Poisson’s ratio.
A final, minor, modification considers the role of rock matrix permeability in hydraulic fracturing. In Fazio et al. (2021), Eq. 3 is assumed to be only valid under conditions whereby the bulk rock permeability (kw) at the interface between the injection fluids and the wall is below a critical permeability (kwc). Adding these boundary conditions yields:
An accurate charaterisation of the fluid flow through the bulk rock mass is key to understanding reservoir properties (Tan et al. 2018). However, measuring permeability remains challenging due to its sensitivity to heterogeneity. This is further complicated by the strong anisotropy found in typical formations used for unconventional hydrocarbons (such as mudrock, shale and crossbedded/tight sandstone). Nonetheless, numerous studies using wellbore tools and core plugs have attempted to link the fracture process to permeability enhancement via numerical models (Ma et al. 2016). To calibrate these models and in situ data, laboratory measurements of flow through fractures under controlled conditions have used images of the post-test fracture aperture (e.g. Stanchits et al. 2014) or morphology of the post-test shear fracture planes (Kranz et al. 1979; Bernier et al. 2004; Gillard et al. 2010, Zhang 2015a, 2015b), as a function of flow rate or permeability. Collectively, these experiments have provided useful data on fracture behavior, but have tended to focus on mudrocks (shale) over other rock types.
There is a large body of laboratory research examining the controlling elements that affect the propagation of hydraulic fractures, such as stress controls, injection parameters, and interactions with preexisting structures (e.g. bedding planes and/or fractures). Hubbert and Willis (1957) were the first to explore stress controls on fracture propagation, determining the anticipated orientation of fractures with regard to tectonic stresses, assuming tensile (Mode I) failure. Chitrala et al. (2013) found that both shear and tensile failure modes are prevalent in hydraulic fracturing, as revealed by focal mechanism data from Acoustic Emissions (AEs), while Solberg et al. (1977) found that whether shear or tensile failure is the primary mechanism is related to stress ratio. The fluid viscosity, pressurisation (injection) rate, and, more recently, cyclic injection schemes have all been noted as key injection parameters.
Data from Ishida et al. (2004), Stanchits et al. (2015), and Zoback et al. (1977) all indicate that high viscosity fluid is more likely to lead to stable fracture propagation, likely due to high viscosity fluids being less able to easily penetrate tight fractures. Breakdown pressures have also been reported to be influenced by the rate of pressurisation or injection, with higher injection rates leading to higher breakdown pressures (e.g., Cheng et al. 2020; Haimson and Zhao 1991; Lockner and Byerlee 1977; Zhuang et al. 2019). Finally, fluid injection is not limited to constant pressure or flow rates. Hofmann et al. (2018), Patel et al. (2017), and Zhuang et al. (2019, 2020) presented experimental and field work on cyclic injection systems, noting that fracture breakdown pressure is generally lower than comparable constant pressurisation methods, and likewise resulting in a lower maximum amplitude of associated AE events produced by fracture formation. Such methods may be useful for lowering seismic energy releases in a production environment.
The analysis of fracture propagation with respect to anisotropic mechanical qualities and preexisting interfaces is a key challenge, given that the rocks most targeted for unconventional oils (shale and tight sandstone) have pervasive layered structure. This bedding, from m to mm in scale, is a key factor that leads to anisotropy in rocks (Vernik and Nur 1992; Hornby 1998) in terms of both rock physics and permeability (e.g. Benson et al. 2003, 2005). Anisotropy of the rock also affects the strength (Amann et al. 2012; Ulusay 2014; Zhou et al. 2008) which invariably control the fracture orientation during tensile fracture due to hydraulic fracture. Experimental and numerical studies have revealed that a larger differential horizontal stress induces dominant cross‐cutting hydraulic fractures (Hou et al. 2019; Tan et al. 2017; Xu et al. 2015). Fluid flow through this fleshly generated tensile fracture is then controlled by the fracture properties such as aperture, length, asperity and tortuosity (Kamali and Ghassemi 2017; Ye et al. 2017). Permeability enhancement in rocks through hydraulic fracture processes is a key application and has been widely reported (Nara et al. 2011; Zhang et al. 2015a, b; Patel et al. 2017) to measure the increased effectiveness of tight oil and gas reservoirs (Tan et al. 2019).
However, the focus of the bulk of past research in this area has tended to be on shale. Here, we report a new laboratory study designed to measure the fluid flow rate through tensile fractures in a tight anisotropic sandstone (Crab Orchard), with respect to its anisotropy, generated mainly by mm-scale crossbedding. Whilst less extensive than shale, such tight sandstone is frequently encountered in a range of hydrocarbon exploration scenarios. Fractures are freshly generated in the tensile mode using water, via the method of Gehne and Benson (2019) before fluid flow data are taken, up to simulated reservoir conditions to 0.5 km. Fracture aperture data are then imaged post-test using X-ray Computed Tomography (CT) to analyze the final fracture aperture to measured flow rate. Our laboratory setup is designed to eliminate the possibility of altering the fracture properties when extracting the fractured sample as flow rate data is taken immediately after the main macro-scale fracture, and so allows better comparison between the fluid-driven tensile fracture processes (and the associated flow enhancement), to reservoir conditions. Finally, we link these fracture mechanics and fluid flow through the fracture to the accompanying Acoustic Emission (AE, the laboratory proxy to tectonic seismicity) as an additional guide to the timing and development of fracture properties with respect to the mm-scale crossbedding.
2 Experimental Methods
2.1 Sample Materials and Preparation
Crab Orchard sandstone (COS) has a relatively low permeability and porosity for a sandstone of approximately 10–18 m2 and 5%, respectively (Benson et al. 2003). The rock, from the Cumberland Plateau, Tennessee (USA), is a fine grained cross bedded fluvial sandstone, with sub-hedral to sub-rounded grains of about 0.25 mm size. It consists predominantly of quartz (> 80%) with little feldspar and lithic fragments cemented by sericitic clay (Benson et al. 2006). This material exhibits a high anisotropy (up to 20% P-wave velocity anisotropy and up to 100% permeability anisotropy), and has a tensile strength calculated through the Brazilian Disc (Ulusay 2014) of 9.8 MPa perpendicular to bedding and 8.6 MPa parallel to bedding.
Cylindrical samples of 36 mm diameter and approximately 90 mm in length were cored from blocks with a long axis either parallel (defined as the x-orientation) or normal (z-orientation) to the visible bedding plane (Fig. 1A). Samples were then water-saturated by immersing in water using a vacuum pump to extract void space air for a minimum of 24 h (for ‘saturated’ hydraulic fracture experiments). Each core sample had a central axially drilled conduit of 10.5 mm diameter through the length of the sample, generating a ‘thick-walled’ cylinder arrangement (Fig. 1A) that can be accommodated into a standard triaxial apparatus. The samples are inserted into a 3D-printed liner (Fig. 1B) that is, in turn, is encapsulated in a rubber jacked (Fig. 1C). This allows water from generated tensile fractures to be received, regardless of their radial orientation, by a water outlet port (Gehne and Benson 2019).
a Sample cored in Z and X orientations with respect to the visible mm-scale crossbedded sandstone. b 3D printed water transport liner. c Sample assembled in the liner and rubber jacket. d Cross section of sample with water guide showing the pressurized zone (modified after Gehne and Benson 2019)
The sample setup is completed by fitting two steel waterguides (Fig. 1D) into the central conduit. These waterguides direct pressurized fluid (water) into a sealed section of the drilled conduit (using O-rings), allowing fluid to apply a uniform pressure to the inner surface of the sealed section, leading to tensile fracture in the central section from which water flow is received via the outlet port, measured using a volumeter.
3 Hydraulic Fracture Procedure and Protocol
Sample assemblies were mounted within a conventional servo-controlled triaxial machine capable of confining pressures up to 100 MPa (Fig. 2). Four 100 MPa servo-controlled pumps provide: (i), axial stress through a piston-mounted pressure intensifier to provide a maximum of 680 MPa, (ii), confining pressure up to 100 MPa. Both these pumps use heat transfer oil (Julabo Thermal HS) as pressurizing medium. Two pore pumps independently provide fluid pressure to (iii), the bottom of the sample (via the lower waterguide) and (iv), receive water through the generated tensile fracture and exiting via the fluid outlet. After fracture, pumps (iii) and (iv) are set to maintain a set pressure gradient and thus establish steady fluid flow through the freshly generated tensile fracture. The final flow rate value is only taken when the flow between the two pumps have achieved a steady, but equal and opposite rate to signify no leaks in the system and to allow transients to settle (approximately 2 min).
Mechanical data (stress, strain, fluid pressures) are recorded at both a ‘low’ recording rate of 1 sample/second and high sampling rates (10 k samples/s), for axial strain and fluid injection pressure only, to record fast changing transients (Gehne et al. 2019). In addition, a suite of 11 acoustic emission sensors, fitted to ports in the engineered rubber jacket (Fig. 1C), received Acoustic Emission (AE) data to monitor fracture speed and progress. The AE signals are first amplified by 60 dB and then received on an ASC “Richter” AE recorder at 10 MHz. For accurate seismo-mechanical data synchronisation during the dynamic tensile fracture, the fluid injection pressure output is split across both mechanical and a single channel of the AE data acquisition systems through an amplified circuit as described by Gehne (2018). This allows data synchronization with an accuracy of ± 0.01 ms.
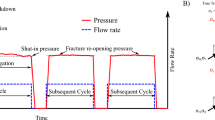
The experimental procedure spans three stages (Fig. 3). First, hydrostatic pressure is established by increasing the confining pressure and the axial pressure concomitantly to attain the target pressure, and a pre-fracture measurement of fluid flow is taken by setting a differential pressure of 2 MPa between central conduit and the fluid outlet port. Second, pore fluid injection was activated at a constant flow rate of 5 mL/min resulting in an increasing conduit pressure, until failure (hydraulic fracture) occurred (Fig. 3). Evidence of fracture development includes a sharp decrease in injection (pore) pressure, accompanied by a swarm of AE. Third, after tensile failure, a fluid pressure gradient (differential fluid pressure of 2 MPa) was re-established between the conduit pressure and the fluid outlet port to initiate a steady-state flow through the freshly generated tensile fracture(s). The volume of the two pressure pumps were monitored independently; steady-state flow is reached when the volume change with time is equal and opposite for the two pumps, averaged across a 4-min time period and after an initial 2 min elapsed to allow transient effects to decay away. This procedure was repeated as a function of confining pressure increase (and decrease) to investigate the effect of confining pressure and pressure hysteresis on flow rate.
Overview plot of a typical experiment with injection pressure (blue), confining pressure (black) and axial stress (red) with time, showing the 3 experiment stages: (i) Pre-hydraulic fracture (pre HF) flow (after hydrostatic conditions are established); (ii) The hydraulic fracturing stage (HF): axial stress (σax) is increased simultaneously with the injection (pore) pressure increase to maintain approximate hydrostatic conditions during fluid injection; (iii) Post hydraulic fracture (Post HF) flow (with hydrostatic conditions re-established) (colour figure online)
The experimental procedure is summarised in the flowchart (Fig. 4). Initially, the sample assembly is loaded in the the triaxial apparatus, the AE sensors are installed and system integrity is tested for leaks by pressurising the chamber with Nitrogen gas. If there is no leak, indicated by pressure communication between the chamber and the injection pressure pump, the chamber is filled with oil and pressurised until the initial pressure conditions (axial stress and confining pressure) are established. During this process of initial setup, a servo feedback loop is used to maintain a differential stress (Axial stress – Confining pressure) of 0.5 MPa to hold the assembly securely. The target confining pressure is then set for the experiment, with axial stress tracking confining pressure and set higher by approximately 5 MPa. An initial (pre hydraulic fracture) flow rate is measured for about 10 min; during this time the AE activity is monitored and decays to background level. The hydraulic fracture (HF) experiment is then performed by injecting water into the sample chamber using a constant injection rate of 5 mL/Min until breakdown is recorded. Finaly, the post-experiment flow rate through the fracture is measured by setting a differential pressure of 2 MPa between central conduit and the fluid outlet. The chamber is de-pressurised, sample retrieved, and XCT scan is conducted for fracture visualisation and analysis.
4 Results
Six experiments were conducted on COS at initial confining pressures (before injection) of 5 MPa, 11 MPa, and 16 MPa. At each pressure, a pair of samples were cored with long axis either parallel or perpendicular to bedding. As detailed above, for each sample an initial fluid flow is measured by setting a differential pore pressure (difference between conduit and outlet pressure) and measuring at the upstream and downstream reservoir (Fig. 3). These initial flow rate data are tabulated in Table 1.
4.1 Hydraulic Fracture
Results from sample COSx-1 (5 MPa initial confining pressure, core axis parallel to bedding) is shown in Fig. 5. As fluid was injected, a concomitant increase in injection pressure is recorded. This continues until an experiment time of approximately 1276 s where tensile fracture is recorded at an injection pressure (or breakdown pressure, Pb) of 11.29 MPa, accompanied by a swarm of AE which increases steadily from 1260 s, reaching a peak of 225 counts/s. After fracture, the injection pressure rapidly decreases to 2 MPa, and cumulative AE reaches a steady value.
At 5 MPa confining pressure with the sample axis perpendicular to bedding (sample COSz-1), we see the injection pressure building until a breakdown pressure of 15.4 MPa (Fig. 6), some 4 MPa higher than parallel to bedding for the same pressure. Again, after the hydro-fracture event injection pressure decreases rapidly to approximately 2 MPa (Fig. 6). Relatively few AE events (and rather sparsely distributed in time) were recorded during the time of fluid injection (2344 s to 2366 s), however, a swarm of activity was recorded at the moment of fracture, as expected. The cumulative AE count increases rapidly at this point up to a peak of 4 × 104 counts at 2367 s.
At 11 MPa and parallel to bedding (experiment COSx-2), breakdown occurs at an injection pressure of 27.7 MPa (Fig. 7). Breakdown occurred at a fluid pressure of 27 MPa, and is again accompanied with a swarm of AE at 2364 s (Fig. 7). The cumulative AE steadily increases from 4598 s to 2 × 102 counts after approximately 4630 s, followed by a significant and rapid final increase at the moment of fracture at 4634 s and a peak of 105 counts.
Mechanical data for sample COSz-2 (11 MPa and perpendicular to bedding) are shown in Fig. 8. Data exhibit a similar trend in injection pressure as seen for sample COSz-1, with a sharp decrease as tensile fracture is generated accompanied by a peak in AE events. A breakdown pressure of 27.3 MPa is recorded in COSz-2, which decreases rapidly to approximately 6 MPa, again accompanied by a swarm of AE events which decrease in counts over time until approximately 3540 s. However, the trend in AE leading up to failure is different, with no build-up in AE prior to the prominent swarm of activity failure time, resulting in a large cumulative AE count of 1.2 × 106 counts at 3531 s.
At 16 MPa and parallel to bedding (experiment COSx-3), breakdown occurs at an injection pressure of 40.4 MPa which decreases rapidly to approximately 15 MPa after fracture, again accompanied with a swarm of AE (Fig. 9). Abundant AEs were recorded from approximately 4955 s, rapidly increasing at the moment of breakdown pressure when compared with samples COSx-1 and COSx-2 (Fig. 9). Cumulative AE count increases at 4956 s to a peak of 7 × 105 at 4981 s.
Finally, for sample COSz-3 (16 MPa and parallel to bedding), tensile fracture was recorded at injection pressure of 43.5 MPa accompanied once again by a swarm of AE (Fig. 10). The conduit pressure decreases rapidly after fracture, reaching 16 MPa just a few seconds after the tensile failure event. Similar to previous experiments, abundant AEs were recorded with an increase in cumulative AE count first registered at 5120 s, increasing in a number of swarms at 5140 s and 5160 s until maximum was recorded at 5180 s of 1 × 104 counts (Fig. 10).
4.2 Post-fracture Fluid Flow
With the tensile (radial) fracture established across samples at three different initial confining pressures, and across two different orientations with respect to anisotropy, a set of fluid flow measurements are made. Fluid flow is measured in cycles of increasing confining pressure followed by a ‘re-set’ to the original confining pressure; this is followed by a second cycle of increasing confining pressure. Figure 11 shows data from COSx-1 and COSz-1 (5 MPa initial conditions). Here, an increase in confining pressure (from 5 to 26 MPa) for COSx-1 (parallel) results in flow rate decreasing from 1.67 mL/min to 0.043 mL/min, respectively. During the re-set of confining pressure from 26 to 5 MPa, flow rate recovered only marginally, increasing from 0.043 mL/min to 0.134 mL/min. The second cycle of confining pressure increase gives a further reduction of flow rate from 0.134 mL/min to 0.028 mL/min, lower than the minimum of the first cycle. Sample COSz-1 (perpendicular) shows a decreasing flow rate from 0.6 mL/min at 5 MPa confining pressure to 0.027 mL/min at 26 MPa confining pressure. During the ‘re-set’ of confining pressure from 26 MPa, flow rate recovered from 0.027 to 0.099 mL/min. The second cycle of confining pressure increase resulted to a further reduction in flow rate from 0.099 mL/min to 0.014 mL/min.
Average flow rate for first cycle (continuous cyan line) and average flow rate for second cycle (discontinuous cyan line) for COSx-1 and average flow rate for first cycle (continuous pink line) and average flow rate for second cycle (discontinuous pink line) for COSz-1 are calculated at each steady-state condition for every confining pressure step, plotted as a confining pressure (colour figure online)
Figure 12 shows data from COSx-2 and COSz-2 (11 MPa initial conditions). For sample COSx-2 (parallel), a general decreasing trend in flow rate was measured for a confining pressure increase from 11 to 31 MPa (Fig. 12). In the first cycle, the flow rate decreases from 0.043 to 0.0073 mL/min, respectively. The confining pressure re-set resulted in a flow rate recovery from 0.0073 to 0.014 mL/min. The second cycle of confining pressure increase generates a reduction in flow rate from 0.014 to 0.0067 mL/min. Conversely, for COSz-2 (perpendicular), the flow rate decreases from 0.0375 to 0.0042 mL/min at 11 and 31 MPa confining pressure, respectively. Pressure is again re-set, resulting in a flow rate recovery from 0.0042 to 0.0105 mL/min. The second cycle of confining pressure increase gives a further reduction of flow rate from 0.0105 to 0.0013 mL/min.
Average flow rate for first cycle (continuous cyan line) and average flow rate for second cycle (discontinuous cyan line) for COSx-2 and average flow rate for first cycle (continuous pink line) and average flow rate for second cycle (discontinuous pink line) for COSz-2 are calculated at each steady-state condition for every confining pressure step, plotted as a confining pressure (colour figure online)
Figure 13 shows data from COSx-3 and COSz-3 (16 MPa initial conditions). For sample COSx-3 (parallel), flow rate decreases from 0.27 to 0.05 mL/min from 16 to 31 MPa, respectively (Fig. 13). Confining pressure re-set results in a marginal flow rate recovery from 0.05 to 0.09 mL/min. The second cycle of confining pressure increase then results in a further decrease in the flow rate from 0.09 to 0.029 mL/min. Conversely, for sample COSz-3 (perpendicular), flow decreases from 0.09 mL/min at 16 MPa confining pressure to 0.017 mL/min at 31 MPa. Confining pressure is again ‘re-set’ from 31 to 16 MPa resulting in almost no recovery (0.017 to 0.018 mL/min) followed by a final confining pressure increase which resulted to a further decrease in the flow rate from 0.018 to 0.011 mL/min.
Average flow rate for first cycle (continuous cyan line) and average flow rate for second cycle (discontinuous cyan line) for COSx-3 and average flow rate for first cycle (continuous pink line) and average flow rate for second cycle (discontinuous pink line) for COSz-3 are calculated at each steady state condition for every confining pressure step, plotted as a confining pressure (colour figure online)
5 Discussion
Hydraulic fracturing has been established as a key process in both a natural environment (e.g. magma intrusion, and mineralization) as well as the engineered geo-environment, most frequently to develop hydraulic fractures in unconventional reservoirs (Guo et al. 2013; Gehne and Benson 2017, 2019; Tan et al. 2018). The ultimate aim of these methods is to generate a higher permeability in the rock mass for developing the reservoir that would otherwise be uneconomic. However, whilst there have been a large number of studies investigating the fluid flow and permeability properties of highly anisotropic rocks such as shale (e.g.; Walsh 1981; Benson et al. 2005; Gehne and Benson 2017), studies investigating the fracture mechanics of shale (e.g. Hubbert and Willis 1972; Zoback et al. 1977; Teufel and Clark 1981; Rubin et al. 1993; Reinicke et al. 2010), and studies combining these two elements (e.g. Fredd et al. 2001; Guo et al. 2013; Zhang et al. 2015a, b), there are far fewer studies investigating low porosity or ‘tight’ sandstone. This is important as the hydraulic properties of low porosity rocks, like shale, is also significantly modified by both pressure and are often highly anisotropic due to small scale crossbedding, such as in COS (e.g. Gehne and Benson 2019). In addition, like unconventional shale reservoirs, tight sandstone (and limestone) reservoirs are increasingly being targeted for new hydrocarbon exploration.
Here, we have conducted a series of hydraulic fracture experiments in a tight sandstone (nominally 5% porosity and 10–18 m2 permeability) with fluid flow measurement directly after this stage in order to assess fluid flow enhancement as a function of anisotropy across cycles of confining pressure. In our experiments, we note a distinct interplay between the inherent anisotropy of the fracturing materials, with samples cored with long axis perpendicular having a higher breakdown pressure than those parallel to bedding, and the effect of the overall confining pressure. We develop our discussion along these two lines of enquiry below. In general, the cycles of effective pressure have a largely irreversible effect on fluid flow. This is consistent with past studies, including from large sample volumes (Guo et al. 2013; Tan et al. 2018).
5.1 Effect of Anisotropy
Results from the mechanical data show that bedding plane orientation has an effect on the strength and energy release (using AE as a proxy) during tensile fracture at two of the three pressures tested. At low confining pressure (5 MPa) a breakdown pressure of 11.3 MPa (parallel) and 15.4 MPa (perpendicular), respectively (Table 1; Figs. 4 , 5) is measured, a difference of 4.1 MPa. At the highest confining pressure (16 MPa), a breakdown pressure of 40.5 MPa (parallel) and 43.5 MPa (perpendicular), respectively (Table 1; Figs. 9, 10) is measured, a slightly lower difference of 3.0 MPa. This observation suggest that mechanical properties of the rock is influenced by confining pressure (Wang et al. 2021) and the orientation of the bedding (Chong et al. 2019; Guo et al. 2021). However, this mechanical anisotropy is not measured at the intermediate pressure of 11 MPa. At every pressure, breakdown is accompanied by a significant swarm in AE output, and for 5 MPa and 11 MPa confining pressures, with higher cumulative AE counts in experiments conducted perpendicular to bedding compared to parallel to bedding, suggesting these orientations release more energy as supported by previous data (Guo et al. 2021). However, this pattern is not seen in the data from 16 MPa (Figs. 9, 10); we posit that the higher confining pressure increases the energy required to hydraulically fracture the sample irrespective of fracture orientation by increasing the tensile strength and compliance of the rock (Jaeger et al. 2009). This is further reinforced by AE data with more events recorded at 5 MPa (Figs. 5, 6), and parallel to bedding at 11 MPa (Fig. 7), but no AE data were recorded before 4955 s and 6918 s at 16 MPa (Figs. 9, 10, respectively).
Anisotropy also provides the major influence on fluid flow, with samples cored parallel to the bedding orientation recording a high fluid flow rate at a given confining pressure compared to perpendicular to the bedding orientation. Our data reveal an initial fluid flow anisotropy (the ratio of flow in samples fractured perpendicular to parallel to bedding) of 0.4 at 5 MPa, 0.9 at 11 MPa, and 0.3 at 16 MPa, illustrating a very low fluid flow anisotropy even at high effective pressures. This general result is consistent with that obtained by Gehne and Benson (2017), which shows that fluid flow is significantly influenced by bedding plane orientation. However, the fluid flow anisotropy as measured on our tensile fracture samples is generally lower than the equivalent permeability anisotropy measured in unfractured samples (Benson et al. 2005; Gehne and Benson 2017) particularly at high effective pressures. Our data compare to fluid flow (permeability) anisotropy of 16.5–25% as reported for unfractured Crab Orchard sandstone at 5–30 MPa confining pressure (Gehne and Benson 2017).
To better understand the complexities of heterogeneity and fluid flow, we have collected X-Ray Computed Tomography (XCT) data on each sample post-test (Fig. 14). These images were segmented in Avizio to extract an approximate fracture tortuosity with respect to bedding plane orientation (Fig. 15). Using these images, we note that samples cored parallel to bedding exhibit a slightly lower fracture thickness of about 35 microns (Fig. 15A), while samples cored perpendicular to bedding have fracture thickness of about 45 microns (Fig. 15B). However, we also note that the fluid flow data, both pre- and post-fracture, is likely to follow a largely radial pathway, whereas the comparison to past permeability data (e.g. Gehne and Benson 2017) is specific to Darcy flow. Hence, we present fluid flow in this study rather than permeability. Combined, this analysis suggest that a single fracture tends to develop in samples at a low confining pressure (5 MPa), irrespective of anisotropy. Whereas at elevated confining pressure (11 MPa and 16 MPa), two fractures were favoured parallel to bedding (Fig. 14C, E), and a single fracture in samples perpendicular to bedding (Fig. 14D, F).
X-ray Computed Tomography showing tensile fracture: A fracture geometry in COSx-1, B fracture geometry in COSz-1, C fracture geometry in COSx-2, D fracture geometry in COSz-2, E fracture geometry in COSx-3, F and fracture geometry in COSz-3. In all cases a prominent fracture is seen orientated lower-left to top-right, and favoring two fractures in samples cored in the ‘x’ direction for COSx-2 and COSx-3 (panels C and E), one fracture for COSx-1 (panel A) and one fracture in samples cored in the ‘z’ direction (panels B, D, F)
Analysis of the tensile fracture showing thickness and pore connectivity; The insert is a histogram distribution of the thickness for both fracture and pore space: A fracture thickness in COSx-1, average 35 μm, B fracture thickness in COSz-1, average 45 μm, C fracture thickness distribution in COSx-2, average 100 μm, D tensile fracture thickness for COSz-2, average 145 μm, E tensile fracture thickness in COSx-3, average 75 μm, F fracture thickness in COSz-3, averaging 40 μm
5.2 Effect of Confining Pressure
The increase of initial confining pressure from 5 MPa, through 11 MPa, and to 16 MPa has the overall effect of increasing the breakdown pressure, respectively, to 10, 27, and 40 MPa for samples parallel to bedding, and to 15, 27, and 43.5 MPa perpendicular to bedding. This is consistent with the findings of Jaeger et al. (2009) and Haimson and Fairhurst (1969) who postulated that an increase in confining pressure increases the horizontal stresses and hence a resultant increase in breakdown pressure as expressed in equation(s) 1–4. A key output when considering fluid flow through newly generated tensile fracture is the pressure history on fracture properties (a key control on the bulk fluid flow).
Previous data focusing on cyclical fluid flow on solid samples of COS have reported a reduction of permeability in subsequent cycles of between approximately 66–70% (Gehne and Benson 2017). For fluid flow through a tensile fracture, as shown here, the equivalent decrease per fluid flow cycles ranges from 92% (COSx-3) to 68% (COSx-2) to 95% (COSx-1). This suggests that the addition of the tensile fracture increases the compliance of the rock, and therefore, makes the application of confining pressure more sensitive when measured in terms fluid flow. Similar effects were also reported by Nara et al. (2011). Conversely, in hydraulically fractured samples, we find that the hysteresis in fluid flow is more sensitive to the overall specimen anisotropy (i.e. whether fluid flow is parallel to perpendicular to bedding). At each initial pressure, post-fracture flow rate is lower in the z-orientation samples (Fig. 1) compared to x-orientation despite larger fracture aperture (Fig. 15). This suggests that these larger average apertures are generally more tortuous, resulting in a lower flow rate, which is consistent with fracture in the z-orientation, or so-called divider orientation, where the tensile fracture crosses multiple layers of bedding (Gehne et al. 2020). This is consistent with previous work linking tortuosity to permeability (Tsang 1984), with data suggesting that fluid flow through a highly tortuous path depends on both fracture aperture and roughness (Murata and Saito 2003; Xiao et al. 2013). In our study, we see similar complexity resulting in overall lower flow rates, despite having reasonably high aperture width; we attribute instead the low flow rate to the high tortuosity of the flow path, as verified by our post-test XCT analysis (e.g. Fig. 15D).
Finally, we note that once confining pressure is released, the fluid flow does tend to recover but not to its initial value at injection. This phenomenon is known as flow hysteresis and has been widely studied and reported (e.g. Gehne and Benson 2017). It is likely that rocks with significant clay and fine crossbedding, such as this tight sandstone, promotes the formation of tensile fractures of low compliance, therefore causing them to fail to reopen during subsequent pressure cycles. This would be manifested as an irreversible decrease in the fracture aperture and, therefore, lower permeability (Walsh 1981; Vinciguerra et al. 2004), as observed in our experiments.
6 Conclusions and Recommendations
In this study, we have investigated the influence of confining pressure and anisotropy on fluid flow through tensile fracture under simulated in situ pressures relevant to hydraulic fracture in a low porosity (tight) sandstone (Crab Orchard). We find that a general increase trend in breakdown pressure and cumulative acoustic emission when confining pressure increases, which leads to an irreversible decrease in fluid flow through the tensile fracture when confining pressure is cycled. In addition, breakdown pressure is higher in experiments with samples cored parallel to bedding at a lower confining pressure (5 MPa), this effect decreases at higher confining pressure (11 MPa and 16 MPa) at injection. We conclude that anisotropy is a significant contributing factor to both the fluid flow hysteresis effect and breakdown stress, with the tortuosity a key factor rather than fracture aperture alone in describing fluid flow rate through the fracture.
In general, the fluid flow is higher in experiments with samples cored parallel to bedding and additionally has weaker recoverability when confining pressure is ‘re-set’. We observed two stages of flow rate reduction during in the two cycles of confining pressure. The first cycle of confining pressure is identified by a rapid decrease in flow rate (e.g. 97% for COSx-1 and 95% for COSz-1), while the second cycle is characterized by a slow decrease in flow rate (e.g. 79% for COSx-1 and 86% for COSz-1). We conclude that it is likely that a combination of mechanisms operate, and must be considered in determining the overall permeability of tight sandstone to regional stresses during burial and uplift (expressed as confining pressure cycles and ‘re-set’). This is not limited to tight sandstone but also a low permeability anisotropic rock material such as shale and mudstone. Finally, we suggest that the open fracture compliance is also important, particularly with regards to cyclical pressure and stress, which is further complicated for rocks such as Crab Orchard that have significant clay content.
This study also highlights the effect of scale and heterogeneity. The smaller grain and finer layering of shale has likely led to more consistent and reliable experiments as previously reported by Gehne et al. (2020) compared to the tight sandstone used in this study. With coarser, mm-scale anisotropy, as seen here in the Crab Orchard Sandstone, it is likely that cm-scale samples are below the minimum size for reliable measurements of breakdown pressure and hydraulic fracture. As such we recommend that larger samples of the dm-scale are used for future studies of hydraulic fracture in coarser grained (250micron and above) samples.
Abbreviations
- P b :
-
Breakdown pressure
- S h :
-
Minor horizontal stress
- S H :
-
Major horizontal stress
- σ T :
-
Tensile strength
- P 0 :
-
Pore pressure
- α :
-
Biot poroelastic coefficient
- ν :
-
Poisson’s ratio
- σ ax :
-
Axial pressure
- k w :
-
Wall permeability
- k wc :
-
Critical wall permeability
References
Amann F, Kaiser P, Button EA (2012) Experimental study of brittle behavior of clay shale in rapid triaxial compression. Rock Mech Rock Eng 45(1):21–33
Aydin G (2014a) Production modeling in the oil and natural gas industry: an application of trend analysis. Pet Sci Technol 32(5):555–564
Aydin G (2014b) Modeling of energy consumption based on economic and demographic factors: the case of Turkey with projections. Renew Sustain Energy Rev 35:382–389
Aydin GÖKHAN (2015) Regression models for forecasting global oil production. Pet Sci Technol 33(21–22):1822–1828
Benson PM, Meredith PG, Platzman ES (2003) Relating pore fabric geometry to acoustic and permeability anisotropy in Crab Orchard Sandstone: a laboratory study using magnetic ferrofluid. Geophys Res Lett 30(19)
Benson PM, Meredith PG, Platzman ES, White RE (2005) Pore fabric shape anisotropy in porous sandstones and its relation to elastic wave velocity and permeability anisotropy under hydrostatic pressure. Int J Rock Mech Min Sci 42(7–8):890–899
Benson P, Schubnel A, Vinciguerra S, Trovato C, Meredith P, Young RP (2006) Modeling the permeability evolution of microcracked rocks from elastic wave velocity inversion at elevated isostatic pressure. J Geophys Res Solid Earth 111(B4)
Bernier F, Bastiaens W (2004) Fracturation and self-healing processes in clays–the SELFRAC project. Proc EURADWASTE 4:478–491
Chang Y, Lee J, Yoon H (2012) Alternative projection of the world energy consumption-in comparison with the 2010 international energy outlook. Energy Policy 50:154–160
Cheng Y, Zhang Y, Yu Z, Hu Z, Yang Y (2020) An investigation on hydraulic fracturing characteristics in granite geothermal reservoir. Eng Fract Mech 237:107252
Chedid R, Kobrosly M, Ghajar R (2007) A supply model for crude oil and natural gas in the Middle East. Energy Policy 35:2096–2109
Chitrala Y, Moreno C, Sondergeld C, Rai C (2013) An experimental investigation into hydraulic fracture propagation under different applied stresses in tight sands using acoustic emissions. J Petrol Sci Eng 108:151–161
Chong Z, Yao Q, Li X (2019) Experimental investigation of fracture propagation behavior induced by hydraulic fracturing in anisotropic shale cores. Energies 12(6):976
Fazio M, Ibemesi P, Benson P, Bedoya-González D, Sauter M (2021) The role of rock matrix permeability in controlling hydraulic fracturing in sandstones. Rock Mech Rock Eng, pp. 1–26
Fredd CN, McConnell SB, Boney CL, England KW (2001) Experimental study of fracture conductivity for water-fracturing and conventional fracturing applications. SPE J 6(03):288–298
Gehne S (2018) A laboratory study of fluid-driven tensile fracturing in anisotropic rocks. Doctoral dissertation, University of Portsmouth
Gehne S, Benson PM (2017) Permeability and permeability anisotropy in Crab Orchard sandstone: experimental insights into spatio-temporal effects. Tectonophysics 712:589–599
Gehne S, Benson PM (2019) Permeability enhancement through hydraulic fracturing: laboratory measurements combining a 3D printed jacket and pore fluid over-pressure. Sci Rep 9(1):1–11
Gehne S, Forbes Inskip ND, Benson PM, Meredith PG, Koor N (2020) Fluid-driven tensile fracture and fracture toughness in Nash point shale at elevated pressure. J Geophys Res Solid Earth 125(2):971
Gillard MR, Medvedev OO, Hosein PR, Medvedev A, Peñacorada F, d'Huteau E (2010) A new approach to generating fracture conductivity. In: SPE Annual Technical Conference and Exhibition. Society of Petroleum Engineers.
Golden JM, Wiseman HJ (2014) The fracking revolution: Shale gas as a case study in innovation policy. Emory LJ 64:955
Guo T, Zhang S, Gao J, Zhang J, Yu H (2013) Experimental study of fracture permeability for stimulated reservoir volume (SRV) in shale formation. Transp Porous Media 98(3):525–542
Guo P, Li X, Li S, Yang W, Wu Y, Li G (2021) Quantitative analysis of anisotropy effect on hydrofracturing efficiency and process in shale using X-ray computed tomography and acoustic emission. Rock Mech Rock Eng 54(11):5715–5730
Haimson BC, Zhao Z (1991) Effect of borehole size and pressurization rate on hydraulic fracturing breakdown pressure. In The 32nd US symposium on rock mechanics (USRMS). OnePetro
Haimson B, Fairhurst C (1969) In-situ stress determination at great depth by means of hydraulic fracturing. In: The 11th US symposium on rock mechanics (USRMS). American Rock Mechanics Association
Hofmann H, Zimmermann G, Zang A, Min KB (2018) Cyclic soft stimulation (CSS): a new fluid injection protocol and traffic light system to mitigate seismic risks of hydraulic stimulation treatments. Geotherm Energy 6(1):1–33
Hornby BE (1998) Experimental laboratory determination of the dynamic elastic properties of wet, drained shales. J Geophys Res: Solid Earth 103(B12):29945–29964
Hou ZK, Cheng HL, Sun SW, Chen J, Qi DQ, Liu ZB (2019) Crack propagation and hydraulic fracturing in different lithologies. Appl Geophys 16(2):243–251
Hu SC, Tan YL, Zhou H, Guo WY, Hu DW, Meng FZ, Liu ZG (2017) Impact of bedding planes on mechanical properties of sandstone. Rock Mech Rock Eng 50(8):2243–2251
Hubbert MK, Willis DG (1972) Mechanics of hydraulic fracturing
Ishida T, Chen Q, Mizuta Y, Roegiers JC (2004) Influence of fluid viscosity on the hydraulic fracturing mechanism. J Energy Resour Technol 126(3):190–200
Jaeger JC, Cook NG, Zimmerman R (2009) Fundamentals of rock mechanics. John Wiley & Sons
Kamali A, Ghassemi A (2017) Reservoir stimulation in naturally fractured poroelastic rocks. In 51st US Rock Mechanics/Geomechanics Symposium. OnePetro
Kennedy RL, Knecht WN, Georgi DT (2012) Comparisons and contrasts of shale gas and tight gas developments, North American experience and trends. In: SPE Saudi Arabia Section Technical Symposium and Exhibition. Society of Petroleum Engineers
Kranz R, Frankel A, Engelder T, Scholz C (1979) The permeability of whole and jointed Barre granite. Int J Rock Mech Min Sci Geomech Abstr 16(4):225–234
Lee WJ, Hopkins CW (1994) Characterization of tight reservoirs. J Petrol Technol 46(11):956–964
Lockner D, Byerlee JD (1977) Hydrofracture in Weber sandstone at high confining pressure and differential stress. J Geophys Res 82(14):2018–2026
Ma L, Taylor KG, Lee PD, Dobson KJ, Dowey PJ, Courtois L (2016) Novel 3D centimetre-to nano-scale quantification of an organic-rich mudstone: the Carboniferous Bowland Shale, Northern England. Mar Pet Geol 72:193–205
Martin CD, Chandler NA (1993) Stress heterogeneity and geological structures. Int J Rock Mech Min Sci Geomech Abstr 30(7):993–999
Murata S, Saito T (2003) Estimation of tortuosity of fluid flow through a single fracture. J Can Petrol Technol 42(12)
Nara Y, Meredith PG, Yoneda T, Kaneko K (2011) Influence of macro-fractures and micro-fractures on permeability and elastic wave velocities in basalt at elevated pressure. Tectonophysics 503:52–59
Patel SM, Sondergeld CH, Rai CS (2017) Laboratory studies of hydraulic fracturing by cyclic injection.Int J Rock Mech Min Sci 95:8–15
Reinicke A, Rybacki E, Stanchits S, Huenges E, Dresen G (2010) Hydraulic fracturing stimulation techniques and formation damage mechanisms—Implications from laboratory testing of tight sandstone–proppant systems. Geochemistry 70:107–117
Richards JP (2003) Tectono-magmatic precursors for porphyry Cu-(Mo-Au) deposit formation. Econ Geol 98(8):1515–1533
Rubin AM (1993) Tensile fracture of rock at high confining pressure: implications for dike propagation. J Geophys Res Solid Earth 98(B9):15919–15935
Solberg P, Lockner D, Byerlee J (1977) Shear and tension hydraulic fractures in low permeability rocks. Pure Appl Geophys 115(1):191–198
Sone H, Zoback MD (2013) Mechanical properties of shale-gas reservoir rocks—Part 1: Static and dynamic elastic properties and anisotropy. Geophysics 78(5):D381–D392
Stanchits S, Surdi A, Gathogo P, Edelman E, Suarez-Rivera R (2014) Onset of hydraulic fracture initiation monitored by acoustic emission and volumetric deformation measurements. Rock Mech Rock Eng 47(5):1521–1532
Stanchits S, Burghardt J, Surdi A (2015) Hydraulic fracturing of heterogeneous rock monitored by acoustic emission. Rock Mech Rock Eng 48(6):2513–2527
Tan P, Jin Y, Han K, Zheng X, Hou B, Gao J, Chen M, Zhang Y (2017) Vertical propagation behavior of hydraulic fractures in coal measure strata based on true triaxial experiment. J Petrol Sci Eng 158:398–407
Tan Y, Pan Z, Liu J, Feng XT, Connell LD (2018) Laboratory study of proppant on shale fracture permeability and compressibility. Fuel 222:83–97
Tan P, Jin Y, Yuan L, Xiong ZY, Hou B, Chen M, Wan LM (2019) Understanding hydraulic fracture propagation behavior in tight sandstone–coal interbedded formations: an experimental investigation. Pet Sci 16(1):148–160
Teufel LW, Clark JA (1981) Hydraulic-fracture propagation in layered rock: experimental studies of fracture containment (No. SAND-80-2219C; CONF-810518-7). Sandia National Labs. Albuquerque, NM (USA)
Tsang YW (1984) The effect of tortuosity on fluid flow through a single fracture. Water Resour Res 20(9):1209–1215
Tuffen H, Dingwell D (2005) Fault textures in volcanic conduits: evidence for seismic trigger mechanisms during silicic eruptions. Bull Volcanol 67(4):370–387
Ulusay R (2014) The ISRM suggested methods for rock characterization, testing and monitoring: 2007–2014. Springer, Berlin
Vernik L, Nur A (1992) Ultrasonic velocity and anisotropy of hydrocarbon source rocks. Geophysics 57(5):727–735
Vinciguerra S, Meredith PG, Hazzard J (2004) Experimental and modeling study of fluid pressure‐driven fractures in Darley Dale sandstone. Geophys Res Lett 31(9)
Walsh JB (1981) Effect of pore pressure and confining pressure on fracture permeability. Int J Rock Mech Min Sci Geomech Abstr 18(5):429–435
Wang Q, Chen X, Jha AN, Rogers H (2014) Natural gas from shale formation–the evolution, evidences and challenges of shale gas revolution in United States. Renew Sustain Energy Rev 30:1–28
Wang J, Xie H, Li C (2021) Anisotropic failure behaviour and breakdown pressure interpretation of hydraulic fracturing experiments on shale. Int J Rock Mech Min Sci 142:104748
Xiao W, Xia C, Wei W, Bian Y (2013) Combined effect of tortuosity and surface roughness on estimation of flow rate through a single rough joint. J Geophys Eng 10(4):045015
Xu D, Hu R, Gao W, Xia J (2015) Effects of laminated structure on hydraulic fracture propagation in shale. Petrol Explor Dev 42(4):573–579
Ye Z, Liu HH, Jiang Q, Liu Y, Cheng A (2017) Two-phase flow properties in aperture-based fractures under normal deformation conditions: Analytical approach and numerical simulation. J Hydrology 545:72–87
Zhang J, Kamenov A, Zhu D, Hill AD (2015a) Development of new testing procedures to measure propped fracture conductivity considering water damage in clay-rich shale reservoirs: an example of the Barnett Shale. J Petrol Sci Eng 135:352–359
Zhang J, Kamenov A, Zhu D, Hill AD (2015b) Measurement of realistic fracture conductivity in the Barnett shale. J Unconvent Oil Gas Resour 11:44–52
Zhou J, Chen M, Jin Y, Zhang GQ (2008) Analysis of fracture propagation behavior and fracture geometry using a tri-axial fracturing system in naturally fractured reservoirs. Int J Rock Mech Min Sci 45(7):1143–1152
Zhuang L, Kim KY, Jung SG, Diaz M, Min KB (2019) Effect of water infiltration, injection rate and anisotropy on hydraulic fracturing behavior of granite. Rock Mech Rock Eng 52(2):575–589
Zhuang L, Jung SG, Diaz M, Kim KY, Hofmann H, Min KB, Zang A, Stephansson O, Zimmermann G, Yoon JS (2020) Laboratory true triaxial hydraulic fracturing of granite under six fluid injection schemes and grain-scale fracture observations. Rock Mech Rock Eng 53(10):4329-4344
Zoback MD, Rummel F, Jung R, Raleigh CB (1977) Laboratory hydraulic fracturing experiments in intact and pre-fractured rock. Int J Rock Mech Min Sci Geomech Abstr 14(2):49–58
Acknowledgements
The authors acknowledge Emily Butcher for technical support in the Rock Mechanics Laboratory, and Smart Osarenogowu for thoughtful discussions. This research was funded by a Petroleum Technology Development Fund (PTDF, Nigeria) to Peter Ibemesi and Philip Benson. This work was supported by the National Research Facility for Lab X-ray CT (NXCT) through EPSRC grant EP/T02593X/1.
Author information
Authors and Affiliations
Contributions
PI performed the experiments, processed/analyzed the data, and drafted the manuscript. PB designed the experiments, supervised data curation and analysis, and cowrote the manuscript.
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ibemesi, P., Benson, P. Effect of Pressure and Stress Cycles on Fluid Flow in Hydraulically Fractured, Low-Porosity, Anisotropic Sandstone. Rock Mech Rock Eng 56, 19–34 (2023). https://doi.org/10.1007/s00603-022-03043-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00603-022-03043-y