1 Introduction

Rockfall represents one of the most dangerous landslide events, due to its abruptness and high energy involved (Crosta and Agliardi 2003; Jaboyedoff et al 2005; Scavia et al 2020). Among the mitigation measures, net fences (or rockfall barriers, or also catchment fences) are widely adopted due to their easiness of installation, to their relatively low weight not to instabilise the slope, as well as to their very high-energy absorption capacity, today up to 11,000 kJ. Despite the development of numerical models to analyse the behaviour of the system (Govoni et al 2011; Coulibaly et al 2019; Mentani et al 2018; Previtali et al 2021), their design procedure has been recently standardised (Peila and Ronco 2009; Grimod and Giacchetti 2014; Volkwein et al 2019), first thanks to the publication of ETAG 027 (2008), now EAD 340059-00-0106 (2018), which have regulated the placing on the EEA (European Economic Area) market. The approach consists in the execution of codified impact tests allowing to characterise each product based on its performance in terms of energy absorption capacity and nominal height. As this harmonised technical specification has been developed and tailored specifically for net fences, a performance based design is adopted by the producers while a prescriptive design simply based on the requirement of specific values of the above mentioned performance characteristics has been endorsed by engineers. In this sense, the net fence is considered as a kit, i.e. an assembly or a system, which, in the Eurocodes (EN 1990:2002 2002) framework, has to satisfy the following requirements:

$$\begin{aligned} E_{d}\le E_{b,d}, \end{aligned}$$
(1)

and

$$\begin{aligned} h_{d} + t \le h_{b,d}, \end{aligned}$$
(2)

where \(E_{d}\) and \(h_{d}\) are the design kinetic energy and height of the impacting block, while \(E_{b,d}\) and \(h_{b,d}\) are the design energy absorption capacity and design height of the barrier. The term t, i.e. the tolerance, serves to account for the shape of the impacting block, as its kinematic characteristics are evaluated in its centre of mass. Equations 1 and 2 reveal that two failure modes are considered: (i) the failure for block kinetic energy exceeding the energy absorption capacity of the barrier, and (ii) the failure for block passing height greater than the nominal height of the barrier. In the framework of partial safety factors design approach promoted in the Eurocodes Standards for civil structures (EN 1990:2002 2002; EN 1997-1:2004 2004), these inequalities can be achieved through either a partial safety factor approach or a reliability based design approach (Bourrier et al 2014; Vagnon et al 2018, 2020; De Biagi et al 2020; Marchelli et al 2020, 2021). Probabilistic propagation (or trajectory) analyses consist in a series of throwings, i.e. simulations, from the individuated source area, in which the input parameters, e.g. the interaction between block and slope and the initial detachment conditions, are selected among a predefined range of variability representative of the real possible situation. These analyses allow thus to obtain the kinematic properties of the blocks, i.e. velocity or energy and passing height, as distributions from which reference, i.e. characteristic, values can be selected and used for the design by applying partial safety factors. Two National standards, i.e. UNI 11211-4 (2018) for Italy and ONR 24810 (2021) for Austria, provide the specifications in evaluating the effects of actions and in properly choosing both reference values and partial safety factors for the design parameters of both actions and resistances, as reported in Sect. 2.

The aforementioned design procedure has been developed for a net fence line only, disregarding the possibility to split the energy absorption capacity and retention into different lines. Nevertheless, in particular morphological situations, e.g. involving block high rebounds or very steep slopes, a single line of net fences cannot be sufficient to stop some blocks and, assuming no problems with the construction site, two adverse and complementary situations can often verify: (i) the installation of a single line on the very top of the slope, just below the source area, or in the middle, could not be effective for high trajectories; (ii) the installation of a line on the slope toe could not be effective for the high kinetic energy reached by the block along its path. Even in presence of low design value of passing height but very high for energy, products with the required performances in some cases cannot be installed at the highest part of the slope. Indeed, even though products with improved performance have been developed, sometimes they are not affordable in terms of environmental impacts, installation difficulties, and foundations related problems. With reference to the last point, it is worth highlighting that products with very high-energy absorption capacity imply strong actions on the foundations. In addition, the allowable deformation of high capacity barriers is up to 8.5 m, not spatially suitable for an installation close to the elements at risk.

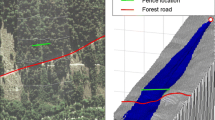
Consequently, a double (or even multiple) line of net fences, i.e. lines on approximately parallel isohypses, could provide a profitable solution to minimise rockfall risk (Fig. 1).

In addition, due to their environmental exposure, net fences require a constant monitoring and maintenance, to guarantee their effectiveness and efficiency in time (Luciani et al 2018; Marchelli 2020; Jaccard et al 2020). A periodic inspection to assess the degree of conservation is thus suggested (Marchelli et al 2019). In areas affected by a high frequency of rockfall events, even of size lower than the design one, this task is difficult to achieve and, thus, a huge amount of small blocks or debris lean on the net can lower the efficiency of the system against larger events. In this particular case, a multiple line of net fence could guarantee that, almost one line maintains design conditions.

Although effective, the solution is not codified in the aforementioned regulations. The aim of this paper is to propose a design approach for double line of net fences, allowing a powerful solution to mitigate rockfall risk in particularly steep slopes or disadvantaged areas from a morphological point of view. An example of application is then provided to illustrate the potentiality of the method.

Fig. 1
figure 1

Double line system in Donnas, Aosta Valley, Northwestern Italy

Full size image

2 Methods

Double line of net fences can be defined as a system of two lines, intercepting blocks from the same source area, located above the uphill line. The situation in which another rockfall source area is identified in between the two lines is not considered herein, where each line has to be designed separately according the standard procedures. In the following, a new design procedure is described. Before going deeply into the method, the preliminary steps of a correct design procedure for rockfall protective measures are summarised.

2.1 Principles of Rockfall Protective Measures Design

As for the other passive mitigation measures, the design flowchart starts from some fundamental steps, aiming at characterising the source area and creating possible release scenarios:

  1. 1.

    source areas identification, i.e. localisation of the potentially starting zones (Fanos et al 2018; Fanos and Pradhan 2018);

  2. 2.

    geo-mechanical characterisation of the blocks potentially unstable, i.e. their shape, volume, unit weight (Wang et al 2003; Elmouttie and Poropat 2012; Umili et al 2020), as well as a volume–frequency relationship (De Biagi et al 2017; De Biagi 2017);

  3. 3.

    evaluation of the possible triggering kinematics and blocks release probability (Macciotta et al 2017; Matasci et al 2018);

  4. 4.

    presence of silent witness and in situ survey of the rockfall block size distribution (Ruiz-Carulla et al 2015; Marchelli and De Biagi 2019).

The following steps have been generally performed in a hazard and risk analysis to individuate the kinematic parameters of the possibly detaching blocks:

  1. 5.

    characterisation of the slope, i.e. terrain/rock materials, roughness, debris conditions, and presence of vegetation;

  2. 6.

    realisation of an accurate Digital Terrain Model of the slope (Zieher et al 2012);

  3. 7.

    execution of trajectory analyses with an accurate choice of model and input parameters (Dorren et al 2011; Li and Lan 2015).

The results obtained from the last point serve to define the requirements of a possible protective measure and to evaluate in each point of the slope the relevant data of blocks trajectories, i.e. their energy (or velocity) and passing height, expressed as unique values, in a deterministic analysis, or, in a probabilistic analysis, through appropriate empirical probability distributions. In the framework of partial safety factors design approach, these kinematic parameters should be expressed in terms of characteristic values, generally assumed as a percentile of the above mentioned distributions. UNI 11211-4 (2018) and ONR 24810 (2021) propose to assume the 95th percentile of the height distribution for the characteristic height. For computing the characteristic energy ONR 24810 adopts the 99th percentile, while UNI 11211-4 the 95th applied on the distribution of the velocity and, consequently, on the energy. Also considering the partial safety factors to adopt, both National Standards provide suggestions, even though UNI 11211-4 indicates fixed values, while ONR 24810 proposes factors varying according to the consequence class of the element at risk and the occurrence probability of a rockfall event, i.e. its frequency. It should be noted that following Eqs. 1 and 2, considering the suggestions provided by these Standards, trajectories height and energy are considered as uncoupled, meaning that, neglecting partial safety factors, the minimum percentage of intercepted and stopped blocks is the \(k_{\min }=(k_h \cdot k_E )\%\) of the total, where \(k_h\) and \(k_E\) are the characteristic percentiles adopted for height and velocity, respectively. As an example, for the Italian Standards, it represent the 90\(\%\) of the total, i.e. \(0.95\cdot 0.95\), while for the Austrian Standard the 94\(\%\). Nevertheless, even though a general trend cannot be individuated, it is almost improbable that none of the \((1-k_h)\) blocks not intercepted belongs to the \((1-k_E)\) blocks not stopped by the barrier, resulting thus in a \(k_\mathrm{tot}\%\) of stopped blocks higher than \(k_{\min }\).

A double line is suggested when a single alignment is not effective or feasible because of the high trajectories of the blocks, their energy level, or if the operating space (deformation allowance) is limited. The next section details the newly proposed design method for double line rockfall protection system. In continuity with what suggested by the National Standards, the double line design method is applied in the framework of partial safety factor approach, and the most general situation is outlined. In particular, considering the capabilities of the existing and widely adopted probabilistic trajectory models, a rigorous method is delineated. This method accounts for considering together the kinematic parameters of each trajectory, thus coupling the height and velocity of blocks. This design philosophy could be expanded also to a single line design, even though it is beyond the scope of the present work. Moreover, to follow the common practice, i.e. to consider height and velocity as independent variables, under the assumption of a linearisation of the right-tail in the cumulative distributions of the output (Ditlevsen 1981), simplified equations that can be used for preliminary design are reported.

2.2 Double-Line Design

The suggested design method is based on the assumption that the double line acts as a unique system, for which the effects of actions and resistances, i.e. the performances, must be evaluated as a whole, i.e. upper line plus lower line barriers. In this context, the characteristic values of the variables, the partial coefficients and, consequently, the design values, must be understood as pertaining to the system, and the design concept is that the performances of whole system should be at least equal or greater than the effects of the actions. This means that, neglecting the partial safety factors, the minimum required performances for the entire system are those for which the upper plus the lower lines intercept and stop at least a \(k\%\) of the blocks reaching the system. As a result, as a percentage of the simulations are stopped by the upper line, the actions for which the lower line should be designed pertain to a percentile lower than the kth, say the qth percentile.

The design should consider some important aspects: (i) in case of very high-energy blocks, the upslope barrier considerably reduces the velocities of the blocks, which are then stopped by the downslope barrier; (ii) in case of blocks trajectories with a considerable variability in height, the upslope barrier intercepts and, possibly, stops part of the blocks and the downslope barrier stops the remaining fraction.

Once the performance characteristics and the location of the two lines have been chosen, checking that the distance between the two rows is greater than the design deformation at the impact of the upper barrier and that the limit deformation requirement of the downslope barrier is satisfied (i.e. the distance between the downslope barrier and the element at risk is greater than the lower line elongation), the verification of the system involves the steps described below.

The method is explained in the most general situation, assuming to perform probabilistic trajectory analyses. Starting from the source zone insisting on both the upper and the lower lines, N simulations are considered. From here on, the terms “blocks” stands for “simulations”, while all symbols are listed in specific section. Depending on the configurations, a number of blocks stops before reaching the upper line, while the remaining \(N_1\) blocks arrive at the upper line location. In this line, two quantities can be defined: \(\alpha _1\), i.e. the percentage of the \(N_1\) blocks intercepted but not arrested, and \(\alpha _2\), i.e. the percentage of the \(N_1\) blocks higher than the height of the upper barrier. Hence, \((\alpha _1+\alpha _2)N_1\) blocks continue their motion along the slope. In the partial safety factor approach, the maximum intercepted height is

$$\begin{aligned} h_{b,\max }=\frac{h_{b,l}}{\gamma _h}-t, \end{aligned}$$
(3)

being \(h_{b,l}\) the design barrier height, generally equal to its commercial nominal height, and \(\gamma _h\) the partial safety factor related to blocks trajectories height.

Following the principles stated above, the upper line reduces thus the velocity of the \(\alpha _1\) fraction of intercepted blocks. Some of the blocks can stop in between the two lines, a reduced number of blocks arrive at the lower line location. Considering separately \(\alpha _1 N_1\) and \(\alpha _2 N_1\), a percentage of each of them arrive on the lower line location, namely \(\beta\) and \({\tilde{\beta }}\), respectively. Similarly, at the lower line, the blocks can be intercepted, or not, and the ratio \(\delta\) between the number of blocks not intercepted and those arrived can be defined. To accomplish the safety requirement, the sum of the blocks not intercepted and not stopped by the system should be lower or equal the \((1-k_{tot})\)% of \(N_1\). To achieve the target of the double line system, the capacity of the lower line must be selected in such a way that the ratio q between the arrested and the intercepted blocks by the lower line satisfies

$$\begin{aligned} q=\frac{{\tilde{\beta }}\alpha _2+\beta \alpha _1(1-\alpha _2)-(1-k_\mathrm{tot})}{[{\tilde{\beta }}\alpha _2+\beta \alpha _1(1-\alpha _2)](1-\delta )}. \end{aligned}$$
(4)

The characteristic value of blocks velocity for the design of the lower line, can thus be obtained taking the qth percentile of the distribution of the velocities among those intercepted by the barrier, namely \(v_{q,i,l}\). This expression can be simplified if (i) all blocks are intercepted, but not all arrested, by the upper line, i.e. \(\alpha _2=0\), and/or (ii) if all blocks are intercepted by the lower line, i.e. \(\delta =0\). If both \(\alpha _2=0\) and \(\delta =0\), Eq. 4 turns into

$$\begin{aligned} q=\frac{\beta \alpha _1-(1-k_\mathrm{tot})}{\beta \alpha _1}. \end{aligned}$$
(5)

In the current practice, trajectory codes, while allowing inserting a physical barrier with its specific performance, do not accomplish considering a reduction of velocity in blocks impacting the barrier with an energy greater than barrier capability. To tackle this problem, a suitable solution is to decompose the problem into separate trajectory analyses.

  1. 1.

    A preliminary trajectory analysis in absence of any mitigation measure (TA0) is performed. This analysis is fundamental to understand if a single line can fulfil the safety requirement. If a barrier for which both Eqs. 1 and 2 verify, a double line system is not necessary.

  2. 2.

    A trajectory analysis (TA1) inserting at the upper line a barrier with a height \(h_{b,\max ,u}\), according to Eq. 3, and with an infinite capacity is performed. Considering the real source zone (top of the slope), in this case, blocks not intercepted by the barrier, i.e.\(\alpha _2 N_1\), continue their motion along the slope. Knowing the nominal capacity of the barrier, as provided by the producer \(E_{b,u}\), the maximum value of block velocity that can be stopped is

    $$\begin{aligned} v_{b,\max ,u}=\sqrt{\frac{2E_{b,u}}{m_k\gamma _m\gamma _v^2\gamma _{E,b}}}, \end{aligned}$$
    (6)

    providing that \(m_k\) is the characteristic value of the block mass, while \(\gamma _m\), \(\gamma _v\), \(\gamma _{E,b}\) are the partial safety factors related to the block mass, its velocity, and the barrier capacity, respectively.

  3. 3.

    If \(\alpha _1\ne 0\), an additional trajectory analysis (TA2) is performed. The analysis has a source area at the upper line, with an initial velocity equal to

    $$\begin{aligned} v_\mathrm{in}=\gamma _v\sqrt{v^2_{k,i,u}-v^2_{b,u,\max }}, \end{aligned}$$
    (7)

    being \(v_{k,i,u}\) the \(k_E\)th percentile of the velocities distribution of only blocks impacting the upper line. The initial height of blocks can be computed, precautionary, as

    $$\begin{aligned} h_\mathrm{in}=\gamma _h h_{k,i,u}, \end{aligned}$$
    (8)

    being \(h_{k,i,u}\) the \(k_h\)th percentile of the height distribution of the only blocks impacting the upper line. It is suggested to consider a direction of motion parallel to that of the slope, in accordance with the observations from the real tests in real size where the deformation of the net tends to guide the block in such a direction. The number of starting blocks should be consistent, i.e. at least 1000 throws are suggested.

  4. 4.

    If \(\alpha _1\ne 0\) and \(\alpha _2\ne 0\), the results from TA1 and TA2 should be merged, while if \(\alpha _1=0\) or \(\alpha _2=0\), the results of either TA1 or TA2 should be considered, only. In the first case, it should be noted that, to achieve consistent results, the number \(N^*\) of simulations in TA2 differs from blocks not stopped by the upper line, i.e. \(\alpha _1 N_1\), and thus, the number of blocks arrived at the location of the lower line barrier, when merged to those of TA1, should be reduced to be consistent with the effective number of simulations that have not be stopped by the upper line barrier. Hence, a subset of \(n^*\) values for blocks height and velocities must be created, where \(n^*\) is computed as

    $$\begin{aligned} n^*={\hat{\beta }}\alpha _1(1-\alpha _2)N_1. \end{aligned}$$
    (9)

    Considering the x kinematic parameter, i.e. height or velocity, the \(n^*\) values can be obtained, considering the empirical cumulative probability distribution of x obtained in TA2, dividing the cumulative frequency in \(n^*\) equally spaced bins and extracting for each bin the correspondent x value, taken in its centre.

  5. 5.

    Once \(\delta\) is computed (from TA1 + TA2 or TA1 or TA2, only, according to the case), considering a maximum intercepting height \(h_{b,\max ,l}\) according to Eq. 3, the qth percentile of the distribution of the velocities, for to the trajectories intercepted by the barrier, only, can be computed from Eq. 4, obtaining the minimum absorption capacity required by the lower line barrier.

The flowchart of the proposed design procedure is highlighted in Fig. 2.

Fig. 2
figure 2

Flowchart of the proposed rigorous method for the design of the double line system

Full size image

For preliminary design purposes, a simplification of the proposed method can be performed allowing (i) analysing separately the results of TA1 and TA2 and (ii) considering uncoupled the blocks height and velocity. In this case, the design parameters of the lower barrier should satisfy safety requirements of each analysis and of each Eqs. 1 and 2, separately. For each analysis, the cumulative frequency distributions of the outputs should be assumed as starting from \((1-\alpha _2)\), and \((1-\alpha _1)\) for TA1 and TA2, respectively, to consider that some of the blocks are stopped by the upper line. To achieve such goal, for each output, the distribution is simplified with a linear trend starting from either \((1-\alpha _2)\) or \((1-\alpha _1)\) and ending in the maximum value, which is generally a conservative assumption for \(\alpha _1\) or \(\alpha _2\) values, provided that they are limited to 20%. The \(k_h\)th, or \(k_E\)th, percentile of this linear cumulative distributions is a \(q'\)th percentile of the real distribution obtained for TA1 or TA2. This value should be used for the design, according to the following equations:

$$\begin{aligned} h_{d,l}= & {} \max \left[ \frac{\alpha _2-(1-k_h)}{k_h\alpha _2}h_{k,l,\mathrm{TA1}}\gamma _h;\right. \nonumber \\&\left. \frac{\alpha _1-(1-k_h)}{k_h\alpha _1}h_{k,l,\mathrm{TA2}}\gamma _h\right] , \end{aligned}$$
(10)
$$\begin{aligned} E_{d,l}= & {} \max \left[ \frac{\alpha _2-(1-k_E)}{k_E\alpha _2}E_{k,l,\mathrm{TA1}}\gamma _E; \right. \nonumber \\&\left. \frac{\alpha _1-(1-k_E)}{k_E\alpha _1}E_{k,l,\mathrm{TA2}}\gamma _E\right] , \end{aligned}$$
(11)

being \(h_{k,l,\mathrm{TA1}}\), \(E_{k,l,\mathrm{TA1}}\), \(h_{k,l,\mathrm{TA2}}\), \(E_{k,l,\mathrm{TA2}}\), the characteristic values of height and energy in TA1 and TA2, respectively. It reveals that \(\alpha _1\) and \(\alpha _2\) should be greater than \((1-k_h)\) and \((1-k_E)\). For lower values, blocks of either TA1 or TA2 eventually arriving in the lower barrier might not be considered. It must be noted that the \(q'\)th percentile should be considered as pertained to the distribution of the kinematic parameters of all the blocks arriving in the lower line location, while the qth percentile of the rigorous methods refers to the blocks intercepted only. In the following an example of calculation, with both methodologies, is performed.

3 Discussion

In this section, a discussion on the practicality and efficiency of a double line system is presented. Although it is beyond the scope of this discussion, it must be stressed that, in the framework a partial safety factor design approach, the definition of the design block volume, among the possible detachable and impactable, represent the starting point in the design phase of mitigation measures, affecting both the trajectories and the energy of the possible impacting blocks. It means that, if a volume–frequency law can be derived for the specific site, the return period to which the design volume refers should be carefully selected in relation to the importance class of the exposed elements at risk. Assuming this choice as carefully performed, Fig. 3 depicts the same flowchart procedure visually represented thanks to the sketches of trajectory analyses on two-dimensional profiles. The picture serves to show also typical topographic configurations into which a double line system is strongly recommended. The first depicted situation (Fig. 3a) represents a case in which the altitude difference between the source zone and the element at risk, e.g. an infrastructure or a building, is significant and the initial unstable volume is very high. In this case, sometimes, a single line of net fences located just below the source area might not be an affordable solution due to the difficulties that often emerge in cliff works and due to the high costs in the maintenance of the net fences after small detachments. Positioning a sacrificial line with low or moderate performances approximately in the middle of the slope, or in a suitable position according to the topography, just to reduce blocks velocities and to drive their motion near to the slope surface could represent a profitable solution. In the framework of a unique system, the upper line serves to reduce the required energy absorption capacity and height of the downslope barrier. Although simple, this example can be reasonably real if economic and technical constraints are considered: no available net fences, deep foundations, works and safety management.

The case represented in (Fig. 3b) stands for a very steep slope, or for a double gradient slope, with a source area located in a quasi-vertical face. In this case, the issues presented in the case a) are emphasised and the upper line system might not be able to intercept all the trajectories. The upslope line decreases the number of trajectories impacting on the downslope line and, meanwhile, reduces the velocities of a portion of the trajectories impacted on it.

It is worth mentioning that, in the hypothesis of a single line able to intercept and stop all the blocks, in sites with a high or very high frequency of rockfall events, even of magnitude lower than the design one, the presence of a double line system allows for a greater safety during maintenance and restoration operations following small events.

Fig. 3
figure 3

Visual flowchart of the proposed rigorous method for the design of the double line system: in case of a a full or b partially interception of blocks by the upslope net fence. In both cases, \(\alpha _1\ne 0\), i.e. not all the intercepted blocks are stopped by the upper line. The element at risk (E.R.) is indicated schematically with a black line. The upper barrier (u.p.) and lower barrier (l.b.) are highlighted with green lines

Full size image

3.1 Example of Application

An example of application of the developed method is performed considering a real slope profile in the Northwestern Italian Alps, characterized by some rocky cliffs, with different soil materials, insisting on a road infrastructure. Figure 4 reports the profile of the slope. The source area (Fig. 4a) is identified at an altitude between 425 m and 445 m a.s.l., where rocky outcrops are found. The characteristic volume \(V_b\) of the possible impacting block is equal to 5 m\(^3\), according to both investigations on the slope surface, i.e. by analysing the discontinuities sets, and on blocks surveyed on the slope. The trajectory analyses are conducted with a bi-dimensional lumped-mass code, RocFall v 8.017 (RocScience Inc. 1998–2002). In the adopted model, the block-slope interaction properties are represented by the normal \(R_N\) and tangential \(R_T\) coefficients of restitution, and by the friction angle \(\phi\). The former should be carefully estimated by both surveys to characterize the slope soil type and, if possible, back-analysis of pasts events to calibrate them as function of the particular site, accounting also for the simplifications and assumptions in the model. The friction angle \(\phi\) is evaluated from \(R_T\) as \(\phi =\arctan {\left( \frac{1-R_T}{R_T}\right) }\) (Wyllie 2014). Although the selection of inputs of the model is beyond the scope of the example, it is assumed that an accurate choice was performed, even though, as an example, no back-analysis was possible. The values of the restitution coefficients are listed in Table 1. The partial safety factors approach suggested by the Italian Standards (UNI 11211-4 2018) is adopted to compute the design value of both kinetic energy and height, i.e. the 95th percentile of both velocity and height as characteristic values, and the same safety factor is applied to both, i.e. \(\gamma _h\) and \(\gamma _v\) assumed equal to 1.122 (UNI 11211-4 2018), as no back-analysis could be performed but only a very accurate topographic survey providing a highly precise digital model of the terrain, as well as source area and slope terrain characteristics. For this reason, a partial safety factor \(\gamma _m\) equal to 1.02 is considered (UNI 11211-4 2018) for the spherical block mass, i.e. applied to \(m_k\). Considering the performances of the selected products for the barriers, the nominal height \(h_b\) can be considered as design value, while for the energy absorption capacity \(E_b\), generally characterized with the maximum energy level (MEL) \(E_{\mathrm{MEL}}\) determined with the standardized tests described in EAD 340059-00-0106 (2018), a partial safety factor \(\gamma _{E,b}\) equal to 1.2 should be taken to account for the uncertainties related to the fact that the test procedures might differ from reality. It should be noted that the Italian Standard provides site-independent partial safety factors and do not account for a specific failure probability (De Biagi et al 2020). As a way to compensate this fact, the author suggests to consider a \(k_{\mathrm{tot}}\%\) of blocks that should be intercepted and stopped equal to \(95\%\). In the framework of a probabilistic approach, 10,000 throws of blocks are selected as statistically representative of the rockfall phenomenon.

Fig. 4
figure 4

Trajectory analyses on the considered path (RocFall v 8.017). See Table 1 for details on input parameters: a simulation TA0 without any barrier (a), simulations TA1 (b) and TA2 (c) with the selected barriers. The element at risk (E.R.), i.e. the infrastructure, is indicated with a black line. The upper barrier (u.p.) and lower barrier (l.b.) are highlighted with green lines, while source areas with blue lines (TA0 and TA1) and a blue cross (TA2)

Full size image
Table 1 Soil input parameters for lumped-mass analysis with RocFall
Full size table

A first trajectory analysis has been performed (TA0), as shown in Fig. 4a without any mitigation measure. Very high trajectories can be observed, especially due to the three topographic leaps along the profile. For site constraint, the highest possible position for installing a net fence is at 400 m a.s.l. A first check to evaluate the possibility of installing a single line is performed. Considering the products available on the market, the required performances satisfying safety requirements at 400 m a.s.l. are \(E_\mathrm{MEL}\) of 5000 kJ and \(h_b\) equal to 6 m, while none of the existing products is able intercept all the blocks with the calculated design height in the hypothesis of a single line for lower altitude, as from 400 m a.s.l. downwards, the trajectories increase considerably their heights, not allowing to be intercepted. Referring to the absorption capacity, neglecting the height, \(E_\mathrm{MEL}\) higher than 8000 kJ should be necessary (Table 2, TA0), being that

$$\begin{aligned} h_{b}\ge & {} h_k\gamma _h+t, \end{aligned}$$
(12)
$$\begin{aligned} E_\mathrm{MEL}\ge & {} \frac{1}{2}m_k\gamma _mv_k^2\gamma _v^2\gamma _{E,b}. \end{aligned}$$
(13)

In the case herein proposed, as usually occurs in similar conditions, due to the inherent difficulties in installing such high-capacity products on inaccessible slopes, the suitable product might hardly been installed in the upper part of the slope. Assuming herein that the maximum MEL of the net fence that can be installed along the slope is equal to 3000 kJ, a barrier with \(h_{b,u}\) and \(E_{b,u}=E_\mathrm{MEL}\) equal to 6 m and 3000 kJ, respectively, is adopted, resulting in \(h_{b,\max ,u}=\) 4.29 m and \(v_{b,\max ,u}=\) 16.98 m/s.

With the procedure suggested in Sect. 2.2, TA1 is performed (Fig. 4b.). All the inputs and results are reported in Table 2. The great majority of the blocks are intercepted by the upper line (i.e. \(\alpha _2\)=0.17), even though it is calculated from Eq. 6 that 34% of blocks (i.e. \(\alpha _1\)) is not stopped. A lower line is also inserted, at 360 m a.s.l., sufficiently far from the element at risk (E.R. in Fig. 4), i.e. almost 10 m. In the lower line location, a 7 m–5000 kJ product is considered. The calculations reported in Table 2 prove that this product satisfies the safety requirements. The totality of blocks not intercepted by the upper barrier arrives at the lower line location. Figure 4c displays the results obtained with TA2. In this case, the source zone is related to the blocks intercepted but not arrested by the upper line barrier, with an initial velocity of 11.53 m/s, oriented as the slope angle and an initial height of 3 m, according to Eqs. 7 and 8, respectively. Merging TA1 and TA2 results in the lower line location, as suggested in Sect. 2.2, among the blocks arrived in the upper line, i.e. \(\delta ({\hat{\beta }}\alpha _1+({\tilde{\beta }}\alpha _1)\), about 4\(\%\) of the blocks is not intercepted by the lower line. Consequently, the qth percentile for the velocity, among the intercepted blocks, according to Eq. 4, becomes equal to the 96\(\%\), corresponding to a \(v_{q,i,l}\) equal to 19.8 m/s. Consequently, the minimum required \(E_\mathrm{MEL}\) is equal to 4078 kJ, thus, considering the existing product, 5000 kJ.

Conversely, if a 8 m high product is selected for the lower line (see Table 3), almost the totality of the blocks is intercepted (Fig. 5), and the qth percentile for the velocity, becomes equal to the 85%, resulting in \(v_{q,i,l}\) equal to 19.43 m/s, and, thus in a minimum \(E_\mathrm{MEL}\) of 3927 kJ. In the present case a small difference between the two values of \(v_{q,i,l}\) appears as the trend of the velocity cumulative distribution in very narrow. Nevertheless, generally speaking, a common trend cannot be observed but it varies for each situation, and in some cases the results span in a very wide range. In this case, the difference between qth and \(k_E\)th values could be significant, allowing a product with a small dissipation capacity.

To assess the effectiveness of the approximated method, being \(\alpha _2\) lower than \(k_h\%\), Eqs. 10 and 11 provide a \(q'\) equal to 0.90, meaning that the 90th percentile of the velocity distribution of all blocks arriving in the lower line location should be considered for the assessment of the barrier. In the present case, the 90th percentile of height and velocity corresponds to 5.27 m and 19.53 m/s, respectively, resulting in a minimum barrier height, considering a tolerance t equal to the block radius (i.e. 1.06 m), of 6.97 m and a minimum required \(E_\mathrm{MEL}\) of 3967 kJ, lower than 7.16 m (\(-3\%\)) and 4036 kJ (\(-2\%\)) obtained with the 95th percentile.

Fig. 5
figure 5

Trajectory analyses on the considered path (RocFall v 8.017). See Table 1 for details on input parameters: simulations TA1 (a) and TA2 (b) with a 8 m height net fences. The element at risk (E.R.), i.e. the infrastructure), is indicated with a black line. The upper barrier (u.p.) and lower barrier (l.b.) are highlighted with green lines, while source areas with blue lines (TA0 and TA1) and a blue cross (TA2)

Full size image
Table 2 Input and output parameters of the performed simulations in case of a lower barrier 7 m high
Full size table
Table 3 Input and output parameters of the performed simulations in case of a lower barrier 8 m high
Full size table

Considering the double line as a system allows to obtain design values lower than in the hypothesis of single lines. It is worth mentioning that the reduction depends on both \(\alpha _1\), \(\alpha _2\) and the shape of the cumulative distribution. In the proposed example, as the velocity distributions, considering either the only impacted blocks or the total arrived, are very narrow, resulting in \(v_{q,i,l}\), \(v_{k,i,l}\), \(v_{q',l}\) and \(v_{k,l}\) that are almost equal. Although this represents an example, it can be noticed that a single line in the lower part cannot be adopted at a first solution. On the contrary, a double line system composed of a 6 m–3000 kJ barrier for the upper line, and a 7 m–5000 kJ for the lower line can be installed.

4 Conclusion

Net fences represent one of the most adopted solution for mitigating rockfall risk. The existing design procedures, based on two failure modes, i.e. the exceeding of kinetic energy or height of the block, have been conceived and defined for a single net line system, only. Nevertheless, in particularly complex morphological situations, a single line cannot be effective or the required product, if existing, cannot be applicable for installation constraints, e.g. large foundations. The present work deals with net fences disposed along double lines, i.e. lines on approximately parallel isohypses which have to arrest blocks from the same source area. The upper line serves to stop the great majority of the blocks, or at least decelerate them, while the lower line to stop the remaining part. The leading idea is that the entire set of net fences can represent a system, for which the effects of actions and resistances should be evaluated as a whole. Consequently, the characteristic values of the variables, the partial safety coefficients and, thus, the design values should be considered as pertaining to the double line system.

Starting from trajectory analyses from the identified source areas, the upslope line is designed first. The design of the lower line depends on the results of supplementary trajectory analysis whose source area is located at the upper barrier position, with an initial height and velocity depending on the retention capacity of the upper barrier. The system assumption allows to consider a reduction of the required energy absorption capacity and height of the lower line based on the amount of blocks stopped by the upper line. It follows that designing with the proposed method enables to choose products whose global energy absorption capacity, i.e. obtained by their sum, is generally lower than the one required by a single line positioned on the slope toe. Moreover, in sites with a high or very high frequency of rockfall events, even of magnitude lower than the design one, a double line system allows for a greater safety during maintenance and restoration operations following small events. Further developments could consider different configurations for the source zone starting from the upslope line in the integrative analysis.