Finite Element Analysis of Expansive Bedrock Considering Electro-chemo-mechanical Coupling Phenomena in Crystal Layers of Clay Minerals and Internal Structural Degradation

Abstract

This research proposes a novel model targeting expansive bedrock by combining an elastoplastic model considering electro-chemo-mechanical phenomena with the Cam-clay model, based on considerations of cementation and its degradation owing to plastic deformation. Additionally, tunnel excavation and swelling analyses are demonstrated by incorporating the proposed model into a finite element analysis code. Specifically, swelling analysis is conducted by decreasing the bedrock ion concentration and by considering the groundwater supply to the tunnel. The simulation results indicate that considerable swelling occurs in a limited area, such as the bottom part of the tunnel, even though changes in ion concentration are uniformly set in the entire analysis area; moreover, swelling phenomena develop instantaneously analogous to the observational records. The simulation reveals that shear stress increases while excavating an area and that softening with plastic expansion occurs in bedrock skeleton owing to decreasing ion concentration. In addition, the yielding of the bedrock skeleton triggers a rapid internal structural degradation and swelling of the clay mineral interlaminar layers based on simulations. Thus, this study clarifies the tunnel swelling deformation mechanism as an interaction problem between coupled electro-chemo-mechanical phenomena occurring in crystal layers and a plastic phenomenon involving the internal structural degradation of the bedrock skeleton.

Highlights

• A model for expansive bedrock is proposed by considering electro-chemo-mechanical coupling phenomena in crystal layers of clay minerals and internal structural degradation.

• Tunnel excavation and swelling analyses are demonstrated by incorporating the proposed model into a finite element analysis code.

• Interactions between the expansion of interlaminar layers due to decreasing ion concentration and the plastic deformation of the rock skeleton causes swelling deformation.

• Significant tunnel swelling deformation occurs approximately 5 m below the tunnel base, because high-shear stress is applied subject to the influence of excavation.

• Yielding of the rock skeleton triggers rapid tunnel swelling deformation owing to the groundwater supply, and internal structural degradation accelerates the deformation.

1 Introduction

Pore fluid composition affects the mechanical behavior of bedrock containing expansive clay minerals. Moreover, swelling of expansive bedrock often causes problems during tunnel excavation and earth cutting. For example, the deformation of the Mount (Mt.) Sakazuki Tunnel on the Yamagata Expressway in Japan led to bumps and cracks which emerged instantaneously on the road due to the swelling of expansive bedrock approximately 17 years after the initiation of the service. The road surface uplift was up to 494 mm, and it developed at a rapid rate of 10 mm/day from the onset of deformation. These tunnel deformations constitute a severe problem because of the subsequent significant costs for necessary tunnel modifications. Thus, it is necessary to elucidate the mechanism behind the emergence of bumps and cracks as well as quantitatively evaluate the deformation caused by swelling.

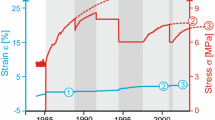
Electro-chemo-mechanical interactions between the crystal layers of expansive clay minerals are one of the predisposing factors for the swelling phenomenon in bedrock. Di Maio (1996) conducted one-dimensional compression tests on Ponza bentonite in various stress conditions by changing the cell fluid from distilled water to NaCl solution, and vice versa, and researched the osmotic compression and swelling behavior of expansive soils. Figure 1 shows that swelling and osmotic compression occur when the ion concentration of pore fluid decreases and increases, respectively; moreover, they depend on confining pressure. The arrows in Fig. 1 represent the moment at which the distilled water solution is replaced by the NaCl solution.

Fig. 1

Experimental results by Di Maio (1996)

Various mechanical models focusing on the microscopic behavior at the surface of clay minerals have been proposed to explain consistently the characteristic behavior of expansive soils. Alonso et al. (1990) proposed the Barcelona expansive model that targeted unsaturated expansive clay. This model assumes that expansive clays have double-porous structures consisting of a macrostructure (soil skeleton) and a microstructure (mineral level), and that the behavior of the macrostructure can be expressed as a function of the effective stress for the saturated soil. Subsequently, Gens and Alonso (1992) extended the Barcelona basic model, and targeted nonexpansive soils. Musso et al. (2013) proposed a model for compacted active clay based on the concept of a double-porous structure, and described a microstructure using the van’t Hoff equation (van’t Hoff 1884). Kyokawa et al. (2020) proposed an elastoplastic constitutive model of expansive soils that focused not only microphenomena, such as electro-chemical phenomena on the surface of clay minerals but also on macrophenomena, using the Cam-clay model.

As such, various studies have been conducted on swelling clays. However, the swelling behavior of bedrock is more complicated because of various factors, such as high stiffness and internal structural degradation, which are absent in clays. Additionally, there are few studies on mechanical modeling of bedrock containing swelling clay minerals which is relevant to actual tunnel construction. Only a few models that describe the behavior of swelling bedrock simultaneously account for the electro-chemical microphenomena on mineral surfaces and macroscopic reduction in cementation caused by internal structural degradation.

Our study proposes a novel model targeting expansive bedrock that combines an elastoplastic model considering electro-chemo-mechanical phenomena (Kyokawa et al. 2020) in conjunction with the use of the Cam-clay model, and based on considerations of cementation and its degradation owing to plastic deformation (Yamada et al. 2022). In addition, an algorithm is constructed to implicitly update stresses and internal variables for numerical analyses using the proposed model. Finally, this research investigates the mechanism of swelling phenomena in bedrock that are responsible for problems in tunnel construction based on finite element analysis using the proposed model.

2 Modeling the Mechanical Behavior of Swelling Bedrock

2.1 Electro-chemo-mechanical Phenomena in Crystal Layers of Clay Minerals

An elastoplastic model considering the electro-chemo-mechanical phenomena in the crystal layers of clay minerals (Kyokawa et al. 2020) is used herein to investigate swelling bedrock. This section describes the model framework.

This model assumes that swelling soils are composed of expansive clay minerals and nonexpansive soil particles, and possess a double-porous structure consisting of soil skeleton and interlaminar voids, as shown in Fig. 2.

Fig. 2

Schematic of expansive soil and its volumetric structure

Variables related to the interlaminar and soil skeleton aspects are indicated by a sub/superscripts “il” and “ss” , respectively; moreover, the variables representing volume are illustrated in Fig. 2. In this model, the void ratios (total void ratio $e$, interlaminar void ratio $e^{il}$, and soil skeleton void ratio $e^{ss}$) are defined as

$$ e = \frac{{V_{{\text{v}}} }}{{V_{{\text{s}}} }},\;e^{il} = \frac{{V_{{{\text{il}}}} }}{{V_{{\text{s}}} }},\;e^{ss} = \frac{{V_{{{\text{ss}}}} }}{{V_{{\text{s}}} }}. $$

(1)

When the volume changes from $V_{0}$ to $V$, the volumetric strain $\varepsilon_{{\text{v}}}$ (compression is positive) is expressed as

$$ \varepsilon_{{\text{v}}} = - \frac{{V - V_{0} }}{{V_{0} }} = - \frac{{\Delta V_{{{\text{ss}}}} + \Delta V_{{{\text{il}}}} }}{{V_{{{\text{s}}0}} + V_{{{\text{ss}}0}} + V_{{{\text{il}}0}} }}. $$

(2)

Consequently, the interlaminar volumetric strain is defined as

$$ \frac{{\Delta V_{{{\text{il}}}} }}{{V_{{{\text{il}}0}} }} = \frac{{2(d - d_{0} )S(n - 1)N}}{{2d_{0} S(n - 1)N}} = \frac{{d - d_{0} }}{{d_{0} }}, $$

(3)

where $d$ is equal to half the distance of the interlaminar space, $d_{0}$ is its initial value, $S$ is the specific surface area of the crystals, $n$ is the number of mineral layers, and $N$ is the number of minerals in the soil element (Fig. 3).

Fig. 3

Crystal structure

Similarly, the soil skeleton volumetric strain $\varepsilon_{{\text{v}}}^{ss}$ is defined as follows:

$$ \varepsilon_{{\text{v}}}^{ss} = - \frac{{\Delta V_{{{\text{ss}}}} }}{{V_{{{\text{s}}0}} + V_{{{\text{ss}}0}} + V_{{{\text{il}}0}} }}. $$

(4)

From Eqs. (2)–(4), the total volumetric strain in the doubly porous structure is defined in terms of $d$ as follows:

$$ \begin{aligned} \varepsilon_{{\text{v}}} & = - \frac{{\Delta V_{{{\text{ss}}}} }}{{V_{{{\text{s}}0}} + V_{{{\text{ss}}0}} + V_{{{\text{il}}0}} }} - \frac{{\Delta V_{{{\text{il}}}} }}{{V_{{{\text{s}}0}} + V_{{{\text{ss}}0}} + V_{{{\text{il}}0}} }} \\ & = \varepsilon_{{\text{v}}}^{ss} - \frac{{V_{{{\text{il}}0}} }}{{V_{{{\text{s}}0}} + V_{{{\text{ss}}0}} + V_{{{\text{il}}0}} }} \cdot \frac{{\Delta V_{{{\text{il}}}} }}{{V_{{{\text{il}}0}} }} \\ & = \varepsilon_{{\text{v}}}^{ss} - \theta^{*} \frac{{d - d_{0} }}{{d_{0} }}, \\ \end{aligned} $$

(5)

where $\theta^{*}$ is defined in terms of $e_{0}^{ss}$ and $e_{0}^{il}$ as follows:

$$ \theta^{*} = \frac{{V_{{{\text{il}}0}} }}{{V_{{{\text{s}}0}} + V_{{{\text{ss}}0}} + V_{{{\text{il}}0}} }} = \frac{{e_{0}^{il} }}{{1 + e_{0}^{ss} + e_{0}^{il} }}. $$

(6)

Therefore, the total strain ${{\varvec{\upvarepsilon}}}$ using infinitesimal deformation theory is defined as the sum of the strain in the soil skeleton ${{\varvec{\upvarepsilon}}}^{ss}$ and isotropic strain with changing interlaminar distance, as follows:

$$ {\varvec{\varepsilon}} = {\varvec{\varepsilon}}^{ss} - \frac{1}{3}\theta^{*} \frac{{d - d_{0} }}{{d_{0} }}{\varvec{I}}, $$

(7)

where ${\mathbf{I}}$ is a second-order unit tensor, and its components are expressed by the Kronecker delta $\delta_{ij}$.

The swelling behavior is determined by the changes in $d$, and $d$ is determined by the following equilibrium equation of the electro-chemo-mechanical forces between the crystal layers:

$$ F^{il} (c,d,{\varvec{\sigma}}) = f_{{\text{a}}} (d) - f_{{\text{r}}} (c,d) - f_{{\text{h}}} (d) + f_{{\text{e}}} ({\varvec{\sigma}}) = 0, $$

(8)

where c is the ion concentration of the pore fluid, $f_{{\text{a}}}$ is the Van der Waals force, $f_{{\text{r}}}$ is the osmotic pressure from the double diffusion layers, $f_{{\text{h}}}$ is the hydration force, and $f_{{\text{e}}}$ is the force from the (mean) effective stress ${{\varvec{\upsigma}}}$. Hereafter, Eq. (8) is referred to as “the interlaminar equilibrium.” The osmotic pressure, Van der Waals force, and hydration force are monotonically decreasing functions with respect to the interlaminar distance; moreover, the osmotic pressure changes with ion concentration. The osmotic repulsive pressure increases with decreasing ion concentration and vice versa. Therefore, increasing or decreasing the interlaminar distance can describe swelling or osmotic compression. The interlaminar equilibrium is a function of the interlaminar distance $d$, ion concentration $c$, and the effective stress ${{\varvec{\upsigma}}}$. The characteristic mechanical behavior of swelling clay minerals, which depends on the pore fluid composition and confining pressure, can be expressed by adding the effective stress to the electro-chemical force. The osmotic repulsive pressure and Van der Waals force are based on the equations given by Komine and Ogata (1996), and the hydration force is based on the equations given by Afzal et al. (1984). Each of these forces and relevant other variables are defined as follows:

$$ f_{{\text{r}}} = \frac{1}{{{\text{CEC}}}}\sum\limits_{{i = {\text{Na}}^{ + } ,{\text{Ca}}^{2 + } , \ldots }} {{\text{EXC}}_{i} \cdot f_{{{\text{r}}i}} (c_{i} ,d)} , $$

(9)

$$ \left\{ \begin{gathered} f_{{{\text{r}}i}} (c_{i} ,d) = 2c_{i} N_{{\text{A}}} kT\{ \cosh u_{i} - 1\} \times 10^{ - 3} \hfill \\ u_{i} = 8\tanh^{ - 1} \left\{ {\exp ( - \omega_{i} d) \cdot \tanh \frac{{z_{i} }}{4}} \right\} \hfill \\ \omega_{i} = \sqrt {\frac{{2c_{i} N_{{\text{A}}} {\text{v}}^{2} e^{\prime 2} }}{\varepsilon kT}} \hfill \\ z_{i} = 2\sinh^{ - 1} \left( {96.5\frac{{{\text{EXC}}_{i} }}{S}\sqrt {\frac{1}{{8\varepsilon c_{i} N_{{\text{A}}} kT}}} } \right) \hfill \\ \end{gathered} \right., $$

(10)

$$ f_{{\text{a}}} (d) = \frac{{A_{{\text{h}}} }}{24\pi }\left\{ {\frac{1}{{d^{3} }} + \frac{1}{{(d + t)^{3} }} - \frac{2}{{\left( {d + \frac{t}{2}} \right)^{3} }}} \right\} \times 10^{ - 3} , $$

(11)

$$ f_{{\text{h}}} (d) = \frac{{W_{0} }}{{\chi_{0} }}\exp \left( { - \frac{d}{{\chi_{0} }}} \right) \times 10^{3} , $$

(12)

$$ f_{{\text{e}}} ({\varvec{\sigma}}) = p, $$

(13)

where ${\text{CEC}}$ $[{\text{mEq/g}}]$ is the cation exchange capacity, ${\text{EXC}}_{i}$ $[{\text{mEq/g}}]$ is the exchange capacity of exchangeable ion $i$, $T$ $[{\text{K}}]$ is the absolute temperature, ${\text{v}}$ is the ionic valence, $e^{\prime}$ $[{\text{C}}]$ is the electronic charge, $\varepsilon$ ${[}{{{\text{C}}^{2} } \mathord{\left/ {\vphantom {{{\text{C}}^{2} } g}} \right. \kern-\nulldelimiterspace} g}]$ is the static permittivity of pore water, and $t$ ${\text{[m]}}$ is the thickness of the clay mineral crystals, and $S$ $[{{{\text{m}}^{{2}} } \mathord{\left/ {\vphantom {{{\text{m}}^{{2}} } {\text{g}}}} \right. \kern-\nulldelimiterspace} {\text{g}}}]$ is the specific surface. $\chi_{0}$ ${\text{[m]}}$ and $W_{0}$ ${[}{{{\text{MJ}}} \mathord{\left/ {\vphantom {{{\text{MJ}}} {{\text{m}}^{2} }}} \right. \kern-\nulldelimiterspace} {{\text{m}}^{2} }}]$ are the material parameters related to hydration force. $A_{{\text{h}}}$ ${\text{[J]}}$, $N_{{\text{A}}}$ ${[}{{{\text{mol}}} \mathord{\left/ {\vphantom {{{\text{mol}}} {\text{L}}}} \right. \kern-\nulldelimiterspace} {\text{L}}}{]}$, and $k$ ${[}{{\text{J}} \mathord{\left/ {\vphantom {{\text{J}} {\text{K}}}} \right. \kern-\nulldelimiterspace} {\text{K}}}]$ are the Hamaker, Avogadro, and Boltzmann constants, respectively. These parameters are examined on a mineral-by-mineral basis or are physical constants.$p = {{({\text{tr}} {\varvec{\sigma}})} \mathord{\left/ {\vphantom {{({\text{tr}} {\varvec{\sigma}})} 3}} \right. \kern-\nulldelimiterspace} 3}$ is the mean effective stress. Moreover, the shear stress $q = \sqrt {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}} \left\| {\mathbf{s}} \right\|$ with ${\mathbf{s}} = {{\varvec{\upsigma}}} - p{\mathbf{I}}$ and stress ratio $\eta = \sqrt {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}} \left\| {{\varvec{\upeta}}} \right\| = {q \mathord{\left/ {\vphantom {q p}} \right. \kern-\nulldelimiterspace} p}$ with ${{\varvec{\upeta}}} = {\mathbf{s}}/p$ are defined as such.

In addition to the above equilibrium model, bedrock skeleton behavior is described with Cam-clay model considering cementation and its degradation in Sect. 2.2.

2.2 Cementation and Internal Degradation of Swelling Bedrock

Kyokawa et al. (2020) described the soil skeleton behavior with the Cam-clay model to target expansive soils. However, the target of this study is not soft expansive soil but swelling bedrock. Therefore, a method that considers the cementation effect and its degradation proposed by Yamada et al. (2022) is introduced into the Cam-clay model to describe the degradation of internal structure due to swelling. This model determines the tensile strength owing to the cementation effect of the material in soil skeletons, such as cement-treated soil and bedrock, by translating the yield surface to the tensile side, as shown in Fig. 4a. It can also express high cementation, because confining pressure virtually increases by treating translations of the yield surface as modifications of the effective stress. Moreover, it describes the transition from cement-treated soil and bedrock into normal soil by eliminating the deviation of the yield surface from the origin owing to progressive plastic deformation. Specifically, the model is expressed with modified effective stress ${\overline{\mathbf{\sigma }}}$, which is the effective stress ${{\varvec{\upsigma}}}$ plus the amount of isotopically parallel shifts of the yield surface $\Psi$:

$$ \overline{\varvec{\sigma }} = {\varvec{\sigma}} + \Psi {\varvec{I}}, $$

(14)

Fig. 4

Parallel shift of the yield function

$\overline{p}$, $\overline{q}$, ${\overline{\mathbf{s}}}$, $\overline{\eta }$, and ${\overline{\mathbf{\eta }}}$, which are the derived quantities of ${\overline{\mathbf{\sigma }}}$, are defined in the same manner as those of ${{\varvec{\upsigma}}}$. The yield surface with cementation passes through the origin in the modified effective stress space, as shown in Fig. 4b, such that the formulation of the model is common in many aspects to the standard Cam-clay model. Hereafter, quantities defined using the modified effective stresses considering cementation are denoted by an overline.

$\Psi$ is referred to as cementation, and is assumed to asymptotically approach zero with plastic deformation. The evolution rule of $\Psi$ is as follows:

$$ \dot{\Psi } = V(\Psi )\left\| {{\dot{\mathbf{\varepsilon }}}^{p} } \right\|,\;\,V(\Psi ) = - \frac{{\tilde{d}}}{{\tilde{D}}}\Psi , $$

(15)

where $\tilde{d}$ is the material constant that controls the decreasing rate of cementation and $\tilde{D} = {{(\tilde{\lambda } - \tilde{\kappa })} \mathord{\left/ {\vphantom {{(\tilde{\lambda } - \tilde{\kappa })} {{(}Mv_{0}^{ss} }}} \right. \kern-\nulldelimiterspace} {{(}Mv_{0}^{ss} }})$ is the dilatancy coefficient. $\tilde{\lambda }$ is the compression index, $\tilde{\kappa }$ is the swelling index, $M$ is the critical state constant, and $v_{0}^{ss}$ is the initial value of a soil skeleton specific volume expressed as $v_{{}}^{ss} = 1 + e_{{}}^{ss}$.

This study applies the Cam-clay model by considering cementation and its degradation owing to plastic deformation in the soil skeleton of the elastoplastic model that satisfies the interlaminar equilibrium for a double-porous structure.

3 Formulation and Computational Algorithm of the Proposed Model

3.1 Fundamental Equations of the Proposed Model

The fundamental equations of the modified Cam-clay model are given by

$$ {\text{Strain rate:}}\quad \dot{\varvec{\varepsilon }}^{ss} = \dot{\varvec{\varepsilon }}^{e} + \dot{\varvec{\varepsilon }}^{p} , $$

(16)

$$ {\text{Elastic constitutive law:}}\quad \varvec{\dot{\overline{\sigma }}} = {\mathbb{C}}^{e} :\dot{\varvec{\varepsilon }}^{e} ,\,\,{\mathbb{C}}^{e} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\mathbb{C}}^{e} \overline{p}, $$

(17)

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\mathbb{C}}^{e} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{K} - \frac{2}{3}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} } \right){\varvec{I}} \otimes {\varvec{I}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} \left( {{\mathbb{I}} + {\overline{\mathbb{I}}}} \right),\,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} = \frac{{3\left( {1 - 2\nu } \right)}}{{2\left( {1 + \nu } \right)}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{K} ,\,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{K} = \frac{{v_{0}^{ss} }}{{\tilde{\kappa }}}\,, $$

$$ {\text{Yield function:}}\quad F(\overline{\varvec{\sigma }},p_{c} ) = f\left( {\overline{p},\overline{\eta }} \right) - M\tilde{D}\ln \left( {\frac{{p_{c} }}{{p_{c0} }}} \right), $$

(18)

$$ f(\overline{p},\overline{\eta }) = M\tilde{D}\ln \left( {\frac{{\overline{p}}}{{p_{c0} }}} \right) + M\tilde{D}\ln \left( {\frac{{M^{2} + \overline{\eta }^{2} }}{{M^{2} }}} \right), $$

$$ {\text{Hardening rule:}}\quad p_{{\text{c}}} = p_{{{\text{c}}0}} \exp \left( {\frac{{\varepsilon_{{\text{v}}}^{p} }}{{M\tilde{D}}}} \right), $$

(19)

$$ {\text{Associated flow rule:}}\quad {\varvec{\varepsilon}}^{p} = \dot{\Lambda }\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}, $$

(20)

$$ {\text{Load criterion:}}\quad F \le 0\;,\;\,\,\dot{\Lambda } \ge 0\;,\,\,\;\dot{\Lambda }F \le 0, $$

(21)

where $({\mathbb{I}})_{ijkl} = \delta_{ik} \delta_{jl}$, $({\overline{\mathbb{I}}})_{ijkl} = \delta_{il} \delta_{jk}$, $\nu$ is the Poisson’s ratio, and $\dot{\Lambda }$ is the plastic multiplier.

In addition to these fundamental equations, the equations for the interlaminar equilibrium, double-porous structure, cementation, and its evolution rule mentioned in the previous section are used in this study

$$ {\text{Interlaminar equilibrium:}}\quad F^{il} (c,d,{\varvec{\sigma}}) = f_{{\text{a}}} (d) - f_{{\text{r}}} (c,d) - f_{{\text{h}}} (d) + f_{{\text{e}}} ({\varvec{\sigma}}) = 0, $$

(22)

$$ {\text{Double-porous structure:}}\quad \dot{\varvec{\varepsilon }} = \dot{\varvec{\varepsilon }}^{ss} + \dot{\varvec{\varepsilon }}^{il} , $$

(23)

$$ {\text{Modified effective stress:}}\quad \overline{\varvec{\sigma }} = {\varvec{\sigma}} + \Psi {\varvec{I}}, $$

(24)

$$ {\text{The evolution rule of cementation:}}\quad \Delta \Psi = V(\Psi )\left\| {\dot{\varvec{\varepsilon }}^{p} } \right\|. $$

(25)

Note that the ion concentration $c$ of the interlayer pore fluid is a known condition for each incremental step.

3.2 Elastoplastic Computation Algorithm

In numerical calculations, the equations in the velocity form are approximated by backward difference as follows:

$$ {\text{Strain increment:}}\,\Delta {\varvec{\varepsilon}}^{ss} = \Delta {\varvec{\varepsilon}}^{e} + \Delta {\varvec{\varepsilon}}^{p} , $$

(26)

$$ {\text{Elastic constitutive law:}}\overline{\varvec{\sigma }}_{n + 1} = \overline{\varvec{\sigma }}_{n} + {\mathbb{C}}_{n + 1}^{e} :\Delta {\varvec{\varepsilon}}^{e} , $$

(27)

$$ {\text{Yield function:}}\quad F_{n + 1} (\overline{\varvec{\sigma }}_{n + 1} ,p_{{\text{c}}} ) = f\left( {\overline{p},\overline{\eta }} \right) - M\tilde{D}\ln \left( {\frac{{p_{{\text{c}}} }}{{p_{{{\text{c}}0}} }}} \right), $$

(28)

$$ {\text{Hardening rule:}}\quad p_{{\text{c}}} = p_{{{\text{c}}0}} \exp \left( {\frac{{\varepsilon_{v\:n + 1}^{p} }}{{M\tilde{D}}}} \right), $$

(29)

$$ {\text{Associated flow rule:}}\quad {\varvec{\varepsilon}}_{n + 1}^{p} = {\varvec{\varepsilon}}_{n}^{p} + \Delta \Lambda \frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}, $$

(30)

$$ {\text{Interlaminar equilibrium:}}\quad f_{{\text{a}}} (d_{n + 1} ) - f_{{\text{r}}} (c_{n + 1} ,d_{n + 1} ) - f_{{\text{h}}} (d_{n + 1} ) + f_{{\text{e}}} ({\varvec{\sigma}}_{n + 1} ) = 0, $$

(31)

$$ {\text{Double-porous structure:}}\quad \Delta {\varvec{\varepsilon}} = \Delta {\varvec{\varepsilon}}^{ss} + \Delta {\varvec{\varepsilon}}^{il} , $$

(32)

$$ {\text{Modified effective stress:}}\quad \overline{\varvec{\sigma }}_{n + 1} = {\varvec{\sigma}}_{n} + \Psi_{n + 1} {\varvec{I}}, $$

(33)

$$ {\text{Evolution rule of cementation:}}\quad \Psi_{n + 1} = \Psi_{n} + V(\Psi_{n + 1} )\left\| {{{\varvec{\upvarepsilon}}}_{n + 1}^{p} - {{\varvec{\upvarepsilon}}}_{n}^{p} } \right\|\;, $$

(34)

$$ {\text{Load criterion:}}\quad F_{n + 1} \le 0\;,\;\,\,\Delta \Lambda \ge 0\;,\;\,\,\Delta \Lambda F_{n + 1} \le 0. $$

(35)

$\Delta$ denotes that the quantity is an incremental amount. Variables of the $n + 1$ step are unknowns, and are computed by the updated algorithm described in the next section. In the formulation described above, $\overline{p}$, $\overline{\eta }$, $p_{{\text{c}}}$, and ${{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial {\overline{\mathbf{\sigma }}}}}} \right. \kern-\nulldelimiterspace} {\partial {\overline{\mathbf{\sigma }}}}}$ use the value in the $n + 1$ step. Similarly, the subscripts which represent steps are omitted for variables other than those used to store history and for differential quantities.

3.2.1 Elastic Predictor Step

An elastic predictor step, which assumes $\Delta \Lambda = 0$ and implies $\Delta {{\varvec{\upvarepsilon}}}^{p} = {\mathbf{0}}$, was performed at first. Moreover, the values obtained from this step are marked with the superscript “trial.” In this step, the trial modified stress $\overline{\varvec{\sigma }}_{n + 1}^{{{\text{trial}}}}$ and trial interlaminar distance $d_{n + 1}^{{{\text{trial}}}}$, which simultaneously satisfy Eqs. (36)–(38), are obtained. Note that in this trial step, convergence calculation by the Newton–Raphson method is required, because the elastic modulus matrix ${\mathbb{C}}_{n + 1}^{{e\:{\text{trial}}}}$ depends on stress

$$ \Delta {\varvec{\varepsilon}} = \Delta {\varvec{\varepsilon}}^{ss} + \Delta {\varvec{\varepsilon}}^{il} , $$

(36)

$$ {\varvec{N}}_{n + 1}^{{{\text{trial}}}} (\overline{\varvec{\sigma }}_{n + 1}^{{{\text{trial}}}} ) = \overline{\varvec{\sigma }}_{n + 1}^{{{\text{trial}}}} - \overline{\varvec{\sigma }}_{n} - {\mathbb{C}}_{n + 1}^{{e,\:{\text{trial}}}} :\Delta {\varvec{\varepsilon}}^{ss} = {\mathbf{0}}, $$

(37)

$$ F_{n + 1}^{{il\:{\text{trial}}}} ({\varvec{\sigma}}_{n + 1}^{{{\text{trial}}}} ,d_{n + 1}^{{{\text{trial}}}} ) = f_{a} (d_{n + 1}^{{{\text{trial}}}} ) - f_{r} (c_{n + 1} ,d_{n + 1}^{{{\text{trial}}}} ) - f_{h} (d_{n + 1}^{{{\text{trial}}}} ) + f_{e} ({\varvec{\sigma}}_{n + 1}^{{{\text{trial}}}} ) = 0. $$

(38)

The first residual equation used in the Newton–Raphson method is obtained by substituting Eq. (36) into Eq. (37) as follows:

$$ {\mathbf{R}}_{1}^{{{\text{trial}}}} (\overline{\varvec{\sigma }}_{n + 1}^{{{\text{trial}}}} ,d_{n + 1}^{{{\text{trial}}}} ) = \overline{\varvec{\sigma }}_{n + 1}^{{{\text{trial}}}} - \overline{\varvec{\sigma }}_{n}^{{{\text{trial}}}} - {\mathbb{C}}_{n + 1}^{{e,\:{\text{trial}}}} :(\Delta {\varvec{\varepsilon}} - \Delta {\varvec{\varepsilon}}^{il} ), $$

(39)

where $\Delta {\varvec{\varepsilon}}^{il}$ can be expressed as a function of $d_{n + 1}^{{{\text{trial}}}}$ as follows:

$$ \Delta {\varvec{\varepsilon}}^{il} = - \frac{1}{3}\theta^{*} \frac{{d_{n + 1}^{{{\text{trial}}}} - d_{n} }}{{d_{0} }}{\varvec{I}}\;,\,\,\;\theta^{*} = \frac{{e_{0}^{il} }}{{1 + e_{0}^{ss} + e_{0}^{il} }}. $$

(40)

As $\Psi$ does not change in the trial elastic calculation, effective stress ${\varvec{\sigma}}_{n + 1}^{{{\text{trial}}}}$ can be expressed with modified effective stress $\overline{\varvec{\sigma }}_{n + 1}^{{{\text{trial}}}}$ as follows:

$$ {\varvec{\sigma}}_{n + 1}^{{{\text{trial}}}} = \overline{\varvec{\sigma }}_{n + 1}^{{{\text{trial}}}} - \Psi_{n} {\varvec{I}}. $$

(41)

Considering that $f_{{\text{e}}} ({{\varvec{\upsigma}}}_{n + 1}^{{{\text{trial}}}} )$ is a function of $\overline{\varvec{\sigma }}_{n + 1}^{{{\text{trial}}}}$, the interlaminar equilibrium is used as the second residual equation as follows:

$$ R_{2}^{{{\text{trial}}}} (\overline{\varvec{\sigma }}_{n + 1}^{{{\text{trial}}}} ,d_{n + 1}^{{{\text{trial}}}} ) = f_{a} (d_{n + 1}^{{{\text{trial}}}} ) - f_{r} (c_{n + 1} ,d_{n + 1}^{{{\text{trial}}}} ) - f_{h} (d_{n + 1}^{{{\text{trial}}}} ) + f_{e} ({{\varvec{\upsigma}}}_{n + 1}^{{{\text{trial}}}} ). $$

(42)

The corrections to stress and interlaminar distance in the Newton–Raphson method are obtained by solving the linearized equations of both residual equations as follows:

$$ \delta \overline{\varvec{\sigma }}^{{{\text{trial}}}} = - {\mathbb{B}}_{n + 1}^{{{\text{trial}}}} :{\mathbf{R}}_{1}^{{{\text{trial}}}} + \left( {\frac{{\theta^{*} }}{{3d_{0} }}\widetilde{\mathbb{C}}_{n + 1}^{{e,\,{\text{trial}}}} :{\varvec{I}}} \right)\delta d^{{{\text{trial}}}} , $$

(43)

$$ \delta d^{{{\text{trial}}}} = \frac{{\frac{1}{3}{\varvec{I:}}{\mathbb{B}}_{n + 1}^{{{\text{trial}}}} :{\mathbf{R}}_{1}^{{{\text{trial}}}} - {R}_{2}^{{{\text{trial}}}} }}{{\frac{{\theta^{*} }}{{9d_{0} }}{\varvec{I:}}\widetilde{\mathbb{C}}_{n + 1}^{{e,\,{\text{trial}}}} :{\varvec{I}} + \frac{{\partial f^{*} }}{\partial d}}}, $$

(44)

where ${{\partial f^{ * } } \mathord{\left/ {\vphantom {{\partial f^{ * } } {\partial d}}} \right. \kern-\nulldelimiterspace} {\partial d}}$, ${\mathbb{B}}_{n + 1}^{{{\text{trial}}}}$, and $\widetilde{\mathbb{C}}_{n + 1}^{{e,\:{\text{trial}}}}$ are given by

$$ \frac{{\partial f^{*} }}{\partial d} = \frac{{\partial f_{{\text{a}}} }}{\partial d} - \frac{{\partial f_{{\text{r}}} }}{\partial d} - \frac{{\partial f_{{\text{h}}} }}{\partial d}, $$

(45)

$$ {\mathbb{B}}_{n + 1}^{{{\text{trial}}}} = \left[ {\frac{1}{2}({\mathbb{I}} + \overline{{\mathbb{I}}} ) - \frac{1}{3}\overline{\mathbb{C}}^{{e,\:{\text{trial}}}} :(\Delta {\varvec{\varepsilon}} - \Delta {\varvec{\varepsilon}}^{il} ) \otimes {\varvec{I}}} \right]^{ - 1} , $$

(46)

$$ \widetilde{\mathbb{C}}_{n + 1}^{{e,\:{\text{trial}}}} = {\mathbb{B}}_{n + 1}^{{{\text{trial}}}} :{\mathbb{C}}_{n + 1}^{{e\:{\text{trial}}}} . $$

(47)

The specific forms of ${{\partial f_{{\text{a}}} } \mathord{\left/ {\vphantom {{\partial f_{{\text{a}}} } {\partial d}}} \right. \kern-\nulldelimiterspace} {\partial d}}$, ${{\partial f_{{\text{r}}} } \mathord{\left/ {\vphantom {{\partial f_{{\text{r}}} } {\partial d}}} \right. \kern-\nulldelimiterspace} {\partial d}}$, and ${{\partial f_{{\text{h}}} } \mathord{\left/ {\vphantom {{\partial f_{{\text{h}}} } {\partial d}}} \right. \kern-\nulldelimiterspace} {\partial d}}$ are showcased in Appendix 7.1.

Upon convergence of the aforementioned iterative calculation, if the yield function value is negative, the loading judgment is designated as “unloading.” Moreover, the internal variables are updated as $\overline{\varvec{\sigma }}_{n + 1} = \overline{\varvec{\sigma }}_{n + 1}^{{{\text{trial}}}}$, $d_{n + 1} = d_{n + 1}^{{{\text{trial}}}}$, and $\varepsilon_{v\:n + 1}^{p} = \varepsilon_{v\:n}^{p}$ before terminating the update procedure. However, if the yield function value is positive, the loading judgment is designated as “loading,” and a plastic corrector step is performed.

3.2.2 Plastic Corrector Step

The equations to be satisfied in the plastic corrector step are Eqs. (26)–(35). The number of unknowns in this step is reduced to three ($\overline{\varvec{\sigma }}_{n + 1}$, $\Delta \Lambda$, and $d_{n + 1}$) by eliminating variables from these equations. This step sets up three residual equations to find these unknowns by the Newton–Raphson method.

Combining Eqs. (26) and (32) gives the following:

$$ \Delta {\varvec{\varepsilon}}^{e} = \Delta {\varvec{\varepsilon}} - \Delta {\varvec{\varepsilon}}^{p} - \Delta {\varvec{\varepsilon}}^{il} . $$

(48)

The first residual equation is obtained by substituting Eqs. (48) and (30) into Eq. (27), as follows:

$$ {\mathbf{R}}_{1}^{{}} (\overline{\varvec{\sigma }}_{n + 1} ,\Delta \Lambda ,d_{n + 1} ) = \overline{\varvec{\sigma }}_{n + 1} - \overline{\varvec{\sigma }}_{n} - {\mathbb{C}}_{n + 1}^{e} :\left( {\Delta {\varvec{\varepsilon}} - \Delta \Lambda \frac{\partial f}{{\partial \overline{\varvec{\sigma }}}} - \Delta {\varvec{\varepsilon}}^{il} } \right), $$

(49)

where $\Delta {\varvec{\varepsilon}}^{il}$ can be expressed as a function of $d_{n + 1}^{{{\text{trial}}}}$ in the same way as in Eq. (40) as follows:

$$ \Delta {\varvec{\varepsilon}}^{il} = - \frac{1}{3}\theta^{*} \frac{{d_{n + 1}^{{}} - d_{n} }}{{d_{0} }}{\varvec{I}}. $$

(50)

Subsequently, the yield function, including the hardening rule, is defined as the second residual equation. As the plastic volumetric strain in $n + 1$ step can be expressed as Eq. (51) from the associated flow rule, the second residual equation is expressed by Eq. (52) as follows:

$$ \varepsilon_{{\rm v}\:n + 1}^{p} = \varepsilon_{{\rm v}\:n}^{p} + \Delta \Lambda {\varvec{I:}}\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}, $$

(51)

$$ R_{2}^{{}} (\overline{\varvec{\sigma }}_{n + 1} ,\Delta \Lambda ) = M\tilde{D}\ln \frac{{\overline{p}}}{{p_{c0} }} + M\tilde{D}\ln \frac{{M^{2} + \overline{\eta }^{2} }}{{M^{2} }} - \varepsilon_{{v{\kern 1pt} n}}^{p} - \Delta \Lambda {\varvec{I:}}\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}. $$

(52)

Finally, the third residual equation is established. Substituting Eq. (30) into Eq. (34) gives the following:

$$ \Psi_{n + 1} = \frac{{\Psi_{n} }}{{1 + \Delta \Lambda \frac{{\tilde{d}}}{{\tilde{D}}}\left\| {\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}} \right\|}}. $$

(53)

Note that $\Psi_{n + 1}$ can be expressed as a function of $\overline{\varvec{\sigma }}_{n + 1}$ and $\Delta \Lambda$. Therefore, $f_{{\text{e}}} ({\varvec{\sigma}}_{n + 1} )$ is also a function of $\overline{\varvec{\sigma }}_{n + 1}$ and $\Delta \Lambda$, because ${\varvec{\sigma}}_{n + 1}^{{}}$ can be expressed using Eq. (33) as follows:

$$ {\varvec{\sigma}}_{n + 1}^{{}} = \overline{\varvec{\sigma }}_{n + 1}^{{}} - \Psi_{n + 1} {\varvec{I}}. $$

(54)

Consequently, the interlaminar equilibrium equation is designated as the third residual equation as follows:

$$ R_{3}^{{}} (\overline{\varvec{\sigma }}_{n + 1} ,\Delta \Lambda ,d_{n + 1} ) = f_{{\text{a}}} (d_{n + 1} ) - f_{{\text{r}}} (c_{n + 1} ,d_{n + 1} ) - f_{{\text{h}}} (d_{n + 1} ) + f_{{\text{e}}} ({\varvec{\sigma}}_{n + 1} ). $$

(55)

The corrections in the Newton–Raphson method are obtained by solving linearized equations of the three residual equations (Eqs. (49), (52), and (55)) as follows:

$$ \delta (\Delta \Lambda ) = \frac{{Df_{1} - Bf_{2} }}{K}, $$

(56)

$$ \delta d = \frac{{ - Cf_{1} + Af_{2} }}{K}, $$

(57)

$$ \delta \overline{\varvec{\sigma }} = - {\mathbb{B}}_{n + 1} :{\mathbf{R}}_{1}^{{}} - \delta (\Delta \Lambda )\widetilde{\mathbb{C}}_{n + 1}^{e} :\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}} + \delta d\frac{{\theta^{*} }}{{3d_{0} }}\widetilde{\mathbb{C}}_{n + 1}^{e} :{\varvec{I}}, $$

(58)

where ${\mathbb{B}}_{n + 1}$, $\widetilde{\mathbb{C}}_{n + 1}^{e}$, and ${{\partial \tilde{f}} \mathord{\left/ {\vphantom {{\partial \tilde{f}} {\partial \overline{\varvec{\sigma }}}}} \right. \kern-\nulldelimiterspace} {\partial \overline{\varvec{\sigma }}}}$ are given by

$$ {\mathbb{B}}_{n + 1} = \left[ {\frac{1}{2}({\mathbb{I}} + \overline{{\mathbb{I}}} ) - \frac{1}{3}\overline{\mathbb{C}}^{e} :\left( {\Delta {\varvec{\varepsilon}} - \Delta {\varvec{\varepsilon}}^{il} - \Delta \Lambda \frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}} \right) + \Delta \Lambda {\mathbb{C}}_{n + 1}^{e} \frac{{\partial^{2} f}}{{\partial \overline{\varvec{\sigma }}\partial \overline{\varvec{\sigma }}}}} \right]^{ - 1} , $$

(59)

$$ \widetilde{\mathbb{C}}_{n + 1}^{e} = {\mathbb{B}}_{n + 1} :{\mathbb{C}}_{n + 1}^{e} , $$

(60)

$$ \frac{{\partial \tilde{f}}}{{\partial \overline{\varvec{\sigma }}}} = \frac{\partial f}{{\partial \overline{\varvec{\sigma }}}} - \Delta \Lambda {\varvec{I:}}\frac{{\partial^{2} f}}{{\partial \overline{\varvec{\sigma }}\partial \overline{\varvec{\sigma }}}}. $$

(61)

The coefficients used in Eqs. (56) and (57) are

$$ A = \frac{{\partial \tilde{f}}}{{\partial \overline{\varvec{\sigma }}:}}\widetilde{\mathbb{C}}_{n + 1}^{e} :\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}} + {\varvec{I:}}\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}, $$

(62)

$$ B = - \frac{{\theta^{*} }}{{3d_{0} }}\frac{{\partial \tilde{f}}}{{\partial \overline{\varvec{\sigma }}:}}\widetilde{\mathbb{C}}_{n + 1}^{e} :{\varvec{I}}, $$

(63)

$$ C = \frac{{\partial F_{n + 1}^{il} }}{{\partial \overline{\varvec{\sigma }}:}}\widetilde{\mathbb{C}}_{n + 1}^{e} :\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}} - \frac{{\partial F_{n + 1}^{il} }}{\partial \Delta \Lambda }, $$

(64)

$$ D = - \left( {\frac{{\theta^{*} }}{{3d_{0} }}\frac{{\partial F_{n + 1}^{il} }}{{\partial \overline{\varvec{\sigma }}:}}\widetilde{\mathbb{C}}_{n + 1}^{e} :{\varvec{I}} + \frac{{\partial f^{*} }}{\partial d}} \right), $$

(65)

$$ K = AD - BC, $$

(66)

$$ f_{1} = F_{n + 1} - \frac{{\partial \tilde{f}}}{{\partial \overline{\varvec{\sigma }}:}}{\mathbb{B}}_{n + 1} :{\varvec{N}}_{n + 1} , $$

(67)

$$ f_{2} = F_{n + 1}^{il} - \frac{{\partial F^{il} }}{{\partial \overline{\varvec{\sigma }}:}}{\mathbb{B}}_{n + 1} :{\varvec{N}}_{n + 1} . $$

(68)

The specific forms of ${{\partial F_{n + 1}^{il} } \mathord{\left/ {\vphantom {{\partial F_{n + 1}^{il} } {\partial {\overline{\mathbf{\sigma }}}}}} \right. \kern-\nulldelimiterspace} {\partial {\overline{\mathbf{\sigma }}}}}$, ${{\partial F_{n + 1}^{il} } \mathord{\left/ {\vphantom {{\partial F_{n + 1}^{il} } {\partial \Delta \Lambda }}} \right. \kern-\nulldelimiterspace} {\partial \Delta \Lambda }}$, ${{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial {\overline{\mathbf{\sigma }}}}}} \right. \kern-\nulldelimiterspace} {\partial {\overline{\mathbf{\sigma }}}}}$, and ${{\partial^{2} f} \mathord{\left/ {\vphantom {{\partial^{2} f} {\partial {\overline{\mathbf{\sigma }}}\partial {\overline{\mathbf{\sigma }}}}}} \right. \kern-\nulldelimiterspace} {\partial {\overline{\mathbf{\sigma }}}\partial {\overline{\mathbf{\sigma }}}}}$ are demonstrated in Appendix 7.2.

The modified stress, interlaminar distance, and plastic multiplier are determined by repeatedly correcting the solution until the values of the residual equations, i.e., Eqs. (56)–(58) yield values which are lower than the designated tolerances. After convergence, other hysteresis variables are updated using Eqs. (51), (53), and (54).

3.2.3 Consistent Tangent Modulus

A tangent modulus consistent with the aforementioned plastic corrector step is derived, such that the global Newton–Raphson method for satisfying the force equilibrium equation can converge to second order. Equations (49), (52), and (55) are linearized around current $\Delta {\varvec{\varepsilon}}$. Herein, the coefficients are defined in the same manner as in the previous section

$$ {\mathbb{B}}_{n + 1}^{ - 1} :{\text{d}}\overline{\varvec{\sigma }}_{n + 1} - {\mathbb{C}}_{n + 1}^{e} :{\text{d}}(\Delta {\varvec{\varepsilon}}) + {\mathbb{C}}_{n + 1}^{e} :\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}{\text{d}}(\Delta \Lambda ) - \frac{{\theta^{*} }}{{3d_{0} }}\widetilde{\mathbb{C}}_{n + 1} :{\varvec{I}}\,{\text{d}}(d) = {\mathbf{0,}} $$

(69)

$$ \frac{{\partial \tilde{f}}}{{\partial \overline{\varvec{\sigma }}:}}{\text{d}}\overline{\varvec{\sigma }}_{n + 1} - {\varvec{I:}}\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}{\text{d}}(\Delta \Lambda ) = 0, $$

(70)

$$ \frac{{\partial F^{il} }}{{\partial \overline{\varvec{\sigma }}:}}{\text{d}}\overline{\varvec{\sigma }}_{n + 1} + \frac{{\partial F^{il} }}{\partial \Delta \Lambda }{\text{d}}(\Delta \Lambda ) + \frac{{\partial f^{*} }}{\partial d}{\text{d}}(d) = 0. $$

(71)

The relations between ${\text{d}}\overline{\varvec{\sigma }}_{n + 1}$, ${\text{d}}(\Delta \Lambda )$, and ${\text{d}}(d)$ are obtained from these equations as follows:

$$ {\text{d}}\overline{\varvec{\sigma }}_{n + 1} = \widetilde{\mathbb{C}}_{n + 1}^{e} :\left[ {{\text{d}}(\Delta {\varvec{\varepsilon}}) - \frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}{\text{d}}(\Delta \Lambda ) + \frac{{\theta^{*} }}{{3d_{0} }}{\varvec{I}}\,{\text{d}}(d)} \right], $$

(72)

$$ {\text{d}}(\Delta \Lambda ) = \frac{{D\left( {\frac{{\partial \tilde{f}}}{{\partial \overline{\varvec{\sigma }}:}}\widetilde{\mathbb{C}}_{n + 1}^{e} :{\text{d}}(\Delta {\varvec{\varepsilon}})} \right) - B\left( {\frac{{\partial F^{il} }}{{\partial \overline{\varvec{\sigma }}:}}\widetilde{\mathbb{C}}_{n + 1}^{e} :{\text{d}}(\Delta {\varvec{\varepsilon}})} \right)}}{K}, $$

(73)

$$ {\text{d}}(d) = \frac{{ - C\left( {\frac{{\partial \tilde{f}}}{{\partial \overline{\varvec{\sigma }}:}}\widetilde{\mathbb{C}}_{n + 1}^{e} :{\text{d}}(\Delta {\varvec{\varepsilon}})} \right) + A\left( {\frac{{\partial F^{il} }}{{\partial \overline{\varvec{\sigma }}:}}\widetilde{\mathbb{C}}_{n + 1}^{e} :{\text{d}}(\Delta {\varvec{\varepsilon}})} \right)}}{K}. $$

(74)

The following consistent tangent modulus for the plastic corrector step is obtained by substituting Eqs. (74) and (75) into Eq. (73) as follows:

$$ {\text{d}}\overline{\varvec{\sigma }}_{n + 1} = \widetilde{\mathbb{C}}_{n + 1}^{ep} :{\text{d}}(\Delta {\varvec{\varepsilon}}), $$

(75)

$$ \begin{aligned} \widetilde{\mathbb{C}}_{n + 1}^{ep} & = \widetilde{\mathbb{C}}_{n + 1}^{e} - \frac{1}{K}\left[ {D\left( {\widetilde{\mathbb{C}}_{n + 1}^{e} :\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}} \right) \otimes \left( {\widetilde{\mathbb{C}}_{n + 1}^{{e\:{\text{T}}}} :\frac{{\partial \tilde{f}}}{{\partial \overline{\varvec{\sigma }}}}} \right) - B\left( {\widetilde{\mathbb{C}}_{n + 1}^{e} :\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}} \right) \otimes \left( {\widetilde{\mathbb{C}}_{n + 1}^{{e\:{\text{T}}}} :\frac{{\partial F^{il} }}{{\partial \overline{\varvec{\sigma }}}}} \right)} \right. \\ & \quad \left. { + \frac{{\theta^{*} }}{{3d_{0} }}C(\widetilde{\mathbb{C}}_{n + 1}^{e} :{\varvec{I}}) \otimes \left( {\widetilde{\mathbb{C}}_{n + 1}^{{e\:{\text{T}}}} :\frac{{\partial \tilde{f}}}{{\partial \overline{\varvec{\sigma }}}}} \right) - \frac{{\theta^{*} }}{{3d_{0} }}A(\widetilde{\mathbb{C}}_{n + 1}^{e} :{\varvec{I}}) \otimes \left( {\widetilde{\mathbb{C}}_{n + 1}^{{e\:{\text{T}}}} :\frac{{\partial F^{il} }}{{\partial \overline{\varvec{\sigma }}}}} \right)} \right]. \\ \end{aligned} $$

(76)

A similar procedure is used to derive tangent coefficients consistent with the elastic predictor step. The following relations are obtained from linearizing Eqs. (39) and (42) around current $\Delta {\varvec{\varepsilon}}$, as follows:

$$ {\text{d}}\overline{\varvec{\sigma }}_{n + 1}^{{{\text{trial}}}} = \widetilde{\mathbb{C}}_{n + 1}^{{e\:{\text{trial}}}} :\left[ {{\text{d}}(\Delta {\varvec{\varepsilon}}) + \frac{{\theta^{*} }}{{3d_{0} }}{\varvec{I}}\,{\text{d}}(d)} \right], $$

(77)

$$ {\text{d}}(d) = \frac{{{\varvec{I:}}\widetilde{\mathbb{C}}_{n + 1}^{{e\:{\text{trial}}}} :{\text{d}}(\Delta {\varvec{\varepsilon}})}}{{ - 3\frac{{\partial f^{*} }}{\partial d} - \left( {\frac{{\theta^{*} }}{{3d_{0} }}{\varvec{I:}}\widetilde{\mathbb{C}}_{n + 1}^{{e\:{\text{trial}}}} :{\varvec{I}}} \right)}}. $$

(78)

The consistent tangent modulus for the elastic predictor step is obtained by substituting Eq. (79) into Eq. (78) as follows:

$$ {\text{d}}\overline{\varvec{\sigma }}_{n + 1}^{{{\text{trial}}}} = \widetilde{\mathbb{C}}_{n + 1}^{{ep\:{\text{trial}}}} :{\text{d}}(\Delta {\varvec{\varepsilon}}), $$

(79)

$$ \widetilde{\mathbb{C}}_{n + 1}^{{ep\:{\text{trial}}}} = \widetilde{\mathbb{C}}_{n + 1}^{{e\:{\text{trial}}}} - \frac{{\frac{{\theta^{*} }}{{3d_{0} }}(\widetilde{\mathbb{C}}_{n + 1}^{{e\:{\text{trial}}}} :{\varvec{I}}) \otimes ({\varvec{I:}}\widetilde{\mathbb{C}}_{n + 1}^{e} )}}{{3\frac{{\partial f^{*} }}{\partial d} + (\frac{{\theta^{*} }}{{3d_{0} }}{\varvec{I:}}\widetilde{\mathbb{C}}_{n + 1}^{{e\:{\text{trial}}}} :{\varvec{I}})}}. $$

(80)

The computational flow based on the above algorithm is summarized in Appendix 8.

4 Numerical Analysis Model

4.1 Tunnel Excavation and Swelling Analysis Methods

Tunnel excavation and swelling analyses were conducted by representing the model proposed in Sect. 2 with our in-house finite element analysis code to achieve the main study objectives of (a) reproducing the qualitative tendency of the deformation in the Mt. Sakazuki Tunnel, and (b) elucidating the mechanism of rapidly developing swelling phenomena. In this finite element analysis, the primary support was not modeled; only the swelling bedrock was analyzed.

4.1.1 Tunnel Excavation Analysis

Figure 5 shows the considered case of excavating a circular hole in an area of ground. Moreover, first, it is assumed that there exists a horizontally stratified ground without a circular hole subjected to the action of overburden and dead weight with a known stress state satisfying the equilibrium equation. Here, the lateral pressure coefficient $K_{0}$ is also known. Unbalanced forces ${\mathbf{R}}$ (= external nodal forces—internal nodal forces) act on the surface of the circular hole due to the presence of a circular hole in reality. These unbalanced forces are computed from the initial stress state and self-weight; moreover, tunnel excavation analysis is conducted by gradually decreasing these forces.

Fig. 5

Calculation of unbalanced forces

4.1.2 Swelling Analysis

Swelling analysis is conducted after the unbalanced forces are completely removed. Herein, the ion concentration $c$ is lowered in the analysis area by assuming that groundwater is supplied from the surrounding ground toward the tunnel-cavity subject to the influence of excavation. When the ion concentration decreases, the osmotic pressure changes according to the interlaminar equilibrium, which induces swelling behavior. Accompanying this change, the state variables vary to satisfy the dominant equations, i.e., Eqs. (16)–(25). This process is tracked by incremental analysis. In reality, the decrease in ion concentrations is thought to occur non-uniformly depending on the heterogeneity of groundwater flow within the bedrock. In this study, however, ion concentrations are reduced uniformly over the entire analysis region to distinguish the regions around the tunnel that are likely to be deformed, independent of the heterogeneity of the ion concentrations.

4.1.3 Finite Element Model and Boundary Conditions

Figure 6 shows a finite element model (5040 nodes and 2400 elements). Note that 8-node hexahedral elements were used (Fig. 7).

Fig. 6

Finite element model and boundary conditions

Fig. 7

Schematic of the shape of the tunnel

A tunnel was placed at the center of the analysis region (100 m × 100 m × 1 m), and calculations were performed by assuming planar strain conditions. Horizontal displacements were fixed on the left and right boundaries; furthermore, vertical displacements were fixed on the lower boundary. An equally distributed load of 1000 kPa, equivalent to the earth pressure of approximately 50 m, was applied to the top boundary to reproduce approximately 100 m of earth cover at the point where the deformation occurred in Mt. Sakazuki Tunnel.

4.2 Parameter Setting

The analyzed parameters were set based on the report for the deformation at Mt. Sakazuki Tunnel (Okui et al. 2009). The geological profile of the Mt. Sakazuki Tunnel was dominated by Cenozoic Tertiary Miocene rhyolite and homogeneous tuff. Soft rhyolitic tuffs subjected to hydrothermal alteration were distributed in the deformed section and are known to contain large amounts of smectite. Based on these considerations, stiffness and initial specific volume in bedrock are assumed to be the soft rock properties of volcanic origin.

Table 1 lists the material constants. The specific volume is set uniformly for all elements to easily conduct self-weight analyses. The reference specific volume on normal consolidation line $N$, critical state constant $M$, compression index $\tilde{\lambda }$, swelling index $\tilde{\kappa }$, and reference stress $p_{{\text{r}}}$ were set based on the material properties of London clay (Atkinson and Bransby 1978). The parameters of the Cam-clay model were substituted with the properties of the London clay, because it was difficult to collect samples locally. The soil particle density of expansive clay $\rho_{{{\text{sw}}}}$ was set as the material property of bentonite sampled in Yamagata Prefecture in Japan (Konishi et al. 2010). The soil particle density $\rho_{{\text{s}}}$, Poisson’s ratio $\nu$, and lateral pressure coefficient $K_{0}$ were set as the general material properties of nonexpansive clay.

Table 1 Material constants

Table 2 lists the physical constants, and Table 3 lists the parameters for osmotic pressure, Van der Waals force, and hydration force (Kyokawa et al. 2020). In this research, only sodium ions were considered.

Table 2 Physical constants

Table 3 Parameters for electro-chemical action

Table 4 lists the initial conditions and other parameters. The initial specific volume was calculated from the dry density of pyroclastic rock, classified as soft rock (Japan Rock Mechanics Committee 2002). The initial cementation was set to be consistent with the estimated uniaxial compressive strength of the soft rock (Kobayashi and Adachi 1982). Additionally, the uniaxial strength was the assumed strength of soft rocks classified as fresh-to-slightly weathered based on the engineering classification of bedrock (Japan Rock Mechanics Committee 2004, JGS 3811-2004). The calculation method for the initial values is explained in Appendix 9. The degradation index of cementation was set with reference to Yamada et al. (2022). Initial and critical ion concentrations (lower limit) were set with reference to Komine and Ogata (2003). The mass ratio of expansive to nonexpansive clay is a parameter used to determine the initial interlaminar void rate, and their relationship is explained in Appendix 10.

Table 4 Initial conditions and other parameters

5 Computational Results and Discussion

First, the proposed model was validated to determine whether it can represent the mechanical behavior of swelling rock.

Figures 8 and 9 show the distributions of cementation $\Psi$ and volumetric strain in an interlaminar void after excavation and swelling analyses. Hereafter, a volumetric strain of an interlaminar void is referred to as the “expansion amount.” In the swelling analysis following the excavation analysis, cementation degradation and swelling progress within a limited area, such as that just below the bottom part of the tunnel, despite the fact that the ion concentration was reduced uniformly in the entire analysis area.

Fig. 8

Cementation distribution

Fig. 9

Distributions of expansion amount

Figure 10 shows distributions of vertical displacement and expansion amount in bedrock just below the tunnel bottom. Depth from the bottom is plotted on the vertical axis, and the cumulative values are plotted at a fixed point approximately 10 m from the bottom. Herein, the vertical displacement is only due to swelling. Note that the expansion and vertical displacement increase remarkably from approximately 5 m just below the bottom. These figures show that the proposed model can describe the mechanical behavior of swelling bedrock adequately, because this tendency in the vertical displacement distribution matches the observed results at Mt. Sakazuki Tunnel, which are shown in Fig. 11. Herein, Fig. 11 shows the displacement distribution after lining observed 17 years after service entry. According to calculations completed separately, it was confirmed that the expansion amount and vertical displacement distribution were not affected considerably by ground surface loading.

Fig. 10

Distributions of vertical displacement and expansion amount in bedrock just below the bottom part of the tunnel

Fig. 11

Observed results of underground displacement in the Mt. Sakazuki Tunnel (Okui et al. 2009, partially reorganized)

Figure 12 shows the relationship between change in ion concentration and expansion amount of Element A. Pronounced swelling is observed, as marked in Fig. 9d. The dashed and solid lines show the excavation and swelling processes, respectively. The expansion amount increases rapidly when the ion concentration falls below a certain value. Considering the changing ion concentrations as equivalent to evolving time, this figure suggests that deformation due to swelling develops in a short time when the ion concentration falls below a certain value, because the ion concentration changes in actual bedrock due to a continuous supply of groundwater. In fact, deformations due to swelling were reported to be sudden and grew rapidly in the Mt. Sakazuki Tunnel (Okui et al. 2009).

Fig. 12

Relationship between ion concentration and expansion amount of Element A from Fig. 9d

In the next section, we investigate this remarkable swelling behavior that occurs approximately 5 m below the bottom part of the tunnel and its rapid growth after a certain point in time. Figure 13 shows the shear stress distribution just below the bottom part of the tunnel after excavation. The shear stress reaches a minimum at 7 m below the bottom and increases rapidly from approximately 5 m below the bottom part of the tunnel. This distribution of the shear stress is similar to that of the expansion amount after swelling analysis shown in Fig. 10. This correlation suggests that as the shear stress generated during tunnel excavation increases, the swelling increases when ion concentration decreases.

Fig. 13

Shear stress distribution after excavation

Considering the stress paths of the two elements shown in Fig. 9d, Element A is located at the bottom of the tunnel where swelling is considerable; moreover, Element B is located at increased depths in which the shear stress after excavation is minimal. Figures 14 and 15 show both the stress path and relationship between the ion concentration and volumetric strain in Elements A and B, respectively. Stress paths are plotted in the $\overline{p} - \overline{q}$ plane considering the amount of translation due to cementation. The dashed and solid lines show the excavation and swelling processes, respectively.

Fig. 14

Behaviors of Element A

Fig. 15

Behavior of Element B

In the stress paths, Element A (Fig. 14a) achieves a stress state above the critical state line at the initiation of swelling analysis owing to the influence of the large shear stress caused by excavation. During swelling analysis, the effective stress increases because of interlayer spreading as the ion concentration decreases and the bedrock skeleton yields outcomes above the critical state line. In the Cam-clay model, the area above the critical state line is the softening zone with plastic expansion (Asaoka et al. 1994). In the stress path of Element A, the shear and mean effective stresses decrease after yielding. These indicate that softening occurs in the region with pronounced swelling. As the mean effective stress decreases due to softening, the distance between the crystalline layers also increases according to the mechanism described by Eq. (8), thus resulting in significant swelling just below the tunnel base. The proposed model describes the high stiffness of bedrock owing to the introduction of cementation, which also increases shear stress during the excavation and decreases ion concentration; in turn, these events lead to softening with plastic expansion. In addition, Figs. 8 and 9 show that as the degradation of the internal structure becomes more extensive, swelling becomes more pronounced. This means that the cementation reduction caused by degrading internal structure promotes swelling.

Moreover, it becomes clear that the rapid swelling begins when the bedrock skeleton reaches yield after comparison of Fig. 14a, b. This illustrates that the changing ion concentrations induce the bedrock skeleton to yield; moreover, the softening initiated by the yielding of the bedrock skeleton leads to significant swelling of the interlaminar layers. Consequently, the yielding of the bedrock skeleton triggers rapid expansion.

In contrast, Fig. 15a shows that Element B is in an almost isotropically stress state after excavation and continues to be compressed elastically during the swelling analysis. In addition, the volumetric expansion is neither sudden nor significant like in Element A, because the behavior of the bedrock skeleton has a minor influence on the behavior of the interlaminar in Element B. Therefore, swelling is suppressed in Element B.

The results outlined above conclude that the distribution of shear stress during excavation below the tunnel’s bottom part is such that the minimum point exists at approximately 6–7 m (below the bottom part of the tunnel) and that significant swelling tends to occur in the high-shear stress region which is at lower depths than the depth at which the shear stress is minimized. Moreover, numerical simulations reveal that the yielding of the bedrock skeleton triggers considerable swelling deformation produced by the interaction of coupled electro-chemo-mechanical phenomena in the crystalline layers of swelling clay minerals and elastoplastic phenomena with internal structural degradation within the rock matrix.

6 Conclusions

This study proposed a novel model targeting expansive bedrock by combining an elastoplastic model considering electro-chemo-mechanical phenomena with the Cam-clay model based on cementation considerations and its degradation due to plastic deformation. The proposed model was represented by finite element analysis code. Moreover, tunnel excavation and swelling analyses were conducted to clarify the characteristics and mechanism responsible for tunnel deformation in swelling bedrock. Some of the key results and insights are the following:

• (1) Tunnel deformation caused by swelling in crystal layers tends to occur just below the tunnel base. Moreover, extensive swelling starts from approximately 5 m just below the bottom part of the tunnel.

• (2) There was extensive swelling in a limited area approximately 5 m below the bottom part of the tunnel, because high-shear stress was already acting in this region after the excavation; additionally, softening with plastic expansion occurred above the critical state line when the ion concentration decreased.

• (3) During excavation, the uplift of the tunnel bottom grew rapidly after a certain time owing to decreasing ion concentration in the bedrock caused by groundwater supply to the tunnel. The yielding of the bedrock skeleton triggered this rapid uplift.

• (4) The mechanism behind the aforementioned observation began with swelling in crystal layers owing to the influence of decreasing ion concentration that caused the yielding of the bedrock skeleton. Additionally, as high-stress ratios were acting owing to tunnel excavation at depths just below the bottom part of the tunnel, the bedrock skeleton yielded above the critical state line, and caused softening with plastic expansion. To elaborate, a decrease in confining pressure is associated with softening, which in turn causes expansion between crystal layers. The swelling then progressed rapidly, accompanied by reduced cementation owing to internal structural degradation that resulted in tunnel deformation. Therefore, the rapid swelling in the bottom part of the tunnel was attributed to the interactions between coupled electro-chemo-mechanical phenomena which occurred between the crystal layers as well as elastoplastic phenomena which involved internal structural degradation of the bedrock skeleton.

Appendices

Appendices

Appendix A: Linearization of Residual Equations

2.1 A.1 Specific Forms of Linearization Terms in the Elastic Predictor Step

This section presents the specific forms of linearization terms used in the elastic predictor step in Sect. 3.2. First, the linearized forms of the residual equations in the elastic predictor step are

$$ {\mathbf{R}}_{1}^{{{\text{trial}}}} + \frac{{\partial {\mathbf{R}}_{1}^{{{\text{trial}}}} }}{{\partial \overline{\varvec{\sigma }}:}}\delta \overline{\varvec{\sigma }}^{{{\text{trial}}}} + \frac{{\partial {\mathbf{R}}_{1}^{{{\text{trial}}}} }}{\partial d}\delta d^{{{\text{trial}}}} = {\mathbf{0,}} $$

(81)

$$ R_{2}^{{{\text{trial}}}} + \frac{{\partial R_{2}^{{{\text{trial}}}} }}{{\partial \overline{\varvec{\sigma }}:}}\delta \overline{\varvec{\sigma }}^{{{\text{trial}}}} + \frac{{\partial R_{2}^{{{\text{trial}}}} }}{\partial d}\delta d^{{{\text{trial}}}} = 0. $$

(82)

Additionally, each linearization term is

$$ \frac{{\partial {\mathbf{R}}_{1}^{{{\text{trial}}}} }}{{\partial \overline{\varvec{\sigma }}}} = \frac{1}{2}({\mathbb{I}} + \overline{{\mathbb{I}}} ) - \frac{1}{3}\overline{\mathbb{C}}^{e} :(\Delta {\varvec{\varepsilon}} - \Delta {\varvec{\varepsilon}}^{il} ) \otimes {\varvec{I}}, $$

(83)

$$ \frac{{\partial {\mathbf{R}}_{1}^{{{\text{trial}}}} }}{\partial d} = - \frac{{\theta^{*} }}{{3d_{0} }}{\mathbb{C}}_{n + 1}^{e} :{\varvec{I}}, $$

(84)

$$ \frac{{\partial R_{2}^{{{\text{trial}}}} }}{{\partial \overline{\varvec{\sigma }}}} = \frac{{\partial \overline{p}}}{{\partial \overline{\varvec{\sigma }}}} = \frac{{\varvec{I}}}{3}, $$

(85)

$$ \frac{{\partial R_{2}^{{{\text{trial}}}} }}{\partial d} = \frac{{\partial f_{{\text{a}}} }}{\partial d} - \frac{{\partial f_{{\text{r}}} }}{\partial d} - \frac{{\partial f_{{\text{h}}} }}{\partial d}. $$

(86)

Partial differentiation of osmotic repulsive pressure, Van der Waals force, and hydration force by interlaminar distance are

$$ \frac{{\partial f_{{{\text{r}}i}} }}{\partial d} = \frac{{\partial f_{{{\text{r}}i}} }}{{\partial u_{i} }}\frac{{\partial u_{i} }}{\partial d}, $$

(87)

$$ \left\{ \begin{gathered} \frac{{\partial f_{{{\text{r}}i}} }}{{\partial u_{i} }} = c_{i} N_{{\text{A}}} kT(e^{{u_{i} }} - e^{{ - u_{i} }} ) \times 10^{ - 3} \hfill \\ \frac{{\partial u_{i} }}{\partial d} = \frac{{ - 8\omega \exp ( - \omega_{i} d)\left( {\tanh \frac{{z_{i} }}{4}} \right)}}{{1 - \exp ( - 2\omega_{i} d)\left( {\tanh \frac{{z_{i} }}{4}} \right)}} \hfill \\ \end{gathered} \right., $$

$$ \frac{{\partial f_{{\text{a}}} }}{\partial d} = - \frac{{A_{{\text{h}}} }}{8\pi }\left[ {\frac{1}{{d^{4} }} + \frac{1}{{(d + t)^{4} }} - \frac{2}{{\left( {d + \frac{t}{2}} \right)^{4} }}} \right] \times 10^{ - 3} , $$

(88)

$$ \frac{{\partial f_{{\text{h}}} }}{\partial d} = - \frac{{W_{0} }}{{\chi_{0}^{2} }}\exp \left( { - \frac{d}{{\chi_{0} }}} \right) \times 10^{3} . $$

(89)

2.2 A.2 Specific Forms of Linearization Terms in the Plastic Corrector Step

The linearized forms of residual equations in the plastic corrector step are

$$ {\mathbf{R}}_{1}^{{}} + \frac{{\partial {\mathbf{R}}_{1}^{{}} }}{{\partial \overline{\varvec{\sigma }}:}}\delta \overline{\varvec{\sigma }} + \frac{{\partial {\mathbf{R}}_{1}^{{}} }}{\partial \Delta \Lambda }\delta (\Delta \Lambda ) + \frac{{\partial {\mathbf{R}}_{1}^{{}} }}{\partial d}\delta d = {\mathbf{0,}} $$

(90)

$$ R_{2}^{{}} + \frac{{\partial R_{2}^{{}} }}{{\partial \overline{\varvec{\sigma }}:}}\delta \overline{\varvec{\sigma }} + \frac{{\partial R_{2}^{{}} }}{\partial \Delta \Lambda }\delta (\Delta \Lambda ) = 0, $$

(91)

$$ R_{3}^{{}} + \frac{{\partial R_{3}^{{}} }}{{\partial \overline{\varvec{\sigma }}:}}\delta \overline{\varvec{\sigma }} + \frac{{\partial R_{3}^{{}} }}{\partial \Delta \Lambda }\delta (\Delta \Lambda ) + \frac{{\partial R_{3}^{{}} }}{\partial d}\delta d = 0. $$

(92)

Additionally, each linearization term is

$$ \frac{{\partial {\mathbf{R}}_{1}^{{}} }}{{\partial \overline{\varvec{\sigma }}}} = \frac{1}{2}({\mathbb{I}} + \overline{{\mathbb{I}}} ) - \frac{1}{3}\overline{\mathbb{C}}^{e} :\left( {\Delta {\varvec{\varepsilon}} - \Delta {\varvec{\varepsilon}}^{il} - \Delta \Lambda \frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}} \right) + \Delta \Lambda {\mathbb{C}}_{n + 1}^{e} :\frac{{\partial^{2} f}}{{\partial \overline{\varvec{\sigma }}\partial \overline{\varvec{\sigma }}}}, $$

(93)

$$ \frac{{\partial {\mathbf{R}}_{1}^{{}} }}{\partial \Delta \Lambda } = {\mathbb{C}}_{n + 1}^{e} :\frac{\partial f}{{\partial \overline{{\varvec{\sigma}}} }}, $$

(94)

$$ \frac{{\partial {\mathbf{R}}_{1}^{{}} }}{\partial d} = - \frac{{\theta^{*} }}{{3d_{0} }}{\mathbb{C}}_{n + 1}^{e} :{\varvec{I}}, $$

(95)

$$ \frac{{\partial R_{2}^{{}} }}{{\partial \overline{\varvec{\sigma }}}} = \frac{\partial f}{{\partial \overline{\varvec{\sigma }}}} - \Delta \Lambda {\varvec{I:}}\frac{{\partial^{2} f}}{{\partial \overline{\varvec{\sigma }}\partial \overline{\varvec{\sigma }}}}, $$

(96)

$$ \frac{{\partial R_{2}^{{}} }}{\partial \Delta \Lambda } = - {\varvec{I:}}\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}, $$

(97)

$$ \frac{{\partial R_{3}^{{}} }}{{\partial \overline{\varvec{\sigma }}}} = \frac{{\partial F_{n + 1}^{il} }}{{\partial \overline{\varvec{\sigma }}}} = \frac{{\varvec{I}}}{3} + \frac{{\Psi_{n} \Delta \Lambda \frac{{\tilde{d}}}{{\tilde{D}}}}}{{\left\| {\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}} \right\|\left( {1 + \Delta \Lambda \frac{{\tilde{d}}}{{\tilde{D}}}\left\| {\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}} \right\|} \right)^{2} }}\frac{{\partial^{2} f}}{{\partial \overline{\varvec{\sigma }}\partial \overline{\varvec{\sigma }}:}}\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}, $$

(98)

$$ \frac{{\partial R_{3}^{{}} }}{\partial \Delta \Lambda } = \frac{{\partial F_{n + 1}^{il} }}{\partial \Delta \Lambda } = \frac{{\Psi_{n} \frac{{\tilde{d}}}{{\tilde{D}}}\left\| {\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}} \right\|}}{{\left( {1 + \Delta \Lambda \frac{{\tilde{d}}}{{\tilde{D}}}\left\| {\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}} \right\|} \right)^{2} }}, $$

(99)

$$ \frac{{\partial R_{3}^{{}} }}{\partial d} = \frac{{\partial f_{{\text{a}}} }}{\partial d} - \frac{{\partial f_{{\text{r}}} }}{\partial d} - \frac{{\partial f_{{\text{h}}} }}{\partial d}. $$

(100)

Finally, the first- and second-order derivatives of the yield function with stress are

$$ \frac{\partial f}{{\partial \overline{\varvec{\sigma }}}} = \frac{{M\tilde{D}}}{{(M^{2} + \overline{\eta }^{2} )^{2} \overline{p}}}\left[ {\frac{1}{3}(M^{2} - \overline{\eta }^{2} ){\varvec{I}} + 3\overline{\varvec{\eta }}} \right], $$

(101)

$$ \begin{aligned} \frac{{\partial^{2} f}}{{\partial \overline{\varvec{\sigma }}\partial \overline{\varvec{\sigma }}}} & = \frac{{M\tilde{D}}}{{(M^{2} + \overline{\eta }^{2} )^{2} \overline{p}^{2} }}\left\{ {\frac{3}{2}(M^{2} + \overline{\eta }^{2} )({\mathbb{I}} + \overline{{\mathbb{I}}} ) - 9\overline{\varvec{\eta }} \otimes \overline{\varvec{\eta }}} \right. \\ & \quad \left. { - 2M^{2} ({\varvec{I}} \otimes \overline{\varvec{\eta }} + \overline{\varvec{\eta }} \otimes {\varvec{I}}) - \left[ {\frac{1}{9}(M^{4} - 4M^{2} \overline{\eta }^{2} - \overline{\eta }^{4} ) + M^{2} + \overline{\eta }^{2} } \right]{\varvec{I}} \otimes {\varvec{I}}} \right\}. \\ \end{aligned} $$

(102)

Appendix B: Calculation Flow

This section summarizes the computational flow based on the stress and internal variables update algorithm in Sect. 3.2.

The algorithm for the proposed model is as follows:

1. For load increment $n + 1$.

2. For gobal Newton–Raphson iteration $k$.

3. Compute ${\varvec{\sigma}}_{n + 1}^{k}$ and $\tilde{\mathbb{C}}_{n + 1}^{ep}$ from given $\Delta {\varvec{\varepsilon}}^{k} ,\,c_{n + 1} ,\,{\varvec{\sigma}}_{n} ,\,{\varvec{\varepsilon}}_{v,\,n}^{p} ,\,\Psi_{n} ,\,d_{n}$ ($k$ now implied)

$$ {\overline{\varvec{\sigma }}}_{n} = {\varvec{\sigma}}_{n} + \Psi_{n} {\varvec{I}} $$

4. Trial calculation

4.1 For trial Newton–Raphson iteration $l$.

4.2 Find ${\varvec{\sigma}}_{n + 1}^{{l\,\,{\rm trial}}} \,,\,d_{n + 1}^{{l\,\,{\rm trial}\,\,}}$ ($l$ now implied)

$$ \Delta {\varvec{\varepsilon}}_{{}}^{{e,\,{\text{trial}}}} = \Delta {\varvec{\varepsilon}} - \Delta {\varvec{\varepsilon}}^{il} ,\,\,\Delta {\varvec{\varepsilon}}^{il} = - \frac{1}{3}\theta^{*} \frac{{d_{n + 1}^{{{\text{trial}}}} - d_{n} }}{{d_{0} }}{\varvec{I}} $$

$$ {\varvec{\sigma}}_{n + 1}^{\text{trial}} = {\overline{\varvec{\sigma }}}_{n + 1}^{\text{trial}} - \Psi_{n} {\varvec{I}} $$

${\mathbf{R}}_{1}^{{{\text{trial}}}} = \overline{\varvec{\sigma }}_{n + 1}^{{{\text{trial}}}} - \overline{\varvec{\sigma }}_{n}^{{}} - {\mathbb{C}}_{n + 1}^{{e,\,{\text{trial}}}} :\Delta {\varvec{\varepsilon}}_{{}}^{{e,\,{\text{trial}}}}$ Elastic constitutive law (see Eqs. (17), (39), (40))

$$ {R}_{2}^{{{\text{trial}}}} = f_{a} \left( {d_{n + 1}^{{{\text{trial}}}} } \right) - f_{r} \left( {d_{n + 1}^{{{\text{trial}}}} ,c_{n + 1} } \right) - f_{h} \left( {d_{n + 1}^{{{\text{trial}}}} } \right) + f_{e} \left( {{\varvec{\sigma}}_{n + 1}^{{{\text{trial}}}} } \right) $$

Interlaminar equilibrium (see Eqs. (9)–(13))

If (${\mathbf{R}}_{1}^{{{\text{trial}}}}$ tolerance or ${R}_{2}^{{{\text{trial}}}}$ tolerance).

Then

$\delta d^{{{\text{trial}}}} = \frac{{\frac{1}{3}{\varvec{I}}:{\mathbb{B}}_{n + 1}^{{{\text{trial}}}} :{\mathbf{R}}_{1}^{{{\text{trial}}}} - {\text{R}}_{2}^{{{\text{trial}}}} }}{{\frac{{\theta^{*} }}{{9d_{0} }}{\varvec{I}}:\tilde{\mathbb{C}}_{n + 1}^{{e,{\text{trial}}}} :{\varvec{I}} + \frac{{\partial f^{*} }}{\partial d}}}$(see Eqs. (45)–(47)))

$\delta \overline{\varvec{\sigma }}^{{{\text{trial}}}} = - {\mathbb{B}}_{n + 1}^{{{\text{trial}}}} :{\mathbf{R}}_{1}^{{{\text{trial}}}} + \left( {\frac{{\theta^{*} }}{{3d_{0} }}\tilde{\mathbb{C}}_{n + 1}^{{e,{\text{trial}}}} :{\varvec{I}}} \right)\delta d^{{{\text{trial}}}}$(see Eqs. (45)–(47)))

$d_{n + 1}^{{{\text{trial}}}} = d_{n + 1}^{{{\text{trial}}}} + \delta d^{{{\text{trial}}}}$ Correct interlaminar distance.

$\overline{\varvec{\sigma }}_{n + 1}^{{{\text{trial}}}} = \overline{\varvec{\sigma }}_{n + 1}^{{{\text{trial}}}} + \delta \overline{\varvec{\sigma }}^{{{\text{trial}}}}$ Correct modified stress.

$l \Leftarrow l + 1$ GO TO 4.1

Else

GO TO 5

Endif

5. Check for yielding

If $f\left( {\overline{\varvec{\sigma }}_{n + 1}^{{{\text{trial}}}} } \right) \le 0$.

Then

Elastic state

${\varvec{\sigma}}_{n + 1}^{{}} = {\varvec{\sigma}}_{n + 1}^{{{\text{trial}}}}$; $\varepsilon_{v,n + 1}^{p} = \varepsilon_{v,n}^{p}$; $\Psi_{n + 1}^{{}} = \Psi_{n}^{{}}$; $d_{n + 1}^{{}} = d_{n + 1}^{{{\text{trial}}}}$

$$ \tilde{\mathbb{C}}_{n + 1}^{ep} = \tilde{\mathbb{C}}_{n + 1}^{{e,{\text{trial}}}} - \frac{{\frac{{\theta^{*} }}{{3d_{0} }}\left( {\tilde{\mathbb{C}}_{n + 1}^{{e,{\text{trial}}}} :{\varvec{I}}} \right) \otimes \left( {{\varvec{I}}:\tilde{\mathbb{C}}_{n + 1}^{{e,{\text{trial}}}} } \right)}}{{3\frac{{\partial f^{*} }}{\partial d} + \left( {\frac{{\theta^{*} }}{{3d_{0} }}{\varvec{I}}:\tilde{\mathbb{C}}_{n + 1}^{{e,{\text{trial}}}} :{\varvec{I}}} \right)}} $$

Compute tangent modulus (see Eqs. (45)–(47))

GO TO 7

Else

Plastic state

GO TO 6

Endif

6. Return-Mapping algorithm

6.1 For Return-Mapping Newton–Raphson iteration $m$.

6.2 Find $\overline{\varvec{\sigma }}_{n + 1}^{m} \,,\,d_{n + 1}^{m} \,,\,\Delta \Lambda^{m}$ ($m$ now implied)

$$ \Delta {\varvec{\varepsilon}}_{{}}^{e} = \Delta {\varvec{\varepsilon}} - \Delta {\varvec{\varepsilon}}^{p} - \Delta {\varvec{\varepsilon}}^{il} ,\,\,\Delta {\varvec{\varepsilon}}^{p} = \Delta \Lambda \frac{\partial f}{{\partial \overline{\varvec{\sigma }}}},\,\,\Delta {\varvec{\varepsilon}}^{il} = - \frac{1}{3}\theta^{*} \frac{{d_{n + 1}^{{{\text{trial}}}} - d_{n} }}{{d_{0} }}{\varvec{I}} $$

$$ \varepsilon_{v,n + 1}^{p} = \varepsilon_{v,n}^{p} + \Delta \Lambda {\varvec{I}}:\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}} $$

$$ {\varvec{\sigma}}_{n + 1}^{{}} = \overline{\varvec{\sigma }}_{n + 1}^{{}} - \Psi_{n + 1} {\varvec{I}},\,\Psi_{n + 1} = \frac{{\Psi_{n} }}{{1 + \Delta \Lambda \frac{{\tilde{d}}}{{{\tilde{\text{D}}}}}\left\| {\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}} \right\|}} $$

${\mathbf{R}}_{1}^{{}} = \overline{\varvec{\sigma }}_{n + 1}^{{}} - \overline{\varvec{\sigma }}_{n}^{{}} - {\mathbb{C}}_{n + 1}^{e} :\Delta {\varvec{\varepsilon}}^{e}$ Elastic constitutive law

${R}_{2}^{{}} = {{M\tilde{D}}}\left( {\ln \frac{{\overline{p}}}{{p_{c0} }}\frac{{{\text{M}}^{2} + \overline{\eta }^{2} }}{{\text{M}}}} \right) - \varepsilon_{v,n + 1}^{p}$ Yield function and Hardening

${R}_{3}^{{}} = f_{a} \left( {d_{n + 1}^{{}} } \right) - f_{r} \left( {d_{n + 1}^{{}} ,c_{n + 1} } \right) - f_{h} \left( {d_{n + 1}^{{}} } \right) + f_{e} \left( {{\varvec{\sigma}}_{n + 1}^{{}} } \right)$ Interlaminar equilibrium (see Eq. (55))

If (${\mathbf{R}}_{1}^{{}} >$ tolerance or ${R}_{2}^{{}} >$ tolerance or ${R}_{3}^{{}} >$ tolerance).

Then (see Eqs. (60)–(68))

$$ \delta d = \frac{{ - Cf_{1} + Af_{2} }}{K} $$

$$ \delta \left( {\Delta \Lambda } \right) = \frac{{Df_{1} + Bf_{2} }}{K} $$

$$ \delta \overline{\varvec{\sigma }} = - {\mathbb{B}}_{n + 1} :{\mathbf{R}}_{1} - \delta \left( {\Delta \Lambda } \right)\tilde{\mathbb{C}}_{n + 1}^{e} :\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}} + \delta d\frac{{\theta^{*} }}{{3d_{0} }}\tilde{\mathbb{C}}_{n + 1}^{e} :{\varvec{I}} $$

$d_{n + 1}^{{}} = d_{n + 1}^{{}} + \delta d^{{}}$ Correct interlaminar distance

$\Delta \Lambda = \Delta \Lambda + \delta \left( {\Delta \Lambda } \right)$ Correct incremental plastic multiplier

$\overline{\varvec{\sigma }}_{n + 1}^{{}} = \overline{\varvec{\sigma }}_{n + 1}^{{}} + \delta \overline{\varvec{\sigma }}^{{}}$ Correct modified stress

$m \Leftarrow m + 1$ GO TO 6.1

Else

$$ \begin{gathered} \tilde{\mathbb{C}}_{n + 1}^{ep} = \tilde{\mathbb{C}}_{n + 1}^{e} - \frac{1}{K}\left[ {D\left( {\tilde{\mathbb{C}}_{n + 1}^{e} :\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}} \right) \otimes \left( {\tilde{\mathbb{C}}_{n + 1}^{{e\,\,{\text{T}}}} :\frac{{\partial \tilde{f}}}{{\partial \overline{\varvec{\sigma }}}}} \right) - B\left( {\tilde{\mathbb{C}}_{n + 1}^{e} :\frac{\partial f}{{\partial \overline{\varvec{\sigma }}}}} \right) \otimes \left( {\tilde{\mathbb{C}}_{n + 1}^{{e\,\,{\text{T}}}} :\frac{{\partial F^{il} }}{{\partial \overline{\varvec{\sigma }}}}} \right)} \right. \hfill \\ \left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{\theta^{*} }}{{3d_{0} }}C\left( {\tilde{\mathbb{C}}_{n + 1}^{e} :{\varvec{I}}} \right) \otimes \left( {\tilde{\mathbb{C}}_{n + 1}^{{e\,\,{\text{T}}}} :\frac{{\partial \tilde{f}}}{{\partial \overline{\varvec{\sigma }}}}} \right) - \frac{{\theta^{*} }}{{3d_{0} }}A\left( {\tilde{\mathbb{C}}_{n + 1}^{e} :{\varvec{I}}} \right) \otimes \left( {\tilde{\mathbb{C}}_{n + 1}^{{e\,\,{\text{T}}}} :\frac{{\partial F^{il} }}{{\partial \overline{\varvec{\sigma }}}}} \right)} \right] \hfill \\ \end{gathered} $$

Compute tangent modulus (see Eqs. (59)–(68))

GO TO 7

Endif

7. Check equilibrium

If ${\mathbf{R}} >$ tolerance

Then

$k \Leftarrow k + 1$ GO TO 2

Else

Update internal variables ${\varvec{\sigma}}_{n}^{{}} \,,\,\varepsilon_{v,n}^{p} ,\,\Psi_{n} ,\,d_{n}^{{}} \,$

$n \Leftarrow n + 1$ GO TO 1

Endif

Appendix C: Determination of Initial Values

4.1 C.1 Calculation of Initial Specific Volume

This section describes the method used to determine the initial specific volume. In this research, the initial specific volume was calculated from the dry density of a pyroclastic rock. Dry density $\rho_{{\text{d}}}$ and initial bedrock skeleton void $e_{0}^{ss}$ are related as follows:

$$ \rho_{{\text{d}}} = \frac{{\rho_{{\text{s}}} }}{{1 + e_{0}^{ss} }}. $$

(103)

Therefore, from the dry density $\rho_{{\text{d}}}$ and soil particle density $\rho_{{\text{s}}}$, the initial specific volume of the bedrock excluding interlaminar void is obtained as follows:

$$ v_{0}^{ss} = 1 + e_{0}^{ss} = \frac{{\rho_{{\text{s}}} }}{{\rho_{{\text{d}}} }}. $$

(104)

The method of determination of initial interlaminar void is described in Appendix 10.

4.2 C.2 Calculation of Initial Cementation

This section describes the method used to determine the initial cementation. The uniaxial tensile strength of a rock is in the range of 5–20% of the uniaxial compressive strength (Kobayashi and Adachi 1982). In this research, the initial cementation is determined from the uniaxial tensile strength $\overline{q}_{{\text{u}}}$ calculated from the rock's uniaxial compressive strength. Figure 16 shows the relationship between the stress path in a uniaxial tensile test and yield function considering a parallel shift. Herein, a uniaxial tensile strength test is assumed to perform with no confining pressure. In Fig. 16, the initial cementation $\Psi_{0}$ is equal to the deviation from the origin of the yield surface based on cementation considerations if the yield surface considering the parallel shift by cementation and the stress path of a uniaxial tensile test intersect at the point satisfying $\overline{q} = \overline{q}_{{\text{u}}}$ on the tensile side. Therefore, the initial cementation is determined by finding $\Psi_{0}$, such that the two curves intersect at $\overline{q} = \overline{q}_{{\text{u}}}$.

Fig. 16

Stress path in a uniaxial tensile test and yield surface

4.3 C.3 Calculation of the Size of the Initial Yield Surface

This section describes the method used to calculate the size of the initial yield surface. When the initial yield surface and initial stress state are as shown in Fig. 17, the initial and yielding states must lie on the same elastic wall in the $p - q - v^{ss}$ space. In this case, on $p - v_{{}}^{ss}$ plane, Point A (initial state) and Point B (foot of the initial yield surface) have the positional relationship shown in Fig. 18.

Fig. 17

Initial yield surface

Fig. 18

Positional relationship on $p - v_{{}}^{ss}$ plane

As points A and B lie on the same swelling line, it follows that:

$$ v_{0}^{ss} = v_{{\tilde{\kappa }}}^{ss} - \tilde{\kappa }\ln \frac{{p_{0} }}{{p_{{\text{r}}} }}, $$

(105)

$$ v_{{{\text{c}}0}}^{ss} = v_{{\tilde{\kappa }}}^{ss} - \tilde{\kappa }\ln \frac{{p_{{{\text{c}}0}} }}{{p_{{\text{r}}} }}. $$

(106)

Moreover, as point B lies on the normal consolidation line

$$ v_{{{\text{c}}0}}^{ss} = N - \tilde{\lambda }\ln \frac{{p_{{{\text{c}}0}} }}{{p_{{\text{r}}} }}, $$

(107)

where $v_{{{\text{c}}0}}^{ss}$ is the soil skeleton specific volume on the NCL at $p = p_{{{\text{c}}0}}$.

The relationship obtained for the size of the initial yield surface by eliminating $v_{{\tilde{\kappa }}}^{ss}$ and $v_{{{\text{c}}0}}^{ss}$ from Eqs. (105)–(107) is

$$ p_{{{\text{c}}0}} = p_{0} \exp \frac{{N - v_{0}^{ss} - \tilde{\lambda }\ln ({{p_{0} } \mathord{\left/ {\vphantom {{p_{0} } {p_{{\text{r}}} }}} \right. \kern-\nulldelimiterspace} {p_{{\text{r}}} }})}}{{\tilde{\lambda } - \tilde{\kappa }}}. $$

(108)

As showcased in Eq. (108), the size of initial yield surface $p_{{{\text{c}}0}}$ is determined with material constants, initial stress state, and initial soil skeleton specific volume.

Appendix D: Relationship Between Mass Ratio and Initial Interlaminar Void

This section explains the relationship between mass ratio and initial interlaminar void. The simplified double structure in the initial period is shown in Fig. 19. $A$ is the bottom area, $a$ is the soil particle height of nonexpansive clay, $b$ is the soil particle height of expansive soil, and $c$ is the representative height of interlaminar void. Additionally, $d_{0}$ is the initial interlaminar distance determined from the interlaminar equilibrium with initial ion concentration and stress state, and $t$ is the thickness of expansive clay minerals.

Fig. 19

Geometric parameters of double structure

Herein, the initial interlaminar void $e_{0}^{il}$ is described using the initial interlaminar volume $V_{{\text{v}}}^{il}$, soil particle volume of nonexpansive clay $V_{{\text{s}}}^{s}$, and soil particle volume of expansive clay $V_{{\text{s}}}^{sw}$ as follows:

$$ \begin{aligned} e_{0}^{il} & = \frac{{V_{{\text{v}}}^{il} }}{{V_{{\text{s}}}^{s} + V_{{\text{s}}}^{sw} }} \\ & = \frac{Ac}{{A(a + b)}} \\ & = \frac{c}{a + b}. \\ \end{aligned} $$

(109)

The relationship between the initial interlaminar distance and thickness of expansive clay mineral is

$$ \frac{c}{b} = \frac{{d_{0} }}{t}. $$

(110)

Additionally, the mass ratio of nonexpansive clay to swelling clay $r$ for soil particle densities $\rho_{{{\text{sw}}}}$ and $\rho_{{\text{s}}}$ is

$$ r = \frac{{b\rho_{{{\text{sw}}}} }}{{a\rho_{{\text{S}}} }}. $$

(111)

Using the mass ratio, the ratio of $a$ and $b$ is set as

$$ \frac{b}{a} = r\frac{{\rho_{{\text{s}}} }}{{\rho_{{{\text{sw}}}} }}. $$

(112)

Finally, the initial interlaminar void is set by substituting Eqs. (109) and (110) into Eq. (112) as follows:

$$ \begin{aligned} e_{0}^{il} & = \frac{c}{a + b} = \frac{{b\frac{{d_{0} }}{t}}}{a + b} \\ & = \frac{{\frac{b}{a}\frac{1}{t}}}{{1 + \frac{b}{a}}}d_{0} = \frac{{r\frac{{\rho_{{\text{s}}} }}{{\rho_{{{\text{sw}}}} }}\frac{1}{t}}}{{1 + r\frac{{\rho_{{\text{s}}} }}{{\rho_{{{\text{sw}}}} }}}}d_{0} . \\ \end{aligned} $$

(113)