Abstract
With the increased use of cable bolts in mining and civil projects worldwide, it is important to understanding the performance of these support structures in different scenarios. The axial load transfer mechanisms of six cable bolts were investigated experimentally in this research study. A large-scale pull-out testing apparatus with a capacity of 1000 kN was designed and manufactured as part of the investigation. A common commercial cementitious grout with a uniaxial compressive strength of 60 MPa was used to encapsulate 300 mm length samples. Passive confinement encapsulated each sample to ensure the concrete’s integrity during the testing. The encapsulated cable bolts were then subjected to axial loads using a hydraulic ram, with the axial load and displacement measured using a load cell and LVDTs. Two scenarios were investigated: free rotation and restricted rotation. The results demonstrated that the apparatus effectively recorded the behaviour of the cable during pull-out and identified that the radial stiffness of the samples had a significant impact on the overall load of the system. The results also indicated that rotation had a limited influence on the load behaviour of the samples tested.
Highlights
-
Design and manufacturing of a high-capacity 1000 kN pull-out apparatus for newer cables,
-
Rotation investigation showed less adverse effect than previously reported. It was concluded that a zero-rotation test is not feasible as the rotation of the cable inside the annulus is not uniform,
-
Cable modifications such as surface indentation and bulbing significantly change the failure mode from strain hardening or perfectly plastic to strain softening,
-
Interaction of cable strands with grout ridges inside the grout annulus creates relative movements and oscillations in the post-peak loading zone, and
-
Failure is not uniformly distributed in the grout annulus, with higher damage observed at the cable’s exit point and minor damage toward the entry point.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The popularity of cable bolts as support elements has increased in recent years, particularly with their lower bending moduli, flexible lengths, and higher capacity. This flexibility has enabled cable bolts to be used in situations where rock bolting is not practical. Cable bolts are also available in various designs and characteristics to suit different support scenarios. A cable bolt’s surface may be smooth or indented, and may include a bulb (enlarged structure) and a hollow central grout tube. These variations in characteristics make cable bolts a versatile support choice. The first use of cable bolts in mines can be traced back to the 1960s and by the 1970s (Clifford, 1974). The idea of “rock reinforcement” proposed by Lang (1962) and later by Rabcewicz (1964) provided the modern understanding of stabilisation where the role of rock bolts and cable bolts is to help rocks support themselves.
Fuller and Cox (1975) considered the effect of embedment length, cable rusting, and cable indentation, and designed a pull-out apparatus called the Split-Pipe Pull Test (SSPT) which consisted of two fully grouted sections that were tightly secured to mitigate rotation when pulled apart. The SSPT has since been used in numerous studies (Cox and Fuller 1977; Goris and Conway 1987; Mah 1994; Thomas 2012 and Farmer 1975). Cox and Fuller (1977) extended Farmer’s study to measure the W:C ratio of the grout and reported an increase in strength with a decrease in W:C.
Hutchins et al. (1990) proposed a pull-out apparatus identified as the Double Embedment Pull Test (DEPT) where, unlike the SSPT, debonding could occur in either section of the testing apparatus. The relative simplicity and lower cost of this method compared to the SSPT led to its increased adoption for pull-out testing (Renwick 1992; Satola and Hakala 2001; Satola and Aromaa 2004; Satola 2007). Hutchinson and Diederichs (1996) proposed an even simpler design with only one encapsulated section. The design was called the Single Embedment Pull Test (SEPT) in which the embedded cable was pulled against a barrel and wedge. A modified SSPT was developed by Reichert (1991) to be a split push test instead of a split pull test.
Over the years, different confining media with variable mechanical properties have been used to simulate the surrounding rock. MacSporran (1993) designed a Modified Hoek Cell (MHC) which enabled researchers to study the effect of stiffness and pressure confinement during the pull-out test. This cell was later used to study various axial load-bearing capacity properties (Hyett et al. 1995, 1996; Moosavi et al. 1996). Clifford et al. (2001) combined the idea of DEPT and the MHC to propose the Laboratory Short Encapsulation Pull Test (LSEPT). This method was later used by Altounyan and Clifford (2001), Bigby and Reynolds (2005), Martin (2012), and Thenevin et al. (2017) for various experimental testing.
To simplify the LSEPT, the biaxial cell was later substituted by a thick pipe. Thomas (2012), Chen et al. (2015), Hagan (2015), and Hagan and Li (2017) conducted studies on the various characteristics of cable bolts using a Modified Laboratory Short Encapsulation Pull Test (MLSPET). Aziz et al.(2016) and Li (2019) reported on a series of pull-out tests on cable bolts using the Minova Axially Split Embedment Apparatus (MASEA). This setup used the double embedment concept of SSPT with the unequal embedment length concept of the LSEPT.
Table 1 summarises the development of the various testing apparatus categorised by the two main differences: the confinement condition and embedment condition. Embedment ensures that debonding happens at the appropriate location and can be used to minimise rotation. The confinement material simulates the rock medium in which the cable will be installed and embedded.
While various researchers have studied the axial load-bearing capacity of cable bolts, there is a gap in the understanding of the role of rotation in axial load transfer mechanisms. In addition, there is limited research on the pull-out performance of recently developed cable bolts. This paper reports on 12 tests of various cable bolts using a modified single embedment pull-out apparatus. The new test apparatus in this paper makes use of the advantages of the previous studies with efficiency and scalability in mind. The cable bolts were all encapsulated using high-strength cementitious grout. The two variables of rotation and radial stiffness were investigated.
2 Experimental Design
2.1 Apparatus Design Presentation
The experiment in this study utilised a modified version of the well-known large-scale double embedment test which provides a comprehensive platform to study the cable, bonding agent, and confining medium. The initial modification was the introduction of an ungrouted cable section at the bottom of the borehole. As the cable is pulled during the test, the encapsulated length gets shorter. This means that the load during the post-peak behaviour is compromised. To address this problem, an ungrouted section was added to the bottom of the samples which was fed steadily through the grout annulus during the test. This was achieved by utilising a tightly wrapped closed cell foam around the cable.
In the conventional double embedment test, a long anchor tube is used to transfer the axial load to the cable and to minimise rotation. As these anchor tubes are load bearing, they need to be structurally capable of withstanding the axial capacity of the cables, which in some cases can reach to up to 1000 kN. Additionally, these tubes need to be replaced for each experiment which makes procurement and machining of the hollow tubes very expensive. Consequently, the second modification was the use of a barrel and wedge to transfer the axial force to the cable instead of a long-grouted anchor tube. The barrel and wedge arrangement was considered to be a better match for the tensile capacity of the cables, more affordable and could be readily replaced. This meant that the anchor tubes could be considerably smaller and only act in rotation mitigation.
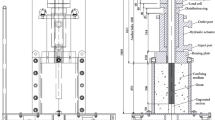
As explained later, the design incorporated an anti-rotation measure to minimise rotation of the anchor tubes during the testing. In five of the tests, the anti-rotation setup was not utilised, and free rotation was allowed to investigate the effect of the rotation on the test results. Furthermore, the concrete samples were passively confined using a large split pipe which was joined using a series of high-grade bolts. It is recognised that torque may not be directly related to radial stiffness; however, as the radial load develops in the sample prior to failure, the confinement bolts become axially loaded, pushing the nut out of the bolt. The interaction of these loads is related to the radial stiffness of the test. As shown later in the paper, the torque values on the bolts can influence the performance of the cable bolt. Figure 1 illustrates the final testing apparatus design.
2.2 Rotation Mitigation
As cable bolts consist of multiple metal strands wound together in a spiral pattern, they rotate naturally when pulled out. The rotational movement consists of an unscrewing and untwisting phenomena (Martin 2012). The former is similar to the unscrewing motion of a fastener bolt and nut assembly where the bolt represents the cable, and the nut represents the confining medium. The untwisting stems from the tendency of the individual strands of the cable to straighten under high axial load. Regardless of origin or type, it was identified that any rotation may negatively impact the axial load, and so, significant effort was made to mitigate any unnecessary rotation during the laboratory tests.
In the apparatus designed for this study, two 300 mm-long internally rifled anchor tubes were bonded to the cable bolt with high-strength grout. These tubes were then welded with a 50 mm-long key, 5 mm wide. This key could slide inside an internally slotted 300 mm-long hollow tube welded to a 32 mm-thick circular base plate that sat on top of the concrete sample (Fig. 2). This base plate assembly distributed the vertical load evenly, and more importantly, transferred the rotation from the cable to the external confinement.
2.3 External Confinement
The concrete cylinders were grouted into an external confinement split pipe of 330 mm diameter, 12.7 mm thick, and 500 mm length that provided confinement of the concrete. Six high-grade bolts securing the split pipe were torqued before the experiment to understand the impact of different torque values on the results. The difference between the 300 mm diameter concrete samples and 330 mm inside diameter of the external confinement meant that a 15 mm space was available around the concrete samples. This space was filled with grout prior to the tests to avoid stress concentration and to bond the concrete and the external confinement. The external confinement had 50 mm-deep slits on both sides of the pipe to lock in the anti-rotation plate wings and therefore mitigate the rotational movement of the whole assembly (Fig. 3).
2.4 Cable Bolts
Cable bolts come in a variety of shapes and configurations. In this study, six cable bolts commonly used in the Australian mining industry were tested. These cable bolts are used in soft and hard rock applications and their specifications are detailed in Table 2. The study used three full-core plain cables (Superstrand, indented Superstrand, and Goliath) and three stranded hollow-core bulbed cables (Sumo 9, 10, and 12 strand) with a metal central grout tube. In this study, the term bulbed was used as opposed to plain, and the term indented (ID) as opposed to smooth. The bulbed cables were custom-made by Jennmar Australia with the bulbs ranging between 100 and 200 mm in length with their centre located 250 mm from the end of the cable. This meant that the bulbs were encapsulated 100 mm from the bottom and 200 mm from the top in the grout annulus (encapsulation length was 300 mm). Figure 4 illustrates the cables’ cross-section.
2.5 Concrete Samples
In this study, the rock behaviour was simulated by concrete for ease of use and repeatability. PVC column formwork moulds with an internal diameter of 300 mm and length of 450 mm were used as concrete moulds. To create the borehole, PVC pipes based on the manufacturer’s recommended borehole size for each cable were utilised and cut into 500 mm lengths. To replicate the effect of rifling on the borehole surface, the pipes were wrapped with a 5 mm ethernet cable with a 25 mm spacing (Fig. 5). Rifling replicates the drill pattern and is necessary in the lab experiments to minimise grout/rock interface failure.
Finally, the boreholes were fixed into the middle of the concrete moulds, and then, a commercial 40 MPa concrete mix with 150 mm slump was cast. The samples were hydrated and covered with plastic bags for 28 days of curing. After the extraction of the PVC pipes, the internal ethernet cables were pulled out and a rifled borehole was created to anchor the cable bolts. Figures 6 and 7 illustrate the compression testing of the concrete sample cores (200 mm length samples).
2.6 Grouting
Before grouting the cables into the borehole in the concrete sample, the first 150 mm of the cable bolts were first wrapped with a non-porous foam to keep this section of the cable ungrouted (Fig. 8). The cable bolts were then inserted into their corresponding concrete samples, and a grout mix of 0.3 water-to-grout (W:G) ratio was poured inside the rifled boreholes. The cables were then agitated to ensure full encapsulation of the cables, bulbs, and the rifled crevices on the borehole surface.
A similar 0.3 W:G Stratabinder grout mix was used to grout the upper cable section in the anchor. The anchor tubes utilised were 300 mm long with a 50 mm internal diameter and a 4.5 mm wall thickness. The inside of the tubes was rifled with a 5 mm pitch and 1 mm depth to reduce slippage. The tubes also had an anti-rotation sliding key welded to their outside to minimise rotation (Fig. 1). A non-porous foam was used to centre the cable bolts in the anchor tubes and to stop the grout from seeping from the bottom of the tube. Finally, the anchor tubes were grouted with the same grout as the boreholes and then both were cured for 28 days.
Timber blocks were placed under the tubes to elevate them 100 mm higher than the concrete. The gap between the anchor tube and the concrete surface, while not optimal, was necessary to facilitate manoeuvrability for the heavy assembled samples and to create space for the large hollow ram and loadcell on the top. However, having a naked section of the cable creates a higher untwisting potential than a zero-gap setup.
The last part of grouting was completed prior to the tests. The samples were placed inside the external confinement pipes with the bolts torqued to the specific values before each test. A mix of 6.5 L of 0.4 W:G grout was used to fill the space between the external confinement and the concrete sample. This mix ensured an easy flow of grout around the large surface area of the concrete samples and provided a minimum of 35 MPa UCS after 48 h.
Figure 9 illustrates sample preparation for uniaxial compression test on the grout samples according to the British Standard (50 × 50 × 50 mm samples), and Fig. 10 exhibits the UCS results. Four samples were representative of the concrete embedment length and anchor tubes with 0.3 W:G after 28 days of curing. Two samples were from the external confinement grouting with 0.4 W:G after 72 h of curing. As shown in Fig. 10, the longer curing time increased both the ultimate load and the stiffness of the grout.
3 Testing Procedure
To test the impact of the rotation constraint, the experiments were undertaken in pairs, one sample with rotation constrained and the other with rotation allowed. As seen in Fig. 1, the externally confined samples were assembled as follows:
-
First, the base plate with the anti-rotation plate was placed over the concrete surface with the external wings inserted in the slots in the external confinement. The welded key on the anchor tube was free to slide vertically inside the slotted guide of the base plate,
-
A 100-tonne hollow ram jack was placed around the slotted guide and on top of the base plate,
-
A 1000 kN load cell mounted on a 32 mm base plate was then placed on the hydraulic jack’s saddle,
-
Another circular 32 mm top plate was placed on top of the load cell to transfer the load,
-
The testing apparatus was closed off with a barrel and wedge which was fixed firmly in place with the assistance of a hammer to avoid initial slippage.
A 225 mm stroke Linear Variable Differential Transformer (LVDT) was installed on the body of the hydraulic jack to measure the ram stroke, and a 10 mm stroke LVDT was mounted on the top section of the load cell to measure the relative movement of the barrel against the cable. The two LVDTs and load cell fed the signal to a data logger at a rate of 10 Hz. The loading was performed using a slow-speed hydraulic pump. Each test was run to at least 120 mm of ram stroke at a rate of approximately 6 mm/min. Figure 11 illustrates the typical outputs of the experiment from all three channels of data logger over the duration of the test. Displacement over time. After each test, the external confinements were opened and cleaned for the next test, and the concrete cylinder was broken apart to investigate the failure (Fig. 12).
4 Results
Table 3 summarises the overall results from the experiments. The maximum recorded load indicates the highest load, which did not necessarily occur at the first peak (for instance, Sumo 12 strand cable). The torque values reported in the table are the torque values applied to the confinement bolts before the test. The rotation column indicates whether the anti-rotation assembly was used in the test. The rotation amount is an approximate value of the observed rotation during or after the test.
An initial observation from the tests was that smooth cables (Superstrand and Goliath) generally possessed a strain hardening behaviour without significant failure in the concrete cylinder. However, the bulbed and indented cables showed multiple failures in the post-peak section. The bulbed cables also split the concrete with at least two large radial cracks, whereas the indented cable did not show radial cracking. The Goliath, a smooth unbulbed cable with a relatively large diameter, showed a combined behaviour with a minimal load drop at the first peak followed by a high residual load resulting in radial cracks in the sample.
As suggested by Figs. 13, 14, and 15, the effect of rotation on the cable pull-out load was relatively small and similar to the findings of Li (2019). This was more evident in the larger diameter cables compared to the smaller cable such as the Superstrand cable. However, in the case of the Superstrand cable, the rotated sample resulted in a slightly higher load value. More importantly, for all the cases, the overall trends were very similar. In the case of the Goliath cable, although initially the non-rotational sample had a slightly higher load, the overall maximum values for both cases were almost identical.
Figures 16 and 17 report the impact of load due to different torque values of the external confinement bolts. It is evident that an increase in the bolt torques has a relationship to radial stiffness and significantly changed the ultimate pull-out load. Figure 17 illustrates the combined effect of confinement and rotation which reduced the ultimate load and stiffness of the system.
Finally, Fig. 18 highlights the effect of indentation on the performance of the cable. The presence of indentation on the surface of the cable resulted in an almost threefold increase in load and changed the post-peak behaviour from strain hardening to softening with a residual value. It is postulated that the indentation effect stems from increased friction and increased surface area. The angle of the indentations (as seen in Fig. 19) significantly inhibits both the vertical movement and radial rotational movement of the cable (unscrewing).
5 Discussion
From the results, it is evident that confining stiffness influences the final load values. This effect is more noticeable in the bulbed cables compared to the plain (non-bulbed) cables. To slip axially, a bulb needs to damage a relatively large section of the grout column. The dilation causes radial cracks to travel to the weakest point in the confining medium, which was a small gap where the external split pipe flanges join. The large radial forces that were generated caused the external confinement bolts to lock and become extremely difficult to open after each test (Fig. 20). The increased radial forces made it difficult to apply more than 80 Nm of torque to the confinement bolts, as opening the bolts after the tests would result in stripping of the bolt’s head or damage to the tools.
Another key finding from the test results was the effect of rotation. The results suggest that the tests which allowed rotation were very similar to those in which the rotation had been constrained. It is also worth noting that even in the tests where rotation was constrained, a sudden rotation was observed when the base plate was released after the test. This suggests that, although the cable was not physically rotated at the anchor tube during the experiment, it actually had been rotating (unscrewing and untwisting) relative to itself, resulting in stored energy.
It is important to note that cables are not a single unit, but many elements wound together. Therefore, the rotation at the entry point (bottom of the concrete samples) and exit point (top of the concrete sample) can vary significantly. More interestingly, the amount of rotation for the tests with unconstrained rotation was very similar to those with constrained rotation during the test. The only difference was that in one case the rotation occurred gradually throughout the experiment, whereas in the other samples, it occurred as one sudden movement once the sample was disassembled.
After the experiment, the samples were broken open to further investigate the failure mechanism. The condition of the ridges (imprints of the cable surface on the grout) is a good indicator of the damage during the test. Again, no visual differences between the two rotation scenarios were observed, as evidenced in Fig. 22.
The broken samples showed that the damage on the annulus was non-uniformly distributed, with the more ridge damage toward the top of the sample and less ridge damage further down the hole. This suggests that the exit point of the cable at the very top section of the borehole had greater untwisting and unscrewing tendencies, while the entry point was probably free to rotate inside the annulus. This would have not happened in a pull-out test of rock bolts, since a rock bolt is one coherent structural unit that shears off the annulus on its way out and has minimal rotational tendencies.
As for confinement stiffness, the comparison between 60 and 80 Nm of torque values on the Sumo 10 Strand cables in Fig. 22 shows that the surface of the grout/cable interface in the higher torque experiments showed more damage than the lower torque samples. This was expected due to the higher loads of the system (i.e., higher radial stiffness). Furthermore, the same observation from Fig. 21 was witnessed in Fig. 22, where there was greater damage to the ridges on the top of the sample and relatively little damage at the entry point on the bottom.
6 Conclusions
This study is part of a more extensive research program investigating the axial behaviour of cable bolts used in the Australian mining industry. In this paper, a new large-scale high-capacity pull-out apparatus was designed based on the experience of previous researchers. The design enabled a 1000 kN testing capacity to accommodate the testing of the newer and stronger tendons. A total of six commonly used cable types in the Australian mining industry, each representing a unique characteristic, were tested using the testing apparatus. The two parameters of confining stiffness and rotation were investigated during 12 experiments.
The results suggested that the confining medium is of paramount importance in the axial study of cable bolts. This appeared to be more significant in bulbed cables due to the increased dilation forces as the result of bulb mobilisation. It can also be inferred that the impact of rotation on the behaviour and performance of cable bolts may not be as significant as previously identified in studies such as Bawden et al. (1992). Most importantly, the cables all experienced rotational movement regardless of the anti-rotation measures put in place. Unlike rock bolts which can be considered to be a single integrated element, cable bolts consist of a complex structure of multiple elements interacting with one another with minimum unifying constraints. This means that to conduct an absolute zero-rotation test in the laboratory is virtually impossible. Each section of the cable, regardless of being naked or embedded, can rotate relative to the adjacent sections.
Based on the results reported, cable modifications, such as surface indentation or bulbing, increase the ultimate load of the system. Moreover, the diameter of the cable seems to change the behaviour of the cable from strain hardening to softening even when modifications are not present (i.e., Goliath cable). Based on the results, it can be inferred that bulbed cables are in a separate class regardless of their other properties. In these cables, the bulb will significantly influence the behaviour of the cable under loading. By comparison, the plain smooth cables yielded comparable results when their diameters were similar. Larger diameter cables were more likely to have radial cracking behaviour, not unlike the bulb cable; however, the overall pull-out load behaviour was closer to a smooth plain cable than a bulbed cable. Indentation of the cable appears to create a strain-softening response similar to bulbed cables but with no radial cracking.
It is recommended that the impact of the cable diameter, surface, and structural modifications be studied in more depth in newer cables. Moreover, a systematic study of the effect of confining stiffness may be beneficial in quantifying this parameter. The study also recognised that the understanding of rotation in cable bolts is more complex than previously expected, and further studies are recommended to evaluate the positive or negative effects of rotation under axial load. This study can also be further extended to investigate the scale effects on the axial bearing capacity of grout encapsulated cable bolts for further geotechnical implementations.
References
Altounyan P and Clifford B (2001) Suitable long tendon technologies and practices. In: Safety in Mines Research Advisory Committee (SIMRAC). Rock mechanics technology limited, pp 1–55
Aziz N, Mirza A, Nemick J, Li X, Rasekh H, Wang GG, Nemcik J, Li X, Rasekh H and Wang GG (2016) Load transfer characteristics of plain and spiral cable bolts tested in new non rotating pull testing apparatus. In: Coal Operators’ Conference. Wollongong. https://ro.uow.edu.au/coal/591
Bawden WF, Hyett AJ, Lausch P (1992) An experimental procedure for the in situ testing of cable bolts. Int J Rock Mech Min Sci Geomech. https://doi.org/10.1111/scs.12327
Bigby, D. and Reynolds, C. (2005) ‘Development of the laboratory short encapsulation pull test for a revised British standard on rock reinforcement components used in coal mining’, in Proceedings of the 24th international conference on ground control in mining, p. 2–4.
Chen J, Saydam S, Hagan PC (2015) ‘An analytical model of the load transfer behavior of fully grouted cable bolts. Construct Build Mater 101:1006–1015. https://doi.org/10.1016/j.conbuildmat.2015.10.099 (Elsevier Ltd)
Clifford RL (1974) Long rockbolt support at New Broken Hill Consolidated Limited. Proc Aus Inst Min Metall 251:21–26
Clifford B, Kent L, Altounyan P and Bigby D (2001) Systems used in coal mining development in long tendon reinforcement. In: Proceedings 20th international conference on ground control in mining, p 7–9
Cox RHT and Fuller PG (1977) Load transfer behaviour between steel reinforcement and cement based grout. Australia
Farmer IW (1975) stress distribution along a resin grouted rock anchor. Int J Rock Mech Min Sci 23(11):347–351. https://doi.org/10.1016/0148-9062(75)90168-0
Fuller PG, Cox RHT (1975) Mechanics of load transfer from steel tendons to cement based grout. 5th Australian Conference on Structures and Materials. Civil Engineering Departments, Melbourne and Monash University, Melbourne, pp 189–203
Goris JM and Conway JP (1987) Grouted flexible tendons and scaling investigation. In: 13th World Mining Congress. Stockholm, p. 783–792
Hagan P, Jianhang C. (2015) Optimising the selection of cable Bolts in varying geotechnical environments, ACARP(C22010)
Hagan P and Li D (2017) Performance of cable bolts under axial loading subjected to varying geotechnical conditions, ACARP(C24018)
Hutchins WR, Bywater S, Thompson AG and Windsor CR (1990) A versatile grouted cable dowel reinforcing system for rock. In: AusIMM, p. 25–29
Hutchinson CDJ, Diederichs MS (1996) Cable bolting in underground hard rock mines, training. BiTech Publishers Ltd, Richmond
Hyett AJ, Bawden WF, Macsporran GR, Moosavi M (1995) A constitutive law for bond failure of fully-grouted cable bolts using a modified hoek cell. Int J Rock Mech Min Sci Geomech Abstract 32(1):11–36 (Elsevier)
Hyett AJ, Moosavi M, Bawden WF (1996) Load distribution along fully grouted bolts, with emphasis on cable bolt reinforcement. Int J Numer Anal Meth Geomech 20(7):517–544
Jennmar Australia (2020) Product catalogue coal mining, Jennmar Australia.
Lang TA (1962) Notes on rock mechanics and engineering for rock construction. Univ Calif Berkeley 1:1962–1964
Li X (2019) Load transfer characteristics of a cable bolt in DEPT. Shock Vibr. https://doi.org/10.1155/2019/2106741 (Hindawi Limited)
MacSporran GR (1993) An empirical investigation into the effects of mine induced stress change on standard cable bolt capacity. Queen’s University
Mah GP (1994) The development of a fibreglass cable bolt. University of British, Columbia
Martin LB (2012) Theoretical and experimental study of fully grouted rock bolts and cable bolts under axial loads. ParisTech, Berlin
Moosavi M, Bawden WF and Hyett AJ (1996) A comprehensive laboratory test program to study the behavior of modified geometry cable bolt support. In: Rock mechanics tools and techniques, p. 209–216
Rabcewicz LV (1964) 1965. The New Austrian Tunnelling Method. Water power, p. 453–457
Reichert RD (1991) A Laboratory and field investigation of the major factors influencing bond capacity of grouted cable bolts. Queen’s University
Renwick MT (1992) ‘Ultrastrand—an innovative cable bolt’. In: Fifth underground operators’ conference. Ballarat: Australasian Institute of Mining and Metallurgy, p. 151–156
Satola I (2007) The axial load-displacement behavior of steel strands used in rock reinforcement. Helsinki University of Technology
Satola I, Hakala M (2001) Corrosion protected cable bolts in long-term reinforcement. In: Särkkä P, Eloranta P (eds) ISRM regional symposium Eurock. Lisse, BALKEMA, pp 377–382
Satola I and Aromaa J (2004) The corrosion of rock bolts and cable bolts. In: Proceedings ground support in mining and underground construction, pp 521–528
Thenevin I, Blanco-Martín L, Hadj-Hassen F, Schleifer J, Lubosik Z, Wrana A (2017) ‘Laboratory pull-out tests on fully grouted rock bolts and cable bolts: results and lessons learned. J Rock Mech Geotech Eng 9(5):843–855. https://doi.org/10.1016/j.jrmge.2017.04.005 (Institute of Rock and Soil Mechanics, Chinese Academy of Sciences)
Thomas R (2012) The load transfer properties of post-groutable cable bolts used in the Australian coal industry. In: Proceedings 31st international conference on ground control in mining, 12:1–10
Acknowledgements
The authors wish to acknowledge the help and in-kind support of Minova and Jennmar Australia, and their provision of the samples used in this research. In particular, Robert Hawker, Peter Craig, Tom Meikle, and Arya Gao.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors have no conflicts of interest to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rastegarmanesh, A., Mirzaghorbanali, A., McDougall, K. et al. Axial Performance of Cementitious Grouted Cable Bolts Under Rotation Constraint Scenarios. Rock Mech Rock Eng 55, 5773–5788 (2022). https://doi.org/10.1007/s00603-022-02950-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00603-022-02950-4