Abstract
Soft or weakly consolidated sand refers to porous materials composed of particles (or grains) weakly held together to form a solid but that can be easily broken when subjected to stress. These materials do not behave as conventional brittle, linear elastic materials and the transition between these two regimes cannot usually be described using poro-elastic models. Furthermore, conventional geotechnical sampling techniques often result in the destruction of the cementation and recovery of sufficient intact core is, therefore, difficult. This paper studies a numerical model that allows us to introduce weak consolidation in granular packs. The model, based on the LIGGGHTS open source project, simply adds an attractive contribution to particles in contact. This simple model allows us to reproduce key elements of the behaviour of the stress observed in compacted sands and clay, as well as in poorly consolidated sandstones. The paper finishes by inspecting the effect of different consolidation levels in fluid-driven fracture behaviour. Numerical results are compared qualitatively against experimental results on bio-cemented sandstones.
Highlights
-
A grain-scale numerical study of the behaviour under stress of weakly consolidated granular packs (soft-sands) of different strengths.
-
The role of the material strength in the development of fluid-driven fracture is examined.
-
The outcomes of the model are compared against experimental results utilising synthetic soft-sands.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Soft sands are granular materials in which particles are weakly held together resulting in very low strength. Mechanisms that hold particles together include weak grain-to-grain cementation, external compressing forces and the physical interlocking arising from the irregular shape of the grains. Many engineering applications, such as groundwater remediation, slope stabilisation, hydrocarbon extraction, or in situ leaching from mining, involve soft-sands and thus, the ability to predict their response to fluid injection is of great importance.
These materials usually have low unconfined compressive strength and high permeability, although the literature lacks precise definitions for these ranges. They are intermediate between soils and rocks, sharing common characteristics with both (Collins and Sitar 2009; Sitar et al. 1980). Therefore, their behaviour is expected to be in-between sand and competent sandstone (Nakagawa and Myer 2001). An encompassing description for them is “poorly-consolidated weakly-cemented sandstones”: They have low strength and stiffness, poor core integrity and stress dependent porosity and permeability.
Experimental evidence has shown that fluid-driven fractures in soft sands are often shaped as flow channels (narrow paths presenting higher permeability than the matrix) with some degree of branching (Huang et al. 2012; Johnsen et al. 2006; Konstantinou 2021; Chang 2004; Chang et al. 2003). Elasto-plastic deformation likely plays a significant role in soft sand fracture initiation and propagation. Although it is frequently assumed that shear mechanisms dominate the fracture tip dynamics, it is not clear whether tensile fracturing takes place. The mode of failure is particularly important as it is seen to describe the fracturing behaviour. In cohesionless sands, tensile stress cannot be transmitted, and therefore, only failure shear occurs; however, in soft rocks of low strength, dislocation of particles along with pure fractures might take place. Some authors, identified this and linked the mode of failure with the unconfined compressive strength (UCS) of the host rock (Olson et al. 2011). It is, therefore, particularly important to test materials across various strengths to examine this transition in behaviour from pure shear failure to pure tensile failure. The research on this topic remains very limited. The majority of the aforementioned studies makes use of cohesionless sand (Zhang et al. 2013; Johnsen et al. 2006; Huang et al. 2012; Chang et al. 2003; Chang 2004; de Pater et al. 2007; Dong 2010; Dong et al. 2008; Xu et al. 2010; Konstantinou 2021) whose “softness” derives from inter-locking due to the particle shape, without cementation between the grains.
Contrary to the case of rock specimens, with virtually limitless quantities of a material for testing purposes, of any shape and size, obtaining soft rocks samples is particularly challenging: Conventional geotechnical sampling techniques often result in destruction of the cementation and recovery of sufficient intact core is, therefore, difficult. In addition, material properties are expected to change upon chemical and mechanical degradation. As a consequence, reliable information about the stress–strain behaviour is rare (Sitar et al. 1980). The task of generating artificial specimens that closely resemble the engineering properties of natural geological formations has been central in the fields of soil and rock mechanics (Maccarini 1987; Wygal 1963; Vogler et al. 2017; Whiffin 2004; Konstantinou 2021; Konstantinou et al. 2021c).
Konstantinou et al. (2021c), used a bio-cementation technique termed as microbially induced carbonate precipitation (MICP) to generate artificially cemented rocks with mechanical and physical properties closely resembling those of natural weakly cemented carbonate sandstones. Those properties were well defined and reproducible. This technique involves the use of urease-producing bacterial strains which are flushed through the granular material together with a cementation solution supply consisting of urea and a calcium source. As a result, calcium carbonate precipitates bonding the particles (Whiffin 2004; DeJong et al. 2006). The method allows for control of the cementation level, and therefore, materials of various strengths can be produced. The preparation of such samples is, nevertheless, time consuming and weaker samples are harder to obtain because of practical limitations, such as disaggregation at the grain scale during extraction from the molds.
This paper uses a discrete element method (DEM) to model soft sands/poorly consolidated sandstones. The model, although simple, successfully reproduces qualitatively key elements characteristic of fracture development in these materials. Numerical results are compared against those obtained experimentally via MICP.
The structure of this work is as follows: Sect. 2 presents the experimental MICP technique and the main experimental observations relevant to the present study. The numerical model is described in Sect. 3. Section 4, addresses the preparation of the “numerical” samples and and discusses the results obtained for the stress–strain tests performed on them. The results are discussed in the context of the information provided by the experimental evidence. To finish, preliminary results of the effect of the consolidation on the hydraulic fracture response of these materials (Sect. 5) are analysed.
2 Bio-cemented Sandstones
The experimental samples utilised in this work are weakly cemented carbonate sandstones. They were created using microbially induced carbonate precipitation (MICP) following the experimental protocol presented in Konstantinou et al. (2021c), Konstantinou (2021). This bio-process builds up cement within a granular network producing a range of sandstone-like materials. The authors have conducted a parametric study to characterise the engineering properties of these bio-treated products (with fine and coarse particles) across a range of cementation levels (from about 3 to \(11\%\) mass concentration of calcium carbonate). The authors aimed at assessing the reproducibility and repeatability of the MICP process as a method to generate these synthetic specimens and at determining whether the resulting mechanical and physical properties would sufficiently resemble those of real weakly cemented sandstones.
For their first objective, Konstantinou et al. (2021c) used three metrics to assess the ability of MICP to produce suitable specimens, namely, chemical efficiency, repeatability and uniformity. The MICP strategy was proven to be reliable in delivering both fine and coarse-grained uniform specimens of varying cementation levels in a repeatable manner. This was achieved via slowing down the MICP reactions which allowed full permeation through the specimens and via the identical bio-treatment ensuring consistency in shape and size of carbonate crystals.
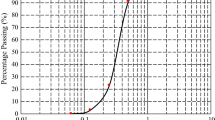
The main properties considered in the aforementioned study are unconfined compressive strength (UCS) and porosity with the aim to assess whether the resulting properties were similar to those of natural weak sandstones. In the current research only the coarse sand specimens are considered for which the relevant information is consolidated and presented. The base material was a uniformly graded (with a narrow particle size distribution) sand with an average particle size of 0.180 mm (\(D_{50}\)), for which there is very limited data in the literature as most studies use fine graded sands. The UCS tests were performed on oven-dried cylindrical specimens (diameter of 70 mm, height 140 mm) across various cementation levels. The samples were prepared for mechanical testing and tested according to ASTM (2004). The loading was displacement-controlled with a rate of 1.14 mm/min. Examples of stress strain curves obtained for low and high cementation levels are shown in Fig. 1a.
a Examples of stress strain curves obtained in experimental UCS testing for samples with low (5.5 %) and high (10%) cementation levels (continuous and dotted curves, respectively). Characteristic failure patterns for the specimens during the compression test: b tensile failure (left) and c shear failure (right)
Figure 1b, c shows the characteristic modes of failures obtained during unconfined compression tests. At very low cementations (up to 3 %, corresponding to UCSs of less than 200 kPa) the specimens disaggregated at the grain scale during the compression test, because they were very weak. For cementation levels of 3–8%, corresponding to UCS values of 200–1000 kPa, the specimens showed a characteristic axial splitting mode. At degrees of cementation above 8%, shearing along a single plain was evident.
Another important parameter is the microstructure of the bio-treated specimens which can be used to compare with the numerical settings. The distribution of the cementation within the granular network and the location of the carbonate crystals on the grain surfaces was examined with X-ray imaging. Figure 2 shows a microCT image for an MICP sample which was generated following the same protocol as described by Konstantinou (2021) and Konstantinou et al. (2021a, 2021c). The enhancement of strength is attributed to the amount of cementation that is present at the contact points between particles. This is because the strength is transmitted to the particles via those contact points, and any addition of carbonate crystals results in a higher strength at the macro-scale level. The carbonate crystals themselves appear to be of the same size, much smaller compared to the size of the grains; however, they accumulate as the amount of cementation increases generating clusters. A detailed discussion on this is presented by Konstantinou et al. (2021c) and Konstantinou (2021).
MicroCT imaging of a moderately cemented (5 %) bio-treated coarse sand specimen: the carbonate crystals accumulate on the surface of the grains, while it acts as a bridge for transmission of stresses at the contact points creating the sense of overlapping. X-ray \(\mu \)-CT high energy micro-tomography scanner (X-Tec Systems) settings: resolution at 8 um, 160 kV, 110 uA with a use of a 0.5 mm copper filter
Figure 3 shows the behaviour of the unconfined compressive strength (UCS) of the bio-cemented coarse sands as a function of the calcium carbonate in the sample (Konstantinou 2021; Konstantinou et al. 2021c).
Strength of bio-cemented coarse sands as a function of the calcium carbonate content in the sample preparation. An exponential curve provided the best fit for this data: \(UCS=56.544*exp(0.3568*C)\), where C is the cementation level. The light shaded area signifies axial splitting mode, while the dark shaded area shows the range at which specimens failed along a single shear plane. The very weak specimens which disaggregated at the grain scale were treated as having null strength and are not presented here, since they failed as soon as the load was applied to the specimen during the UCS test
The UCS varies from about 100 to 1600 kPa, which is a similar range to that found in natural weakly cemented sandstones reported in the literature. The lower boundary of this range is, nevertheless, still uncertain, as weaker samples are harder to obtain because of practical limitations. Numerical modelling enables the generation of even weaker samples which is the focus of this research.
3 Numerical Model
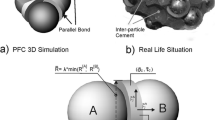
We use a discrete element method (DEM) to model the dynamics of soft spheres (Shäfer et al. 1996) and in particular, the implementation provided by the LIGGGHTS (Kloss et al. 2012) open source project). This model allows for a small overlapping \(\delta \) of the spherical grains. The contact forces acting on each grain are calculated based on this overlap. The dynamics of the system is then obtained by numerically integrating Newton’s laws for all degrees of freedom in the system. A Hertz potential (Brilliantov et al. 1996) is used to model a “repulsive” force (due to volume exclusion) between two particles and a simplified Johnson–Kendall–Roberts (JKR) (Johnson et al. 1971; Johnson 1996) is used to model particle–particle cohesion.
Hertz model for the normal force has an elastic (conservative) term that depends on \(\delta ^{3/2}\) (with \(\delta \) the linear overlap between the two particles in contact) and a dissipative term proportional to the normal component of the relative velocity. [This last term is used to account for the loss of kinetic energy due to plastic deformation, visco-elasticity of the material, etc. (Shäfer et al. 1996; Stevens and Hrenya 2005)]. The tangential component \(F_{\text {tang}}\) implements an elastic shear force, proportional to the tangential displacement \(\delta _{t}\) between two grains in contact, since the moment at which the contact has been established. This tangential (frictional) force is limited using \(F_{\text {tang}} \le \mu \times F_{\text {normal}}\), where \(\mu \) is the friction coefficient. A viscous (dissipative) force, proportional to the tangential component of the relative velocity between particles is also implemented by the model.
Adhesive force consists in adding an additional (attractive) term to the contact force: \(F_{\text {coh}}=C_{h} \times A\), where A is the cross- sectional area of the overlap between the particles and \(C_{h}\) (in units of Pa) is called the cohesion energy density and will be the control parameter for varying the system strength throughout this paper. The reason for selecting this simplified JKR model (among the many models existing that incorporate cohesion to granular systems) was due to its low computational requirements: it does not required the tracking and storage of the “bonds” or the incorporation of a “skin” effect (increase of the effective grain radius) to calculate forces. Although the model allows for the formation of new bonds during the simulation (similarly to a water bridge model) the initial sample preparation (as it will be described in the following section) applies “high” confining forces to the granular pack, creating stronger bonds (higher overlaps) compared to the ones that could potentially develop afterwards (Details of the model implementation can be found in (CFDEM [4]).
We are interested in the quasi-static dynamics of these systems (particle velocities equal to zero), and therefore, the normal force for two particles i and j in contact can be written as
where \(\delta \) is the linear overlap between the two particles in contact, Y(\(=1 \times 10^{7}~\) Nm\(^{-2}\)) is the Young’s modulus, \(\nu \) (\(=0.15\)) is the Poisson’s ratio. The model also uses a friction coefficient \(\mu =0.7\) and a restitution coefficient \(\epsilon = 0.055\). The low values used for \(\nu \) and \(\epsilon \) are selected to decrease the time needed to reach the initial static configuration (by dissipating energy faster). These parameters have otherwise little impact in the quasi-static behaviour of the system.
It is possible to see that for this model \(f_{n}\) can reach both, positive (cohesion dominant) and negative (compression dominant) values. This will lead to a (non-linear) inter-play between the “stress” (due to external compression) and that due to cohesion. This will be discussed in Sect. 5).
4 Stress–Strain Test
The grains are spheres with diameters distributed as a truncated Gaussian distribution (\(d=[0.9-1.8]~\)mm with mean diameter \(d=1.363~\) mm and a standard deviation \(\sigma _{d}\sim 0.3~\)mm).
Cylinders of \(h=10\) cm height and \(D=0.5~\)cm diameter (formed by \(N \approx 10^{5}\) grains) were constructed to perform the stress–strain tests. The protocol followed to create these samples is presented in Fig. 4.
Schematic representation of the setup used to create the samples for the stress–strain test. a and initially loose configuration of cohesionless grains, confined between two parallel, horizontal plates (in the z direction) is laterally compressed (\(F_{lat}\)) until reaching a static, mechanically stable, dense condition. b Cementation is added by setting \(C_{h}>0\) (Eq. (1)) while maintaining the effect of \(F_{lat}\) and applying a vertical force \(F_{v}=30~\)N. All lateral walls are removed after a static configuration is achieved. c A cylinder of diameter \(D=5~\)cm and height \(h-10~\)cm is cut from the sample created in (b) (elimination the particles outside the region). d A constant displacement (\(v=2.5~\)mm s\(^{-1}\)) is imposed in the upper wall. The force acting on this wall is measured during the test
Initially, a loose configuration of \(N=5 \times 10^{5}\) spherical, non-cohesive (\(C_{h}=0\)) grains, is placed between two parallel plates separated by a constant distance h (\(=10~\) cm) in the vertical (z) direction. These grains are laterally compressed (in the \(x-y\) plane) using 8 piston-like walls applying a constant lateral force \(F_{\text {lat}}\) until a mechanically stable configuration is reached (Fig. 4a). This methodology was chosen to reduce stress anisotropy and minimise the creation of preferential stress directions in the system. Once a mechanically stable configuration is reached, “cementation” is incorporated to the system by setting a value to the parameter \(C_{h}>0\). During this step the piston-like walls keep applying \(F_{\text {lat}}\) and the upper wall applies a constant vertical force \(F_{v}\) (\(=30~\)N) (Fig. 4b). The system is allowed to relax under this condition until a new equilibrium state is achieved. All lateral walls are removed at this stage and a cylindrical core of 5 cm diameter is obtained by “deleting” particles outside that region (Fig. 4c).
The system is again allowed to relax before the stress–strain test starts. For the test, the upper horizontal wall moves at a constant speed v (\(=2.5~\)mms\(^{-1}\)) (Fig. 4d), inducing deformation to the probe. The force acting on the wall due to the grains is measured and plotted against the strain \(\epsilon =h-vt/h)\) (with t being the time in seconds).
Each complete test takes, depending on the cementation level of the sample (\(C_{h}\)), between 1 and 3 days [running on 32 processors on Imperial College Research Computing Service (see DOI: 10.14469/hpc/2232)]. It is worth noting that due to this limitation in computational time, v was chosen about ten times faster than that recommended in the literature (ASTM 2004). Although no systematic analysis performed to evaluate this dependence due to constrains in computational time, a series of preliminary tests was conducted suggesting that the resulting strength may be slightly under-estimated as a consequence of this selection.
To achieve lower strength levels, consistent with subsurface situations but hard to achieve experimentally, gravity was not considered, preventing that the sample breaks under its own weight.
Figure 5 shows, in the left column, the characteristic stress–strain curves for three different degrees of cementation (increasing from bottom to top). In the right column of the figure, the fracture patterns for the corresponding cases, obtained just after the system has reached the peak-stress (as marked by the red stars).
Left: stress–strain curves corresponding to different cohesion levels, a \(C_{h}=7 \times 10^{5}\), b \(C_{h}=5.5 \times 10^{5}\) and c \(C_{h}=4 \times 10^{5}\). Right: fracture patterns for the corresponding cases represented in the left after the system reaches the peak-stress (red stars in the left panels marking the corresponding state)
Key elements observed experimentally, are present in these results. One such behaviour is the effect known as post-peak strain softening. It can be observed in Fig. 5c as a soft decay in the stress supported for the system after the maximum strength value is achieved. This behaviour has been reported as characteristic of cemented soils and clay (Riman et al. 2014; Abdulla and Kiousis 1997) and attributed to the re-orientation of the sliding surfaces creating a residual shear strength (the lowest possible) (Culshaw et al. 2017).
It can also be noticed that a transition occurs as the material strength increases. This continuum deformation gives place to a more sudden “brittle-like” fracturing process (Fig. 5a). This type of behaviour can be compared with that displayed in Fig. 1c, corresponding to moderate cementation levels in the MICP samples (\(\sim 300~\)kPa), where an axial splitting mode was observed. At lower strengths or equivalently lower cementation levels, disaggregation at the grain scale was observed in the UCS experiments. This behaviour is mapped to the behaviour of the numerical setup, where expansion of the cylinder (consistent with Reynolds’ dilatancy (Reynolds 1885) is observed near the failure point. The focus on lower strengths or cementation levels, which were not possible in the experimental part, because specimens of such low cohesion break when extracting from the mould, is one of the objectives of this study.
To assess the impact of the initial condition on the resulting strength of the sample, three different values were investigated for the confining force \(F_{lat}\).
The inset of Fig. 6 shows UCS for these different initial conditions as a function of the model parameter \(C_{h}\) (Eq. (1)). As stated in Sect. 3 Eq. (1), the interplay between the compressive (external) and the cohesive forces is not linear indicating that \(C_{h}\) is not a good parameter to characterise the system’s strength; a higher \(F_{\text {lat}}\) results in a higher degree of particle overlapping, and this overlapping increases both, the repulsive and the atractive (cohesive) forces.
Strength of the numerical samples as a function of the model cohesion energy density \(C_{h}\) times \(\Phi _{c}\), the density of contacts in the volume \(\Phi _{c}=\phi \times z_{c}\) with \(\phi \) the packing fraction and \(z_{c}\) the mean coordination number of the particles in the system. The different curves were obtained on samples built using different values of \(F_{lat}1=33\)N,\(F_{lat}2=166\)N,\(F_{\text {lat}}3=333\)N (see Fig. 4a). The dashed black line corresponds to the function \(UCS=0.01 \times (C_{h} \times \Phi )^{3}\) (obtained from fitting the data). Inset: Same than main figure but as a function \(C_{h}\)
To scale these results as a function of a more meaningful parameter, we define the density of contacts in the system \(\Phi _{c}\):
with \(z_{c}\) the mean coordination number of the system and \(\phi \) the corresponding packing fraction (\(\phi =1-porosity\)).
Figure 6 shows UCS as a function of \(C_{h} \times \Phi _{c}\) for the same systems than in the inset. This parameter provides a closer collapse among the curves obtained with different initial conditions (\(F_{lat}\)) suggesting that the overlap between particles could be interpreted as similar to the role of the calcium carbonated bonds in MICP specimens (Fig. 2).
5 Hydraulic Fractures
In this section, we use the cohesion model presented above to study the behaviour of fluid-driven fractures created in quasi-two-dimensional Hele–Shaw cells.
Initial configurations are created following the protocol presented in Sect. 3, but compressing \(N=10^{4}\) loose grains between two parallel plates having a constant separation \(h=1.5~\)mm (in the vertical z direction). The effective cell diameter is \(r \sim 4.8~\)cm, (the cell is in fact octagonal). A central inlet of radius \(r_{0}=3.5~\)mm, is created during the compaction process by preventing particles from occupying the cylindrical region in the centre of the cell (using a wall-like constraint). After reaching a static configuration (Fig. 4c) all the walls in the system were fixed in position. The volume of the cell is not allowed to change during fluid injection.
Fluid injection is simulated using (Gago et al. 2020b), a variation of the CFDEM (Kloss et al. 2012) open source software. This software couples LIGGGTHS with OPENFoam, computational fluid dynamics (CFD) model to simulate spatially resolved solid–fluid interaction. We simulate an incompressible fluid with viscosity \(\nu =0.1~\)cP, density \(\rho =1000~\)km\(^{-3}\). As this model needs to resolve the movement of the fluid around the solid interface a fine CFD mesh is required (of at least four grid-blocks per particle diameter (Kloss et al. 2012). A mesh refinement of 1/6 of the mean particle diameter was chosen.
Fluid is injected from the central inlet at a constant pressure \(p_{i}\), while the outlet (the external cell perimeter) is considered to be open to the atmosphere (\(p_{\text {outlet}}=0\)). Figure 7 shows characteristic patterns of the fracture behaviour for different injection pressures (increasing from left to right), and consolidation levels (increasing from top to bottom).
Fracture patterns obtained numerically. Injection pressures \(p_{i}\) increases from left to right and cohesion energy density \(C_{h}\) from top to bottom. a–c \(C_{h}=0~\) Pa and \(p_{i}\) = 25–100–200 kPa. d–f \(C_{h}=4 \times 10^{5}~\) Pa and \(p_{i}\) = 25–200–300 kPa, g–i \(C_{h}=6 \times 10^{5}~\)Pa and \(p_{i}=25-200-300~\) kPa
These patterns show that the fracture patterns corresponding to more consolidated systems (bottom) tend to present more branched-like behaviour than those of unconsolidated ones (top). This finding is not surprising: weaker materials spend more of the input energy in permanent deformation, while stronger materials open up defects, those defects (or voids) increases the local pressure and “self-drive” the fracture development. This kind of behaviour is consistent with experimental observations.
Figure 8 (top) shows the fracture patterns obtained experimentally for an unconsolidated system with fine sand for three different values of the injection pressure (increasing from left to right). The system was constrained by the boundary walls and the injection was from the bottom to the top. The borehole inlet was 1 cm away from the observation window (placed at the top). For the test with the lower applied inlet pressure, the fluid infiltrates through the permeable granular matrix without any visible fractures being induced. For the other two tests, where the inlet pressure was higher, particle rearrangement (grain dislocation) is observed resulting in an opening or borehole expansion. As in Fig. 7 (top and middle), the fracture area is “symmetrically” distributed around the fluid inlet. Although the sand is cohesionless, it possesses some strength due to interlocking of the particles and capillary forces. Figure 8 (bottom) shows a test before and after a fracture was obtained on bio-cemented coarse sands with a UCS \(\sim \) 300–350 kPa. This experimental setup differs from the one used in unconsolidated sand as no walls were used to constrain the specimen (the specimen possesses strength that is higher than any potential reaction from the walls). Multiple crack-like fractures can be observed (bottom right) without any evidence of grain dislocation or borehole expansion. The damage was extensive and was produced in a very small time window. These patterns are similar to those in Fig. 7 (bottom).
Top: An example of fracture behaviour in cohesionless fine sand, for three different values of the fluid pressure [from left to right: 60, 130, 250 kPa Konstantinou et al. (2021b)]. Bottom: An example of an experimental injection test in a bio-cemented coarse carbonate coarse sandstone with strength of approximately 300–350 kPa
To assess the effect of consolidation level in the development of the hydraulic fractures, a series of numerical experiments were performed. A combination of confining stresses \(\Sigma \) (obtained by varying \(F_{\text {lat}}\) in Fig. 4a) and material UCS (obtained with different values of \(C_{h}\)) were considered. Material stress \(\Sigma \) is defined as in Gago et al. (2020a) as the average value of the trace of the compressive stress tensor \(S^{i}_{ab}\) of the particles in the system:
where i is the particle index and the sum runs over all the particles c in contact with the particle i, \(V^{i}\) is the particle volume, \(r^{ic}_{a}\) (\(a=\{x,y,z\}\)) is the component in the a direction of the vector connecting the centre of the particle i with the centre of the particle c and \(f^{ic}_{b}\) is the b component of the contact force. Only positive contact forces [repulsive net force in Eq. (1)] are considered in this definition.
As stated previously (Sect. 3—Eq. (1)), there is a non-linear interplay between the (external) compressive and the cohesive forces, since an increase of \(C_{h}\) leads to a decrease of the absolute value of the contact forces between grains. This interplay can be observed in Fig. 9, where for initial conditions created using the same confining forces (\(F_{\text {lat}}\)), \(C_{h}\) is varied and as a consequence different \(\Sigma \) are obtained.
Compressive stress \(\Sigma \) acting on the system as a function of the unconfined compressive strength UCS (evaluated through the relation proposed in Fig. 6). As expressed in Eq. (1) compressive (repulsive) and cohesive (attractive) forces acting on the grains are not independent and initial conditions created under the same protocol (\(F_{\text {lat}}\)) do not necessarily present the same effective stress. The \(\Sigma _{i}\) (\(i=1-4\)) labels present in the figure highlight initial conditions having the same compressive stress but different UCS values
Here, the value of UCS was obtained through the power-law relation presented in Fig. 6. It is important to mention here that the cases corresponding to UCS = 0 (\(C_{h}=0\)) do not really represent a realistic situation: although experiments have been performed in non-cohesive sands (Huang et al. 2012; Johnsen et al. 2006), grains in such systems still present certain degree of collective behaviour, mainly due to the interlocking caused by the irregular shape of the grains, an effect that is not present in our model of perfectly spherical grains. These resutls (UCS = 0) are, therefore, presented only for reasons of completeness.
Figure 10 shows the fracture area for the numerical experiments, as a function of the inlet pressure for samples with different cohesion level-s and the same compressive stress \(\Sigma \) (represented by the horizontal lines in Fig. 9).
Fracture area for the numerical experiments, as a function of the inlet pressure for samples with different UCS (numbers on the arrows, reported in kPa) and same stress \(\Sigma \) (represented by the horizontal lines in Fig. 9)
Fracture area was measured using the protocol explained in Ref. Gago et al. (2020c). In short, the particle positions were mapped onto a (500, 500, 8) cubic grid and each grid-block was set with a value in the range \([0-1]\) proportional to the amount of it covered by a particle. Only the slice \(z=4\) of the grid was considered (this is represented in Fig. 7). Grid-blocks containing a fraction of particle smaller than 0.2 were taken as fluid. To ignore the pore size volumes, only clusters of such grid-blocks, bigger than 10 units were considered as a “fracture”. The fracture area as a function of \(p_{i}\) was defined as the difference between the amount of those grid-blocks before and after the fluid injection.
This figure shows that, as expected, fractures in more consolidated materials require higher pressure to initiate, although, as has been discussed in Gago et al. (2020a), the effective stress also strongly influences fracture development. Curves corresponding to lower \(\Sigma _{1}\) show a clear deviation for a change of consolidation of \(\sim 25~\)kPa, while for intermediate stress/cohesion this deviation is less evident (\(\Sigma _{2}\) \(UCS=63-11~\)kPa and \(\Sigma _{3}\) \(UCS=5-35~\)kPa)). This deviation becomes evident again for higher stress and UCS jumping from 0 to a small, non-zero value, although, as explained before, UCS = 0 does not really represent a realistic condition.
6 Conclusions
We presented a discrete element method that allows for modelling key elements of the behaviour of soft sand under stress. We have compared the numerical results with experimental results obtained on bio-cemented sandstones. Although the range of strength for the numerical specimens are on the “weaker” end of the experimental samples, both overlap for moderate strength, providing confidence on the validity of the model. The model is successful in reproducing shear-failure, observed experimentally for materials with moderate strength (UCS 300 kPa) and characteristic branched-like fracture patterns driven by fluid-injection. The model expands the experimentally possible strength values to an even lower range which could not be achieved in the experiments. In this lower range, the model is able to account for the post-peak strain softening, characteristic of compacted sands. Since it is believed that any transition in the hydraulic fracturing behaviour will occur in this lower region, the results presented here are encouraging that the method presented can help towards a better understanding of this transition. A more systematic analysis of the fracture behaviour with consolidation/stress dependence, with special emphasis on the soft-brittle transitional UCS values will be addressed in future work.
Availability of Data and Materials
The data that support the findings of this study are available from the corresponding authors, upon reasonable request.
Code Availability
Not applicable.
References
Abdulla AA, Kiousis PD (1997) Behavior of cemented sands—I. Testing. Int J Numer Anal Methods Geomech 21(8):533–547
ASTM (2004) Compressive strength and elastic moduli of intact rock core specimens under varying states of stress and temperatures. Stress. https://doi.org/10.1520/D7012-14.1.5.1.1
Brilliantov NV, Spahn F, Hertzsch J-M, Pöschel Thorsten (1996) Model for collisions in granular gases. Phys Rev E 53(5):5382
Chang H (2004) Hydraulic fracturing in particulate materials. PhD thesis, Georgia Institute of Technology
Chang H, Germanovich LN, Wu R, Santamarina JC, Dijk PE (2003) Hydraulic fracturing in cohesionless particulate materials. In: AGU Fall Meeting Abstracts 2003:H51B-03
Collins Brian D, Nicholas Sitar (2009) Geotechnical properties of cemented sands in steep slopes. J Geotech Geoenviron Eng 135(10):1359–1366. https://doi.org/10.1061/(ASCE)GT.1943-5606.0000094 (ISSN 1090-0241)
Culshaw MG, Entwisle DC, Giles DP, Berry T, Collings A, Banks VJ, Donnelly LJ (2017) Material properties and geohazards. Geol Soc Lond Eng Geol Spec Publ 28(1):599–740
de Cornelis JP, Yufei D, Bahman B et al (2007) Experimental study of hydraulic fracturing in sand as a function of stress and fluid rheology. In: SPE hydraulic fracturing technology conference. Society of Petroleum Engineers
DeJong JT, Fritzges MB, Nüsslein K (2006) Microbially induced cementation to control sand response to undrained shear. J Geotech Geoenviron Eng 132(11):1381–1392. https://doi.org/10.1061/(ASCE)1090-0241(2006)132:11(1381) (ISSN 1090-0241)
Dong Y (2010) Hydraulic fracture containment in sand
Dong Y, De Pater CJ et al (2008) Observation and modeling of the hydraulic fracture tip in sand. In: The 42nd US Rock Mechanics Symposium (USRMS). American Rock Mechanics Association
Gago PA, Raeini AQ, King P (2020a) A spatially resolved fluid-solid interaction model for dense granular packs/soft-sand. Adv Water Resour 136:103454
Gago PA, Wieladek K, King Peter (2020b) Fluid-induced fracture into weakly consolidated sand: impact of confining stress on initialization pressure. Phys Rev E 101(1):012907
Gago PA, Konstantinou C, Biscontin G, King P (2020c) Stress inhomogeneity effect on fluid-induced fracture behavior into weakly consolidated granular systems. Phys Rev E 102(4):040901
Huang H, Zhang F, Callahan P, Ayoub Joseph (2012) Granular fingering in fluid injection into dense granular media in a hele-Shaw cell. Phys Rev Lett 108(25):258001
Johnsen Ø, Toussaint R, Måløy KJ, Flekkøy EG (2006) Pattern formation during air injection into granular materials confined in a circular hele-Shaw cell. Phys Rev E 74(1):011301
Johnson KL (1996) Continuum mechanics modeling of adhesion and friction. Langmuir 12(19):4510–4513
Johnson KL, Kendall K, Roberts AD (1971) Surface energy and the contact of elastic solids. Proc R Soc Lond A 324(1558):301–313
Kloss C, Goniva C, Hager A, Amberger S, Pirker S (2012) Models, algorithms and validation for opensource dem and CFD-DEM. Progress Comput Fluid Dyn 12(2–3):140–152
Konstantinou C (2021) Hydraulic fracturing of artificially generated soft sandstones. PhD thesis, University of Cambridge
Konstantinou C, Biscontin G, Logothetis F (2021a) Tensile strength of artificially cemented sandstone generated via microbially induced carbonate precipitation. Materials 14(16):4735
Konstantinou C, Kandasami RK, Wilkes C, Biscontin G (2021b) Fluid injection under differential confinement. Transport Porous Media 139(3):627–650
Konstantinou C, Biscontin G, Jiang N-J, Soga K (2021c) Application of microbially induced carbonate precipitation (MICP) to form bio-cemented artificial sandstone. J Rock Mech Geotech Eng 13(3):579–592 (Accepted Paper)
Maccarini M (1987) Laboratory studies of a weakly bonded artificial soil. PhD thesis, Imperial College of Science and Technology
Nakagawa S, Myer LR (2001) Mechanical and acoustic properties of weakly cemented granular rocks. In: The 38th US Symposium on Rock Mechanics (USRMS), Washington, DC, p 1–8
Olson JE, Holder J, Hosseini M et al (2011) Soft rock fracturing geometry and failure mode in lab experiments. In: SPE Hydraulic Fracturing Technology Conference. Society of Petroleum Engineers
Reynolds O (1885) Lvii. on the dilatancy of media composed of rigid particles in contact with experimental illustrations. Lond Edin Dublin Philos Mag J Sci 20(127):469–481
Riman A, Sadek S, Najjar S (2014) Predicting the behavior of sand columns in soft clays using hypoplastic finite element modeling. In: Publication Name: Numerical Methods in Geotechnical Engineering-Proceedings of the 8th European Conference on Numerical Methods in Geotechnical Engineering, NUMGE 2014; Conference Title: 8th European Conference on Numerical Methods in Geotechnical Engineering, NUMGE 2014; Conference Date: 18 June 2014 through 20 June 2014; Conference Location: Delft; Publication Year: 2014; Volume: 1. Taylor and Francis-Balkema, pp 565–570
Shäfer J, Dippel S, Wolf DE (1996) Force schemes in simulations of granular materials. Journal de Physique I 6(1):5–20
Sitar N, Clough GW, Bachus RG (1980) Behavior of weakly cemented soil slopes under static and seismic loading conditions. Technical report, US Geological Survey
Stevens AB, Hrenya CM (2005) Comparison of soft-sphere models to measurements of collision properties during normal impacts. Powder Technol 154(2–3):99–109
Vogler D, Walsh SDC, Dombrovski E, Perras MA (2017) A comparison of tensile failure in 3D-printed and natural sandstone. Eng Geol 226:221–235. https://doi.org/10.1016/j.enggeo.2017.06.011
Whiffin VS (2004) Microbial CaCO3 precipitation for the production of biocement. PhD thesis, Murdor University. URL http://researchrepository.murdoch.edu.au/399/2/02Whole.pdf
Wygal RJ (1963) Construction of models that simulate oil reservoirs. Soc Petrol Eng J 3(04):281–286. https://doi.org/10.2118/534-PA
Xu B, Yuan Y, Wong RCK et al (2010) Modeling of the hydraulic fractures in unconsolidated oil sands reservoir. In: 44th US Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium. American Rock Mechanics Association
Zhang F, Damjanac B, Huang H (2013) Coupled discrete element modeling of fluid injection into dense granular media. J Geophys Res Solid Earth 118(6):2703–2722
Acknowledgements
Simulations were performed at the Imperial College Research Computing Service (see DOI: 10.14469/hpc/2232).
Funding
The authors would like to acknowledge the funding and technical support from bp through the bp International Centre for Advanced Materials (bp-ICAM) which made this research possible.
Author information
Authors and Affiliations
Contributions
PAG and CK conceptualised the study with inputs from GB and PK. PAG conducted the numerical simulations and produced the numerical results. CK conducted the experimental analysis and produced the experimental figures. PAG and CK wrote the manuscript with the help of GB and PK. GB and PK acquired the funding and supervised the project.
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that they have no conflicts of interest.
Additional Declarations
Not applicable.
Ethics Approval
Not applicable.
Consent to Participate
Not applicable.
Consent for Publication
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gago, P.A., Konstantinou, C., Biscontin, G. et al. A Numerical Characterisation of Unconfined Strength of Weakly Consolidated Granular Packs and Its Effect on Fluid-Driven Fracture Behaviour. Rock Mech Rock Eng 55, 4565–4575 (2022). https://doi.org/10.1007/s00603-022-02885-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00603-022-02885-w