Method for Measuring Three-Dimensional Strain Tensor of Rock Specimen Using Strain Gauges

Abstract

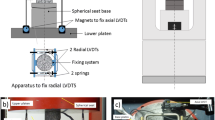
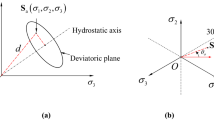
We propose a method for identifying a three-dimensional strain tensor using six or more strain gauges. This purely theoretical method assumes elementary deformation of the target object. To derive the strain tensor, six independent strain components must be measured using six or more strain gauges. The effect of measurement errors of the strain gauges on the strain tensor varies with the arrangement and orientations of the strain gauges. Thus, we also propose a method for evaluating the quality of the arrangement and orientations of the strain gauges. In this evaluation method, the determinant and condition number $\kappa$ of the matrix obtained from the unit direction vector in the attachment direction of the strain gauge are analyzed. The quality of each strain gauge arrangement is evaluated based on an assumption of 2–4 rosette gauges attached to a cylindrical specimen. The results of the proposed numerical analysis demonstrated that it is disadvantageous to install strain gauges at axisymmetric positions, and that it is better to have strain gauges attached to the sides in different directions. Furthermore, to evaluate one of the methods verified in this analysis, a triaxial compression test of Neogene-period tuff was conducted for comparison. It was determined that the strain tensor can be specified with high accuracy even though the three-rosette-gauge method had a medium accuracy. The accuracy improved as the number of strain gauges increased, and it was demonstrated that the strain tensor could be identified with sufficient accuracy even when only three rosette gauges are used.

Highlights

• A theoretical method for measuring strain tensor is proposed.

• Strain tensor is obtained from normal strain components measured by strain gauges.

• The method was experimentally validated via comparison with triaxial tests.

• Arrangements of strain gauges that stably identify the strain tensor were determined.

Appendix

Calculations for two examples of matrices are demonstrated here to clarify the good and ill conditions of matrices for solving simultaneous linear equations (Kreyszig 2011). An example of a good-condition matrix is

$$\begin{aligned} \underbrace{\begin{pmatrix} -1 &{} -1 \\ 1 &{} -1 \\ \end{pmatrix}}_{{\varvec{A}}} \underbrace{\begin{pmatrix} y_1 \\ y_2 \\ \end{pmatrix}}_{{\varvec{y}}} = \underbrace{\begin{pmatrix} 1\\ 1+\epsilon \\ \end{pmatrix}}_{{\varvec{a}}}, \end{aligned}$$

(22)

where $\epsilon$ is a small error. This equation can be transformed using det${\varvec{A}}$, as follows:

$$\begin{aligned} \begin{pmatrix} y_1 \\ y_2 \\ \end{pmatrix} = \underbrace{\frac{1}{\mathrm{det}{\varvec{A}}} \begin{pmatrix} -1 &{} 1 \\ -1 &{} -1 \\ \end{pmatrix}}_{{\varvec{A}}^{-1}} \begin{pmatrix} 1\\ 1+\epsilon \\ \end{pmatrix}. \end{aligned}$$

(23)

For this equation, det${\varvec{A}}=2$, and both the $l_1$ and $l_\infty$ norms for ${\varvec{A}}$ have a value of $\kappa ({\varvec{A}}) =||{\varvec{A}}||~||{\varvec{A}}^{-1}||=2$. For a good-condition matrix, the values of det and $\kappa$ should not be small. The solutions of this equation are $y_1=0.5\epsilon$ and $y_2=-1-0.5\epsilon$. The correct solutions of this equation without error are $y_1=0$ and $y_2=-1$. Therefore, this equation is not affected by a small error $\epsilon$.

On the other hand, an example of an ill-condition matrix is

$$\begin{aligned} \underbrace{\begin{pmatrix} 0.9999 &{} -1.0001 \\ 1 &{} -1 \\ \end{pmatrix}}_{{\varvec{B}}} \underbrace{\begin{pmatrix} y_1 \\ y_2 \\ \end{pmatrix}}_{{\varvec{y}}} = \underbrace{\begin{pmatrix} 1\\ 1+\epsilon \\ \end{pmatrix}}_{{\varvec{b}}}, \end{aligned}$$

(24)

where $\epsilon$ is a similarly small error. This equation can be transformed to

$$\begin{aligned} \begin{pmatrix} y_1 \\ y_2 \\ \end{pmatrix} = \underbrace{\frac{1}{\mathrm{det}{\varvec{B}}} \begin{pmatrix} -1 &{} 1.0001 \\ -1 &{} 0.9999 \\ \end{pmatrix}}_{{\varvec{B}}^{-1}} \begin{pmatrix} 1\\ 1+\epsilon \\ \end{pmatrix}. \end{aligned}$$

(25)

For this equation, det${\varvec{B}}=0.0002$, and both the $l_1$ and $l_\infty$ norms for ${\varvec{B}}$ have a value of $\kappa ({\varvec{B}}) =||{\varvec{B}}||~||{\varvec{B}}^{-1}||= 20001$. For an ill-condition matrix, the value of det should be much smaller, and the value of $\kappa$ should be much larger than that of a good-condition matrix. The solutions of this equation are $y_1=0.5 + 5000.5\epsilon$ and $y_2=-0.5-4999.5\epsilon$. The correct solutions of this equation without error are $y_1=0.5$ and $y_2=-0.5$. Therefore, this equation is significantly affected by a small error $\epsilon$. The influence of error on the solutions is 10000 times greater than that for the good-condition matrix.