Probabilistic Stability Analysis of a Tunnel Face in Spatially Random Hoek–Brown Rock Masses with a Multi-Tangent Method

Abstract

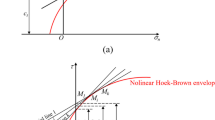
Tunnel excavations in heavily fractured rock masses are often subjected to the high risk of face instability. To solve this problem, the probabilistic stability analysis of tunnel face is performed in this contribution, in which the fractured rock masses are modelled as spatially random media that follow the Hoek–Brown failure criterion. The method of Karhunen–Loève expansion is adopted to characterize the spatial variabilities of Hoek–Brown parameters. Under this circumstance, the conventional tangent technique fails to integrate the Hoek–Brown failure criterion into the kinematical approach of limit analysis framework. Thus, the multi-tangent method which permits to use multiple tangent lines to represent the nonlinear Hoek–Brown failure envelope is proposed. A discretized three-dimensional failure mechanism of tunnel face is adopted to determine critical face pressures within the framework of limit analysis. Due to a large number of input variables required by the generation of random fields, the global sensitivity analysis and a sparsity scheme are employed to reduce the problem dimension. The method of spare polynomial chaos expansion is then employed to perform Monte Carlo simulation with a significant reduction of calls to the computationally expensive original model. Finally, the parametric analysis on the deterministic model and probabilistic model is performed to gain an insight into the proposed approach.

Highlights

• The three-dimensional stability of a tunnel face driven in Hoek-Brown rock masses is evaluated by combining the limit analysis and random field theory.

• The method of Karhunen-Loève expansion is adopted to characterize the spatial variabilities of Hoek-Brown parameters.

• A multi-tangent method is proposed to determine the equivalent shear strength parameters of rock masses.

• A fast and accurate probabilistic model for tunnel face reliability analysis is obtained with the sparse polynomial chaos expansion method.

Appendix: Work rate equation for face stability analysis

Let σ_T denotes the pressure provided by the shield machine to retain tunnel face stability, so its work rate can be calculated by

$$W_{{\sigma_{T} }} = \iint_{S} {\overrightarrow {{\sigma_{T} }} \cdot \overrightarrow {v\;} {\text{d}}S} = - \omega \sigma_{T} \sum\limits_{j} {\left( {S_{j0} R_{j0} \cos \beta_{j0} } \right)} ,$$

(32)

where S_j0 is the area of the j-th element on tunnel face; R_j0 is the corresponding rotation radius; β_j0 is the angle between the rotation radius and the negative direction of the Y-axis.

The work rate done by gravity of rock masses can be calculated as

$$W_{\gamma } = \iiint_{V} {\overrightarrow {{\gamma_{{}} }} \cdot \overrightarrow {{v_{{}} }} {\text{d}}V} = \omega \gamma \sum\limits_{i} {\sum\limits_{j} {\left( {V_{ij} R_{ij} \sin \beta_{ij} } \right)} } ,$$

(33)

where γ is the unit weight of rock masses; V_ij is the volume of the element determined by local coordinate system; R_ij is the corresponding rotation radius; β_ij is the angle between the rotation radius and the negative direction of the Y-axis.

The internal energy dissipation can be expressed by

$$W_{D} = \sum {\iint_{S} {c_{t} \cdot v} \cdot \cos \varphi_{t} {\text{d}}S} = \omega \sum\limits_{i} {\sum\limits_{j} {\left( {\left[ {c_{t} } \right]_{ij} \cos \left[ {\varphi_{t} } \right]_{ij} S_{ij} R_{ij} } \right)} } ,$$

(34)

where [c_t]_ij and [φ_t]_ij represent the corresponding equivalent cohesion and internal friction angle of the element; S_ij denotes the elementary area on the failure surface and R_ij is the corresponding rotation radius.

By equating the internal energy dissipation and external work rate, the required face pressure can be obtained as

$$\sigma_{T} = \gamma dN_{\gamma } - N_{c} ,$$

(35)

where N_γ, N_c are non-dimensional coefficients as

$$N_{\gamma } = \frac{{\sum\nolimits_{i} {\sum\nolimits_{j} {\left( {V_{ij} R_{ij} \sin \beta_{ij} } \right)} } }}{{d\sum\nolimits_{j} {\left( {S_{j0} R_{j0} \cos \beta_{j0} } \right)} }},$$

(36)

$$N_{c} = \frac{{\sum\nolimits_{i} {\sum\nolimits_{j} {\left( {\left[ {c_{t} } \right]_{ij} \cos \left[ {\varphi_{t} } \right]_{ij} S_{ij} R_{ij} } \right)} } }}{{\sum\nolimits_{j} {\left( {S_{j0} R_{j0} \cos \beta_{j0} } \right)} }}.$$

(37)

The expressions of [c_t]_ij and [φ_t]_ij are specified by Eqs. (5) and (6). They are determined by the Hoek–Brown parameters and the stress state of the element of interest. More details for the derivation can be obtained from (Mollon et al. 2011a).