True Mode $\mathrm {III}$ Fracturing of Rocks: An Axially Double-Edge Notched Brazilian Disk Test

Abstract

A new test, referred to as axially double-edge notched Brazilian disk (ANBD), is proposed to measure true mode $\mathrm {III}$ fracture toughness ($K_{\mathrm {IIIc}}$) of rock materials. The term true denotes a shear-induced fracturing via self-planar crack extension as opposed to a twisted tension-based one commonly observed in many mode $\mathrm {III}$ experiments of rocks. The ANBD test follows a straightforward procedure thanks to its simple core-based geometry and diametrical compression loading setup. Finite element analyses are employed to evaluate the stress intensity variations along the crack front and to calculate the point-wise stress intensity factors (SIFs) for different geometry and loading configurations. The results of ANBD tests conducted on granitic samples demonstrate the good performance of this test in yielding true mode $\mathrm {III}$ fracturing. The influences of the test parameters of ligament length and loading angle on $K_{\mathrm {IIIc}}$ are also investigated. A comparison study shows that $K_{\mathrm {IIIc}}$ values are similar to $K_{\mathrm {IIc}}$ but almost 2.5 times greater than $K_{\mathrm {Ic}}$. This demonstrates that the true mode $\mathrm {III}$ test offers a similar shear-based fracturing mechanism to the true mode $\mathrm {II}$, which is significantly more energy-consuming than the tension-based mode $\mathrm {I}$ failure type.

Highlights

• A new test named ANBD is introduced to measure true mode III fracture toughness.

• The test performance was evaluated by conducting experiments on granite samples.

• The effects of loading angle and ligament length were investigated.

• Measured values of KIIIc were compared to the ones of KIc and KIIc.

• Fracture surfaces of true and apparent mode III experiments were analysed.

1 Introduction

Rock fracturing is an important topic in many geo-science and geo-engineering applications such as $\mathrm {CO_2}$ sequestration, wastewater injection, geothermal energy, tunnelling, mining, etc. Fractures in rock masses are often subjected to the combinations of mechanical and hydraulic loadings, and as a result, they may evolve in complex three-dimensional trajectories. Fracture toughness, defined as the resistance of a rock against crack propagation, plays a key role in predicting the fracture growth path in rock masses. Hence, precise knowledge on the fracture toughness values of rocks under different tensile or shear loadings is of great importance in rock mechanics and engineering.

The singular stress field near the crack front is presented in the form of the superposition of three loading modes $\mathrm {I}, \mathrm {II}, \mathrm {III}$. Let us define the coordinate system xyz, with xy ($r, \theta$) being normal to the crack front, as shown in Fig. 1. The singular stress field within xy plane is characterised by Eq. (1a), where point-wise mode $\mathrm {I}$ and mode $\mathrm {II}$ stress intensity factors, $K_\mathrm {I}$ and $K_\mathrm {II}$, determine the intensity of in-plane stresses. The out-of-plane shear stresses are also characterised by Eq. (1b), with $K_\mathrm {III}$ being the point-wise mode $\mathrm {III}$ stress intensity factor (Sun and Jin 2012).

$$\begin{aligned} \left[ \begin{array}{l} {\sigma _{rr}}\\ {\sigma _{\theta \theta }}\\ {\tau _{r\theta }}\\ \end{array} \right]&= \dfrac{K_\mathrm {I}}{{4\sqrt{2\pi r} }}\left[ \begin{array}{l} 5\cos \dfrac{\theta }{2} - \cos \dfrac{{3\theta }}{2} \\[10pt] 3\cos \dfrac{\theta }{2} + \cos \dfrac{{3\theta }}{2} \\[10pt] \sin \dfrac{\theta }{2} + \sin \dfrac{{3\theta }}{2} \\[10pt] \end{array} \right] \nonumber \\&\quad + \dfrac{K_\mathrm {II}}{4{\sqrt{2\pi r} }}\left[ \begin{array}{l} - 5\sin \dfrac{\theta }{2} + 3\sin \dfrac{{3\theta }}{2}\\[10pt] 3\sin \dfrac{\theta }{2} + 3\sin \dfrac{{3\theta }}{2}\\[10pt] \cos \dfrac{\theta }{2} + 3\cos \dfrac{{3\theta }}{2}\\[10pt] \end{array} \right] \end{aligned}$$

(1a)

$$\begin{aligned} \left[ \begin{array}{l} {\tau _{\theta z}}\\ {\tau _{rz}} \end{array} \right]&= \dfrac{{K_\mathrm {III}}}{{\sqrt{2\pi r} }}\left[ \begin{array}{l} \cos \dfrac{\theta }{2} \\[10pt] \sin \dfrac{\theta }{2}\\[10pt] \end{array} \right] \end{aligned}$$

(1b)

Fig. 1

a Mode $\mathrm {III}$ vs. b true mode $\mathrm {III}$ fracturing

In the context of linear elastic fracture mechanics, a crack under pure mode $\mathrm {I}$ loading condition ($K_{\mathrm {II}}=K_{\mathrm {III}}=0$) propagates once $K_{\mathrm {I}}$ reaches a critical value referred to as the mode $\mathrm {I}$ fracture toughness, $K_{\mathrm {Ic}}$. This parameter represents the resistance of the material against mode $\mathrm {I}$ crack growth. Due to its importance, procedures to measure $K_{\mathrm {Ic}}$ in rocks have received a lot of attention. For example, various studies have been conducted to propose new test specimens (Kuruppu et al. 2014; Wei et al. 2018b; Bahrami et al. 2020a; Nejati et al. 2020a), to determine the size and shape of the fracture process zone (Dutler et al. 2018; Wu et al. 2018; Wei et al. 2016b), to evaluate the influence of notch types and loading methods (Wei et al. 2015, 2017b, 2018a), and to analyse the effects of specimen size (Bažant 1984; Ayatollahi and Akbardoost 2014; Nejati et al. 2020d), and rock anisotropy (Nejati et al. 2020a, c).

Mode $\mathrm {II}$ tests indicate two distinct types of rock fracturing mechanisms under mode $\mathrm {II}$ loading. The first is tension-based fracturing which occurs when a mode $\mathrm {II}$ crack kinks towards the direction normal to the maximum tensile stress. The kink angles in these mode $\mathrm {II}$ tests can be predicted by tension-based criteria such as the maximum tangential stress or strain (Akbardoost et al. 2014; Wei et al. 2017a; Lin et al. 2019), thus indicating that this form of failure is indeed tension-induced. The fracture toughness associated to tension-based tests should be referred to as apparent mode $\mathrm {II}$ fracture toughness ($K^a_\mathrm {IIc}$) (Nejati et al. 2021). This is because the fracture toughness in these tests is not an independent material property, and depends on $K_\mathrm {Ic}$ of the material (Ayatollahi and Aliha 2008; Aliha et al. 2017; Razavi et al. 2018; Wei et al. 2017a; Lin et al. 2019). The second type is shear-based mode $\mathrm {II}$ fracturing, referred to as true mode $\mathrm {II}$, that takes place when both loading and fracturing mechanism are shear-based. In order to achieve true mode $\mathrm {II}$ fracturing, a self-planar shear-induced crack extension must precede any tensile-induced crack kinking. Three testing methods are available to conduct true mode $\mathrm {II}$ experiments: punch through shear test (Backers and Stephansson 2012), shear box test (Rao et al. 2003) and double-edge notched Brazilian disk test (Bahrami et al. 2020b). In contrast to the apparent mode $\mathrm {II}$ fracture toughness, true mode $\mathrm {II}$ fracture toughness, $K_{\mathrm {IIc}}$, is considered as an independent material property. In rocks, $K_{\mathrm {IIc}}$ is roughly two to five times $K_{\mathrm {Ic}}$ (Backers and Stephansson 2012; Bahrami et al. 2020b).

Similar to mode $\mathrm {II}$, mode $\mathrm {III}$ cracks also show two distinct fracturing mechanisms of tension- and shear-based. Most mode $\mathrm {III}$ fracturing studies on rocks report tension-based failure, where a mode $\mathrm {III}$ crack twists to orient itself at angle $45^{\circ }$ with respect to the notch plane, as schematically shown in Fig. 1a. These studies include the research by Rao and Liao (2005) who used two non-core-based rock specimens of anti-plane punch-thorough shear and anti-plane four-point bending, and the work by Aliha et al. (2015a), Aliha and Bahmani (2017), Bidadi et al. (2020) and Bahmani et al. (2021) who utilized the core-based edge-notched disc bend specimen. The fracture path and load in these tests are effectively predicted by the tension-based fracture growth criteria like the maximum tangential strain energy density criterion (Aliha and Bahmani 2017). The tension-based mode $\mathrm {III}$ fracturing has also been studied in other brittle materials such as PMMA (Aliha et al. 2015a, 2016; Safaei et al. 2017; Ayatollahi et al. 2019), foam (Aliha et al. 2019), asphalt (Aliha et al. 2015a; Mansourian et al. 2018), and graphite (Aliha et al. 2015a). The fracture toughness associated to these tests may be referred to as apparent mode $\mathrm {III}$ fracture toughness ($K^a_\mathrm {IIIc}$) since it truely depends on $K_\mathrm {Ic}$ of the material.

On the other hand, shear-based mode $\mathrm {III}$ fracturing, referred to as true mode $\mathrm {III}$, is based on the co-planar extension of a mode $\mathrm {III}$ crack due to the shear stresses, as shown in Fig. 1b. We employ the term true to distinguish this shear-based fracturing from the conventional tension-based one. Unlike $K^a_\mathrm {IIIc}$ of tension-based tests, true mode $\mathrm {III}$ fracture toughness ($K_\mathrm {IIIc}$) is expected to be an independent intrinsic material property. A major contribution on true mode $\mathrm {III}$ fracturing of rocks was made by Goldstein and Osipenko (2012, 2014). They designed a non-core-based specimen and showed that several small ruptures or facets develop near the crack front, while a co-planar true mode $\mathrm {III}$ fracture takes place. A drawback of their test is the non-core-based sample which is difficult to prepare from rock materials. In another study, Ko (2008) used core-based cylindrical specimens subjected to torsional loading in order to measure $K_\mathrm {IIIc}$ of sandstone. However, the need for a special fixture to apply torsion severely limits the usage of this test.

Beside rock materials, mode $\mathrm {III}$ shear fracturing has been investigated in other materials such as PMMA and concrete. For instance, Pham and Ravi-Chandar (2014, 2016) and Pham (2015) designed different mode $\mathrm {III}$ fracturing tests on PMMA, and showed the generation of daughter cracks in addition to the parent (main) fracture. These findings along with the observations made by Zehnder and Zella (2015) from torsion tests on PMMA further confirm the previous observations of Goldstein and Osipenko (2012) and Goldstein and Osipenko (2014) about the development of facets or daughter cracks in true mode $\mathrm {III}$ fracturing. Literature also contains several studies to measure $K_\mathrm {IIIc}$ of concrete (Bažant and Prat 1988; Golewski 2017), and metallic materials (Liu et al. 2004; Zheng et al. 2008; Song et al. 2016).

Our survey shows that the literature currently lacks reliable testing methods to measure true mode $\mathrm {III}$ fracture toughness of rock materials. The present paper introduces a novel testing procedure to reliably measure $K_{\mathrm {IIIc}}$ in rocks. This test is based on the diametrical compression of an axially double-edge notched Brazilian disk (ANBD) specimen. The simple core-based specimen as well as the simple loading configuration makes this testing procedure straightforward and attractive. We first analyse the variations of $K_{\mathrm {I}}$, $K_{\mathrm {II}}$ and $K_{\mathrm {III}}$ along the crack front of the ANBD specimen, and show that the ANBD test induces dominant mode $\mathrm {III}$ loading along the crack front. Then, the procedure of the specimen preparation and testing is elaborated. Finally, we present the results of the fracture toughness on Bedretto granite and give a discussion on the influence of the ligament length and loading angle on the value of $K_{\mathrm {IIIc}}$.

2 Axially Double-Edge Notched Brazilian Disk (ANBD)

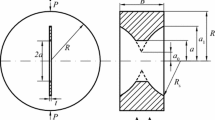
Figure 2a shows the schematic view of the axially double-edge notched Brazilian disk (ANBD) test. To prepare an ANBD sample, two axial notches of length a are introduced to a core of radius R and thickness 2t. This yields a ligament of length $2l = 2t-2a$ between the two notches. Due to the geometrical and loading symmetry along the core axis, both notches sustain the same level of stress. As seen, two wooden jaws are utilized to reduce the localisation of stress at the loading points, thereby preventing possible fracture initiation from those areas. The angle between the loading direction and the notch plane, $\alpha$, controls the combination of mode $\mathrm {I}$ and mode $\mathrm {III}$ loadings. As $\alpha$ increases, the intensity of $K_\mathrm {III}$ decreases while the magnitude of mode $\mathrm {I}$ stress intensity grows.

Fig. 2

a Schematic view of the ANBD test; b mesh pattern and boundary conditions used in finite element modelling of the ANBD sample

To find optimum geometry and loading conditions for the ANBD test, we performed finite element (FE) simulations by means of the commercial finite element package Abaqus. Modes $\mathrm {I}$, $\mathrm {II}$ and $\mathrm {III}$ stress intensity factors were determined using a three-dimensional FE model discretised with quadratic hexahedral elements (see Fig. 2b). Collapsed wedge-shaped elements were used at the tip of the cracks to achieve a square-root stress singularity along the crack front. A specimen of $R = 42$ mm was numerically subjected to the normalized diametrical load of $F/2t = 100$ N/mm. A wide range of crack lengths $a/t= 0.3, 0.4, 0.5, 0.6, 0.7$, corresponding to the ligament lengths $l/t = 0.7, 0.6, 0.5, 0.4, 0.3$, at different loading angles $\alpha = 10^{\circ }, 20^{\circ }, 30^{\circ },40^{\circ }$ were considered in the simulations. Note that no contact between the two notch faces was modelled. This is because in the rock experiments, the initial gap between the two notch surfaces is significantly larger than the deformation that attempts to close the distance between the notch surfaces. At first, the wooden jaws and their contact with the sample were modelled in FE simulations for some sample cases. Then, the results were compared with the more simple model which directly applies the line load to the specimen. It was found out that both the models reveal the same results. Therefore, to reduce computational cost, we did not simulate the wooden jaws any further and instead simulated the specimens under directly applied loads. Figure 3 illustrates two stress nephograms obtained from the finite element simulations of the ANBD specimen. As seen, the majority of the crack ligament is subjected to large shear stresses, whereas only a very small portion of the ligament area is under positive tensile stresses. This indicates that tensile stresses cannot contribute much to the fracturing process.

Fig. 3

Stress nephograms obtained from finite element simulation of the ANBD test ($l/t = 0.7$ and $\alpha = 30^{\circ }$); a $\tau _{yz}$; b $\sigma _{yy}$

Once the stress intensity factors (SIFs) are obtained from the FE models, normalized SIFs are determined from

$$\begin{aligned} K_\mathrm {I}^*&=K_\mathrm {I} \dfrac{2 \pi R t}{F \sqrt{\pi a}} , K_\mathrm {II}^*=K_\mathrm {II} \dfrac{2 \pi R t}{F \sqrt{\pi a}} , \nonumber \\ K_\mathrm {III}^*&=K_\mathrm {III} \dfrac{2 \pi R t}{F \sqrt{\pi a}} . \end{aligned}$$

(2)

Figure 4 shows the variations of $K_\mathrm {I}^*$, $K_\mathrm {II}^*$ and $K_\mathrm {III}^*$ along the crack front in two different configurations of the ANBD test. Here, z is the distance from the middle of the crack front. As seen, the contribution of $K_\mathrm {III}^*$ is dominant in a large section of crack front. Also, $K_\mathrm {III}^*$ follows considerable variations along the crack front. We point out that obtaining a uniform $K_\mathrm {III}^*$ in a sample is rather unfeasible, and almost all mode $\mathrm {III}$ tests show significant variations of $K_\mathrm {III}^*$ along the crack front (Ahmadi-Moghadam and Taheri 2013; Aliha et al. 2015b). The pure torsion of a shaft can apply uniform mode $\mathrm {III}$ loading, but conducting such a test on rocks is rather unfeasible. A good mode $\mathrm {III}$ test should provide the least possible variations of $K_\mathrm {II}^*$ and $K_\mathrm {III}^*$ along the crack front in order to prevent crack kinking and twisting (Lin et al. 2010). Figure 4 also shows that the magnitude of $K_\mathrm {II}^*$ is negligible in a large section of the crack front. In fact, $K_\mathrm {II}^*$ becomes significant only in a very small region near the corner points. Lastly, $K_\mathrm {I}^*$ holds negative values along the majority of the crack front, and the region with positive $K_\mathrm {I}^*$ shrinks as $\alpha$ increases.

We point out that a corner singularity occurs at the intersection of a crack front and free surfaces. At this point, the order of the singularity is different from the square-root crack singularity (Benthem 1977; Bazant and Estenssoro 1979). The order of corner singularity depends on the loading conditions and the Poisson’s ratio. As a result, the definition of crack stress intensity factor loses its meaning at the corner point, and an inverse square root singular field no longer exists (Nakamura and Parks 1988, 1989). In addition, modes $\mathrm {II}$ and $\mathrm {III}$ become coupled, meaning that applying primary modes $\mathrm {II}$ and $\mathrm {III}$ also generates a coupled mode $\mathrm {III}$, or mode $\mathrm {II}$ crack deformation, respectively. This coupling occurs due to the Poisson’s ratio effects or the redistribution of stresses near the free surfaces (Kotousov et al. 2013; Nejati et al. 2015).

Fig. 4

Variations of $K_\mathrm {I}^*$, $K_\mathrm {II}^*$ and $K_\mathrm {III}^*$ along the crack tip for a a/t = 0.4, $\alpha$ = 10$^{\circ }$, b a/t = 0.6, $\alpha$ = 30$^{\circ }$

Table 1 reports the average values and the maximum of the absolute values of modes $\mathrm {I}$, $\mathrm {II}$ and $\mathrm {III}$ SIFs and the average values of mode $\mathrm {I}/\mathrm {III}$ and $\mathrm {II}/\mathrm {III}$ SIF ratios as obtained from the FE simulations. Note that for mode $\mathrm {II}$ SIF, the average value in one-half of the crack front is considered, as the average on the entire crack front is equal to zero. According to Table 1, as $\alpha$ increases, the contribution of $K_\mathrm {I}^*$ rises while the contributions of $K_\mathrm {II}^*$ and $K_\mathrm {III}^*$ drop. In the next section, the values reported in Table 1 are employed to design the experiments for determining $K_\mathrm {IIIc}$ in rocks.

Table 1 Normalized stress intensity factors of the ANBD specimen for various values of a/t and $\alpha$

3 Experiments

3.1 Rock Samples

Rock cores of Bedretto Granite were employed to conduct the experimental study on true mode $\mathrm {III}$ fracture toughness measurement. Rock cores were taken from the Bedretto Underground Laboratory for Geoenergies (BULG) of ETH Zurich, that is situated in the Bedretto tunnel, a 5.2 km long access gallery to the Furka railway tunnel in southern Switzerland (Gischig et al. 2020). BULG is situated in a cavern with 100 m length, under an overburden of about 1000–1200 m, and is hosted in a granitic intrusion called Rotondo (Bedretto) granite. Bedretto Granite is a rather homogeneous rock with small to medium grain size, and a mild anisotropic behaviour (David et al. 2020). Experimental data show that the Bedretto Granite holds to following mechanical properties: the secant Young’s modulus of 75 GPa, the uniaxial compressive strength of 170 MPa and the indirect tensile strength of 8 MPa (David et al. 2020).

Two sets of experiments were conducted on Bedretto Granite in order to investigate the effects of ligament length (2l) and loading angle ($\alpha$) on the measured values of $K_\mathrm {IIIc}$ using the ANBD test. To do so, first 2 m rock cores of radius of 42 mm were cut into samples with lengths of 60 mm. Then, two longitudinal notches of same length were cut in the samples using a rotating sawing machine. Table 2 reports the geometrical and loading details of the test samples in both sets.

Table 2 Detailed geometry and loading conditions of the ANBD test samples

3.2 Test Details

Zwick/Roell 1474 RetroLine universal testing machine was used to conduct the ANBD tests. In all tests, the displacement rate was set to 1 mm/min. Figure 5a shows the test setup employed for the ANBD tests. It is seen in Fig. 5b that the force-displacement curves of the tests are non-linear in the beginning (mainly due to the deformation of wooden jaws), and then show a rather linear behaviour up to the fracture load. This demonstrates the applicability of linear elastic fracture mechanics (LEFM) theory for analysing the fracture behaviour of Bedretto granite.

Fig. 5

a Test setup; b sample force-displacement curves of ANBD tests

4 Results and Discussion

4.1 Results

Figure 6a shows samples of fracture path and surface resulted from the ANBD tests. As seen in this figure, the fracture growth direction does not have the butterfly shape which is usually observed in tension-based fracture growth of mode $\mathrm {III}$ cracks. Additionally, Fig. 6b demonstrates two more important characteristics of the shear-based mode $\mathrm {III}$ fracture surfaces. The first one is the pulverised surface of the fracture, which was identified among important features of shear fracture surfaces by Bobet and Einstein (1998). The second feature is the jagged fracture surfaces consisted of several cavities. Zehnder and Zella (2015) also reported such features in the surface for shear-based fracturing of PMMA, and referred to it as faceted surface. The jagged fracture surfaces in shear-based mode $\mathrm {III}$ fracture was also observed by Pham and Ravi-Chandar (2014) and Goldstein and Osipenko (2012) who called the emanated cracks from the main fracture as daughter cracks and recognised the local tensile stresses as the reason of initiation of such daughter cracks.

Fig. 6

Samples of a fracture path and b fracture surfaces of the ANBD specimen ($a = 15$ mm, $\alpha = 10^{\circ }$)

Table 3 reports the fracture loads and their corresponding true mode $\mathrm {III}$ fracture toughness values measured from ANBD specimens. In order to calculate $K_\mathrm {IIIc}$, measured fracture loads together with average values of $K_\mathrm {III}^*$ in Table 1 were substituted into Eq. (2). One can alternatively use the maximum values of $K_\mathrm {III}^*$ in Table 1 to obtain $K_\mathrm {IIIc}$. However, we expect that the average values of $K_\mathrm {III}^*$ yield more accurate estimations of $K_\mathrm {IIIc}$. This is because the gradual development of the fracture process zone (FPZ) along the crack front allows the redistribution of stresses in a more uniform manner. Once the FPZ starts developing along crack front sections with higher $K_\mathrm {III}$, the damaged material in those sections sustains less stress, which causes the redistribution of stress along the crack front in a more uniform manner.

Table 3 Fracture loads and the corresponding true mode $\mathrm {III}$ fracture toughness values measured from ANBD tests

4.2 Effects of Ligament Length on $K_\mathrm {IIIc}$

Figure 7a shows the variations of $K_{\mathrm {IIIc}}$ against the ligament length (2l) in the ANBD specimens. It is seen that the measured $K_{\mathrm {IIIc}}$ increases with the ligament length of the ANBD specimen. However, both Fig. 7a and Table 3 indicate a sign of convergence at higher ligament length. Similar observation has been reported for mode $\mathrm {I}$ and true mode $\mathrm {II}$ fracture toughness tests, where fracture toughness values increase with the ligament length and tend to converge at higher ligament lengths (Wei et al. 2016a, 2021; Ghouli et al. 2021; Bahrami et al. 2021). This phenomenon, which is also referred to as size or scale effect, introduces a minimum size requirement for obtaining the size independent fracture toughness (Kuruppu et al. 2014; Backers and Stephansson 2012). The reason is that the fracture process zone (FPZ) develops more closely into its full extent at higher values of ligament length. In small ligament lengths, the FPZ size is underdeveloped due to the geometrical constraints, which leads to the underestimation of energy dissipation and consequently fracture toughness values. This restriction on the FPZ development occurs mainly out of the fact that the FPZ exceeds beyond the K-dominant region in small samples. The K-dominant zone is the region where the singular terms of the crack tip fields characterise the stress field well.

The results presented in this article can be used for specimens with similar range of sizes and it would be very useful to extend this study in future for different specimen sizes in order to achieve a better insight into size effects in true mode $\mathrm {III}$ fracturing of rocks. We note that suggesting a minimum sample size for the ANBD specimen requires an independent theoretical and experimental study that includes the results of a comprehensive set of tests on different rock types at various ligament lengths. As the ligament size increases, it is expected that the fracture toughness values also increase, but eventually reach a plateau, where more accurate and size-independent fracture toughness values are measured. It is also noteworthy that one of the main advantages of the ANBD test is the possibility of designing a straightforward size effect experimental procedure. This is because the ligament size in the ANBD specimen is controlled by the specimen length, and not by its diameter. This is an important attribute since a major size restriction factor for the rock cores in geo-mechanical projects is the core diameter, which is restricted by the borehole size (2–3 in.). This feature of the ANBD sample is an important advantage over most mode $\mathrm {I}$ and true mode $\mathrm {II}$ test specimens in which the ligament size is controlled by the core diameter, and achieving a large ligament size from the normal core samples is unfeasible.

Fig. 7

Variations of $K_\mathrm {{IIIc}}$ against a ligament length and b contribution of mode $\mathrm {I}$ loading

4.3 Effects of Loading Angle on $K_\mathrm {IIIc}$

Figure 7b demostrates the variations of $K_\mathrm {IIIc}$ against $K_\mathrm {I}^*/K_\mathrm {III}^*$ which represents the contribution of compressive mode $\mathrm {I}$ loading in the tests. As seen, $K_\mathrm {IIIc}$ increases as the contribution of compressive mode $\mathrm {I}$ loading grows. Similar observation has been made for true mode $\mathrm {II}$ fracture toughness measurements (Backers and Stephansson 2012). To find a relation between the applied compressive mode $\mathrm {I}$ loading and the resulted $K_\mathrm {IIc}$, Bahrami et al. (2020b) proposed the following relation:

$$\begin{aligned} {{\hat{K}}_\mathrm {IIc}} = {K_\mathrm {IIc}} \Bigg (1 - \mu \displaystyle \left|\frac{{K_\mathrm {I}^*}}{{K_\mathrm {II}^*}} \right|\Bigg ) , \quad K_\mathrm {I}^*<0 . \end{aligned}$$

(3)

Here, ${{\hat{K}}_\mathrm {IIc}}$ denotes the value of $K_\mathrm {IIc}$ in the case that the contribution of mode $\mathrm {I}$ is zero, and $\mu$ is the friction coefficient. Equation (3) takes into account the effects of friction as a resistive force against the true mode $\mathrm {II}$ fracture growth. To develop this relation, Bahrami et al. (2020b) used the simple Coulomb frictional model which is based on the linear relationship between the applied normal load the resulting frictional forces. Since the nature of failure in true mode $\mathrm {II}$ is similar to that one of true mode $\mathrm {III}$, we can also propose a similar relation for true mode $\mathrm {III}$:

$$\begin{aligned} {{\hat{K}}_\mathrm {IIIc}} = {K_\mathrm {IIIc}}\Bigg (1 - \mu \displaystyle \left|\frac{{K_\mathrm {I}^*}}{{K_\mathrm {III}^*}} \right|\Bigg ) , \quad K_\mathrm {I}^*<0 , \end{aligned}$$

(4)

where ${{\hat{K}}_\mathrm {IIIc}}$ is the estimated value of $K_\mathrm {IIIc}$ at zero mode $\mathrm {I}$ contribution (zero-confinement condition prependicular to the crack). We point out that the test data in Fig. 7b do not obviously follow such linear relationship. Indeed, Eq. (5) is based on the simplest form of frictional constitutive law, and more complicated nonlinear models can potentially provide more accurate predictions. However, it is also noted that the test data in Fig. 7b are not comprehensive enough to disapprove the linear model, and significantly more data over a wide range of $K_\mathrm {I}^*/K_\mathrm {III}^*$ are required to test the linear frictional model. In addition, there is a possibility that at large values of $K_\mathrm {I}^*/K_\mathrm {III}^*$ (large angles $\alpha$), potential failure at the loading points influences the fracture toughness results. The reason is that fracture load significantly grows with $\alpha$, and such large loads at the contact points may induce local failure. Indeed, testing the validity of Eq. (5) requires more test data.

Figure 8a presents the estimated values of ${\hat{K}}_\mathrm {IIc}$ and ${\hat{K}}_\mathrm {IIIc}$ (using $\mu =0.6$) together with $K_\mathrm {Ic}$ of the Bedretto Granite against the ligament length in the notched samples. To report the results in Fig. 8a, $K_{\mathrm {Ic}}$ and $\mathrm {K_{IIc}}$ values were extracted from Bahrami et al. (2021) and Eqs. (3) and (5) were used to calculate $\mathrm {\hat{K}_{IIc}}$ and $\mathrm {\hat{K}_{IIIc}}$ from $\mathrm {K_{IIc}}$ and $\mathrm {K_{IIIc}}$. Note that to calculate $\mathrm {\hat{K}_{IIIc}}$ for the samples with the ligament length 20 mm, all of the tested loading angles ($\alpha = 10^{\circ }, 20^{\circ }, 30^{\circ }$) were considered. As Fig. 8a demonstrates, at each ligament length, the estimated $\mathrm {\hat{K}_{IIc}}$ and $\mathrm {\hat{K}_{IIIc}}$ values are close to each other, and almost two times greater than $K_{\mathrm {Ic}}$. These results again confirm similar shear-based nature of true mode $\mathrm {II}$ and true mode $\mathrm {III}$ fracturing, which in essence differs from the mode $\mathrm {I}$ or tension-based fracturing.

Let us now employ the LEFM theory to estimate the fracture energy associated to each individual mode of failure. The relationship between the stress intensity factor and the fracture energy of each mode of failure for the plane strain condition is given by Anderson (2004)

$$\begin{aligned} {G_\mathrm {Ic}}&= \dfrac{K^2_\mathrm {Ic}}{E/(1-\nu ^2)} , \quad {{\hat{G}}_\mathrm {IIc}} = \dfrac{\hat{K}^2_\mathrm {IIc}}{E/(1-\nu ^2)} \quad ,\nonumber \\ {{\hat{G}}_\mathrm {IIIc}}&= \dfrac{\hat{K}^2_\mathrm {IIIc}}{E/(1+\nu )} \end{aligned}$$

(5)

where E and $\nu$ are the Young’s modulus and Poisson’s ratio of the material. Substituting the measured data for the fracture toughness, as well as the estimated material constants reported in David et al. (2020), individual mode fracture energies can be estimated. Figure 8b illustrates the variations of the fracture energies associated with the three modes of failure against the ligament size. As clearly seen in this figure, true mode $\mathrm {II}$ and true mode $\mathrm {III}$ fracture energies are in a very good agreement, which indicates that they both perhaps represent an identical shear fracture energy. This is yet another supporting evidence on the similar shear-based fracturing mechanisms in true mode $\mathrm {II}$ and true mode $\mathrm {III}$ fracturing tests. Also seen in Fig. 8b is that shear fracture energy is significantly greater than the tensile (mode $\mathrm {I}$) one.

Fig. 8

Variations of a fracture toughness and b fracture energy for the three individual modes of failure against the ligament length

4.4 Comparison with an Alternative Sample

An alternative sample to the ANBD specimen is its single-edge counterpart, that is referred to as the axially single-edge notched Brazilian disk (ASNBD). It is basically prepared by cutting the ANBD sample at the symmetry plane into two halves. The preparation of ASNBD is simpler than ANBD since it contains only one notch and does not require the alignment of notches in one plane, that is a critical step in ANBD sample preparation. This specimen has been employed in a few studies for mode $\mathrm {I}$ and mixed-mode $\mathrm {I/III}$ tests (Bahmani et al. 2019, 2021; Ko 2008). We conducted a set of mode $\mathrm {III}$ tests to evaluate the effectiveness of this specimen for measuring true mode $\mathrm {III}$ fracture toughness. The details of the specimen preparation and test results are presented in Appendix A. The results show that although $K_\mathrm {IIIc}$ measured from ASNBD and ANBD tests are in agreement in some cases, the single-edge sample is not as reliable as the double-edge counterpart since it allows crack kinking as shown in Appendix A. Hence, we conclude that ANBD is much more reliable than ASNBD for $K_\mathrm {IIIc}$ measurement.

It should be mentioned that the torsional bar test can also be suggested for measuring true mode $\mathrm {III}$ fracture toughness of rocks as has been previously used by Ko (2008). The paramount advantage of the torsional bar test is its non-confinement loading condition which leads to directly measuring $\mathrm {\hat{K}_{IIIc}}$ without using the hypotheses considered in Eq. (5). Conducting such a test on rock samples is however not simple and straightforward. Future research should focus on the comparison between $\mathrm {\hat{K}_{IIIc}}$ values measured from ANBD and torsional bar tests for rocks as well as other types of materials.

As a final point, we note that although the actual deformation modes are not measured experimentally, we believe that mainly non-opening condition and shear-based fracturing happens in the ANBD tests, because of the following reasons. (1) Finite element simulations show that most of the ligament area is under a considerable shear stress, and only a very small region is subjected to a positive normal stress (see Fig. 3). This suggests that the failure is induced mainly by shear stresses. (2) Comparing $K_\mathrm {IIIc}$ and $K_\mathrm {IIc}$ in Fig. 8a shows a good agreement between these two properties. This indicates that both tests involve similar nature of fracturing process. (3) The generation of daughter cracks and cavities in the fracture surface has been reported to be a unique characteristic of the true mode $\mathrm {III}$ fracture surface (Pham and Ravi-Chandar 2014, 2016; Pham 2015). Such fracture growth mechanism is also observed in the tests reported in the present paper (see Fig. 6). 4) The load-deformation and acoustic emission response of the samples are very similar to the ones of true mode $\mathrm {II}$ tests, suggesting that both tests show a similar failure initiation and propagation within the notch ligament.

5 Summary

A new testing method called axially double-edge notched Brazilian disk (ANBD) for true mode $\mathrm {III}$ fracture toughness determination of rock samples was presented. Core-based shape, easy preparation and straightforward testing procedure are among the major advantages of the proposed test. First, the FE method was employed to compute the stress intensity factors at the crack front. Subsequently, in the experimental program of the paper, Bedretto Granite was used as the testing material and the influence of the loading angle and the ligament size on the measured fracture toughness was investigated. It was demonstrated that fractures grow without kinking and the fracture surfaces are pulverized, which demonstrates the shear-based nature of fracturing. The results were also compared with the results of mode $\mathrm {I}$ and true mode $\mathrm {II}$ fracture toughness values reported in the literature for the same rock type. While a good agreement between true mode $\mathrm {III}$ and true mode $\mathrm {II}$ fracture toughness values was observed, $K_{\mathrm {IIIc}}$ values were found to be almost 2.5 times greater than $K_{\mathrm {Ic}}$.

Appendix 1: Results of Axially Single-Edge Notched Brazilian Disk Tests

As a similar test to ANBD is axially single-edge notched Brazilian disk (ASNBD) which has been employed for mode $\mathrm {I}$ and mixed-mode $\mathrm {I/III}$ fracture toughness tests (Bahmani et al. 2019, 2021; Ko 2008). In this appendix, we evaluate the applicability of this specimen for true mode $\mathrm {III}$ fracture toughness measurement of rocks. The ASNBD specimen is basically generated by cutting an ANBD specimen at the symmetry-plane into two halves. ASNBD samples of radius 42 mm, notch lengths of 10, 15, 20 mm and thickness of $t = 30$ mm (half of the thickness in ANBD specimens) were prepared for testing. Sample preparation of ASNBD specimens is more straightforward than ANBD specimens as the operator should not be concerned about the alignment of the two notches in one plane. Table 4 compares the measured values of true mode $\mathrm {III}$ fracture toughness from ASNBD tests with the ones of ANBD tests.

Table 4 Comparison of $K_\mathrm {IIIc}$ values obtained from ASNBD and ANBD tests

According to Table 4, the results obtained from ASNBD tests underestimate $K_{\mathrm {IIIc}}$ values in comparison with the results of ANBD tests, particularly at high loading angles. In order to justify this behaviour, we also performed a FE analysis for the ASNBD specimen. Figure 9a shows the variations of the SIFs along the crack front in the ASNBD specimen with the configuration $l/t = 0.33, \alpha = 30^{\circ }$. For the sake of comparison, we also show in Fig. 9b the plot for the SIFs of the counterpart ANBD specimen. As seen, $K_{\mathrm {II}}^*$ has much higher magnitudes and variations in the ASNBD specimen compared to ANBD.

Lin et al. (2010) showed the important role of $K_{\mathrm {II}}$ in causing crack twisting under dominant mode $\mathrm {III}$ loading conditions. They demonstrated that high values of $K_{\mathrm {II}}$ in dominant mode $\mathrm {III}$ loadings facilitate the twist of the crack and its consequent reorientation to become normal to the direction of maximum tensile stress. Figure 10 shows such kinking tendency in the ASNBD specimen, that is completely different from the co-planar crack extension in the ANBD specimen. This supports the conclusion put forward by Lin et al. (2010) that the presence of $K_{\mathrm {II}}$ is likely the reason for twisting in dominant mode $\mathrm {III}$ cracks.

As seen in Fig. 10, the kink angle in the sample with the configuration $l/t = 0.33, \alpha = 30^{\circ }$ is more than twice the one with $l/t = 0.5, \alpha = 10^{\circ }$. The fracture toughness values in these two configurations are also about 14% and 53% less than the ones of their ANBD counterparts (see Table 4). This indicates that crack twisting in ASNBD samples is the main reason for significant differences between fracture toughness results obtained from ASNBD and ANBD specimens. To avoid such twisting, one should select specimens that induce low values of $K_\mathrm {II}$. The ANBD test suggested in this paper is indeed one of those choices that simply allows the measurement of true mode $\mathrm {III}$ fracture toughness in a reliable manner.

Fig. 9

Variations of normalized SIFs along the crack front for the configuration $l/t = 0.33, \alpha = 30^{\circ }$: a ASNBD; b ANBD

Fig. 10

Sample fracture growth path in ASNBD specimens: a $l/t = 0.5, \alpha =10^{\circ }$; b $l/t = 0.33, \alpha = 30^{\circ }$