Hydro-mechanical Response to Gas Transfer of Deep Argillaceous Host Rocks for Radioactive Waste Disposal

Abstract

During recent decades, argillaceous sedimentary formations have been studied as potential host formations for the geological disposal of long-living and heat-emitting radioactive waste—Boom Clay in Belgium and Opalinus Clay and Brown Dogger in Switzerland. A significant issue in the long-term performance of these potential host rocks concerns the generation and transport of gases. The pressure resulting from the generation of gas in an almost impermeable geological medium in the near field of a repository will increase. Under high gas pressures, the mechanical and hydraulic properties of the host rock are expected to change significantly. Preferential gas pathways may develop which exploit material heterogeneity, anisotropy (bedding planes), rock discontinuities, or interfaces between the different components of the repository, and may eventually lead to the release of the produced gases. Gas flow through these clayey rocks is investigated on the basis of laboratory work. Priority has been given to studying the volume change response of these initially water-saturated materials through relatively fast and controlled volume-rate gas injections. The effect of the gas injection rate, the confining pressure and the bedding orientation on the gas transport properties have been studied with particular attention paid to the coupling with strain behaviour. The results have shown features common to the three formations concerning the gas transfer process through preferential pathways, despite their initially differential properties.

1 Introduction

Radioactive wastes conditioned for deep geological disposal in low-permeability formations will produce a significant amount of gas as a result of the anaerobic corrosion of metals (which produces H₂), degradation of organic matter (which may produce CO₂ and CH₄) and radiolysis of water (which principally produces H₂). The generation, accumulation and release of gases from the disposal system may affect several processes that influence the long-term radiological safety of the repository (NEA 2001). In particular, some of the gases produced may be radioactive (e.g., those containing ¹⁴C and ³H); thus, their release from the repository into the biosphere may present a radiological hazard. Furthermore, gas accumulation may eventually result in gas pressure build-up sufficient to affect the mechanical integrity of the engineered barrier system (EBS) or the geological barriers (host rock), or influence groundwater movement, potentially enhancing the transport of dissolved radionuclides by the expulsion of contaminated water from the waste packages. Therefore, to establish confidence in the safety case for deep geological disposal of radioactive wastes, all significant processes associated with repository performance and safety should be quantitatively evaluated, even if radiological risks are low.

Clay-rich rocks have been identified as a class of candidate host rock formations in radioactive waste disposal, distinguished by their particular suitability for the long-term isolation of waste forms. Furthermore, the capacity of argillaceous formations to efficiently self-seal both naturally occurring and excavation induced fractures, together with their favourable radionuclide retention characteristics, have been the subject of comprehensive international research programmes [e.g., (NEA 2010); SELFRAC (Bastiaens et al. 2007); TIMODAZ (Li et al. 2007)].

Significantly, clay-rich materials' excellent radionuclide retention behaviour entails low gas transport capacity. Therefore, after repository closure, the accumulation of corrosion and degradation gases, added to the build-up of excessive gas pressures on the backfilled repository structures, could impair the performance of long-term safety functions for the EBS and host rock, respectively. The development of a mechanistic understanding of the release of gases from the backfilled structures through argillaceous host rock formations has been addressed in various national radioactive waste disposal programmes (e.g., Marschall et al. 2005; ONDRAF/NIRAS 2011) and on international RD&D platforms for radioactive waste management organisations worldwide [e.g., EUP7-FORGE/(Shaw 2013)]. Even so, laboratory data that might facilitate the development of conceptual models for predicting the long-term behaviour of the repositories are scarce.

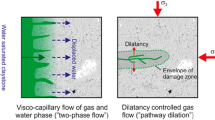
There is more and more evidence (Marschall et al. 2005; Olivella and Alonso 2008; Xu 2013; Harrington et al. 2015; Liu et al. 2016) that gas transfer through saturated argillaceous rocks will first be driven by the diffusion of dissolved gases in pore water, and via the immiscible displacement of the wetting fluid by the non-wetting gas phase (“two-phase flow”). However, these formations present low diffusion coefficients and low hydraulic conductivity, leading to a continuous increase in gas pressure. This fact, in conjunction with the relatively low tensile strength properties of these clay rocks, may generate a micro-crack network (two-phase flow coupled with mechanical effects or gas flow through dilatant pathways). As a result, gas pathways may develop, thereby exploiting material heterogeneity and anisotropy (bedding planes), previously sealed discontinuities in the EDZ (Excavation Damaged Zone) or along EBS/EDZ interfaces (Davy et al. 2009; Harrington et al. 2012b, 2017b; Cuss et al. 2014, 2015; Lanyon et al. 2014; Le and Nguyen 2014; Senger et al. 2014; Gonzalez-Blanco et al. 2016; Liu et al. 2016). Therefore, the mechanical properties, the total stresses at the interfaces and the deformation response become key parameters for describing gas flow through dilatant pathways.

A comprehensive series of gas injection tests were performed to enhance understanding of the response of argillaceous rocks to gas transfer through preferential pathways. The gas tests were carried out at stress states equivalent to the repository conditions of three different formations, candidates for hosting radioactive waste in Belgium (Boom Clay formation) and Switzerland (Opalinus Clay formation and Brown Dogger). The laboratory tests aimed at investigating the effect of the gas injection rate, the confining pressure and the bedding orientation on the gas transport properties in fully saturated samples, with a special attention paid to the stress–strain response. In contrast to previous works (Harrington et al. 2012a, 2017a; Arnedo et al. 2013; Liu et al. 2016), sample volume changes were permitted during tests (oedometer or isotropic conditions) and gas injection was limited to a maximum gas pressure below the minimum principal stress, ensuring gas flow through the sample and avoiding gas flow through interfaces or gas-frack (gas migration through macro-cracks).

The discussion of the experimental results provides some clues to the common features of the three formations concerning the gas transfer process through preferential pathways and seeks to promote interaction between different national agencies through European Joint Programmes such as the recently launched HORIZON 2020 project EURAD (www.ejp-eruad.eu).

2 Materials

2.1 Mineralogical Origin and In Situ Stress State

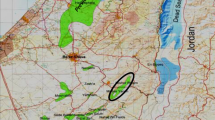
Three different argillaceous formations were considered in this study. Boom Clay (BC) is marine sediment of the Cenozoic, specifically of the Rupelian age (~ 30 My). At the Mol–Dessen nuclear site, the Boom Clay lies 190–290 m below ground level (Fig. 1). Samples of BC were retrieved by the ESV EURIDICE at a depth of 223 m in the HADES-URF (Underground Research Facility) at Mol, Belgium (Core references: CGR70_71W_Core8, CGR70-71W_Core7, CGR66-67W_Core 8_Sectiona). On the other hand, two different shales were recovered by NAGRA from a deep geothermal well, Schlattingen-1, near the village of Schlattingen in the Molasse Basin of Northern Switzerland (Wersin et al. 2013). The so-called “Brown Dogger” (BD) corresponds to a sequence of clay-rich layers with sandy and carbonate-rich intercalations from the Upper Dogger unit of the Bathonian/Bajocian age (~ 168 My), whilst the Opalinus Clay formation (OPA) is from the Lower Dogger unit of Aalenian age (~ 170 My). Figure 1 also shows a section of the stratigraphic column of the geothermal well from which OPA and BD were retrieved. Cored samples in this study correspond to depths of 781.55–781.85 m for BD and 936.26–936.49 m for OPA.

Fig. 1

Left: Stratigraphic column of the Mol–Dessen nuclear site (Belgium) [modified after (Vandenberghe et al. 2014)]; right: Stratigraphy of the geothermal well Schlattingen-1 (SLA-1) (modified after Wersin et al. 2013)

In terms of mineralogy, Boom Clay is very homogeneous in the vertical profile. However, variations exist in the quantitative mineralogy related to different grain-size distributions in silt-dominated and clay-dominated layers. It consists mainly of clay minerals (30–70%) dominated by illite (15–35%), kaolinite (5–20%) and smectite (10–30%). The complementary non-argillaceous fraction is mainly constituted by quartz (5–60%) and feldspar (1–10%) (De Craen et al. 2004).

Mineralogical compositions of rock samples from the Opalinus Clay (Aalenian stage) and Brown Dogger section (comprising Callovian, Bathonian, Bajocian) in the Schlattingen borehole were determined by X-ray diffractometry, as reported in Wersin et al. (2013). Further information was obtained from petrophysical logging. Three rock samples were taken at the depth interval 929.5–939.5 m in the lower section of the Opalinus Clay formation, displaying a total clay content of 34–63%, with 7–18% of illite, 14–31% of illite/smectite mixed layers, 7–17% of kaolinite and < 6% of chlorite. Among the non-clay minerals, quartz (9–40%), calcite (11–36%) and siderite (1–8%) dominate. In the Parkinsoni-Württembergica Beds within the BD section, the mineralogical information was derived from three core samples at a depth range between 778.5 and 787.5 m. The total content of clay minerals is about 34–52%, consisting of 10–13% illite, 16–25% illite/smectite mixed layers, 7–12% kaolinite and 2–4% chlorite. The non-clay minerals are comprised of 21–24% quartz and 19–33% carbonates. These data points are broadly comparable to the ones published by Ferrari and Laloui (2013) and Ferrari et al. (2014), where the BD is classified as silty to clay-rich marl with a clay content of 25–45%, 30–50% carbonate and 20–25% quartz.

Given that the planned tests are intended to reproduce the samples’ in situ stress states as precisely as possible, the conditions before the injection should mimic the field stresses. BC at the depth of the HADES-URF presents the lithostatic pressure or total vertical stress, ${\sigma }_{\mathrm{v}}$, imposed by the weight of the overlying material, of about 4.5 MPa. The undisturbed pore pressure ${u}_{\mathrm{w}}$ at the HADES depth (but measured at a sufficient distance from the galleries) is about 2.2 MPa and corresponds closely to hydrostatic distribution up to the water table close to the surface. The effective vertical stress is thus ${\sigma {^{\prime}}}_{\mathrm{v}}= {\sigma }_{\mathrm{v}}- {u}_{\mathrm{w}}=2.3 \mathrm{MPa}$. The ${K}_{0}$ value (the ratio of horizontal to vertical effective stresses) was determined by laboratory tests (oedometer cell with lateral stress measurement) as being close to 0.9 (Bernier et al. 2007; Dao 2015; Gonzalez-Blanco et al. 2016) for an overconsolidation ratio between 2.1 and 2.3 at HADES level.

In situ stress state data from the SLA-1 borehole (Vietor et al. 2012; Giger and Marschall 2014), at the depth of BD samples (782 m), yielded values for minimum and maximum horizontal stresses of ${\sigma }_{\mathrm{h}}=15.0 \mathrm{MPa}$ and ${\sigma }_{\mathrm{H}}=21.0 \mathrm{MPa}$, whilst the calculated vertical stress was ${\sigma }_{\mathrm{v}}=19.5 \mathrm{MPa}$, resulting in a value for total mean stress of $p=18.5 \mathrm{MPa}$. Hydrostatic water pressure was assumed to be ${u}_{\mathrm{w}}=7.8 \mathrm{MPa}$, and therefore, the result for vertical effective stress yielded ${\sigma {^{\prime}}}_{\mathrm{v}}=11.7 \mathrm{MPa}$, whereas the effective mean stress was $p {^{\prime}}=10.7 \mathrm{MPa}$. In the case of the stress state at the OPA depth (936 m), the vertical stress was calculated using the same overburden unit weight, resulting in ${\sigma }_{\mathrm{v}}=23.4 \mathrm{MPa}$. Giger and Marschall (2014) reported a total stress K-ratio $({\sigma }_{\mathrm{h}}/{\sigma }_{\mathrm{v}})$ of 0.82 for a depth of 900 m, which denotes a horizontal stress ${\sigma }_{\mathrm{h}}=19.2 \mathrm{MPa}$. Hydraulic head distributions in Opalinus Clay can be considered hydrostatic (Giger and Marschall 2014). Therefore, the water pressure at OPA depth is ${u}_{\mathrm{w}}=9.4 \mathrm{MPa}$, giving an effective mean stress $p {^{\prime}}=11.2 \mathrm{MPa}$ and effective vertical stress ${\sigma {^{\prime}}}_{\mathrm{v}}=14.0 \mathrm{MPa}$.

2.2 Geotechnical Properties

Table 1 shows the main geotechnical properties of the three materials, together with volumetric and gravimetric properties as well as initial state variables. To form a complete picture, the plasticity chart obtained for the studied samples according to ASTM D2487 is shown in Fig. 2 together with data reported by several authors (Belanteur et al. 1997; Romero 1999; Dehandschutter et al. 2004; Volckaert et al. 2005; Li et al. 2007; François et al. 2009; Lima 2011; Ferrari et al. 2012; Ferrari and Laloui 2013; Romero and Gómez 2013). Boom Clay is classified as a high–medium plastic inorganic clay (CH), Opalinus Clay as low plastic inorganic clay (CL), whilst Brown Dogger is in between low plastic inorganic clay (CL) and low plastic inorganic silt (ML).

Table 1 Main geotechnical, volumetric and gravimetric properties of the three tested materials

Fig. 2

Plasticity chart including data from other authors (Belanteur et al. 1997; Romero 1999; Dehandschutter et al. 2004; Volckaert et al. 2005; Li et al. 2007; François et al. 2009; Lima 2011; Ferrari et al. 2012; Ferrari and Laloui 2013; Romero and Gómez 2013)

In addition, the bulk density and void ratio at the initial state, as well as the initial degree of saturation and the initial total suction, are profiled and depicted in-depth to compare these argillaceous materials (Fig. 3). Again, values reported in the literature (Le 2008; Lima 2011; Ferrari et al. 2012; Ferrari and Laloui 2013; Dao 2015) at different depths have been used to complement the information of the three formations. As expected, the void ratio decreases with depth in BC samples. However, samples from the Schlattingen borehole, both OPA and BD, which are very deep, do not illustrate that tendency, the void ratio being around 0.1 for all of them, although the bulk density values are slightly scattered. In terms of the degree of saturation, it is notable that all samples are highly saturated, even though they display relatively high initial total suctions (some desiccation during retrieval and storage caused the increase of the initial total suction in some samples). The increase of matric suction is due to the water undrained retrieval of the samples since the pore water follows the change in total stress during the undrained unloading at constant effective stress.

Fig. 3

Depth profiles of bulk density, void ratio and degree of saturation of BC, OPA and BD and  total suction induced on retrieval and storage complemented with data from other authors (Le 2008; Lima 2011; Ferrari et al. 2012; Ferrari and Laloui 2013; Dao 2015)

2.3 Microstructural Analyses

Gas transfer in argillaceous rocks reveals some specific mechanisms (the diffusion and advection of dissolved gas, two-phase flow of gas and water, gas flow through dilatant pathways and gas transport in tensile fractures) (Marschall et al. 2005; Olivella and Alonso 2008; Gerard et al. 2014; Damians et al. 2020; Nguyen et al. 2020; Yang and Fall 2021). These mechanisms are complex, as they seem to be highly dependent on the initial heterogeneity and microstructure. The existence of macro-pores or initial discontinuities, such as bedding planes, may impact gas transport properties. Therefore, a good initial characterisation of the microstructure will allow for the identification of possible variations that may affect gas permeability, which is very sensitive to microstructural changes, due to the growth of micro-cracks or fissures in the rock mass (Gonzalez-Blanco et al. 2017).

Mercury Intrusion Porosimetry (MIP) tests were carried out to characterise the microstructure of the three formations at the initial state (Romero and Simms 2008; Gonzalez-Blanco et al. 2017). In addition, the pore-network description was complemented by nitrogen adsorption tests to cover a wider range of pore sizes following the Barrett, Joyner and Halenda (BJH) method using the desorption information (Webb and Orr 1997). Figure 4 presents the cumulative void ratio ($e$) and the pore size density ($\mathrm{PSD}$) function obtained with MIP and BJH for the different entrance pore sizes ($x$) of the three formations.

Fig. 4

Cumulative void ratio (top) and $\mathrm{PSD}$ functions (bottom) for different entrance pore sizes for BC samples (left), BD samples (middle) and OPA samples (right)

The cumulative void ratio estimated via both techniques reaches the initial void ratio (see Table 1) of the samples, except for the deepest sample—OPA (936 m)—in which a porosity of 0.02 was not intruded. MIP data show a mono-modal pore size distribution at the intact state. The pore volume at the macro-scale is very low for the three materials. According to the study carried out by Keller et al. (2013) in Opalinus Clay from Mont Terri, the dominant entrance pore size is possibly related to the bedding aperture, which showed a higher frequency of longer and larger pores in the direction of the bedding planes using several microstructural techniques. This fact allows us to estimate the air-entry value (AEV), resulting in a value of 4.8 MPa for BC and 118 MPa for BD according to the Young–Laplace equation for capillary pressure (Bear 2018), indicated in Table 1. However, these values, associated with the $\mathrm{PSD}$ peaks, are large and AEV is also determined by water retention results described below. For the OPA (936 m) sample, the peak was not detected using MIP; instead, in this case, the nitrogen desorption information revealed a dominant pore mode of 3 nm (peaks at 0.6 and 4 nm were reported in Gimmi and Fernandez 2017). Smaller peaks were also detected for the other samples at the nano-metre level. The figure is complemented by data reported by Romero and Gómez (2013) for BD and OPA samples at similar depths.

2.4 Water Retention Properties

The determination of water retention curves (WRC) is essential to interpret better the suction induced on water undrained retrieval, the AEV on drying at a given degree of saturation and the hysteresis response on wetting and drying cycles (Romero and Vaunat 2000; Ferrari et al. 2014). This study obtained the water retention curve using a dew-point psychrometer (Cardoso et al. 2007) in the total suction range from 1 to 100 MPa under unstressed conditions (Fig. 5). The specimens were dried in steps starting from the initial state; they were stored for 1 day for equalisation and then weighed, and finally, the total suction was measured. Afterwards, samples were wetted in steps from the dry state by adding a drop of synthetic water, corresponding to that of the formation prepared according to De Craen et al. (2004) for BC, and to Mäder (2011) for OPA and BD. These synthetic water preparations were also used in the tests described below, but are labelled as water for the sake of simplicity. The values obtained are in close correspondence with those published by Lima (2011) for BC and Ferrari et al. (2014) for OPA and BD samples at similar depths.

Fig. 5

Water retention curves in terms of degree of saturation for BC, BD and OPA samples

The figure also includes fitting curves for the drying (solid line) and wetting (dashed line) branches for each material, using a modified version of van Genuchten’s expression

$${S}_{\mathrm{r}}={{S}_{\mathrm{r min}}+\left(1-{S}_{\mathrm{r min}}\right)\left[1+{(s/{P}_{0})}^{n}\right]}^{(-\lambda )},$$

(1)

where ${S}_{\mathrm{r min}}$ is the residual degree of saturation and $n$, $\lambda$ and ${P}_{0}$ are fitting parameters; the latter being related to the AEV. For the gas migration process in saturated clayey rocks, the ${P}_{0}$ value for the drying path is, at first, the most relevant one, and yields values reported in Table 1. This means that the gas pressure needed to start to desaturate the samples should be very high, and Table 1 also includes information on the total suction required to reach a degree of saturation of 0.90. However, as described in the next section, pressures as large as those are not required during the gas injections, since stress-dependent pathways may develop through the bedding planes, though initially closed, still represent a weakness within the clay matrix. Nonetheless, the data provided by the water retention curve do not consider the changes in the fabric of the material, due to the gas pressurisation process, and the AEV only describes the initial state. Consequently, for the gas transport in pressure-dependent pathways, the behaviour may not follow these initial water retention curves.

3 Experimental Set-Ups and Protocols

A high-pressure oedometer cell was used to perform the hydro-mechanical (HM) tests (samples of 50 mm in diameter and 20 mm in height). This equipment was also used for gas injection tests in BC, whereas in OPA and BD samples, gas injection tests were performed in a high-pressure isotropic cell (samples of 50 mm in diameter and 25 mm in height). Details of both set-ups are well described in Romero et al. (2013), Gonzalez-Blanco et al. (2016) and Gonzalez-Blanco (2017). Briefly, both set-ups consist of the cell and several controllers for the application of the boundary conditions: a pressure/volume controller (PVC) for applying vertical or isotropic stress; two water PVCs for injecting or collecting fluids in the upstream or downstream lines; and a gas PVC located in the upstream line at the bottom of the sample. In addition, an LVDT was installed to measure the vertical displacements in each piece of equipment.

The HM behaviour was addressed by testing the three materials in the oedometer cell. The test stages are described below and include common features, whilst specific characteristics for each stage for the different materials are explained along with the results for the sake of clarity.

• i. A pre-conditioning path to restore the in situ effective stress conditions was first applied to all samples. It consisted of two steps. Initially, a water undrained loading stage at a rate of 15 kPa/min at constant water content was carried out, followed by the flooding of the samples to ensure full saturation and the increase of the pore water pressure.

• ii. Water permeability was determined at steady-state conditions by imposing a pressure gradient through the samples at constant vertical stress mimicking the in situ stress.

• iii. Continuous loading to a target vertical stress was carried out at a controlled stress rate of 0.5 kPa/min to ensure drained conditions.

• iv. Water permeability was determined at steady-state conditions by imposing a pressure gradient through the samples at constant vertical stress.

• v. Continuous unloading at a controlled stress rate of 0.9 kPa/min to ensure drained conditions.

Concerning the gas injection tests in BC, the same oedometer cell was used, whereas OPA and BD were tested in the isotropic cell. Nonetheless, equivalent protocols were established. For these tests, the two initial stages were the same as described above. The continuous loading was performed at the same rate, but the maximum target pressure was limited in order not to exceed the yield stress. After the water permeability determination (stage iv in the HM protocol), the protocol changed to include the gas injection stage. It began with fast drainage of the bottom line (upstream boundary) to replace water with gas at the same pressure, whilst in the top line (downstream boundary), the water pressure remained the same. Then, the gas injection started at a constant controlled volume rate until reaching maximum gas pressure. At this maximum gas pressure, the injection piston was stopped (shut-off), and gas pressure was left to dissipate at constant gas volume of the inlet line. Finally, an undrained unloading stage was carried out to preserve the fabric of the samples after the injection.

4 Results

4.1 Hydro-mechanical Behaviour on Loading and Unloading

The first protocol was established primarily to obtain HM parameters, such as the compressibility coefficient, or to calculate water permeability in the oedometer cell. A pre-conditioning path was initially applied to all samples, since this was a prerequisite for the correspondence of the geostatic conditions of the material at the in situ state, and to ensure maximum parity in terms of effective stress. In addition, it is essential to take into account that argillaceous rocks display a high initial suction level due to the significant stress relief upon sampling, despite being close to saturation. Therefore, they can undergo expansion and degradation as a straightforward consequence of suction reduction effects due to water contact at low-stress levels (Della Vecchia et al. 2011; Lima 2011; Bésuelle et al. 2014). To minimise these effects, the samples were always loaded at a target total stress at constant water content, reducing the initial suction, and only then put in contact with water under atmospheric pressure. Thus, once the water pressure is applied, the effective stress will be equivalent to the stress in situ, thereby avoiding damage to the samples.

As described above, the pore water pressure of the materials, at their corresponding depth, is 2.2 MPa for BC, 7.82 MPa for BD and 9.36 for OPA. However, in our laboratory tests, due to the operating range of the boundary condition controllers (PVC), the applied water pressure cannot exceed 2 MPa. Consequently, to achieve correspondence with the value of the in situ effective stress, the total stress to be applied should be lower. At oedometer conditions, vertical total stress of 3 MPa for BC samples was considered for the initial loading at constant water content in the pre-conditioning stage. After flooding at atmospheric pressure to ensure full saturation, the water pressure was increased to 0.5 MPa, resulting in a vertical effective stress of 2.5 MPa, very close to the value in situ. In the case of deep OPA and BD samples, the in situ vertical effective stresses are 14 and 12 MPa approximately. Therefore, a determination was made to load both materials to 12.5 MPa in terms of total stress and apply the same increase in water pressure (0.5 MPa), resulting in a vertical effective stress of 12 MPa, equivalent to the in situ effective stress of the BD but slightly lower than the OPA one.

This first loading stage to the target total pressure was carried out at a relatively fast rate of 15 kPa/min and at constant water content. A reduction in the initial suction down to zero was expected during this path, since the total stress would affect the pore pressure. According to the Barcelona Basic Model (Alonso et al. 1990), small deformations were predicted during these total stress and suction paths. This model computes the elastic deformation with two parameters, $\kappa$ and ${\kappa }_{\mathrm{s}}$, which represent the stiffness due to changes in net stress and changes in suction, respectively, where the net stress is defined as the total stress minus the maximum fluid pressure, either water or gas pressure. For instance, values of $\kappa$ = 0.005 and ${\kappa }_{\mathrm{s}}$= 0.002 were used for the BC sample with bedding planes parallel to the axis, given an axial deformation of around 0.58% and a remaining suction of 0.6 MPa at the end of the load, which cohere closely with the experimental results (Gonzalez-Blanco 2017). Figure 6 presents the continuous loading results at controlled stress rates measuring axial strain (positive in compression) as a function of the vertical total stress on a logarithmic scale for representative samples. OPA and BD were tested with the bedding planes orthogonal to the axis, whilst BC was tested with bedding planes in both directions—orthogonal (BC_⊥) and parallel (BC_//), to study the effects of anisotropy. The loading and reduction in suction caused less than 1.5% of deformation for the BC and BD, whilst OPA underwent a slightly higher compression. The elastic anisotropy of BC is also observed, since BC_⊥ presented higher compressibility for this initial loading.

Fig. 6

Axial deformation against total stress during fast loading at constant water content

During flooding at constant vertical stress, all samples underwent some expansion due to some remaining suction after the initial loading. In this case, the Barcelona Basic Model predicted the expansion of the material due to suction changes (i.e., using the same parameters as above, the deformation at the end of the flooding stage on the BC_// sample was − 0.08%). Figure 7 presents the time evolution of the swelling strains (negative in expansion) for the three materials. BC results are presented for both orientations, showing the distinctive behaviour of anisotropy due to the bedding orientation. Samples with bedding planes orthogonal to the axis underwent more significant expansions during soaking. Surprisingly, the compressibility behaviour of BD and OPA at this initial stage, pre-conditioning and flooding, is very similar to the behaviour displayed by BC samples with bedding planes parallel and orthogonal to the axis, respectively. BD is stiffer than OPA and swells less, which is consistent with its lower clay mineral content.

Fig. 7

Evolution of swelling (negative axial deformation) during flooding at atmospheric water pressure and constant total stress

After reaching steady-state conditions for deformation during flooding, water pressure at the downstream and upstream boundaries was increased to 0.5 MPa, and once the pore pressure was equalised, vertical effective stress was equivalent to in situ stress for the three samples.

Water permeability was calculated subsequently at constant vertical stress by applying a pressure gradient and recording the inlet and outlet water volumes. Water pressure at the upstream boundary was increased to 0.6 MPa for BC samples and 2.0 MPa for BD and OPA samples.

After the complete saturation of the samples, a drained continuous loading was carried out in all the oedometer tests at a slow stress rate of 0.5 kPa/min to ensure drained conditions. This rate was checked by stopping the loading and recording the deformations with time, which were negligible. BD and OPA samples were loaded to 25 MPa of vertical total stress; for BC, maximum vertical total stresses of 9 and 14 MPa were selected to study post-yield behaviour. Nonetheless, for gas injection tests, the maximum applied stress for the three materials was lower than indicated above to avoid inducing plastic deformations. At these stress levels, water permeability was again determined by applying the same hydraulic gradient described above. Afterwards, a drained unloading was carried out in all the HM tests at a 0.9 kPa/min rate, checking again that pore pressure changes were not generated.

Figure 8 shows the compressibility curves of the materials. In the case of BC, selected results on samples with bedding planes orthogonal and parallel to the axis up to maximum effective stresses of 8.5 and 13.5 MPa, respectively, are plotted in the figure. Despite being natural samples, good consistency was observed during this hydro-mechanical loading. Anisotropy behaviour during this stage was not as evident as in the pre-conditioning stage. However, samples with bedding planes orthogonal to the axis still presented slightly higher compressibility. BD and OPA are significantly stiffer than BC. To facilitate the comparison, the drained constrained modulus for the different loading stages was defined as ${E {^{\prime}}}_{\mathrm{k}}=\delta {\sigma {^{\prime}}}_{\mathrm{v}}/\delta {\varepsilon }_{\mathrm{a}}$ (Fig. 9), ${\sigma {^{\prime}}}_{\mathrm{v}}$ being the effective vertical stress and ${\varepsilon }_{\mathrm{a}}$ the axial strain. It should be noted that during the first loading in the pre-conditioning stage, OPA and BC_⊥ present similar values, as well as BD and BC_//, the latter being considerably higher. This behaviour was not replicated during the drained loading. OPA and BD samples still present an increase of the modulus along with the effective stress, whilst BC samples change the tendency; their moduli are slightly decreasing with stress.

Fig. 8

Axial deformation against vertical effective stress during drained loading/unloading paths: a BC samples at both bedding orientations; b BD and OPA samples

Fig. 9

Drained constrained moduli during the two steps of loading in terms of net/effective stress

Drained unloading paths on BC samples produced a marked change in the structure of the sample, even increasing the porosity of the initial state. It is readily apparent that BC presents two different trends for stiffness in unloading. Typically, the first stiffer slope is associated with a mechanically driven mechanism and the second one with a hydraulically driven mechanism due to the damage to the structure when applying high stresses, which facilitate the water uptake at low stresses (Lima 2011; Cui et al. 2013). The loading to high stresses leads to a progressive degradation (presumably bond breakage) of the argillaceous rock fabric. When stresses are released, swelling takes place easily, since it is now only partially constrained by the damaged mineral skeleton. Therefore, this behaviour has been interpreted as the coupled response of the damaged rock microstructure and the swelling of the active minerals (Alonso and Alcoverro 2002). On the other hand, BD and OPA also underwent swelling during the drained unloading, recovering the initial porosity in the case of the former and slightly higher for the latter. For both materials, the double slope of the curve was not so evident, because they were less affected by the degradation on loading.

4.2 Water Permeability

Results on water permeability for the three materials, obtained at different constant vertical stresses, are shown in Fig. 10 as a function of the average void ratio together with values reported by other authors (Horseman et al. 2007; Le 2008; Lima 2011; Ferrari et al. 2012; Nguyen 2013; Romero and Gómez 2013).

Fig. 10

Water permeability as a function of the void ratio together with data reported by other authors (Horseman et al. 2007; Le 2008; Lima 2011; Ferrari et al. 2012; Nguyen 2013; Romero and Gómez 2013)

The BC results highlighted the clear dependence of the water permeability on porosity. Furthermore, higher water permeability was observed with flow parallel to bedding planes as expected, which indicated a marked anisotropic feature as indicated in Aertsens et al. (2004) and Lima (2011). The fitting of the experimental data obtained in this study is presented in Fig. 10 for each orientation. Regarding the values for BD and OPA samples, very small changes in void ratio resulted in relatively significant variations of permeability in these deep indurated clays. To study the anisotropy of these materials, there are not much data with the bedding planes parallel to the water flow in the case of OPA, and none were found in the case of BD, so that no clear conclusion can be drawn.

Water permeability values for the three materials are plotted in a depth profile (Fig. 11). Compiled results for BC and OPA at Mont Terri level present dispersion of less than two orders of magnitude. The deeper materials present the same variation if only the results of this study are considered; however, taking into account the collected data, the scattering increased up to three orders of magnitude. This variation could be attributed to the depth at which these samples were obtained, whereas the boreholes drilled directly from the underground research facilities may be of higher quality and therefore present less dispersion.

Fig. 11

Depth profile of water permeability including data reported by other authors (Horseman et al. 2007; Le 2008; Lima 2011; Ferrari et al. 2012; Nguyen 2013; Romero and Gómez 2013)

4.3 Gas Injection Tests

4.3.1 Experimental Methods

Selected results of gas migration experiments are presented in this section for the three materials, to find comparable features. To achieve this, samples were tested following similar procedures but at different stress levels, using different injection rates or with different bedding plane orientations with respect to the gas flow. Air was used as the injected gas in all the experiments.

For BC samples, the oedometer cell was used for the gas injection tests, reproducing the same protocol as for the HM tests but loading to a maximum total vertical stress of 6 MPa so as not to incur damage to the sample on the post-yield range. In the case of OPA and BD samples, the air injection was carried out in an isotropic cell, reproducing the same steps as described above (pre-conditioning, flooding, drained loading and water permeability determination). The confining pressure reached before the air injection was 15 MPa, but in the case of OPA samples, another injection was performed at a higher confining pressure of 19 MPa to study its influence.

The protocol for the gas injection stage was the same for all the tests. Just before the gas injection phase, fast drainage of the bottom line was carried out to replace water with air. Immediately afterwards, air pressure at the upstream boundary was increased from the initial (${u }_{\mathrm{a ini}}^{\mathrm{bottom}}$) to the maximum air pressure (${u }_{\mathrm{a max}}^{\mathrm{bottom}}$) at a constant-volume injection rate ($r$). At this moment, the injection piston was stopped, which is the shut-off of the system, and air pressure was subsequently left to decay at constant air volume of the inlet line during the dissipation phase. During the entire stage, the vertical (${\sigma }_{\mathrm{v}}$) or isotropic stress ($p$) were kept constant. The recovery lines were initially full of water, and the pressure (${u }_{\mathrm{w}}^{\mathrm{top}}$) was kept constant in both set-ups. The selected rates were relatively fast (gas pulse tests) to minimise gas diffusion mechanisms through the matrix and enhance gas flow mechanisms through discontinuities (Marschall et al. 2005). Furthermore, the maximum gas pressure was targeted lower than the vertical stress to avoid overpassing the minimum principal stress and prevent the gas passage between the interfaces. Finally, after the gas injection, undrained unloading was carried out to avoid water uptake during this process, resulting in negligible expansion. In this manner, suction developed due to the stress relief preserved the pore-network, which allowed the microstructure to be studied after the gas injection (Gonzalez-Blanco et al. 2017).

The maximum gas pressure of these tests was limited and held below the estimated air-entry pressure of the intact materials. The tests did not follow the typically called ‘breakthrough tests’ (Volckaert et al. 1995; Harrington and Horseman 1999; Rodwell 2000; Hildenbrand et al. 2004; Harrington et al. 2012a; Wiseall et al. 2015; Liu et al. 2016), in which gas pressure is continuously increased until some outflow volume is recorded indicating the breakthrough pressure. Instead, the gas pressure was increased until the (shut-off) maximum pressure, and then, gas volume in the inflow line was kept constant. Therefore, the gas pressure decay indicated the gas entrance into the sample, which was corroborated by the volume change of the PVC located at the outflow line.

4.3.2 Time Evolution of Gas Injection and Dissipation

Gas injection tests with different characteristics were performed to analyse the influence of each one on the coupled hydro-mechanical response. Selected results for BC samples involved different injection rates for the same bedding orientation and the same injection rate with different orientations. Tests on OPA samples were carried out at different confining pressures and the same injection rate. In contrast, confining pressure was identical during injection tests on BD samples, but three different injection rates were used. The different values for each studied case are gathered in Table 2. The recorded data during the tests include the time evolution of the gas injection pressure at the upstream boundary, the outflow pressure and volume at the downstream boundary, jointly with the axial displacement at the top, which permits for the calculation of the average axial strain.

Table 2 Main characteristics of the gas injection tests

Figure 12 shows the results of the gas injection tests in two BC samples with the bedding planes orthogonal to the gas flow (BC_⊥); and one sample with the bedding parallel (BC_//) to the gas flow at two different injection rates, 2 and 100 mL/min. For all of them, the total vertical stress was 6 MPa and was kept constant during gas injection and dissipation. The gas pressure at the upstream boundary increased from 0.5 to 4 MPa (A to B in the figures), followed by shut-off (point B) and dissipation at closed gas injection line (B to C). The increase in injection pressure was accompanied by expansion (negative axial strains), followed by compression strains throughout the dissipation stage.

Fig. 12

Time evolution of air pressure at the bottom boundary (bottom), average axial strain (centre) and outflow volume (top) for BC samples at the same vertical stress but different bedding orientations and different injection rates

When comparing the tests at different injection rates and with the same bedding orientation, it is noticeable that minimal displacements were recorded during the fast injection phase and that the sample underwent most of the expansion after the shut-off. Conversely, expansion of the samples tested at the slower rate occurred during the injection phase, reaching its maximum at the shut-off. This fact could be explained by examining the gas pressure-front propagation into the sample, which induces a local increase in the pore pressure and, consequently, a local decrease in the effective stress. When the injection rate was fast, there was a delay in the deformation response, since the pore pressure increase was restricted to the lower boundary of the sample. In contrast, when the injection rate was slow enough, samples expanded during the injection stage, reaching their peak expansion at the maximum gas pressure (the slow pore pressure increase propagated into the sample reaching minimum local effective stress). Hence, expansion after shut-off was not observed. In fact, the first outflow detection in the slow injection tests occurred during the injection phase, indicating that the pressure front had propagated into the sample.

The effect of bedding orientation is analysed based on the results of Fig. 12 and on those reported by Gonzalez-Blanco (2017), reinforcing the consistency of the results. BC samples with bedding planes orientated orthogonal to flow, systematically showed higher expansions regardless of the injection rate, since the material is less constrained from expanding due to the oedometer conditions compared to the samples with bedding planes parallel to the flow. In the case presented here, the sample BC_⊥ underwent larger expansion strains on gas pressure-front propagation and more significant compression on gas dissipation, which is consistent with the anisotropic behaviour observed on loading. The sample BC_// underwent the breakthrough (the outflow volume rapidly increased) just after attaining the maximum injection pressure (point B in the figure). On the contrary, the sample BC_⊥ could sustain the maximum pressure for a slightly more extended period after shut-off (point B) without a perceptible increase in volume. After the breakthrough, the injection pressure in both samples started to decrease during the dissipation phase towards the value indicated by point C, leading to progressive compression of the material.

Figure 13a presents the comparison of the behaviour during gas injection and dissipation phases for BD samples tested at three different controlled-volume rates (0.04, 2 and 100 mL/min) and at constant isotropic stress (15 MPa). It was possible for the gas pressure to increase up to the target pressure of 14 MPa. Samples tested at the fast and medium rates displayed some small expansion at the end of the air injection phase (A to B in the figure), reproducing the same behaviour as the BC sample tested at 100 mL/min. Expansion continued in both samples after shut-off (point B in the figure), as the gas pressure front propagated into the sample, causing an increase in the pore pressure and decreasing local effective stress (at constant isotropic stress). The time at which the first gas outflow occurred depended on the injection rate. In the sample tested at 100 mL/min, the first outflow was detected during the dissipation phase, whereas in the sample tested at 2 mL/min, it had already occurred during the last phase of the injection stage. At fast and medium rates (100 and 2 mL/min), the expansion of the BD samples took place with some delay in the dissipation stage (some time was needed for the pressure front to propagate into the sample). When the maximum strain was reached, and the outflow volume rate speeded up, the samples underwent compression. In contrast, the sample tested at the lowest rate (0.04 mL/min) behaved differently and was equivalent to BC tested at 2 mL/min. Indeed, all the expansion took place during the injection phase, and the maximum strain was recorded at the maximum air pressure. As the BC samples tested at 2 mL/min, the expansion after shut-off was not observed. The main difference is that in the case of the BC, 2 mL/min is slow enough for the pore pressure equilibration during the injection, whilst for the BD, the rate is somewhat slower, which is a consequence of its lower porosity. Again, the first outflow detection in this slow injection regime occurred during the injection phase. Immediately after that, the sample underwent compression due to the local effective stress increase during pore pressure dissipation (B to C in the figure).

Fig. 13

Time evolution of air pressure at the bottom boundary (bottom), average axial strain (centre) and outflow volume (top) for a OPA samples at two different confining stresses and the same injection rate; and b BD samples at the same confining stress and different injection rates

Figure 13b presents the air injection results for the OPA sample at two different constant isotropic confining stresses of 15 MPa and 19 MPa tested with the bedding planes orthogonal to the gas flow. In the first test, gas injection pressure was increased to 14 MPa, whilst in the second, the maximum gas pressure was 18 MPa, both at a constant volumetric injection rate of 100 mL/min. In both cases, it was possible for the injection pressure to increase up to the target value (14 or 18 MPa). At the end of the injection stage (A to B in the figure), the samples underwent some small expansion, being more significant at the higher confining pressure. The sample degradation might cause this behavioural feature after the first gas injection, but more research is needed to draw firm conclusions. However, any outflow was recorded in either case during the injection. After the shut-off, the gas pressure essentially remained flat in the recovery stage at constant volume without appreciable outflow volume detected for both tests (the outflow pressure remained at 0.5 MPa). For the test at confining stress of 15 MPa, the outflow volume slightly increased after 1000 min, and a steep decline in gas pressure was recorded. The outflow continued in parallel with the sample expansion and the pressure decay until it sharply increased, and as a result, the sample underwent some compression. In the second case, at higher confining stress, the behaviour is fairly similar. Nonetheless, after 4000 min approximately, the outflow volume presented a sharp change (not visible due to the graph scale), with faster gas pressure dissipation. Again, significant pressure decay occurred after the maximum expansion of the sample. The results of these fast injections are equivalents and very consistent with those for the faster injections of BC (100 mL/min) and BD (100 and 2 mL/min).

4.3.3 Gas Permeability

Gas permeability calculations were performed using the pressure decay method. Although the gas transfer is expected to occur through localised pathways, both the ideal gas law and generalised Darcy law for compressible fluid for a gas phase were assumed and applied to the entire sample area (Yoshimi and Osterberg 1963; Arnedo et al. 2013; Pineda et al. 2014; Gonzalez-Blanco 2017). The contribution of the diffusion mechanism of dissolved air through the saturated clayey matrix was neglected, since the materials present very low diffusion coefficients (Jacops et al. 2013). Numerical simulations of equivalent gas injection tests in Boom Clay indicated that the diffusive gas flux through the sample was between three and four orders of magnitude lower than the advective gas flux (Gonzalez-Blanco et al. 2016). Similar behaviour is expected for the shale samples, since the diffusion coefficients are equivalent to those of Boom Clay (Jacops et al. 2016). The pressure decay method required the constant volume $V$ of the upstream reservoir (dead and piston volumes) at varying absolute pressures ${\overline{u} }_{\mathrm{a}}$, as well as the constant downstream pressure ${\overline{u} }_{at}$ at the top cap. The evolution of the absolute pressure decay $\mathrm{d}{\overline{u} }_{\mathrm{a}}/\mathrm{d}t$ was recorded and used to estimate the mass of gas flowing through the sample.

$${k}_{\mathrm{a}}=\frac{{k}_{\mathrm{i }}{{k}_{\mathrm{r}}\rho }_{\mathrm{a}} g}{{\mu }_{\mathrm{a}}}=-\frac{2 L V {\rho }_{\mathrm{a}} g}{A\left({{\overline{u} }_{\mathrm{a}}}^{2}-{{\overline{u} }_{\mathrm{at}}}^{2}\right)}\frac{\mathrm{d}{\overline{u} }_{\mathrm{a}}}{\mathrm{d}t}$$

(2)

$${k}_{\mathrm{i }}{k}_{\mathrm{r}}=-\frac{2 {\mu }_{\mathrm{a}} L V}{A\left({{\overline{u} }_{\mathrm{a}}}^{2}-{{\overline{u} }_{\mathrm{at}}}^{2}\right)}\frac{\mathrm{d}{\overline{u} }_{\mathrm{a}}}{\mathrm{d}t},$$

(3)

where ${k}_{\mathrm{i}}$ is the intrinsic permeability; ${k}_{\mathrm{r}}$ is the relative permeability to air (${k}_{\mathrm{i }}{k}_{\mathrm{r}}$ represents the effective permeability to air as a measure of the ability of this phase to flow in the presence of water); $A$ and $L$ are the cross-sectional area and length of the sample; ${\mu }_{\mathrm{a}}$ is the air dynamic viscosity at standard temperature and pressure; ${\rho }_{\mathrm{a}}$ is the air density at standard temperature and pressure; and $g$ is the acceleration of gravity. ${k}_{\mathrm{i }}{k}_{\mathrm{r}}$ was used, since the degree of saturation of the material was not known during the dissipation stage (the outlet of water was not measured during the tests).

It was assumed that the air pathways were desaturated and that the relative permeability to air was maximum in these paths (relative permeability close to one, even though the matrix is saturated and the global degree of saturation is higher than 95%). This way, the expression allowed for approximately obtaining intrinsic permeability values to air flow that could be compared to those obtained for water and used later to study the influence of sample deformation on gas transport properties.

Figure 14 presents the time evolution of the effective permeability to gas flow for the selected tests during the dissipation phase assuming quasi-steady-state conditions. Gas effective permeability values for BC samples were around 10^–18 m², whilst BD and OPA samples presented values between two and three orders of magnitude lower, consistent with their lower porosity.

Fig. 14

Time evolution of the air effective permeability for the selected tests

5 Discussion of the Results

Gas injection experiments on these three formations displayed common behavioural features. The gas pressurisation process acted as an unloading stage at constant vertical or isotropic stress, inducing some expansion of the samples during local pore pressure increase (local effective stress increase).

The stress–strain response during the injection stage is plotted in Fig. 15 in terms of the local vertical/isotropic stress minus the gas pressure at the bottom of the sample to assess the deformational behaviour better. As shown in Figs. 12 and 13, the injection phase was identified from point A to point B. Samples tested at slower rates only presented expansion during this phase, whilst for samples tested at faster rates, point B′ was marked as the moment when the outflow speeded up, concurrent with the maximum expansion. For these latter cases, the expansion was delayed due to the progressive increase of the pore pressure. The rate at which this behaviour changed undoubtedly depended on the porosity of the samples; this rate was between 100 and 2 mL/min for BC samples, whilst for BD, and very likely for OPA, the rate was between 2 and 0.04 mL/min.

Fig. 15

Local axial strain changes associated with local net stress changes at the bottom of the sample during air injection/dissipation stages for BC samples (top), BD samples (middle) and OPA samples (bottom)

The deformational response during the gas injection tests was consistent with the results obtained during loading and unloading paths, namely that BD samples were the stiffer ones and BC the more compressible samples. In that regard, it was interesting to consider whether or not the mechanical response to the gas injection affected the samples. For this purpose, the mean air permeability values were compared with those obtained for water as a function of the average void ratio calculated accounting for the deformation during the injection stage (Fig. 16). For BC samples, intrinsic permeability to water, which depended on sample orientation, consistently displayed lower values compared to air (assuming air relative permeability equal to one in the preferential pathways). Higher water intrinsic permeability values were observed when bedding planes were parallel to flow. This was not the case for air intrinsic permeability values, which highlighted the role played by the deformation of the material and the opening of gas pathways along the injection and dissipation stages. On the contrary, similar values for both fluids were found on OPA and BD samples. These indurated rocks presented significant changes in intrinsic permeability with very small changes in porosity.

Fig. 16

Water and air intrinsic permeability values as a function of the void ratio for BC samples (top) and BD and OPA samples (bottom)

To better understand the consequences of gas injection, MIP tests were performed on freeze-dried samples to compare the pore size density ($\mathrm{PSD}$) functions before (intact state) and after the gas tests. Figure 17 presents the PSD functions obtained for BC and OPA samples at their intact state and after the gas injection tests. The results are plotted on a log–log scale to highlight the changes at the macro-scale. Special care was taken during the unloading stage (after the air tests) that was carried out under undrained conditions to prevent further expansion of the material. The micropores (below 2 μm) did not undergo significant changes. However, larger macroporosity was detected after the injection tests in both materials, which might have developed during the expansion produced at the early stage of the injection/dissipation experiments. The influence of the previous mechanical paths on the pore size distribution was disregarded. This assumption was based on MIP tests performed in BC samples subjected to the same stress paths but without gas injection (Gonzalez-Blanco 2017). The obtained $\mathrm{PSD}$ functions after these stress paths were similar to the intact ones. By contrast, a new family of large pores, which was not detected in intact samples, was systematically observed after the gas injection tests in BC samples. These new pores at entrance sizes larger than 2 µm (dominant pore modes around 10 µm and representing around 10% of the total pore volume) were associated with fissure openings that acted as preferential gas pathways. In fact, further analyses in BC samples with other microstructural techniques (Micro-Focus-X-ray Computed Tomography and Field-Emission Scanning Electron Microscopy) were performed and confirmed that gas injection led to the opening of preferential pathways that considerably modify the gas transport properties (Gonzalez-Blanco and Romero Submitted). Only one MIP test was performed after the injection tests on OPA, showing the same behaviour as BC. Despite the scarcity of data on the indurated clays, similar trends are expected regarding the increase at the macro-scale level on OPA samples after gas tests, implying the opening of preferential paths for gas transport even in these low-porosity samples.

Fig. 17

PSD functions from MIP on intact samples and after gas injection tests for BC and OPA samples

6 Conclusions

The present work was motivated by the challenging task of better understanding the gas transfer process on argillaceous formations intended to host radioactive waste in deep geological disposals. Gas transport through these low-permeability rocks seems to be controlled not only by the hydraulic and mechanical properties of the intact state (intrinsic permeability, porosity distribution, rock strength, etc.) but also by the gas pressure at the generation locus and the hydro-mechanical paths undergone by the material during gas injection/dissipation.

To this aim, laboratory-scale experiments were launched, which provided useful data for understanding theoretical frameworks and validating predictive tools. Tests under oedometer and isotropic conditions followed robust protocols, given the priority to restoring in situ conditions for the materials together with their full saturation. The hydro-mechanical response was studied during the initial stages. Relatively fast controlled volume-rate gas injection tests (air pulse tests) were performed to study gas flow mechanisms associated with the opening of stress-dependent discontinuities, rather than on slower displacement flow (displacement of the wetting fluid by the invading non-wetting fluid) and gas diffusion mechanisms through the matrix. The tests were designed specifically on samples with oriented bedding planes, at different gas injection rates and stress states to investigate their effects on the coupled hydro-mechanical mechanisms dominating gas transfer. Volume changes were allowed in the experimental set-ups, and the deformation response was analysed during gas injection, gas pressure increase and dissipation.

The gas injection rate strongly influenced the stress–strain response during gas injection and dissipation. At slower rates, expansions occurred during the injection stage, since pore pressure was nearly equilibrated, whereas, at faster rates, this response was delayed in time. The rate at which these different behavioural features occur depends on the porosity of the rock. For BC samples, an injection rate of 2 mL/min can be considered slow. However, for the low-porosity BD, the 2 mL/min rate gives results comparable to the faster rate of 100 mL/min. The effect of the bedding plane orientation was also studied in BC samples and played a fundamental role in the volume change behaviour during gas migration. Samples with bedding planes orthogonal to flow were less constrained and consistently displayed more significant expansions than samples with bedding planes parallel to flow. For the tests performed on OPA samples, a minor impact of the confining pressure was found.

Estimation of the effective permeability to air flow of the materials during the dissipation stages was found, in general, to be higher than the measured for water flow, which indicated a possible opening of preferential pathways for the gas flow that controls the permeability.

To detect the opening of fissures or discontinuities due to gas transfer, pore size distributions were obtained from mercury intrusion porosimetry tests before and after the gas injection experiments. The results showed an increase in the pores/fissures larger than 2 μm, which is evidence of preferential pathways formed during gas injection and pressurisation.

The compiled information in this paper, concerning three different argillaceous formations as potential hosts of nuclear waste disposals, gives some clues to their common features, particularly regarding the gas transfer process, and would endorse the joining of forces between different national agencies through European Joint Programmes such as the recently launched HORIZON 2020 project EURAD WP-GAS.