3D Cutting Force Model of a Stinger PDC Cutter: Considering Confining Pressure and the Thermal Stress

Abstract

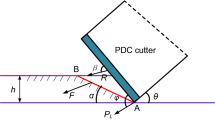
Cutting force prediction of the Stinger PDC cutter is a critically important work for the hybrid PDC bit design, which will directly affect the working stability and rock-breaking efficiency of drill bits. Thermal stress caused by drilling fluid cooling high temperature rock has significant influence on cutting force in geothermal drilling. However, to our best knowledge, the investigation of thermal stress in cutting force models for Stinger PDC is still limited. This paper presents a 3D cutting force analytical model of a Stinger PDC cutter based on the rock stress analysis, which considers the comprehensive influences of in-situ stress, hydrostatic pressure, and thermal stress. The model accuracy is validated by experimental data with less than 7% error in atmosphere condition. The simulation results show that a spherical shape stress concentration zone around the Stinger PDC cutter tip is formed, where the rock is mainly subjected to tensile stress. With the increase of in-situ stress and hydrostatic pressure, the cutting force increases linearly, but the hydrostatic pressure has smaller influence on the cutting force than in-situ stress. The induced thermal stress belongs to tensile stress, which can sharply decrease the cutting force, and the amplitude of cutting force reduction reaches 74% at cutting depth of 1 mm when the formation temperature is 300 °C. In addition, the cutting force also reduces with the increase of the formation temperature and the heat transfer coefficient. The key findings of the work will be expected to help design the hybrid PDC bit used in geothermal drilling.

Appendices

Appendix A: Derivation of force ${{\varvec{F}}}_{{\varvec{c}}1}$, ${{\varvec{F}}}_{{\varvec{c}}2}$ and ${{\varvec{F}}}_{{\varvec{n}}}$

In this section, the detailed derivation process of Eq. (6) is shown. According to Eq. (2), Eq. (3), Eq. (4), and Eq. (5), the known conditions can be expressed as:

$$\gamma { = }\theta - \Omega .$$

(26)

$$\sin \Omega = \sin \beta \sin \alpha .$$

(27)

$$\cos \phi = \sin \beta \sin \alpha .$$

(28)

$$\begin{gathered} F_{1} = {{N \cdot \sin \gamma } \mathord{\left/ {\vphantom {{N \cdot \sin \gamma } {\sin \phi }}} \right. \kern-\nulldelimiterspace} {\sin \phi }} + {{S_{1} \cdot \cos \gamma } \mathord{\left/ {\vphantom {{S_{1} \cdot \cos \gamma } {\sin \phi }}} \right. \kern-\nulldelimiterspace} {\sin \phi }} \hfill \\ F_{2} = {{N \cdot \sin \gamma } \mathord{\left/ {\vphantom {{N \cdot \sin \gamma } {\tan \phi }}} \right. \kern-\nulldelimiterspace} {\tan \phi }} + {{S_{1} \cdot \cos \gamma } \mathord{\left/ {\vphantom {{S_{1} \cdot \cos \gamma } {\tan \phi }}} \right. \kern-\nulldelimiterspace} {\tan \phi }} \hfill \\ F_{3} = {{N \cdot \cos \gamma - S_{1} \cdot \sin \gamma - N \cdot \sin \gamma } \mathord{\left/ {\vphantom {{N \cdot \cos \gamma - S_{1} \cdot \sin \gamma - N \cdot \sin \gamma } {\tan \phi }}} \right. \kern-\nulldelimiterspace} {\tan \phi }} - {{S_{1} \cdot \cos \gamma } \mathord{\left/ {\vphantom {{S_{1} \cdot \cos \gamma } {\tan \phi }}} \right. \kern-\nulldelimiterspace} {\tan \phi }}. \hfill \\ \end{gathered}$$

(29)

Thus, according to Eq. (26), the $cos\gamma$ and $sin\gamma$ can be express as:

$$\begin{gathered} \cos \gamma = \cos (\theta - \Omega ) = \cos \theta \cos \Omega + \sin \theta \sin \Omega \hfill \\ \sin \gamma = \sin (\theta - \Omega ) = \sin \theta \cos \Omega - \cos \theta \sin \Omega . \hfill \\ \end{gathered}$$

(30)

Substitute Eq. (30) into Eq. (29):

$$\begin{gathered} F_{c1} = 2\int_{0}^{{\frac{\pi }{2}}} {F_{3} \sin \beta } d\beta { = }2\int_{0}^{{\frac{\pi }{2}}} {N \cdot \cos \gamma \cdot \sin \beta } d\beta - 2\int_{0}^{{\frac{\pi }{2}}} {S_{1} \cdot \sin \gamma \cdot \sin \beta } d\beta \hfill \\ \quad \quad \quad \quad \quad - 2\int_{0}^{{\frac{\pi }{2}}} {N \cdot {{\sin \gamma } \mathord{\left/ {\vphantom {{\sin \gamma } {\tan \phi }}} \right. \kern-\nulldelimiterspace} {\tan \phi }}} \cdot \sin \beta d\beta - 2\int_{0}^{{\frac{\pi }{2}}} {S_{1} \cdot {{\cos \gamma } \mathord{\left/ {\vphantom {{\cos \gamma } {\tan \phi }}} \right. \kern-\nulldelimiterspace} {\tan \phi }}} \cdot \sin \beta d\beta . \hfill \\ \end{gathered}$$

(31)

(1) the detailed derivation process of: $2N{\int }_{0}^{\frac{\pi }{2}}cos\gamma sin\beta d\beta -2{S}_{1}{\int }_{0}^{\frac{\pi }{2}}sin\gamma sin\beta d\beta$

$$\begin{gathered} 2N\int_{0}^{{\frac{\pi }{2}}} {\cos \gamma \sin \beta d\beta } - 2S_{1} \int_{0}^{{\frac{\pi }{2}}} {\sin \gamma \sin \beta d\beta } \hfill \\ = 2N\int_{0}^{{\frac{\pi }{2}}} {\left( {\cos \theta \cos \Omega + \sin \theta \sin \Omega } \right)\sin \beta } d\beta - 2S_{1} \int_{0}^{{\frac{\pi }{2}}} {\left( {\sin \theta \cos \Omega - \cos \theta \sin \Omega } \right)\sin \beta d\beta } \hfill \\ = \left( {2N\cos \theta - 2S_{1} \sin \theta } \right)\int_{0}^{{\frac{\pi }{2}}} {\cos \Omega \sin \beta d\beta } + \left( {2N\sin \theta + 2S_{1} \cos \theta } \right)\int_{0}^{{\frac{\pi }{2}}} {\sin \Omega \sin \beta d\beta } . \hfill \\ \end{gathered}$$

(32)

the detailed derivation process of: ${\int }_{0}^{\frac{\pi }{2}}cos\Omega sin\beta d\beta$

$$\int_{0}^{{\frac{\pi }{2}}} {\cos \Omega \sin \beta d\beta = } \int_{0}^{{\frac{\pi }{2}}} {\sqrt {1 - \sin^{2} \Omega } \sin \beta d\beta } .$$

(33)

Substitute Eq. (27) into Eq. (33):

$$\int_{0}^{{\frac{\pi }{2}}} {\cos \Omega \sin \beta d\beta = } \int_{0}^{{\frac{\pi }{2}}} {\sqrt {1 - \sin^{2} \beta \sin^{2} \alpha } \sin \beta d\beta = } \int_{0}^{{\frac{\pi }{2}}} {\sqrt {1 - \sin^{2} \alpha + cos^{2} \beta \sin^{2} \alpha } \sin \beta d\beta } .$$

(34)

Set $x=cos\beta$, Eq. (34) can be expressed as:

$$- \int_{0}^{{\tfrac{\pi }{2}}} {\sqrt {\cos^{2} \alpha + \sin^{2} \alpha cos^{2} \beta } d\left( {\cos \beta } \right)} = \int_{0}^{1} {\sqrt {\cos^{2} \alpha + \sin^{2} \alpha \cdot x^{2} } dx} .$$

(35)

Set $a=cos\alpha$, $b=sin\alpha$, Eq. (35) can be expressed as:

$$\begin{gathered} \int_{0}^{1} {\sqrt {a^{2} + b^{2} x^{2} } dx = b} \int_{0}^{1} {\sqrt {\left( \frac{a}{b} \right)^{2} + x^{2} } dx} \hfill \\ = b \cdot \left[ {\frac{x}{2}\sqrt {\left( \frac{a}{b} \right)^{2} + x^{2} } + \frac{1}{2}\left( \frac{a}{b} \right)^{2} \ln \left( {x + \sqrt {\left( \frac{a}{b} \right)^{2} + x^{2} } } \right)} \right]\left| {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right. \hfill \\ { = }b \cdot \left[ {\frac{1}{2}\sqrt {\left( \frac{a}{b} \right)^{2} + 1} + \frac{1}{2}\left( \frac{a}{b} \right)^{2} \ln \left( {1 + \sqrt {\left( \frac{a}{b} \right)^{2} + 1} } \right) - \frac{1}{2}\left( \frac{a}{b} \right)^{2} \ln \frac{a}{b}} \right]. \hfill \\ = \frac{b}{2} \cdot \left[ {\sqrt {\left( \frac{a}{b} \right)^{2} + 1} + \left( \frac{a}{b} \right)^{2} \ln \left( {1 + \sqrt {\left( \frac{a}{b} \right)^{2} + 1} } \right) - \left( \frac{a}{b} \right)^{2} \ln \frac{a}{b}} \right] \hfill \\ { = }\frac{1}{2}{ + }\frac{{a^{2} }}{2b}\ln \frac{b + 1}{a} \hfill \\ \end{gathered}$$

(36)

So

$$\int_{0}^{{\frac{\pi }{2}}} {\cos \Omega \sin \beta d\beta = } \frac{1}{2} + \frac{{\cos^{2} \alpha }}{2\sin \alpha }\ln \frac{\sin \alpha + 1}{{\cos \alpha }}.$$

(37)

the detailed derivation process of: ${\int }_{0}^{\frac{\pi }{2}}sin\Omega sin\beta d\beta$

$$\begin{gathered} \int_{0}^{{\frac{\pi }{2}}} {\sin \Omega \sin \beta d\beta } { = }\int_{0}^{{\frac{\pi }{2}}} {\sin \alpha \sin^{2} \beta d\beta } = \sin \alpha \int_{0}^{{\frac{\pi }{2}}} {\sin^{2} \beta d\beta } \hfill \\ = \sin \alpha \int_{0}^{{\frac{\pi }{2}}} {\frac{1 - \cos 2\beta }{2}d\beta } = \sin \alpha \cdot \left[ {\frac{\beta }{2} - \frac{\sin 2\beta }{4}} \right]\left| {\begin{array}{*{20}c} {\frac{\pi }{2}} \\ 0 \\ \end{array} } \right. = \frac{\pi }{4}\sin \alpha . \hfill \\ \end{gathered}$$

(38)

Substitute Eq. (37) and Eq. (38) into Eq. (32), $2N{\int }_{0}^{\frac{\pi }{2}}cos\gamma sin\beta d\beta -2{S}_{1}{\int }_{0}^{\frac{\pi }{2}}sin\gamma sin\beta d\beta$ can be expressed as:

$$\begin{gathered} 2N\int_{0}^{{\frac{\pi }{2}}} {\cos \gamma \sin \beta d\beta } - 2S_{1} \int_{0}^{{\frac{\pi }{2}}} {\sin \gamma \sin \beta d\beta } \hfill \\ = \left( {N\cos \theta - S_{1} \sin \theta } \right)\left( {1 + \frac{{\cos^{2} \alpha }}{\sin \alpha }\ln \frac{\sin \alpha + 1}{{\cos \alpha }}} \right) + \left( {N\sin \theta + S_{1} \cos \theta } \right)\left( {\frac{\pi }{2}\sin \alpha } \right). \hfill \\ \end{gathered}$$

(39)

(2) the detailed derivation process of: $2N{\int }_{0}^{\frac{\pi }{2}}sin\gamma /tan\upphi sin\beta d\beta +2{S}_{1}{\int }_{0}^{\frac{\pi }{2}}cos\gamma /tan\upphi sin\beta d\beta$

$$\begin{gathered} 2N\int_{0}^{{\frac{\pi }{2}}} {\frac{\sin \gamma }{{\tan \phi }}} \sin \beta d\beta + 2S_{1} \int_{0}^{{\frac{\pi }{2}}} {\frac{\cos \gamma }{{\tan \phi }}} \sin \beta d\beta \hfill \\ = 2N\int_{0}^{{\frac{\pi }{2}}} {\frac{\sin \theta \cos \Omega - \cos \theta \sin \Omega }{{\tan \phi }}} \sin \beta d\beta + 2S_{1} \int_{0}^{{\frac{\pi }{2}}} {\frac{\cos \theta \cos \Omega + \sin \theta \sin \Omega }{{\tan \phi }}} \sin \beta d\beta \hfill \\ = 2N\int_{0}^{{\frac{\pi }{2}}} {\frac{\sin \theta \cos \Omega \sin \alpha - \cos \theta \sin \Omega \sin \alpha }{{\tan \phi \sin \alpha }}} \sin \beta d\beta + 2S_{1} \int_{0}^{{\frac{\pi }{2}}} {\frac{\cos \theta \cos \Omega \sin \alpha + \sin \theta \sin \Omega \sin \alpha }{{\tan \phi \sin \alpha }}} \sin \beta d\beta \hfill \\ = 2N\int_{0}^{{\frac{\pi }{2}}} {\left( {\sin \theta \sin \alpha \sin^{2} \beta - \frac{{\cos \theta \cos^{3} \phi }}{\sin \phi \sin \alpha }} \right)} d\beta + 2S_{1} \int_{0}^{{\frac{\pi }{2}}} {\left( {\cos \theta \sin \alpha \sin^{2} \beta + \frac{{\sin \theta \cos^{3} \phi }}{\sin \phi \sin \alpha }} \right)} d\beta \hfill \\ { = }\left( {2N\sin \theta \sin \alpha + 2S_{1} \cos \theta \sin \alpha } \right)\int_{0}^{{\frac{\pi }{2}}} {\sin^{2} \beta d\beta } + \left( { - 2N\cos \theta + 2S_{1} \sin \theta } \right)\int_{0}^{{\frac{\pi }{2}}} {\frac{{\cos^{3} \phi }}{\sin \phi \sin \alpha }d\beta } . \hfill \\ \end{gathered}$$

(40)

The following is the detailed derivation process of: ${\int }_{0}^{\frac{\pi }{2}}\frac{{cos}^{3}\upphi }{sin\phi sin\alpha }d\beta$

$$\int_{0}^{{\frac{\pi }{2}}} {\frac{{\cos^{3} \phi }}{\sin \phi \sin \alpha }} d\beta {\text{ = - sin}}^{2} \alpha \int_{0}^{{\frac{\pi }{2}}} {\frac{{{\text{sin}}^{2} \beta }}{{\sqrt {1 - \sin^{2} \alpha + \cos^{2} \beta \sin^{2} \alpha } }}} d\left( {\cos \beta } \right).$$

(41)

Set $x=cos\beta$, Eq. (41) can be expressed as:

$${\text{ - sin}}^{2} \alpha \int_{0}^{{\frac{\pi }{2}}} {\frac{{{\text{sin}}^{2} \beta }}{{\sqrt {1 - \sin^{2} \alpha + \cos^{2} \beta \sin^{2} \alpha } }}} d\cos \beta {\text{ = sin}}^{2} \alpha \int_{0}^{1} {\frac{{1 - x^{2} }}{{\sqrt {\cos^{2} \alpha + x^{2} \sin^{2} \alpha } }}} dx.$$

(42)

Set $a=cos\alpha$, $b=sin\alpha$, Eq. (42) can be expressed as:

$$\begin{gathered} {\text{sin}}^{2} \alpha \int_{0}^{1} {\frac{{1 - x^{2} }}{{\sqrt {\cos^{2} \alpha + x^{2} \sin^{2} \alpha } }}} dx \hfill \\ = b\int_{0}^{1} {\frac{{1 - x^{2} }}{{\sqrt {\left( \frac{a}{b} \right)^{2} + x^{2} } }}} dx = b\int_{0}^{1} {\frac{1}{{\sqrt {\left( \frac{a}{b} \right)^{2} + x^{2} } }}} dx - b\int_{0}^{1} {\frac{{x^{2} }}{{\sqrt {\left( \frac{a}{b} \right)^{2} + x^{2} } }}} dx \hfill \\ = b\left[ {\ln (x + \sqrt {\left( \frac{a}{b} \right)^{2} + x^{2} } )} \right]_{0}^{1} - b\left[ {\frac{x}{2}\sqrt {\left( \frac{a}{b} \right)^{2} + x^{2} } - \frac{1}{2}\left( \frac{a}{b} \right)^{2} \ln (x + \sqrt {\left( \frac{a}{b} \right)^{2} + x^{2} } )} \right]_{0}^{1} \hfill \\ = b\left[ {\ln (1 + \sqrt {\left( \frac{a}{b} \right)^{2} + 1} )} \right] - b\ln (\frac{a}{b}) - b\left[ {\frac{1}{2}\sqrt {\left( \frac{a}{b} \right)^{2} + 1} - \frac{1}{2}\left( \frac{a}{b} \right)^{2} \ln (1 + \sqrt {\left( \frac{a}{b} \right)^{2} + 1} )} \right] - \frac{a}{2b}^{2} \ln (\frac{a}{b}) \hfill \\ { = }\frac{{a^{2} + 2b^{2} }}{2b}\ln \left( {\frac{b + 1}{b}} \right) - \frac{{a^{2} + 2b^{2} }}{2b}\ln (\frac{a}{b}) - \frac{1}{2} \hfill \\ = \frac{{1 + b^{2} }}{2b}\ln \left( {\frac{b + 1}{a}} \right) - \frac{1}{2}. \hfill \\ \end{gathered}$$

(43)

So

$$\int_{0}^{{\frac{\pi }{2}}} {\frac{{\cos^{3} \phi }}{\sin \phi \sin \alpha }d\beta = } \frac{{1 + \sin^{2} \alpha }}{2\sin \alpha }\ln \frac{\sin \alpha + 1}{{\cos \alpha }} - \frac{1}{2}.$$

(44)

Substitute Eq. (38) and Eq. (44) into Eq. (40), $2N{\int }_{0}^{\frac{\pi }{2}}sin\gamma /tan\upphi sin\beta d\beta +2{S}_{1}{\int }_{0}^{\frac{\pi }{2}}cos\gamma /tan\upphi sin\beta d\beta$ can be expressed as:

$$\begin{gathered} 2N\int_{0}^{{\frac{\pi }{2}}} {\frac{\sin \gamma }{{\tan \phi }}} \sin \beta d\beta + 2S_{1} \int_{0}^{{\frac{\pi }{2}}} {\frac{\cos \gamma }{{\tan \phi }}} \sin \beta d\beta \hfill \\ { = }\left( {N\sin \theta \sin \alpha + S_{1} \cos \theta \sin \alpha } \right)\frac{\pi }{2} + \left( { - N\cos \theta + S_{1} \sin \theta } \right)\left( {\frac{{1 + \sin^{2} \alpha }}{\sin \alpha }\ln \frac{\sin \alpha + 1}{{\cos \alpha }} - 1} \right). \hfill \\ \end{gathered}$$

(45)

Substitute Eq. (39) and Eq. (45) into Eq. (31), the formula of ${F}_{c1}$ can be obtained:

$$F_{c1} = \frac{2N}{{\sin \alpha }}\ln \frac{\sin \alpha + 1}{{\cos \alpha }}\cos \theta - \frac{{2S_{1} }}{\sin \alpha }\ln \frac{\sin \alpha + 1}{{\cos \alpha }}\sin \theta .$$

(46)

The formula of ${F}_{c2}$ and ${F}_{n}$ can be expressed as:

$$\begin{gathered} F_{c2} = 2\int_{0}^{{\frac{\pi }{2}}} {F_{1} \sin \alpha } d\beta = 2\sin \alpha \int_{0}^{{\frac{\pi }{2}}} {\left( {N{{\sin \gamma } \mathord{\left/ {\vphantom {{\sin \gamma } {\sin \phi }}} \right. \kern-\nulldelimiterspace} {\sin \phi }} + {{S_{1} \cdot \cos \gamma } \mathord{\left/ {\vphantom {{S_{1} \cdot \cos \gamma } {\sin \phi }}} \right. \kern-\nulldelimiterspace} {\sin \phi }}} \right)d\beta } \hfill \\ F_{n} = 2\int_{0}^{{\frac{\pi }{2}}} {F_{1} \cos \alpha } d\beta = 2\cos \alpha \int_{0}^{{\frac{\pi }{2}}} {\left( {N{{\sin \gamma } \mathord{\left/ {\vphantom {{\sin \gamma } {\sin \phi }}} \right. \kern-\nulldelimiterspace} {\sin \phi }} + {{S_{1} \cdot \cos \gamma } \mathord{\left/ {\vphantom {{S_{1} \cdot \cos \gamma } {\sin \phi }}} \right. \kern-\nulldelimiterspace} {\sin \phi }}} \right)d\beta } . \hfill \\ \end{gathered}$$

(47)

The detailed derivation process of: $2{\int }_{0}^{\frac{\pi }{2}}\left(Nsin\gamma /sin\phi +{S}_{1}cos\gamma /sin\phi \right)d\beta$

$$\begin{gathered} 2\int_{0}^{{\frac{\pi }{2}}} {\left( {N{{\sin \gamma } \mathord{\left/ {\vphantom {{\sin \gamma } {\sin \phi }}} \right. \kern-\nulldelimiterspace} {\sin \phi }} + {{S_{1} \cdot \cos \gamma } \mathord{\left/ {\vphantom {{S_{1} \cdot \cos \gamma } {\sin \phi }}} \right. \kern-\nulldelimiterspace} {\sin \phi }}} \right)} d\beta \hfill \\ = 2\int_{0}^{{\frac{\pi }{2}}} {\left( {N\frac{\sin \theta \cos \Omega - \cos \theta \sin \Omega }{{\sin \phi }} + S_{1} \frac{\cos \theta \cos \Omega + \sin \theta \sin \Omega }{{\sin \phi }}} \right)} d\beta \hfill \\ = 2\int_{0}^{{\frac{\pi }{2}}} {\left( {N\sin \theta - N\frac{\cos \theta \cos \phi }{{\sin \phi }} + S_{1} \cos \theta + S_{1} \frac{\sin \theta \cos \phi }{{\sin \phi }}} \right)} d\beta \hfill \\ = \pi N\sin \theta + \pi S_{1} \cos \theta + 2\left( {S_{1} \sin \theta - N\cos \theta } \right)\int_{0}^{{\frac{\pi }{2}}} {\frac{\cos \phi }{{\sin \phi }}d\beta } . \hfill \\ \end{gathered}$$

(48)

The following is the detailed derivation process of: ${\int }_{0}^{\frac{\pi }{2}}\frac{cos\upphi }{sin\phi }d\beta$

$$\begin{gathered} 2\int_{0}^{{\frac{\pi }{2}}} {\frac{\cos \phi }{{\sin \phi }}} d\beta = 2\int_{0}^{{\frac{\pi }{2}}} {\frac{\sin \beta \sin \alpha }{{\sqrt {1 - \sin^{2} \beta \sin^{2} \alpha } }}} d\beta \hfill \\ = - 2\sin \alpha \int_{0}^{{\frac{\pi }{2}}} {\frac{1}{{\sqrt {1 - \sin^{2} \alpha + \cos^{2} \beta \sin^{2} \alpha } }}} d\cos \beta . \hfill \\ \end{gathered}$$

(49)

Set $a=cos\alpha$, $b=sin\alpha$, Eq. (49) can be expressed as:

$$\begin{gathered} 2\int_{0}^{{\frac{\pi }{2}}} {\frac{\cos \phi }{{\sin \phi }}} d\beta = - 2\int_{0}^{{\frac{\pi }{2}}} {\frac{1}{{\sqrt {\left( \frac{a}{b} \right)^{2} + \cos^{2} \beta } }}} d\cos \beta \hfill \\ = 2\int_{0}^{1} {\frac{1}{{\sqrt {\left( \frac{a}{b} \right)^{2} + x^{2} } }}} dx = 2\left[ {\ln (x + \sqrt {\left( \frac{a}{b} \right)^{2} + x^{2} } )} \right]_{0}^{1} = 2\ln \frac{b + 1}{a}. \hfill \\ \end{gathered}$$

(50)

So

$$2\int_{0}^{{\frac{\pi }{2}}} {\frac{\cos \phi }{{\sin \phi }}} d\beta = 2\ln \frac{\sin \alpha + 1}{{\cos \alpha }}.$$

(51)

Substitute Eq. (51) into Eq. (47), the formula of ${F}_{c2}$ and ${F}_{n}$ can be obtained:

$$\begin{gathered} F_{{{\text{c}}2}} = \pi N\sin \theta \sin \alpha + \pi S_{1} \cos \theta \sin \alpha - 2N\cos \theta \sin \alpha \ln \frac{\sin \alpha + 1}{{\cos \alpha }} + 2S_{1} \sin \theta \sin \alpha \ln \frac{\sin \alpha + 1}{{\cos \alpha }} \hfill \\ F_{n} = \pi N\sin \theta \cos \alpha + \pi S_{1} \cos \theta \cos \alpha - 2N\cos \theta \cos \alpha \ln \frac{\sin \alpha + 1}{{\cos \alpha }} + 2S_{1} \sin \theta \cos \alpha \ln \frac{\sin \alpha + 1}{{\cos \alpha }}. \hfill \\ \end{gathered}$$

(52)

Appendix B: Derivation of governing equation of thermal stress

In this section, the governing equation of thermal stress, Eq. (19) is derived. Assuming that the temperature distribution inside the material is $T(x,y,z,t)$, the Hooke's law considering the thermal expansion can be expressed as:

$$\varepsilon_{ij} = \frac{1}{2G}\sigma_{ij} - \frac{v}{E}\Theta \delta_{ij} + \alpha \cdot \Delta T \cdot \delta_{ij} .$$

(53)

where, $v$ is Poisson’s ratio, $\alpha$ is the thermal expansion coefficient, $\Delta T=T\left(x,y,z,t\right)-{T}_{r}$, ${T}_{r}$ is the initial formation temperature, $G=\frac{E}{\left[2\left(1+v\right)\right]}$, $={\sigma }_{x}+{\sigma }_{y}+{\sigma }_{z}$

According to Eq. (53), the equation for stress expressed by strain is:

$$\sigma_{ij} = \lambda e\delta_{ij} + 2G\varepsilon_{ij} - \frac{E}{1 - 2v}\alpha \cdot \Delta T \cdot \delta_{ij} .$$

(54)

where, $e={\varepsilon }_{x}+{\varepsilon }_{y}+{\varepsilon }_{z}$ is volumetric strain,$\lambda =Ev/[(1+v)(1-2v)]$.

The thermoelastic equilibrium equation can be expressed as:

$$\sigma_{ij,j} + f_{i} = \rho \ddot{u}_{i} .$$

(55)

where, $\rho$ is density, ${\ddot{u}}_{i}(i=\mathrm{1,2},3)$ are the acceleration in the $x$,$y$, z directions, ${f}_{i}(i=\mathrm{1,2},3)$ are the body forces in the $x$,$y$, z directions.

The strain–displacement relationship can be expressed as:

$$\varepsilon_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right).$$

(56)

The bottom hole rock is assumed to be semi-infinite body. Thus, there is only deformation along the $Z$-axis, and no deformation along the $X$-axis and $Y$- axis, which can be expressed as:

$$w = w\left( {z,t} \right),\quad u = v = 0.$$

(57)

Substitute Eq. (57) into Eq. (56):

$$\varepsilon_{z} = \frac{\partial w}{{\partial z}},\quad \varepsilon_{x} = \varepsilon_{y} = \varepsilon_{xy} = \varepsilon_{yz} = \varepsilon_{zx} = 0.$$

(58)

Substitute Eq. (58) into Eq. (54):

$$\begin{gathered} \sigma_{z} = 2G\left( {\frac{1 - v}{{1 - 2v}}\varepsilon_{z} - \frac{1 + v}{{1 - 2v}}\alpha \cdot \Delta T} \right) \hfill \\ \sigma_{x} = \sigma_{y} = 2G\left( {\frac{v}{1 - 2v}\varepsilon_{z} - \frac{1 + v}{{1 - 2v}}\alpha \cdot \Delta T} \right). \hfill \\ \tau_{xy} = 0,\quad \tau_{yz} = 0,\quad \tau_{zx} = 0 \hfill \\ \end{gathered}$$

(59)

According to Eq. (59), the following equation can be obtained:

$$\varepsilon_{z} = \frac{\partial w}{{\partial z}} = \frac{1}{1 - v}\left[ {\frac{1 - 2v}{{2G}}\sigma_{z} \left( {z,t} \right) + \left( {1 + v} \right)\alpha \cdot \Delta T\left( {z,t} \right)} \right].$$

(60)

According to Eq. (55), the following equation can be obtained by ignoring the body force:

$$\frac{{\partial \sigma_{z} }}{\partial z} = \rho \frac{{\partial^{2} w}}{{\partial t^{2} }}.$$

(61)

Derivative of Eq. (61) with respect to z:

$$\frac{{\partial^{2} \sigma_{z} }}{{\partial z^{2} }} = \rho \frac{\partial }{{\partial {\text{z}}}}\left( {\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) = \rho \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\frac{\partial w}{{\partial {\text{z}}}}} \right).$$

(62)

Substitute Eq. (60) into Eq. (62), the governing equation of thermal stress can be expressed:

$$\frac{{\partial^{2} \sigma_{z} }}{{\partial z^{2} }} - \frac{{\rho \left( {1 - 2v} \right)}}{{2G\left( {1 - v} \right)}}\frac{{\partial^{2} \sigma_{z} }}{{\partial t^{2} }} = \frac{{\rho \cdot \alpha \left( {1 + v} \right)}}{1 - v}\frac{{\partial^{2} T}}{{\partial t^{2} }}.$$

(63)