Determination of Fracture Toughness of Mode I Fractures from Three-Point Bending Tests at Elevated Confining Pressures

Abstract

Fracture toughness is one of the key parameters for the characterization of brittle rock fracturing. Yet, constraints on it mainly rest on measurements performed at ambient pressure, although rock fracturing frequently occurs at elevated pressures even in geotechnical applications. To address the lack of a generally accepted evaluation procedure for tests at elevated pressure we explored the conditions for initiation and propagation of mode I fractures in samples subjected to bending at elevated pressure by numerical modeling and analytical considerations of the involved angular moments. We derived an evaluation procedure and applied it to experimental observations for specimens with either a chevron or a single-edge notch of four different rocks (a granite, a limestone, a marble and a sandstone) subjected to three-point bending at confining pressures up to 30 MPa. Two sealing methods were considered. Specimens were either varnished or jacketed by a rubber tube, differing in whether pressure is allowed to build up inside the pre-fabricated notch or not, respectively. Irrespective of notch geometry and sealing method, the determined toughness values increase significantly with confining pressure. The apparent toughness determined for jacketed specimens is, however, larger than that for varnished specimens, for which toughness seems to reach a plateau with increasing pressure. The similarity of the pressure dependence of the toughness determined for varnished, i.e., uniformly pressurized, samples with that of other physical properties suggests that it is controlled by the closure of pre-existing micro-cracks; the absence of pressure dependence beyond some tens of MPa suggests that non-linearity effects may not be as severe at depths beyond a few kilometers as previously discussed. Our study points to the necessity of resolving numerical issues associated with compressed fractures and of further improving experimental facilities for the determination of fracture toughness at elevated pressure.

1 Introduction

Fracture mechanics has proven to be a useful tool for the investigation of brittle failure of rocks during natural processes or anthropogenic activities, such as tunnelling or mining (e.g., Scavia 1990, Rubin 1993, Kemeny 2003). The critical stress intensity or fracture toughness is the central material parameter of fracture mechanics, which describes the resistance to fracture initiation distinguishing between the three fundamental loading modes, tensile (mode I), in-plane shear (mode II), or anti-plane shear (mode III), and mixed mode.

At ambient pressure, fracture toughness testing has been extensively carried out using a variety of methods, including several suggested by the International Society for Rock Mechanics, ISRM (e.g., Ouchterlony 1988, Backers and Stephansson 2012, Kuruppu et al. 2014), transferrable also to testing at elevated temperature (e.g., Chandler et al. 2017). However, an extension of these methods to testing at elevated confining pressure is neither commonly accepted nor straightforward. Previous experimental studies (Schmidt and Huddle 1977; Winter 1983; Müller 1986; Al-Shayea et al. 2000; Vásárhelyi 2001; Balme et al. 2004; Funatsu et al. 2004, 2014; Backers 2005; Sato and Hashida 2006; Kataoka et al. 2017) indicate that fracture toughness increases with confining pressure, with the relation reported to be either linear (e.g., Al-Shayea et al. 2000) or logarithmic (e.g., Funatsu et al. 2004). Yet, no noticeable increase in fracture toughness with pressure has also been reported (Müller 1986; Balme et al. 2004). The different observations may be a result of different experimental procedures and data reduction, the latter actually not fully disclosed in cases.

The sealing method significantly influences the toughness results (Winter 1983; Kataoka et al. 2017). At elevated confining pressure, sealing of samples is necessary to prevent penetration of the confining medium into the samples’ pore space. In previous studies, specimens were coated with urethane (Schmidt and Huddle 1977), silicone (Funatsu et al. 2004, 2014; Kataoka et al. 2017), varnish (Winter 1983), or glossy spray paint (Al-Shayea et al. 2000) exhibiting variable suitability for rocks with high porosity. Specimens were also jacketed with flexible materials, e.g., rubber tubes (Müller 1986; Vásárhelyi 2001), scotch tape (Al-Shayea et al. 2000; Funatsu et al. 2004) or copper sheets (Kataoka et al. 2017), covering the notch such that confining fluid does not penetrate it. The sealing methods thus correspond to different scenarios regarding the difference between pressure acting on the bulk sample and in the notch.

When the confining fluid can penetrate the notch, the toughness can be determined using the methods developed for testing at ambient pressure. Uniform hydrostatic loading of the sample’s entire surface does not change the stress distribution during bending compared to that at ambient pressure. Only, the mechanical state of the sample material potentially changes, as micro-crack closure may, for example, occur due to the application of elevated pressure. Penetration of a newly formed crack section by the confining medium may, however, be delayed depending on bending rate and viscosity of the confining fluid. A further problem may arise regarding the newly formed fracture surfaces during crack growth; the confining-pressure fluid may penetrate the interior of porous or micro-fractured samples to cause build-up of a pore pressure of unknown magnitude.

Application of confining pressure to a sample with a covered notch leads to a pressure difference between the sample’s bulk surface and the surface of the notch and thus the stress distribution in these samples differs from that in samples tested at ambient pressure, requiring a different evaluation strategy for toughness. Only in two such cases, the evaluation procedure was actually documented (Funatsu et al. 2004; Kataoka et al. 2017). Using single-edge-crack round bar specimens, Funatsu et al. (2004) determined toughness by two strategies. On the one hand, they corrected the measured force by subtracting the force required to open the notch—against the external pressure—back to the initial state based on separately recording crack-opening displacement curves for bending and pressurization. On the other hand, they subjected the specimen to several unloading–reloading cycles to obtain the crack evolution as a function of applied stress-intensity factor, the K-resistance curve. Yet, the toughness determined from the former strategy is consistently smaller than that from the latter and the differences become larger with confining pressure. Kataoka et al. (2017) used numerical simulations to obtain a correction factor that is linearly proportional to confining pressure to amend the standard procedure for semi-circular bend tests. The two studies only employed specimens with a single-edge crack. It is unclear how to reconcile the results from the two studies; consensus on the evaluation method for tests at elevated pressure has yet to be reached.

We present an evaluation method for three-point bending tests performed on notched round bar specimens subjected to elevated confining pressure. To determine mode I-fracture toughness, we combined an analysis of the moments induced by bending and pressurization and numerical modeling of the stress-intensity factors related to the two loading modes. In the accompanying experiments, we explored two sealing methods, jacketing the specimens with rubber tubes and spraying the specimens’ surfaces with varnish, and investigated samples of four different rocks prepared with either single-edge cracks (SEC) or chevron-edge notches (CEN).

2 Background

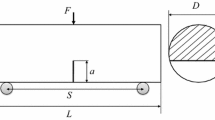
The mode I stress intensity, K_I, on a crack with length $a$, that extended from a pre-fabricated notch of length ${a_{\text{0}}}$ due to three-point bending of a sample with diameter D using a support span S, depends on current load $F$ according to

$$K_{{\text{I}}}^{{\text{b}}} (F,\alpha ,\alpha_{0} ) = \frac{S}{4D}Y^{{\text{b}}} (\alpha ,\alpha_{0} )\frac{F}{{D^{1.5} }},$$

(1)

where $Y^{{\text{b}}}$ denotes the dimensionless stress-intensity factor depending on the dimensionless crack length $\alpha = a/D$ and the superscript “b” indicates bending. Ouchterlony (1981, 1984) determined the dimensionless stress-intensity factors

$$Y_{{{\text{CEN}}}}^{{\text{b}}} \left( {\alpha ,\alpha_{0} } \right) = 0.6006\left( {C_{0} \frac{{C_{1} \alpha^{1.5} + C_{2} \alpha^{5.5} + C_{3} \alpha^{15} }}{{\alpha - \alpha_{0} }}} \right)^{0.5} ,$$

(2)

with

$$\begin{aligned} C_{0} & = 15.672\left( {1.455 + 1.796\alpha_{0} + 4.308\alpha_{0}^{2} } \right) \\ C_{1} & = 2.5\left( {6.675 - 12.275\alpha_{0} + 3.639\alpha_{0}^{2} } \right) \\ C_{2} & = 6.5\left( {40.2 - 75.3\alpha_{0} + 71.2\alpha_{0}^{2} } \right) \\ C_{3} & = 16\left( {393 - 394\alpha_{0} - 394\alpha_{0}^{2} } \right), \\ \end{aligned}$$

and

$$Y_{{{\text{SEC}}}}^{{\text{b}}} \left( {\alpha = \alpha_{0} } \right) = 12.7527\alpha_{0}^{0.5} \frac{{\left( {1 + 19.646\alpha_{0}^{4.5} } \right)^{0.5} }}{{\left( {1 - \alpha_{0} } \right)^{0.25} }},$$

(3)

for chevron-edge notches (CEN, Fig. 1) and single-edge cracks (SEC), respectively. Relations (2) and (3) are valid for $S/D = 3.33$; (2) holds for an initial dimensionless crack length $\alpha_{0} = a_{0} /D$ in the range from 0.05 to 0.25. The two sample types differ regarding the evolution in crack geometry. While the current crack geometry depends on the initial notch depth for CEN samples, it does not for SEC samples, for which any initial configuration can also be considered a current one, i.e., $\alpha = \alpha_{0}$ in (3), assuming that the stress concentration at the notch tip is identical to that at a fracture tip.

Fig. 1

Geometry of a single-edge crack (SEC) and b chevron-edge notch (CEN)

The condition for crack initiation, the failure criterion of linear-elastic fracture mechanics, reads $K_{{\text{I}}} = K_{{{\text{IC}}}}$ for mode I-fractures, i.e., the actual stress intensity reaches a critical (subscript C) value, the fracture toughness $K_{{{\text{IC}}}}$ of the material. According to (1), the critical force required to initiate a crack and propagate it quasi-statically is thus inversely proportional to the dimensionless stress-intensity factor

$$F_{{\text{C}}} (K_{{{\text{IC}}}} ,\Delta p,\alpha ,\alpha_{0} ) = \frac{{4D^{2.5} K_{{{\text{IC}}}} }}{S}\frac{1}{{Y^{{\text{b}}} (\alpha ,\alpha_{0} )}}.$$

(4)

The determination of $K_{{{\text{IC}}}}$ relies on the ability to associate the current crack geometry (specified by α) with a well-determined point on the load curve. The stress intensity for CEN (2) exhibits a minimum. According to the critical load relation (4), a minimum in stress intensity means that the crack extends at increasing loads up to a peak, after which further crack growth occurs at a decreasing load. Fracturing initiates at the “sharp” tip of a CEN before the load reaches its maximum. Ouchterlony (1988) approximated the minima of (2) by polynomial regression as

$$Y_{{\text{CEN,min}}}^{{\text{b}}} \left( {\alpha_{0} } \right) = 7.34 + 28.6\alpha_{0} + 39.4\alpha_{0}^{2} .$$

(5)

Fracture toughness is evaluated using (5) in (1) and $F_{{\text{C}}} = F_{\max }$, corresponding to level I estimation (Ouchterlony 1988).

For SEC specimens, the stress intensity (3) increases monotonically, indicating that the stress intensity at the tip of a growing crack continuously increases and that once initiated, propagating the crack requires decreasing force according to (4). Thus, critical conditions are reached at the maximum in load and the initial notch length a₀ also constitutes the critical crack length. Accordingly, fracture toughness is determined using (3) evaluated for ($F_{{\text{C}}} = F_{\max }$, $\alpha = \alpha_{0}$) in (1) (Ouchterlony 1981). When evaluated for a notch in a cylindrical sample aligned with the loading point, the results of Hua et al. (1982), obtained modeling rectangular specimens with a SEC using a finite-element method, give

$$K_{{{\text{IC}}}} = \frac{{M_{{\text{C}}} }}{{D^{2.5} }}\frac{4}{\pi }f_{{\text{b}}} \left( {\alpha_{0} } \right),$$

(6)

where $f_{{\text{b}}}$ is a non-dimensional function of initial dimensionless crack length α₀ ranging from 0.2 to 0.7. Using the critical moment $M_{{\text{C}}} = F_{\max } S/4$, we find that $Y_{{\text{SEC,C(Hua)}}}^{{\text{b}}} = 4f_{{\text{b}}} \left( {\alpha_{0} } \right)/\pi$ when (6) is cast in the notation of (1). Hua et al.’s (1982) dimensionless stress-intensity factors, $Y_{{\text{SEC,C}}}^{{\text{b}}}$, closely agree with Ouchterlony’s (1981) up to $\alpha$ of about 0.5, above which Ouchterlony’s (1981) function exceeds the results by Hua et al. (1982) up to 10% (Fig. 2).

Fig. 2

Comparison of dimensionless stress-intensity factor $Y_{{{\text{SEC}}}}^{{\text{b}}}$ obtained from numerical simulation with that of Ouchterlony (1981) and Hua et al. (1982) for SEC. The dimensionless stress-intensity function $Y_{\text{CEN}}^{\text{b}}$ from Ouchterlony (1984) is also included to highlight the lack of convergence of the functions for the two geometries for large α

The commonly applied evaluation of bending tests entails known problems. The dimensionless stress intensity $Y_{{{\text{CEN}}}}^{{\text{b}}}$ (2) was approximated by Ouchterlony (1984) from results gained for SEC. Dai et al. (2015) showed from numerical simulations that the crack front is curved rather than straight as assumed by Ouchterlony (1984), indicating that the approximation (2) for $Y_{{{\text{CEN}}}}^{{\text{b}}}$ is not accurate but these authors did not provide an improved expression. Furthermore, the dimensionless stress-intensity factors of CEN and SEC do not coincide when crack growth extends to the point where the two geometries do not differ anymore. While this discrepancy does not pose an immediate problem for evaluation of tests at ambient pressure that entails only crack lengths below this point of coincidence, it may for tests at elevated pressure. Therefore, we derived the dimensionless stress-intensity functions $Y^{{\text{b}}}$ for CEN and SEC specimens from numerical simulations using the contour-integral method.

3 Numerical Simulations

To the best of our knowledge, a comprehensive analysis of the stress-intensity distribution in samples subjected to confining pressure, considering different notch geometries and sealing procedures, has not been presented so far. We, therefore, performed numerical modeling of typical three-point bending configurations accounting for a difference between the confining pressure and the pressure applied to the notch flanks, not considered by the conventional analysis. We exploit the superposition principle of stress intensities

$$K_{{\text{I}}}^{{{\text{tot}}}} = K_{{\text{I}}}^{{\text{b}}} + K_{{\text{I}}}^{{\text{p}}} ,$$

(7)

valid in the framework of linear elastic fracture mechanics and investigate separately the bending (superscript b) and the subjection of all of the sample but the notch to pressure, i.e., differential pressurization (superscript p). Re-investigating the stress concentrations associated with simple bending has the two purposes of (a) assessing the validity of the assumptions involved in the conventional analysis and the empirical fits, and (b) providing a consistently derived set of stress-intensity functions for bending and differential pressurization.

3.1 Set-Up of Numerical Model

We employed the finite-element software ABAQUS (Abaqus 2019) to determine the stress-intensity factor around the crack tip by the J-integral method, embedded in the software. The numerical set up followed previous studies that used the same method but for different sample geometries (i.e., Tutluoglu and Keles 2011, Kuruppu et al. 2014). We took advantage of the sample symmetry, i.e., only half of the specimen was modeled (Fig. 3a) with the same dimensions as that of the samples used in the experiments (Table 2). All numerical samples had the same set of elastic parameters (Young’s modulus of 20 GPa, Poisson’s ratio of 0.28), relying on the result of Tutluoglu and Keles (2011) that these parameters have insignificant effects on the obtained stress-intensity factor. The support and the piston were modeled as analytic rigid shells. The contact between either support or top piston and specimen was realized with a constraint and a surface-to-surface contact.

Fig. 3

a Schematic illustration of crack treatment for CEN and SEC. The red circle indicates the integrations contour. b Typical finite element mesh used for half of a CEN specimen with a close-up view of the crack tip. The red semi-circle of radius 0.4 mm represents the nodes used for numerical determination of the J-integral.

The entire sample was first meshed using hexahedral elements with a global mesh size of 1.1 mm, i.e., less than 4% of the diameter. Mesh refinement was then conducted in a circular region around the crack front using wedge elements (Fig. 3a). The crack itself is modeled as an internal surface without width (Fig. 3b, c). For SEC samples, we refrained from actually modeling the notch with finite width, because exploratory calculations showed that it did not affect the stress intensity at the crack tip. The radius of the circular region around the crack front was 0.4 mm. A radius larger than 0.5 mm, i.e., half the notch width specified by Ouchterlony (1988), leads to problems with mesh generation. The dimensionless crack length $\alpha$ was prescribed and constant in a simulation; crack growth was implicitly modeled by a sequence of simulations with $\alpha$ varying from typically 0.1 (depending on the initial notch length for CEN) to 0.9 in steps of 0.033. The stress-intensity factor was computed from the defined contour integrals as the average of all nodes along the crack front. Our approach did not allow us to calculate the stress intensity at the initial Chevron notches but only for cracks that extended from them to a length exceeding the chosen integration radius.

We did not investigate the mesh dependence of the results at depth. Exploratory calculations with a two times coarser mesh yield dimensionless stress intensity that was smaller than for the smaller mesh size, less than 5% for $\alpha < 0.8$ but around 20% for $\alpha > 0.8$, differences slightly increasing with increasing $\alpha_{0}$. The run duration increases by about a factor of 4, when the mesh size is reduced by half; the performed calculations took several minutes with a standard desktop computer. The agreement of our results with the numerical study by Wei et al. (2016) (see 3.2) suggested that the chosen mesh size constitutes a good compromise between precision and calculation time, considering the need to perform several hundred calculations.

3.2 Simulations for Uniformly Pressurized Samples

We simulated the three-point bending of SEC and CEN specimens at uniform pressure (i.e., either ambient pressure or elevated pressure acting on the entire surface including the notch). For SEC specimens with $\alpha$ ranging from 0.2 to 0.7, our simulated dimensionless stress-intensity factors are smaller by less than 12% than the ones from Ouchterlony (1981) and from Hua et al. (1982) (Fig. 2). Deviations larger than 20% occur for α larger than approximately 0.7, i.e., well outside the range of 0.2–0.6 in $\alpha$ that Ouchterlony (1981) used for polynomial fitting of experimental results.

The simulated dimensionless stress intensity of bended CEN specimens (for initial dimensionless crack lengths $\alpha_{0}$ of 0.05, 0.067, 0.083, 0.15 and 0.25) exhibits general agreement with those predicted by (2) (Fig. 4). Our numerical simulations, however, give smaller values and correspondingly smaller minima in $Y_{{{\text{CEN}}}}^{{\text{b}}}$ than (2) by up to 10% (Fig. 5) for $\alpha$ smaller than about 0.5. Similar results (~ 12% less than Ouchetrlony’s) have also been reported by Wei et al. (2016), who also used the contour-integral method. The simulation results exceed the predictions of (2) for $\alpha$ larger than about 0.5, actually eliminating the discrepancy between stress intensities inherent in Ouchterlony’s approximations for crack lengths, for which SEC and CEN geometries do not differ anymore, i.e., 0.55, 0.63 and 0.71 for $\alpha_{0} = 0.05$, 0.15 and 0.25, respectively. The simulated dimensionless stress-intensity factors for CEN and SEC specimens agree well (within 2% difference) for such large crack lengths (Fig. 4), but agree less well (around 15% difference) at $\alpha$ larger than 0.87 that is close to the limit of 0.9, beyond which meshing was not possible. High-order fitting is necessary to capture the simulation data (Fig. 4b, Appendix 2); extrapolation may thus be problematic. For example, our $Y_{{{\text{CEN}}}}^{{\text{b}}}$ at the initial alpha-values is finite in contrast to the infinite values of Ouchterlony (1984)’s expression (2). Therefore, caution should be exercised when extrapolating the polynomial fits beyond the explored range of α-values from around 0.1 to 0.9.

Fig. 4

Comparison of dimensionless stress-intensity factors obtained from numerical simulation a with that of Ouchterlony (1981, 1984) and b with polynomial fits of 7th order for CEN and 8th order for SEC (for clarity simulation data for $\alpha_{0} = 0.067$ and 0.083 are not shown). Cross-markers indicate the crack length where the two notch geometries do not differ any more

Fig. 5

Comparison of a dimensionless crack length α_min corresponding to the minima in stress intensity obtained from our numerical modeling and Ouchterlony (1984)’s polynomial fit (B2), and of b the corresponding $Y_{{\text{CEN,min}}}^{{\text{b}}}$ values (legend applies to both plots)

3.3 Simulations for Finite Pressure Differences

3.3.1 Stress-Intensity Function

In contrast to a uniform pressure applied to the entire sample surface, a difference in pressure on the notch flanks and the outer sample surfaces causes a heterogeneous stress distribution in the sample even without bending (Fig. 6a, b). In analogy to the approach chosen by Ouchterlony (1988) for the dimensionless stress-intensity factor at ambient pressure (1), we formulate the stress-intensity contribution by the difference between the pressure acting on the bulk specimen and that acting on the notch flanks, $\Delta p$, as

$$K_{{\text{I}}}^{{\text{p}}} (\Delta p,\alpha_{0} ,\alpha ) = D^{0.5} Y^{{\text{p}}} (\alpha_{0} ,\alpha )\Delta p.$$

(8)

Fig. 6

Stress distributions of jacketed samples subjected to 10 MPa confining pressure with a CEN ($\alpha_{0} = 0.05$) and b SEC from numerical simulations at $\alpha = 0.5$. The zoom-ins show a central axial section through the crack tip. Contours indicate the von Mises stress in kPa. Samples experience only pressurization but no bending; the rigid shell (simulating the loading piston) is necessary to ensure stability

The negative stress intensities $Y^{{\text{p}}}$ decrease with increasing crack length for both SEC and CEN specimens but for CEN with the largest initial notch depths, for which a weak maximum is observed at small crack lengths. The results for the two notch types converge at large crack lengths (Fig. 7). The stress intensity $Y^{{\text{p}}}$ of CEN specimens decreases with increasing $\alpha_{0}$ and is consistently smaller than the intensity for SEC specimens. In general, the curves of $Y^{{\text{p}}}$ resemble that of $Y^{{\text{b}}}$ but are inverted due to their negative sign.

Fig. 7

Comparison of the dimensionless stress intensity induced by a pressure difference obtained from numerical simulations with the ones based on moment analysis (9) for SEC and CEN (at indicated $\alpha_{0}$)

Considering the moment induced by the pressure difference acting on the area of the crack surface, $A$, with a lever arm, $x_{{{\text{Lever}}}}$, determined by the distance from the center of $A$ to the loading point (Appendix 3), the two stress intensities for pressurization and bending should obey

$$Y_{{}}^{{\text{p}}} (\alpha ,\alpha_{0} ) = - \frac{{A(\alpha ,\alpha_{0} )x_{{{\text{lever}}}} (\alpha ,\alpha_{0} )}}{{D^{3} }}Y^{b} (\alpha ,\alpha_{0} ).$$

(9)

A semi-analytical result, $Y_{{\text{semi-analytical}}}^{{\text{p}}}$, can be derived from (9) using the numerically obtained stress intensity for bending at uniform pressure $Y_{{{\text{numerical}}}}^{{\text{b}}}$ for SEC and CEN, respectively. For SEC specimens, these semi-analytical dimensionless stress intensities $Y_{{\text{SEC,semi-analytical}}}^{{\text{p}}}$ exhibit general agreement with the results from the numerical simulations, $Y_{{\text{SEC, numerical}}}^{{\text{p}}}$, but differences increase with increasing $\alpha$ (Fig. 7). The difference is more pronounced for CEN than for SEC specimens. The discrepancy between $Y_{{\text{semi-analytical}}}^{{\text{p}}}$ and $Y_{{{\text{numerical}}}}^{{\text{p}}}$ may reflect limitations of the assumption of fixed sample geometry underlying the analytical moment calculation.

3.3.2 Critical Force

Assuming that superposition of stress-intensity factors is valid, the total stress intensity becomes

$$K_{{\text{I}}}^{{{\text{tot}}}} (F,\Delta p,\alpha ,\alpha_{0} ) = \frac{S}{{4D^{2.5} }}Y^{{\text{b}}} (\alpha ,\alpha_{0} )F + D^{0.5} Y^{{\text{p}}} (\alpha ,\alpha_{0} )\Delta p,$$

(10)

where $Y^{{\text{b}}}$ and $Y^{{\text{p}}}$ denote the dimensionless stress intensities associated with bending and differential pressurization, respectively. When the pressure applied to the notch surface equals the confining pressure, $Y^{{\text{p}}}$ is 0, as applies to varnished specimens. When the pressure applied to the notch surface is smaller than the confining pressure, then $Y^{{\text{p}}} < 0$, as is the case for jacketed specimens, counterbalancing the stress intensity due to bending. Using the result of the moment analysis (9) in (10) gives

$$K_{{\text{I}}}^{{{\text{tot}}}} (F,\Delta p,\alpha ,\alpha_{0} ) = \underbrace {{\frac{S}{{4D^{2.5} }}Y^{{\text{b}}} (\alpha ,\alpha_{0} )F}}_{{ = K_{{\text{I}}}^{{\text{b}}} }}\left( {1 - 4\frac{{x_{{{\text{lever}}}} (\alpha ,\alpha_{0} )}}{S}\frac{{A(\alpha ,\alpha_{0} )\Delta p}}{F}} \right),$$

(11)

showing how an increasing differential pressurization reduces the total stress intensity compared to that from the bending alone.

The condition for crack initiation and quasi-static propagation is $K_{{\text{I}}}^{{{\text{tot}}}} = K_{{{\text{IC}}}}$. Inverting (11), the critical force for crack extension depends on current crack length according to

$$F_{{\text{C}}} (K_{{{\text{IC}}}} ,\Delta p,\alpha ,\alpha_{0} ) = \frac{4}{S}\left( {\frac{{D^{2.5} }}{{Y^{{\text{b}}} (\alpha ,\alpha_{0} )}}K_{{{\text{IC}}}} + A(\alpha ,\alpha_{0} )x_{{{\text{lever}}}} (\alpha ,\alpha_{0} )\Delta p} \right),$$

(12)

which when normalized by the force $F_{\lim } = \pi D^{3} \Delta p/(2S)$ gained from moment analysis for a fully broken sample (Appendix 3) becomes

$$\frac{{F_{{\text{C}}} (K_{{{\text{IC}}}} ,\Delta p,\alpha ,\alpha_{0} )}}{{F_{{{\text{lim}}}} }} = \frac{{8K_{{{\text{IC}}}} }}{{\pi D^{0.5} \Delta p}}\frac{1}{{Y^{{\text{b}}} (\alpha ,\alpha_{0} )}} + \underbrace {{\frac{{A(\alpha ,\alpha_{0} )}}{{A_{{\text{s}}} }}\frac{{2x_{{{\text{lever}}}} (\alpha ,\alpha_{0} )}}{D}}}_{{\text{purely geometrical summand}}}.$$

(13)

Here, $A_{{\text{s}}} = \pi D^{2} /4$ denotes the cross-sectional area of the cylindrical samples. Equation (13) demonstrates that with increasing pressure difference $\Delta p$ the effect of fracture toughness on force decreases, i.e., the resolution for the determination of toughness vanishes. The purely geometrical summand monotonically increases with crack length for either notch geometry (Fig. 8); at infinitely small crack lengths, it assumes a finite value of 0.5 and zero for CEN and for SEC, respectively.

Fig. 8

Geometrical factor, defined as a product of relative fracked area and relative lever length (13), as a function of current dimensionless crack length

We determined the evolution of the normalized critical force with crack length for alternative choices of stress-intensity functions (Fig. 9). On the one hand, we relied on the semi-analytical results based on the moment analysis (9) using $Y^{{\text{b}}}$ from either our numerical simulations or Ouchterlony’s expressions (2) and (3). On the other hand, the force was calculated using exclusively our numerical results for, $Y^{{\text{b}}}$ and $Y^{{\text{p}}}$; then the second term in (13) becomes $- 8{{Y^{{\text{p}}} (\alpha ,\alpha_{0} )} \mathord{\left/ {\vphantom {{Y^{{\text{p}}} (\alpha ,\alpha_{0} )} {\left[ {\pi Y^{{\text{b}}} (\alpha ,\alpha_{0} )} \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {\pi Y^{{\text{b}}} (\alpha ,\alpha_{0} )} \right]}}$.

Fig. 9

Critical force normalized by the limiting force from moment analysis versus current dimensionless crack length at ${{8K_{{{\text{IC}}}} } \mathord{\left/ {\vphantom {{8K_{{{\text{IC}}}} } {\left( {\pi D^{0.5} \Delta p} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\pi D^{0.5} \Delta p} \right)}} = 37.5, \, 9.4$ for a CEN and b SEC and at ${{8K_{{{\text{IC}}}} } \mathord{\left/ {\vphantom {{8K_{{{\text{IC}}}} } {\left( {\pi D^{0.5} \Delta p} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\pi D^{0.5} \Delta p} \right)}} = 3.7, \, 0.7$ for c CEN and d SEC. Legend applies to all subfigures. Curves are exemplified at $\alpha_{0} = 0.07$ for CEN. Red crosses indicate maxima of the curves generated for moment analysis with $Y_{{{\text{numerical}}}}^{{\text{b}}}$, the polynomial fit to numerical simulations performed at $\alpha$ from about 0.1–0.9. Thus, the curves rely on extrapolating the polynomial fits to α values larger than 0.9 (indiated by dotted red lines) for all specimens and smaller than about 0.1 for SEC specimens. The solid and dashed vertical red lines indicate the notch depths used in the accompanying experiments

Since the dimensionless toughness–pressurization ratio ${{8K_{{{\text{IC}}}} } \mathord{\left/ {\vphantom {{8K_{{{\text{IC}}}} } {\left( {\pi D^{0.5} \Delta p} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\pi D^{0.5} \Delta p} \right)}}$ controls the contribution of fracture toughness to the result of a bending experiment on a differentially pressurized sample, we modeled normalized forces (13) for values of 0.7, 3.7, 9.4, and 37.5 corresponding to $\Delta p = 50$, 10, 4, and 1 MPa for $K_{{{\text{IC}}}} = 2.55$ MPa m^0.5. When calculated according to the relation based on moment analysis (13), the critical load and its dependence on current crack length do not strongly depend on the choice of the stress-intensity function for bending, irrespective of notch geometry or the level of pressurization. The similarity between the critical load determined from $Y_{{{\text{numerical}}}}^{{\text{b}}}$ and that from $Y_{{{\text{Ouchterlony}}}}^{{\text{b}}}$ lends support to the validity of the extrapolation. The critical loads relying exclusively on the numerically determined stress-intensity functions for bending and differential pressurization differ significantly from that relying on the moment-analysis results, the more the smaller the dimensionless toughness-pressurization ratio. The purely numerical results also do not obey the physical limit $F_{{\text{C}}} = F_{{{\text{lim}}}}$ for fully broken samples; this mismatch does not seem to be solely a consequence of extrapolating the numerical results beyond the range of crack lengths, for which they were determined, i.e., $\alpha < 0.9$.

When the dimensionless toughness–pressurization ratio is large (i.e., Fig. 9a, b), toughness dominates and the normalized critical force versus crack length curves resemble that at ambient pressure, i.e., monotonically decreasing load for SEC specimens and an evident peak for CEN specimens occurring at an $\alpha$ value comparable to $\alpha_{\min }$-values for bending alone (Fig. 5). As the toughness–pressurization ratio decreases, the normalized critical load calculated according to the moment analysis decreases leading to little load variations (less than about 10%) for $\alpha > 0.1$ for CEN specimens (Fig. 9c) and a minimum load at $\alpha < 0.2$ for SEC specimens (Fig. 9d). For either notch geometry, a weak (local) maximum in force (i.e., $F_{{\text{C}}} > F_{{{\text{lim}}}}$) may occur at large dimensionless crack lengths and toughness–pressurization ratios between about 1 and 10 (Fig. 9c, d). The curves mimic the purely geometrical summand at the smallest considered ratios but for small crack lengths < 0.1, where SEC samples exhibit the mentioned minimum in load owing to the counterbalancing effect of the stress-intensity function.

4 Three-Point-Bending Tests

4.1 Experimental Procedure

4.1.1 Testing Apparatus

For testing at ambient pressure, a conventional three-point-bending test apparatus was used that comprises a loading frame equipped with a hydraulic cylinder (loading capacity up to 109 kN), a load cell (range of 0–2 kN, accuracy of 0.1%) and a displacement transducer (range of 0–20 mm, accuracy of 0.1%). For the testing at elevated pressure, a custom-designed apparatus (Fig. 10) was used, composed of a vessel and a loading system (Winter 1983; Müller 1986). The vessel accommodates a specimen immersed in pressurized oil that applies the confining pressure. The loading system includes a piston with a self-made internal load cell (Fig. 10c compare Heard and Carter 1968, distance measurement based on change in capacitance, accuracy ± 10 N) attached to a hydraulic cylinder (capacity up to 13 kN) and an externally mounted displacement transducer (range of 0–20 mm, accuracy 0.1%). The advancement of the piston of the hydraulic cylinder was servo-hydraulically controlled using the displacement transducer as feedback signal. A nominal piston velocity of 1 × 10^–3 mm/s, comparable to the ones used in previous studies (Al-Shayea et al. 2000; Funatsu et al. 2004, 2014), was applied in all tests, constituting an upper bound for the actual load-point velocity because we did not correct for system deformation. It took several minutes to reach the maximum in force for the chosen piston velocity.

Fig. 10

a Assembly of testing apparatus consisted of a displacement transducer (1), a hydraulic cylinder (2), a differential pressure transducer (3), pressure transducers of upper (4) and lower (5) chamber of the hydraulic cylinder and a pressure vessel (6); b specimen holder with sealing plug and c self-made internal load cell. (7) hollow steel cylinder, (8) seal, (9) brass housing, (10) connecting stem, (11) counterplate for capacitor, (12) device for initial adjustment of the two capacitor plates.

4.1.2 Sample Material and Preparation

Four different rocks were used, Padang granite, Carrara marble, Solnhofen limestone, and Bentheim sandstone, that differ in composition and grain size (Table 1). To constrain sample-to-sample variability, we measured bulk density relying on geometric volume determination, connected porosity by water imbibition, and axial P-wave velocity by ultrasound transmission (Table 1). In the majority of cases, the standard deviations of the performed measurements exceed the uncertainty indicating that the blocks used for sampling are not fully homogeneous on the spatial scale of the specimens.

Table 1 Mineralogical composition, grain size, bulk density, p-wave velocity of dry samples, and porosity of rocks used

Cylindrical specimens with single-edge crack (SEC) and chevron-edge notch (CEN) were prepared from the blocks according to the suggested methods of ISRM (Ouchterlony 1988, 1989) (Table 2). Drilled and sawn to length, specimens were dried in an oven at 60 °C for at least 48 h before they were either varnished or jacketed to prevent the confining medium (oil) from penetrating them. For varnished specimens, the varnish was sprayed on the entire sample surface. Thus, oil can flow into the notch and all sample surfaces are equally pressurized.

Table 2 Geometrical specifications of samples and notches

Jacketed specimens were sealed by a rubber tube and two metal end plugs. The three load points were strengthened with copper plates (Fig. 11). The notch was filled with Teflon to prevent the jacket from failing due to the missing support upon application of confining pressure. Limited penetration of the jacket into the notch and deformation of the Teflon filler may exert some pressure against the notch flanks. We did not find evidence for substantial flow of the Teflon filler, e.g., limited penetration of Teflon into the pores on the notch flanks of GBS samples and none into the fractures emanating from the notch, after experiments, although the highest applied confining pressures probably reach or exceed the strength of Teflon. A rough but conservative estimate indicates that the combined effect of reduced area experiencing the pressure difference due to jacket intrusion into the notch and counter-pressure associated with flow of Teflon reduces the nominal pressure difference by at most 10 % at the onset of tests on jacketed samples, with the reduction diminishing with progressing fracture growth.

Fig. 11

Assembly of jacketed specimen, a notch (in Bentheim sandstone) filled with Teflon, b loading point and supporting points reinforced with copper plates, underlying holes cut into the jacket sealed by glue

4.2 Results

4.2.1 Load–Displacement Curves

Tests at ambient pressure exhibit the typical pronounced maxima followed by extended softening with absolute loads of SEC samples exceeding those of CEN samples (Fig. 12a). For tests performed at elevated pressure, the load–displacement curves differ significantly for the two sealing methods. For all rocks, the shape as well as the reproducibility of the load–displacement curves are similar to the ones of Solnhofen limestone (SL) used as examples in Fig. 12. For varnished specimens tested at elevated pressure, the load–displacement curves show an approximately linear increase before the maximum force is reached (Fig. 12b), at which the specimens fail as marked by the sudden loss of load-bearing capacity indicating unstable crack growth. In contrast, the curves for jacketed specimens exhibit a yield-like change from the initial slope to modest displacement hardening irrespective of notch geometry (Fig. 12a). Only after an extended section of slightly pressure-dependent hardening, rapid drops in the bending force occurred that indicate total specimen failure. The load–displacement curves for CEN and SEC specimens exhibit similar shapes for tests at elevated pressure, but loads recorded for SEC samples tend to be higher or reach higher maxima than the ones for CEN samples.

Fig. 12

Load–displacement curves for a varnished specimens and b jacketed specimens of Solnhofen limestone at indicated confining pressures. Geometrical specifications of samples and notches are given in Table 2. The circles in a indicate total loss of load-bearing capacity of varnished samples. The tests on jacketed samples in cases also reached the point of total failure but in a number of cases had to be terminated when the capacity of the piston was reached. (The examples shown here for samples of Solnhofen limestone are qualitatively representative of the curves recorded for all rocks.)

The maximum load recorded in tests on jacketed samples seldom exceeds the limiting force, $F_{\lim }$, gained from moment analysis for a fully broken sample (Fig. 13). In the light of the modeling results for the normalized critical load based on the moment analysis (Fig. 9), this observation correlates well with the modest hardening observed. Not all of the load–displacement curves exhibiting hardening actually could reach the limiting force, because some tests had to be terminated when the capacity of the loading piston was exhausted, before the sample was fully broken.

Fig. 13

Comparison of the limiting force (obtained from moment analysis, Appendix 3, corresponding to fully broken samples) with maximum force recorded in the experiments on jacketed specimens. Error bars have a comparable size to the symbol size and are not shown

We could not successfully perform tests on varnished samples of Bentheim sandstone; samples were full soaked by oil after pressurization. For the samples of the other rock varieties, we did not observe oil penetration, neither on the varnished surfaces nor on the newly created fracture surfaces. For the latter, however, wiping of the oil is not as definite as it is for the varnished surfaces. Samples tested with a jacket did not show any oil penetration after the tests.

4.2.2 Procedure for Toughness Determination

Our determination of fracture toughness depends on the pressure difference. The recorded load–displacement curve is the pivotal input for toughness determination and is influenced greatly by whether a sample is uniformly pressurized or not (Fig. 12). For the varnished samples that experienced uniform pressurization, we apply the same procedure as for tests at ambient pressure, i.e., level I estimation using the maximum recorded load either with the initial depth of the SEC or the minimum relation (5) for CEN.

The presented numerical simulations and moment analysis (Sect. 3.3) guided our analysis strategy for jacketed samples. We discard the fully numerical solutions that, in addition to the problem of not obeying the expected limits, predict weakening for SEC samples at all toughness–pressurization ratios in contrast to the experimental observations. The relation between normalized critical load and crack length (Sect. 3.3.2) reveals that the increase in load with crack length becomes modest when the toughness–pressurization ratio becomes small. Interpreting the evolution of recorded loads, i.e., strengthening vs. softening, is not straightforward since we recorded only the axial displacement, while the theoretical analysis refers to current dimensionless crack length. Yet, forces recorded for jacketed samples do not significantly exceed the limiting force deduced from the moment analysis of a fully broken sample, and thus the force–displacement curves fall in the category with a toughness–pressurization ratio ${{8K_{{{\text{IC}}}} } \mathord{\left/ {\vphantom {{8K_{{{\text{IC}}}} } {\left( {\pi D^{0.5} \Delta p} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\pi D^{0.5} \Delta p} \right)}}$ of less than about 10 according to the results of our numerical modeling (Fig. 9). This upper limit for the toughness–pressurization ratio corresponds to an upper limit for toughness of about $K_{{{\text{IC}}}} < 7{\text{ MPa m}}^{0.5}$.

The modest variation in load observed for the tests conducted on jacketed samples at elevated confining pressures exacerbates the challenge to determine the force corresponding to crack initiation or any other known crack length. In the light of the used initial notch depths and the resemblance between the F_C–α curves calculated using (13) and the recorded force–displacement curves, we suggest to use the yield point in the force–displacement curves as an estimate of the critical load for toughness evaluation. We determined the load corresponding to “yield”, denoted $F_{{\text{y}}}$, as the intersection of the two tangents fitted to recorded curves at their points of largest slope and largest curvature (Fig. 21).

The initial notch depth of our SEC samples of 0.2 slightly exceeds the crack lengths, at which the minimum in load is predicted by the modeling based on moment analysis and thus the chosen $F_{{\text{y}}}$ likely overestimates the force at crack initiation corresponding to an overestimation of K_IC using $\left( {F_{C} = F_{y} ,\alpha_{C} { = }\alpha_{0} } \right)$. The methodological advantage, exploited for the analysis of tests on CEN specimen performed at uniform pressure, of associating the peak load to a known crack length gradually vanishes with a decreasing toughness–pressurization ratio eliminating the pronounced load maxima. The nominally infinite stress intensity $Y_{{{\text{CEN}}}}^{{\text{b}}}$ for the initial notch depth $\alpha_{0}$ characteristic of CEN samples hinders a toughness determination from crack initiation. We determined K_IC at $\left( {F_{{\text{C}}} { = }F_{y} , \, \alpha { = }\alpha_{\min }^{0} } \right),$ where $\alpha_{\min }^{0}$ denotes the crack length at minimum dimensionless stress-intensity factor for uniform pressurization.

When a maximum in force, i.e., $F_{{{\text{lim}}}} < F_{{{\text{max}}}}$, occurred, an alternative evaluation point is $\left( {F_{{\text{C}}} { = }F_{{{\text{max}}}} , \, \alpha_{C} { = }\alpha_{\min }^{{\text{p}}} } \right)$ with $\alpha_{\min }^{{\text{p}}}$ determined as the minimum of (11) for an experimental pair of $F_{{{\text{max}}}}$ and $\Delta p$. The few experiments, for which K_IC could be evaluated at $\left( {F_{{\text{C}}} { = }F_{{{\text{max}}}} , \, \alpha_{C} { = }\alpha_{\min }^{{\text{p}}} } \right)$ and either $\left( {F_{{\text{C}}} { = }F_{{\text{y}}} , \, \alpha_{C} { = }\alpha_{\min }^{0} } \right)$ for CEN specimens or $\left( {F_{{\text{C}}} { = }F_{{\text{y}}} , \, \alpha_{C} { = }\alpha_{0} } \right)$ for SEC specimens, indicate fair agreement but for Bentheim sandstone (Fig. 14).

Fig. 14

Comparison of K_IC evaluated at $\left( {F_{{{\text{max}}}} , \, \alpha_{\min }^{{\text{p}}} } \right)$ and $\left( {F_{{\text{y}}} , \, \alpha_{0} } \right)$ for SEC specimens or $\left( {F_{{\text{y}}} , \, \alpha_{\min }^{0} } \right)$ for CEN specimens for tests where $F_{\max } > F_{{\text{y}}}$. Filled marker: SEC specimens; open marker: CEN specimens. Vertical error bars have a comparable size to the symbol size and are not shown

4.2.3 Fracture Toughness

The K_IC determined for uniformly pressurized SEC and CEN specimens, evaluated at $\left( {F_{{{\text{max}}}} , \, \alpha_{0} } \right)$ and $\left( {F_{{{\text{max}}}} , \, \alpha_{\min } } \right)$, respectively, agree well (Fig. 15, Table 3). For either Padang granite or Bentheim sandstone, repeated tests at ambient pressure indicate that sample-to-sample variability may account for a variability in toughness of up to 13%. While toughness values seem to scatter evenly around the SEC–CEN identity line for Padang granite, toughness values for Bentheim sandstone indicate that toughness derived for SEC samples is higher than that for CEN samples. A conservative upper bound for the uncertainty in yield force of 5% converts to an uncertainty in the K_IC for jacketed specimens of 15%, slightly less than the observed 20% variability in fracture toughness associated with sample-to-sample variability (Table 3).

Fig. 15

Comparison of toughness from specimens with CEN or SEC tested at uniform pressure. Error bars have a comparable size to the symbol size and are not shown

Table 3 Testing conditions and the associated toughness parameters

For all tested rocks, the fracture toughness deduced for uniformly pressurized samples significantly increases with confining pressure, reaching 2–5 times the toughness at ambient pressure depending on rock type. For Solnhofen limestone and Carrara marble, the toughness values appear to reach a plateau at about 20–30 MPa. The apparent reversal of the trend for Padang granite at 30 MPa hinges on a single data point, mandating further substantiation.

The increase in toughness with increasing pressure for jacketed samples is even more pronounced than the one for varnished ones. For example, the toughness of jacketed CM samples with SEC increases from 0.7 MPa m^0.5 at ambient pressure up to approximately 4.4 MPa m^0.5 at 20 MPa in comparison to approximately 2.9 MPa m^0.5 at 20 MPa for varnished specimens. The relation between toughness and confining pressure is fairly linear, but for samples of Bentheim sandstone with CEN, exhibiting little difference in the linearity between rock varieties (Fig. 16).

Fig. 16

Fracture toughness K_IC as a function of confining pressure for samples of a Solnhofen limestone, b Carrara marble, c Padang granite, and d Bentheim sandstone with indicated notch geometry and sealing procedure. Error bars indicate the uncertainty in $F_{y}$ estimation for jacketed specimens and the uncertainty in the measurements of load (± 10 N) and initial notch depth (± 0.1 mm) for varnished specimens. Error bars of varnished specimens have a comparable size to the symbol size and are not shown

5 Discussion

5.1 How Well is Fracture Toughness Constrained from Ambient Pressure Experiments?

Our toughness results gained at ambient pressure agree for samples with the two different notch types (Fig. 15). The scatter of results around the identity line suggests that the differences reflect sample-to-sample variability rather than severe methodological issues. At face value, SEC samples of Bentheim sandstone seem to yield a larger toughness than CEN samples though, which contrasts the report by Khan and Al-Shayea (2000), who determined K_IC at ambient pressure from Brazilian disk specimens with either CEN or SEC and concluded that K_IC is approximately 15% larger for CEN specimens than for SEC specimens. However, the reported difference might be a result of Khan and Al-Shayea (2000) applying the same dimensionless stress-intensity function for the two notch types.

Local damage caused by preparing the notches may bias the determination of fracture toughness of rocks. Microcracks surrounding the notch may result from mechanical and/or thermal interaction of saw blade and specimen. Since the evaluation procedures for samples with SEC and CEN differ regarding the association of crack state and actual load (for SEC samples, nucleation of the crack at the initial notch is used to derive fracture toughness, while a state of advanced crack growth is considered for CEN samples, see Sect. 2) the general agreement in K_IC determined for SEC and CEN specimens found in our study suggests that damage induced by preparation plays a subordinate role. This general agreement also suggests that the numerically determined stress-intensity functions for bending account consistently for the geometrical differences of the two notch types. Consistency, likely however, does not say much about accuracy, whose assessment will need a comprehensive examination of the dependence of the numerical results for the stress-intensity functions on details of the calculation, in particular meshing.

5.2 The Dependence of Fracture Toughness on Uniform Pressure

In principle, the experiments on varnished samples at elevated confining pressure constrain the dependence of fracture toughness on pressure. Fracture toughness of SEC-samples is determined from the maximum in force and the initial notch depth because crack initiation requires the highest stress intensity. For CEN samples, the critical crack length associated with the force maximum used for evaluation of toughness is only reached after some crack extension. Thus, the K_IC determined for varnished CEN specimens may be biased by a delayed penetration of the confining medium into the growing crack or by oil penetrating the rock from the newly formed fracture surfaces. Delayed penetration constitutes a loading situation similar to that of the differential pressurization experienced by the jacketed samples. Severe penetration into the pore space of the rocks may lead to build-up of a pore pressure of unknown magnitude. Previous experiments indicated that an effective pressure law holds for toughness; when the confining fluid penetrated cracks and pores right from the start of an experiment (samples without any jacketing), an effect of absolute pressure on K_IC was not observed (Balme et al. 2004; Müller 1986). We address whether penetration issues affect our results for toughness by comparing the results for the two notch geometries and estimating penetration times.

A difference in K_IC between CEN specimens and SEC specimens would be an indicator for issues related to oil penetration into the propagating crack and/or the surrounding rock material. As for ambient pressure, we, however, do not see a systematic difference between fracture toughness of varnished samples with different notch geometry tested at elevated pressure (Fig. 15). The scatter exhibited by the limited observations may well represent sample-to-sample variability.

Using Darcy’s law, the time it takes to penetrate a conduit or a permeable material by a distance $l_{{{\text{pene}}}}$ can be approximated by $t_{{{\text{pene}}}} \approx l_{{{\text{pene}}}}^{2} \eta_{{\text{f}}} /(k\Delta p)$, where $k$ denotes permeability and $\eta_{{\text{f}}}$ fluid viscosity (here ~ 0.03 Pa.s for the used hydraulic oil). With constraints for fracture permeability of $k_{{\text{F}}} \approx 10^{ - 13... - 11} {\text{ m}}^{{2}}$ (Padang granite, Hernández-Castañeda 2020) and for rock permeability of $k_{{{\text{CM}}}} \approx 3 \cdot 10^{ - 22} {\text{ m}}^{{2}}$ and $k_{{{\text{SL}}}} \approx 3 \cdot 10^{ - 19} {\text{ m}}^{{2}}$ (Fischer and Paterson 1992), and $k_{{{\text{PG}}}} \approx 10^{ - 19... - 18} {\text{ m}}^{{2}}$ (Hernández-Castañeda 2020), we estimate that penetration of 1 mm takes less than 0.03 s for a fracture but more than 3000 s for the most permeable of the three fairly dense rocks. Bentheim sandstone exhibits a permeability of $k_{{{\text{BS}}}} \ge 10^{ - 13} {\text{ m}}^{{2}}$ (Vajdova et al. 2004), i.e., at the lower end of fracture permeability, and we, thus, estimate a penetration time of less than 0.03 s, too. In the light of the typical duration of our experiments of 100 s, the calculations predict that penetration into the fracture is instantaneous, as it is for Bentheim sandstone, but penetration into Padang granite, Solnhofen limestone, and Carrara marble is insignificant. The analysis neglects a potential increase in permeability near the fracture tip associated with a brittle process zone and capillary effects that, however, likely hinder penetration of the oil into the rocks’ pores. Our qualitative observations on samples retrieved from the vessel agree well with the predictions and we infer that oil penetration does not affect fracture toughness determination on the varnished CEN samples of the fairly impermeable rocks.

The general increase of K_IC with confining pressure (Fig. 16) is in qualitative agreement with previous studies; specifically for limestones either a linear (e.g., Schmidt and Huddle 1977, e.g., Al-Shayea et al. 2000) or logarithmic (Perkins and Krech 1966) relation between toughness and pressure was reported (Fig. 17). The fracture toughness K_IC for varnished specimens with SEC and CEN of Solnhofen limestone is comparable with that of Lueders limestone and falls within the range bounded by data for Indiana limestone of Schmidt and Huddle (1977) and Roegiers and Zhao (1991) (Fig. 17). This quantitative comparison is, however, hampered by different analysis procedures suggested (Müller 1986; Funatsu et al. 2004; Kataoka et al. 2017) or the lack of clear information on evaluation methods.

Fig. 17

Comparison of fracture toughness for various limestones and its relation to pressure observed in this study and previously reported in the literature. IL Indiana limestone, LL Lueders limestone. Error bars of varnished specimens have a comparable size to the symbol size and are not shown

A variation in toughness with uniform pressure reflects a change in the state of the material induced by the pressurization. Rock samples typically contain pre-existing micro-cracks that are known to progressively close with increasing pressure (e.g., Bieniawski 1967, Wawersik and Brace 1971, Fortin et al. 2007). The observed pressure dependence of fracture toughness of varnished samples indeed resembles the evolution of other physical properties with confining pressure that lead to the notion of critical closing pressure for micro-cracks (Walsh 1965; Mavko and Nur 1978). For Solnhofen limestone and Carrara marble, the plateaus in fracture toughness are reached at about 20 and 30 MPa, agreeing with 20 MPa and ~ 30 MPa, at which significant crack closure in samples of these rocks were deduced from observations of P-wave velocity (Ahrens 2019) and from the evolution of elastic modulus (Sarout et al. 2017) with pressure, respectively. For Solnhofen limestone, however, the pressure, at which the plateau in fracture toughness of varnished samples is presumably reached, is a factor of two to three smaller than the values reported for “ultimate” critical crack-closure pressure from analyses of volumetric strain or ultrasonic P- and S-wave velocity (Baud et al. 2000; Ahrens 2019). The gradual changes in these properties demonstrate the presence of fractures with a range of geometrical properties. Extensive micromechanical modeling revealed the key role of aspect ratio for the pressure dependence of volumetric strain and ultrasonic velocity (Kachanov 1992; David and Zimmerman 2012). In contrast, Griffith’s fundamental concept for flaws under tension suggests that absolute length of pre-existing fractures is critical for fracture toughness. Lawn and Evans (1977) documented how spatial variability in stress, as applies to the bending in our tests, leads to a maximum in fracture length, for which the maximum stress intensity is reached. In this scenario, the diminishing effect on fracture toughness is exhausted once the fractures fulfilling this criterion are closed. While still other fractures may be open, their effect on fracture toughness would be less pronounced. Thus, the quantitative difference in critical closing pressures for the different physical properties likely simply reflects the difference in dominating aspect of fracture geometry and/or the characteristic length scale of stress heterogeneity in bending tests. Therefore, we suppose that tests on varnished specimens give the intrinsic pressure dependence of toughness as related to changes in microstructure with pressure, i.e., crack closure.

5.3 Is There An Effect of Differential Pressurization on Fracture Toughness?

Several issues are related to the tests on jacketed samples and their results. First of all, they may be biased by the deformation of the Teflon filler and the jacket penetration into the notch exerting a pressure on the—nominally unpressurized—fracture flanks and, thus, reducing the differential pressure difference. We did not find evidence for Teflon penetrating the newly formed cracks, though, meaning that the biasing effect evolves and gradually diminishes as cracks extend. A finite pressure on all or parts of the notch flanks leads to an overestimation of pressure difference and thus to an underestimation of $K_{{{\text{IC}}}}$, because a smaller $\Delta p$ leads to a smaller absolute value of $K_{{\text{I}}}^{{\text{p}}}$ (8), i.e., a smaller reduction of total stress intensity, and hence a larger toughness value according to (7). An overestimation of the pressure difference by 10% leads to an underestimation of actual fracture toughness by about 20% for CEN specimens and 5% for SEC specimens. This uncertainty related to the experimental set-up is, however, unlikely to be responsible for the observation that the K_IC values for jacketed SEC specimens seem to exceed systematically that for jacketed CEN specimens. The discrepancy rather indicates that the chosen evaluation procedure has its deficiencies, a suspicion supported by the absence of variation in K_IC values with rock type, for jacketed specimens, at stark contrast to the results for varnished samples (Fig. 16). The increase of toughness with pressure difference for jacketed specimens is linear with a slope of approximately 0.2 m^0.5 for all rocks investigated here, but for CEN samples of Bentheim sandstone, and also for Kimachi sandstone (Fig. 18). When the maximum loads recorded in tests differ little from the limiting force $F_{\lim }$, (11) automatically yields a linear relation between fracture toughness and pressure difference as long as it is evaluated for a fixed dimensionless crack length:

$$K_{{{\text{IC}}}}^{{{\text{app}}}} (F_{\lim } ,\Delta p,\alpha ,\alpha_{0} ) = \frac{{\pi D^{0.5} }}{8}Y^{{\text{b}}} (\alpha ,\alpha_{0} )\left( {1 - 8\frac{{x_{{{\text{lever}}}} (\alpha ,\alpha_{0} )A(\alpha ,\alpha_{0} )}}{{\pi D^{3} }}} \right)\Delta p.$$

(14)

Fig. 18

Comparison of fracture toughness for samples of Bentheim sandstone with indicated notch type (this study) and SEC-samples of Kimachi sandstone (Funatsu et al. 2004; Kataoka et al. 2017) and its relation to pressure. Lines are meant to help identifying groups of data

In these cases, the linear relation between “apparent toughness” and pressure difference is an artifact that arises due to the diminishing contribution of toughness to the total load with increasing confining pressure on jacketed samples. To determine toughness from tests on jacketed samples that do not exhibit significant load maxima reliably, better criteria for the association of current load and current crack length had to be developed than the ones used here.

In addition to the problems regarding the relation between load and crack length, the correction of stress intensity for the counter-bending associated with pressurization of jacketed samples remains a matter of discussion. Kataoka et al. (2017) determined the $K_{{{\text{IC}}}}$ from three-point bending tests on semi-circular specimens with SEC notches sealed by jacketing up to a confining pressure of 4 MPa. In their evaluation, they used superposition of stress-intensity factors, in which the one induced by pressure difference was based on numerical modeling, and toughness was determined using initial crack length and load at yielding. Funatsu et al. (2004) determined the $K_{{{\text{IC}}}}$ from jacketed SEC specimens and corrected the measured force by simply deducting a force that is required to open the notch—against the external pressure—back to the initial state. The correction associated with pressurization determined by Kataoka et al. (2017) and Funatsu et al. (2004) correspond to linear reductions with coefficients of − 0.15 m^0.5 and − 0.26 m^0.5, respectively, possibly explaining the quantitative difference between their fracture toughness values (Fig. 18). Our coefficients of − 0.13 m^0.5 from numerical simulation and − 0.10 m^0.5 from the semi-analytical results are closer to the one of Kataoka et al. (2017).

5.4 Implications

Non-linear effects lead to an apparent toughness when described by linear elastic fracture mechanics; furthermore, toughness depends on the size of the fracture and the loading configuration for non-linear behavior (e.g., Rubin 1993). Toughness values determined for a non-linear material relying on linear-elastic fracture mechanics are “effective or equivalent” ones in the sense that they correspond to that of a hypothetical linear material that would withstand the same maximum load using the same test configuration. Pressure sensitivity of the physical properties of rocks is a frequent and well-documented expression of non-linear elastic behavior and is commonly attributed to the existence of micro-cracks (Walsh 1965; Mavko and Nur 1978; David and Zimmerman 2012). The potentially large bias between true and equivalent toughness is critically relevant for quantitative analyses of fluid-driven fractures in fundamental science (e.g., earthquake mechanics and magma transport) and industry applications (e.g., hydro-fracturing). For both fields, we face depths of a few km and more associated with mean stresses of 100 MPa and more, exceeding the range currently explored by experiments. It is, thus, crucial to substantiate the indication of our test results that toughness loses its sensitivity to pressure already at pressures of tens of MPa. The similarity between the pressure dependence of toughness observed for varnished samples and that of other physical rock properties indicates that they share micro-crack closure as the underlying micromechanical mechanism. Diminishing pressure sensitivity translates to vanishing non-linearity with depth; thus, the commonly applied linear treatment may actually be valid for applications at several kilometre depth and beyond but with toughness values increased compared to that determined at ambient pressure. If true at all, a dependence of toughness on differential pressurization may, for example, favor episodic growth of hydraulically driven fractures, when rapid growth causes a significant drop of the fluid pressure or in the extreme case of a “dry” crack trip (e.g., Ishida et al. 2004; Shimizu et al. 2011).

The significant dependence of $K_{{{\text{IC}}}}$ observed for all rocks when uniformly pressurized (a factor of 2–4 increase in the range of investigated pressure, Fig. 16) hints at a potential shortcoming of fracture-mechanics-based modeling of experimental results from deformation tests at elevated confining pressure, e.g., micromechanical modeling of triaxial deformation tests (e.g., Ashby and Sammis 1990), using $K_{{{\text{IC}}}}$ determined at ambient pressure. An increase in fracture toughness with pressure increases the problem of these models in explaining the diminishing strengthening effect of confining pressure, expressed for example by a decrease in the coefficient of internal friction (see review by Lockner 1995). The key strength parameter of fracture mechanical models is the ratio of fracture toughness and the square root of the length of the failure controlling, pre-existing micro-cracks, i.e., $K_{{{\text{IC}}}} /\sqrt c$. Thus, our results suggest that these models tentatively underestimate crack length $c$, when employing fracture toughness determined at ambient pressure. While it is debatable whether fracture toughness of individual minerals or of aggregates, as determined here, should be used in these models for triaxial compressive strength, the aggregate values are relevant for the propagation of fluid-pressure-driven tensile fractures during borehole stimulation. Such nominally purely tensile hydro-fractures propagate in the direction perpendicular to the least principal stress and their growth characteristics exhibit a switch from a “strength controlled” to a “viscous-dissipation controlled” regime with increasing fracture length (Detournay 2004). Estimates of fracture lengths, at which this transition occurs, may need re-evaluation; a higher fracture toughness extends the regime of “strength control” to larger length.

The fracture-mechanics-based micromechanical models for triaxial compressive strength rest on the concept that deviatoric compressive loading leads to local tension and, thus, constitute the reason for the focus on experimental determination of characteristics of mode I failures. When the “local” scale of the stress field reaches the grain scale of rocks, mineral anisotropy, variability of elastic properties of the rock-forming minerals, and other imperfections, such as pores and fluid inclusions, may perturb local stresses and/or crack paths. Similarly, the expected stabilization of tensile cracks with increasing pressure likely leads to fracture planes with curvature on a range of scales, again associated with heterogeneities, in rock formations obviously not restricted to the grain scale. Such phenomena require the consideration of mixed-mode fractures that pose a challenge for experimental approaches and reliable data evaluation.

6 Conclusions

We investigated the fracture toughness for tensile (mode I) fractures by numerical modeling and three-point bending tests on notched round-bar specimens subjected to different pressurization scenarios. Numerical simulations and experiments were performed on specimens with either a Chevron-edge notch (CEN) or single-edge crack (SEC) subjected to either uniform pressure or a difference between the pressure applied to the outer sample surfaces and that acting on the notch, resulting from sample jacketing. Our analysis of the latter rests on superposition of stress-intensity factors induced by the bending force and the pressure difference. In addition to the numerical analysis, we accounted for the pressure difference by a semi-analytical solution resting on a moment analysis, highlighting toughness–pressurization ratio as the central scaling parameter of experiments that employ differential pressurization.

The toughness of specimens of four rocks, Padang granite (PG), Solnhofen limestone (SL), Carrara marble (CM) and Bentheim sandstone (BS), pressurized up to 30 MPa increases significantly with confining pressure. The pressure dependence for varnished specimens seems to reflect the gradual closure of micro-cracks with pressure, i.e., the less the number of pre-existing micro-cracks, the growing fracture can exploit the higher the toughness. The strengthening effect is exhausted when pre-existing cracks are closed at elevated pressure leading to a plateau in toughness. We conclude that the toughness determined for varnished specimens represents an intrinsic, yet state-dependent material property. Unstable crack growth from either notch type is an aspect of our tests on varnished samples that should receive further attention in the future. While it is plausible that due to the combination of an external displacement sensor and the rather compliant internal load cell, the stored elastic energy exceeds the fracture energy, a detailed analysis may provide further constraints on the stress-intensity functions.

The toughness determined for jacketed specimens appears to be insensitive to rock type, tends to exceed that of varnished ones, and exhibits an approximately linear increase with differential pressure. The performed moment analysis indicates that such a linear relation results as an “artifact” of the decreasing contribution of toughness to the total recorded force.

The numerically determined dimensionless stress-intensity factors for uniform pressure give comparable toughness for specimens with either CEN or SEC experimentally tested at uniform pressure. Yet, for differential pressurization, the predictions of the superposed stress-intensity functions for bending and pressurization do not comply with the limits from the moment analysis and we, thus, have to question their reliability. We suspect that appropriate modeling of a crack under compression constitutes the core challenge.

Since critical applications of fracture propagation in geoscience refer to depths of several kilometer and probably involve differential pressurization, it is crucial to ensure that experimental techniques permit to subject samples to pressures of some hundred MPa, be it uniformly or differentially, and to improve analysis methods, probably requiring in-depth evaluation of numerical determination of stress-intensity factors. The use of SEC samples with short initial notch depth is most promising for resolving toughness at high differential pressure, because this sample geometry ensures the highest possible contribution of the toughness to the total recorded load. Our results for uniformly pressurized samples suggest that non-linearity may cease with increasing depth, possibly reducing or eliminating the effects of fracture size and loading configuration on effective toughness.

Appendices

Appendix 1: Tabulated Test Results

See Table 3.

Appendix 2: Polynomial Fits for Y from Numerical Simulations

The polynomial forms of the stress intensities Y obtained from our numerical simulations (Figs. 4, 5) read:

$$\begin{aligned} Y_{{{\text{SEC}}}}^{{\text{b}}} & = {27479}{\text{.47}}\alpha_{0}^{8} - {83743}{\text{.94}}\alpha_{0}^{7} + {104065}{\text{.15}}\alpha_{0}^{6} - {66380}{\text{.20}}\alpha_{0}^{5} \\ & \quad + {22475}{\text{.14}}\alpha_{0}^{4} - {3529}{\text{.19}}\alpha_{0}^{3} + {74}{\text{.56}}\alpha_{0}^{2} + {51}{\text{.75}}\alpha_{0} \\ \end{aligned}$$

(15)

for SEC and

$$\begin{aligned} Y_{{{\text{CEN}}}}^{{\text{b}}} & = \left( \begin{gathered} - 5.5207e + 08\alpha_{0}^{4} + 4.4926e + 07\alpha_{0}^{3} + 2.1882e + 07\alpha_{0}^{2} \hfill \\ - 2.6488e + 06\alpha_{0} + 9.2523e + 04 \hfill \\ \end{gathered} \right)\alpha^{7} \\ & \quad + \left( \begin{gathered} 2.4274e + 09\alpha_{0}^{4} - 4.4569e + 08\alpha_{0}^{3} - 2.016e + 07\alpha_{0}^{2} \hfill \\ + 5.2050e + 06\alpha_{0} - 2.0745e + 05 \hfill \\ \end{gathered} \right)\alpha^{6} \\ & \quad + \left( \begin{gathered} - 4.2951e + 09\alpha_{0}^{4} + 1.0578e + 09\alpha_{0}^{3} - 4.67661e + 07\alpha_{0}^{2} \hfill \\ - 2.2198e + 06\alpha_{0} + 1.5815e + 05 \hfill \\ \end{gathered} \right)\alpha^{5} \\ & \quad + \left( \begin{gathered} 4.0120e + 09\alpha_{0}^{4} - 1.1494e + 09\alpha_{0}^{3} + 9.3053e + 07\alpha_{0}^{2} \hfill \\ - 2.1215e + 06\alpha_{0} - 2.5589e + 05 \hfill \\ \end{gathered} \right)\alpha^{4} \\ & \quad + \left( \begin{gathered} - 2.1526e + 09\alpha_{0}^{4} + 6.7301e + 08\alpha_{0}^{3} - 6.7219e + 07\alpha_{0}^{2} \hfill \\ + 2.6110e + 06\alpha_{0} - 2.8261e + 04 \hfill \\ \end{gathered} \right)\alpha^{3} \\ & \quad + \left( \begin{gathered} 6.6705e + 08\alpha_{0}^{4} - 2.1978e + 08\alpha_{0}^{3} + 2.4299e + 07\alpha_{0}^{2} \hfill \\ - 1.1053e + 06\alpha_{0} + 1.7092e + 04 \hfill \\ \end{gathered} \right)\alpha^{2} \\ & \quad + \left( \begin{gathered} - 1.1108e + 08\alpha_{0}^{4} + 3.7746e + 07\alpha_{0}^{3} - 4.4062e + 06\alpha_{0}^{2} \hfill \\ + 2.1483e + 05\alpha_{0} - 3.6993e + 03 \hfill \\ \end{gathered} \right)\alpha \\ & \quad + \left( \begin{gathered} 7.7071e + 06\alpha_{0}^{4} - 2.6627e + 06\alpha_{0}^{3} + 3.2002e + 05\alpha_{0}^{2} \hfill \\ - 1.6109e + 04\alpha_{0} + 297.1065 \hfill \\ \end{gathered} \right) \\ \end{aligned}$$

(16)

for CEN with α₀ in the range from 0.05 to 0.25 (the same range as in the ISRM-suggested method for testing at ambient pressure Ouchterlony 1988), applicable to α in the range from α₀ to $\alpha_{\lim }$ given as:

$$\alpha_{\lim } = \frac{1}{2}\left( {0.5 + \alpha_{0} + \sqrt {0.25 + \alpha_{0} - \alpha_{0}^{2} } } \right).$$

(17)

At α larger than $\alpha_{\lim }$, SEC and CEN geometries do not differ anymore and $Y_{{{\text{CEN}}}}^{{\text{b}}}$ is given by $Y_{{{\text{SEC}}}}^{{\text{b}}}$. The polynomial fitting to the 7th order is necessary to capture the minima in the curves. The high-order fitting may cause instability at points outside the fitting range. Therefore, caution should be exercised when extrapolating (15) and (16) beyond the explored range of α-values from around 0.1 (exact value depending on α₀) to 0.9.

Appendix 3: Moment Analysis

A moment analysis is performed based on the assumption that the deflection is small and the geometry of the specimen does not change significantly, which is usually the case for the three-point bending of rock specimens. The moment by differential pressure, Δp, depends on α according to:

$$M_{{\text{p}}} (\alpha ,\alpha_{0} ,\Delta p) = A(\alpha ,\alpha_{0} )x_{{{\text{Lever}}}} (\alpha ,\alpha_{0} )\Delta p,$$

(18)

where

$$A_{{{\text{SEC}}}} = \left\{ {\begin{array}{*{20}c} {\frac{{{\text{arc}}\cos \left( {1 - 2\alpha } \right)D^{2} }}{4} - D\sqrt {\alpha - \alpha^{2} } \left( {\frac{D}{2} - \alpha D} \right)} \\ {\frac{{\pi D^{2} }}{4} - \left[ {\frac{{{\text{arc}}\cos \left( {2\alpha - 1} \right)D^{2} }}{4} - D\sqrt {\alpha - \alpha^{2} } \left( {\frac{D}{2} - \alpha D} \right)} \right]} \\ \end{array} \begin{array}{*{20}c} {{\text{for }}\alpha \le \frac{1}{2}} \\ {{\text{ for }}\alpha \ge \frac{1}{2}} \\ \end{array} } \right.$$

(19)

$$x_{{\text{Lever,SEC}}} = \left\{ {\frac{{D^{3} \sqrt {\alpha - \alpha^{2} } }}{6} - \frac{{4D^{2} \left( {\alpha - \alpha^{2} } \right)}}{3}\left( {\frac{D}{2} - \alpha D} \right)^{2} } \right\}\frac{1}{{A_{{{\text{SEC}}}} }} + \frac{D}{2},$$

(20)

for SEC and

$$A_{{{\text{CEN}}}} = \left\{ {\begin{array}{*{20}c} \begin{gathered} \frac{{\pi D^{2} }}{4} - \left\{ \begin{gathered} \frac{{\arcsin \left( {\frac{{2L_{{{\text{CEN}}}} }}{D}} \right)D^{2} }}{4} - \hfill \\ L_{{{\text{CEN}}}} \left[ {L_{{{\text{CEN}}}} - \frac{D}{2} + D\alpha_{0} } \right] \hfill \\ \end{gathered} \right\} - L_{{{\text{CEN}}}}^{2} + D^{2} \left( {\alpha - \alpha_{0} } \right)^{2} \hfill \\ \hfill \\ \end{gathered} & {{\text{for }}\left( {\alpha - \alpha_{0} } \right)D \le L_{{{\text{CEN}}}} } \\ {A_{{{\text{SEC}}}} } & {{\text{for }}\left( {\alpha - \alpha_{0} } \right)D \ge L_{{{\text{CEN}}}} } \\ \end{array} } \right.$$

(21)

$$x_{{\text{Lever,CEN}}} = \left\{ {\begin{array}{*{20}c} \begin{gathered} \left[ \begin{gathered} \frac{{D^{2} L_{{{\text{CEN}}}} }}{6} - \frac{{2L_{{{\text{CEN}}}} }}{3}\left( {L_{{{\text{CEN}}}} - \frac{D}{2} + \alpha_{0} D} \right)^{2} \hfill \\ + L_{{{\text{CEN}}}}^{2} \left( {\frac{D}{2} - \alpha_{0} D - \frac{{2L_{{{\text{CEN}}}} }}{{3}}} \right) \hfill \\ - D^{2} \left( {\alpha - \alpha_{0} } \right)^{2} \left( {\frac{D}{2} - \frac{{2D\left( {\alpha - \alpha_{0} } \right)}}{3} - \alpha_{0} D} \right) \hfill \\ \end{gathered} \right]\frac{1}{{A_{{{\text{CEN}}}} }} + \frac{D}{2} \hfill \\ \hfill \\ \end{gathered} & {{\text{for }}\left( {\alpha - \alpha_{0} } \right)D \le L_{{{\text{CEN}}}} } \\ {\left[ {\frac{{D^{2} L_{{{\text{CEN}}}} }}{6} - \frac{{2L_{{{\text{CEN}}}} }}{3}\left( {L_{{{\text{CEN}}}} - \alpha_{0} D} \right)^{2} } \right]\frac{1}{{A_{{{\text{CEN}}}} }} + \frac{D}{2}} & {{\text{for }}\left( {\alpha - \alpha_{0} } \right)D \ge L_{{{\text{CEN}}}} } \\ \end{array} } \right.$$

(22)

$$L_{{{\text{CEN}}}} = \frac{D}{2}\left( {0.5 + \alpha_{0} + \sqrt {0.25 + \alpha_{0} - \alpha_{0}^{2} } } \right),$$

(23)

for CEN (Fig. 19).

Fig. 19

Geometrical parameters underlying the calculation of bending moment

The moment with respect to the loading point induced by differential pressure can be calculated when the specimen geometry and the pressure difference are known (Fig. 20). The limiting force in the figure corresponds to a fully broken sample at α = 1, and is calculated irrespective of notch geometry as:

$$F_{{{\text{lim}}}} = \frac{{\pi D^{3} \Delta p}}{2S}.$$

(24)

Fig. 20

Moment induced by a pressure difference of 10 MPa as a function of dimensionless crack length

Appendix 4: Determination of Yield Force

The load–displacement curve is fitted using polynomials. Then, the two points corresponding to maximum slope and maximum radius of curvature (inverse of the second derivative) are determined. The yield force $F_{{\text{y}}}$ is then determined as the intersection of the tangents to the two points. It is noted that when data are badly recorded, i.e., an irregular zigzag curve, $F_{{\text{y}}}$ may not be determined correctly due to polynomial fitting. Therefore, a visual monitoring of this automatic procedure to find $F_{{\text{y}}}$.shall be conducted (Fig. 21).

Fig. 21

An example for the determination of the yield force F_y