Estimation of Fracture Orientation Distributions from a Sampling Window Based on Geometric Probabilistic Method

Abstract

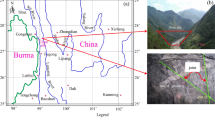
Accurate orientation distributions are crucial to generating a reliable discrete fracture network (DFN) model for rock mass, while conventional one-dimensional (1D) and two-dimensional (2D) observation data have significant sampling bias. The study proposes a complete analytical method for estimating the orientation distributions of three-dimensional (3D) fractures in rock mass in conjunction with trace statistics in a sampling window, which is suitable for most continuous distributions by reducing the sampling bias. Traces are divided into three categories to derive the geometric probabilistic relationships between 2D trace statistics and 3D fracture orientation distributions. The moment estimation, number estimation, and normalization error functions are derived, and the distribution parameters are determined by minimizing the total error function. The proposed method is compared with the Terzaghi family methods and validated by multiple sets of stochastic fracture networks with different orientation distributions and sampling windows generated by the Monte Carlo method. The results indicate that the estimated continuous orientation distributions subjected to the error functions from a large single sampling window are well matched with the true distributions after removing the number estimation error functions of trace samples fewer than 20. Daxiagu tunnel is selected as a case study and the distributions estimated by the proposed method are more coincident with the field observation than those fitted by the orientations of the rock outcrops on the excavation face.

Appendices

Appendix A

Number of Dissecting Traces

The bottom area of the distribution space of the centers of fractures with $x \in (x,\;x + dx)$, $\gamma \in (\gamma ,\;\gamma + d\gamma )$, and $\varphi \in (\varphi ,\;\varphi + d\varphi )$, intersecting the rectangular infinitesimal with one censored end and one observable end, is the shadow area surrounded by the red line in Fig. 

Fig. 17

On the $uO^{\prime\prime}v$ coordinate plane, the distribution region of the centers of fractures intersecting the rectangular infinitesimal with one censored end and one observable end. Note that the solid and hollow circles represent the centers of fractures of the above type and the others, respectively. a $x < h(w)$. b $x \ge h(w)$

17. According to the relationship between the fracture diameter x and the height of the rectangular infinitesimal h(w), the bottom area is determined according to the following two situations.

(a) When $x < h(w)$, the shadow region boundary in the positive v-axis satisfies the following function in Fig. 17a.

$$v = \left\{ \begin{aligned}& \sqrt {\frac{{x^{2} }}{4} - u^{2} } ,{\text{ }} - \frac{x}{2} \le u < \frac{x}{2} \hfill \\ & 0,{\text{ }}\frac{x}{2} \le u < h(w) - \frac{x}{2} \hfill \\& \sqrt {\frac{{x^{2} }}{4} - \left[ {u - h(w)} \right]^{2} } ,{\text{ }}h(w) - \frac{x}{2} \le u \le h(w) + \frac{x}{2} \hfill \\ \end{aligned} \right.$$

(43)

The bottom area $dS_{D1}$ of the distribution space of the centers of fractures, intersecting the rectangular infinitesimal with one censored end and one observable end, is expressed as:

$$\begin{aligned} dS_{{D1}} =&\, 2\int_{{u = - x/2}}^{{u = h(w) + x/2}} {vdu} \cdot dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ) \hfill \\ &\,= 2\left\{ {\int_{{u = - x/2}}^{{u = x/2}} {\sqrt {\frac{{x^{2} }}{4} - u^{2} } } du + \int_{{u = h(w) - x/2}}^{{u = h(w) + x/2}} {\sqrt {\frac{{x^{2} }}{4} - \left[ {u - h(w)} \right]^{2} } } du} \right\} \cdot dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ) \hfill \\ = &\,\frac{\pi }{2}x^{2} \cdot dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ) \hfill \\ \end{aligned}$$

(44)

b) When $x \ge h(w)$, the shadow region boundary in the positive v-axis in Fig. 17b satisfies the following equation.

$$v = \left\{ {\begin{array}{*{20}c} {\sqrt {\frac{{x^{2} }}{4} - u^{2} } , \, - \frac{x}{2} \le u < h(w) - \frac{x}{2}} \\ {\sqrt {\frac{{x^{2} }}{4} - u^{2} } - \sqrt {\frac{{x^{2} }}{4} - \left[ {u - h(w)} \right]^{2} } , \, h(w) - \frac{x}{2} \le u < \frac{h(w)}{2}} \\ {\sqrt {\frac{{x^{2} }}{4} - \left[ {u - h(w)} \right]^{2} } - \sqrt {\frac{{x^{2} }}{4} - u^{2} } , \, \frac{h(w)}{2} \le u < \frac{x}{2}} \\ {\sqrt {\frac{{x^{2} }}{4} - \left[ {u - h(w)} \right]^{2} } , \, \frac{x}{2} \le u \le h(w) + \frac{x}{2}.} \\ \end{array} } \right.$$

(45)

The bottom area $dS_{D2}$ of the distribution space of the centers of fractures, intersecting the rectangular infinitesimal with one censored end and one observable end, is expressed as:

$$\begin{aligned} dS_{D2} &= 2\int_{u = - x/2}^{u = h(w) + x/2} {vdu} \cdot dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ) \\& = 2\left\{ {\int_{u = - x/2}^{u = h(w) - x/2} {\sqrt {\frac{{x^{2} }}{4} - u^{2} } du} + \int_{u = h(w) - x/2}^{u = h(w)/2} {\sqrt {\frac{{x^{2} }}{4} - u^{2} } - \sqrt {\frac{{x^{2} }}{4} - \left[ {u - h(w)} \right]^{2} } du} } \right. \\ &\quad\, \left. { + \int_{u = x/2}^{u = h(w) + x/2} {\sqrt {\frac{{x^{2} }}{4} - \left[ {u - h(w)} \right]^{2} } - \sqrt {\frac{{x^{2} }}{4} - u^{2} } du} + \int_{u = h(w)/2}^{u = x/2} {\sqrt {\frac{{x^{2} }}{4} - \left[ {u - h(w)} \right]^{2} } du} } \right\} \\& \quad\, \cdot dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ) \\ &= \left[ {h(w)\sqrt {x^{2} - h^{2} (w)} + x^{2} \arcsin \frac{h(w)}{x}} \right] \cdot dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ). \\ \end{aligned}$$

(46)

Equation (44) and Eq. (46) can be expressed by the unified formula. The bottom area $dS_{D}$ of the distribution space of the centers of fractures, intersecting the rectangular infinitesimal with one censored end and one observable end, is expressed as:

$$\begin{aligned} dS_{D} &= \left\{ {h(w)\sqrt {x^{2} - \left\{ {\min \left[ {h(w),\;x} \right]} \right\}^{2} } + x^{2} \arcsin \frac{{\min \left[ {h(w),\;x} \right]}}{x}} \right\} \\&\quad \, \cdot dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ). \\ \end{aligned}$$

(47)

The volume $dV_{D}$ of the distribution space of the centers of fractures, intersecting the rectangular infinitesimal with one censored end and one observable end, is determined by multiplying Eq. (18) and Eq. (47).

$$\begin{aligned} dV_{D} &= dS_{D} \cdot dH \\ &= \left\{ {h(w)\sqrt {x^{2} - \left\{ {\min \left[ {h(w),\;x} \right]} \right\}^{2} } + x^{2} \arcsin \frac{{\min \left[ {h(w),\;x} \right]}}{x}} \right\} \\ &\, \cdot dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ) \cdot \sqrt {1 - \sin^{2} \gamma \sin^{2} \varphi } dw. \\ \end{aligned}$$

(48)

$dn_{FD}$ is the number of fractures intersecting the rectangular infinitesimal with one censored end and one observable end. According to the definition, $dn_{FD}$ is determined by multiplying the volume of the distribution space and the volume density of fracture centers.

$$\begin{aligned} dn_{FD} =&\, \rho_{V} dV_{D} \\ = &\,\rho_{V} \left\{ {h(w)\sqrt {x^{2} - \left\{ {\min \left[ {h(w),\;x} \right]} \right\}^{2} } + x^{2} \arcsin \frac{{\min \left[ {h(w),\;x} \right]}}{x}} \right\} \\ &\, \cdot dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ) \cdot \sqrt {1 - \sin^{2} \gamma \sin^{2} \varphi } dw. \\ \end{aligned}$$

(49)

The number $n_{FD}$ of fractures, intersecting the whole sampling window with one censored end and one observable end, is derived by integrating Eq. (49) over $w \in (0,\;D)$.

$$\begin{aligned} n_{FD} &= \int_{{w = w_{1} }}^{{w = w_{2} }} {dn_{FD} } \\ &= \rho_{V} \int_{{w = w_{1} }}^{{w = w_{2} }} {\left\{ {h(w)\sqrt {x^{2} - \left\{ {\min \left[ {h(w),\;x} \right]} \right\}^{2} } + x^{2} \arcsin \frac{{\min \left[ {h(w),\;x} \right]}}{x}} \right\}dw} \\& \quad\cdot \sqrt {1 - \sin^{2} \gamma \sin^{2} \varphi } dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ). \\ \end{aligned}$$

(50)

The number $N_{FD}$ of fractures of arbitrary size and orientation, intersecting the whole sampling window with one censored end and one observable end, is derived by integrating Eq. (50) over $x \in (x,\;x + dx)$, $\gamma \in (\gamma ,\;\gamma + d\gamma )$, and $\varphi \in (\varphi ,\;\varphi + d\varphi )$.

$$\begin{aligned} N_{FD} &= \int_{\varphi = 0}^{\varphi = 2\pi } {\int_{\gamma = 0}^{\gamma = \pi /2} {\int_{x = 0}^{x = \infty } {n_{FD} } } } \\& = \int_{\varphi = 0}^{\varphi = 2\pi } {\int_{\gamma = 0}^{\gamma = \pi /2} {\int_{x = 0}^{x = \infty } {\rho_{V} \int_{{w = w_{1} }}^{{w = w_{2} }} {\left\{ {h(w)\sqrt {x^{2} - \left\{ {\min \left[ {h(w),\;x} \right]} \right\}^{2} } + x^{2} \arcsin \frac{{\min \left[ {h(w),\;x} \right]}}{x}} \right\}} dw} } } \\& \, \cdot \sqrt {1 - \sin^{2} \gamma \sin^{2} \varphi } dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ) \\ &= \rho_{V} \int_{x = 0}^{x = \infty } {\left\{ {\int_{{w = w_{1} }}^{{w = w_{2} }} {\left\{ {h(w)\sqrt {x^{2} - \left\{ {\min \left[ {h(w),\;x} \right]} \right\}^{2} } + x^{2} \arcsin \frac{{\min \left[ {h(w),\;x} \right]}}{x}} \right\}} dw} \right\}dD(x)} \\ &\quad\, \cdot \int_{\varphi = 0}^{\varphi = 2\pi } {\int_{\gamma = 0}^{\gamma = \pi /2} {\sqrt {1 - \sin^{2} \gamma \sin^{2} \varphi } dG_{\gamma } (\gamma )dG_{\varphi } (\varphi )} } . \\ \end{aligned}$$

(51)

The number of fractures intersecting with one censored end and one observable end is equal to that of dissecting traces because of the one-to-one correspondence between fractures and traces. $N_{TD}$ is the expected number of dissecting traces in the sampling window, and Eq. (51) can be rewritten as:

$$\begin{aligned} N_{TD} = &\,\rho_{V} \int_{x = 0}^{x = \infty } {\left\{ {\int_{{w = w_{1} }}^{{w = w_{2} }} {\left[ {h(w)\sqrt {x^{2} - \left\{ {\min \left[ {h(w),x} \right]} \right\}^{2} } + x^{2} \arcsin \frac{{\min \left[ {h(w),x} \right]}}{x}} \right]} dw} \right\}dD(x)} \\ &\, \cdot \int_{\varphi = 0}^{\varphi = 2\pi } {\int_{\gamma = 0}^{\gamma = \pi /2} {\sqrt {1 - \sin^{2} \gamma \sin^{2} \varphi } dG_{\gamma } (\gamma )dG_{\varphi } (\varphi )} } . \\ \end{aligned}$$

(52)

Number of contained traces

The bottom area of the distribution space of the centers of fractures with $x \in (x,\;x + dx)$, $\gamma \in (\gamma ,\;\gamma + d\gamma )$, and $\varphi \in (\varphi ,\;\varphi + d\varphi )$, intersecting the rectangular infinitesimal with both observable ends, is the shadow area surrounded by the red line in Fig. 

Fig. 18

On the $uO^{\prime\prime}v$ coordinate plane, the distribution region of the centers of fractures is intersecting the rectangular infinitesimal with both observable ends. Note that the solid and hollow circles represent the centers of fractures of the above type and the others, respectively. a $x < h(w)$. b $x \ge h(w)$

18. According to the relationship between the fracture diameter x and the height of the rectangular infinitesimal h(w), the bottom area is determined according to the following two situations.

(a) When $x < h(w)$, the shadow region boundary in the positive v-axis in Fig. 18a satisfies the following equation.

$$v = \left\{ \begin{gathered} \frac{x}{2} - \sqrt {\frac{{x^{2} }}{4} - u^{2} } ,{\text{ }}0 \le u < \frac{x}{2} \hfill \\ \frac{x}{2},{\text{ }}\frac{x}{2} \le u < h(w) - \frac{x}{2} \hfill \\ \frac{x}{2} - \sqrt {\frac{{x^{2} }}{4} - \left[ {u - h(w)} \right]^{2} } ,{\text{ }}h(w) - \frac{x}{2} \le u \le h(w) \hfill \\ \end{gathered} \right.$$

(53)

The bottom area $dS_{C1}$ of the distribution space of the centers of fractures is intersecting the rectangular infinitesimal with both observable ends.

$$\begin{aligned} dS_{C1} = &\,2\int_{u = 0}^{u = h(w)} {vdu} \cdot dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ) \\ =&\, 2\left\{ {\int_{u = 0}^{u = x/2} {\left[ {\frac{x}{2} - \sqrt {\frac{{x^{2} }}{4} - u^{2} } } \right]du} + \int_{{u = \frac{x}{2}}}^{u = h(w) - x/2} {\frac{x}{2}du} + \int_{u = h(w) - x/2}^{u = h(w)} {\left\{ {\frac{x}{2} - \sqrt {\frac{{x^{2} }}{4} - \left[ {u - h(w)} \right]^{2} } } \right\}du} } \right\} \\& \, \cdot dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ) \\ = &\,\left[ {xh(w) - \frac{\pi }{4}x^{2} } \right] \cdot dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ). \\ \end{aligned}$$

(54)

b) When $x \ge h(w)$, the shadow region boundary in the positive v-axis in Fig. 18b satisfies the following equation.

$$v = \left\{ \begin{gathered} \frac{x}{2} - \sqrt {\frac{{x^{2} }}{4} - u^{2} } ,{\text{ }}0 \le u < \frac{{h(w)}}{2} \hfill \\ \frac{x}{2} - \sqrt {\frac{{x^{2} }}{4} - \left[ {u - h(w)} \right]^{2} } ,{\text{ }}\frac{{h(w)}}{2} \le u \le h(w) \hfill \\ \end{gathered} \right.$$

(55)

The bottom area $dS_{C2}$ of the distribution space of the centers of fractures intersecting the rectangular infinitesimal with both observable ends, and is expressed as:

$$\begin{aligned} dS_{{C2}} =&\, 2\int_{{u = 0}}^{{u = h(w)}} {vdu} \cdot dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ) \hfill \\ =&\, 2\left\{ {\int_{{u = 0}}^{{u = h(w)/2}} {\left[ {\frac{x}{2} - \sqrt {\frac{{x^{2} }}{4} - u^{2} } } \right]du} + \int_{{u = h(w)/2}}^{{u = h(w)}} {\left\{ {\frac{x}{2} - \sqrt {\frac{{x^{2} }}{4} - \left[ {u - h(w)} \right]^{2} } } \right\}du} } \right\} \hfill \\ &\cdot dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ) \hfill \\ =&\, \left[ {xh(w) - h(w)\sqrt {\frac{{x^{2} }}{4} - \frac{{h^{2} (w)}}{4}} - \frac{{x^{2} }}{2}\arcsin \frac{{h(w)}}{x}} \right] \cdot dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ) \hfill \\ \end{aligned}$$

(56)

Equation (54) and Eq. (56) can be expressed by the unified formula. The bottom area $dS_{C}$ of the distribution space of the centers of fractures intersecting the rectangular infinitesimal with both observable ends is expressed as:

$$\begin{aligned} dS_{C} =& \,\left\{ {xh(w) - \frac{h(w)}{2}\sqrt {x^{2} - \left\{ {\min \left[ {h(w),\;x} \right]} \right\}^{2} } - \frac{{x^{2} }}{2}\arcsin \frac{{\min \left[ {h(w),\;x} \right]}}{x}} \right\} \\ &\, \cdot dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ). \\ \end{aligned}$$

(57)

The volume $dV_{C}$ of the distribution space of the centers of fractures intersecting the rectangular infinitesimal with both observable ends is determined by multiplying Eq. (18) and Eq. (57).

$$\begin{aligned} dV_{C} =&\, dS_{C} \cdot dH \\ =& \left\{ {xh(w) - \frac{h(w)}{2}\sqrt {x^{2} - \left\{ {\min \left[ {h(w),\;x} \right]} \right\}^{2} } - \frac{{x^{2} }}{2}\arcsin \frac{{\min \left[ {h(w),\;x} \right]}}{x}} \right\} \\ \, &\cdot dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ) \cdot \sqrt {1 - \sin^{2} \gamma \sin^{2} \varphi } dw. \\ \end{aligned}$$

(58)

$dn_{FC}$ is the number of fractures intersecting the rectangular infinitesimal with both observable ends. According to the definition, $dn_{FC}$ is determined by multiplying the volume of the distribution space and the volume density of fracture centers.

$$\begin{aligned} dn_{FC} = &\,\rho_{V} dV \\ = &\,\rho_{V} \left\{ {xh(w) - \frac{h(w)}{2}\sqrt {x^{2} - \left\{ {\min \left[ {h(w),\;x} \right]} \right\}^{2} } - \frac{{x^{2} }}{2}\arcsin \frac{{\min \left[ {h(w),\;x} \right]}}{x}} \right\} \\ &\, \cdot dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ) \cdot \sqrt {1 - \sin^{2} \gamma \sin^{2} \varphi } dw. \\ \end{aligned}$$

(59)

The number $n_{FC}$ of fractures intersecting the whole sampling window with both observable ends is derived by integrating Eq. (59) over $w \in (0,\;D)$.

$$\begin{aligned} n_{FC} = &\int_{{w = w_{1} }}^{{w = w_{2} }} {dn_{FC} } \\ = &\rho_{V} \int_{{w = w_{1} }}^{{w = w_{2} }} {\left\{ {xh(w) - \frac{h(w)}{2}\sqrt {x^{2} - \left\{ {\min \left[ {h(w),\;x} \right]} \right\}^{2} } - \frac{{x^{2} }}{2}\arcsin \frac{{\min \left[ {h(w),\;x} \right]}}{x}} \right\}} dw \\ &\cdot \sqrt {1 - \sin^{2} \gamma \sin^{2} \varphi } dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ). \\ \end{aligned}$$

(60)

The number $N_{FC}$ of fractures of arbitrary size and orientation intersecting the whole sampling window with both observable ends is derived by integrating Eq. (60) over $x \in (x,\;x + dx)$, $\gamma \in (\gamma ,\;\gamma + d\gamma )$, and $\varphi \in (\varphi ,\;\varphi + d\varphi )$.

$$\begin{aligned} N_{FC} = &\,\int_{\varphi = 0}^{\varphi = 2\pi } {\int_{\gamma = 0}^{\gamma = \pi /2} {\int_{x = 0}^{x = \infty } {n_{FC} } } } \\ =&\, \int_{\varphi = 0}^{\varphi = 2\pi } {\int_{\gamma = 0}^{\gamma = \pi /2} {\int_{x = 0}^{x = \infty } {\rho_{V} \int_{{w = w_{1} }}^{{w = w_{2} }} {\left\{ {xh(w) - \frac{h(w)}{2}\sqrt {x^{2} - \left\{ {\min \left[ {h(w),\;x} \right]} \right\}^{2} } - \frac{{x^{2} }}{2}\arcsin \frac{{\min \left[ {h(w),\;x} \right]}}{x}} \right\}dw} } } } \\& \, \cdot \sqrt {1 - \sin^{2} \gamma \sin^{2} \varphi } dD(x)dG_{\gamma } (\gamma )dG_{\varphi } (\varphi ) \\ =&\, \rho_{V} \int_{x = 0}^{x = \infty } {\left\{ {\int_{{w = w_{1} }}^{{w = w_{2} }} {\left\{ {xh(w) - \frac{h(w)}{2}\sqrt {x^{2} - \left\{ {\min \left[ {h(w),x} \right]} \right\}^{2} } - \frac{{x^{2} }}{2}\arcsin \frac{{\min \left[ {h(w),x} \right]}}{x}} \right\}} dw} \right\}dD(x)} \\& \, \cdot \int_{\varphi = 0}^{\varphi = 2\pi } {\int_{\gamma = 0}^{\gamma = \pi /2} {\sqrt {1 - \sin^{2} \gamma \sin^{2} \varphi } dG_{\gamma } (\gamma )dG_{\varphi } (\varphi )} } . \\ \end{aligned}$$

(61)

The number of fractures intersecting with both observable ends is equal to that of contained traces because of the one-to-one correspondence between fractures and traces. $N_{TC}$ is the expected number of contained traces in the sampling window, and Eq. (61) can be rewritten as:

$$\begin{aligned} N_{TC} = &\rho_{V} \int_{x = 0}^{x = \infty } {\left\{ {\int_{{w = w_{1} }}^{{w = w_{2} }} {\left\{ {xh(w) - \frac{h(w)}{2}\sqrt {x^{2} - \left\{ {\min \left[ {h(w),\;x} \right]} \right\}^{2} } - \frac{{x^{2} }}{2}\arcsin \frac{{\min \left[ {h(w),\;x} \right]}}{x}} \right\}dw} } \right\}dD(x)} \\ &\, \cdot \int_{\varphi = 0}^{\varphi = 2\pi } {\int_{\gamma = 0}^{\gamma = \pi /2} {\sqrt {1 - \sin^{2} \gamma \sin^{2} \varphi } dG_{\gamma } (\gamma )dG_{\varphi } (\varphi )} } . \\ \end{aligned}$$

(62)