Verification of Coupled Hydraulic Fracturing Simulators Using Laboratory-Scale Experiments

Abstract

In this work, we aim to verify the predictions of the numerical simulators, which are used for designing field-scale hydraulic stimulation experiments. Although a strong theoretical understanding of this process has been gained over the past few decades, numerical predictions of fracture propagation in low-permeability rocks still remains a challenge. Against this background, we performed controlled laboratory-scale hydraulic fracturing experiments in granite samples, which not only provides high-quality experimental data but also a well-characterized experimental set-up. Using the experimental pressure responses and the final fracture sizes as benchmark, we compared the numerical predictions of two coupled hydraulic fracturing simulators—CSMP and GEOS. Both the simulators reproduced the experimental pressure behavior by implementing the physics of Linear Elastic Fracture Mechanics (LEFM) and lubrication theory within a reasonable degree of accuracy. The simulation results indicate that even in the very low-porosity (1–2 %) and low-permeability (${10}^{-18}\ {\mathrm{m}}^{2}- {10}^{-19}\ {\mathrm{m}}^{2}$) crystalline rocks, which are usually the target of EGS, fluid-loss into the matrix and unsaturated flow impacts the formation breakdown pressure and the post-breakdown pressure trends. Therefore, underestimation of such parameters in numerical modeling can lead to significant underestimation of breakdown pressure. The simulation results also indicate the importance of implementing wellbore solvers for considering the effect of system compressibility and pressure drop due to friction in the injection line. The varying injection rate as a result of decompression at the instant of fracture initiation affects the fracture size, while the entry friction at the connection between the well and the initial notch may cause an increase in the measured breakdown pressure.

1 Introduction

Over the past few decades, the technique of hydraulic stimulation has received considerable attention in both renewable and fossil energy sector. Advancements in hydraulic stimulation technology have not only elevated the estimates of energy production from tight gas reservoirs (Arukhe et al. 2009) or Enhanced Geothermal Systems (EGS) (Brown et al. 2012), but also has important implications for managing CO₂ storage performance (Fu et al. 2017). In the field of geothermal energy, hydraulic stimulation is employed for permeability enhancement, in otherwise low porous and low permeable rocks, whereby, fluid is injected at high pressure into the deep-seated, hot and dry rocks activating the natural fracture network or creating new fractures. Reservoirs created through this process are also known as Enhanced or Engineered Geothermal Systems (EGSs), e. g., Soultz-sous-Forêts in France (Kölbel and Genter 2017), Rittershofen in France (Baujard et al. 2017) and Cooper Basin in Australia (Holl 2015). Despite its great energy potential and negligible carbon footprint, this technology has experienced significant backlash and criticism in the past decade due to the associated environmental risks particularly related to induced seismicity, such as the earthquakes in Basel, Switzerland in 2009 (Häring et al. 2008; Deichmann et al 2014) and in Pohang, South Korea in 2017 (Grigoli et al. 2018). Studies have confirmed injection-related fault reactivation as the cause for both earthquakes.

As a result, intensive research has been performed to study experimentally and theoretically the coupled hydro-mechanical processes during reservoir stimulation. Amann et al. (2018) provide a detailed review of studies addressing seismically and hydromechanically coupled processes at different scales (reservoir, laboratory and intermediate). One major challenge in EGS remains to accurately predict the growth, propagation and interaction of fractures by numerical modeling and subsequently design a safe, efficient and sustainable heat exchange system in the deep-seated subsurface structure. To this end, it is indispensable that the numerical models are capable of accurately solving the associated coupled partial differential equations describing the complex physical processes. As the solutions from different numerical simulators can differ significantly depending on the assumptions made and the implemented physics, the reliability of the predictions has always been a subject of concern (Sorey and Fradkin 1979; Molloy and Sorey 1981). The necessity of verifying numerical codes against field-scale or laboratory-scale experimental data has been emphasized in several studies before (Leampion et al. 2015; White et al. 2016). Field-scale tests, however, suffer from low resolution (Amann et al. 2018) and uncontrollable boundary conditions, which cannot be used for investigating specific physical processes and analysis of sensitive factors. Therefore, controlled laboratory-scale experiments are not only necessary to generate benchmark datasets for verification of the numerical codes, they also provide detailed insights regarding the parameters that influence the initiation, propagation and closure of hydraulic fractures.

To this end, numerous laboratory-scale hydraulic fracturing experiments have been performed using samples of different sizes and materials such as granite (Chen et al. 2015; Matsunaga et al. 1993), casted cement (Bai et al 2016; De Pater et al. 1994) and sandstone (Zoback et al. 1977; Patel et al. 2017). Many studies have also been performed experiments in transparent blocks of polymethyl methacrylate (PMMA) (Bunger and Detournay 2008; Wu et al. 2008; Khadraoui et al. 2020), which offers the possibility for real-time monitoring of crack propagation. Laboratory-scale experiments in casted cement and PMMA have also been used for comparing numerical predictions in many studies (Lecampion et al. 2017; Bai et al 2016; De Pater et al. 1994). Very rarely, however, well-controlled laboratory-scale experiments on real rocks, such as, granite have been used as a benchmark for numerical code verification studies. This is primarily due to the inherent complexity associated with the brittle failure mechanism in real rock involving microcracks from stress concentrators, such as dissimilar grain contacts, voids and inclusions (Lockner 1993) and the coupling of this deformation process with fluid flow in the matrix and the fracture (Detournay 2016).

Our main objective in this paper is to present an experimental study in low-permeability granite samples and compare the experimental results with predictions of two numerical codes. In the process, we also evaluate the most sensitive factors, which affect the initiation, growth and propagation of radial, penny-shaped fractures in the granite samples. The experiments were performed on samples of size $30\ \mathrm { cm }\times 30\ \mathrm { cm }\times 45\ \mathrm { cm}$. The experimental data are reported in Deb et al. 2020. The dataset is unique due to the large sample sizes, detailed characterization of the experimental set-up and the accurate knowledge of the initial notch size, the boundary conditions, and the geometry of the induced fracture. Both the finite element simulators—Complex Systems Modelling Platform (CSMP) (Salimzadeh et al. 2017a) and GEOS (Settgast et al. 2016) modeled the entire pressure response curve and the final geometry of the fracture solving simultaneously for deformation and fluid flow. To consider the effect of leak-off, coupled with the effects of system compressibility, viscosity and material toughness, the numerical codes implemented wellbore solver models, which modeled the different components of the experimental set-up.

The paper is organized as follows: Sect. 2 briefly explains the theoretical background and the governing equations for numerical modeling of the hydraulic fracturing process, Sect. 3 presents the experiment description and protocol. In Sect. 4 the simulations are compared to the experimental results, followed by discussion in Sect. 5.

2 Theoretical Background

Hydraulic fracturing is a complex, multi-physics, and multi-dimensional problem. It requires robust models that can simultaneously account for matrix and fracture deformation, fluid flow through the matrix and fractures, fluid exchange between fractures and matrix, and fracture propagation and interaction, all fully-coupled and in three dimensions. The first basic models to explain the process of hydraulic fracturing were presented in Sneddon (1946), Khristianovic and Zheltov (1955), Perkins and Kern (1961) and Geertsma and de Klerk (1969). Since then, several advanced numerical models have been developed to account for the complexities related to moving boundary conditions and their influences (Detournay and Pierce 2014) (see Adachi et al. 2007 for review on the development of hydraulic fracturing models).

In this experimental and simulation study, we concentrate on the evolution of a single 3D radial, Mode-I, penny-shaped fracture along a plane normal to the minor principal stress and initiated from a pre-existing known crack (an initial notch) at uniform initial stress. Despite being one of the basic hydraulic fracture models, its numerical prediction demands the coupling of complex non-linear equations. Fluid flow through the fracture is commonly modelled using lubrication theory, which is derived from the general Navier–Stokes equation for the flow of a fluid between two parallel plates (Zimmerman and Bodvarsson 1996). The fracture aperture is calculated using linear elasticity in conjunction with Linear Elastic Fracture Mechanics (LEFM) to compute the Mode-I stress intensity factor at the fracture tip. The energy spent in hydraulic fracturing is used either in the toughness regime for overcoming the fracture toughness and creating new fracture surfaces, or in the viscosity regime to propagate a viscous fluid in the fracture (Detournay 2004). The fluid used for hydraulic fracturing may remain either, in the storage regime, within the fracture, or dissipate, in the leak-off regime, into the rock matrix (Detournay 2016). For each of the end-member regimes, storage vs. leak-off and toughness vs. viscosity, there are analytical solutions for simple reference geometries. However, intermediate regimes or complex hydraulic fracture geometries require a numerical solution of the coupled governing equations.

The two simulation codes used in this study, CSMP and GEOS, are based on the same fundamental theories but implement slightly modified mathematical equations. Therefore, the coupled equations governing the rock matrix deformation, flow through fracture and flow through rock matrix are reviewed separately for both codes in the following sub-sections:

2.1 Simulator 1: Complex Systems Modelling Platform (CSMP)

CSMP is an object-oriented application program interface, for the simulation of complex geological processes and their interactions. The CSMP hydraulic fracturing module is a fully coupled, three-dimensional finite element model for hydraulic fracturing in permeable rocks. It models simultaneously the elastic deformation of the matrix, fluid flow in the fracture and the matrix, as well as heat transfer in the fracture and the matrix Salimzadeh et al. (2017a; 2019b, 2020a, b). In this module, fractures are modelled as surface discontinuities in the three-dimensional matrix.

2.1.1 Deformation of Rock Matrix

The deformation model assumes equilibrium in a representative elementary volume of the porous medium. Fracture surfaces are not traction-free in the model, and hydraulic loading is applied on the fracture walls. The differential equation describing the deformation field for a saturated rock matrix is given by

$$\mathrm{div}\left({\varvec{D}}{\varvec{\varepsilon}}-\alpha {p}_{m}{\varvec{I}}\right)+{\varvec{F}}-{p}_{f}{\mathbf{n}}_{c}\updelta \left(\mathbf{x}-{\mathbf{x}}_{c}\right)=0,$$

(1)

where, ${\varvec{D}}$ is the drained stiffness matrix, ${\varvec{\varepsilon}}=\mathrm{sym}\left(\nabla {\varvec{u}}\right)$ is the strain tensor in the porous medium, u denotes the displacement vector in the porous medium, ${\alpha }$ is the Biot coefficient, ${p}_{m}$ is the fluid pressure in the rock matrix, ${\varvec{F}}$ is the body force per unit volume, I is the second-order identity tensor, ${p}_{f}$ is the fracture pressure, $\delta$ is the Dirac delta, ${{\varvec{x}}}_{\mathrm{c}}$ represents the position of the fracture and ${{\varvec{n}}}_{\mathrm{c}}$ is the outward unit normal to the fracture wall (Salimzadeh et al. 2017a).

2.1.2 Fracture Propagation Model

Within the framework of Linear Elastic Fracture Mechanics (LEFM), the stress intensity factors (SIFs) for three modes of fracture opening are computed using the energy-based interaction integral (Nejati et al. 2015). This ‘disk method’ is less prone to numerical error and yields better approximations for coarse meshes. The three stress intensity factors are Mode-I (${K}_{I}$) for opening due to tensile loading, Mode-II (${K}_{II}$) for in-plane shearing due to sliding, and Mode-III (${K}_{III}$) for out-of-plane shearing due to tearing. A propagation event occurs when the equivalent stress intensity factor ${K}_{\rm eq}$ at a fracture tip overcomes the fracture toughness (${K}_{\mathrm{ic}}$). The equivalent SIF in the direction of propagation (${\theta }_{p}$) is calculated as (Schöllmann et al. 2002)

$${K}_{\rm eq}=\frac{1}{2}\cos\left(\frac{{\theta }_{p}}{2}\right)\left\{{K}_{cs}+\sqrt{{K}_{cs}^{2}+4{K}_{III}^{2}}\right\}$$

(2)

where

$${K}_{cs}={K}_{I}{\cos}^{2}\left(\frac{{\theta }_{p}}{2}\right)-\frac{3}{2}{K}_{II}\sin\left({\theta }_{p}\right)$$

(3)

and ${\theta }_{p}$ is the propagation angle. The in-plane propagation angle (${\theta }_{p}$) and out-of-plane deflection angle (${\psi }_{p}$) are determined using a modified maximum circumferential stress method that considers modal stress intensity factors under mixed loading (Schöllmann et al. 2002). Since the hydraulic fracturing in the present experiments occurs mainly under tensile mode and the induced fracture is planar, the equivalent SIF becomes equal to ${K}_{I}$. At each timestep, the stress intensity factors are computed at forty locations along the fracture front, i.e. the fracture tips. If the stress intensity factor ${K}_{I}$ reaches the fracture toughness at least at one tip, a propagation event occurs. The other fracture tips, however, advance proportional to the equivalent SIF value at each tip.

2.1.3 Fluid Flow in Fracture and Matrix

Assuming a planar fracture in which the area of the fracture plane is much larger than the fracture aperture, the governing equation describing fluid flow along the fracture plane, based on the cubic law, can be written as (Salimzadeh et al. 2017a)

$$\mathrm{div}\left(\frac{{{a}_{f}}^{3}}{12{\mu }_{f}}\nabla {p}_{f}\right)=\frac{{a}_{f}}{{K}_{f}}\frac{\partial {p}_{f}}{\partial t}+\frac{\partial {a}_{f}}{\partial t}+\frac{{k}_{n}}{{\mu }_{f}}\frac{\partial p}{\partial {n}_{c}}$$

(4)

where ${a}_{f}$ is the fracture aperture, ${\mu }_{f}$ is the fluid viscosity, ${p}_{f}$ is the fracture fluid pressure, ${K}_{f}$ is the fluid bulk modulus, ${k}_{n}$ is the permeability of the rock matrix in the direction normal to the fracture, and $\partial p/({\partial n}_{c })$ is the gradient of the pressure perpendicular to the fracture. The aperture is given by the differential displacement between two sides of the fracture,${a}_{f}=\left({\mathbf{u}}^{+}-{\mathbf{u}}^{-}\right).{\mathbf{n}}_{c}$, where ${\mathbf{u}}^{+}$ and ${\mathbf{u}}^{-}$ are the displacements of the two opposing faces of the fracture. Note that the term $\partial {a}_{f}/\partial t=\partial \left({\mathbf{u}}^{+}-{\mathbf{u}}^{-}\right).{\mathrm{n}}_{c}/\partial t$ provides direct coupling between the displacement field and the fracture flow field, which is symmetric to the fracture pressure loading term, ${p}_{f}{\mathbf{n}}_{C}$ in Eq. 1. Also, the last term in Eq. 4 provides coupling between the fracture and matrix flows, known as leak-off.

2.1.4 Hydro-Mechanical Coupling and Discretization

The fluid leak-off from the hydraulic fracture into the surrounding rock matrix affects both the fluid mass balance in the fracture and induces poroelastic deformation in the rock. These effects cannot be simply ignored, and a coupled flow-deformation model for flow through the porous rock matrix is required. The governing equation for the flow model, combining the fluid mass balance equation with Darcy’s law, may be expressed as (Salimzadeh et al. 2017a)

$$\mathrm{div}\left[\frac{{{\varvec{k}}}_{{\varvec{m}}}}{{\mu }_{f}}\left(\nabla {p}_{m}+{\rho }_{f}\mathbf{g}\right)\right]=\alpha \frac{\partial \left(\mathrm{div }\mathbf{u}\right)}{\partial t}+\left(\frac{\phi }{{K}_{f}}+\frac{\alpha -\phi }{{K}_{m}}\right)\frac{\partial {p}_{m}}{\partial t}+\updelta \left(\mathbf{x}-{\mathbf{x}}_{c}\right)\frac{{k}_{n}}{{\mu }_{f}}\frac{\partial p}{\partial {n}_{c}}$$

(5)

where ${{\varvec{k}}}_{{\varvec{m}}}$ is the intrinsic permeability of the rock matrix, ${\rho }_{f}$ is the fluid density, $\mathbf{g}$ is the gravity vector, $\phi$ is rock porosity, and ${K}_{m}$ is the bulk modulus of rock matrix material (i.e. solid grains).

The governing coupled equations are solved numerically using the finite element method. Space and time are discretized using the Galerkin method and finite difference techniques, respectively. Displacements u and fluid pressures (${p}_{f}$ in the fracture and ${p}_{m}$ in the matrix) are defined as the primary variables. Using the standard Galerkin method, the primary variable ${\mathbb{X}}=\left\{\mathbf{u}, {\mathrm{p}}_{f}, {\mathrm{p}}_{\mathrm{m}}\right\}$ within an element is approximated from its nodal values as

$${\mathbb{X}}={\varvec{N}}\widehat{\mathbb{X}}$$

(6)

where ${\varvec{N}}$ is the vector of shape functions and $\widehat{\mathbb{X}}$ is the vector of nodal values. Using the finite difference technique, the time derivative of ${\mathbb{X}}$ is defined as

$$\frac{\partial {\mathbb{X}}}{\partial t}=\frac{{\mathbb{X}}^{t+dt}-{\mathbb{X}}^{t}}{dt}$$

(7)

where ${\mathbb{X}}^{t+dt}$ and ${\mathbb{X}}^{t}$ are the values of ${\mathbb{X}}$ at time t + dt and t, respectively. The set of discretized equations can be written in matrix form as ${\mathbb{S}}{\mathbb{X}}={\mathbb{F}}$, in which ${\mathbb{S}}$ is the element’s general stiffness matrix, and ${\mathbb{F}}$ is the vector of right-hand-side loadings. Flow through the deforming fracture is a highly nonlinear problem, thus a Picard iteration procedure is adopted to reach the correct solution within acceptable tolerance. For the current iteration $s+1$ in current timestep $n+ 1$, the solution-dependent coefficient matrices in the stiffness matrix are updated using the weighted average solution vector ${\mathbb{X}}_{n+1}^{s+\theta }$ defined as

$${\mathbb{X}}_{n+1}^{s+\theta }=\left(1-\theta \right){\mathbb{X}}_{n+1}^{s-1}+\theta {\mathbb{X}}_{n+1}^{s}$$

(8)

where ${\mathbb{X}}_{n+1}^{s-1}$ and ${\mathbb{X}}_{n+1}^{s}$ are the solution vectors of two most recent iterations in the current timestep $n+1$, and $\theta=2/3$ is the weighing coefficient. For the first iteration $s=1$, the previous timestep solution is used as

$${\mathbb{X}}_{n+1}^{0}={\mathbb{X}}_{n+1}^{1}={\mathbb{X}}_{n}$$

(9)

where ${\mathbb{X}}_{n}$ is the solution vector for timestep $n$. The iterations are repeated, until consecutive values of ${\mathbb{X}}_{n+1}^{s}$ agree to within a specified tolerance $\varepsilon$:

$$\frac{\Vert {\mathbb{X}}_{n+1}^{s+1}-{\mathbb{X}}_{n+1}^{s}\Vert }{\Vert {\mathbb{X}}_{n+1}^{s+1}\Vert }< \varepsilon$$

(10)

The tolerance used in the present simulations was set to 1%. The set of linear algebraic equations is solved with the algebraic multigrid method for systems, SAMG (Stüben 2001). Between three to five Picard iterations are needed for each timestep to converge to the prescribed tolerance. At each timestep, the equivalent SIF at each fracture tip is computed and if they reach the fracture toughness, the fracture is propagated. In CSMP, the fracture geometry evolves independently of the mesh (Paluszny and Zimmerman 2011). Propagation events, controlled by SIFs, results in the deformation of the crack geometry instead of the mesh. Once a new fracture geometry is established, a new mesh is regenerated where the elements conform with the new geometry. The jump in displacement is calculated explicitly from the displacements on two sides of a given fracture. The CSMP finite element hydraulic fracturing simulator has been extensively verified against analytical, numerical and experimental data (Salimzadeh et al. 2019a, b, 2017b; Vik et al. 2018; Usui et al. 2017).

2.2 Simulator 2: GEOS

GEOS is a massively parallel multiphysics framework developed at Lawrence Livermore National Laboratory. Hydro-mechanical processes are fully coupled using a finite element method to model solid body deformation and a finite volume method to model fluid flow in fractures and the matrix. A more detailed description can be found in Settgast et al. (2016).

2.2.1 Deformation of Rock Matrix

Consider a body Ω with external boundaries Γ, and a fracture surface Γ^c. A standard Galerkin finite element method is applied to the equations of static equilibrium on Ω, which leads to a discrete solid body residual R in the solid domain for an element

$${(R}_{\mathrm{solid}}^{e}{)}_{ai}={\int }_{ {\Gamma }_{i}^{c}}{\Phi }_{a}{{\varvec{t}}}_{i} dA+ {\int }_{ {\Gamma }_{i}^{c}}{\Phi }_{a}{({\varvec{f}}}_{i}^{c}-{p}_{f}{{\varvec{n}}}_{i})dA + {\int }_{{\Omega }^{e} }{\Phi }_{a,j} {{\varvec{T}}}_{ij} dV,$$

(11)

where $a$ is the nodal index, i is the spatial dimension, $\Phi$ is the finite element shape function, ${T}_{ij}$ is the Cauchy stress tensor with indices i and j, ${t}_{\mathrm{i}}$ is the externally applied traction, ${f}_{\mathrm{i}}^{\mathrm{c}}$ is the contact force, ${p}_{\mathrm{f}}$ is the fluid pressure in the fracture and ${n}_{\mathrm{i}}$ is the outward normal to the external surface.

2.2.2 Fracture Propagation Model

To attain a reasonable fracture criterion, we apply the assumptions of Linear Elastic Fracture Mechanics to the solid material. In GEOS, a 3D fracture front is represented by a collection of line segments or FEM ‘edges’. The rupture criterion is evaluated by calculating stress intensity factors (${K}_{I}, {K}_{II}, {K}_{III}$) for each edge based on the deformation and stress states of the elements surrounding this edge. For this purpose, a modified virtual crack closure technique (Krueger 2004; Leski 2007) is applied, whereby the energy release rate (G) is computed for every splitting edge. The vector components of G, ${G}_{I}, {G}_{II}$ and ${G}_{III}$ represent the energy release rate in directions normal to the fracture plane, direction of propagation and direction of the fracture front, respectively (Settgast et al. 2016). This energy release rate is compared with the critical energy release rate ${G}_{c}$ given by,

$${G}_{c}={K}_{IC}^{2} \left(\frac{1-{\nu }^{2}}{E}\right)$$

(12)

where E is Young’s modulus and $\nu$ is Poisson’s ratio.

Once the energy release rate (G), exceeds the critical energy release rate ($G>{G}_{C})$, the fracture is ready to propagate from this edge into the solid medium. The topology of the mesh is then modified to allow for the extension of the fracture. For a detailed discussion of the modified virtual crack closure technique, and topology change in a distributed memory computing environment. (see Settgast et al. 2016)

2.2.3 Fluid Flow in Fracture and Matrix

As is standard in hydraulic fracturing simulations, the fluid flow in the fracture is modeled using the lubrication assumptions (i.e. parallel plate flow) on volumes that are bounded between fractured element faces.

$$\frac{\partial }{\partial t}\left({\rho }_{f}{\alpha }_{f}\right) - \frac{1}{12{\mu }_{f } } \nabla \cdot {\rho }_{f}{\alpha }_{f}^{3} \nabla \left({p}_{f}\right)=0,$$

(13)

with the fluid dynamic viscosity ${\mu }_{f}$, the fluid pressure in the fracture ${p}_{f}$, the fracture aperture ${\alpha }_{f }=\mathbf{u}\cdot \mathbf{n}$, and the fluid density ${\rho }_{f}.$ The aperture ${\alpha }_{f}$ is then computed as ${\alpha }_{f}=\mathrm{u} \bullet \mathrm{n},$ where $\mathrm{u}$ is the displacement jump across the fracture surface.

The fluid flow in the rock is modeled by a two-point finite volume method applied to the mass conservation equations.

$$\frac{\partial }{\partial t}\left({\rho }_{f}\phi \right) - \nabla \cdot ({\rho }_{f}\frac{{k}_{m}}{{\mu }_{f}} \nabla ({p}_{m}))=0,$$

(14)

where ${k}_{m}$ is the matrix permeability tensor.

The flow equation is discretized using a finite volume method with individual finite volumes ${V}_{r}$, where r is the index over all finite volumes on fracture surface Γ^c. The residual for the rate of fluid mass in a finite volume is given by

$$({R}_{\mathrm{fluid}}{)}_{r}=\frac{d({\rho }_{r}{V}_{r})}{dt} - \sum_{e\epsilon r}{\stackrel{-}{\rho }}_{er} {\kappa }_{er} \left({p}_{e}-{p}_{r}\right)-{q}_{r}^{in},$$

(15)

where

$${\kappa }_{er}=\frac{{a}_{f }^{3}{l}_{e}}{12\mu {l}_{er}},$$

(16)

where, ${p}_{r}$ is fluid pressure on face r, ${p}_{e}$ is the fluid pressure on edge e, the density of the fluxed volume into the cell from edge e is ${\stackrel{-}{\rho }}_{er}$, ${q}_{r}^{in}$ is a source or sink term, ${l}_{e}$ and ${l}_{er}$ are the distances from the effective cross-section for flow across edge e and the distance from the center of face r to the center of edge e, respectively. The coupling of flow between the fracture and matrix is simulated intrinsically by placing flux connectors between the fracture and matrix finite volume cells.

2.2.4 Hydro-Mechanical Coupling and Discretization

The fracture aperture and storativity can be computed by coupling the fluid pressure of the fracture surface and the solid deformation in the rock mass. Thus, fluid pressure applied to the crack surfaces results in a direct influence of the fluid pressure solution on the displacement solution. The fluid volume, in turn, is directly linked to the displacements of the nodes on the fracture surfaces, thus resulting in direct hydro-mechanical coupling. The residuals for the equations of deformation (11) and the conservation of fluid mass in the fracture (15), satisfied over a discrete timestep, defined as $\Delta t={t}_{n+1}-{t}_{n}$, are coupled in a fully implicit method, and linearized to form a block-structured system of equations for fully coupled deformation and flow

$$\left[{R}^{n+1}\right]=\left[\frac{{R}_{\mathrm{solid}}^{n+1}}{{R}_{\mathrm{fluid}}^{n+1}}\right]=\left[0\right] .$$

(17)

Equation (17) is referred to as a “fully-coupled” system because of the tight coupling of solid displacements and fluid pressures. The residuals are minimized using an iterative non-linear Newton's method with a standard line search and the fracture criterion is evaluated after the solution of the nonlinear system of equations. The finite element face along which the fracture extends is controlled by a mixed-mode rupture criterion applied at the fracture tip. According to this criterion, the face with the highest hoop stress is assigned the highest rupture priority. However, one face reaching the rupture criteria does not immediately trigger a topology update. Once all the rupture-ready faces are identified in a time step, the nodes associated with the faces are inspected to find a closed path around the node. If such a closed path is found, the nodes are selected for splitting, and the mesh topology is updated (Settgast et al. 2016).

3 Experiment Description

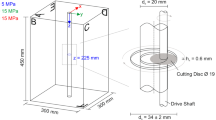
The triaxial apparatus was developed under a project funded by BMU (Federal Ministry for Environment, Nature Conservation and Nuclear Safety), Germany (Siebert 2017; Clauser et al. 2015) while the experiments presented in this paper are funded by European Union’s H2020 project GEMex (GEMex 2016–2020). The photograph of the testing facility is shown in Fig. 1. It comprises of the loading system, the injection system and the acoustic emission data acquisition system. The different components of the system are explained briefly in the following sub-sections and shown schematically in Fig. 2.

Fig. 1

modified from Siebert 2017)

Testing facility showing the loading, injection and acoustic emission data acquisition (AE DAQ) systems (

Fig. 2

Schematic figure of injection system and loading system

The dataset represents the development of an ideal penny-shaped crack (Mode-1 fracture) perpendicular to the direction of minimum stress in two samples (TFK01 and TFK02) under confining pressure. The flow in the crack is assumed to be laminar and the injection fluid is assumed to behave like an incompressible Newtonian fluid.

3.1 Loading System

Confining pressure in the sample is applied using loading plates, which are connected to flat jacks, applying uniform stress in x-, y- and z-direction. Flat jack pairs of the opposite directions are connected to a hand pump for regulating the fluid supply for achieving the desired stress states and to syringe pumps for keeping the applied stress constant and for monitoring the volumetric changes in the flat jacks resulting from the dilation of the specimen during the experiment. In the set-up, the stresses can be varied from zero to 15 MPa in the horizontal direction and from zero to 30 MPa in the vertical direction. In our experiments, the horizontal confining stresses ${\sigma }_{x}$ and ${\sigma }_{y}$ are set to 15 MPa while the applied vertical stress ${\sigma }_{z}$ is 5 MPa.

3.2 Injection System

The Syringe-Pump ‘Teledyne Isco 260 HP’ is used for the injection of the hydraulic fracturing fluid. Figure 2 shows the pump and the injection system. The pipes of the injection system have an inner diameter of 1.76 mm. During the experiment, Valve A and Valve C are closed and the volume of the pump cylinder is reduced to pressurize the injection system. The volume of the injection system is approximately 12 cm³ plus the variable volume of the pump. The injection interval is isolated from the rest of the borehole by a packer. Figure 2 also shows the location of the pressure transmitters p1 and p2. As it is not possible to measure the fluid pressure in the injection interval, the pressure transmitter $p2$ (before) and $p1$ (behind) are placed at equal distance to the injection interval. Sensors of type ‘Keller P33x/1000 bar/80794’ with an accuracy of  $0.1\ \mathrm {MPa}$ are used. The fluid pressure in the injection interval is assumed to be the mean value of p1 and p2.

The injection fluid in the experiment is a mixture of 98% glycerol and 2% ink. The ink is added to visualize the penetration depth of the fluid when the samples are opened after the experiment. As the viscosity of injection fluid depends on both temperature and pressure and may vary in each experiment, the dynamic viscosity of the injection fluid is measured in a separate test using a rotary rheometer for temperatures recorded during the experiment. The properties of the injection fluid are provided in Table 1.

Table 1 Model parameters used in numerical simulations: experimentally measured values versus values used in simulation

3.3 Acoustic Emission (AE) Data Acquisition

The seismic data acquisition is performed using GMuG data acquisition software and GMuG acoustic sensors. The 32 piezoelectric sensors, operating in a bandwidth from $20\ \mathrm{kHz}\ \mathrm{to}\ 1\ \mathrm{MHz}$, can be used both as transmitters and receivers and are directly attached to the surface of the sample: six sensors at each vertical face and four at each of the upper and lower surfaces (Fig. 3).

Fig. 3

Polished granite sample with drilled borehole (left); schematic showing the distribution of the AE sensors (hollow circles) projected on the sample surface, the borehole of diameter 2 cm and length 45 cm, the saw-cut notch in the borehole at z = 22.5 cm

There are two modes of data acquisition: Active transmission for computing the average seismic velocity of the sample and passive monitoring for collecting acoustic emission data during fracturing. During active transmission, all the 32 sensors attached to the samples are activated one at a time as transmitters to generate pressure pulses, while the others act as receivers. Each input pulse is repeated eight times to improve the statistics, generating a total number of 7936 records, which are processed to detect first arrivals using the Akaike Information Criterion (AIC) (Akaike 1998) and subsequently compute the average P-wave velocity. In passive monitoring mode, the energy pulses generated during the fracturing processes are recorded by all the sensors. The first arrivals are again picked using the AIC. Then, the events are localized in space using the average P-wave velocity determined in the previous step. The detailed seismic data processing and event localization workflow is discussed in Deb et al. (2020).

3.4 Samples

The samples used for the experiment are low-porosity and low-permeability granite with the trade name Tittlinger Feinkorn (TFK) collected from the Höhenberg Quarry in Bavaria. The samples were fine-grained and appear macroscopically to be homogeneous and isotropic. As a preparation, each sample was cut and polished to a final dimension of $30\ \mathrm{cm} \times 30\ \mathrm{cm} \times 45\ \mathrm{cm}$. A borehole of radius 1 cm was drilled through the center of the sample and a circumferential notch of radius $1.7 \pm 0.1\ \mathrm{cm}$ was cut into the borehole wall at a depth of $z=22.5\ \mathrm{cm}$ in the borehole for guiding the crack initiation (Fig. 3).

The petrophysical and mechanical properties of the samples are reported in Table 1. The petrophysical properties of the rock samples—porosity, bulk density, P-wave velocity—are measured in separate tests using different techniques, such as Gas Pycnometer, Archimedes method and Multi-Sensor Core Logger. The P-wave velocity of the sample was measured on cores in both dry and water-saturated conditions and was used for comparing the average velocity of the samples obtained from the active transmission experiment. The intrinsic permeability of each sample was measured using a gas permeameter (Schütt et al. 2013). These measurements were performed at 1.5 MPa confining pressure with Argon gas and converted to fluid-independent permeability according to Klinkenberg (e.g., Schön 1996).

The mechanical properties for this material are directly taken from Siebert (2017), who performed a detailed characterization of the TFK granite. The value of Poisson’s ratio and compressive strength were measured by performing a uniaxial compression test, while the fracture toughness and Young’s modulus were determined by a Chevron-Bend Test. The tensile strength was calculated from an indirect tensile test.

3.5 Protocol

The two experiments reported in this paper were performed under identical experimental boundary conditions. The steps followed in the experiments are explained in their order as follows:

• 1. The experiment starts by applying the confining stresses (${\sigma }_{x}, {\sigma }_{y}=15\ \mathrm{MPa}, {\sigma }_{z}=5\ \mathrm{MPa}$) around the sample using the loading system.

• 2. After the initial loading, a leakage test is performed to ensure that there are no leakages in the injection system and the installed packer in the loaded state. This is done by pressurizing the closed injection system with a fluid pressure of 3 MPa and then maintaining this pressure constant for about 600 s. It takes approximately 0.03 mL of injection fluid to keep the pressure constant for this time, which confirms the tightness of the system.

• 3. Once the desired stress state is reached, an active transmission experiment is performed to obtain the average velocity of the sample.

• 4. Following this, the pump is filled with $5\ \mathrm{mL}$ of injection fluid, after which the injection for the hydraulic fracturing begins. This starting time of injection is used as a time reference (t = 0 s) for all recorded data. To ensure a controlled and stable fracture growth, and retain the fracture within the specimen, a special injection procedure is followed (Siebert 2017). The fluid is pumped at a constant injection rate of $0.1\ \mathrm{mL}/\mathrm{min}$ while the pressure response within the injection system is recorded. With the start of the injection, the seismic sensors are activated to start the passive acquisition of any induced AE events.

• 5. Once the peak pressure is reached, a defined volume, $\Delta V=$ $1.5\ \mathrm{mL}$ is injected further. This volume leads to a controlled fracture growth within the sample of this size and has been determined from previous experiments (Siebert 2017)

• 6. After the injection of $\Delta V$ is completed, the pump is stopped. This phase of the experiment is referred to as ‘shut-in’.

• 7. The standard post-shut-in procedure consists of releasing the pressure of the injection system by opening valve C connected to the bleeding line (Fig. 2). However, to estimate the amount of fluid lost into the rock, the pump cylinder is driven back to achieve atmospheric pressure conditions. The total fluid loss is then calculated as the difference between the pump volumes at atmospheric pressure before and after injection.

• 8. Following shut-in, when the pressure drops below the minimum confining stress, another active transmission experiment is performed, which is followed by unloading the sample and removing it from the set-up for further investigation.

• 9. Finally, the fractured sample is split along the fracture plane to view the dimension and shape of the created fracture. The fracture extent is outlined according to the spread of the red ink. A 3D photogrammetry model is then created to digitize the fracture radius.

4 Results

4.1 Experiment

The pressure response from the hydraulic fracturing experiments on two samples TFK01 and TFK02, shown in Fig. 4, presents the classic response expected during a hydraulic fracturing operation (Lesage et al. 1991). The pressure response during the entire injection cycle and finally the shut-in can be divided into five distinctive parts as described below.

• 1. Pressure build-up: This part includes a linear increase in pressure due to the constant injection rate (‘1’ in Fig. 4). The response is linear, apart from the very initial part of the pressure curve, which is affected by the compression of the air bubbles in the injection system. The slope of the pressure curve represents the compressibility of the injection system plus some effects of the fluid leak-off. Separate experiments were performed to study the compressibility of the individual components of the injection system, viscosity of the injection fluid, and amount of air contained in the system. These experiments are reported in the Appendix.

• 2. Breakdown pressure: Due to the continuous fluid injection, the fluid pressure in the wellbore keeps increasing, until it reaches the maximum pressure (also called breakdown pressure), required to open the initial-notch and initiate fracture propagation. The breakdown values for both experiments agree well, with TFK01 showing a slightly higher breakdown pressure (‘2’ in Fig. 4). Apart from the rock elastic properties, the magnitude of the maximum pressure is also influenced by the viscosity of injection fluid, rock permeability and entry friction (Deb et al. 2018; Lecampion and Desroches 2015; Matsunaga et al. 1993).

• 3. Propagation pressure: This decaying pressure response corresponds to the propagation of the fracture (‘3’ in Fig. 4), which increases the fracture volume which, in turn, reduces the resistance against further propagation.

• 4. Instantaneous shut-in pressure: This pressure is measured immediately after the shut-in (‘4’ in Fig. 4) when the pressure drops due to the elimination of flow resistances. It corresponds to pressure equilibrium in the fracture and in the well (injection system), removing any pressure gradient across the hydraulic fracture or between the well and the fracture. It is the pressure required to keep the fracture open (Zoback et al. 1977).

• 5. Leak-off pressure: Finally, the last part of the pressure response represents the pressure dissipation due to leak-off (‘5’ in Fig. 4), where the slope of the pressure curve represents the leak-off rate. The leak-off rate in TFK01 is slightly higher than in TFK02.

Fig. 4

Pressure response P (left y axis) and injection rate Q (right y axis) with time during the hydraulic fracturing experiments in TFK01 (solid line) and TFK02 (dashed line); the different stages of the pressure response are annotated as 1 for pressure build-up, 2 for breakdown pressure, 3 for fracture propagation, 4 for instantaneous shut-in and 5 for leak-off or pressure decay (left figure); and final fracture size in TFK01 (solid line) and TFK02 (dashed line) (right figure)

In the previous experiments (Siebert 2017), the volume change of the flat jacks parallel to the fracture plane was evaluated. The flat jacks were operated at a constant pressure mode by automatically adjusting the fluid volume inside the flat jacks. As a result of fracture propagation, the specimen deforms perpendicular to the fracture plane, causing a volume change of the flat jacks. As the rock samples were assumed to be incompressible and impermeable, the volume change of the flat jacks was expected to correspond to the fracture volume. However, it was found that the change in the volume of the flat jacks could account for only 10% of the injected volume. This indicated a considerable fluid loss into the system. In the experiments presented in this paper, the volume of fluid loss is calculated as the difference between the pump volumes at atmospheric pressure conditions before and after injection (see point 7 of Protocol). It was estimated that around 44% of the injected fluid was lost into the rock matrix in TFK01 and 38% was lost in TFK02.

In Fig. 4, we also observe the quasi-circular shape of the final fracture in both the experiments due to the uniform horizontal stresses in x- and y-direction. In addition to minor differences in breakdown pressure ($\sim 1.5\ \mathrm{MPa}$), we also observe that the final fracture size of TFK01 is slightly smaller than TFK02. Considering the natural differences in the grain contacts and internal texture in rocks, these minor differences are to be expected even in identical experimental conditions. Additionally, the slight differences in fluid viscosity in the two experiments ($0.51\ \mathrm{Pa}\ \mathrm{s}$ in TFK01 and $0.6\ \mathrm{Pa}\ \mathrm{s}$ in TFK02) may have resulted in more leak-off in the former experiment and consequently resulted in a smaller fracture. The higher breakdown pressure in TFK01, among other parameters, may also explain the smaller fracture radius as relatively higher energy was spent in overcoming the resistance to initiate fracturing than in TFK02. This pattern can also be observed in Fig. 5, where we see the cumulative number of AE events before breakdown for TFK01 is much higher than for TFK02. In both the experiments, the maximum number of events is recorded between 500 and 1500 s, i.e., between breakdown and shut-in. Very few events are also located during the post-shut-in pressure release phase, which may be triggered by friction while the fracture is closing due to the roughness of the fracture surfaces.

Fig. 5

Cumulative number of acoustic events generated during the experiments of TFK01 (left) and TFK02 (right)

In Fig. 6, we present the localized AE foci or hypocenters (left) and the image of the split samples showing the fracture outline (right) for the experiments TFK01 (top) and TFK02 (bottom). The samples were split along the fracture plane, and the fracture extent was outlined by the spread of the red ink. This colored fracture extent correlates well with the localized AE events.

Fig. 6

Hypocenters of the acoustic emission data with color-coded arrival time (left) and fracture radius from the experiments (right), image of the split samples with fracture outline (dashed line) are shown

4.2 Numerical Modeling: CSMP

4.2.1 Model Parameters

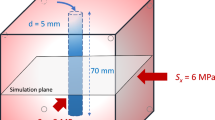
A three-dimensional model of the hydraulic fracturing experiment (Fig. 7) is constructed using a block with dimensions 300 mm × 300 mm × 450 mm, with an initial fracture of radius 17 mm located horizontally in the center of the block (22.5 cm from the top of block).

Fig. 7

3D model of the experiment in CSMP, showing the vertical well (white line), fluid pressure in fracture plane ${p}_{f}$ and in matrix ${p}_{m}$, as well as the mesh used for simulations (Color figure online)

The parameters used in the simulations are listed in Table 1. Among them, the values for Young’s modulus, Poisson’s ratio, porosity, fluid viscosity and the volume of injection system measured in laboratory experiments, are used directly in the numerical simulations. However, some parameters including the matrix permeability, bulk modulus of the injection system and fracture toughness had to be modified to improve the fit with the experiment results.

The fluid flow through the well (or injection system) also affects the pressure response during the hydraulic fracturing process by providing additional compressibility and modifying the actual flowrate entering the hydraulic fracture. The volume of the injection system has been modelled using a vertical well of length 22.5 cm and radius 0.49 cm connected to the center of the initial fracture. The well is modelled using line elements. A constant injection rate of 0.1 mL/min is applied at the top of the well. The flow through the well is given by

$$\mathrm{div}\left(\frac{\pi {{r}_{w}}^{4}}{8{\mu }_{f}}\nabla {p}_{f}\right)=\frac{\pi {{r}_{w}}^{2}}{{K}_{f}}\frac{\partial {p}_{f}}{\partial t}$$

(18)

where, ${r}_{w}$ is the radius of the well. Direct leak-off from the wellbore into the rock matrix is disregarded, and the wellbore is directly connected to the hydraulic fracture.

4.2.2 Simulation

A first set of simulations were performed using the values measured in the laboratory for matrix permeability (${k}_{m}=5 \times {10}^{-18}\ {\mathrm{m}}^{2}$), fracture toughness (${K}_{ic}=1.66\ \mathrm{MPa}\ {\mathrm{m}}^{0.5}$), and bulk modulus of the injection system (${K}_{f}=0.47\ \mathrm{GPa}$) calculated from the slope of the pressure build-up curve. As can be seen in Fig. 8, the simulated initial pressure build-up (‘1’) agrees very well with the one in experiment TFK02. However, the lack of any post-shut-in pressure decay (‘5’) in the simulation indicated that the matrix permeability of $5 \times {10}^{-18}\ {\mathrm{m}}^{2}$ (measured in the laboratory) was insufficient for simulating the pressure decay in the experiment. Following this, a systematic parameter sensitivity analysis is performed to identify the important parameters and their best value for an optimal fit.

Fig. 8

Pressure response from TFK02 experiment (in red) compared with simulated pressure response for different matrix permeabilities (in ${\mathrm{m}}^{2}$, in black) (Color figure online)

Permeability The pressure dissipation observed in the experiment indicates that fluid is lost into the matrix. This may occur due to different reasons (i) if the matrix permeability of block TFK02 is greater than the one measured on the small granite plugs. Increasing the matrix permeability by one order of magnitude, to $5 \times {10}^{-17}\ {\mathrm{m}}^{2}$, yielded the best fit for the slope of the leak-off pressure dissipation (‘5’) as well as the instantaneous shut-in pressure (‘4’) in Fig. 8. For sensitivity analysis, other simulations with two different values of matrix permeability are also plotted in Fig. 8. The permeability value smaller than $5 \times {10}^{-17}\ {\mathrm{m}}^{2}$ yields higher pressures during post-shut-in, while the permeability value higher than $5 \times {10}^{-17}\ {\mathrm{m}}^{2}$ yields lower pressures (‘5’ on Fig. 8). However, with increased permeability, additional deviations from the experimental curve can be observed for the build-up pressure (‘1’), breakdown pressure (‘2’), propagation pressure (‘3’) and instantaneous shut-in pressure (’4’).

Bulk Modulus of Injection System The pressure reaction to the volume change of the pump is determined by the bulk modulus of the entire injection system which comprises the pump, pipes, injection interval, and fluid. The slope of the pressurization curve prior to breakdown can provide the overall system compressibility. However, with matrix permeability in the order of ${k}_{m}=5 \times {10}^{-17}\ {m}^{2}$, leak-off into the matrix from the initial-notch cannot be excluded and therefore the pressurization phase is also affected by matrix permeability in addition to the compressibility of the system, particularly at pressures higher than 15 MPa (the maximum horizontal stress). As can be seen in Fig. 8, the higher the permeability (in the order of ${10}^{-17}\ {\mathrm{m}}^{2}$), the more delayed is the pressure build-up compared to the experiment. Therefore, the compressibility of the injection system has been slightly reduced by increasing the bulk modulus of the injection system to $0.56\ \mathrm{GPa}$. This improved the match of the build-up pressure response between simulation and experimental results for both TFK01 and TFK02 samples as shown in Fig. 9.

Fig. 9

CSMP simulations for TFK01 (top) and TFK02 (bottom) experiments for pressure response (left) and fracture size (right) with matrix permeability ${k}_{m}=5 \times {10}^{-17}\ \mathrm{m}^{2}$, bulk modulus of injection set-up ${K}_{f}=0.56\ \mathrm{GPa}$ and two different values of fracture toughness

Fracture Toughness In Fig. 9, we also see the predicted versus experimentally observed final fracture size for both experiments. CSMP simulations with $1.5\ \mathrm{MPa}\ {\mathrm{m}}^{0.5}$ reproduced the fracture radius of TFK02 but predicted a smaller fracture for TFK01, perhaps due to the different fluid viscosity values in the two experiments. To simulate a hydraulic fracture of the same size as in the experiments, the fracture toughness was lowered to $1.0\ \mathrm{MPa}\ {\mathrm{m}}^{0.5}$. The pressure responses and fracture sizes from simulations using different values of fracture toughness (${K}_{Ic}=1.5\ \mathrm{MPa}\ {\mathrm{m}}^{0.5}, {K}_{Ic}=1.0\ \mathrm{MPa}\ {\mathrm{m}}^{0.5}$) are compared with experimental data of TFK01 and TFK02 in Fig. 9. Inspecting Fig. 9, one may suspect that a higher fracture toughness is associated with a small fracture size and that the fracture toughness decreases as the fracture propagates. Since a higher fracture toughness corresponds to a higher fracture aperture, future measurements of the fracture aperture may reveal if this scenario is relevant to this experiment. Decreasing the fracture toughness to ${K}_{Ic}=1.0\ \mathrm{MPa}\ {\mathrm{m}}^{0.5}$, yields the correct fracture size but, at the same time, reduces the breakdown pressure (by ~ 4 MPa) in both TFK01 and TFK02 (Fig. 9).

Effect of Entry Friction A possible explanation for the lower prediction of breakdown pressure is the local pressure drop (a function of the entering flow rate) at the connection between the well and the fracture, i.e., a choke-like effect, also referred to as entry friction (Lecampion and Desroches 2015). This effect is expected to be highest initially as the fracture is closed under stress and diminishes as the fracture aperture increases towards the end of fluid injection. Two simulation tests were performed to test this effect. In CSMP, the flow between the wellbore and the fracture is continuous, i.e., the pressure at the connection between the wellbore and the fracture is the same on both sides (fracture and wellbore). Therefore, to mimic the entry friction (pressure loss), a pressure gradient is developed along the wellbore. To this end, the hydraulic conductivity of the well has been artificially reduced to force the pressure to drop from the injection pressure to the fluid pressure inside the hydraulic fracture. Figure 10 shows the injection pressures for low and high entry friction in the TFK01 experiment. Initially high entry friction may explain the high break-down pressure measured during the hydraulic fracturing experiment. However, the entry friction has become smaller as the fracture propagated and its aperture at the intersection with the wellbore increased. Entry friction effects, as expected, diminish when the injection stopped.

Fig. 10

Pressure response from simulation for low and high entry friction in TFK01 experiment

4.3 Numerical Modeling: GEOS

4.3.1 Model Parameters

The experimental system was modeled as a quarter system to make use of the symmetry axis through the origin in x- and y-planes (Fig. 11). This results in a system measuring 150 mm × 150 mm × 550 mm. In the z-direction, the 550 mm are composed of the 450 mm of the rock specimen, as well as 50 mm of solid steel plate that were used in the experiment to apply the stress boundary condition of 5 MPa evenly on the top and bottom of the specimen. The numerical resolution was set to an edge length of 1.875 mm in x- and y-direction respectively. To enable a finer resolution around the fracture zone, element edge lengths were refined in z-direction as follows: 5 mm edge length in the solid steel plates (between − 275 mm and − 225 mm; and between 225 and 275 mm), 6.7 mm edge length in the rock specimen with exception of 1.5 mm edge length between the z-coordinates of − 30 mm and 30 mm in the center of the system. This resulted in a total element number of 755 200 for the solid domain. The saw-cut notch in the wellbore with a radius of 17 mm is accounted for by a locally variable fracture aperture of 0.6 mm thickness. For each element in this region, a local cubic law approach is employed for fluid flow while mechanical contact is solved with a penalty method. Further information on this variable aperture approach can be found in Vogler 2016; Vogler et al. (2016, 2018).

Fig. 11

Schematic of the numerical system used for GEOS simulations

Rock properties such as density, bulk modulus, shear modulus, uniaxial compressive strength, rock fracture toughness, and matrix porosity were taken directly from experimental measurements (Table 1). For the fluid viscosity, the arithmetic mean ($0.55\ \mathrm{Pa\ s}$) of the two measurements ($0.51\ \mathrm{Pa\ s}$ and $0.6\ \mathrm{Pa\ s}$) was used to represent an average fluid viscosity. For the steel plates on the top and bottom of the domain, a density of $8000\ \mathrm{kg}/\mathrm{m}^3$, bulk modulus of $159\ \mathrm{GPa}$ and a shear modulus of $77\ \mathrm{GPa}$ were used.

The wellbore is discretized using the same finite volume approach as the fracture and matrix, considering frictional losses along the pipes and through the perforation holes in the wellbore, using standard relations for these terms (Brown 2002). A volumetric compliance is introduced to model the stiffness of the wellbore packer and correlated with the experimentally measured stiffness modulus of the packer. An incremental pressure increase in the wellbore then leads to an incremental expansion of the wellbore volume, which can be calculated with the volumetric compliance. The wellbore solver also accounts for the total volume of the injection system and pump.

The traction boundary condition on the top and bottom of the experimental set-up was applied on the steel plates on the specimen. Zero-displacement conditions in x- and y-direction were applied on the symmetry planes in yz- and xz-directions (going through the origin of the system), respectively (Fig. 11). The initial stress states applied to the specimen were used as initial conditions for the stress fields in all three directions. To initialize the simulation, the pressure in the wellbore was ramped up to $2\ \mathrm{MPa}$ during the first $220\ \mathrm{s}$. This reflects a time period during which compression of air occurs in the experimental system, which is difficult to replicate in the numerical system without more detailed knowledge of the exact air content in the system.

4.3.2 Simulation

Numerical simulations of the fracture growth during pressurization of the system were compared with the experimental results of fracture radius and pressure response at the pump (Fig. 12). While the simulation correctly predicts the pressure build-up, propagation pressure and shut-in pressure, the breakdown pressure is underestimated by almost 6 MPa. Figure 13 shows the resulting vertical stress and displacement fields. The bounding plates on the system wall are not shown in the figure. The vertical stress ${\sigma }_{z}$ at the time of shut-in (Fig. 13, left) exhibits the expected stress shadows of higher compressive stresses above and below the fracture, caused by the compression of the rock mass. Vertical stress at the fracture tip, however, is tensile, resulting in further fracture propagation once the tensile stresses increase sufficiently. The opening of the fracture then results in a radially symmetric displacement field (Fig. 13, right). Very little displacement occurs beyond the fracture tip, as most of the displacement is concentrated near the center of the fracture. The most sensitive parameters affecting the GEOS simulations are:

Fig. 12

Simulation of TFK01 and TFK02 using code GEOS: pressure (in MPa) response versus time (s) (left) and fracture radius (mm) (right)

Fig. 13

Vertical stress z and displacement in the solid domain d (in $\mu \mathrm{m}$) at the time of shut-in. Only the rock specimen is displayed, without the loading plates. The hydraulic fracture is visible in the center of the specimen

Permeability Compared to the value measured in the laboratory ($5 \times {10}^{-18}\ {m}^{2}$), matrix permeability had to be increased to 10^‒16 m² to obtain a faster pressure decay similar to the experiments. The fluid pressure declined more rapidly in the experiments between breakdown and shut-in as well as after shut-in, indicating a significant fluid leak-off out of the fracture and into the matrix (Fig. 12).

Bulk Modulus of Injection System GEOS uses an analytical wellbore solver to account for frictional pressure losses in the pipe as well as at the perforations and deformation of the wellbore. The total fluid volume of the experimental system of $17\ \mathrm{mL}$ is incorporated in the wellbore solver of the numerical simulations where a bulk modulus of the injection system of $0.5\ \mathrm{GPa}$ was found to reproduce the initial fluid pressure build-up before breakdown.

Effect of Entry Friction To account for pressure losses due to piping and perforation holes, three perforation holes were included in the wellbore solver. This results in frictional losses that are mostly observable after peak pressure (when fluid flow out of the wellbore and into the fracture increases) up until shut-in, after which the pressure curve shows a significant pressure loss. In GEOS, the connection between the wellbore and the fracture finite volume cells is described by the standard conservation equations which account for perforation friction pressure as a function of pump rate, number of perforations taking fluid, diameter of each perforation and the discharge coefficient (Bell and Cuthill 2008). The experimental system additionally shows frictional losses at the notch and fracture entry, which were not explicitly reproduced by the wellbore solver.

5 Discussion

The results obtained by both the codes show that, despite differences in modeling approaches, the implemented physics based on LEFM and lubrication theory captures the coupled processes in the experiment sufficiently well. Both the numerical codes (CSMP and GEOS) correctly predict the pressure build-up (‘1’) by implementing the wellbore solver models to consider the influence of system compressibility (pumps, pipes, well and fluid) during the initial pressurization phase.

While the measured intrinsic rock permeability in the laboratory was in the order of $5 \times {10}^{-18}\ {\mathrm{m}}^{2}$, the pressure decline observed in the experiments could only be matched by increasing the matrix permeability by one–two orders of magnitude in both the simulators. This variation in permeability may have been influenced by the modeling assumptions. In the experiments, owing to the large size of the samples, it was not possible to ensure that the samples were fully dry or in a fully water-saturated condition. As estimated at the end of the experiment that approximately 38% and 44% of fluid was lost into the rock in TFK01 and TFK02, respectively. Both CSMP and GEOS, assumed that the rock was in a fully-saturated condition, and as a result the amount of flow into the dry rock is not properly represented by this fully saturated approach, and a higher permeability was required to fit experimental results. Salimzadeh and Khalili (2015) showed numerically that assuming a fully saturated rock reduces the amount of leak-off in the simulations relative to the actual leak-off in an unsaturated (dry) rock for a given permeability. This is because the amount of water required to saturate a dry rock is not considered in single-phase fluid (saturated) models. This assumption may have also caused the smaller computed breakdown pressure relative to the experiments.

Additionally, microcracks developed due to pressurization of the sample exceeding the maximum applied stresses (15 MPa) may have contributed to the permeability enhancement even before the main fracturing event. The possibility of creating microcracks before the main tensile event can be supported by the numerous seismic events recorded before the breakdown pressure in both TFK01 and TFK02 (Fig. 5). In similar hydraulic fracturing studies (Matsunaga et al. 1993; Lockner 1993; Ishida et al. 2004), first motion studies of the seismic events before the breakdown pressure indicated that most source mechanisms are double couple shear events and not pure tensile events. Therefore, the possibility of occurrence of shear-induced fractures and subsequent permeability enhancement of the rock before the creation of the main tensile hydraulic fracture cannot be excluded. A further analysis of the focal mechanisms of the AE events might reveal in greater detail the characteristics of the seismic events, but this topic is beyond the scope of our study.

GEOS simulated the final fracture size of TFK01 using the given fracture toughness value of ${K}_{Ic}=1.66\ \mathrm{MPa}\ {\mathrm{m}}^{0.5}$. However, the breakdown pressure was underestimated by around 6 MPa (Fig. 12). CSMP simulations with $1.5\ \mathrm{MPa}\ {\mathrm{m}}^{0.5}$ resulted in different final fracture radii for the two experiments [smaller in TFK01 than in TFK02 (Fig. 9)], perhaps due to the different fluid viscosity values used in the simulations. Reducing the fracture toughness to ${K}_{Ic}=1.0\ \mathrm{MPa}\ {\mathrm{m}}^{0.5}$ yielded in larger fracture radius and good match with the experiments but also a decreased breakdown pressure. As mentioned before, the predicted smaller breakdown pressure could be the result of the model approach, which assumed fully saturated rock, thereby underestimating the amount of fluid leak-off into the matrix. This ambiguity can only be resolved by future experiments on a fully saturated sample.

6 Conclusion

In this paper, we compared experimental results and numerical simulations of the growth and propagation of Mode-I tensile fractures from a pre-existing weak zone in granite samples. The simulation results emphasize the complexity of predicting hydraulic fracturing process in low-permeability rocks, where different stages of pressure response (build-up, breakdown, propagation, shut-in, and decay of pressure) evince the coupling of different parameters (matrix permeability, fluid viscosity, influence of injection system, material toughness).

By modeling the response of the injection system, both simulators perfectly reproduce the initial pressure build-up phase and the early stages of fracture growth This was achieved by including the wellbore models. The differences observed in the breakdown pressure and post-breakdown pressure decay between the experiment and the simulation may be due to the significant fluid loss into the matrix and the model assumption of a fully saturated rock. Inducing fluid loss into the matrix by increasing the rock matrix permeability in the simulations, partly improved the match of pressure response with the experiment. However, the under-determined saturation state of the granite samples may have contributed to higher breakdown pressure in the experiments. Due to the large size of the samples, it was not possible to ensure that the rock is fully-saturated before the hydraulic fracturing experiment. This is therefore a limitation of the current experimental study. To avoid such ambiguities, future experiments must ensure fully saturated condition in a rock.

Both the numerical models were verified in this study, as they reproduced the hydraulic fracturing process in the observed scale well, although some differences remain owing to the different approaches chosen. It is important to emphasize that laboratory-scale experiments are influenced by several small-scale processes such as decompression of injection set-up, stress field near the borehole, boundary influences due to limited sample size and frictional force encountered by the fluid in the injection line. These specific processes may have very limited or no influence in the field-scale fracturing process, where the cracks generated through hydraulic fracturing spread very far in a short time. The field-scale problem, on the other hand, is generally governed by different regimes of loading than the experimental case. The experiments reported in this study are performed with the objective of verification of numerical predictions and may not be directly extended to field scale on their own. Nevertheless, the verification of these simulators against laboratory-scale experiments builds up confidence in the verified simulators and justifies their application to future field-scale problems.

7 Appendix

7.1 Injection System Characterization

During the experiment, the entire injection system comprising pump, pipes, injection interval and fluid is pressurized by reducing the pump cylinder volume. In addition to the compression of the fluid, the surrounding parts (e.g., pipes, pump, pressure transmitters) are deformed by the pressure. The pressure reaction to the volume change of the pump is therefore determined by the entire injection system and not only by the compressibility of the fluid. In this context, Siebert (2017) calculated a compressibility of the system of $2.75\pm 0.12\ {\mathrm{GPa}}^{-1}$ (bulk modulus ~ $0.4\ \mathrm{GPa}$) for the experiments he performed.

In this work the compressibility of the individual components of the injection system was investigated and characterized in more detail. The compressibility effects within a hydraulic system may be considered as a series of springs that describe the stiffness of the individual components (Manning and Fales 2019). Various experiments were carried out to determine these stiffnesses. Parts of the injection system were pressurized with fluids of the known bulk modulus. The bulk modulus of the components of the injection system was then calculated from the pressure response of the system. The injection system comprising pump, pipes, valves, pressure transmitters and the packer was divided into two subsystems. Subsystem 1 refers to the components between valve A and valve B, while Subsystem 2 refers to the components between valve B and valve C (see Fig. 2 for details).

The first step was to determine the bulk modulus of subsystem 1. The pump was filled with a volume of $5\ \mathrm{ml}$, which corresponds to the volume of the pump in the hydraulic fracturing tests. According to the fracturing experiments, the volume of the pump was reduced at a rate of $0.1\ \mathrm{mL}/\mathrm{min}$ until a pressure of $40\ \mathrm{MPa}$ was reached. The effective bulk modulus ${K}_{\mathrm{e}}$ of the subsystem1 was then calculated using Eq. (A). V_e is the effective volume which is deformed, so in this case the volume of the pump and the pipes to valves A and B.

$${K}_{\mathrm{e}}=-{V}_{\mathrm{e}}\frac{\mathrm{d}P}{\mathrm{d}{V}_{\mathrm{e}}}$$

(A)

According to Manning and Fales (2019), the effective bulk modulus of a container filled with fluid be calculated from equation B. In Equation B, K_f is the bulk modulus of the fluid and K_c is the bulk modulus of the container, in this case the pump, pipes and valves between valves A and B:

$${K}_{e}={\left(\frac{1}{{K}_{\mathrm{f}}}+\frac{1}{{K}_{\mathrm{c}}}\right)}^{-1}$$

(B)

Rearranging equation B and using the known bulk modulus for the fluid yields the bulk modulus of subsystem 1: ${K}_{\mathrm{c},1}=0.18\pm 0.003\ \mathrm{GPa}$.

In the next step, the compressibility of subsystem 2 was determined. For this purpose, the entire injection system consisting of subsystem 1 and subsystem 2 was loaded similar to the previous test. The packer was installed in a steel cylinder with an inner diameter of 20 mm and an outer diameter of 120 mm. Due to the wall thickness of the cylinder, it is considered to be undeformable. Using a steel cylinder instead of rock prevents the effects of fluid leak-loss into the matrix. The effective bulk modulus of total system (subsystem 1 and subsystem 2 combined) was calculated using Eq. A.

To calculate the bulk modulus of subsystem 2, ${K}_{\mathrm{c},2}$ (components between valves B and C) equation B is modified as follows.

$${K}_{e}={\left(\frac{{V}_{\mathrm{c},1}}{{V}_{\mathrm{f}}}\frac{1}{{K}_{\mathrm{c},1}}+\frac{{V}_{\mathrm{c},2}}{{V}_{\mathrm{f}}}\frac{1}{{K}_{\mathrm{c},2}}+\frac{1}{{K}_{\mathrm{f}}}\right)}^{-1}$$

(C)

Using Eq. (C) the bulk modulus of subsystem 2 was determined to ${K}_{\mathrm{c},2}=2.7\pm 0 .15\ \mathrm{GPa}$

7.2 Estimation of Air Content

The experiments to determine the bulk moduli were carried out with de-aired fluids of known bulk moduli. Furthermore, the bulk moduli were derived in a pressure range in which any remaining residual air in the system is completely compressed and has no influence on the overall system. However, in the actual fracturing experiment, a mixture of glycerol and ink is used as injection fluid. Despite all efforts, it is impossible to completely exclude entrained air from the system. Therefore, the injection fluid must be considered as a mixture of glycerol, ink and air. The proportion of air varies in the individual experiments and must be determined anew each time. To estimate the air content in the individual experiments, the method presented in Kim and Murrenhoff (2012) and Jinghong et al. (1994) is used. The method is referred to as volume-change approach. Based on the initial volume V₀ the change in fluid volume during pressurization is calculated. By applying a tangent to the pressure versus volume change curve the effective bulk modulus can be estimated. The intersection of this tangent with atmospheric pressure provides the proportion of entrained air (Fig. 14). The method is applied on the pressurization path in each fracturing experiment. Figure 14 shows the results for the experiments TFK01 (~ 6% air) and TFK02 (~ 4.4% air). The presence of air delays the pressure increase during the initial injection. In previous experiments (Siebert 2017), an air content of around 0.5–9 % was estimated.

Fig. 14

Estimation of air content X₀ for TFK01 (left) and TFK02 (right)