1 Introduction

The hydraulic properties of fractured geological formations have been of interest for many purposes such as developing fluid resources (e.g., geothermal fluids, shale oil, and groundwater), geological storage or disposal, and seismic events (fault reactivation and induced seismicity). It is known that fracture permeability and preferential flow paths within fractures are controlled by the heterogeneous distribution of apertures, which can vary as stress changes (Krantz et al. 1979; Raven and Gale 1985; Thompson and Brown 1991; Watanabe et al. 2008; Ishibashi et al. 2015; Chen et al. 2017; Vogler et al. 2018). In-situ stress is never constant during geoengineering developments or on the geological time scale, and consequently, the aperture distribution and associated hydraulic properties also must change in natural settings (e.g., Manga et al. 2012). These changes produce transitions in the patterns of fracture flow that in turn control the fault reactivation cycle (Sibson et al. 1988) and characterize the transport behavior of fluid resources.

Geophysical observations can detect changes in electrical resistivity or elastic wave velocity that may reflect subsurface stress changes associated with hydraulic stimulation, earthquakes, or geothermal fluid production (Peacock et al. 2012, 2013; Didana et al. 2017; Mazzella and Morrison 1974; Park 1991; Gunasekera et al. 2003; Brenguier et al. 2008; Nimiya et al. 2017; Taira et al. 2018). It would be beneficial if changes in aperture-related hydraulic properties triggered by subsurface stress changes could be linked to geophysical properties that can be remotely monitored. Studies based on synthetic or simulated single fractures have related hydraulic properties to electrical properties (Stesky 1986; Brown 1989; Volik et al. 1997; Kirkby et al. 2016) and to elastic properties (Pyrak-Nolte and Morris 2000; Petrovitch et al. 2013, 2014; Pyrak-Nolte and Nolte 2016; Wang and Cardenas 2016). These studies have confirmed that the relationships of these properties depend on features of the fracture microstructure (e.g., pore connectivity, tortuosity, apertures, and contacts), which varies with the initial fracture roughness and changes with normal stress. On one hand, connected apertures are characterized by pore connectivity and tortuosity, both of which are strongly related to the permeability–resistivity relationship. On the other hand, discrete points of contact (asperities) contribute to hydro-mechanical properties. Therefore, both hydraulic–electrical and hydraulic–elastic relations may reflect similar microstructures; however, the underlying mechanisms do not necessarily have a mutual correlation. Simultaneous measurements in identical samples may shed light on the nature of variations in rock properties and their relationships. To our knowledge, no study has simultaneously investigated hydraulic, electrical, and elastic properties of natural rock fractures.

This study took advantage of recent advances in Digital Rock Physics (e.g., Tsuji et al. 2019; Sain et al. 2014) that enabled us to simultaneously determine multiple properties in the same sample while visualizing its microstructure. In this study, we explored the simultaneous changes in fracture permeability, electrical resistivity, and elastic wave velocity of natural rock fractures that occur with increasing normal stress. By coupling experiments and digital fracture simulations, we investigated the correlations between hydraulic–electrical–elastic properties and addressed their governing mechanisms. Many studies have reported a correlation between permeability and fracture specific stiffness, which is related to the amplitude of the seismic response (i.e., attenuation), but have not established a direct correlation between permeability and seismic velocity (Pyrak-Nolte and Nolte 2016; Wang and Cardenas 2016). Some experimental studies have observed velocity changes with aperture closure (e.g., Nara et al. 2011; Choi et al. 2013), but none has established a direct relationship between seismic velocity and fracture permeability. As an alternative to fracture specific stiffness, in this study, we adopted finite-element modeling of static elasticity to calculate elastic wave velocity. In this paper, we also evaluate the local behavior of the fluid flow (i.e., preferential flow paths) within fractures to investigate the connectivity of flow paths, flow area, and their transient changes. Our lattice Boltzmann simulation of digitized rock fractures reveals transitions in 3D fracture flow patterns that accompany stress changes, which are difficult to observe in laboratory experiments or in the field. We discuss how transient changes of the fracture flow pattern are correlated with hydraulic and geophysical properties, and suggest possible applications of our findings to seismogenic zones and geothermal reservoirs.

2 Methods

2.1 Sample and Experimental Procedure

We evaluated the dependency of the fracture permeability on the effective normal stress in fluid-flow experiments. These employed two cylindrical fractured samples of Inada granite 50 mm in diameter and 80 mm long, in which the fracture plane was parallel to the central axis. The two samples differed in the roughness characteristics of their fracture surfaces, as determined from the surface topographies of the hanging wall and footwall which we mapped in a grid of cells 23.433 µm square with a 3D measuring microscope (Keyence, VR-3050). The surface of one sample, called the smooth fracture hereafter, had a fractal dimension of 2.5 and a root-mean-square (rms) roughness of 1.3 mm, whereas the surface of the other sample, called the rough fracture hereafter, had a fractal dimension of 2.4 and rms roughness of 1.7 mm (Power et al. 1987; Power and Durham 1997). The fractal dimension describes the scaling characteristics of surface topographies and is a measure of fracture surface roughness (Brown 1995). The rms roughness, called roughness hereafter, represents an rms height of fracture surface topographies. The initial aperture distribution of each fracture and the corresponding probability histogram are shown in Fig. 1. Note that initial aperture models are created by numerically mating the mapped fracture surfaces, where they are assumed to be in contact at one point. The aperture distribution in the smooth fracture (Fig. 1a) shows less spatial variation than that of the rough fracture (Fig. 1b). Consequently, the aperture distribution of the smooth fracture shows a sharp peak of probability, whereas the rough fracture shows a broad distribution (Fig. 1c).

Fig. 1
figure 1

Fracture aperture distribution of a smooth and b rough fracture and c probability histogram of apertures. Color in (a) and (b) represents the fracture aperture (color figure online)

Full size image

After measuring the fracture surfaces, we conducted fluid-flow experiments on these two samples. Distilled water was injected into jacketed samples under various effective normal stresses between 5 and 30 MPa. The pore-inlet, pore-outlet, and confining-oil pressures were independently controlled by syringe pumps. For each stress state, we measured flow rates and thereby evaluated the fracture permeability based on the cubic law (e.g., Witherspoon et al. 1980), where we assumed Darcy flow and a negligible matrix permeability of granite (between 10–19 and 10–22 m2).

2.2 Numerical Simulation

We performed a series of numerical simulations on digitized fractures. Three-dimensional digital fracture models were prepared for each sample directly from the mapped surface topographies described above in a system of 0.1 mm cubic voxels. The use of a three-dimensional fractured sample enabled us to model local transport properties along with the rough-walled fractures. Although the voxel size potentially affects absolute values of permeability and resistivity to some degree, we confirmed that a 0.1 mm voxel system is small enough for our qualitative interpretations (Appendix 1). The distance between the two surfaces was adjusted in each model by uniformly reducing the local apertures, so that the digitized fracture had a simulated permeability equivalent to that measured in the real fractures (Watanabe et al. 2008; Ishibashi et al. 2015).

Subsequently, we simulated 3D local flows within the fractures by the lattice Boltzmann method, which is suitable for modeling heterogeneous local flows with complex boundaries (He and Luo 1997; Jiang et al. 2014). The governing equation for the lattice Boltzmann method in the D3Q19 model is given by (Ahrenholz et al. 2008):

$$\begin{array}{c}{f}_{i}\left({\varvec{x}}+\varvec{e}_{i} \Delta t, t+\Delta t\right)={f}_{i}\left({\varvec{x}}, t\right)+{\boldsymbol{\Omega }}_{{\varvec{i}}}, i=0, \cdots 18,\end{array}$$
(1)

where \(\Delta t\) is the time step and \({f}_{i}\left({\varvec{x}}, t\right)\) is the particle distribution function that represents the probability of finding a particle at node \({\varvec{x}}\) and time \(t\) with velocity \({{\varvec{e}}}_{i}\). Collision operators \({\varvec{\Omega}}\) are defined by:

$$\begin{array}{c}\varvec{\Omega} ={{\varvec{M}}}^{-1}\varvec{S}\left[\left({\varvec{M}}{\varvec{f}}\right)-{{\varvec{m}}}^{{eq}}\right], \end{array}$$
(2)

where \({\varvec{M}}\) is a transformation matrix that transforms the particle distributions into moment space. The equilibrium vector \({{\varvec{m}}}^{{eq}}\) is composed of equilibrium moments, and the matrix \({\varvec{S}}\) is a diagonal collision matrix indicating the relaxation rates (Jiang et al. 2014). We implemented this model using advanced memory-saving schemes and parallel-GPU techniques to simulate digital fracture systems with a large domain and high resolution (Jiang et al. 2014). At the fracture surfaces, bounce-back boundaries (a no-slip scheme at fluid–solid interfaces) were implemented. Provision of a constant body force from the inlet to the outlet boundaries and the periodic boundary along the fracture plane enabled us to simulate the fracture flow (Fig. 2). Permeability along the fracture was estimated from the macroscopic flow velocity that was calculated from the particle distribution function (\({f}_{i}\)). A series of lattice Boltzmann simulations enabled us to explore the changes with stress state in permeability and in the flow area, defined as the ratio of the area of preferential flow paths to the area of the fracture plane (Watanabe et al. 2009).

Fig. 2
figure 2

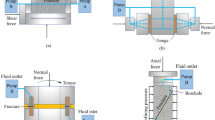
Model setup of the 3D digital fracture simulation. Fluid flow and applied voltage are defined as parallel to the fracture plane, whereas elastic wave velocity is defined as perpendicular to the fracture plane. Both the lattice Boltzmann simulation and finite-element modeling adopt a periodic boundary condition

Full size image

Once the lattice Boltzmann simulations yielded estimates of the heterogeneous distribution of flow within the fracture, we evaluated both the resistivity and the elastic wave velocity using the finite-element method, which is a well-established method of computing rock properties from three-dimensional microstructure (Garboczi 1998; Andrä et al. 2013; Saxena and Mavko 2016). Both analyses implemented a periodic boundary along the fracture plane. Resistivity in the direction parallel to the fracture plane (and the fluid-flow direction) was calculated from Ohm’s law, where the electric current was simulated from the potential difference between the inlet and outlet boundaries. Parameters used in our finite-element modeling are summarized in Table 1. For the electrical conductivity of the solid, we used the experimental value of Inada granite under dry conditions, measured by the four-electrode method with an impedance analyzer (Solartron Analytical, SI 1260A) at 10 MHz.

Table 1 Physical properties used for finite-element modeling of resistivity and elastic wave velocity
Full size table

Elastic wave velocity in the direction perpendicular to the fracture plane was estimated from the simulated static elasticity under the triaxial stress state. The finite-element analysis of static elasticity enabled us to simulate the elastic wave velocity under the low-frequency limit, where a wavelength much longer than the fracture aperture was assumed. The linear stress–strain relationship is expressed as Hooke’s law:

$$\begin{array}{c}{\sigma }_{i}={C}_{ij} {\varepsilon }_{j}, i,j=1,\cdots 6,\end{array}$$
(3)

where \({C}_{ij}\) is the stiffness tensor (in Voigt notation). \({\sigma }_{i}\) and \({\varepsilon }_{j}\) are stress and strain tensors, both of which are solved in a finite-element analysis associated with engineered strain (Garboczi 1998). Because our fracture models can be assumed to be transversely isotropic material along the z-axis (perpendicular to the fracture plane), \({C}_{ij}\) has five independent elements (Mavko et al. 2009):

$$\begin{array}{c}{C}_{ij}= \left[\begin{array}{cccccc}{C}_{11}& {C}_{12}& {C}_{13}& 0& 0& 0\\ {C}_{12}& {C}_{11}& {C}_{13}& 0& 0& 0\\ {C}_{13}& {C}_{13}& {C}_{33}& 0& 0& 0\\ 0& 0& 0& {C}_{44}& 0& 0\\ 0& 0& 0& 0& {C}_{44}& 0\\ 0& 0& 0& 0& 0& \frac{{C}_{11}-{C}_{12}}{2}\end{array}\right].\end{array}$$
(4)

By solving macroscopic stress and strain in the finite-element analysis, we can estimate all of the elements of macroscopic stiffness based on Eq. (3). Thus, P-wave velocity \({V}_{p}\) and S-wave velocity \({V}_{\mathrm{s}}\) in the direction perpendicular to the fracture plane are obtained by:

$$\begin{array}{c}{V}_{p}= \sqrt{\frac{{C}_{33}}{d}} , {V}_{s}= \sqrt{\frac{{C}_{44}}{d}}, \end{array}$$
(5)

where \(d\) is the average density of the solid and the fluid (Table 1). The elastic constants of the solid were taken from experimental values; in dry, intact Inada granite under 200 MPa of confining pressure, and measured P- and S-wave velocities were 6.14 and 3.42 km/s, respectively.

To explore how geophysical properties vary with variations in the fluid distribution within fractures, we investigated the correlations between fracture permeability, flow area, resistivity, and elastic wave velocity in detail.

3 Results

3.1 Changes in Fracture Permeability and Preferential Flow with Aperture Closure

Figure 3 shows the three-dimensional fluid-flow paths on the smooth and rough fracture surfaces. Flow paths in all models are channelized by asperity contacts (i.e., preferential flow paths). As the fracture aperture closes, both the flow velocity and the number of preferential flow paths decrease. Permeability in each model was calculated from these simulated flow velocities for comparison with the experimental results (Fig. 4). Our digital fracture simulations closely reproduced our experimental results for the smooth (Fig. 4a) and rough (Fig. 4b) surfaces. Plots of the logarithmic permeability against stress show a change with increasing effective normal stress from curving trends to linear trends. Figure 4c and d shows representative simulation results for the distribution of apertures (in grayscale) and associated flow rates (in color online) through the smooth and rough fractures, respectively. Note that the flows in Fig. 4 represent the vertically summed flow rates (perpendicular to the fracture plane), so that the three-dimensional flows in rough fracture walls can be projected on the x–y plane. These flows are then normalized with respect to their maximum value, and regions with > 1% of the maximum flow rate are visualized to accentuate the dominant flow paths. At low stresses, preferential flow paths form that cover most of the area with open (non-zero) apertures (images i in Fig. 4). Isolated apertures also form, few at first, that are surrounded by contacting asperities (zero aperture points), where the fluid is stagnant (white patches in Fig. 4c, d).

Fig. 3
figure 3

Three-dimensional flow paths calculated by the lattice Boltzmann simulation on the surface of the a–c smooth and d–f rough fracture under various effective normal stress (σeff). Flow velocity (in color online) is illustrated on the footwall of each fracture surface

Full size image
Fig. 4
figure 4

Experimental and simulated fracture permeabilities with increasing effective normal stress of the a smooth and b rough fractures and representative images derived from the simulation showing fracture flow distribution (color) within the heterogeneous aperture distribution (grayscale) with aperture closure of the c smooth and d rough fractures. Black and white diamonds in (a) and (b) represent experimental and simulated results, respectively. Red diamonds in (a) and (b) are the representative results that are illustrated in (c) and (d). The normalized flow in (c) and (d) represents the vertical summed flow, normalized by the maximum value in each condition, and the regions with < 1% of the maximum flow rate are colorless (color figure online). Dashed red ellipses in (c) and (d) show regions that are disconnected from the dominant flow paths

Full size image

As stress increases, larger fractions of the fracture surfaces are in contact, and hence, the dominant flow paths decrease in number. As the dominant flow paths become less significant, the flow paths from the inlet to outlet are progressively disconnected (images iii and iv in Fig. 4). Accordingly, the permeability–stress relationship includes a transition: logarithmic permeability changes exponentially with stress, while the flow paths are connected (images i and ii) and linearly while the flow paths are disconnected (images iii and iv). The stress level where this change occurs can be defined as the hydraulic percolation threshold \({\sigma }_{\mathrm{HPT}}\), which signifies the creation of continuous flow paths through rocks (Guéguen et al. 1997; Kirkby et al. 2016). Roughness does not appear to greatly affect this threshold (see Fig. 5a). Interestingly, the disconnection of dominant electrical flow paths coincides with that of the fluid-flow paths (Fig. 12 in Appendix 3), even though electrical flow is spread more diffusely over the fracture than fluid flow (Fig. 13 in Appendix 3). Note that both hydraulic and electrical flow do not pass through the matrix owing to its negligibly low permeability and electrical conductivity.

Fig. 5
figure 5

Graphs showing changes in a permeability, b resistivity, c elastic wave velocity, and d porosity in relation to effective normal stress. Dashed lines are extrapolations from the data in the regions of disconnected flow (gray), as defined by the value of \({\sigma }_{\mathrm{HPT}}\). Gray symbols in (c) and (d) (green in the online version) represent pairs of data points that have comparable porosity (~ 1.2%)

Full size image

3.2 Effect of Stress and Asperity Contact

We present the evolution of several rock properties with stress changes in Fig. 5. Note that we discuss only P-wave velocity here as P- and S-wave velocities show similar tendencies (see Fig. 5c). Permeability and resistivity show a linear trend at stresses higher than \({\sigma }_{\mathrm{HPT}}\), but deviate from a linear trend at lower stresses, and neither property displays any dependence on fracture roughness (Fig. 5a, b). Elastic wave velocity varies notably with roughness, and unlike the case with porous rocks, there is no clear correlation between velocity and porosity; even at the same porosity (for example, ~ 1.2%), P- and S-wave velocities show variations (Fig. 5c, d).

Contact area increases with increasing stress, and hence, the hydro-mechanical properties vary likewise (Jaeger et al. 2007; Wang and Cardenas 2016); therefore, we examined the effect of contact area on rock properties (Fig. 6). Permeability and resistivity are strongly correlated with contact area and insensitive to roughness (Fig. 6a, b). Previous research has explored the relationship between fracture permeability and contact area in synthetic fractures with identical mean aperture (Zimmerman et al. 1992). Our results, from natural rock fractures with different apertures, also support a stable relationship between permeability and contact area. In contrast, elastic wave velocity is not a single function of contact area, particularly when contact area is larger; instead, velocity generally increases with roughness (Fig. 6c). Although porosity may partially contribute to this velocity variation (Fig. 5c, d), the correlation between them appears to be weak. Another difference arising from the different roughness characteristics is the size variation of fracture asperity contacts. Figure 7 shows the distribution of contacting asperities along with their size (in color online) in the smooth and rough fractures. Although both fractures have almost the same contact area (~ 28%), the rough fracture contains larger asperities than the smooth fracture, and the contact area in the smooth fracture consists mostly of small asperities. This difference in spatial distribution of the asperities also produces the velocity difference. The effect of the asperity distribution on the velocity is small when the contact area is low, as contacting asperities in both fracture surfaces are few and small under these conditions.

Fig. 6
figure 6

Graphs showing changes in a permeability, b resistivity, and c elastic wave velocity in relation to the contact area. Gray symbols in (c) (green in the online version) represent pairs of data points with comparable contact area (~ 28%), whose asperity distributions are shown in Fig. 7

Full size image
Fig. 7
figure 7

Distribution of asperity contacts on the a smooth and b rough fractures, both of which have a contact area of ~ 28%. Color represents the asperity size (color figure online)

Full size image

3.3 Relations of Hydraulic and Geophysical Properties

We examine the initial hypothesis of the link between hydraulic–electrical–elastic properties in the two plots of Fig. 8. The relationship of P-wave velocity with logarithmic permeability is sensitive to roughness, whereas resistivity clearly shows a simple relationship with permeability on a log–log basis that does not vary with roughness (Fig. 8a). The relationship between logarithmic resistivity and flow area (the areal fraction of preferential flow paths, i.e., the colored areas in Fig. 4c–d) is also insensitive to roughness (Fig. 8b), reflecting the positive correlation between permeability and flow area (Watanabe et al. 2009; Nemoto et al. 2009). The relationship between P-wave velocity and flow area is roughness-dependent when flow areas are below 60% but not so when flow areas exceed 60% (Fig. 8b). This roughness-independent relationship between velocity and flow area at flow areas > 60% arises from the roughness independence of velocity in the fracture with lower asperity contacts (Fig. 6). The transition at ~ 60% flow area coincides with the mechanical percolation threshold, as discussed below.

Fig. 8
figure 8

Graphs showing correlations between a permeability and geophysical properties and b flow area and geophysical properties. Orange diamonds and green circles (color online) represent resistivity and P-wave velocity, respectively, and open and solid symbols represent smooth and rough fractures, respectively

Full size image

4 Discussion

4.1 Effect of Roughness on Rock Properties

We observe that all rock properties change markedly at elevated stresses that increase fracture asperity contacts. Changes in permeability and resistivity with stress (or contact area) are insensitive to roughness, whereas the change in velocity with stress varies notably with roughness. Permeability and resistivity are generally sensitive to pore connectivity (Walsh and Brace 1984; Guéguen and Palciauskas 1994), and hence, their roughness-independent tendencies may imply that connectivity is unlikely to change with differences in roughness even at the same stress. Although detailed investigations with various samples are needed to assess the correlation of connectivity with these transport properties, the close similarity of the percolation threshold \({\sigma }_{\mathrm{HPT}}\) in different roughness models also supports our hypothesis. The theoretical study of Zimmerman et al. (1992) shows that transport properties are strongly dependent on the contact area and less sensitive to the microstructure. Because the contact area of different roughness models is almost the same under similar stress conditions in our mated fracture (Table 2  in Appendix 2), the roughness independence of transport properties in our results may be related to the roughness independence of the contact area. The roughness-independent relationship between resistivity and permeability (Fig. 8) also suggests that at least the mechanisms underlying changes in both properties are the same and do not depend on roughness. Note that such roughness independences may be limited to mated fractures, as the contact area of sheared fractures may be found to change with roughness. The slope of the resistivity–permeability relationship is related to the tortuosity of the pore structure (Brown 1989). The smaller change in resistivity at higher ranges of permeability (> 10–11) indicates that tortuosity also changes relatively little, whereas the larger change in resistivity at lower permeability ranges (< 10–11) implies that tortuosity responds dramatically to aperture closure. This change in slope marks a transition of the flow pattern. At higher permeabilities (images i in Fig. 4), flow paths are largely channelized and the flow area is sufficient (> 60%), whereas at lower permeabilities (images ii–iv in Fig. 4), flow paths are sinuous (or have fewer connected channels).

The roughness dependence of the velocity change arises mainly from differences in porosity and contact area, velocity being higher in samples with lower porosity or larger contact area even at the same stress condition (Figs. 5 and 6). In addition, different roughness characteristics produce size variations of the fracture asperity contacts, which also affect the velocity difference (Fig. 7). On one hand, larger contact sizes generally contribute to stiffening the rock (Guéguen and Boutéca 2004), and hence, elastic energy propagates dominantly in the larger asperity due to its high bond energy. On the other hand, a large number of small asperities reduce the bulk elastic stiffness. In the case of cracked materials, thin cracks (i.e., smaller aspect ratio) reduce the bulk elastic energy more than stiff cracks (i.e., lower aspect ratio) even at the same volume, because the stress strongly concentrates on the edges of thin cracks rather than those of stiff cracks (e.g., Budiansky and O’connell 1976; Kachanov 1994). Similarly, our fractured sample also shows a stress concentration on small asperities that are dominant in smooth fractures (Appendix 4). Therefore, we infer that the velocity difference (Fig. 6) may also arise from the size variation of contacting asperities. Figure 9 depicts our conceptual model of roughness-induced variation of asperity contacts and possible changes in velocity. Aperture closure with increasing stress enlarges asperity contacts, and hence, the velocity increases in both smooth and rough fractures (Fig. 6). Under higher stress conditions (Fig. 9b and d), even at the same stress and similar proportions of contact area, the asperity size differs due to the roughness, and thus, the roughness dependency of velocity is especially marked at higher contact areas. This effect of asperity size is small when the contact area is low, as contacting asperities are few and small under these conditions. Because our results also incorporate the porosity effect, further study is needed to confirm the effect of asperity distribution on velocity by investigations of various natural fractures having identical porosity. It may be of interest that permeability and resistivity do not vary with the size and distribution of asperities, because they are integrated properties (Zimmerman et al. 1992), which are insensitive to the microscopic structure but sensitive to the macroscopic structure (i.e., contact area).

Fig. 9
figure 9

Schematic images of the voxel model of the fracture aperture structure and asperity contacts, showing their changes with stress for a, b smooth and c, d rough fractures. The apertures are shown in blue, matrix in gray, and contacting asperities as black solid boxes (color figure online)

Full size image

4.2 Transitions in the Fracture Flow Pattern and Associated Changes in Geophysical Properties

Although many experimental studies in intact rocks have revealed the evolution of rock properties with stress change (Brace and Orange 1968; Scholz 2002; Paterson and Wong 2005), some observations have detected unusual changes of rock properties that cannot be explained by these experimental results (Park 1991; Xue et al. 2013). The presence of mesoscale fractures may account for these discrepancies. To investigate this issue, we compiled our results on the evolution of rock properties in single fractures and compared them with the changes in flow rate distribution within the fracture. These changes in rock properties can be categorized as roughness-dependent (Fig. 10a) or roughness-independent (Fig. 10b).

Fig. 10
figure 10

Schematic diagram of changes with respect to pressure in a roughness-dependent properties and b roughness-independent properties and c schematic images of the three-stage transition of fracture flow patterns. All rock physical properties in (a) and (b) are normalized based on our results. Gray lines in (a) represent mechanical percolation thresholds \({\sigma }_{\mathrm{MPT}}\) and \(\sigma ^{\prime } _{{{\text{MPT}}}}\) of smooth and rough fractures, respectively, which distinguish aperture-dependent and aperture-independent flows (Stages I and II). The gray line in (b) represents the hydraulic percolation threshold \({\sigma }_{\mathrm{HPT}}\), which represents the boundary between connected flow (Stages I and II) and disconnected flow (Stage III)

Full size image

Elastic wave velocity and flow area are both roughness-dependent, and thus, we can distinguish separate mechanical percolation thresholds for smooth fractures (\({\sigma }_{\mathrm{MPT}}\)) and rough fractures (\(\sigma ^{\prime } _{{{\text{MPT}}}}\)), defined in both cases as the stress at which velocity reaches 90% of its maximum value (Fig. 10a). Because \({\sigma }_{\mathrm{MPT}}\) is smaller than \(\sigma ^{\prime } _{{{\text{MPT}}}}\), velocity increases more sharply with stress in smooth fractures than in rough fractures. The difference arises from a discrepancy in the heterogeneous aperture distribution (Fig. 1c). In cracked rock samples, it is well known that a rapid velocity increase with stress implies the closure of a dominant set of cracks with a similar aspect ratio (i.e., a sharp bend in the aspect ratio spectrum), whereas a monotonic increase results from closure of cracks of various aspect ratios (i.e., a broader bend in the aspect ratio spectrum) (Tsuji et al. 2008; Mavko et al. 2009). By analogy with this model, a more rapid velocity increase with stress in the smooth fracture may reflect a biased distribution of aperture sizes, such that velocity increases rapidly with the closure of apertures of the dominant size and changes only slightly afterward. Resistivity and permeability are both roughness-independent (Fig. 10b). Tendencies of these changes depend on the hydraulic percolation threshold \({\upsigma }_{\mathrm{HPT}}\), which is higher than \({\upsigma }_{\mathrm{MPT}}\) (Guéguen et al. 1997).

Figure 9c schematically illustrates these changes in rock properties as three stages (Stage I–Stage III) defined by transitions of the fracture flow pattern within a subsurface fracture with increasing stress. At lower stresses, Stage I represents aperture-dependent flow, where fluid flows within most of the void space (the aperture) and the flow area decreases as the mean aperture decreases (Fig. 10a). This stage is typified by largely connected flow paths and sufficient flow area, in which tortuosity is insensitive to stress changes. All rock properties change rapidly with increasing stress in this stage. Stage II, at stresses higher than \({\sigma }_{\mathrm{MPT}}\) but lower than \({\sigma }_{\mathrm{HPT}}\), represents aperture-independent flow, in which isolated apertures appear and become areas without flow. In this stage, tortuosity becomes sensitive to stress change, connected channels decrease, and as a result, flow area decreases markedly with increasing stress. Unlike Stage I, the rate of decrease in flow area exceeds the decrease in mean aperture size (Fig. 10a), suggesting that the fracture flow at this stage is not fully characterized by aperture size, but instead is controlled by asperity contacts. Although elastic wave velocity remains nearly constant with rising stress, permeability and resistivity change exponentially, because flow paths are still connected, and thus, these attributes are less sensitive to the spatial distribution of asperity contacts. In Stage III, at stresses higher than \({\sigma }_{\mathrm{HPT}}\), flow paths become disconnected and result in disconnected flow. In this stage, logarithmic permeability and resistivity change linearly with stress, and areas without flow become a significant fraction of the fracture area. Because Stage II begins when the velocity ceases to change with rising stress, the transition from Stage I to II can be detected by velocity monitoring, whereas resistivity is sensitive to the transition from Stage II to III. This means that, if monitoring detects the combination of almost constant velocity and exponential change in the logarithmic resistivity, it may signal the presence of aperture-independent (Stage II) flow.

If crustal stress can be considered constant (i.e., on relatively short timescales), then changes in the fracture flow pattern with changes in effective normal stress represent changes in pore pressure. This finding may show promise in two applications. One application involves the evolution of fluid flow along faults, which is part of the fault reactivation cycle triggered by pore pressure perturbations. Our model of Stage I reproduces observations of high permeability (Xue et al. 2013; Kinoshita et al. 2015), low resistivity (Mazzella and Morrison 1974; Park 1991), and low seismic velocity (Brenguier et al. 2008; Taira et al. 2018) resulting from high pore pressures associated with earthquakes. The changes in elastic wave velocity and permeability from Stage I–II (Fig. 10a, b) are in good agreement with observations after earthquakes (Xue et al. 2013; Nimiya et al. 2017). Under Stage II conditions, a resistivity change of ~ 10–20% (Park 1991) corresponds to a stress perturbation of 0.2–1.4 MPa, and a permeability change of ~ 30–40% (Xue et al. 2013) corresponds to a stress perturbation of 0.9–3.2 MPa. Moreover, during Stage II, seismic velocity is nearly constant after healing stabilizes the mechanical properties of faults (Nimiya et al. 2017). Nevertheless, subsurface fracture flow could be changing, because our results show that seismic velocity is insensitive to pressure above \({\upsigma }_{\mathrm{MPT}}\). Fault healing eventually leads to large areas of little or no flow (Stages II and III), where mineral precipitation is favored. Pore pressure changes following earthquakes, triggered by several mechanisms such as mineral precipitation (Sibson 1992; Tenthorey et al. 2003), lead rapidly to decreases in seismic velocity, increases in permeability, and decreases in resistivity, after which all of these properties recover (Mazzella and Morrison 1974; Xue et al. 2013; Taira et al. 2018), which suggests that fracture flow patterns return to their initial condition (Stage I). Thus, our inferred transitions in the fracture flow pattern may explain how the cycle of earthquake recurrence is correlated with geophysical observations, complementing the fault-valve model (Sibson et al. 1988).

The other application involves the changes in productivity of fluid resources in fractured reservoirs (for example, geothermal reservoirs) during development. Because increased elastic wave velocity coincides with decreased permeability during Stage I, a gradual velocity increase in geothermal fields implies a slight decrease in reservoir permeability (Taira et al. 2018). If a point is reached where velocity remains steady, while resistivity decreases, the fracture flow pattern would be at Stage II or III, where the flow area shrinks considerably. A limited flow area could lead to poorer thermal performance during a geothermal development (Hawkins et al. 2018) and could lower reservoir permeability by as much as two orders of magnitude (Fig. 9).

To apply our results to real field locations, we need to consider the scale dependencies of rock properties. For example, although longer fracture lengths generally mean higher roughness values (Brown and Scholz 1985; Power et al. 1987; Power and Durham 1997; Jaeger et al. 2007), fracture permeability in joints is only partially dependent on fracture length (Ishibashi et al. 2015). This suggests that roughness-independent properties, including resistivity (Fig. 10b), may have a weak dependence on fracture length, and thus, resistivity monitoring could be effective for detecting changes in hydraulic properties at field scale. On the other hand, elastic wave velocity is a roughness-dependent property (Fig. 10a) and thus varies with the fracture scale. However, this scaling effect on velocity can be modified by considering the ratio of the wavelength and the fracture length (Mavko et al. 2009). Although our study adopted a zero-frequency assumption for the velocity calculation, the scaling effect on velocity can be addressed by considering finite wavelengths. Because finite-difference time-domain modeling of wave fields in fractured media requires more complex assumptions, such as fracture compliance (Bakulin et al. 2000; Minato and Ghose 2016; Pyrak-Nolte et al. 1990), the scale dependency on velocity needs to be further explored.

5 Conclusions

We investigated the correlated changes in fracture permeability, flow area, resistivity, and elastic wave velocity of joints under increasing normal stress by coupling experimental data with digital fracture simulations. We found that changes in permeability and resistivity are controlled by fluid connectivity, which is more dependent on stress than on fracture roughness. The relationship between hydraulic and electrical properties is independent of roughness, owing to the roughness independence of fluid connectivity (as expressed by the hydraulic percolation threshold). The roughness dependence of elastic wave velocity arises from spatial distributions of contacting asperities as well as the roughness dependency of porosity. These relationships show promise for improving geophysical interpretations. Our lattice Boltzmann fluid-flow simulation revealed that the fracture flow pattern undergoes transitions through three stages as effective normal stress increases: aperture-dependent flow (Stage I), aperture-independent flow (Stage II), and disconnected flow (Stage III). Elastic wave velocity may be a useful indicator of the Stage I–II transition, and resistivity may be a sensitive indicator of the Stage II–III transition. The relationships we have revealed may enable geological regimes associated with stress changes, such as seismogenic zones and geothermal reservoirs, to be monitored remotely on the basis of their geophysical properties.