A Bayesian Approach for Uncertainty Quantification in Overcoring Stress Estimation

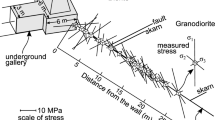
Abstract

In civil and mining engineering, three-dimensional in situ stress states are commonly measured using overcoring (OC) techniques. With these techniques, stresses are usually estimated by classical least-squares regression analysis of measured OC data. However, the estimated stresses are uncertain and may even be unreliable, due to factors such as rock heterogeneity, measurement errors and inadequacy of the regression model. Quantifying such uncertainty is crucial, as doing so both permits quantitative assessment of the reliability of the measured stress state and facilitates application of probabilistic design approaches in rock engineering such as reliability-based design. The classical approach to OC stress estimation suffers various limitations in this respect, particularly the failure in quantifying uncertainty in estimates of principal stresses, and the inability to improve stress estimation by incorporating stress information from other sources (say, stress states measured at nearby locations and orientation of the major principal stress as determined from observations of borehole breakouts). To overcome these limitations, this paper proposes a novel Bayesian approach to OC data analysis that probabilistically quantifies uncertainty in stress estimations and permits formal incorporation of additional stress information in forms of prior distributions. It also discusses the challenges faced in developing the informative prior distributions that are required to allow incorporation of additional stress information.

Appendices

Appendix A: Overcoring Stress Transformation

The transformation of stress tensors from one (e.g. global) Cartesian coordinate system to another (e.g. local) coordinate system is written as:

$$\begin{aligned} \begin{aligned} \varvec{\mathbf {S}}' = \begin{bmatrix} \sigma _{x'} &{} \tau _{x'y'} &{} \tau _{x'z'} \\ &{} \sigma _{y'} &{} \tau _{y'z'} \\ \text {sym.} &{} &{} \sigma _{z'} \end{bmatrix} = \varvec{\mathbf {R}}\varvec{\mathbf {S}}\varvec{\mathbf {R}}^{\mathrm {T}} = \varvec{\mathbf {R}} \begin{bmatrix} \sigma _x &{} \tau _{xy} &{} \tau _{xz} \\ &{} \sigma _y &{} \tau _{yz} \\ \text {sym.} &{} &{} \sigma _z \end{bmatrix} \varvec{\mathbf {R}}^{\mathrm {T}} \end{aligned}, \end{aligned}$$

(11)

where $\varvec{\mathbf {R}}$ denotes a $3 \times 3$ transformation matrix of stress tensors between the two Cartesian coordinate systems, and can be conveniently calculated using the standard basis of the two coordinate systems (i.e. unit vectors of the axes of a Cartesian coordinate system) by:

$$\begin{aligned} \varvec{\mathbf {R}} = \begin{bmatrix} \varvec{\mathbf {u}}_{x'}&\varvec{\mathbf {u}}_{y'}&\varvec{\mathbf {u}}_{z'} \end{bmatrix}^{\mathrm {T}} \begin{bmatrix} \varvec{\mathbf {u}}_{x}&\varvec{\mathbf {u}}_{y}&\varvec{\mathbf {u}}_{z} \end{bmatrix}. \end{aligned}$$

(12)

In the context of overcoring analysis, given the global geographical coordinate system (x East, y North and z vertically upwards) and the local coordinate system attached to the overcoring borehole with trend $\alpha$ and plunge $\beta$, the transformation matrix $\varvec{\mathbf {R}}$ is obtained as:

$$\begin{aligned} \varvec{\mathbf {R}}= & {} \begin{bmatrix} -\cos \alpha &{} \sin \beta \sin \alpha &{} \cos \beta \sin \alpha \\ \sin {\alpha } &{} \sin \beta \cos \alpha &{} \cos \beta \cos \alpha \\ 0 &{} \cos \beta &{} -\sin \beta \end{bmatrix}^{\mathrm {T}} \begin{bmatrix} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{bmatrix}\nonumber \\= & {} \begin{bmatrix} -\cos {\alpha } &{} \sin \alpha &{} 0 \\ \sin \beta \sin \alpha &{} \sin \beta \cos \alpha &{} \cos \beta \\ \cos \beta \sin \alpha &{} \cos \beta \cos \alpha &{} -\sin \beta \end{bmatrix}. \end{aligned}$$

(13)

Substituting Eq. (13) into Eq. (11) and rearranging in a stress vector form give:

$$\begin{aligned} \begin{aligned} \begin{bmatrix} \sigma _{x'} \\ \tau _{x'y'} \\ \tau _{x'z'} \\ \sigma _{y'} \\ \tau _{y'z'} \\ \sigma _{z'} \end{bmatrix}&= \varvec{\mathbf {T}}\begin{bmatrix}\sigma _{x} \\ \tau _{xy} \\ \tau _{xz} \\ \sigma _{y} \\ \tau _{yz} \\ \sigma _{z} \end{bmatrix} \\&=\begin{bmatrix} \cos ^2\alpha &{} -\frac{1}{2}\sin \beta \sin 2\alpha &{} -\frac{1}{2}\cos \beta \sin 2\alpha &{} \sin ^2\beta \sin ^2\alpha &{} \frac{1}{2}\sin 2\beta \sin ^2\alpha &{} \cos ^2\beta \sin ^2\alpha \\ -\sin 2\alpha &{} -\sin \beta \cos 2\alpha &{} -\cos \beta \cos 2\alpha &{} \sin ^2\beta \sin 2\alpha &{} \frac{1}{2}\sin 2\beta \sin 2\alpha &{} \cos ^2\beta \sin 2\alpha \\ 0 &{} -\cos \beta \cos \alpha &{} \sin \beta \cos \alpha &{} -\sin 2\beta \sin \alpha &{} \cos 2\beta \sin \alpha &{} -\sin 2\beta \sin \alpha \\ \sin ^2\alpha &{} \frac{1}{2}\sin \beta \sin 2\alpha &{} \frac{1}{2}\cos \beta \sin 2\alpha &{} \sin ^2\beta \cos ^2\alpha &{} \frac{1}{2}\sin 2\beta \cos ^2\alpha &{} \cos ^2\beta \cos ^2\alpha \\ 0 &{} \cos \beta \sin \alpha &{} -\sin \beta \sin \alpha &{} -\sin 2\beta \cos \alpha &{} \cos 2\beta \cos \alpha &{} -\sin 2\beta \cos \alpha \\ 0 &{} 0 &{} 0 &{} \cos ^2\beta &{} -\frac{1}{2}\sin 2\beta &{} \sin ^2\beta \\ \end{bmatrix} \begin{bmatrix}\sigma _{x} \\ \tau _{xy} \\ \tau _{xz} \\ \sigma _{y} \\ \tau _{yz} \\ \sigma _{z} \end{bmatrix}, \end{aligned} \end{aligned}$$

(14)

where $\varvec{\mathbf {T}}$ is the transformation matrix of stress vectors from the global geographical coordinate system to the local coordinate system attached to the overcoring borehole.

Appendix B: Basics of Bayesian Statistics

1.1 B.1 Bayes’ Rule

Similar to frequentist methods, Bayesian methods are used to make statistical inference based on observed data. A fundamental theoretical difference between the two approaches is that frequentist methods treat observations (i.e., data) as random variables, and the unobservable quantities we wish to learn about (i.e., statistical parameters such as mean, standard deviation and covariance) as fixed unknowns, while the Bayesian methods treat both the data and statistical parameters as random variables (Gelman et al. 2013).

To make Bayesian inference for a set of statistical parameters $\theta$ (e.g., the mean and variance of a population distribution), we begin by defining a full joint probability distribution for all observable quantities y and unobservable quantities $\theta$ as

$$\begin{aligned} f(\theta ,y) = f(\theta )f(y|\theta ), \end{aligned}$$

(15)

where $f(\theta )$ is known as the prior distribution and reflects the state of knowledge about the parameters $\theta$ in the form of a probability density function prior to observing the data y. The term $f(y|\theta )$ is known as the likelihood function, and is the probability distribution of the data y assuming they arise from a statistical model with the parameters $\theta$.

Normalizing by f(y), a constant that depends only on the known values of the data y to ensure unity of posterior distributions, leads to Bayes’ rule

$$\begin{aligned} f(\theta |y) = \frac{f(\theta ,y)}{f(y)} = \frac{f(\theta )f(y|\theta )}{f(y)}, \end{aligned}$$

(16)

where $f(\theta |y)$ is known as the posterior distribution and reflects the updated state of knowledge about the parameters $\theta$ after observing the data y in terms of probability. The posterior distribution represents the probability of parameters $\theta$ over all plausible values, from which the usual point estimate (i.e. posterior mean) and probabilistic measure of uncertainty (e.g. 95% credible intervals) regarding the parameters $\theta$ can be readily made.

An important feature of the Bayesian approach is that it allows commonsense probabilistic interpretations of statistical conclusions. For instance, a Bayesian credible interval can be directly regarded as an interval that a specified probability of containing the true value of an unknown parameter of interest, in contrast to a frequentist confidence interval that must be strictly interpreted only in relation to a hypothetical sequence of similar inferences that might be made in repeated practice (Gelman et al. 2013).

1.2 B.2 Prior Distribution

A distinctive advantage of the Bayesian approach over the classical frequentist approach is the use of the prior distribution $f(\theta )$ for statistical inference. This allows additional information from other sources to be logically incorporated into statistical analyses. Prior distributions can be summarized from relevant historical data, engineering judgment or a combination of both. For example, the posterior distribution from one relevant Bayesian analysis can be used directly, or with some modification, as a prior distribution for a subsequent analysis.

Prior distributions that are based on information (e.g. historical data or engineering judgment) other than the immediate data at hand are known as informative priors, and can strongly influence the posterior distribution through Eq. (16). On the other hand, priors that have no preference for any particular parameter values over a wide range are called vague (or diffuse, flat) priors, such as a uniform (0, $10^6$) or a half-normal (0, $5\times 10^5$) for a standard deviation parameter. Vague priors are often used as the default prior choice in the absence of specific prior information. However, in cases of limited data and/or complex models, such default priors can sometimes be undesirably informative in that they assign approximately equal probability density to an unrealistically wide range of parameter values, thereby pulling the posterior distributions towards extreme values and hence biasing the inferences (Gelman et al. 2013, 2017).

For the purpose of more robust Bayesian inference, a related prior type—weakly informative priors which are based on the general understanding of the data at hand (i.e. contextual/background knowledge)—has recently been strongly advocated over vague priors as the default prior choice (Gelman et al. 2013, 2008; Chung et al. 2015; Gelman 2006; Lemoine 2019; Gelman et al. 2017). The principled weakly informative priors that carry some amount of realistic information can regularize the posterior distributions and prevent unrealistic posterior parameter values. As weakly informative priors generally allow the data to dominate the posterior distributions while providing regularization, adopting them generally results in statistical inferences similar to those obtained with frequentist methods relying solely on the data. Arguably, for Bayesian analysis of geotechnical data weakly informative priors should be used as the default prior, considering the usual lack of sufficient data in geotechnical engineering.

Appendix C: Stan Model

Stan Model