Combined Viscoplasticity-Embedded Discontinuity Model for 3D Description of Rock Failure Under Dynamic Loading

Abstract

This paper presents a combined viscoplasticity-embedded discontinuity model for 3D analyses of rock failure processes under dynamic loading. Capabilities of a rate-dependent embedded discontinuity model, implemented with the linear tetrahedral element, for mode I (tension) loading induced fractures is extended to compressive (shear) failure description by viscoplastic softening model with the Drucker–Prager yield criterion. The return mapping update formulas are derived for the corner plasticity case exploiting the consistency conditions for both models simultaneously. The model performance is demonstrated in 3D numerical simulations of uniaxial tension and compression test on a heterogeneous rock at various loading rates. These simulations corroborate the conception that the rate sensitivity of rock is a genuine material property in tension while structural (inertia) effects play the major role in compression at high loading rates (up to 1000 s⁻¹). Finally, the model is validated with predicting the experiments of dynamic Brazilian disc test on granite.

1 Introduction

Numerical modelling of the failure of rock is an integral part of modern computational rock mechanics. Rock is particularly challenging engineering material due to its heterogeneity, which consists of different material properties of constituent minerals as well as the inherent microfaults, such as microcracks and voids (Jaeger and Cook 1971; Mahabadi 2012; Liu et al. 2004a, b; Tang 1997; Xia et al. 2008; Wei and Anand 2008; Krajcinovic 1996; Tang and Hudson 2010). Another factor making the rock constitutive modelling even more challenging is the strain rate sensitivity (Forquin 2017; Li et al. 2017, 2018; Qian et al. 2009). The rate sensitivity realizes under dynamic loading as an apparent increase in both tensile and compressive strengths accompanied with a transition from single crack-to-multiple crack/fragmentation failure mode (Denoual and Hild 2000; Xia and Yao 2015; Zhang and Zhao 2014; Zhang et al. 1999). Therefore, ideally a numerical approach for modelling rock should include heterogeneity description and accommodate the strain rate sensitivity.

The modelling approaches to rock fracture can be divided into two basic categories, which are the continuum-based methods, such as the finite-element method (FEM) and the discontinuous or particle-based methods, such as the discrete/distinct-element method (DEM). In the FEM-based methods, the rock failure processes are described only in the smeared sense by damage and/or plasticity models (see e.g. Mardalizad et al. 2020; Saksala 2010; Saksala et al. 2013; Saksala and Ibrahimbegovic 2014; Shao et al. 1999; Shao and Rudnicki 2000; Tang and Yang 2011). On the one hand, the advantages of the continuum models are the computational efficiency and relative simplicity of calibration and, in most cases, the physical meaning of material and model parameters. On the other hand, their most obvious shortcoming is the poor numerical description of fracture and fragmentation.

For this reason, the discontinuum approach based on particle or discrete-element methods has become popular today (see e.g. Ma et al. 2011; Yoon et al. 2012; Lisjak and Grasselli 2014; Ghazvinian et al. 2014; Kazerani and Zhao 2011), as the present computers allow more realistic problems to be tackled (see the examples, e.g. at Itasca and Geomechanica websites). Particle methods in general are superior in rock fracture description but their calibration is more involved because the laboratory sample level properties are emerging from the particle level interaction laws (this is, however, the case in reality as well). Complex fracture processes that the particle methods can realistically mimic include, e.g. the fracture of echelon rock joints (Sarfarazi et al. 2014; Cheng et al. 2019) and the rupture of veined rocks under triaxial compression (Shang 2020). The most critical drawback of particle methods is the computational labour required to keep track and update the particle contacts configurations and neighbours during simulations. Further details on the recent advances on computational rock mechanics can be found in the review Mohammednejad et al. (2018).

There is also the class of hybrid methods combining the advantages of discontinuum and continuum approaches in a single code (see e.g. Klerck et al. 2004; Mahabadi et al. 2010; Mahabadi 2012; Mardalizad et al. 2020; Fukuda et al. 2020). Although the hybrid methods capture the fracture processes very well and are easier to calibrate than pure particle methods, they still inherit the computational labour of the particle methods, which render them often unattractive.

For this reason, intensive research has been devoted during the last couple of decades to extend the ability of FEM, which is computationally cheap as compared to DEM, to better describe discontinuities. This effort has resulted in two classes of enrichment methods, i.e. the embedded discontinuity FEM (Simo et al. 1993; Simo and Oliver 1994) and the extended FEM (Belytschko and Black 1999). In the first version and this contrasts with the second, the enrichment of the displacement field is such that the extra degrees of freedom, representing the crack opening vector, can be eliminated by static condensation. The embedded discontinuity FEM has been applied in modelling dynamic rock fracture analyses by Saksala (2015, 2016) in 2D simulations and by Saksala et al. (2016) in 3D simulations. However, the 3D version of the model suffers from a serious drawback in that it can describe only cracks initiating in tensile (mode I) mode (however, once a crack has initiated it can open in mode II). Therefore, it cannot be applied in 3D problems involving intensive compressive (shear) failure, such as uniaxial compression test.

In 2D setting, the embedded discontinuity approach with a Rankine criterion as a fracture initiation criterion can capture the axial splitting failure mode, originating from tensile microcracks, of rock under uniaxial compression without imposing the crack path continuity over adjacent element boundaries, as demonstrated by Saksala (2015, 2016). However, in 3D this is not possible, at least with the linear tetrahedron, due to locking problems stemming from the discontinuous fracture planes over adjacent elements. Notwithstanding, compressive failure can be captured by the linear tetrahedron when using plasticity models since pressure sensitive plastic deformation does not suffer from locking in this case.

Thereby, this paper presents a 3D constitutive model for rock capable of describing both mode I fracture and compressive (shear) failure, represented in the smeared sense as plastic deformation, by combining a Drucker–Prager viscoplastic softening model with the rate-dependent embedded discontinuity model. The model is tested and validated in representative numerical simulations involving dynamic loading.

2 Theoretical Formulation of the Proposed Model

2.1 Finite Element with a Discontinuity Plane

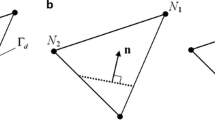
Let a body ${\Omega } \in {\mathbb{R}}^{3}$ be discretized with 4-node tetrahedral elements. Despite the low order kinematics interpolation, this element is well suited for explicit analyses involving transient loads and stress wave propagation (Saksala et al. 2016). Assume now that the discretized body is split into two disjoint parts by a displacement discontinuity, i.e. a crack. Figure 1a illustrates an element with the displacement discontinuity $\Gamma_{{\text{d}}}$ defined by the normal n_d and tangent vectors m₁, m₂. As this element results in constant strain, the displacement jump over the discontinuity plane is also assumed elementwise constant, which considerably simplifies the finite-element implementation of the embedded discontinuity kinematics.

Fig. 1

4-Node tetrahedron with a discontinuity plane (a) and the possible positions (with the same normal vector n) of a discontinuity that determine the value of function φ (Radulovic et al. 2011) (b)

Assuming infinitesimal deformation kinematics justified by brittle nature of rock fracture, the displacement and the strain fields can be written as:

$${\mathbf{u}}\left( {\mathbf{x}} \right) = N_{i} \left( {\mathbf{x}} \right){\mathbf{u}}_{i}^{{\text{e}}} + M_{{\Gamma_{{\text{d}}} }} \left( {\mathbf{x}} \right){{\varvec{\upalpha}}}_{{\text{d}}} \user2{ }\;{\text{with}}\;M_{{\Gamma_{{\text{d}}} }} \left( {\mathbf{x}} \right) = H_{{\Gamma_{{\text{d}}} }} \left( {\mathbf{x}} \right) - \varphi_{{{\Gamma }_{{\text{d}}} }} \left( {\mathbf{x}} \right)$$

(1)

$${{\varvec{\upvarepsilon}}}\left( {\mathbf{x}} \right) = \left( {\nabla N_{i} \otimes {\mathbf{u}}_{i}^{{\text{e}}} } \right)^{{{\text{sym}}}} - \left( {\nabla \varphi_{{\Gamma_{{\text{d}}} }} \left( {\mathbf{x}} \right) \otimes {{\varvec{\upalpha}}}_{{\text{d}}} } \right)^{{{\text{sym}}}} + \delta_{{\Gamma_{{\text{d}}} }} \left( {{\mathbf{n}} \otimes {{\varvec{\upalpha}}}_{{\text{d}}} } \right)^{{{\text{sym}}}} ,$$

(2)

where ${{\varvec{\upalpha}}}_{{\text{d}}}$ denotes the displacement jump and $N_{i}$ and ${\mathbf{u}}_{i}^{{\text{e}}}$ are the standard interpolation functions for the linear tetrahedron and nodal displacements (i = 1,..,4 with summation on repeated indices), respectively. Moreover, $H_{{\Gamma_{{\text{d}}} }}$ and $\delta_{{\Gamma_{{\text{d}}} }}$ denote, respectively, the Heaviside function and its gradient, the Dirac delta function. As the displacement jump is assumed element wise constant, $\nabla {{\varvec{\upalpha}}}_{{\text{d}}} \equiv 0$ and thus (2) follows from taking gradient of (1). It should be noted that the term containing the Dirac’s delta function, $\delta_{{\Gamma_{{\text{d}}} }} \left( {{\mathbf{n}} \otimes {{\varvec{\upalpha}}}_{{\text{d}}} } \right)^{{{\text{sym}}}}$, in (2), is non-zero only when ${\mathbf{x}} \in \Gamma_{{\text{d}}}$. This term is zero outside the discontinuity, i.e. for all ${\mathbf{x}} \in {\Omega }_{{\text{e}}}^{ \pm }$ and can thus be neglected at the global level when solving the discretized equations of motion.

Function $M_{{\Gamma_{{\text{d}}} }}$ in (1) restricts the effect of ${{\varvec{\upalpha}}}_{{\text{d}}}$ inside the corresponding finite element, i.e. ${{\varvec{\upalpha}}}_{{\text{d}}} \equiv 0$ outside that element. This is a considerable facilitation from the implementation point of view, as there is no need for special treatment of the essential boundary conditions. Function $\varphi_{{\Gamma_{{\text{d}}} }}$ appearing in $M_{{\Gamma_{{\text{d}}} }}$ is chosen from among the possible combinations of the nodal interpolation functions, as illustrated in Fig. 1b, so that its gradient is as parallel as possible to the crack normal ${\mathbf{n}}_{{\text{d}}}$:

$$\nabla \varphi_{{\Gamma_{{\text{d}}} }} = {\arg}\left( {\mathop {\max }\limits_{k = 1,2,3} \frac{{\left| {\sum_{i = 1}^{k} \nabla N_{i} \cdot {\mathbf{n}}_{{\text{d}}} } \right|}}{{\left\| {\sum_{i = 1}^{k} \nabla N_{i} } \right\|}}} \right).$$

(3)

Following Mosler (2005), the finite-element formulation of the embedded discontinuity theory is based on the enhanced assumed strains concept (EAS). Accordingly, the variation of the enhanced part of the strain in (2), i.e. the second and the third terms, is constructed in the strain space orthogonal to the stress field. Applying the L₂-orthogonality condition with a special Petrov–Galerkin formulation gives the following expression for the weak form of the traction balance (Mosler 2005; Radulovic et al. 2011):

$$\begin{gathered} \mathop \int \limits_{{\Omega_{{\text{e}}} }}^{{}} \delta \overline{\overline{{{\varvec{\upvarepsilon}}}}} :{{\varvec{\upsigma}}}{\text{d}}\Omega = 0, \quad \delta \overline{\overline{{{\varvec{\upvarepsilon}}}}} = - \frac{1}{{V_{{\text{e}}} }}({{\varvec{\upbeta}}}_{{\text{d}}} \otimes {\mathbf{n}}_{{\text{d}}} )^{{{\text{sym}}}} + \frac{1}{{A_{{\text{d}}} }}({{\varvec{\upbeta}}}_{{\text{d}}} \otimes {\mathbf{n}}_{{\text{d}}} )^{{{\text{sym}}}} \delta_{{\Gamma_{{\text{d}}} }} \hfill \\ \Rightarrow \frac{1}{{V_{{\text{e}}} }}\mathop \int \limits_{{\Omega_{{\text{e}}} { \setminus }\Gamma_{{\text{d}}} }}^{{}} {{\varvec{\upsigma}}} \cdot {\mathbf{n}}_{{\text{d}}} {\text{d}}\Omega - \frac{1}{{A_{{\text{d}}} }}\mathop \int \limits_{{\Gamma_{{\text{d}}} }}^{{}} {\mathbf{t}}_{{\Gamma_{{\text{d}}} }} {\text{d}}\Gamma_{{\text{d}}} = 0, \hfill \\ \end{gathered}$$

(4)

where ${{\varvec{\upbeta}}}_{{\text{d}}}$ is an arbitrary variation of the displacement jump, ${{\varvec{\upsigma}}}$ is the stress tensor, ${\mathbf{t}}_{{\Gamma_{{\text{d}}} }}$ is the traction vector, $V_{{\text{e}}}$ is the volume of the element and $A_{{\text{d}}}$ is the area of the discontinuity $\Gamma_{{\text{d}}}$. As the integrands in (4) are constants for the linear tetrahedron, the weak traction continuity reduces to the strong (local) form of traction continuity. The final FE discretized form of the problem can be written as follows (Saksala 2015; Mosler 2005):

$$\mathop \int \limits_{{\Omega_{{\text{e}}} }} \rho N_{i} N_{j} {\mathbf{\ddot{u}}}_{j} {\text{d}}\Omega + \mathop \int \limits_{{\Omega_{{\text{e}}} }} {{\varvec{\upsigma}}} \cdot \nabla N_{i} {\text{d}}\Omega - \mathop \int \limits_{{\Gamma_{\sigma } }} N_{i} {\hat{\mathbf{t}}}{\text{d}}\Gamma = 0,\quad i,j = 1 \ldots N_{{{\text{nodes}}}}$$

(5)

$$\phi_{{\text{d}}} \left( {{\mathbf{t}}_{{\Gamma_{{\text{d}}} }} } \right) = 0,\quad {\mathbf{t}}_{{\Gamma_{{\text{d}}} }} = {{\varvec{\upsigma}}} \cdot {\mathbf{n}}_{{\text{d}}} ,$$

(6)

where ${\mathbf{\ddot{u}}}_{j}$ is the acceleration vector, $N_{{{\text{nodes}}}}$ is the number of nodes in the mesh, J is the set of elements with an embedded discontinuity and N_i is the interpolation function of node i. In addition, ${\hat{\mathbf{t}}}$ is the traction defined on boundary $\Gamma_{\sigma }$. Equation (5) is the discretized form of the balance of linear momentum and Eq. (6), with $\phi_{{\text{d}}}$ being the loading function, defines the elastic zone of stresses. This EAS based formulation results in a simple implementation without the need to know explicitly neither the exact position of the discontinuity within the element nor its area. Only its relative position with respect to the element nodes is required for the calculation of the ramp function $\varphi_{{\Gamma_{{\text{d}}} }}$.

2.2 Plasticity Inspired Traction–Separation Model For Tensile Fracture

The formal similarity of Eqs. (5) and (6) to the plasticity theory allows the problem of solving the irreversible crack opening increment and the evolution equations to be recast in the computational plasticity format (Mosler 2005). This means that the classical elastic predictor–plastic corrector split is employed here. The relevant model components, i.e. the loading function, softening rules and evolution laws are defined as

$$\phi_{{\text{d}}} \left( {{\mathbf{t}}_{{\Gamma_{{\text{d}}} }} ,\kappa_{{\text{d}}} ,\dot{\kappa }_{{\text{d}}} } \right) = {\mathbf{n}}_{{\text{d}}} \cdot {\mathbf{t}}_{{\Gamma_{{\text{d}}} }} + \left( {\left( {{\mathbf{m}}_{1} \cdot {\mathbf{t}}_{{\Gamma_{{\text{d}}} }} } \right)^{2} + \left( {{\mathbf{m}}_{2} \cdot {\mathbf{t}}_{{\Gamma_{{\text{d}}} }} } \right)^{2} } \right)^{1/2} - \left( {\sigma_{{\text{t}}} + q_{{\text{d}}} \left( {\kappa_{{\text{d}}} ,\dot{\kappa }_{{\text{d}}} } \right)} \right)$$

(7)

$$q_{{\text{d}}} = h_{{\text{d}}} \kappa_{{\text{d}}} + s_{{\text{d}}} \dot{\kappa }_{{\text{d}}} ,\quad h_{{\text{d}}} = - g_{{\text{d}}} \sigma_{t} \exp \left( { - g_{{\text{d}}} \kappa_{{\text{d}}} } \right),\quad g_{{\text{d}}} = \frac{{\sigma_{{\text{t}}} }}{{G_{{{\text{Ic}}}} }}$$

(8)

$${\dot{\mathbf{t}}}_{{\Gamma_{{\text{d}}} }} = - {\mathbf{E}}:\left( {\nabla \varphi \otimes {\dot{\mathbf{\alpha }}}_{{\text{d}}} } \right) \cdot {\mathbf{n}}_{{\text{d}}}$$

(9)

$${\dot{\mathbf{\alpha }}}_{{\text{d}}} = \dot{\lambda }_{{\text{d}}} \frac{{\partial \phi_{{\text{d}}} }}{{\partial {\mathbf{t}}_{{\Gamma_{{\text{d}}} }} }},\quad \dot{\kappa }_{{\text{d}}} = - \dot{\lambda }_{{\text{d}}} \frac{{\partial \phi_{{\text{d}}} }}{{\partial q_{{\text{d}}} }}$$

(10)

$$\dot{\lambda }_{{\text{d}}} \ge 0,\quad \phi_{{\text{d}}} \le 0,\quad \dot{\lambda }_{{\text{d}}} \phi_{{\text{d}}} = 0,$$

(11)

where E is the elasticity tensor, $\kappa_{{\text{d}}} , \dot{\kappa }_{{\text{d}}}$ are the internal variable and its rate related to the softening law $q_{{\text{d}}}$ for the discontinuity and σ_t is the tensile strength while s_d is the viscosity modulus in tension. Parameter $h_{{\text{d}}}$ is the softening modulus of the exponential softening law while parameter $g_{{\text{d}}}$ controls the initial slope of the softening curve and it is calibrated by the mode I fracture energy G_Ic. Moreover, $\dot{\lambda }_{{\text{d}}}$ is crack opening increment. The evolution laws (10) have their equivalent counterparts in the plasticity theory. It should also be noticed that the loading function (7) has a shear term multiplied with the shear parameter β. The Eq. (11) are the Kuhn–Tucker conditions imposing the consistency, meaning thus that this is the viscoplastic consistency formulation by Wang et al. (1997).

A discontinuity (crack) is introduced in an element with the first principal stress exceeding the tensile strength of the material. The crack normal is parallel to the first principal direction and once introduced, the crack orientation is kept fixed.

2.3 Drucker–Prager Viscoplasticity Model for Compressive (Shear) Failure

The linear Drucker–Prager (DP) yield criterion with linear softening and viscosity model is chosen for rock failure description in compression (shear). The model components, given in consistency format, are as follows:

$$\phi_{{{\text{DP}}}} \left( {{{\varvec{\upsigma}}},\kappa_{{\text{c}}} ,\dot{\kappa }_{{\text{c}}} } \right) = \sqrt {J_{2} } + \alpha_{{{\text{DP}}}} I_{1} - k_{{{\text{DP}}}} \left( {c_{0} + q_{{\text{c}}} \left( {\kappa_{{\text{c}}} ,\dot{\kappa }_{{\text{c}}} } \right)} \right)$$

(12)

$$g_{{{\text{DP}}}} \left( {{{\varvec{\upsigma}}},\kappa_{{\text{c}}} ,\dot{\kappa }_{{\text{c}}} } \right) = \sqrt {J_{2} } + \beta_{{{\text{DP}}}} I_{1} - k_{{{\text{DP}}}} \left( {c_{0} + q_{{\text{c}}} } \right)$$

(13)

$$q_{{\text{c}}} = h_{{\text{c}}} \kappa_{{\text{c}}} + s_{{\text{c}}} \dot{\kappa }_{{\text{c}}} ,\quad h_{{\text{c}}} = - \sigma_{{\text{c}}}^{2} d_{{{\text{ele}}}} /2G_{{{\text{IIc}}}}$$

(14)

$${\dot{{\varvec{\sigma}} }} = - {\mathbf{E}}:{{\dot{{\varvec{\varepsilon}} }}}_{{{\text{vp}}}} ,\quad {{\dot{{\varvec{\varepsilon}} }}}_{{{\text{vp}}}} = \dot{\lambda }_{{\text{c}}} \frac{{\partial g_{{{\text{DP}}}} }}{{\partial {{{\varvec{\sigma}} }}}},\quad \dot{\kappa }_{{\text{c}}} = - {\dot{\lambda }}_{{\text{c}}} \frac{{\partial g_{{{\text{DP}}}} }}{{\partial q_{{\text{c}}} }}$$

(15)

$$\dot{\lambda }_{{\text{c}}} \ge 0,\quad \phi_{{{\text{DP}}}} \le 0,\quad \dot{\lambda }_{{\text{c}}} \phi_{{{\text{DP}}}} = 0,$$

(16)

where I₁ and J₂ are the first and the second invariants of the stress tensor, respectively, α_DP and k_DP are the DP parameters and c₀ is the intact cohesion. Moreover, $\kappa_{{\text{c}}} , \dot{\kappa }_{{\text{c}}}$ are the internal variable and its rate related to the softening law $q_{{\text{c}}}$, where h_c are s_c are the constant softening and viscosity modulus in compression. The softening modulus is calibrated with the mode II fracture energy and defined so that, irrespective of the element size d_ele, the same amount of energy dissipates in each element. The DP parameters are expressed in terms of the friction angle φ: α_DP = 2sinφ/(3 − sinφ) and k_DP = 6cosφ/(3 − sinφ), which enables to match the uniaxial compressive strength of rock when the cohesion is expressed as c₀ = σ_c (1 − sinφ)/2cosφ with σ_c being the uniaxial compressive strength. It should be noted that these relations are assumed here to be valid enough for the present purpose to capture the compressive (shear) failure of rock. Moreover, a plastic potential, $g_{{{\text{DP}}}}$, of the same form as ϕ_DP in (12), but with a dilatation angle ψ (≤ φ) is employed to account for correct dilatancy of rock.

2.4 Combination of the Models: Corner Plasticity

The solution, i.e. the stress return mapping, of the models described in Eqs. (7)–(11) and (12)–(16) separately is quite standard (Wang et al. 1997; Saksala 2016; Mosler 2005). However, when both of the criteria (7) and (12) are violated simultaneously, the stress integration is not trivial due to the different nature of the primary variables in the models, i.e. the crack opening vector and the traction vector in the embedded discontinuity model and the viscoplastic strain and the stress tensor in the viscoplasticity model. Notwithstanding, the plasticity inspired formulation allows the simultaneous stress integration since there are relations between these primary variables, namely Eq. (6) and the additive split of the total strain to include also the viscoplastic strain, i.e. ${{\varvec{\upvarepsilon}}} = {{\varvec{\upvarepsilon}}}_{{\text{e}}} - \left( {\nabla \varphi_{{\Gamma_{{\text{d}}} }} \otimes {{\varvec{\upalpha}}}_{{\text{d}}} } \right)^{{{\text{sym}}}} + {{\varvec{\upvarepsilon}}}_{{{\text{vp}}}}$ where ${{\varvec{\upvarepsilon}}}_{{\text{e}}}$ is the elastic strain.

The update formulae are next developed in detail for the corner plasticity case exploiting the standard elastic predictor–plastic corrector split and assuming that a crack (displacement discontinuity) with a normal n_d exists in an element. Moreover, the trial stress violates both criteria, i.e. $\phi_{{\text{d}}}^{{{\text{trial}}}} > 0\,\& \,\phi_{{{\text{DP}}}}^{{{\text{trial}}}} > 0$, where $\phi_{{\text{d}}}^{{{\text{trial}}}} = \phi_{{\text{d}}} \left( {{\mathbf{t}}_{{\Gamma_{{\text{d}}} ,n + 1}}^{{{\text{trial}}}} ,\kappa_{{{\text{d}},n}} ,\dot{\kappa }_{{{\text{d}},n}} } \right)$, $\phi_{{{\text{DP}}}}^{{{\text{trial}}}} = \phi_{{{\text{DP}}}} \left( {{{\varvec{\upsigma}}}_{n + 1}^{{{\text{trial}}}} ,\kappa_{{{\text{c}},n}} ,\dot{\kappa }_{{{\text{c}},n}} } \right)$ with

$${{\varvec{\upsigma}}}_{n + 1}^{{{\text{trial}}}} = {\mathbf{E}}:\left( {{\hat{\mathbf{\varepsilon }}}_{n + 1} - \left( {\nabla \varphi_{{\Gamma_{{\text{d}}} }} \otimes {{\varvec{\upalpha}}}_{{{\text{d}},n}} } \right)^{{{\text{sym}}}} - {{\varvec{\upvarepsilon}}}_{{{\text{vp}},n}} } \right),\quad {\mathbf{t}}_{{\Gamma_{{\text{d}}} ,n + 1}}^{{{\text{trial}}}} = {{\varvec{\upsigma}}}_{n + 1}^{{{\text{trial}}}} \cdot {\mathbf{n}}_{{\text{d}}} ,$$

(17)

where ${\hat{\mathbf{\varepsilon }}}_{n + 1}$ is the new ordinary strain (the first term in the r.h.s of Eq. 2) and ${{\varvec{\upvarepsilon}}}_{{{\text{vp}},n}}$ is the old viscoplastic strain. Now, the task is to derive update formulas for the crack opening and viscoplastic increments $\dot{\lambda }_{{\text{d}}} ,\dot{\lambda }_{{\text{c}}}$. The starting point is the consistency conditions (11) and (16), which state that at t end of the time step the yield criteria must be zero:

$$\left\{ {\begin{array}{*{20}l} {\phi_{{\text{d}}} \left( {{\mathbf{t}}_{{{\Gamma }_{{\text{d}}} ,n + 1}} ,\kappa_{{{\text{d}},n + 1}} ,\dot{\kappa }_{{{\text{d}},n + 1}} } \right) = \hat{\phi }_{{\text{d}}} \left( {{\mathbf{t}}_{{\Gamma_{{\text{d}}} ,n + 1}} } \right) - \left( {\sigma_{{\text{t}}} + h_{{\text{d}}} \kappa_{{{\text{d}},n + 1}} + s_{{\text{d}}} \dot{\kappa }_{{{\text{d}},n + 1}} } \right) = 0} \hfill \\ {\phi_{{{\text{DP}}}} \left( {{{\varvec{\upsigma}}}_{n + 1} ,\kappa_{{{\text{c}},n + 1}} ,\dot{\kappa }_{{{\text{c}},n + 1}} } \right) = \hat{\phi }_{{\text{c}}} \left( {{{\varvec{\upsigma}}}_{n + 1} } \right) - \left( {\sigma_{{\text{c}}} + h_{{\text{c}}} \kappa_{{{\text{c}},n + 1}} + s_{{\text{c}}} \dot{\kappa }_{{{\text{c}},n + 1}} } \right) = 0} \hfill \\ \end{array} } \right.,$$

(18)

where $\hat{\phi }_{{\text{d}}}$ and $\hat{\phi }_{{\text{c}}}$ are homogeneous functions of degree one ($\hat{\phi }\left( {\mathbf{x}} \right) = \partial \hat{\phi }\left( {\mathbf{x}} \right)/\partial {\mathbf{x}}:{\mathbf{x}}$) by their obvious definitions in (7) and (12). Next, the elastic predictor–plastic corrector split and the algorithmic counterparts of the evolution Eqs. (9), (10) and (15), allow the traction and stress at end of the time step to be expressed as:

$${{\varvec{\upsigma}}}_{n + 1} = {{\varvec{\upsigma}}}_{n + 1}^{{{\text{trial}}}} + \Delta {{\varvec{\upsigma}}} = {{\varvec{\upsigma}}}_{n + 1}^{{{\text{trial}}}} - {\mathbf{E}}:\left( {\Delta \lambda_{{\text{c}}} \frac{{\partial g_{{{\text{vp}}}} }}{{\partial {{\varvec{\upsigma}}}}} + \Delta \lambda_{{\text{d}}} \left( {\nabla \varphi_{{\Gamma_{{\text{d}}} }} \otimes \frac{{\partial \phi_{{\text{d}}} }}{{\partial {\mathbf{t}}_{{\Gamma_{{\text{d}}} }} }}} \right)^{{{\text{sym}}}} } \right)$$

(19)

$${\mathbf{t}}_{{\Gamma_{{\text{d}}} ,n + 1}} = {\mathbf{t}}_{{\Gamma_{{\text{d}}} ,n + 1}}^{{{\text{trial}}}} + {\Delta }{\mathbf{t}}_{{\Gamma_{{\text{d}}} }} = {{\varvec{\upsigma}}}_{n + 1} \cdot {\mathbf{n}}_{{\text{d}}} .$$

(20)

The rates of the internal variables need to be replaced by their algorithmic counterparts, which, by noting that according to (10) and (15) $\kappa_{{\text{d}}} \equiv \lambda_{{\text{d}}}$ and $\kappa_{{\text{c}}} \equiv k_{{{\text{DP}}}} \lambda_{{\text{c}}}$, gives $\dot{\lambda }_{{{\text{d}},n + 1}} = \dot{\lambda }_{{{\text{d}},n}} + {\Delta }\lambda_{{\text{d}}} /{\Delta }t$ and $\dot{\lambda }_{{{\text{c}},n + 1}} = k_{{{\text{DP}}}} \left( {\dot{\lambda }_{{{\text{c}},n}} + {\Delta }\lambda_{{\text{c}}} /{\Delta }t} \right)$. With these results in hand, Eq. (18) can be further developed. For the tensile loading function, this gives

$$\begin{gathered} \phi_{{\text{d}}} \left( {{\mathbf{t}}_{{\Gamma_{{\text{d}}} ,n + 1}} ,\lambda_{{{\text{d}},n + 1}} } \right) = \underbrace {{\hat{\phi }_{{\text{d}}} \left( {{\mathbf{t}}_{{\Gamma_{{\text{d}}} ,n + 1}} } \right)}}_{{\frac{{\partial \hat{\phi }_{d} }}{{\partial {\mathbf{t}}_{{\Gamma_{{\text{d}}} }} }}:{\mathbf{t}}_{{\Gamma_{{\text{d}}} ,n + 1}} }} - \left( {\sigma_{{\text{t}}} + h_{{\text{d}}} (\lambda_{{{\text{d}},n}} + {\Delta }\lambda_{{\text{d}}} ) + s_{{\text{d}}} \left( {\dot{\lambda }_{{{\text{d}},n}} + \frac{{{\Delta }\lambda_{{\text{d}}} }}{{{\Delta }t}}} \right)} \right) \hfill \\ = \phi_{{\text{d}}}^{{{\text{trial}}}} + \frac{{\partial \hat{\phi }_{{\text{d}}} \left( {{\mathbf{t}}_{{\Gamma_{{\text{d}}} }} } \right)}}{{\partial {\mathbf{t}}_{{\Gamma_{{\text{d}}} }} }}:\Delta {{\varvec{\upsigma}}} \cdot {\mathbf{n}}_{{\text{d}}} \user2{ } - h_{{\text{d}}} {\Delta }\lambda_{{\text{d}}} - s_{{\text{d}}} \frac{{{\Delta }\lambda_{{\text{d}}} }}{{{\Delta }t}} \hfill \\ = \phi_{{\text{d}}}^{{{\text{trial}}}} - \frac{{\partial \hat{\phi }_{{\text{d}}} }}{{\partial {\mathbf{t}}_{{\Gamma_{{\text{d}}} }} }}:{\mathbf{E}}:\left( {\Delta \lambda_{{\text{c}}} \frac{{\partial g_{{{\text{vp}}}} }}{{\partial {{\varvec{\upsigma}}}}} + \Delta \lambda_{{\text{t}}} \left( {\nabla \varphi_{{\Gamma_{{\text{d}}} }} \otimes \frac{{\partial \phi_{{\text{d}}} }}{{\partial {\mathbf{t}}_{{\Gamma_{{\text{d}}} }} }}} \right)^{{{\text{sym}}}} } \right) \cdot {\mathbf{n}}_{{\text{d}}} - h_{{\text{d}}} {\Delta }\lambda_{{\text{d}}} - s_{{\text{d}}} \frac{{{\Delta }\lambda_{{\text{d}}} }}{{{\Delta }t}}. \hfill \\ \end{gathered}$$

Similarly, for the DP yield function:

$$\phi_{{{\text{DP}}}} \left( {{{\varvec{\upsigma}}}_{n + 1} ,\lambda_{{{\text{c}},n + 1}} } \right) = \phi_{{{\text{DP}}}}^{{{\text{trial}}}} - \frac{{\partial \hat{\phi }_{{{\text{DP}}}} }}{{\partial {{\varvec{\upsigma}}}}}:{\mathbf{E}}:\left( {\Delta \lambda_{{\text{c}}} \frac{{\partial g_{{{\text{vp}}}} }}{{\partial {{\varvec{\upsigma}}}}} + \Delta \lambda_{{\text{t}}} \left( {\nabla \varphi_{{\Gamma_{{\text{d}}} }} \otimes \frac{{\partial \phi_{{\text{d}}} }}{{\partial {\mathbf{t}}_{{\Gamma_{{\text{d}}} }} }}} \right)^{{{\text{sym}}}} } \right) - k_{{{\text{DP}}}} \left( {h_{{\text{c}}} {\Delta }\lambda_{{\text{c}}} + s_{{\text{c}}} \frac{{{\Delta }\lambda_{{\text{c}}} }}{{{\Delta }t}}} \right).$$

These two equations yield the iterative scheme for solving for the crack opening and viscoplastic increments. The final update scheme is summarized below:

Although $\phi_{{{\text{DP}}}} \left( {{{\varvec{\upsigma}}}_{k + 1} ,\lambda_{{{\text{c}},k + 1}} ,\dot{\lambda }_{{{\text{c}},k + 1}} } \right) > {\text{TOL}}\, \& \,\phi_{{\text{d}}} \left( {{\mathbf{t}}_{{\Gamma_{{\text{d}}} ,k + 1}} ,\lambda_{{{\text{d}},k + 1}} ,\dot{\lambda }_{{{\text{d}},k + 1}} } \right) > {\text{TOL}}$ Do.

• 1. Solve for $\delta \lambda_{{{\text{c}},k}}$ and $\delta \lambda_{{{\text{d}},k}}$ from Eq. (20)

• 2.
  $$\Delta \lambda_{{{\text{c}},k + 1}} = \Delta \lambda_{{{\text{c}},k}} + \delta \lambda_{{{\text{c}},k}} ,\quad \dot{\lambda }_{{{\text{c}},k + 1}} = \frac{{\Delta \lambda_{{{\text{c}},k + 1}} }}{\Delta t},\quad \lambda_{{{\text{c}},k + 1}} = \lambda_{{{\text{c}},k}} + \delta \lambda_{{{\text{c}},k}}$$
  $$\Delta \lambda_{{{\text{d}},k + 1}} = \Delta \lambda_{{{\text{d}},k}} + \delta \lambda_{{{\text{d}},k}} ,\quad \dot{\lambda }_{{{\text{d}},k + 1}} = \frac{{\Delta \lambda_{{{\text{d}},k + 1}} }}{\Delta t},\quad \lambda_{{{\text{d}},k + 1}} = \lambda_{{{\text{d}},k}} + \delta \lambda_{{{\text{d}},k}}$$

• 3. $\delta {{\varvec{\upalpha}}}_{{{\text{d}},k}} = \delta \lambda_{{{\text{d}},k}} \frac{{\partial \phi_{{\text{d}}} }}{{\partial {\mathbf{t}}_{{\Gamma_{{\text{d}}} }} }},\quad \delta {{\varvec{\upvarepsilon}}}_{{{\text{vp}},k}} = \delta \lambda_{{{\text{c}},k}} \frac{{\partial g_{{{\text{vp}}}} }}{{\partial {{\varvec{\upsigma}}}}}$

• 4. ${{\varvec{\upalpha}}}_{{{\text{d}},k + 1}} = {{\varvec{\upalpha}}}_{{{\text{d}},k}} + \delta {{\varvec{\upalpha}}}_{{{\text{d}},k}} ,\quad {{\varvec{\upvarepsilon}}}_{{{\text{vp}},k + 1}} = {{\varvec{\upvarepsilon}}}_{{{\text{vp}},k}} + \delta {{\varvec{\upvarepsilon}}}_{{{\text{vp}},k}}$

• 5. ${{\varvec{\upsigma}}}_{k + 1} = {{\varvec{\upsigma}}}_{k} - {\mathbf{E}}:\left( {(\nabla \varphi_{{\Gamma_{{\text{d}}} }} \otimes \delta {{\varvec{\upalpha}}}_{{{\text{d}},k}} )^{{{\text{sym}}}} + \delta {{\varvec{\upvarepsilon}}}_{{{\text{vp}},k}} } \right),\quad {\mathbf{t}}_{{\Gamma_{{\text{d}}} ,k + 1}} = {{\varvec{\upsigma}}}_{k + 1} \cdot {\mathbf{n}}_{{\text{d}}}$

$(\delta \lambda_{{\text{c}}} \delta \lambda_{{\text{d}}} )^{{\text{T}}} = {\mathbf{G}}^{ - 1} {\mathbf{f}}$ where

$${\mathbf{G}} = \left( {\begin{array}{*{20}l} {\frac{{\partial \hat{\phi }_{{\text{d}}} }}{{\partial {\mathbf{t}}_{{\Gamma_{{\text{d}}} }} }}:{\mathbf{E}}:\left( {\nabla \varphi_{{\Gamma_{{\text{d}}} }} \otimes \frac{{\partial \phi_{d} }}{{\partial {\mathbf{t}}_{{{\Gamma }_{d} }} }}} \right)^{{{\text{sym}}}} \cdot {\mathbf{n}}_{{\text{d}}} + h_{{\text{d}}} + \frac{{s_{{\text{d}}} }}{{{\Delta }t}}} \hfill & {\frac{{\partial \hat{\phi }_{{\text{d}}} }}{{\partial {\mathbf{t}}_{{\Gamma_{{\text{d}}} }} }}:{\mathbf{E}}:\frac{{\partial g_{{{\text{vp}}}} }}{{\partial {{\varvec{\upsigma}}}}} \cdot {\mathbf{n}}_{{\text{d}}} } \hfill \\ {\frac{{\partial \hat{\phi }_{{{\text{DP}}}} }}{{\partial {{\varvec{\upsigma}}}}}:{\mathbf{E}}:\left( {\nabla \varphi \otimes \frac{{\partial \phi_{{\text{d}}} }}{{\partial {\mathbf{t}}_{{\Gamma_{{\text{d}}} }} }}} \right)^{{{\text{sym}}}} } \hfill & {\frac{{\partial \hat{\phi }_{{{\text{DP}}}} }}{{\partial {{\varvec{\upsigma}}}}}:{\mathbf{E}}:\frac{{\partial g_{{{\text{vp}}}} }}{{\partial {{\varvec{\upsigma}}}}} + k_{{{\text{DP}}}} (h_{{\text{c}}} + \frac{{s_{{\text{c}}} }}{{{\Delta }t}})} \hfill \\ \end{array} } \right), \quad {\mathbf{f}} = \left( {\begin{array}{*{20}l} {\phi_{{\text{d}}} } \\ {\phi_{{{\text{DP}}}} } \\ \end{array} } \right).$$

(21)

The material tangent stiffness can be derived in a straightforward manner having Eq. (21) in hand. However, it is not used in the present case since the equations of motion are solved with explicit time marching. Finally, the overall flow of the solution process is presented in “Appendix”.

3 Numerical Examples

This section presents the numerical simulations that demonstrate and validate the model performance. First, the model behaviour is tested at the material point level in cyclic loading using a single element mesh. Then, uniaxial compression and tension tests are carried on numerical rock at the laboratory sample level. Third, the dynamic Brazilian test is simulated as a further validation test.

3.1 Material Properties and Model Parameters

The material properties and model parameters used in some of the simulations are given in Table 1. The numerical rock consists of Quartz (33%), Feldspars (60%) and Biotite (7%) minerals and most of their properties are taken from Mahabadi (2012) with some slight modifications [the tensile strength of feldspar is lowered from 10 MPa in Mahabadi (2012) to 8 MPa here]. The shear fracture energies are obtained by multiplying the mode I energies by 30. It should be noted that in the present model these energies represent the amount energy dissipated in a finite element during the uniaxial compression and tensile tests. Therefore, the computational mode II fracture energy, G_IIc, must be substantially larger than that in mode I since the ratio of the compressive to tensile strength is ~ 15 in the present case. The shear control parameter is set to 1 for simplicity, but its effect is tested in numerical examples. The dilation angle is set to a low value of 5° to decrease the volumetric component of plastic flow and thus reduce the dilation effect. However, the effect of associated flow rule (ψ = φ) is also tested in simulations.

Table 1 Material properties and model parameter values

The rock heterogeneity is described by random clusters of finite elements assigned with the material properties of the constituent minerals (see Fig. 3). However, the dynamic Brazilian disc test simulation is carried out using homogenized properties because the experimental results available report only the rock aggregate properties, not the mineral properties. The homogenized properties in Table 1 are calculated by simple rule of mixtures, i.e. they are the weighted average values.

It is assumed here that the compressive strengths for the minerals can be calculated similarly as for the aggregate rock, i.e. by the relation between the compressive strength, cohesion and the friction angle: σ_c = c₀2cosφ/(1 − sinφ). It should be noted that the analysis behind this relation considers rock as homogenous, i.e. made of a single mineral. Therefore, it can be used to calculate the strength of the constituent minerals as well. Moreover, the viscosity values in Table 1 are small enough so as not to cause notable strain rate hardening effect in low rate simulations and also high enough to secure robust solution of Eq. (21). More precisely, the diagonal entries of matrix G should be positive in order to have a meaningful solution, i.e. fulfilling the consistency conditions. However, if the element size is relatively large and, consequently, softening modulus h_c very large, the diagonal entry may be negative in the inviscid case (s_c = 0). Nevertheless, in the viscid case with explicit time marching, the term s_c/Δt is large enough to guarantee positivity of the diagonal entry and hence the robust solution of (21).

3.2 Material Point Level Simulation

The first simulation demonstrates the model prediction in a cyclic uniaxial (low rate) loading at the material point level with the single tetrahedron mesh shown Fig. 2d. The homogenized material properties and model parameters in Table 1 are used. The simulation results are presented in Fig. 2.

Fig. 2

Model response in uniaxial cyclic loading at the material point level: the loading program (a), the stress–strain response (b), magnified detail (c) and the single element mesh (d)

The loading program starts with a tension cycle, which leads to tensile failure accompanied with the introduction and opening of a crack with normal n_d = [0 0 1]^T. This is realized as softening in Fig. 2. The loading then switches to compression, where viscoplastic flow related softening starts upon violation of the DP criterion at the compressive strength of 137 MPa. Then, the loading turns once again to tension and the crack opening and the related softening start at the present tensile strength ($\sigma_{t} + q_{{\text{d}}}$). It should be noted that the loading and off-loading takes place with the intact elasticity modulus, i.e. there is no stiffness degradation or damage component in the model presently.

3.3 Uniaxial Tension and Compression Tests at the Laboratory Sample Scale

Uniaxial tension and compression tests are the most basic problems any rock material model should be able to replicate. The performance of the present model is demonstrated in simulation of these tests with the mineral properties in Table 1 at different loading rates. The tests are carried out on the three numerical rock specimens shown in Fig. 3a. Theses numerical rocks are generated as follows. First, a 1D array with a length of the total number of elements is filled with integers 1, 2 and 3, corresponding to the color code in Fig. 3, so that the number of ones, twos and threes in the array correspond to the percentage of each mineral in the rock. This array is then randomly permutated. As the element numbering in the mesh is kept fixed, this scheme generates simple representations of spatial heterogeneity.

Fig. 3

Numerical rock samples for uniaxial tension and compression test simulations (206,617 elements, color code: 1 = Quartz, 2 = Feldspar, 3 = Biotite) (a) and boundary condition for high strain-rate simulations (b)

The mesh is the same for each specimen consisting of 206,617 linear tetrahedrons with the average element size of 1 mm. The specimen dimensions are D = 25 mm and H = is 50 mm. Figure 4 shows the uniaxial tension test results with a constant velocity boundary condition v₀ = 0.005 m/s ($\dot{\varepsilon }$ = 0.1 s⁻¹). In passing, it is noted that lower strain rates are impractical due to the conditional stability of explicit time marching (time step is ~ 4E−8 s). In order to avoid premature fracture, the tension test at higher velocity must be conducted with a special arrangement shown in Fig. 3b. A linear initial velocity field of form v_z (z) = 2v₀z/H with v₀ = $\dot{\varepsilon }$ H/2 is imposed at each node in z-direction in order to prevent the stress wave oscillations at the top and bottom edges and premature failures close to the edges.

Fig. 4

Uniaxial numerical tension test (v₀ = 0.005 m/s): Final failure modes in terms of crack opening magnitude for numerical rock samples (a), the crack planes for NumRock1 (b), the average stress–strain responses (c) and the crack normals for NumRock1 with every 5th crack plotted (d)

The failure modes of the numerical rock samples attest the experimental transverse splitting mode with a single or double macrocrack (RML 2016). The resulting tensile strength is ~ 8 MPa for each specimen (Fig. 4c). The pre-peak part of the response is virtually identical for each specimen while deviations occur during the post-peak crack opening related softening process. Furthermore, the pre-peak part shows some ductile behaviour, i.e. a short hardening stage, before the peak stress. This feature is caused by the heterogeneous material properties leading to failure at weak elements in the mesh before the average response reaches the peak stress. However, the experimental results on quasi-static uniaxial tension test do not usually display this pre-peak ductility but a sharp peak response instead (see Shang et al. 2016 for example). Notwithstanding, the ductile behaviour attested in Fig. 4c is quite negligible in the practical engineering sense.

Figure 4 also shows the effect of the shear parameter value for β = 0.25 (loading function (7)). With this value, a smooth post-peak softening response and a slightly aligned and slightly thicker macrofailure plane is realized. Finally, Fig. 4b shows the spatial structure of the double crack system realized with NumRock1. The corresponding crack normal distribution, with every 5th crack shown for clarity, is presented in Fig. 4d. Most of the crack normals are parallel to the loading axis (z-axis).

Next, higher loading rates and the effect of viscosity are tested. Figure 5 shows the results for loading rates 10 s⁻¹ and 100 s⁻¹. As the loading rate increases, more macrocracks appear in the samples, which is reflected in the average stress–strain responses as a more ductile response due to a larger amount of energy dissipated. This is the experimental rate-dependent brittle-to-ductile transition (Zhang and Zhao 2014).

Fig. 5

Uniaxial tension test on NumRock1: Final failure modes in terms of crack opening magnitude at v₀ = 0.5 m/s (10 s⁻¹) (a), v₀ = 5 m/s (100 s⁻¹) (b), v₀ = 5 m/s (100 s⁻¹) with s_d = 0.1 MPa s/m (c), corresponding average stress–strain responses (d)

However, no significant increase in tensile strength is predicted even at 100 s⁻¹ while the experiments attest the dynamic increase factor (DIF) of about 2 at this level of strain rate (Zhang and Zhao 2014). The significance of this results is that in tension the rock strain rate sensitivity is not a structural effect but, at least primarily, a material property (see also Saksala 2019).

This inability of predicting the strain rate hardening can be mended by increasing the viscosity modulus. Indeed, Fig. 5d shows that the DIF of 2 is predicted when s_d = 0.1 MPa s/m. However, the corresponding failure mode (Fig. 5c) displays rather weird pattern with the whole specimen having undergone cracking.

Uniaxial compression tests are simulated next. Figure 6 shows the failure modes for the numerical rock specimens at v₀ = − 0.005 m/s ($\dot{\varepsilon }$ = 0.1 s⁻¹). The failure modes predicted with the present DP viscoplastic softening model using the nonassociated flow (ψ = 5°) represent the experimentally documented double shearing and multiple fracture modes (Basu et al. 2013). However, the corresponding average stress–strain responses, with a maximum of 120 MPa, are virtually identical despite the different spatial configuration of the failure planes and the heterogeneous material properties. Another notable feature is that the pre-peak parts of the curves show a decline in the stiffness at around 70 MPa of stress. This realistic feature, which represent microcracking events in real rocks, is due to heterogeneous material properties, which causes failures (tensile and compressive) in weak elements at which the failure criteria is met before the final failure. It should be reminded that the constitutive model does not have a pre-peak nonlinearity description.

Fig. 6

Uniaxial numerical compression test (v₀ = − 0.005 m/s): Final failure modes in terms of viscoplastic multiplier for numerical rock samples (a), corresponding average stress–strain responses (b), failure plane structure (c) and tensile crack normal distribution (every 20th crack normal plotted) (d) for NumRock1

Interestingly, the associated flow rule predicts the partial axial splitting mode and the corresponding stress–strain response does not exhibit notable (upon eye inspection) decline in the pre-peak stiffness. Figure 6c shows the internal structure of the failure mode for the first numerical rock specimen (NumRock1). Despite being compressive test, substantial number of tensile cracks are induced, as attested in Fig. 6d showing tensile crack normal distribution for NumRock1 with every 20th crack normal plotted for clarity.

Figure 7 presents the simulations results on compressive test on NumRock1 at elevated loading rates. As the loading rate rises, the numerical specimen becomes more fragmented, being totally demolished at 1000 s⁻¹. This is, again, the experimentally observed single-to-multiple fracture/fragmentation transition. In the experiments performed by Hokka et al. (2016), a granite sample was fully disintegrated under uniaxial compression at 600 s⁻¹. The compressive strength predicted here at 1000 s⁻¹ is 202 MPa, meaning that the DIF, compared to 120 MPa at 0.1 s⁻¹, is 1.7, which is within the experimental range (Zhang and Zhao 2014). The simulations in Fig. 7 were carried out with a low viscosity value (viscosity was lowered to 0.0001 MPa·s at 1000 s⁻¹), which does not introduce notable strain rate hardening effect. Therefore, these 3D results corroborate the view (see the 2D simulations by Saksala 2019) that in uniaxial compression the rate sensitivity is mostly a structural property, caused by lateral inertia effects at extremely high rates.

Fig. 7

Uniaxial compression test on NumRock1: Failure modes in terms of viscoplastic multiplier at v₀ = − 0.5 m/s (10 s⁻¹) (a), v₀ = − 5 m/s (100 s⁻¹) (b), v₀ = 50 m/s (1000 s⁻¹) (c) and average stress–strain responses (d)

3.4 Dynamic Brazilian Disc Test

The dynamic Brazilian disc test is widely used to determine the indirect dynamic tensile strength of brittle materials such as rock and concrete. The experimental results on Kuru granite by Saksala et al. (2013) are exploited here as a validation case for the present model. The test is performed with the Split Hopkinson pressure bar apparatus. The schematics of the computational model and the finite-element mesh are shown in Fig. 8.

Fig. 8

Schematic model for dynamic Brazilian disc test (a) and the finite-element mesh with 163,177 tetrahedrons (b)

The principle of the computational procedure is as follows. The compressive stress wave induced by the impact of the striker bar is simulated as an external stress pulse, σ_i (t), obtained from the experiments. The incident and transmitted bars are modelled with two-node standard bar elements and the Brazilian disc is discretized with the linear tetrahedral elements. Finally, the contacts between the bars and the numerical rock sample are modelled by imposing kinematic (impenetrability) constraints between the bar end nodes and the rock mesh nodes in form u_bar − u_n = b_n, where u_bar and u_n are the degrees of freedom in axial direction (horizontal in Fig. 8) of the bar node and a rock contact node n, respectively, and b_n is the distance between the bar end and rock boundary node. The contact constraints are imposed using the Lagrange multipliers, corresponding to contact forces P₁ and P₂, which are solved using the forward increment Lagrange multiplier method (see Saksala 2010).

The indirect dynamic tensile strength is calculated based on the exact elasticity solution of the problem of a cylindrical disc under diametral compression. At the center of the disc this solution reads

$$\sigma_{T} = \frac{2F}{{\pi {\text{LD}}}}, F = \frac{1}{2} \left( {P_{1} + P_{2} } \right), P_{1} = A_{{\text{b}}} E_{{\text{b}}} \left( {\varepsilon_{i} + \varepsilon_{r} } \right), P_{2} = A_{{\text{b}}} E_{{\text{b}}} \varepsilon_{t} ,$$

(22)

where F is the force acting on the sample with length (thickness) L and diameter D. In the present case, these dimensions were L = 16 mm and D = 40 mm. The force F can be calculated from strains measured by strain gages from either of the bars or taken, as in (22), as the average of the forces P₁ and P₂. These forces are calculated, respectively, by the incident and reflected strain signals (P₁) or by the transferred strain signal (P₂) using the bas cross section (A_b) and the Young’s modulus (E_b) of bar material. When the test is properly designed and conducted, P₁ ≈ P₂.

Following homogenous properties are used for Kuru granite (Saksala et al. 2013): E = 60 GPa; ν = 0.26; σ_c = 230 MPa; σ_t = 11.4 MPa; G_Ic = 100 J/m²; G_IIc = 50G_Ic; s_d = 0.15 MPa s/m; s_c = 0.1 MPa s. The values of viscosity moduli are found by trial and error to match the experimental results. The rest of the parameters are those in Table 1. The simulation results are shown in Fig. 9.

Fig. 9

Dynamic Brazilian disc test on numerical rock: Final failure mode in terms of (mode I) crack opening magnitude (a), shear failures in terms of viscoplastic multiplier (b), tensile stress vs time at the disc center (c) and the contact forces at the end of the bars as function of time (e) (experimental results after Saksala et al. 2013)

Before commenting on the results, it is noted that a rigorous calibration method for the viscosity parameters is not trivial for the present problem due to its indirect nature: Brazilian disc test is compressive in its primary nature while the lateral tensile stress field is indirectly caused by the geometry. That being the case, the viscosity moduli in compression and tension must be adjusted simultaneously since they both affect the contact forces with which the indirect tensile strength is computed by Eq. (22). However, further elaboration on this topic is beyond the scope of the present paper.

The predicted failure mode is the experimental axial splitting (Saksala et al. 2013) with considerable shearing close to the contact areas, as can be observed in Fig. 9b showing the distribution of the cumulative viscoplastic multiplier at the end of simulation. In the experiments, this is represented as shear fractures and crushing at the contact areas (Saksala et al. 2013; Zhang and Zhao 2014). The experimental indirect tensile strength, 34 MPa as calculated by Eq. (22), is well matched by the simulation when calculated from the simulated bar strains using formula (22). Moreover, the “true” tensile strength, being the average of the stresses recorded in a patch of elements at the center of the top face of the disc, is in good agreement with the one calculated from Eq. (22). This is an important aspect signalling a successful selection of the viscosity moduli values and the validity of the dynamic Brazilian disc test assumptions. Furthermore, the experimental and simulated contact forces plotted as a function of time (shifted to the arrival of the incident stress wave at the contact area) in Fig. 9e are in a good agreement. The “dynamic equilibrium”, i.e. P₁ ≈ P₂, was fulfilled to a degree that could have been better, both in the experiments and simulation. However, this issue is not related to the predictive capabilities of the present model.

Crack normal plot in Fig. 10 shows that there are cracks almost everywhere in the numerical specimen, 152,294 cracks in total, but only a part of them open significantly to form the localization zone or macrocrack (the one in Fig. 9a). This is the present modelling approach representation of the microcrack initiation and coalescence into a macrocrack taking place in the experiments. Moreover, the crack orientations along the edge of the specimen indicate that, given a higher amplitude of the loading pulse, secondary radial cracking would appear.

Fig. 10

Crack normal distribution at the end of simulation (every 40th normal plotted for clarity)

It is finally remarked here that the DIF in this test, both in the simulation and the experiment, was about 3. Given that the strain rate was only ~ 18 s⁻¹, this DIF, while consistent with other experiments (Zhang and Zhao 2014), reflects the discrepancy between the direct and indirect test methods for dynamic tensile strength. Indeed, in the direct tension test simulations above, a strain rate of 100 s⁻¹ was required to achieve DIF of 2. Although this discrepancy is an experimentally established fact (Zhang and Zhao 2014), more research work is still needed to fully understand its origins. This topic is, however, beyond the scope of the present model development paper.

4 Discussion

The applicability and limitations of the presented model are addressed here. First, the presented failure model, based on a combination of a rate-dependent embedded discontinuity model for tensile fracture and a Drucker–Prager viscoplasticity softening model for compressive (shear) failure, cannot account for stiffness degradation. This is a regrettable shortcoming of the present model, shared with the class of pure plasticity models, that should be mended in future developments by adding a damage model.

Second, as the loading rate dependency is accommodated both in tension and compression by linear viscosity terms with constant viscosity moduli, the model is valid only for a fairly narrow range of loading rates. Therefore, it must be recalibrated for each application depending on its loading. Moreover, no calibration method for the viscosity moduli was presented in this work. This nontrivial task should be addressed in future. Moreover, as the model has no equation of state accounting for the shock conditions, it is suitable only for problems involving moderate loading rates.

Third, the model suffers from the inherent weakness of the viscoplasticity models to describe failure planes at elevated loading rates. In was seen in the numerical simulations that as the viscosity moduli is increases, or as the loading rate increases, the predicted failure plane becomes excessively wide. The original viscodamage-embedded discontinuity model by Saksala et al. (2016) does not suffer from this drawback, at least to the same extent, since the rate-dependence is included in the pre-peak viscodamage model governing the fracture process zone development. This component could, in principle, be included in the present model.

Fourth, as the embedded discontinuity part of the present model adopts the fixed crack concept with only a single crack per finite element, it suffers from crack shielding leading to linear elastic response in highly rotated stress states. This drawback could be mended by multiple intersecting discontinuity (in a single element) concept—a possible future development topic for present model. Notwithstanding, this would make the return mapping inconveniently complex in case of corner plasticity when three or more criteria are violated simultaneously.

Finally, the ideal class of problems for the present model (in its present state) is the one involving mixed compressive–tensile loadings at moderate loading rates and the one where cracking induced anisotropy is an important aspect. The dynamic Brazilian disc test successfully simulated here is one such problem. Another problem that could, judging a priori, be addressed is the dynamic indentation, which is the basic problem in percussive drilling.

5 Conclusions

The presented rock failure model has some advantages over the plain plasticity models. First, it can describe damage-induced anisotropy by introduction of the crack orientation. Second, the very introduction of crack orientation gives information about rock fracture processes that plasticity models cannot provide. The present model has also the computational efficiency of continuum methods, which is an advantage over the discontinuum (DEM) approach. It must, however, be immediately admitted that compared to DEM the present model is inferior in multiple fracture and fragmentation description.

The numerical simulations demonstrated that the present model capture the salient features of rock under uniaxial tension and compression at wide range of strain rates. Moreover, the simulations corroborate the conception established earlier (e.g. the 2D simulations by Saksala 2019) that in tension the rock rate sensitivity is a genuine material property while in compression the structural, mainly lateral inertia, effects explain the apparent hardening effects, at least at high rates. The simulations also highlighted the discrepancy of the DIF observed in direct and indirect methods for dynamic tensile strength. More research work is needed in this topic to reveal the ultimate sources of these differences. As the present model has predictive capabilities in simulations of dynamic rock fracture, it could serve as a tool in this field of research.

Appendix

The solution process is presented here as a flowchart in Fig. 

Fig. 11

The flow of the solution process (without contact boundary conditions)

11 for the convenience of the reader.

This chart represents the decision-making process while the actual details of the stress return mapping are presented in Sect. 2.4 above. Moreover, the treatment of boundary conditions is not shown Fig. 11. Finally, the asterisk * means that the stress state is elastic and no plastic correction is needed.