A Three-Dimensional Hydro-mechanical Model for Simulation of Dilatancy Controlled Gas Flow in Anisotropic Claystone

Abstract

Dilatancy controlled gas flow is characterized by a series of gas pressure-induced dilatant pathways in which the pathway aperture is a function of the effective stress within the solid matrix. In this paper, a three-dimensional hydro-mechanical model is presented to simulate the gas migration in initially saturated claystone with considerable anisotropy. The governing equations including mass conservation, momentum balance and energy conservation are presented for the unsaturated rock containing three phases, i.e., gas, water and solid grain. The constitutive model is proposed in which two conceptualized fracture sets with nonlinear mechanical behavior and cubic law controlled permeability are inserted, which have a direct effect on the hydro-mechanical behavior of the equivalent continuum. Finally, the developed model is validated against three gas injection tests on initially saturated Callovo–Oxfordian claystone. In general, the model is capable of capturing the main features of dilatancy controlled flow, i.e., anisotropic radial deformation, major gas breakthrough, and mechanical volume dilation of the sample. The proposed model offers additional insight into the relation between gas flow, solid matrix deformation and fracture opening/closure, which helps us get in-depth understanding of this gas transport mechanism.

1 Introduction

Gas transport processes have gained increasing attention in the research of deep geological repositories (DGRs) for nuclear waste. The safe long-term disposal and isolation of the waste are guaranteed by a multi-barrier system, i.e., engineered barrier and natural barrier system (Nasir et al. 2011, 2013, 2014, 2015; Abdi et al. 2015). Each barrier represents an impediment to the waste migration, in which the host rock is the final impediment. However, a significant volume of gas can be generated in the post-closure phase due to several processes, i.e., metal corrosion, water radiolysis or microbial reaction (Shaw 2015). The integrity of the host rock may be impaired by the accumulated gas pressure (NAGRA 2008). This situation can be even worse when the gas pressure reaches a certain value to which the micro-fracture or macro-fracture forms (Fall et al. 2012, 2014; Harrington et al. 2012b). These gas-induced fractures would enable the easy transport of contaminants, which could jeopardize the biosphere and groundwater. Therefore, the investigation and study of gas migration in host rock are important for assessing DGR safety.

It is widely accepted that there are four kinds of gas transport processes in clay-based porous media, i.e., advection/diffusion of dissolved gas, capillary controlled two-phase flow, dilatancy controlled gas flow, and macro-fracture flow (Harrington et al. 2012a, b; Marschall et al. 2005; NAGRA 2008). The advection/diffusion of dissolved gas is usually a slow transport process in which the efficiency is significantly restricted by the low hydraulic conductivity of the argillaceous rock (Marschall et al. 2005). The conventional capillary-controlled flow process cannot explain some experimental phenomena related to the gas migration process in argillaceous rock, such as gas-induced micro-fracturing, macroscopic volume dilation and associated permeability increase, and the near-zero desaturation occurring after significant gas flux is observed (Angeli et al. 2009; Cuss et al. 2014, 2012; Harrington et al. 2012a, b, 2013, 2017). The ultimate mechanism of gas transport occurs at a condition of high gas production rates such that a macro-fracture is formed to initiate a single-phase (gas) flow process (Marschall et al. 2005). However, this condition is hard to reach in the case of the DGR, where the gas source terms are insufficient (Pazdniakou and Dymitrowska 2018). Most recent experimental results have demonstrated that gas flow through clay-based porous media is along with a series of dilatant pathways that are related to the injected gas pressure, which characterizes the dilatancy controlled gas flow (Angeli et al. 2009; Cuss et al. 2012, 2014; Harrington et al. 2012a, b, 2013, 2017). The aperture of gas pathways is a function of the effective stress within the solid matrix, which dominates the behavior of fluid flow within the sample (Cuss et al. 2014; Harrington et al. 2017). Therefore, figuring out the mathematical relation between gas flow, solid matrix deformation and fracture opening/closure is important to get an in-depth understanding of the dilatancy controlled gas flow.

To simulate the development of gas preferential pathways, the coupling between unsaturated fluid flow, matrix deformation and fracture aperture have been tackled implicitly or explicitly in several numerical studies, i.e., modified two-phase flow models (Senger et al. 2014, 2018), conventional hydro-mechanical (HM) models (Fall et al. 2014; Mahjoub et al. 2018; Nguyen and Le 2015; Xu et al. 2013), the embedded fracture models (Arnedo et al. 2013; Gerard et al. 2014; Gonzalez-Blanco et al. 2016; Olivella and Alonso 2008), and the dilatant crack model (Rozhko 2016). In terms of modified two-phase flow models, a significant increase in both pore space and intrinsic permeability due to pathway dilation was considered by proposing an effective stress-dependent porosity and corresponding permeability function, which reproduced an overall satisfactory HM response (Senger et al. 2014, 2018). As the model was improved from the standard two-phase flow model, some more complex experimental phenomena, i.e., sudden change of axial deformation related to gas breakthrough and gradual pressure decline following the shut-in were not well captured. By contrast, the conventional HM models were more likely to describe the complex HM response related with the dilatant pathways by introducing features such as anisotropy, plasticity, damage, etc. (Fall et al. 2014; Mahjoub et al. 2018; Nguyen and Le 2015; Xu et al. 2013). These models have shown the robustness to capture the effect of rigidity degradation on the hydraulic properties such as the intrinsic permeability, gas entry value, which might be an alternative choice to simulate pathway dilation. To simulate the localized gas pathways in a more physical way, the embedded fracture models have been widely integrated into the HM framework (Arnedo et al. 2013; Gerard et al. 2014; Gonzalez-Blanco et al. 2016; Olivella and Alonso 2008). The conceptualized fracture with strain-controlled permeability was inserted into the coupled HM model, but the fracture shows no mechanical behavior, nor has any mechanical effects on the solid matrix. Correspondingly, the micro-fracturing induced rigidity degradation as well as the anisotropic deformation cannot be represented. To address the deficiency of conceptualized fracture, the dilatant crack model was proposed to explicitly simulate the development of gas pathways (Rozhko 2016). In the model, a single crack-like geometry was inserted into the elastic solid in which wetting fluid occupies the crack tips and nonwetting fluid occupies the crack central parts, and the dilatancy-controlled fluid flow as well as crack deformation were studied in the model. However, the model with approximated geometry is limited by the complex mathematical treatment on the fracture and the application to real cases of gas injection tests.

At present, several methods have been developed to model the HM behavior of a fractured medium, i.e., finite element method (FEM) with remeshing, the extended finite element method (XFEM), discrete element method (DEM), boundary element method (BEM), the hybrid finite-discrete element method (FDEM), etc. If the domain only contains a limited number of discontinuities, the discrete fractures can be modelled by inserting special zero-thickness interface elements to the standard solid elements (Lei et al. 2017). By defining the fracture geometry as part of the mesh, the coupled HM behavior of interface elements can be properly represented in FEM (Paluszny et al. 2018; Segura and Carol 2010). In XFEM, the sharp displacement of the fracture elements is captured by adding jump functions to the finite element approximation without remeshing strategy (Faivre et al. 2016). This approach has been adopted for modelling coupled flow-deformation problems, i.e., soil desiccation (Pouya et al. 2019; Vo et al. 2017), hydraulic fracturing (Salimzadeh and Khalili 2015; Wang 2016). Compared with the XFEM, the combination of DEM with the discrete fracture network (DFN) gives a more straight representation of fractures, as sharp discontinuities are explicitly modelled as a conformed mesh lattice, which is able to capture the opening/shearing of meshed fractures and the interaction between matrix blocks and fractures (Berre et al. 2018; Fu et al. 2013; Sun et al. 2017). However, great computational efforts are needed for the rock mass with many fractures and blocks, in which the BEM may be a reasonable alternative to provide computational efficiency, accuracy and numerical stability (Asgian 1989; Dershowitz and Fidelibus 1999; Lenti and Fidelibus 2003; Fidelibus 2007). By combining the BEM with FEM, fluid flow in complex rock fracture networks can be well represented, see Berrone et al. (2018), Xu et al. (2018). As another numerical option, the FDEM can be used to model the transitional behavior of brittle rocks, where the stress–strain evolution is analyzed in FEM while the contact interaction is analyzed in DEM. This synthetic method has been used to tackle engineering problems such as the progressive failure of rock slopes (Vyazmensky et al. 2010), rock blasting (Munjiza et al. 2000), fracture propagation in the excavation damage zone (EDZ) (Lisjak et al. 2014, 2016), etc. Though these methods provide us multiple choices to explicitly account for the fracture propagation process, these models not only require considerably long computational time but also are limited in the saturated case or have difficulty for fracture crossings, especially in three-dimensional cases.

In general, tremendous computational efforts have been used to investigate the HM behavior of pre-existing or conceptualized fractures. However, little attention is given in the literature to the anisotropic deformation of the fractured rocks accompanied by the fracture propagation, which is a significant observation in the gas injection tess (Cuss et al. 2012, 2014). This anisotropic deformation is induced either due to the presence of the fracture sets or by the matrix containing inherent bedding. There appear to be several numerical difficulties to capturing the phenomenon: (1) the anisotropic deformation in the radial direction of a cylindrical sample can only be captured by using a three-dimensional (3D) geometry, which largely increases the computational efforts; (2) serious convergence issues will occur when the problem is related to the gas breakthrough in saturated clayey material (Guo and Fall 2018, 2019), as this comes to the fracture propagation and self-sealing in unsaturated condition, more details about the problem can be referred to (Angeli et al. 2009; Cuss et al. 2014, 2012; Harrington et al. 2017, 2013, 2012a, b; Skurtveit et al. 2012; Wiseall et al. 2015). To get a balance in simulating the development of gas pathways, simplicity for implementing in real cases of gas injection tests, a 3D HM coupled model based on fundamental physical laws is introduced here to capture more experimental observations, i.e., anisotropic radial deformation, major gas breakthrough, mechanical volume dilation of the sample, etc.

In the remainder of the paper, we will present the mass conservation law, momentum balance equation and energy conservationn in Sect. 2. In Sect. 3, the constitutive framework for unsaturated fractured rocks is proposed. Lastly in Sect. 4, the HM model with 3D geometry is proposed and evaluated against three gas injection tests on initially saturated claystone.

2 Governing Equations

The representative elementary volume (REV) expressed in the following section is extracted from unsaturated fractured rock, in which the matter included consists of a three-phase mixture, i.e., the solid skeleton denoted by $s$ and two fluids, liquid water ($w$) and gas ($g$), respectively.

2.1 Main Assumptions

Prior to derive the governing equations, some basic hypotheses need to be made as follows.

• Infinitesimal deformations.

• Isothermal conditions are made.

• Two fluids are assumed to be immiscible and to stay connected in the porous networks, the porous volume is partially saturated by water while the remaining porous space is infiltrated by gas.

• Gas dissolution and water evaporation as well as gas transport by diffusion are neglected for simplicity in this paper. In the post-closure phase of the deep geological repository, gas transport capacity by diffusion and/or advection of dissolved gas is significantly restricted by the low hydraulic conductivity of argillaceous rocks, which is several orders of magnitude lower than the transport capacity of two-phase flow (NAGRA 2008). Moreover, the contribution of gas transport by diffusion and dissolved gas is very low compared with the capacity of dilatancy controlled flow. The latter is the main focus of this paper.

• Tensile stress is counted positively, while compression is positive for pressure.

2.2 Mass Conservation

For a mixture of three phases (solid, water, gas), the phase change is neglected. The mass balance equations for the solid phase and fluid phase take the following form Coussy (2004):

$$\frac{{\partial [\rho_{{\text{s}}} (1 - n)]}}{\partial t} + \nabla \cdot [\rho_{{\text{s}}} (1 - n){\mathbf{v}}_{{\text{s}}} ] = 0,$$

(1)

$$\frac{{\partial (\rho_{\alpha } nS_{\alpha } )}}{\partial t} + \nabla \cdot (\rho_{\alpha } nS_{\alpha } {\mathbf{v}}_{\alpha } ) = 0,\;\alpha = g,w,$$

(2)

where $\rho_{{\text{s}}}$ and $\rho_{\alpha }$$(\alpha = g,w)$ are the intrinsic mass densities of the solid skeleton, fluid, respectively; $n$ is the Eulerian porosity, $S_{\alpha }$ is the saturation degree of fluid $\alpha$, ${\mathbf{v}}_{{\text{s}}}$ and ${\mathbf{v}}_{\alpha }$ are the velocity vectors of solid and fluid $\alpha$, respectively.

The term of the time derivative of Eulerian porosity contained in the mass balance equations can be obtained by referring to the relationship between Eulerian porosity and Lagrangian porosity (Coussy 2004, 2007), as follows:

$$\phi = (1 + \varepsilon_{v} )n,\;\dot{\phi } = \dot{n} + \phi_{0} \dot{\varepsilon }_{v} ,$$

(3)

$$\phi - \phi_{0} = {{\varvec{\upalpha}}}:{{\varvec{\upvarepsilon}}} + \left( {\frac{\pi }{N} - \frac{{\pi_{0} }}{{N_{0} }}} \right),$$

(4)

where $\phi$ is the Lagrangian porosity, $\varepsilon_{{\text{v}}}$ is the volumetric strain of the porous medium, and notation with subscript ‘0’ denotes the corresponding initial value, the overdot represents the time derivative operator, ${{\varvec{\upalpha}}}$ is the second-order Biot effective stress coefficients tensor, ${{\varvec{\upvarepsilon}}}$ is the strain tensor, $N$ is the Biot’s skeleton modulus, $\pi$ is the equivalent pore pressure, defined by Coussy (2004) and Bui et al. (2017)

$$\pi = \overline{p}_{{\text{f}}} - U = [S_{{\text{w}}} p_{{\text{w}}} + (1 - S_{{\text{w}}} )p_{{\text{g}}} ] - U,$$

(5)

where $\overline{p}_{f}$ is the averaged pore pressure, $U = \int_{{S_{{\text{w}}} }}^{1} {p_{{\text{c}}} {\text{d}}S}$ is the interfacial energy, $p_{{\text{c}}} = p_{{\text{g}}} - p_{{\text{w}}}$ is the capillary pressure.

The variables and poroelastic parameters included in the mass balance equations will be further explored in the constitutive models.

2.3 Momentum Balance

In the study, the inertial and viscous forces are neglected, which means the kinetical effects are zero. The body loads are assumed to solely originate from the gravity. The time derivative of the momentum of all the matter contained in the REV is equal to the sum of external forces acting on the respective matter (Coussy 2004). Thus, the local equation of momentum balance is represented by:

$$\nabla \cdot {{\varvec{\upsigma}}} + \rho {\mathbf{g}} = 0,$$

(6)

where ${{\varvec{\upsigma}}}$ is the total stress tensor, $\rho = \rho_{{\text{s}}} (1 - n) + n(\rho_{{\text{w}}} S_{{\text{w}}} + \rho_{{\text{g}}} S_{{\text{g}}} )$ is the total mass density, ${\mathbf{g}}$ is the gravitational acceleration vector.

2.4 Energy Conservation

The first law of thermodynamics expresses the energy conservation in a form that the time rate of energy associated with the REV is equal to the sum of the work rate applied by the external forces and the rate of the external heat source (Coussy 2004). When the matter within the REV consists of the solid skeleton ($s$), water ($w$) and gas ($g$), the energy balance equation can be represented as (Coussy 2004):

$$\frac{\partial e}{{\partial t}} + \nabla \cdot (e{\mathbf{v}}_{{\text{s}}} ) = {{\varvec{\upsigma}}}:{\dot{\mathbf{\varepsilon }}} - \sum\limits_{\alpha = g,w} {\nabla \cdot (\rho_{\alpha } h_{\alpha } {\mathbf{v}}_{{{\varvec{\upalpha}}}}^{{\mathbf{D}}} ) + \sum\limits_{\alpha = g,w} {(\rho_{\alpha } {\mathbf{g}} \cdot {\mathbf{v}}_{{{\varvec{\upalpha}}}}^{{\mathbf{D}}} } } ),$$

(7)

where $e = \rho_{{\text{s}}} (1 - n)e_{{\text{s}}} + \sum\nolimits_{\alpha = g,w} {\rho_{\alpha } n_{\alpha } e_{\alpha } }$ is the overall density of internal energy per unit of volume, e_s and $e_{\alpha }$ represent the specific internal energy of the skeleton and fluid, respectively; $n_{\alpha } = nS_{\alpha }$ is the volume fraction of fluid $\alpha$, ${\dot{\mathbf{\varepsilon }}}$ is the strain rate tensor associated with the velocity ${\mathbf{v}}_{{\text{s}}}$, or the time derivative of displacement ${\mathbf{u}}$, defined as ${\dot{\mathbf{\varepsilon }}} = \frac{1}{2}[\nabla {\mathbf{v}}_{{\text{s}}} + (\nabla {\mathbf{v}}_{{\text{s}}} )^{T} ] = \frac{1}{2}[\nabla {\dot{\mathbf{u}}} + (\nabla {\dot{\mathbf{u}}})^{T} ]$; ${\mathbf{v}}_{{{\varvec{\upalpha}}}}^{{\mathbf{D}}}$ is Darcy’s velocity of the fluid $\alpha$, defined as ${\mathbf{v}}_{{{\varvec{\upalpha}}}}^{{\mathbf{D}}} = n_{\alpha } ({\mathbf{v}}_{\alpha } - {\mathbf{v}}_{{\text{s}}} )$; $h_{\alpha } = e_{\alpha } + \frac{{p_{\alpha } }}{{\rho_{\alpha } }}$ is the fluid-specific enthalpy.

3 Constitutive Models

3.1 Mechanical Model

The deformation of fractures contained in the potential host rock for DGRs is an unneglectable part of the performance of the argillaceous rock formations, as the produced gas may significantly migrate through the fractures. Besides, natural clayey rocks usually exhibit specific orientation of distinct bedding planes, which leads to a high anisotropy on the macroscopic scale (Hu et al. 2013). These properties all largely affect the mechanical behavior of clayey rocks, which are characterized by fractures and matrix, respectively. Similar treatment of the equivalent mechanical model containing both behaviors of fractures and matrix is also proposed by Bertrand et al. (2017) and Martinez et al. (2013). The effective stress and strain relation contained in the mechanical model can be expressed as

$${\dot{\mathbf{\sigma }}}{\prime } = {\mathbb{C}}:{\dot{\mathbf{\varepsilon }}} \Leftrightarrow {\dot{\mathbf{\varepsilon }}} = {\mathbb{S}}:{\dot{\mathbf{\sigma }}}{\prime ,}$$

(8)

where ${\mathbb{S}}$ is the compliance tensor of the equivalent continuum consisting of the rock matrix and fractures, ${\mathbb{C}}$ is the fourth-order effective stiffness tensor; ${{\varvec{\upsigma}}}{\prime }$ is the effective stress tensor, which can be derived based on the thermodynamic framework; more details can be seen in Coussy (2004), expressed as follows:

$${{\varvec{\upsigma}}}{\prime } = {{\varvec{\upsigma}}} + {{\varvec{\upalpha}}}\pi = {{\varvec{\upsigma}}} + {{\varvec{\upalpha}}}(\overline{p}_{{\text{f}}} - U).$$

(9)

Note that if the interfacial energy $U$ is neglected, Eq. (9) becomes the Bishop-type effective stress law.

For modelling simplicity, the complex structure of host rock is reduced to a series of matrix separated by fracture sets with constant spacing.

3.1.1 Characterization of Matrix

The inherent anisotropy of clayey rock due to bedding is a significant property of sedimentary rock, which has been extensively recorded in the gas injection tests (Cuss et al. 2012; Harrington et al. 2013; Popp et al. 2007). This anisotropic characterization of the matrix may largely affect the formation of gas preferential pathway, as the bedding plane can make a big difference in the HM properties in different directions. Therefore, the matrix is assumed to be a transverse isotropic material with the $z$-axis being the axis of rotational material symmetry. With respect to the local bedding plane in the $xy$ plane, the compliance tensor of rock matrix can be expressed in terms of two Young’s moduli ($E_{//}$, $E_{{ \bot }}$), two Poisson’s ratio ($\nu_{////}$, $\nu_{{{ \bot }//}}$) and a shear modulus ($G_{{//{ \bot }}}$) in the following form (Cheng 1997):

$${\mathbb{S}}_{{\text{m}}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\frac{1}{{E_{//} }}} & { - \frac{{\nu_{////} }}{{E_{//} }}} & { - \frac{{\nu_{{{ \bot }//}} }}{{E_{{ \bot }} }}} \\ { - \frac{{\nu_{////} }}{{E_{//} }}} & {\frac{1}{{E_{//} }}} & { - \frac{{\nu_{{{ \bot }//}} }}{{E_{{ \bot }} }}} \\ { - \frac{{\nu_{{{ \bot }//}} }}{{E_{{ \bot }} }}} & { - \frac{{\nu_{{{ \bot }//}} }}{{E_{{ \bot }} }}} & {\frac{1}{{E_{{ \bot }} }}} \\ \end{array} } & {} \\ {} & {\begin{array}{*{20}c} {\frac{1}{{G_{////} }}} & {} & {} \\ {} & {\frac{1}{{G_{{//{ \bot }}} }}} & {} \\ {} & {} & {\frac{1}{{G_{{//{ \bot }}} }}} \\ \end{array} } \\ \end{array} } \right]$$

(10)

where $E_{//}$ and $E_{{ \bot }}$ are Young’s moduli of intact material parallel to the bedding plane and normal to it, respectively; $\nu_{////}$ and $\nu_{{{ \bot }//}}$ are the Poisson’s ratio for the effect of the stresses in the bedding plane and in the direction normal to it on the strain in the bedding plane, respectively; $G_{{//{ \bot }}}$ is the shear modulus of intact material normal to the bedding plane, $G_{////} = {{E_{//} } \mathord{\left/ {\vphantom {{E_{//} } {2(1 + \nu_{////} )}}} \right. \kern-\nulldelimiterspace} {2(1 + \nu_{////} )}}$ is the shear modulus of intact material in the bedding plane.

3.1.2 Characterization of Fractures

The mechanical properties of fractures under different loading paths have been extensively studied, by both experimental and numerical methods (Bandis et al. 1983; Cammarata et al. 2007; Souley et al. 1995; Ghaffari et al. 2010; Yang et al. 2016). In the gas injection experiments, the stiffness of the pre-existing fractures within the rock sample will decrease with the opening of the gas-induced fracturing. To capture the phenomenon, the hyperbolic relationship of the fracture deformability developed in Bandis et al. (1983) will be applied in this study, as the model satisfies the fact that the fracture stiffness decreases in the gas injection process.

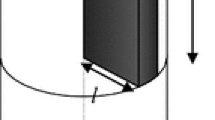
For simplicity, the fractured clayey rock element may be ideally conceptualized by a number of fractures, and each fracture set has a certain parallel direction and fixed spacing, $a$, as shown in Fig. 1. The aperture of each fracture set is represented by $u_{{\text{n}}} = u_{{{\text{n0}}}} + \Delta u_{{\text{n}}}$, in which $u_{{{\text{n0}}}}$ is the initial normal displacement at the initial effective stress field, $\Delta u_{{\text{n}}}$ is the change of normal displacement due to local changes in effective stress normal to the fracture plane. In the model, fracture opening is counted positively, $V_{{\text{m}}}$ is the maximum fracture closure that is negatively expressed in Fig. 1.

Fig. 1

(modified from Martinez et al. (2013))

Conceptual model of fractured rock

The response of a fracture to normal loading can be described by the hyperbolic model (Bandis et al. 1983; Souley et al. 1995), thus the fracture behavior under normal stress is written as

$$\Delta u_{{\text{n}}} = \frac{{\Delta \sigma_{{\text{n}}} {\prime }V_{{\text{m}}} }}{{K_{{{\text{ni}}}} V_{{\text{m}}} + \Delta \sigma_{{\text{n}}} {\prime }}}.$$

(11)

The fracture stiffness ($K_{{\text{n}}}$) normal to the fracture plane can be calculated (Martinez et al. 2013; Souley et al. 1995)

$$K_{{\text{n}}} = \frac{{\partial \sigma_{{\text{n}}} {\prime }}}{{\partial u_{{\text{n}}} }} = \frac{{K_{{{\text{ni}}}} }}{{(1 - {{\Delta u_{{\text{n}}} } \mathord{\left/ {\vphantom {{\Delta u_{{\text{n}}} } {V_{{\text{m}}} }}} \right. \kern-\nulldelimiterspace} {V_{{\text{m}}} }})^{2} }}.$$

(12)

where $\sigma_{{\text{n}}} {\prime } = \vec{n} \cdot {{\varvec{\upsigma}}}{\prime } \cdot \vec{n}$ is the traction of effective stress normal to the fracture set, $K_{{{\text{ni}}}}$ is the initial fracture stiffness and $V_{{\text{m}}}$ is the maximum aperture of the fracture, which can be used as two fitting parameters for a particular dataset in the numerical implementation, the unit vector normal to the fracture plane can be expressed in terms of Euler angle, $\beta_{{\text{f}}}$ shown in Fig. 1, as follows

$$\vec{n} = (\cos \beta_{{\text{f}}} ,0,\sin \beta_{{\text{f}}} ).$$

(13)

Considering a fracture set in the local coordinate system with constant spacing, $a$, see the $x{\prime }z{\prime }$ plane in Fig. 1, the compliance matrix of the persistent fracture can be written as (Amadei and Goodman 1981)

$${\mathbb{S}}_{{\text{f}}} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\frac{1}{{aK_{{\text{n}}} }}} & {} & {} \\ {} & 0 & {} \\ {} & {} & 0 \\ \end{array} } & {} \\ {} & {\begin{array}{*{20}c} {\frac{1}{{aK_{{{\text{fs}}}} }}} & {} & {} \\ {} & 0 & {} \\ {} & {} & {\frac{1}{{aK_{{{\text{fs}}}} }}} \\ \end{array} } \\ \end{array} } \right),$$

(14)

where ${\mathbb{S}}_{{\text{f}}}$ represents the compliance tensor of the facture set, $K_{{{\text{fs}}}}$ is the shear stiffness of the fracture.

3.1.3 Equivalent Continuum

To consider the effect of fracture set on the elastic moduli, a superposition method developed by Yang et al. (2018) may be well applied here, in which the equivalent compliance tensor of the fractured rock is calculated by adding up the individual compliance tensor of intact rock and fracture sets. This method is similar to the method developed by Liu et al. (2009), who conceptualized the fractured rock as an equivalent continuum consisting of hard spring and soft spring. These methods extend the concept of equivalent continuum proposed by Amadei and Goodman (1981), which has been applied in the production of coalbed recovery (Bertrand et al. 2017) and CO₂ sequestration (Martinez et al. 2013).

By using the superposition method, the determination of the compliance tensor of the equivalent continuum is expressed in Fig. 2. Noted here the local coordinate system of both bedding plane and fracture set may not correspond to the global coordinate axis, thus a change of compliance tensor of both matrix and the fracture set has to be computed using a rotation matrix, which depends on the angle between the local and global coordinate system, as can be seen in Fig. 2. The rotation matrix of the bedding plane and the fracture set with respect to the global coordinate axis is expressed as follows

$${\mathbf{R}} = \left( {\begin{array}{*{20}c} {\cos \beta } & 0 & {\sin \beta } \\ 0 & 1 & 0 \\ { - \sin \beta } & 0 & {\cos \beta } \\ \end{array} } \right),$$

(15)

Fig. 2

(modified from Yang et al. (2018))

Determination of the compliance tensor of the equivalent continuum

where $\beta = \beta_{{\text{m}}}$ or $\beta_{{\text{f}}}$ represents the rotation angle for matrix or fracture set, respectively, ${\mathbf{R}}$ is the corresponding rotation matrix of the bedding plane or the fracture set.

The rotation matrix provides the relationships of stress and strain between the local and global coordinate system:

$${{\varvec{\upsigma}}}^{*} = {\mathbf{R\sigma R}}^{T} ,$$

(16)

$${{\varvec{\upvarepsilon}}}^{*} = {\mathbf{R\varepsilon R}}^{T} ,$$

(17)

in which ${{\varvec{\upsigma}}}^{*}$ and ${{\varvec{\upvarepsilon}}}^{*}$ are the stress, strain tensor in the local axes system, respectively. We can further obtain the transformation matrix ${\mathbb{T}}$ if we rearrange Eq. (16) in terms of stress components in the following form:

$$\left( {\begin{array}{*{20}c} {\sigma_{xx}^{*} } \\ {\sigma_{yy}^{*} } \\ {\sigma_{zz}^{*} } \\ {\sigma_{xy}^{*} } \\ {\sigma_{yz}^{*} } \\ {\sigma_{xz}^{*} } \\ \end{array} } \right) = {\mathbb{T}}\left( {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{zz} } \\ {\sigma_{xy} } \\ {\sigma_{yz} } \\ {\sigma_{xz} } \\ \end{array} } \right),\;\;{\mathbb{T}} = \left( {\begin{array}{*{20}c} {\cos^{2} \beta } & 0 & {\sin^{2} \beta } & 0 & 0 & {\sin (2\beta )} \\ 0 & 1 & 0 & 0 & 0 & 0 \\ {\sin^{2} \beta } & 0 & {\cos^{2} \beta } & 0 & 0 & { - \sin (2\beta )} \\ 0 & 0 & 0 & {\cos \beta } & {\sin \beta } & 0 \\ 0 & 0 & 0 & { - \sin \beta } & {\cos \beta } & 0 \\ { - \frac{1}{2}\sin (2\beta )} & 0 & {\frac{1}{2}\sin (2\beta )} & 0 & 0 & {\cos (2\beta )} \\ \end{array} } \right),$$

(18)

After the compliance tensor is obtained by the aforementioned superposition method, the elastic stiffness tensor contained in Eq. (8) can be easily expressed as the inverse of compliance tensor, ${\mathbb{C}} = {\mathbb{S}}^{ - 1}$. Then it remains to define the explicit form of poro-elastic parameters ${{\varvec{\upalpha}}}$ and $N$. Due to the aforementioned characterization of the fractured rock, the Biot’s tensor of the equivalent continuum is highly anisotropic and being affected by the evolution of the inserted fracture set, expressed as

$${{\varvec{\upalpha}}} = {\mathbf{I}} - \frac{1}{{3K_{{\text{s}}} }}{\mathbb{C}}:{\mathbf{I}},$$

(19)

where ${\mathbf{I}}$ is the second-order identity tensor, K_s is the bulk modulus of solid grain.

For an isotropic material with a homogeneous solid phase, the expression of Biot’s modulus is written as ${1 \mathord{\left/ {\vphantom {1 N}} \right. \kern-\nulldelimiterspace} N} = {{(\alpha - \phi_{0} )} \mathord{\left/ {\vphantom {{(\alpha - \phi_{0} )} {K_{{\text{s}}} }}} \right. \kern-\nulldelimiterspace} {K_{{\text{s}}} }}$ (Coussy 2004). Inspired by the micromechanical analysis of anisotropic porous media in Cheng (1997) for micro-homogeneous and micro-isotropic material and the unsaturated thermoporoelasticity analysis in Coussy (2007) for disconnected porous networks, Aichi et al. (2012) extend the expression of Biot’s modulus to micro-heterogeneous media. In this study, the equivalent continuum is assumed to be micro-homogeneous and micro-isotropic material, two fluids are assumed to be immiscible and to stay connected in the porous networks. The porous volume is partially saturated by water while the remaining porous space is infiltrated by gas. The modulus $N$ is expressed as (Guayacán-Carrillo et al. 2017)

$$\frac{1}{N} = \frac{{{\text{tr}}({{\varvec{\upalpha}}})}}{{3K_{{\text{s}}} }} - \frac{{\phi_{0} }}{{K_{\phi } }},$$

(20)

where $K_{\phi }$ is the unjacketed pore bulk modulus (Aichi and Tokunaga 2012). The experimental determination of the modulus $K_{\phi }$ is generally very difficult (Ghabezloo et al. 2008); however, it can be simplified to be equal to the modulus of solid grain (K_s) by assuming the porous medium is made up of a homogeneous solid phase (Guayacán-Carrillo et al. 2017). Thus $K_{\phi } = K_{{\text{s}}}$ is adopted for simplicity in the study.

3.2 Hydraulic Constitutive Models

The mass balance equations described in Eqs. (1), (2) include different variables, i.e., fluid density and water saturation degree, which are linked to the primary variables, i.e., gas pressure, water pressure, and displacement tensor, through some constitutive and equilibrium equations. We will further explore the relations between these variables in this section.

The permeability of the porous material can be largely affected due to the opening/closure of pre-existing fractures, which is a significant characterization of fractured rock, as well as the experimental observation in the gas injection test. The contribution of permeability to the fluid flow within the unsaturated rock is governed by the general Darcy’s law, expressed as follows,

$${\mathbf{v}}_{\alpha }^{D} = - \frac{{{\mathbf{k}}_{{{\text{in}}}} k_{r\alpha } }}{{\mu_{\alpha } }}(\nabla p_{\alpha } - \rho_{\alpha } {\mathbf{g}}),$$

(21)

where ${\mathbf{k}}_{in}$ is the intrinsic permeability tensor, $k_{r\alpha }$ is the relative permeability of fluid $\alpha$, $\mu_{\alpha }$ is the dynamic viscosity of the fluid $\alpha$.

The development of gas preferential pathways activates the opening of the existing fractures, thus increases the value of intrinsic permeability and decreases the gas entry pressure. Accordingly, the relative permeability will be affected indirectly through the coupled variable, i.e., effective saturation degree. The specific model to represent the couplings between the hydraulic variables is described as follows.

3.2.1 Intrinsic Permeability

In the porous material, fluid flow occurs in the pore space between the solid skeleton, including micro-pores and macro-pores. For the case of fractured rock, the pore space consists of the pores and the existing fractures, in which both of their permeabilities contribute to the intrinsic permeability of the material. The change in intrinsic permeability of matrix due to porosity change can be described by Kozeny-Carmen model (Carman 1937), given by

$${\mathbf{k}}_{{\text{m}}} = {\mathbf{k}}_{{\text{m,0}}} \frac{{\phi^{3} }}{{(1 - \phi )^{2} }}\frac{{(1 - \phi_{0} )^{2} }}{{\phi_{0}^{3} }},$$

(22)

where ${\mathbf{k}}_{m}$ is the intrinsic permeability tensor of matrix, notations with subscript ‘0’ denote their corresponding initial values.

According to the conceptualization of the fracture set in this study, a well-known cubic law is adopted to describe the permeability through fracture set $s$(= 1 or 2) oriented parallel to the flow direction $k_{fs}$.

$$k_{{{\text{fs}}}} = \frac{{b_{{{\text{hs}}}}^{3} }}{{12a_{s} }}, \, s = 1,{ 2,}$$

(23)

where $b_{{{\text{hs}}}}$ is the hydraulic aperture of the fracture set $s$(= 1 or 2), $a_{{\text{s}}}$ is the spacing of the fracture set $s$(= 1 or 2).

Then the intrinsic permeability of fractured rock can be expressed in terms of the permeability of matrix and fracture as follows,

$$\begin{aligned} {\mathbf{k}}_{{{\text{in}}}} &= {\mathbf{k}}_{{\text{m}}} + {\mathbf{k}}_{{\text{f}}} = {\mathbf{k}}_{{\text{m,0}}} \frac{{\phi^{3} }}{{(1 - \phi )^{2} }}\frac{{(1 - \phi_{0} )^{2} }}{{\phi_{0}^{3} }} \\ &\quad+ \frac{{b_{{{\text{h}}s}}^{3} }}{{12a_{s} }}({\mathbf{I}} - \vec{n}_{s} \otimes \vec{n}_{s} ), \, s = 1,{ 2,} \end{aligned}$$

(24)

where ${\mathbf{k}}_{{\text{f}}}$ represents the permeability tensor of fracture set, ${\mathbf{I}}$ is the second identity tensor, $\vec{n}_{s}$ is the unit vector normal to the plane of fracture set $s$ (= 1 or 2).

By noting that the hydraulic aperture is generally different with the mechanical aperture in the above equation, the equality is only tenable for smooth fractures (Cappa et al. 2008; Guglielmi et al. 2015; Liu et al. 2013). Fracture roughness and contact area occupied by an obstruction are important factors influencing the couplings between the two apertures. Witherspoon et al. (1980) proposed a modified cubic law to adjust the two apertures in the parallel-plate flow concept, which was verified against numerous laboratory experiments (Alvarez et al. 1995; Detournay 1980). For simplicity, this law will be used in the study, to couple the hydraulic aperture with the mechanical aperture, expressed as follows

$$b_{hs} = b_{hs0} + f_{s} \Delta u_{ns} ,$$

(25)

where $b_{hs0}$ is the initial hydraulic aperture of fracture set $s$(= 1 or 2) at the initial effective stress state, $f_{s}$ is a factor representing the influence of roughness of fracture set $s$(= 1 or 2) on the tortuosity of flow, $\Delta u_{ns}$ is the change of aperture in fracture set $s$(= 1 or 2).

3.2.2 Water Retention Curve

The well-known van Genuchten (vG) model (van Genuchten 1980) is applied here to simulate the two-phase flow process within the rock. The effective water saturation degree $S_{e}$ can be expressed in terms of capillary pressure as follows,

$$S_{{\text{e}}} = \left\{ {\begin{array}{*{20}c} {\left[ {1 + \left( {\frac{{p_{{\text{c}}} }}{{p_{{{\text{gev}}}} }}} \right)^{{\frac{1}{1 - m}}} } \right]^{ - m} } & {p_{{\text{c}}} > 0} \\ 1 & {p_{{\text{c}}} \le 0} \\ \end{array} } \right.,$$

(26)

where $m$ is the model parameter, $p_{{{\text{gev}}}}$ is the gas entry value, which will be significantly affected by the fracture opening/closure. For the fracture set with aperture $b_{hs}$, the gas entry value may be written, in view of the Laplace equation, as

$$p_{{{\text{gev}}}} = \frac{{2T_{s} }}{{b_{{{\text{h}}s}} }} = \frac{{2T_{s} }}{{b_{{{\text{h}}s0}} }}\left( {\frac{{b_{hs0} }}{{b_{hs} }}} \right) = \min (p_{0} ({{k_{{{\text{f0}}}} } \mathord{\left/ {\vphantom {{k_{{{\text{f0}}}} } {k_{fs} }}} \right. \kern-\nulldelimiterspace} {k_{fs} }})^{1/3} ), \, s = 1,{ 2,}$$

(27)

where $T_{s}$ is the surface tension acting on the air–water interface, $p_{0}$ is the initial air entry value, the expression ‘$\min ()$’ in Eq. (27) means a function to get the minimum value of two fracture sets, which means gas can penetrate the sample through the largest pore that corresponds to the smallest gas entry value.

The residual saturation degree of both gas and water are assumed to be zero; thus, the water saturation degree $S_{{\text{w}}}$ is equal to the effective saturation degree, which amounts to writing the following relations:

$$\frac{{\partial S_{{\text{g}}} }}{\partial t} = - \frac{{\partial S_{{\text{w}}} }}{\partial t} = - \frac{{\partial S_{{\text{e}}} }}{\partial t} = C_{{\text{s}}} \frac{{\partial p_{{\text{c}}} }}{\partial t},$$

(28)

$$C_{{\text{s}}} = - \frac{{\partial S_{{\text{e}}} }}{{\partial p_{{\text{c}}} }} = \frac{m}{{p_{{{\text{gev}}}} (1 - m)}}S_{{\text{e}}}^{{\tfrac{1}{m}}} (1 - S_{{\text{e}}}^{{\tfrac{1}{m}}} )^{m} ,$$

(29)

n which $C_{{\text{s}}}$ is a specific storage coefficient.

3.2.3 Relative Permeability

The concept of relative permeability with respect to unsaturated fluid flow can be used to capture the dependency of the coefficient of permeability on effective water saturation degree. The widely used models are from Mualem and van Genuchten (Mualem 1976; van Genuchten 1980), Brooks and Corey (1964). For simplicity, the model by Brooks and Corey (1964) is extended here to describe the relative permeability of gaseous phase with respect to the effective saturation degree, which has been widely used in studies of the research topic at hand (Arnedo et al. 2013; Gerard et al. 2014; Gonzalez-Blanco et al. 2016). The generalized power law is expressed as follows,

$$k_{{{\text{rg}}}} = A_{{\text{k}}} (1 - S_{{\text{e}}} )^{{n_{k} }} { + }\delta ,$$

(30)

where $\delta$ is a small constant (0.001) to ensure a minimum value of relative permeability, a similar treatment can be also found in Guo and Fall (2018), $A_{{\text{k}}}$ and $n_{{\text{k}}}$ are fitting parameters related to the pore size distribution of the material.

For the liquid phase, the relative permeability of the water flow in the rock is given as (Mualem 1976; van Genuchten 1980):

$$k_{{{\text{rw}}}} = \sqrt {S_{{\text{e}}} } [1 - (1 - S_{{\text{e}}}^{1/m} )^{m} ]^{2} .$$

(31)

3.2.4 Fluid Density Variation

If fluid compressibility is not neglected, then the fluid density varies with the respective fluid pressure in the porous medium. By introducing the water compressibility $\chi_{{\text{w}}}$, the time derivative of water density can be expressed as

$$\frac{{\partial \rho_{{\text{w}}} }}{\partial t} = \rho_{{\text{w}}} \chi_{{\text{w}}} \frac{{\partial p_{{\text{w}}} }}{\partial t}.$$

(32)

The gas phase within the fractured rock is assumed to obey the ideal gas law, the assumption amounts to writing the time derivative of gas density as follows,

$$\frac{{\partial \rho_{{\text{g}}} }}{\partial t} = \frac{M}{RT}\frac{{\partial p_{{\text{g}}} }}{\partial t},$$

(33)

where $M$ is the molar mass of the gas, $R$ is a universal gas constant, and $T$ is the absolute temperature.

4 Evaluation of the Model

The proposed HM model is implemented in a FEM code, COMSOL Multiphysics, and then validated against three sets of gas injection test on the clayey rock. The experimental data used in the study were obtained from the tests conducted on Callovo–Oxfordian claystone (COx) at British Geological Survey (BGS, UK), where the first and second gas injection tests are, respectively, conducted on intact sample COx-1 and naturally fractured sample COx-4 under isotropic conditions (Harrington et al. 2013, 2017), the third test is conducted on sample SPP_COx-2 under triaxial conditions (Cuss et al. 2012, 2014). In the specific experimental condition of gas injection tests, gas-induced fracturing initially occurs in the inlet area, then these fractures gradually propagate along with the axial and radial directions and reach the outlet area and sample wall area. This phenomenon can be reflected by the larger fracture opening size close to the gas injection area. However, the 2D axisymmetric model happens to represent an opposite response due to the existence of the constant symmetrical axis. On the other hand, the anisotropic deformation along the radial direction of the sample cannot be represented using the 2D axisymmetric model. With these considerations, a 3D model with anisotropic HM properties is adopted to fully capture the significant phenomena in the gas injection tests.

The procedures of the experimental tests performed are briefly discussed in the following subsection; detailed experimental explanations of individual tests can be found in Cuss et al. (2012) and Harrington et al. (2013).

4.1 Experimental Description

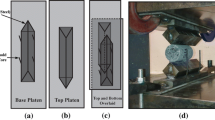
A number of gas injection tests on initially saturated COx samples were conducted at BGS to investigate the gas migration mechanism as well as its potential impact on the performance of host rocks. The samples are either subjected to isotropic confining stress conditions (i.e., COx-1 test, COx-4 test) or triaxial stress conditions (see SPP_COx-2 test). Helium was introduced as a substitute gas for hydrogen and was injected into the sample through the injection filter (IF); see Fig. 3. The water pressure p_w was applied at the backpressure filter (BF) with a constant value. A constant confining pressure $p_{3}$ and axial pressure $p_{1}$ were applied in the sample through all the gas injection process.

Fig. 3

Schematic diagram of the experimental system

The gas outflow rate at standard temperature and pressure condition (STP) was recorded. The pressure in the injection guard ring (IGR) as well as in the back guard ring (BGR) was monitored to provide some useful information, i.e., pore pressure evolution and hydraulic anisotropy. The dimensions of IF, BF, IGR and BGR are shown in Fig. 3. The sample with diameter $D$ and length $L$ was used for specific experiments.

Sample COx-1 and COx-4 with cylindrical axis perpendicular to the bedding were prepared for the gas injection test under isotropic stress condition ($p_{1} = p_{3}$), while sample SPP_COx-2 with cylindrical axis parallel to the bedding was tested under triaxial stress condition ($p_{1} - p_{3} = 0.5$ MPa). Sample COx-4 was designated to contain a natural fracture to investigate the gas flow behavior in the fracture. For the SPP_COx-2 test, radial strain at different points of the mid-plane was measured to investigate the anisotropic deformation accompanied with the gas flow. Full description of gas injection test as well as the explanation of experimental results can be referred to Cuss et al. (2012) and Harrington et al. (2013, 2017).

4.2 Model Parameters

Basic information of the rock samples used in the experimental tests is extracted from Cuss et al. (2014) and Harrington et al. (2017), as listed in Table 1. As recorded in Harrington et al. (2017), sample COx-1 and COx-4 were oriented perpendicular to bedding while COx-3 was parallel to bedding. Thus the Euler’s angle between the bedding plane and the global axes is obtained as 0°, 0° and 90°, respectively, for COx-1, COx-4 and SPP_COx-2. Noted here, due to limited information of sample COx-4, other data excluding length and diameter listed in this paper is adopted from COx-1.

Table 1 Basic information on rock samples

In the mechanical test of SPP_COx-1 conducted by Cuss et al. (2012), anisotropic radial strain was observed in the experiment, which emphasizes the rationality to define the clayey rock as a transverse isotropic material with a higher stiffness value in the direction parallel to the plane of isotropy. Although the elastic constants were measured based on the rule of isotropic material in the experiment, the anisotropic characteristics of COx are considered in the model as it is non-neglectable for sedimentary rocks.

The physical properties of the clayey rock sample have been studied by many researchers with emphasis on anisotropy (Belmokhtar et al. 2017; Homand et al. 2006; Loon et al. 2008; Pardoen et al. 2015), the value of elastic moduli may be different based on the specific loading conditions and experimental apparatus. For simplicity, the isotropic Young’s modulus recorded in the experiments will be used as parameters in the plane of isotropy. The value of solid grain modulus is calculated based on the isotropic elastic constants and Biot’s coefficient recorded in Mahjoub et al. (2018), who also simulated gas migration process in the COx sample. The degree of elastic anisotropy for all the samples is taken as 1.2 from Loon et al. (2008) who studied the anisotropy on the COx sample, which is originally recorded in Andra (2005). The values of shear modulus and Poisson’s ratio are extracted from Pardoen et al. (2015), who modelled the shear behavior of cross-anisotropic COx sample. These mechanical parameters, i.e., Young’s modulus, shear modulus and Poisson’s ratio, are set to the same value for all the samples.

The permeability of sample COx-4 is taken as one order magnitude above that of COx-1 as COx-4 contains a natural fracture (Harrington et al. 2017). The shape parameter, $m$, was set to 1/3 for gas migration modelling through all the COx samples, which is similar to the value used by Mahjoub et al. (2018). As gas migration in claystone is a time-dependent dynamic process, it is difficult to capture using the same value set of relative permeability relations for all the samples. Therefore, these constants contained in Eq. (30) are used as empirical parameters to better capture this process.

The initial gas entry value, $p_{0}$, may be significantly different due to sampling disturbance, pore structure and fracturing degree, etc. Furthermore, this parameter plays a critical role in controlling the gas migration process, but it is not always given for a specific experiment. Therefore, the following reference capillary model given in Chasset et al. (2011) is applied here to acquire an appropriate initial gas entry value for different COx samples, which is expressed as

$$p_{0} = p_{{{\text{ref}}}} \sqrt {\frac{{k_{{{\text{ref}}}} \phi_{0} }}{{\phi_{{{\text{ref}}}} k_{0} }}} ,$$

(34)

where $k_{0}$ is the initial intrinsic permeability of the sample, $p_{{{\text{ref}}}}$, $k_{{{\text{ref}}}}$ and $\phi_{{{\text{ref}}}}$ refer to the gas entry value, intrinsic permeability and porosity of a representative clayey rock sample with a known capillary curve. The reference properties of the clayey rock sample, i.e., $p_{{{\text{ref}}}}$, $k_{{{\text{ref}}}}$ and $\phi_{{{\text{ref}}}}$, are adopted from the existing experimental data (Charlier et al. 2013), which are given as 15 MPa, 1.33 × 10^–20 m² and 0.18, respectively.

The detailed HM parameters are summarised in Table 2.

Table 2 HM parameters of COx sample (1, Mahjoub et al. 2018; 2, Pardoen et al. 2015)

As stated by Cuss et al. (2014), rock samples may contain micro-fractures or macro-fractures to different extents due to variations in the confining pressure, initial sample size, stress state or sample preparation method. These pre-existing fractures can affect the gas migration process significantly and need to be considered in the study. On the other hand, to provide predictive results and avoid the convergence problem, only two fracture sets are inserted in the REV. The normal direction of the two fractures is set to be parallel with $x$-axis and $z$-axis, respectively. The spacing of the two fracture sets is set to be uniform, i.e., 20 mm, while the initial stiffness value and maximum aperture are used as fitting parameters for the specific dataset in the gas injection test. As we only focus on the fracture opening/closure effect, the shear stiffness of fractures is set to have a same value as the initial normal stiffness. Detailed parameters for the two fracture sets can be found in Table 3. Fracture spacing and roughness factor are used as empirical parameters in the calculation to fitting the experimental curve. Similar treatment has been widely adopted in the research topic at hand; for example, see Fall et al. (2014), Gerard et al. (2014), Gonzalez-Blanco et al. (2016), Nguyen and Le (2015), Olivella and Alonso (2008). However, more experimental efforts need to be made in the future to better determine these parameters.

Table 3 Facture parameters used in the model

4.3 Simulation of COx-1 Test

In the COx-1 test, gas injection pressure p_g increased from 6.5 MPa up to 12 MPa and then decreased down to 7 MPa after several steps. The water pressure p_w was controlled with a constant value, i.e., 4.5 MPa at the BF. The confining pressure was kept at a same value with the axial pressure, i.e., $p_{1} = p_{3} = 12.5$ MPa.

4.3.1 Initial and Boundary Conditions

A 3D model is adopted here to simulate the COx-1 test, as the 2D axisymmetric model cannot represent the phenomenon of larger fracture opening close to the gas injection area due to the existence of the constant symmetrical axis. The conceptualized two-fracture sets are set to have uniform parameters, with different normal direction, i.e., along the $x$-axis for the 1st fracture set and $z$-axis for the 2nd fracture set, respectively. The filters, i.e., the IF and BF, the IGR and BGR, are modeled using an equivalent porous material with high permeability and high porosity. The fine-meshed domain including the cylindrical sample and the filters is shown in Fig. 4a. To avoid the convergence problem due to the inconsistent deformation between the filters and the sample, mechanical conditions were only applied to the sample; see Fig. 4b. The detailed HM boundary conditions can be referred to Table 4.

Fig. 4

Fine meshed geometry of the REV and HM boundary conditions (BCs)

Table 4 The HM BCs for COx-1 test

The initial water pressure in the sample was set to 4.5 MPa, which is equal to the pressure applied on the BF. The initial gas pressure was set to 4.7 MPa which was a little higher than the water pressure to avoid the convergence problem and to initiate the gas flow process. The initial water saturation degree and water–solid interfacial energy are calculated to be 99.3% and 1376 Pa, respectively. Accordingly, the initial equivalent pore pressure is obtained as 4.5 MPa. The initial Biot’s tensor is calculated by considering the initial normal stiffness and spacing of the fracture set, which is determined as ${{\varvec{\upalpha}}}_{0} = (\begin{array}{*{20}c} {0.77} & {0.68} & {0.78} & 0 & 0 & 0 \\ \end{array} )^{{\text{T}}}$. The initial effective stress tensor is determined to be ${{\varvec{\upsigma}}}_{0} = (\begin{array}{*{20}c} { - 9.00} & { - 9.42} & { - 8.97} & 0 & 0 & 0 \\ \end{array} )^{{\text{T}}}$ MPa. From Eq. (11), the initial mechanical aperture of the two fracture sets can be calculated as − 1.45 × 10–4 m for the 1st set and − 1.45 × 10–4 m for the 2nd set, respectively. The two fracture sets are assumed to have a very small initial value of intrinsic permeability, i.e., 2.03 × 10^–23 m², to initiate the gas flow process in fractures. This value is much smaller than that of the surrounding matrix in the initial state, which represents a nearly closed state when no gas is injected. To obtain an equilibrium condition from the initial state, a ramp function range from 4.6 to 6.5 MPa was provided for the initial gas injection pressure.

4.3.2 Results and Discussion

Figure 5 presents a comparison between the numerically modeled and experimentally obtained gas outflow rate at STP condition. Figure 6 shows the normal displacement of the inserted fracture sets and the corresponding gas entry value at middle point A. In general, the simulated results are in good agreement with the experimental results. It can be also observed that the model estimates well the flow rate before the gas breakthrough occurs, then underestimates it followed the breakthrough and the simulated onset of gas flow is earlier. Similar modelling discrepancies have also been reported in Harrington et al. (2013) and Gerard et al. (2014), which highlights the instability of dynamic gas pathways.

Fig. 5

Gas outflow rate at STP condition. [i] represents the correlation line and related to the onset of major gas breakthrough

Fig. 6

Gas entry value and normal displacement of fracture sets at middle point A

The early onset of gas flow might be attributed to the relatively low gas entry value at an early time, i.e., lower than 1 MPa in the model since day 110, as can be seen in Fig. 6. Another influence factor is that the fracture opening behavior is related to the gas-induced unloading phenomenon, which can be represented by the increased fracture aperture step by step that corresponds to the applied gas pressure; see Fig. 6. This coupled process can be seen from Eqs. (11), (23), (25) and (27). As gas is injected from the inlet, gas gradually penetrates the sample that has a direct effect on the sample deformation. The deformation can be represented by the increase of effective stress, which leads to the opening of the two fracture sets; see fracture behavior in Fig. 1. By the coupled relation between a mechanical and hydraulic aperture in Eq. (25), the gas entry value decreases with the increasing fracture permeability; see Eqs. (23) and (27). Thanks to the anisotropic characteristics of claystone, the sample deformation is anisotropic in the radial and axial directions, thus leading to different apertures of the fracture sets, as can be seen in Fig. 6. Following a major gas breakthrough, the gas migration process is represented by steady-state flow along pressure-induced preferential pathways, which can be seen by the stepwise gas flux that corresponds to the stepwise increase in the gas injection pressure.

Figure 7 shows the comparison between modelled pressure and experimental data in the IGR and BGR. As reported by Cuss et al. (2012) and Harrington et al. (2013), the pore pressure evolution represented by the observations of guard-ring data is highly complex and no obvious correlation is persistent between IGR and BGR pressure. Thus, it is hard to capture the specific phenomenon using only one formulation. To get a better explanation of the guard-ring data, the formulations used in the COx-1 test are presented based on the specific experimental interpretation (Harrington et al. 2013, 2017) and other published modelling work (Mahjoub et al. 2018).

Fig. 7

Pressure in the IGR and BGR

As gas injection process initiates from 6.5 MPa, gas gradually penetrates the sample and reaches the IGR easily along localized pathways, which can be seen by the IGR pressure slightly lower than the gas injection pressure at the initial testing date; see Fig. 7. As the gas partially interacts with the water-saturated IGR, water is gradually displaced out of the IGR with the increasing gas injection pressure. After the major gas breakthrough occurs, the IGR is almost fully saturated with gas, and then the IGR pressure is represented by the gas pressure. Therefore, the simulated gas pressure in the IGR can well represent the IGR data.

Gas propagates through the sample to as far as the BGR at day 171.5, thus leading to a sudden increase in the BGR pressure; see the red circle in Fig. 7. This sudden increase indicates the development of new conductive gas pathways. When the gas moves along the existing pathways at a relative steady-state, water flows back to the sink until the BGR is saturated with water again. The BGR pressure continues to maintain a constant value, i.e., 4.5 MPa, which is equal to the applied water counterpressure in the BF. Therefore, the simulated water pressure can well represent the BGR pressure.

Figure 8 shows the evolution of volumetric strain between simulated results and experimental data, as well as the evolution of vertical intrinsic permeability at different points within the sample. Although the IGR or BGR pressure cannot be represented by the equivalent pore pressure, it acts to have a direct effect on the deformation; see the constitutive relation Eq. (9). This direct effect shows a satisfactory agreement between the numerically modeled and experimentally obtained volumetric strain, as shown in Fig. 8a. A well-defined increase in volume can be seen in Fig. 8a accompanying the increase of intrinsic permeability (see Fig. 8b), which validates the coupled relation of fracture permeability and mechanical deformation, as captured by the model; see Eqs. (11), (23) and (25). Besides, the area closer to the injection filter shows larger values of vertical intrinsic permeability (see lower point B in Fig. 8b), which represents the inconsistent deformation caused by the gas migration.

Fig. 8

Evolution of volumetric strain and vertical intrinsic permeability

4.4 Simulation of COx-4 Test

In the COx-4 test, gas injection pressure p_g increased from 1 MPa up to 7 MPa either in constant-flow pressure ramps or in constant-pressure mode over 98 days, and then gas was shut-in following the end of the last pumping. The water pressure p_w was controlled with a constant value, i.e., 1 MPa at the BF. The confining pressure was kept at a same value with the axial pressure, i.e., $p_{1} = p_{3} = 9$ MPa.

4.4.1 Initial and Boundary Conditions

The COx-4 test is conducted under a similar experimental condition to that in the COx-1 test, but with different confining pressure and gas injection pressure. A 3D model is used to simulate the COx-4 test for the same numerical considerations with that in the COx-1 test. The computational mesh of the domain can be referred to Fig. 4 as they have the same test apparatus with different sample size and loading conditions. The HM BCs are provided in Table 5.

Table 5 The HM BCs for COx-4 test

The initial water pressure in the sample was set to 1 MPa, which is equal to the pressure applied on the BF. The initial gas pressure was set to 1.1 MPa to avoid the convergence problem and to initiate the gas flow process. The initial water saturation degree and water–solid interfacial energy are calculated to be 98.7% and 1350 Pa, respectively. Accordingly, the initial equivalent pore pressure is obtained as 1 MPa approximately. The initial Biot’s tensor is calculated by considering the initial normal stiffness and spacing of the fracture set, which is determined as ${{\varvec{\upalpha}}}_{0} = (\begin{array}{*{20}c} {0.75} & {0.67} & {0.76} & 0 & 0 & 0 \\ \end{array} )^{{\text{T}}}$. The initial effective stress tensor is determined to be ${{\varvec{\upsigma}}}_{0} = (\begin{array}{*{20}c} { - 8.25} & { - 8.33} & { - 8.24} & 0 & 0 & 0 \\ \end{array} )^{{\text{T}}}$ MPa. From Eq. (11), the initial mechanical aperture of the two fracture sets can be calculated as − 1.89 × 10^–5 m for the 1st set and − 1.88 × 10^–5 m for the 2nd set, respectively. The initial intrinsic permeability of two fracture sets is set to have the same value as that in COx-1 test, i.e., 2.03 × 10^–23 m², which gives an initial value of hydraulic aperture, see Eq. (23), to initiate the fluid flow process in fractures.

4.4.2 Results and Discussion

Figure 9 shows a comparison between the simulated and experimental results with respect to the gas injection pressure and gas flux, respectively. The simulated results agree well with the experimental data in general, but the model overestimates the gas flux at the breakthrough timing (approximately at day 59.3), which may be attributed to the relatively large value of fracture opening size in the model. In the simulation of the gas injection process, the increase of gas pressure is applied through three ramp functions, while the actual increase of gas pressure is applied through a constant flow mode; see the event of gas pumping in Fig. 9a. The discrepancy means that the applied gas pressure may be affected by the gas flux out of the vessel, as gas can penetrate the sample depending on the gas entry value and gas permeability. This is the reason that gas pressure increases in a linear form in the model, while it is in a nonlinear form in the actual experiment; see Fig. 9).

Fig. 9

Comparison between simulated and experimental results. [i] represents the correlation line and related to the onset of gas breakthrough

After reaching the peak value, both the simulated gas pressure and flow rate show rapid decay and then quickly realize an asymptote value, as can be seen in Fig. 9b. However, this asymptote value is not fully realized in the experiment, which shows the incapability of forming interconnected gas pathways. The discrepancy represents that the actual gas preferential pathways close more quickly than the fracture closure in the simulated case once the gas was shut in, thus leading to less gas flux flowing from the inlet to the outlet and subsequent higher gas pressure in the vessel than that in the simulated case. Further improvements need to be made in future studies to capture the unstable dynamic behavior of gas pathways.

Figure 10 shows the mechanical behavior (i.e., change of aperture and normal stiffness) of the 1st fracture set in the gas migration process. Accompanying every event of applied gas pressure, the fracture either gradually opens at constant flow mode as it is an unloading process or keeps with the same aperture at constant pressure mode; see Fig. 10a. The trend in the change of normal displacement is similar to that in the change of gas injection pressure; see Fig. 9a. Corresponding to the fracture opening/closure, the normal stiffness either decreases when fracture continues opening or keeps with the same value when no changes occur on the aperture according to the relation in Eq. (12), as can be seen in Fig. 10b. After the gas was shut in, the fracture quickly closes and the aperture decreases to a value close to that at the initial state, thus resulting in a rapid increase of normal stiffness; see Fig. 10b.

Fig. 10

Mechanical behavior of the 1st fracture set

4.5 Simulation of SPP_COx-2 Test

In the SPP_COx-2 test, gas injection pressure p_g increased from 4.5 MPa up to 10.5 MPa either in constant-flow pressure ramps or in constant-pressure mode. The water pressure p_w was controlled with a constant value, i.e., 4.5 MPa at the BF. The axial pressure was kept at a constant value with 0.5 MPa higher than the confining pressure throughout the test, i.e., $p_{1} = 13$ MPa, $p_{3} = 12.5$ MPa.

4.5.1 Initial and Boundary Conditions

Aside from the aforementioned numerical considerations in the COx-1 and COx-4 tests, the 2D axisymmetric model also cannot capture the anisotropic deformation along the radial direction, which is a significant phenomenon in the SPP_COx-2 test. Therefore, a 3D model with anisotropic HM properties is also adopted here to simulate the SPP_COx-2 test. The computational mesh of the domain in SPP_COx-2 test is similar to that in COx-1 test, as shown in Fig. 4. The detailed HM boundary conditions can be referred to in Table 6.

Table 6 The HM BCs for SPP_COx-2 test

The initial water pressure in the sample was set to 4.5 MPa, which is equal to the pressure applied on the BF. The initial gas pressure was set to 5.0 MPa, which was a little higher than the water pressure to avoid the convergence problem and to initiate the gas flow process. Although the initial capillary pressure is calculated to be 0.5 MPa, the corresponding initial water saturation degree is 99.4% which still represents an almost saturated condition of the sample. Accordingly, the initial water–solid interfacial energy and equivalent pore pressure are calculated to be 3178 Pa and 4.5 MPa, respectively. The initial Biot’s tensor is calculated by considering the initial normal stiffness and spacing of the fracture set, which is determined as ${{\varvec{\upalpha}}}_{0} = (\begin{array}{*{20}c} {0.76} & {0.67} & {0.75} & 0 & 0 & 0 \\ \end{array} )^{{\text{T}}}$. The initial effective stress tensor is determined to be ${{\varvec{\upsigma}}}_{0} = (\begin{array}{*{20}c} { - 9.08} & { - 9.49} & { - 9.63} & 0 & 0 & 0 \\ \end{array} )^{{\text{T}}}$ MPa. The initial mechanical aperture of the two fracture sets is calculated to be − 1.76 × 10^–5 m for the 1st set and − 1.82 × 10^–5 m for the 2nd set, respectively. The initial intrinsic permeability of two fracture sets is set to have the same value as that in the COx-1 test, i.e., 2.03 × 10^–23 m², to initiate the fluid flow process in fractures.

4.5.2 Results and Discussion

Figure 11 shows the comparison of pressure in the IGR and BGR between simulated and experimental results. Although the simulated gas pressure and equivalent pore pressure cannot fully capture the rapid increase of the IGR and BGR pressure, the model still provides some other satisfactory results. In the model, the fracture opening/closure is fully controlled by the normal stress change; see Eq. (11). As gas is injected in the IF, gas gradually migrates along with the existed fractures with increasing gas pressure. This unloading process leads to the increase of effective stress, as can be seen from Eq. (9), which causes the fracture to open correspondingly. Once the gas penetrates to the IGR area, the gas pressure in the IGR increases nonlinearly, as can be seen in Fig. 11.

Fig. 11

Comparison of IGR pressure between simulated and experimental results

As reported by Cuss et al. (2012, 2014), the evolution of BGR pressure was interpreted as the HM coupled response due to gas penetration. Thus, the equivalent pore pressure may be a good choice to capture the change. Although the response of simulated equivalent pore pressure begins at a similar time with that in the experiment, at about day 255, which is indicative of the start of the coupling process between gas migration and fracture opening. However, the change rate is much smaller than expected due to the aforementioned fracture behavior. Compared with the early stabilized BGR pressure at 6.5 MPa in the experiment, the simulated asymptote value, i.e., 6.1 MPa, is finally reached at around day 310) Further work needs to be done in the future to totally capture the complex evolution of pressure observed in the IGR and BGR.

Figure 12 represents the distribution of gas pressure and gas flux at different times. At the initial state, gas pressure is kept to a uniform value, i.e., 5 MPa, so no gas flux occurs. At the second gas pumping time, i.e., day 187 corresponding to the third event shown in Fig. 11, gas penetrates the sample through the IF and concentrates in the IF area. At the third gas pumping time, day 236 in the fifth event, gas gradually migrates in both directions. With continuous increasing of gas injection pressure, large amounts of gas flow into the sample and reach the middle area of the sample, accompanied by the sample volume dilation; see Fig. 12d. As time elapses, gas almost penetrates the BF area; see Fig. 12e. And the preferential gas pathways are along the axial center of the sample, as can be seen in Fig. 12e, f, i.e., the more concentrated arrow line in the central area than that in the sidewall area. This phenomenon occurs for two reasons: (1) a straightway from the inlet to the outlet is the shortest distance for gas transport, and (2) the direction of the first pre-inserted fracture set (i.e., $\beta_{{{\text{f1}}}}$ = 0° in Fig. 1) is along the sample axis, which provides a preferential pathway for gas movement. This characteristic of gas propagation can be also observed from the symmetry of radial deformation; see Fig. 14, which has been reported by Cuss et al. (2012).

Fig. 12

The distribution of gas pressure and flux at a different time (arrow line represents the gas velocity)

Figure 13 represents the normal displacement of two fracture sets at middle point A. Based on the general model proposed by Cuss et al. (2012, 2014), the fracture response due to gas injection is also divided into three stages: fracture initiation, acceleration and stabilization. In the stage of fracture initiation, gas gradually enters the sample, and the fracture opening initiates at a slow rate. Due to the anisotropic material properties, the different change in sample deformation causes the different change in normal stress of the fracture set, thus leading to slightly different opening sizes of the two fracture sets. In the acceleration stage, large amounts of gas flow into the sample, which causes the accelerating deformation of fracture in the normal direction. In the last stage of stabilization, fracture behavior becomes stable as gas has already propagated throughout the sample and kept flowing out of the sample at a steady state.

Fig. 13

Normal displacement of two fracture sets

Figure 14 shows the comparison of radial deformation between simulated and experimental results. Figure 15 shows the comparison between simulated and experimental results of strain data. Generally, both the simulated displacement and strain results get an overall agreement with the experimental data. Thanks to the inherent bedding of the rock matrix and the introduced fracture sets, the determined compliance tensor is significantly anisotropic, see Fig. 2, thus leading to anisotropic radial deformation. Besides, the symmetric radial deformation also corresponds to the direction of gas flow pathways which are mainly concentrated upon the sample axis area, as can be seen from the gas velocity direction in Fig. 12e, f.

Fig. 14

The radial deformation of the sample

Fig. 15

Comparison between simulated and experimental results of strain data

5 Conclusions

A fully coupled hydro-mechanical (HM) model is presented here to simulate the gas migration in initially saturated claystone with considerable anisotropy. The governing equations including mass conservation, momentum balance and energy conservation are presented for the unsaturated rock containing three-phases, i.e., gas, water and solid grain. The constitutive model is proposed by considering the effects of both the solid matrix and the fracture set. The fractured rock is regarded as an equivalent continuum consisting of solid matrix and fractures, in which two conceptualized fracture sets are assumed to be pre-existing with constant spacing in the REV. The fracture shows nonlinear mechanical behavior in the normal direction, fracture permeability is controlled by cubic law. The HM behavior of fracture is coupled through the mechanical aperture and hydraulic aperture, which have a superposed effect on the HM behavior of the solid matrix. As the 2D axisymmetric model cannot represent the phenomenon of larger fracture opening size close to the gas injection inlet due to the existence of the constant symmetrical axis, also it cannot capture the anisotropic deformation along the radial direction, thus a model with three-dimensional geometry is provided here.

The developed model is evaluated against three laboratory gas injection tests on initially saturated COx claystone, i.e., intact sample COx-1, designated fractured sample COx-4, triaxial condition tested sample SPP_COx-2. In general, the simulated results are in good agreement with that in all three experimental studies. The pressure evolution in the IGR and BGR is specifically represented by the simulated fluid pressure, i.e., gas pressure, water pressure, or equivalent pore pressure. The fracture opening/closure is governed by the gas injection pressure as it acts to influence the effective stress of the solid matrix. Correspondingly, the normal stiffness of fracture decreases with the aperture opening which has an implicit weakening effect on the compliance tensor of the equivalent continuum, thus leading to the volume dilation. The dual effects of the matrix containing inherent bedding and fracture induced stiffness reduction to cause the anisotropic deformation in the radial direction, which is well represented by the proposed 3D model.

In summary, the developed HM model has well captured the key experimental observations, i.e., anisotropic radial deformation, major gas breakthrough, and mechanical volume dilation of the sample, offered additional insight into the mathematical relation between gas flow, solid matrix deformation and fracture opening/closure. However, the numerical model either slightly underestimates or overestimates the gas flux for the whole gas migration process, which shows the difficulty of modeling the dynamic behavior of dilatant gas pathways. Further improvements can be made in future studies by introducing the heterogeneous HM properties, which can better represent the real condition. Moreover, the fracture propagation law as well as thermodynamically consistent damage model can be taken into account to improve the model performance, which will be performed in our future work.