1 Introduction

Failure of quasi-brittle materials such as rocks is associated with the localization of strain into a finite band forming macroscopic fracture. Accumulation of these microcracks due to their initiation, growth and coalescence imposes a nonlinear/softening behavior in the stress–strain curve of rocks. In the recent decades, several researchers have developed numerical method (codes) to capture the complicated process of fracturing. Jing and Hudson (2002) have classified the most commonly applied numerical methods in Rock Mechanics in three categories of (1) Continuum method including the Finite Difference Method (FDM), the Finite Element Method (FEM) and the Boundary Element Method (BEM), (2) Discrete Element Methods (DEM), (3) Hybrid continuum/discrete methods.

The DEM was introduced by Cundall (1971) for the analysis of rock-mechanics problems and then applied to soils by Cundall and Strack (1979). Particle Flow Code, PFC (Itasca Consulting Group Inc. 2012) as a DEM based code discretizes the domain by a number of discs in 2D and spheres in 3D which are in contact two by two transferring normal and shear forces in contact bond and also resisting rolling induced by moment in parallel bond version (Potyondy and Cundall 2004). Fractures are formed by breakage of the bonds and their coalescence with other broken bonds. Classical PFC does not use fracture mechanics theories directly, but Potyondy and Cundall (2004) showed that the fracture toughness can be related to the properties of parallel bond model if a definite size of particles (a characteristic length) are chosen with two non-dimensional constants α and β. Marina et al. (2015) obtained a cubic relationship between \(\beta \sqrt \alpha\) and \(K^{\text{I}}\). Huang et al. (2013) also used PFC to calculate the toughness in rock cutting. Moon et al. (2007) developed a general approach to measure fracture toughness under random packing of non-uniform size particles. They used the energy balance approach which is based on the equilibrium state between strain, friction, and kinetic energy as the internal and the total accumulated work done by the loaded boundaries as the external energies. Their second method was collocation method which is determining the coefficients in a series of stress solution based on the complex stress function presented by Westergaard (1939) and expanded by Sanford and Berger (1990). In this method, the result is sensitive to the number of data points. Although, PFC is widely used in modeling of rock failure and fracture propagation, like any other method or code, it has particular drawbacks such as low unconfined compressive to indirect tensile strength ratio, effect of the inherent roughness of interfaces forming discontinuities on frictional behavior. Lisjak and Grasselli (2014) have discussed the major drawbacks and reviewed the recent studies improving them. Among them are the paper by Potyondy and Cundall (2004) where they used cluster of particle together to obtain a more realistic macroscopic friction values. Cho et al. (2007) showed that clumped-particle geometry lead to a more correct compressive to tensile strength ratio. Potyondy (2012) has alternatively, formulated the flat-joint model to capture the effect of clumped-particles.

Hybrid continuum-discontinuum method has recently gained attention among the researchers. Hybrid methods, generally consider the domain as a continuum and as soon as the cracks are about to form, the domain becomes discontinuum in the corresponding region. ELFEN (Rockfield Software Ltd. 2004) is an example of a hybrid code that is based on finite element formulation. The transition from elastic continuum to discontinuum is controlled by dissipation of a definite amount of strain energy during strain localization into a crack band. For details about ELFEN the readers are referred to Klerck (2000) and Profit et al. (2015). Another known hybrid method is the combined finite-discrete element method developed by Munjiza (2004) and extended by Mahabadi et al. (2012) named Y-Geo by improving the limitation of Munjiza’s FDEM such as including a quasi-static friction law, Mohr–Coulomb and rock joints shear failure criterion etc. Guo et al. (2016) have also developed a three dimensional version of the Munjiza’s FDEM that has the ability to capture transition from continuum to discontinuum and the explicit interaction of discrete fractures. Lisjak and Grasselli (2014) have given a comprehensive review on some of DEM and hybrid codes.

Hori et al. (2005) and Alassi (2008) have separately developed methodologies by which the microscopic parameters Kn (contact normal stiffness) and Ks (contact shear stiffness) are calculated using macroscopic Young’s modulus and Poisson’s ratio. The main objective in their works was removing the difficult process to calibrate the PFC model to find the desired condition to capture the effect of Poisson’s ratio. The improper arrangement of particles does not produce a lateral deformation due to the axial loading in DEM (Hori et al. 2005). However, the lateral deformation caused by an axial deformation both globally and locally determines the stress changes in large scale applications especially in oil–gas depletion or fluid injection such as CO2 storage and Enhanced Oil Recovery (EOR) (Fjaer et al. 2008). Therefore, there is no need for the calibration procedure required in PFC. Hori et al. (2005) called their method/code FEM-β which was developed in the framework of FEM. In contrast, Alassi (2008) developed his methodology in the framework of DEM and called it Modified Discrete Element Method (MDEM). MDEM has been successfully applied in reservoir geomechanics and hydraulic fracturing recently (Lavrov et al. 2016; Gheibi et al. 2016, 2017). Like the FEM, MDEM suffers from mesh/particle size dependency in modeling crack propagation. In the local FEM approach, mesh size dependency is treated by correcting the softening modulus for the element size by enforcing a mesh size independent fracture energy (Bazant and Planas 1997). However, in others, a material length scale is incorporated in the formulation of finite elements. In the nonlocal damage model formulation, the stress at a point not only depends on the strain at that point, but also on the strain at a neighborhood of that point (e.g. Bažant and Pijaudier-Cabot 1988; Guy et al. 2012). The gradient-enhanced approach incorporates the dependency on the second gradient of an invariant of the plastic strain (e.g. De Borst and Mühlhaus 1992). In the micropolar elastoplaticity, the Cosserat’s continuum is adopted (e.g. Steinmann and Willam 1991). Considering rate-dependency of the yield surface is also another approach to overcome the instability in strain localization (Wang et al. 1997). Alternatively, a finite width of a localization band is reduced to zero width (or an interface) known as a strong discontinuity. Assumed enhanced strain (Simo and Rifai 1990) and the extended finite element (Moës et al. 1999) methods are classified among the approaches used assuming a strong discontinuity which uses classical plasticity theory without introducing a length scale.

In this paper, we will discuss the new developments in MDEM by presenting two different methodologies that are based on Linear-Elastic Fracture Mechanics (LEFM) and Elastic-Softening Fracture Mechanics to deal with the fracture problem. The application of MDEM in the lab and large scale will be shown by modeling several examples. The general formulation of MDEM will be given in Sect. 2. In Sect. 3, the application of MDEM in LEFM will be discussed by solving several examples. Section 4 covers the application of MDEM in elastic softening fracture mechanics of quasi-brittle materials. Finally, the conclusions will be given in the last section.

2 Modified Discrete Element Method

The Modified Discrete Element Method (MDEM) was proposed by Alassi (2008) to model fracture developments and fault reactivation during fluid withdrawal and injection at reservoir scale. MDEM is a hybrid code that behaves like a continuum model (e.g., finite element method) before failure and like a discontinuum model (e.g., discrete element method) after failure.

Figure 1 shows a triangular element formed by connecting the centers of three discs which are in contact two by two. The triangle element is also called a cluster.

Fig. 1
figure 1

Representation of MDEM element (Alassi 2008)

Full size image

The constitutive relationship of the normal forces, \({\mathbf{f}}_{{\mathbf{n}}} = \left\{ {\begin{array}{*{20}c} {f_{n1} } & {f_{n2} } & {f_{n3} } \\ \end{array} } \right\}^{\text{T}} ,\) and the normal relative displacements, \({\mathbf{u}}_{{\mathbf{n}}} = \left\{ {\begin{array}{*{20}c} {u_{n1} } & {u_{n2} } & {u_{n3} } \\ \end{array} } \right\}^{\text{T}} ,\) of the three contacts of a cluster (Fig. 1) is given as Alassi (2008)

$${\mathbf{f}}_{{\mathbf{n}}} = {\bar{\mathbf{K}}\mathbf{u}}_{{\mathbf{n}}} ,$$
(1)

where, \({\bar{\mathbf{K}}} = \left( {\begin{array}{*{20}c} {k_{n1} } & {a_{12} } & {a_{13} } \\ {a_{21} } & {k_{n2} } & {a_{23} } \\ {a_{31} } & {a_{32} } & {k_{n3} } \\ \end{array} } \right)\).

It is assumed that a contact can only develop normal forces, therefore, the shear stiffness of contact are set to zero. Instead, \(a{}_{ij}\) are introduced to the matrix of stiffness in Eq. (1). \(a{}_{ij}\) represents the contribution of the deformation of \(j{\text{th}}\) contact on the force of \(i{\text{th}}\) contact.

Stress state is related to the internal forces of the contacts. Using Gauss theorem, stresses are retrieved from the internal forces as following (Alassi 2008)

$${\varvec{\upsigma}} = \frac{1}{A}{\mathbf{M}}^{{\mathbf{T}}} {\mathbf{f}}_{{\mathbf{n}}} ,$$
(2)

where, \({\varvec{\upsigma}} = \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } & {\sigma_{yy} } & {\sigma_{xy} } \\ \end{array} } \right\}^{\text{T}}\), \(A\) is the area of the cluster (triangle), the internal forces \({\mathbf{f}}_{{\mathbf{n}}}\) and \({\mathbf{M}}\) is the unit normal vector matrix defined as Alassi (2008)

$${\mathbf{M}} = \left( {\begin{array}{*{20}c} {I^{2}_{11} d_{1} } & {I^{2}_{12} d_{1} } & {I_{11} I_{12} d_{1} } \\ {I^{2}_{21} d_{2} } & {I^{2}_{22} d_{2} } & {I_{21} I_{22} d_{2} } \\ {I^{2}_{31} d_{3} } & {I^{2}_{32} d_{3} } & {I_{31} I_{32} d_{3} } \\ \end{array} } \right),$$
(3)

where \(I_{e1} = \cos \left( {\theta_{e} } \right)\)\(I_{e2} = \sin \left( {\theta_{e} } \right)\) and the angle \(\theta_{e}\) represents the normal vector orientation of contact \(e\) inside the cluster, \(d_{e}\) is the contact length (the distance between the centers of the two particles that are in contact), and \(e = 1,2,3\) is the ID of contacts.

Strain of a cluster is calculated using (Alassi 2008)

$${\mathbf{u}}_{{\mathbf{n}}} {\mathbf{ = M\varepsilon }}.$$
(4)

The geometrical matrix \({\mathbf{M}}\) transforms the strain of a cluster \({\varvec{\upvarepsilon}} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } & {\varepsilon_{yy} } & {\varepsilon_{xy} } \\ \end{array} } \right\}^{\text{T}}\) to the relative displacements \({\mathbf{u}}_{{\mathbf{n}}} ,\) of contacts.

The stress can be related to the strain by using the material conventional constitutive elastic matrix \({\mathbf{C}}\) as

$${\mathbf{\sigma = C\varepsilon }}$$
(5)

So, by combining Eqs. (1)–(5) a relationship can be derived between the conventional elasticity matrix and internal contact stiffness matrix \({\bar{\mathbf{K}}}\) as following (Alassi 2008)

$${\mathbf{C}} = \frac{1}{A}{\mathbf{M}}^{{\mathbf{T}}} {\bar{\mathbf{K}}\mathbf{M}}.$$
(6)

The solution scheme is an explicit one like the regular discrete element method after \({\bar{\mathbf{K}}}\) is retrieved from Eq. (6). The contact forces are updated (\({\mathbf{f}}_{{\mathbf{n}}}^{\text{new}} = {\mathbf{f}}_{{\mathbf{n}}} + {\text{d}}{\mathbf{f}}_{{\mathbf{n}}}\)) based on the incremental change in the forces (\({\text{d}}{\mathbf{f}}_{{\mathbf{n}}} = {\bar{\mathbf{K}}}{\text{d}}{\mathbf{u}}_{{\mathbf{n}}}\)) due to contact’s relative displacement. \({\text{d}}{\mathbf{u}}_{{\mathbf{n}}}\) is calculated based on the difference of velocities of the two particles in contact in time step \({\text{d}}t\).

Newton’s second law is used to update the particle’s motion [see Cundall and Strack (1979) for more details]. Clusters fail in tension or shear after they reach their peak strength value. For a failed cluster, two of the contacts fail.

Discontinuities such as joints and faults can be introduced to the model. A discontinuity is a collection of failed clusters which has two contacts failed. This provides flexibility in introducing preexisting discontinuities even with complex geometries. The direction of the failed contact is updated to the direction of the discontinuity. This is equivalent to the smooth-joint model in DEM introduced by Mas Ivars et al. (2008).

The failure criterion is Mohr–Coulomb with a tension cut-off. After peak strength of an element, the strain localizes into a band with a finite width (Bazant and Planas 1997) and a finite amount of energy is dissipated until the continuum cluster turns to discontinuum. Two of the three contacts of the cluster are allowed to separate or slide. The two failed contacts are selected based on the direction of minimum principal stress i.e. the contacts under lower normal force. Post-peak softening/hardening behavior is captured by dividing the strain \(\left( \varepsilon \right)\) into two elastic \(\left( {\varepsilon^{e} } \right)\) and plastic parts \(\left( {\varepsilon^{p} } \right)\) i.e. \(\varepsilon = \varepsilon^{\text{e}} + \varepsilon^{\text{p}} .\) The plastic strain is calculated as Chen and Han (2007)

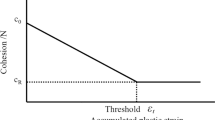
$$\varepsilon^{\text{p}} = \varLambda \frac{\partial F}{\partial \sigma },$$
(7)

where Λ is the plastic multiplier defined by the plastic power equivalence (plastic work) and is a function of the hardening/softening modulus H (Chen and Han 2007). Since the internal calculation of the code is based on displacements rather than strains, \({\mathbf{u}}^{\text{p}}\) as the plastic relative displacement is calculated using \(\varepsilon^{\text{p}}\) and \({\mathbf{u}}^{\text{e}} = {\mathbf{u}} - {\mathbf{u}}^{\text{p}}\) is the elastic relative displacement. \({\mathbf{u}}^{\text{e}}\) is used to update the forces in Eq. (1). Fractures appear if the effective plastic strain in a given cluster reaches a critical value. The critical plastic strain is dictated by H or equivalently the fracture energy. Figure 2 represents the geometrical relation between fracture energy (\(G_{\text{f}}\)), softening modulus (H), tangential modulus \((E_{\text{t}} )\), Young’s modulus (\(E\)) fracture energy density (\(\gamma^{\text{f}}\)), tensile strength (\(f_{\text{t}}\)) for a bar breaks in uniaxial tension.

Fig. 2
figure 2

The crack band model, a system response, b crack band softening (Bazant and Planas 1997; Klerck 2000)

Full size image

According to Bazant and Planas (1997) the crack band has a finite width (\(h_{\text{c}}\)) that is a material constant depending on its maximum particle size. From numerical point of view, the size of the elements should not necessarily be exactly equal to \(h_{\text{c}}\) but larger element size can be used in the model. However, the softening modulus (H) or equivalently \(\varepsilon_{\text{c}}^{\text{f}}\) should be updated to guarantee the correct energy release rate independent of the mesh size. The fracture energy \(G_{\text{f}}\) defines the amount of energy dissipated per unit cross sectional area of the crack band of width \(h_{\text{c}}\). For an arbitrary mesh, strain-softening should necessarily localize into an element of dimension,\(h^{\text{e}}\). The equivalent softening modulus (\(H^{\text{e}}\)) is determined by enforcing a constant fracture energy \(G_{\text{f}}\) as following

$$G_{\text{f}} = h_{\text{c}} \gamma_{\text{f}} = h^{\text{e}} \gamma_{\text{f}}^{\text{e}} \Rightarrow \gamma_{\text{f}}^{\text{e}} = \frac{{h_{\text{c}} }}{{h^{\text{e}} }}\gamma_{\text{f}} \Rightarrow H^{\text{e}} = \frac{{h^{\text{e}} }}{{h_{\text{c}} }}H.$$
(8)

Therefore, the results should be less mesh size sensitive. To avoid a negative value of \(H^{\text{e}}\) for very large mesh sizes, the tensile strength can also be modified to ensure constant fracture energy (Bazant and Planas 1997).

It should be noted that the examples modeled with elastic-softening in this paper have been restricted to tensile mechanism and the softening after shear failure was beyond the goal of this paper. However, Alassi and Holt (2011) modeled softening behavior under compression with MDEM.

The main difference between MDEM and the regular discrete element method is that the material behaves like a continuum before failure, where the conventional elastic properties are given as input values (Eq. (6)). The material behaves like a regular discrete element method after the deformation of an element reaches \(\varepsilon_{\text{c}}^{\text{f}} .\)

2.1 Calculation of \(K^{\text{I}}\) and \(K^{\text{II}}\) in MDEM

For an arbitrarily oriented crack in an isotropic body under a mixed-mode I–II loadings in plane stress or plane strain conditions. The stresses near the crack tip are

$$\sigma_{yy} = {{K^{\text{I}} } \mathord{\left/ {\vphantom {{K^{\text{I}} } {\sqrt {2\pi x} }}} \right. \kern-0pt} {\sqrt {2\pi x} }}$$
(9)
$$\tau_{xy} = {{K^{\text{II}} } \mathord{\left/ {\vphantom {{K^{\text{II}} } {\sqrt {2\pi x} }}} \right. \kern-0pt} {\sqrt {2\pi x} }}.$$
(10)

The total forces over the \(x_{\text{c}} -\) sized ligament (Fig. 3) can be expressed as de Morais (2007)

Fig. 3
figure 3

A pre-existing crack and clusters in front of the crack tip and calculation of forces required to approximate \(K^{\text{I}}\) and \(K^{\text{II}}\) (after Gheibi et al. 2018)

Full size image
$$F_{y} = \int\limits_{0}^{{x_{\text{c}} }} {\sigma_{yy} } {\text{d}}x = K^{\text{I}} \sqrt {{{2x_{\text{c}} } \mathord{\left/ {\vphantom {{2x_{\text{c}} } \pi }} \right. \kern-0pt} \pi }}$$
(11)
$$F_{x} = \int\limits_{0}^{{x_{\text{c}} }} {\tau_{xy} } {\text{d}}x = K^{\text{II}} \sqrt {{{2x_{\text{c}} } \mathord{\left/ {\vphantom {{2x_{\text{c}} } \pi }} \right. \kern-0pt} \pi }} .$$
(12)

And their values can be evaluated from the internal forces of the contacts for a cluster at its center of gravity as shown in Fig. 3. SIFs are estimated using (de Morais 2007)

$$K^{{ * {\text{I}}}} = \sqrt {{\pi \mathord{\left/ {\vphantom {\pi {2x_{\text{c}} }}} \right. \kern-0pt} {2x_{\text{c}} }}} \sum\limits_{i = 1}^{l} {F_{y,i} }$$
(13)
$$K^{{ * {\text{II}}}} = \sqrt {{\pi \mathord{\left/ {\vphantom {\pi {2x_{\text{c}} }}} \right. \kern-0pt} {2x_{\text{c}} }}} \sum\limits_{i = 1}^{l} {F_{x,i} } .$$
(14)

\(K^{\text{I}}\) and \(K^{\text{II}}\) are calculated by extrapolating to \(x_{\text{c}} = 0\) of the linear approximations of \(K^{{*{\text{I}}}}\) and \(K^{{*{\text{II}}}}\) as a function of \(x_{c}\) plots, respectively. The deviation from the analytical \(K^{\text{I}}\) and \(K^{\text{II}}\) values is about 1%. The method provides an acceptable accuracy for reasonably coarser mesh.

2.2 Mixed Mode I–II Cracks and Brittle Fracture Criterion

Erdogan and Sih (1963) proposed the composite criterion of minimum circumferential tensile stress (minimum tensile–stress criterion). This criterion holds that a mixed mode I–II crack propagates along the corresponding direction of minimum tensile stress satisfying the following (modified after Wu et al. 2016)

$$\frac{{\partial \sigma_{\theta \theta } }}{\partial \theta } = 0,\;\frac{{\partial^{2} \sigma_{\theta \theta } }}{{\partial \theta^{2} }} > 0$$
(15)
$$\theta^{\text{IC}} = 2\tan^{ - 1} \frac{{1 - \sqrt {1 + 8w^{2} } }}{4w},\;w = \frac{{K^{\text{II}} }}{{K^{\text{I}} }},$$
(16)

where \(\theta^{\text{IC}}\) is the corresponding direction of minimum tensile stress.

The corresponding SIF of minimum tensile stress or equivalent mode I intensity factor is given by (modified after Wu et al. 2016)

$$K^{\text{Ie}} = \frac{1}{2}\cos \frac{\theta }{2}^{\text{IC}} \left[ {K^{\text{I}} \left( {1 + \cos \theta^{\text{IC}} } \right) - 3K^{\text{II}} \sin \theta^{\text{IC}} } \right].$$
(17)

The fracture criterion for mode I crack grow/rupture is Rao et al. (2003)

$$\left| {K^{\text{Ie}} } \right| \ge K^{\text{IC}} ,$$
(18)

where \(K^{\text{IC}}\) is the fracture toughness in mode I.

To obtain the direction of maximum shear stress, the following condition should be satisfied

$$\frac{{\partial \tau_{\theta r} }}{\partial \theta } = 0,\;\left| {\tau_{\theta r} \left( {\theta = \theta_{\alpha }^{\text{IIC}} } \right)} \right|_{\text{max} } .$$
(19)

This leads to a cubic equation with three roots. We derive the following solution as the corresponding direction of maximum (absolute value) shear stress (Gheibi et al. 2018)

$$\theta_{\alpha }^{{I{\text{IC}}}} = 2\tan^{ - 1} \left( {2\cos \left( {\frac{g}{3} + \left( {\alpha - 2} \right)\frac{\pi }{3}} \right)\sqrt { - \left( {\frac{p}{3}} \right)} + \frac{w}{3}} \right),\;\alpha = 1,2,3,$$
(20)

where, \(p = - \frac{1}{3}\left( w \right)^{2} - \frac{7}{2}\), \(q = \frac{2}{27}\left( w \right)^{3} - \frac{2}{3}w\), \(g = \cos^{ - 1} \left( { - \frac{1}{2}\frac{q}{{\sqrt { - \left( {\frac{p}{3}} \right)^{3} } }}} \right)\) and \(\alpha\) is the index of the three roots and only one of them maximizes the shear stress.

Therefore, the corresponding SIF of maximum shear stress or equivalent mode II intensity factor is given by (modified after Wu et al. 2016)

$$K^{\text{IIe}} = \frac{1}{2}\cos \frac{{\theta^{\text{IIC}} }}{2}\left[ {K^{\text{I}} \sin \theta^{\text{IIC}} + K^{\text{II}} \left( {3\cos \theta^{\text{IIC}} - 1} \right)} \right].$$
(21)

The failure criterion for shear is given by Rao et al. (2003)

$$\left\{ \begin{aligned} \left| {{{K^{\text{IIe}} } \mathord{\left/ {\vphantom {{K^{\text{IIe}} } {K^{\text{Ie}} }}} \right. \kern-0pt} {K^{\text{Ie}} }}} \right| \ge {{K^{\text{IIC}} } \mathord{\left/ {\vphantom {{K^{\text{IIC}} } {K^{\text{IC}} }}} \right. \kern-0pt} {K^{\text{IC}} }} \hfill \\ K^{\text{IIe}} \ge K^{\text{IIC}} \hfill \\ \end{aligned} \right.,$$
(22)

where \(K^{\text{IIC}}\) is the fracture toughness in mode II.

It must be noted that \(K^{\text{I}}\) in Eqs. (17) and (21) is only meaningful if it is negative. Otherwise it should be set to zero.

3 Linear Elastic Fracture Mechanics

3.1 Central Crack Under Uniaxial and Biaxial Loading

Figure 4 represents \(K^{\text{I}}\) and \(K^{\text{II}}\) numerically obtained for a central crack with a length of \(2a = 1\) inclined by \(\beta\) varying from 0° to 90° from the horizontal line. A vertical, constant uniaxial tensile stress was applied on the top edge and the bottom was fixed in y direction. The difference between the exact solution and the numerical one is about 1%.

Fig. 4
figure 4

Comparison of analytical and numerical a\(K^{\text{I}}\) and b\(K^{\text{II}}\) as a function of the central crack inclination \(\beta\)

Full size image

It is also possible to calculate \(K^{\text{I}}\) and \(K^{\text{II}}\) for biaxial stress boundary condition in any ratio of the applied stress, no matter if they are compression–compression, tensile–tensile and tensile-compression. When the crack surface is closed (under compression) the corresponding \(K^{\text{II}}\) is corrected by imposing the effect of the friction coefficient. Based on the fracture criterion proposed by Rao et al. (2003), \(K^{\text{Ie}}\) and \(K^{\text{IIe}}\) are calculated using Eqs. (17 and 21). Figure 5 shows \(K^{\text{Ie}}\), \(K^{\text{IIe}}\) and the corresponding \(\left| {{{K^{\text{IIe}} } \mathord{\left/ {\vphantom {{K^{\text{IIe}} } {K^{\text{Ie}} }}} \right. \kern-0pt} {K^{\text{Ie}} }}} \right|\) for a central crack with \(\beta\) inclination under two uniaxial and compressive–compressive stresses with \(\lambda = 0,0.3\) and friction coefficient \(\mu = 0,0.6\). Figure 5 shows that mode I is more likely to occur for a central crack than mode II, because either \(\left| {{{K^{\text{IIe}} } \mathord{\left/ {\vphantom {{K^{\text{IIe}} } {K^{\text{Ie}} }}} \right. \kern-0pt} {K^{\text{Ie}} }}} \right|\) is lower than \({{K^{\text{IIC}} } \mathord{\left/ {\vphantom {{K^{\text{IIC}} } {K^{\text{IC}} }}} \right. \kern-0pt} {K^{\text{IC}} }}\) for rocks (Al-Shayea and Khan 2000; Rao et al. 2003; Backers and Stephansson 2012) or \(K^{\text{IIe}}\) is very low.

Fig. 5
figure 5

a\(K^{\text{Ie}}\) and \(K^{\text{IIe}}\) and b\(\left| {{{K^{\text{IIe}} } \mathord{\left/ {\vphantom {{K^{\text{IIe}} } {K^{\text{Ie}} }}} \right. \kern-0pt} {K^{\text{Ie}} }}} \right|\) for a central crack under uniaxial (λ = 0) and biaxial compression (λ = 0.3) with friction coefficient μ = 0,0.6

Full size image

3.2 Non-Collinear Cracks

The methodology can be applied to calculate \(K^{\text{I}}\) and \(K^{\text{II}}\) for preexisting cracks with complex geometries such as curved and multiple cracks in different geometries. Figure 6a represents a model of two non-collinear symmetrical cracks with 2a and \(\theta\) inclination with centers that are 2.2a away from one another under uniaxial tensile stress. Figure 6 displays different solutions [by Sih (1973), Chen and Chang (1989), Guo and Ma (2011), Guo et al. (2013)] for \(K^{\text{I}}\) for two symmetrical non-collinear cracks with several inclination \(\theta\). In the figure, the dots are the values obtained by this methodology for the two tips of the crack inclined by 20° and 0° from the horizontal line.

Fig. 6
figure 6

a Schematic of two collinear cracks, and b several solutions for \(K^{\text{I}}\)(after Guo et al. 2013)

Full size image

3.3 Reservoir Scale Application

Figure 7 shows a schematic description of the reservoir model used to study of the stress intensity factor change after injection of a fluid such as CO2. The reservoir is assumed to be closed and the pore pressure is increased inside it to mimic the fluid injection. It was assumed that the pore pressure remains constant in the surrounding rock as well as in the caprock. The reservoir thickness is 200 m and the aspect ratio of the models is 0.25. The elastic constants are the same for the reservoir and the surrounding rock with \(E = 15\;{\text{GPa}}\) and \(\nu = 0.2\). The studied fault with length of 100 m and inclination of 60° were placed at (0, 0). The mechanical boundary condition at the boundaries of the models is a constant stress equal to the far-field stress. The maximum principal stress is considered to be in the vertical direction called normal faulting or extensional stress regime. The ratio of horizontal stress to vertical stress was assumed to be 0.4. The pressure inside the reservoir section was increased by 5, 10, 15, 20, 25, 35 and 40 MPa in separate models. \(K^{\text{I}}\) and \(K^{\text{II}}\) were measured using the method described in 2.1 in both initial and after injection states. The friction coefficient of the fault plane assumed to be 0.6 and 1. Figure 8 shows the variation of K for different pressure change for the fault with different friction coefficients. The stress intensity values were normalized by \(\sigma_{V} \sqrt {50\pi } \left( {{\text{MPa}}\;{\text{m}}^{ - 0.5} } \right)\). Therefore, the results can be used for different initial in situ stress values.

Fig. 7
figure 7

Schematic representation of the general model, which includes a fault at center

Full size image
Fig. 8
figure 8

Variation of \(K^{\text{I}}\) and \(K^{\text{II}}\) vs pore pressure increase

Full size image

It is important to note that positive \(K^{\text{I}}\) is not meaningful. However, the positive values were used here to show to how much degree the fault tip was under compression and how it unloaded due to increase in the pressure. Figure 8 shows the \(K^{\text{I}}\) decreases for increasing pressure and it becomes negative after ΔP > 32 MPa. This means that after this amount of pressure increase mode I failure can occur. As expected, \(K^{\text{I}}\) is independent of friction coefficient. \(K^{\text{II}}\) increases for increasing pore pressure so that the mode II failure occurrence becomes more likely. It is observed that for higher friction coefficient a greater pore pressure increase is needed to have \(K^{\text{II}} > 0\). Increase of \(K^{\text{II}}\) loses its dependency on the friction coefficient after \(K^{\text{I}}\) becomes negative. The reason is that for \(K^{\text{I}} < 0\) the fault plane is open and normal force is zero so no shear resistance.

Equations (17 and 21) were used to calculate the equivalent stress intensity factors to be able to assess the rupture likelihood and plotted vs. pressure increase in Fig. 9. In contrast to Fig. 8, \(K^{\text{I}}\) was restricted to be ≤ 0 in Fig. 9, this also means that only negative \(K^{\text{I}}\) were used in the calculations in Eqs. (17 and 21). Figure 9a indicates that the mode I rupture can occur after 5 and 15 MPa pressure increase for the 0.6 and 1 friction coefficient cases, respectively depending on the toughness value (\(K^{IC}\)). The direction of mode I failure initiation was calculated to be 70.5° in the fault tip. However, the mode I rupture will probably change its direction to grow vertically depending on the level of pressurization. Mode II failure is more complicated because not only it depends on the \(K^{\text{IIC}}\) but also the ratio \(K^{\text{IC}} /K^{\text{IIC}}\). Figure 9b indicates that mode II is more likely for pressure lower than 30 MPa, because the \(K^{\text{Ie}} /K^{\text{IIe}}\) is lower. The reason is that for pressure > 30 MPa \(K^{\text{I}}\) becomes negative (Fig. 8), therefore, \(K^{\text{Ie}}\) has contributions from \(K^{\text{I}}\) and \(K^{\text{II}}\)(Eq. 17). However, for pressure < 30 MPa, \(K^{\text{I}}\) is positive so it does not contribute to \(K^{\text{Ie}}\) in Eq. (17). The mode II rupture (if occurs) will propagate along the fault plane for pressure < 30 MPa, and − 2.2° and − 5.8° (counterclockwise being positive). For more comprehensive discussion on this subject the readers are referred to Gheibi et al. (2018).

Fig. 9
figure 9

Variation of a\(K^{\text{Ie}}\) and b\(K^{IIe}\) vs pore pressure increase and rupture criteria (Eqs. 17 and 22)

Full size image

4 Elastic-Softening Crack Band model

4.1 A Model Without a Preexisting Crack: Brazilian test

First example in this section is modeling rock Brazilian test. This test is performed to obtain the indirect tensile strength of rocks. Brazilian test is also used to calculate the toughness of rock either including (Tang 2017) or excluding (Guo et al. 1993) a preexisting crack. Guo et al. (1993) proposed a method to calculate the KIC from the force curve of a Brazilian test by (after Wang and Xing 1999)

$$K^{\text{IC}} = \frac{{P_{\text{min} } }}{\sqrt R \times t}\varPhi_{\text{max} } ,$$
(23)

where \(P_{\text{min} }\) is the local minimum load which can be obtained from the force curve, \(\varPhi_{\text{max} }\) is the maximum dimensionless SIF and R and t are radius and thickness of the disc, respectively. \(\varPhi_{\text{max} }\) is dependent on the angle of the arc made by the loading plate and the sample. This angle is considered to be ~ 10° for the standard Brazilian test. However, experimental and numerical studies have shown that the standard Brazilian test can lead to a shear failure in the loading region rather than tensile failure at center of the specimen depending on the ratio of the shear to tensile strength (Fairhurst 1964; Gheibi et al. 2015) and deformability of the disc (Gheibi et al. 2015). Therefore, the modeled specimen was loaded by a plate with an arc angle of 30°. The radius of the disc is 52 mm and thickness was assumed to be 26 mm. \(\varPhi_{\text{max} }\) was calculated to be 0.443 (Erarslan et al. 2012). The Young’s modulus, Poisson’s ratio and tensile strength are 10 GPa, 0.25 and 7 MPa, respectively with H varying from 10 to 100 MPa. Figure 10 shows the force-strain curve of the model with several H. Table 1 shows \(P_{\text{max} } ,\)\(P_{\text{min} } ,\) calculated indirect tensile strength (σt), and the toughness value calculated by Eq. (23). As it is expected, the toughness value is greater for lower softening modulus. Lower softening modulus means that the cracks require more energy to proceed. Also, the estimated indirect tensile strength is higher for lower H models. Figure 11 shows the tensile fracture formed for different values of H. The fracture has propagated a longer distance for higher H values.

Fig. 10
figure 10

Brazilian test model with several softening moduli

Full size image
Table 1 Data of the Brazilian test models
Full size table
Fig. 11
figure 11

Load-CMOD curve of experimental and numerical models with several mesh sizes

Full size image

4.2 A Model with a Preexisting Crack: Three Points Bend Test

Three points bend test with a notch is a commonly used test to determine the toughness and fracture energy of quasi-brittle materials. To verify the capability of the code in elastic-softening fracture mechanics a three points bend experiment was modeled. The experiment data was picked up from Fakhimi et al. (2017). The sample used in this study was Berea sandstone. The sandstone specimen was prepared with length = 276 mm (span = 254 mm), height = 99.9 mm, and thickness = 24 mm and a straight notch was cut with length = 15 mm and width = 1.7 mm at the center of the beam (Fakhimi et al. 2017).

A model of the experiment was built in the code based on the geometry given above. A 15 mm crack was applied to the model instead of cutting the notch section in mesh generation. The elements/clusters were equilateral triangular with sides equal to 1 mm in front of the notch. The model matched to the experimental data has a Young’s modulus of 10 GPa (Fakhimi et al., 2017), Poisson’s ratio of 0.25, tensile strength 5.1 MPa and softening modulus, H = 40 MPa. The bending was simulated by applying a velocity boundary and the reaction force and Crack Mouth Opening Displacement (CMOD) were recorded numerically. Similar to the experiment, the model was unloaded at a point close to the 50% of the maximum force after peak (Fakhimi et al. 2017). Figure 12 shows the Force-CMOD curve of the experiment and the simulation with a relatively reasonable match with the two. Fakhimi et al. (2017) inspected the unloaded beam and a crack of about 25 mm in length above the notch was observed with an unaided eye. Interestingly, the propagated crack (cohesionless term was used by Fakhimi et al. 2017) was 22 mm in the model. The Force–deflection curve could not be verified because Fakhimi et al. (2017) did not measure the deflection (personal communication). Three other similar models with the element sizes of 1.5 mm, 3 mm, and 6 mm were built to investigate the effect of mesh size sensitivity. Figure 12 shows that the Force-CMOD curve was reproduced with an acceptable accuracy for different values of mesh size. Figure 13 shows the discretization of the model with 1 mm and 6 mm element sizes overlapping one another. It should be noted the mesh dependency of strain localization is not restricted to only the size of the elements (Guy et al. 2012), but its geometry and its relation to the fracture path. In this example, the geometry and loading condition is such that the fracture formed is in the vertical direction, therefore, the size of the spatial discretization play a more important role compared to its orientation. Jirásek and Bauer (2012) showed that the effective width of a crack band depends on the shape of the element and its orientation with respect to the overall direction of the band.

Fig. 12
figure 12

Load-CMOD curve of experimental and numerical models with several mesh sizes

Full size image
Fig. 13
figure 13

Comparison of the discretization of the model with 1- and 6-mm mesh sizes

Full size image

5 Conclusion

Modified Discrete Element Method (MDEM) and its new developments in fracture problem were presented in the paper. A Linear Elastic Fracture Mechanics (LEFM) based methodology was adopted to calculate stress intensity factors, \(K^{\text{I}}\) and \(K^{\text{II}}\) using the contact forces of particles. It is able to be used in complex boundary condition and geometrical configuration such as curved and interacting multiple cracks with acceptable accuracy. The methodology has been also used in reservoir scale to study the rupture likelihood of faults and fractures. This methodology enables the code to model mode I and mode II failures based on the fracturing model proposed by Rao et al. (2003).

Another development was embedding elastic-softening crack band model into MDEM. The code is able to model the nonlinear behavior of quasi-brittle materials including and excluding preexisting cracks. A Brazilian (without a notch) test was modeled by the second methodology and effect of softening modulus was studied on obtaining the models mode I toughness. Also, an experiment of a three points bend test with a notch was modeled in the paper. The numerically obtained force-crack mouth opening displacement was reasonably comparable the experimental test. The model was repeated for three different meshes 1.5, 3 and 6 time larger than the initial mesh and the results are less mesh size sensitive. Finally, it was shown that MDEM has the capability in studying fracture mechanics of quasi-brittle materials both in the lab size and large-scale investigations.