Effect of Power Plant Operation on Pore Pressure in Jointed Rock Mass of an Unlined Hydropower Tunnel: An Experimental Study

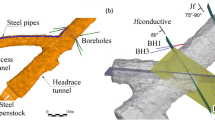
Abstract

Load changes in hydropower plants result in significant pressure transients and unsteady flow in the waterway. It has been observed that instances of block falls in tunnels have increased in unlined pressure tunnels subjected to frequent load changes. To examine this problem, field instrumentation was conducted in the 3.5 km long unlined headrace tunnel of 50 MW Roskrepp hydropower plant in southern Norway. This article describes the methodology of instrumentation, presents the observations and findings. The monitoring clearly demonstrates that frequent load changes have a considerable effect in the rock mass consisting of system of joints. The observations show that pressure transients can travel deep into the rock mass irrespective of their time period. Moreover, pressure transients with longer time periods, i.e. mass oscillations, are seen to induce a higher hydraulic gradient between the rock mass and the tunnel itself. A delayed response from the rock mass is observed during pressure transients, which is the main cause of development of hydraulic gradient and additional pore pressure acting on the rock blocks. Hence, it is evident that the cumulative impact of small but frequent pressure gradients is significant and is responsible for increased instances of block falls over a long period of operation of the unlined tunnels of hydropower plants with frequent start–stop sequences. The overall impact is governed by pore pressure response of the jointed rock mass which depends on the conditions of joint geometry and joint wall properties.

Introduction

The main design principle of unlined tunnels and shafts for hydropower plants is to place them in suitable rock mass with sufficient confinement. The placement is selected to avoid hydraulic jacking, which could lead to water leakages. Local sections with unstable rock mass, including swelling and/or friable materials are mapped and provided with sufficient support (Palmstrøm and Broch 2017). In such tunnels, hydraulic jacking needs to be prevented by ensuring that the maximum water pressure in the tunnel does not exceed the minimum principal in-situ stress in the rock mass. Design requirements and failure mechanisms of unlined pressure tunnels under static loading conditions are a well-studied issue described by several authors including Bergh-Christensen (1975), Buen (1984), Garshol (1988) Benson (1989), Panthi (2014), and Basnet and Panthi (2018). However, long-term instabilities caused by dynamic pressure transients over years of operation are not covered in existing design practices and literatures.

Lang et al. (1976) reported a case study of a hydropower tunnel failure as a result of rapid pressure transients caused by fluctuating power plant operation. A more recent failure of similar nature occurred in the Svandalsflona hydropower plant in southern Norway, where a rockslide occurred in an unlined shaft in 2008 and caused significant damage to the power plant (Panthi 2012; Neupane and Panthi 2018). Further, a list of several tunnel failures that occurred after years of operation is compiled by Brox (2018). Bråtveit et al. (2016) has concluded that compared with results from a previous study (Bruland and Thidemann 1991), the occurrence of rock falls has increased by a factor of 3–4 times in tunnels that have been subjected to frequent start/stop sequences (also referred to as hydropeaking).

The total length of hydropower tunnels and shafts in Norway is close to 4300 km and there are more than 100 unlined tunnels and shafts with maximum static head of up to 1047 m (Panthi and Basnet 2016). Most of Norwegian hydropower plants constructed during the 60s and 70s were designed to be operated as base load plants, providing a continuous supply of electricity throughout the year. Deregulation of the power market in Norway in 1991 has changed the operational regime of hydropower plants significantly. At present, there are far more frequent start–stop sequences and load changes compared to when they were designed and constructed.

In the future, the trend of fluctuating operation is expected to rise because of the increasing share of electricity generation from variable renewable energy (VRE) sources such as solar and wind power in the energy market. Electricity generation from these sources is dependent on weather conditions and most often does not comply with the system demand. Hence, hydropower plants will have more frequent load changes and start–stop sequence of operations in the future, to balance the production and load as the VRE share of production increases.

EPRI (1987) mentioned that the rate of recurrence of dynamic pressure is higher in peaking plants and pumped storage plants than in base load plants. According to Benson (1989), a factor of safety for static and dynamic pressures during normal operation must be used during unlined pressure tunnel design. However, pressure transients with a short time period, i.e. water hammer, does not require a factor of safety since the time of application is too short to cause hydraulic jacking. Helwig (1987) presented a theoretical study to estimate the depth to which significant pressure transients are transferred into the rock mass. It concludes that the effect of water hammer is limited to a relatively shallow depth around the tunnel walls because of the short time period. It also concludes that pressure penetration into the rock mass could be considerably larger during pressure transients with a longer time period, i.e. mass oscillations.

Frequent load changes in hydropower plants result in significant pressure transients and unsteady flow in the waterway. In an unlined pressure tunnel, pore pressure in the surrounding rock mass is dependent on water pressure in the tunnel itself. During long periods of standstill or steady operation, an equilibrium is reached. However, the authors’ hypothesis is that when load changes are occurring, delayed response of rock mass may cause significant pressure gradients between the tunnel and rock mass. This situation may be the leading cause of instabilities in the unlined pressure tunnels that have been occurring more frequently.

The main aim of this article is to describe a full-scale experimental study conducted on the unlined medium pressure headrace tunnel of the 50 MW Roskrepp hydropower plant in southern Norway. The major objective of the instrumentation and monitoring is to measure the changes in pore pressure in the rock mass near the tunnel walls during load changes and start–stop sequence of operation and to simultaneously measure the pressure fluctuations in the headrace tunnel. The methodology of instrumentation and recorded measurements for a period of 356 days are presented in this article. The obtained data provide valuable insights and are comprehensively analyzed. The monitoring will continue for a number of years to come so that possible changes during long-term operation are investigated.

Tunnel Hydraulics and Fluid Flow in the Rock Mass

During steady operation of a hydropower plant, a constant pressure is maintained in the tunnel which tends to push the water out of the tunnel to low-pressure areas such as nearby access tunnels/construction adits and out to the surface. Since hard rocks have relatively low porosity (mostly less than 2%), a system of rock joints act as flow paths governing the overall permeability of the rock mass. The design and construction of an unlined pressure tunnel are carried out such that leakage out of the tunnel is under acceptable limits (Panthi 2013). An equilibrium is reached for the given pressure and flow situation when the power plant is operated at constant load for a long time. This equilibrium is changed when there is a change of load in the power plant. Load changes cause pressure transients in the tunnel, which changes the pore pressure and the flow through system of joints. Hence, the issue under consideration is an interdisciplinary topic which involves two complex and dynamic mechanisms that are occurring simultaneously during the operation of an unlined pressure tunnel of a hydropower plant. They are described in brief in the following sections.

Flow and Pressure Transients in a Hydropower Tunnel

Every start, stop and load change in hydropower plants generate flow and pressure transients in the waterway. In the example of an emergency shutdown at Roskrepp power plant, the turbines close rapidly within 10 s and result in a rapid decrease of the water flow. The resulting deceleration of the water in the waterway causes a pressure increase on the upstream side of the turbine, and a pressure decrease on the downstream side. This pressure transient cannot be calculated simply with Newton’s second law, as water is an elastic medium that can be compressed and decompressed.

The elasticity of water will result in a pressure transient with a short time period, referred to as water hammer (Parmakian 1963). Water is barely elastic and requires a large pressure increase to cause a small compression, resulting in the maximum compression being reached in a short time, which leads to a fast-traveling water hammer. The water hammer starts from turbine and progresses towards the nearest free water surface where the water hammer is reflected back towards the turbine with the opposite pressure, a positive pressure becoming a negative one. In this manner, the water hammer may travel back and forth many times until the energy is dissipated by friction.

To reduce and control the water hammer, hydropower plants are constructed with a surge tank. The surge tank is constructed close to the turbines to reflect the water hammer as soon as possible, reducing the amplitude and the affected tunnel length. However, in hydropower plants with a surge tank, a pressure transient with a long time period will occur, which is referred to as mass oscillations (Chaudhry 1987). Mass oscillations are caused by the inertia of the water in the tunnel between the reservoir and the surge tank. When the turbines close, water cannot flow through the turbine and will instead flow into the surge tank, causing water level to rise. In the opposite case of a power plant startup, the water level in the surge tank will drop as it takes time to accelerate the water in the rest of the headrace tunnel to the reservoir. The rise or drop of the water level in the surge tank will reverse once the water in the main tunnel is accelerated or decelerated. This mass oscillation will oscillate back and forth until the energy is dissipated by friction. Figure 1 presents a principle drawing of a hydropower plant and the effect on water pressure from water hammer and mass oscillations.

Fig. 1

Flow and pressure transients in hydropower plants

The water hammer has a higher potential for pressure increase compared with the mass oscillations and may result in bursting pipes and structural damage if uncontrolled. The purpose of the surge tank is thus to reduce the water hammer, even though the surge tank causes mass oscillations to occur. Some measures other than surge tanks are available, such as pressure relief valves, but are often insufficient in hydropower plants with long waterways. The surge tank may thus be the only viable option, as is the case for Roskrepp power plant. The maximum water hammer pressure peak may be estimated with the following simplified equation: (Joukowsky 1889):

$$\Delta p = \frac{c\Delta v}{g},$$

(1)

where ∆p is the pressure increase by water hammer, c is the speed of sound in water, ∆v is the change in water velocity in the waterway. When there is a surge tank in the system, the rule of thumb is that water hammer is reduced with the factor T_r/T_l, where T_r = 2L/c is the return time of the water hammer and T_l is the closing time of the turbine. The maximum water level rise in surge tank during mass oscillation is calculated by the following equation:

$$z = \frac{{LA_{\text{t}} v^{2} }}{{2gh_{\text{f}} A_{\text{s}} }},$$

(2)

where L is the length of the tunnel between the reservoir and surge tank, A_t is the tunnel cross-section, v is the water velocity in the tunnel, g is the gravitational acceleration, h_f is the headloss in the tunnel between the reservoir and the surge tank, and A_s is the area of the water surface in the surge tank (the horizontal plane cross-section). For more accurate estimation of the water hammer and mass oscillations, numerical simulations are applied (Chaudhry 1987).

Fluid Flow Through Rock Fractures

Fluid flow through rock mass consists of two components: (1) flow through interconnected network of fractures, and (2) seepage through the pores of the rock itself, which is insignificant for crystalline rocks. Therefore, only the first component is considered here since the permeability in the rock mass is mainly controlled by the system of joints and not by the intact rock. According to Jing and Stephansson (2007), the fluid flow and block deformation are coupled through a two-way interaction. The change of fluid pressures on the rock joint surface affects the deformation on the joint wall, which causes the joint aperture to change. This change of hydraulic aperture affects its transmissivity, flow rate and fluid pressure distribution along the fracture surface, which in turn affects the deformation. Hence, the mechanical and hydraulic behaviors of a rock joint are interacting with each other. This hydro-mechanical coupling is shown in Fig. 2.

Fig. 2

(modified from Schleiss 1986)

Hydro-mechanical coupling in rock mass in an unlined tunnel

Significant research has been carried out regarding the hydro-mechanical behavior of single fractures in rocks since the 1960s. Rutqvist and Stephansson (2003) provide a summary of major research carried out in this area. It is an established fact that the void space geometry between fracture surfaces has a major influence on the flow through them. Hakami (1995) highlights the fracture properties affecting the void space geometry consisting of: (1) aperture, (2) roughness, (3) contact area, (4) matedness, (5) spatial correlation, (6) tortuosity, (7) channeling, and (8) stiffness of the fracture. A simplified form of the Navier–Stokes equation of viscous fluid flow through two parallel surfaces having a narrow aperture is used as a conceptual model to define the flow between two planar fractures. This is the most commonly used model in rock mechanics and is referred to as the ¨cubic law¨. The flow rate per unit width of fracture is given by the following expression:

$$q = \frac{{a^{3} }}{12\mu } \frac{\Delta p}{l},$$

(3)

where a is the aperture, μ is the kinematic viscosity of the fluid, ∆p is the pressure difference; and l is the length of joint. Witherspoon et al. (1980) modified the cubic law using lab experiments on artificial tension fractures in granite and marble and introduced the terms ¨apparent aperture¨ and friction factor into the equation which accounts for the roughness of fractures. Barton et al. (1985) propose the use of hydraulic aperture in Eq. (3) instead of the mechanical aperture and relate these two parameters with the following expression:

$$e = \frac{{{\text{JRC}}^{2.5} }}{{\left( {E/e} \right)^{2} }} \mu {\text{m}}\quad \left( {{\text{valid for}}\, E \ge e} \right),$$

(4)

where JRC is the joint roughness coefficient, E is the real physical aperture which can be calculated as the arithmetic mean of the separation between two fracture surfaces which can be measured with a feeler gauge and e is the hydraulic aperture.

Brief on Roskrepp Hydropower Plant

Roskrepp hydropower plant is located in Sirdal municipality in southern Norway and is operated by Sira-Kvina Kraftselskap. The power plant was commissioned in 1979 and has a design discharge of 70 m³/s with operating head between 52 and 109 m depending on the reservoir level. The installed capacity is 50 MW in one Francis turbine unit. The headrace tunnel is an inverted D shape, 6.5 m high, 7.5 m wide and approximately 3500 m long from the intake to the start of steel-lined pressure shaft (Fig. 3).

Fig. 3

Geological plan and profile of Roskrepp hydropower plant

Geological Setting of the Project

The rock mass in the project area consists of a mixture of coarse-grained granite and weakly schistose granitic gneiss. At regional scale, the geological structures are characterized by coarse-grained granite pluton which have intruded the gneiss and caused the foliation of granitic gneiss to follow the boundary of granite plutons (Sira-Kvina kraftselskap, 1977). Surface mapping of the project area revealed that the general orientation of foliation joints vary in the range N 135°–150° E/40°–60° NE (Jf). In addition, two prominent cross-joint sets having strike/dip as N 80°–100° E/70°–80° N (J1) and N 0°–20° E/40°–50° SE (J2) are present in the rock mass. During walkover survey along the dewatered tunnel, it was noted that rock mass along the tunnel is of good quality and very little rock support is provided except few meters of concrete lining when crossing through weakness zones. Most sections of the tunnel have tight-jointed walls and were observed to be dry during the survey. Weakness zones are mostly concentrated along the lower reaches of tunnel. Weakness zones crossing the tunnel are shown in the geological plan and profile of the power plant (Fig. 3).

Joint Conditions at the Instrumentation Location

The summary of comprehensive joint mapping carried out at the instrumentation location is presented in Table 1 following ISRM’s (1978) suggested method for quantitative description of discontinuities in rock mass. A major weakness zone crosses the tunnel approximately 150 m upstream of the instrumentation location (Fig. 3). Dripping flow was observed at several locations downstream of this weakness zone, which indicated relatively open joints in this section as compared to rest of the headrace tunnel. Joint mapping at the instrumentation location in the tunnel (Fig. 3) shows slightly different orientation of the joints as compared to surface mapping. Figure 4 shows typical joint orientation at the surface and the rosette of joints measured at the instrumentation location.

Table 1 Engineering geological properties of joint sets at the instrumentation location

Fig. 4

Orientation of joints a at surface near the instrumentation location and b joint rosette at the instrumentation location in tunnel

A 3D model of the tunnel (Fig. 5) generated using laser-scanned data shows the plan view of the jointing conditions at instrumentation location, along with the orientation of boreholes drilled for pore pressure measurement in the rock mass. The details of boreholes are presented in Sect. 4.2. On the right tunnel wall, BH1 and BH3 are aligned such that they intersect foliation joint set (Jf) and are roughly parallel to cross-joint set (J1). On the left wall, BH2 and BH4 are aligned such that they intersect cross-joint set (J1) and are roughly parallel to foliation joint set (Jf). BH5 intersects through foliation joint set (Jf) on the left wall. The cross-joint (J2) is clearly visible at the tunnel crown and is contributing to most of the inflow into the tunnel. In addition, a conductive single joint is present at the right wall (indicated by plane marked Jf_conductive). It follows the same orientation as foliation joint set (Jf) but has different joint aperture and infilling conditions, especially near the crown where it is in proximity to cross-joint (J2). On the right wall, both boreholes BH1 and BH3 intersect Jf_conductive (Fig. 6b) in addition to foliation joints (Jf). It is noted here that in BH3, the packer is located 4 m from the tunnel wall and the conductive single joint hits this borehole in the grout-filled impermeable section behind the packer. Hence, there is no direct hydraulic connection between the borehole and this single joint. On the left wall, BH4 intersects the cross-joint (J2), while BH2 does not intersect it (Fig. 5). Hence, only BH4 has a direct hydraulic connection to cross-joint (J2).

Fig. 5

Plan view of jointing conditions and orientation of boreholes at instrumentation location

Fig. 6

Joint conditions at a left wall (cross-joint J2 is visible) and b right wall showing Jf_conductive

Figure 6 show the joint conditions at the instrumentation location. Tunnel contour on the right wall is relatively less undulated as compared to left wall where undulations and formation of wedges are more prominent. The formation of wedge was due to blasting through unfavorably orientated joints in the tunnel wall during excavation, which exposed the joints on the left wall. Hence, a relatively larger number of joints are exposed to the tunnel contour on the left wall near BH2 and BH4 as compared to the right wall.

Instrumentation Setup

Selection of Instrumentation Location

The instrumentation is carried out just upstream of the junction between the construction adit and headrace tunnel at the downstream end as shown in Fig. 3. This location has been chosen because of the following reasons:

• 1. Measurement in headrace tunnel section between surge shaft and the steel-lined section will record the maximum pore pressure transient in the rock mass due to both water hammer and mass oscillation.

• 2. This location is nearby a construction adit, making it close to a dry area where pressure transducers and datalogger can be placed safely.

• 3. A detailed survey carried out along the headrace tunnel after 72 h of dewatering revealed that the rock mass at this location is suitable for the instrumentation where water inflow in the tunnel was distinct with a clear hydraulic connection between different joint systems and the tunnel walls.

Instrumentation Layout and Details

In total, five boreholes of 48 mm diameter are drilled at selected locations with varying length and orientation (Figs. 7 and 8). Stainless steel pipe of 10 mm internal diameter is fixed inside each borehole using rubber packers as shown in Fig. 9. The empty length of borehole inside the packer of each hole is used to collect water from the rock mass and to convey through installed stainless steel pipe to the pressure transducer located outside the concrete plug (dry area). As seen in Fig. 9, the packer when tightened fixes the steel pipe tightly in the borehole and creates a barrier between the pore pressure in rock mass and water pressure in the tunnel. In addition, grouting is carried out to achieve complete isolation between water flowing in the tunnel and the borehole beyond the packer. The packer is placed at different distances from the tunnel wall in the boreholes to study the pore pressure variation at various distances from the tunnel wall (Table 2). In addition, one steel pipe is installed in the tunnel to measure water pressure. The open end of this pipe is placed at the junction between headrace tunnel and construction adit as shown in Fig. 7.

Fig. 7

Layout of the instrumentation setup and location of boreholes

Fig. 8

Location of boreholes in the tunnel (looking upstream) and detail (top right corner)

Fig. 9

Schematic detail of borehole showing location of packer (left) and details of packer assembly (right)

Table 2 Borehole details

The steel pipes are laid out along the construction adit, through the concrete plug out to a dry area (Fig. 7). GE Unik 5000 absolute pressure transducers with an accuracy of 0.2% of full scale are connected to each pipe. The frequency of data logging for each sensor is 10 Hz, which is sufficient to record the pressure changes due to both water hammer and mass oscillations. Signals from the transducers are transmitted to an automatic datalogger shown in Fig. 10.

Fig. 10

Location of datalogger in the construction adit. Arrangement of pressure transducers and deaeration valve is shown in top right corner

Possible Error Sources and Remedies

Possible sources of error were identified during the planning process and measures were taken during installation to increase the accuracy of the measurements. They are as follows:

Choking of pipes The boreholes were thoroughly cleaned with a mixture of pressurized air and water to avoid the possibility of choking of pipes from the debris material which may come from the empty borehole. In addition, the boreholes are drilled in downward inclination of about 10° so that larger particles which can clog the pipes can settle towards the far end of the borehole, away from the pipe opening when there is no fluctuation of pressure in the borehole during standstill or steady power plant operation.

Water tightness of packers After the packer was fully tightened, the tightening handle was left in place and welded with the outer pipe (Fig. 9, top right). To ensure that no leakage occurs through the packer, the length of borehole outside the packer is filled with non-shrinking cement grout mix. This ensures that hydraulic connection between tunnel and boreholes is only through the joint systems in the rock mass. The setting of grout was checked with a geological hammer.

Leakage from pipes After installation, all six pipes were pressure tested with a maximum pressure of 30 bars (300 m) to prevent possible leakage from the connections. Detected leakages from some connections were rectified and tested again. This was done for the whole stretch of pipe except the last connection near the boreholes (Fig. 8, top right). This is to make sure that the test pressure does not affect the joints in the rock mass. After the pressure testing was completed, this last connection was installed with extreme caution to avoid leakage.

Removal of entrapped air in pipes Each steel pipe outside of the plug (air side) is equipped with a deaeration valve so that air entrapped in the pipe can be expelled out (Fig. 10, top right). This is to ensure that the readings are not affected by the air present in the pipes.

Pipe vibration due to flowing water It is possible that the pipes could move and vibrate due to flowing water during operation and affect the measurements. To avoid this, all six pipes are fixed rigidly to the tunnel wall/floor using grouted rock dowels and metal clamps at 1 m interval. The data shows that minor vibration still occurred in the pipes during operation and it increases slightly with increasing flow in the tunnel. However, during shutdowns the velocity of water in this tunnel section is zero as it lies downstream of the surge shaft and hence will not affect the quality of the readings.

Condition of setup after 1 year The tunnel was dewatered and inspected after 1 year of installation of pipes to confirm that the setup is still in good condition and that the data produced within this period are free of errors due to any possible damage of the setup. The pipe connected to BH2 was found broken which created a direct hydraulic connection between the sensor and the tunnel. This explains its sudden behavior change in day 168 (Sect. 5.2) and the readings after this being identical to tunnel water pressure. All the other pipes were found to be intact and in good condition. Also, the pipe joints were in good condition and the cement grout filled in boreholes was observed to be free of cracks and in good condition.

Observed Behavior

Continuous monitoring is carried out after the installation. The pressure readings during tunnel filling, plant operation for a period of about 1 year and dewatering are illustrated in Figs. 11 and 12. Although the frequency of data acquisition is 10 Hz, the figures presented in Sects. 5.1 and 5.2 are based on pressure values averaged to a frequency of 1/60 Hz (one data point per minute) for clarity of the figures which represent the behavior over a larger duration. The short-term changes occurring during pressure transients are presented at a frequency of 10 Hz in Sect. 5.3.

Fig. 11

Pressure readings a during tunnel infilling (day 1) and b tunnel dewatering (day 335–337)

Fig. 12

Pressure readings during plant operation

Tunnel Filling and Dewatering

According to Palmstrøm and Broch (2017), the rate of controlled tunnel filling or dewatering in Norwegian unlined headrace tunnel and shafts is generally carried out at a rate of 15 m head increase/decrease per hour with a stop for minimum 2 h per 150 m head change and maximum head of 300 m per day. The tunnel filling and dewatering rates at Roskrepp are shown in Fig. 11a, b, respectively.

During filling, the maximum water pressure of 86 m at the instrumentation location was reached in about 24 h. The deaeration valves for all pipes were opened after 1 week of tunnel filling to release any air entrapped in the pipes, which is indicated by a sharp pressure drop in all pipes (Fig. 12) and plant operation was started afterwards. Simultaneous readings of the pore pressure in the rock mass are also shown and are discussed below.

Pore Pressure Response

At the time of installation, only three sensors were available at site. Therefore, only the pipe directly connected to the tunnel and pipes connected to BH1 and BH2 were equipped with sensors immediately after the installation work was completed. Three remaining sensors were added to the pipes connected to boreholes BH3, BH4 and BH5 on day 63. Hence, the initial pore pressure build-up during tunnel filling could not be recorded in these three holes. Therefore, the general response of BH3, BH4 and BH5, respectively, can be inferred only after day 63.

Borehole 1 (BH1) The pore pressure build-up in BH1 almost follows the same rate as water pressure increase in the tunnel. It regained pressure rapidly (within 5 min) after deaeration. This borehole registered a pressure drop between deaeration and start of operation when the tunnel water pressure was constant which indicates water seepage from the rock mass to the daylight area at the construction adit (i.e. area where the joint is exposed in the tunnel wall). A similar phenomenon is noticed during some intermittent shutdowns (Fig. 12). Also, the pore pressure variations between day 63 and day 166 seem random and did not follow any pattern. During this time, the power plant was shut down and the tunnel water pressure gradually increased due to increased water level in the reservoir. Except for this period, the pressure variations in BH1 during power productions usually follow the same pattern as the tunnel water pressure. Similar behavior is seen during tunnel dewatering. This borehole is responsive to pressure transients in the tunnel such that pore pressure closely follows the pattern of mass oscillation (discussed in Sect. 5.3).

Borehole 2 (BH2) The pore pressure build-up in BH2 is very slow as compared to BH1. It reached a pressure of about 18 m in 7 days. After deaeration, it took about 5 days to regain the same pressure (Fig. 12). This borehole is found to be non-responsive to the pressure transients in the tunnel (discussed in Sect. 5.3). The pore pressure in this borehole is found to be continuously rising as one can see until around day 135 (Fig. 12). This is happening even during intermittent shutdowns (days 72–76) and when water pressure in the tunnel is in static condition.

However, as one can see in Fig. 12, a drastic change in pressure behavior in this borehole occurred after around day 135. At first the water pressure was fluctuating and afterwards a sudden increase in pore pressure was observed making this borehole responsive to plant shutdown and start of operation and also started responding rapidly to the pressure transients.

Borehole 3 (BH3) BH3 registered most of the pressure build-up in 7 days after deaeration. Since the rock mass is already saturated by the time the sensor was installed, pressure build-up in the pipe after deaeration occurred relatively faster as compared to pressure build-up in BH2. It has the lowest magnitude of pore pressure as compared to other boreholes except BH5, which does not respond to pressure transients in the tunnel (discussed in Sect. 5.3).

Between days 78 and 136, the production is stopped and the tunnel water pressure is increasing due to rising water level in the reservoir. During this period the pore pressures in BH2, BH4 and BH5 are also increasing at the same rate. However, pore pressure in BH3 is increasing at a slower rate between days 78 and 102 and further decreasing between days 102 and 136 similar to the behavior seen in BH1, which also indicates water seepage through the rock mass from the daylight area of the construction adit. The rate of pore pressure drop during dewatering is the slowest in this borehole (Fig. 12).

Borehole 4 (BH4) BH4 registered rapid pressure build-up just after deaeration. This borehole has high pore pressure magnitude and is responsive to pressure transients (discussed in Sect. 5.3).

Borehole 5 (BH5) The pressure build-up in BH5 is faster as compared to BH3 but it has the lowest magnitude of pore pressure among all the boreholes. This borehole is non-responsive to pressure transients. However, the pore pressure changes occur much faster during transients as compared to other non-responsive boreholes (Fig. 12). During dewatering, the rate of pressure drop is almost as steep as responsive boreholes to a certain level and then becomes slower, which is similar to the non-responsive boreholes.

Response to Pressure Transients

Figures 13 and 14 show typical events of a normal shutdown and an emergency shutdown, respectively. These events are representative of the load changes and shutdowns that are occurring very frequently in recent years. The difference between these two shutdowns is the speed of closure of the turbine guide vanes. In this case of normal shutdown, complete closure of guide vanes takes place within 160 s. On the other hand, during an emergency shutdown, complete closure of guide vanes takes place within 10 s. The time period of water hammer and mass oscillation is about 2 s and 220 s, respectively.

Fig. 13

Response of boreholes during normal shutdown (day 221) showing a complete transient event and b water hammer

Fig. 14

Response of boreholes during emergency shutdown (day 334) showing a complete transient event and b water hammer

Two distinct behaviors of rock mass response from different boreholes in terms of pore pressure change can be seen in both shutdown cases (Figs. 13 and 14). The behavior of BH1 and BH4 is responsive with pressure variation inside the borehole almost identical to the pressure variation in the tunnel, but with reduced amplitude of pressure. The second behavior shown by BH2, BH3 and BH5 is non-responsive and shows very little or no variation in pore pressure inside the rock mass during load changes.

For the responsive case, the effect of mass oscillation can be clearly seen in both shutdown cases (Figs. 13a and 14a). It is observed that the mass oscillations cause significant changes in rock mass pore pressure. However, the effect of water hammer is different between normal and emergency shutdowns even though they have similar frequencies. It is observed that during normal shutdown the water hammer travels into the rock mass (Fig. 13b) causing the pore pressure to vary with almost the same frequency but with reduced amplitude. This effect is more pronounced in BH1 than BH4. On the other hand, during emergency shutdown, water hammer shows very little impact on the rock mass pore pressure in both BH1 and BH4 (Fig. 14b).

Normally, the magnitude of water hammer should be higher during an emergency shutdown as compared to a normal shutdown but is just the opposite as seen above. This could be explained by the fact that during emergency shutdown at Roskrepp, the guide vanes are closed first, then reopened slightly to reduce water hammer, and then fully closed. This reopening dampens the water hammer but it is triggered two times (Fig. 14b). Further, to confirm that pressure peaks seen during normal shutdown is due to water hammer, a fast Fourier transform (FFT) analysis of the pressure signals after final closure was carried out. The result is shown in Fig. 15.

Fig. 15

Result of FFT analysis on water pressure signal during normal and emergency shutdowns

This figure shows five different peaks of different frequencies during normal shutdown. In a simple system, there should only be one peak, the water hammer traveling from turbine to reservoir and back to the turbine. However, at Roskrepp power plant there is a waterway system consisting of penstock shaft, transition from penstock shaft to unlined tunnel, sand trap, surge shaft and the unlined headrace tunnel. These structures act as obstacles for the pressure waves and reflect parts of the water hammer, resulting in multiple peaks at different frequencies.

It is seen that the two largest peaks during shutdown events have frequencies of 0.38 Hz and 0.52 Hz, which is equivalent to the time periods of 2.6 s and 1.9 s, respectively. The distance between turbine and free water surface at the surge shaft is 560 m and thus the wave propagation speed for these frequencies is 830 m/s and 1166 m/s, respectively. Both these velocities are within the normal range of water hammer propagation speed (800–1200 m/s). However, the water hammer speed is dependent on the stiffness of water and the conduit wall. In stiffer material such as steel pipe, the velocity will be higher as compared to a relatively flexible material such as the rock mass in an unlined tunnel wall. Hence, out of these two pressure waves, it is likely that the pressure wave with the higher velocity could be due to reflection from the cone area at transition between steel-lined and unlined section of the waterway. The one with lower speed could be the water hammer wave traveling through both steel-lined and unlined section between the turbine and free water surface in the surge tank.

Delayed Pore Pressure Response

There is a delayed pore pressure response in the rock mass, which can be observed during pressure transients in one of the responsive borehole BH4 as an example (Fig. 16). As one can see, during negative pressure transients, the drop in rock mass pore pressure is slower than the tunnel water pressure, which causes the rock mass pore pressure to be higher for some time. This situation occurs for the first few cycles of the pressure transient and then the pressure gradient gradually decreases as the mass oscillation attenuates.

Fig. 16

Delayed pore pressure response of BH4

BH1 also shows such time delay but for a shorter time period than BH4 (Fig. 14b). It is interesting to note here that the pore pressure in BH1 becomes equal to the tunnel water pressure faster than in BH4 indicating joint roughness, joint opening and infilling condition have an important role in the pore pressure behavior. After this, the pore pressure changes in BH1 are almost as fast as the tunnel water pressure during the entire period of mass oscillation and hence the pressure gradient does not change during transients. As a result, the rock mass pore pressure is always less than tunnel water pressure.

Interpretation and Discussion

A summary of the most important observed behaviors of all boreholes is presented in Table 3 and logical interpretation and discussions are made in this section.

Table 3 Behavioral summary of the boreholes

General Behavior

Two main behaviors (A and B shown in Fig. 17) are observed. Behavior A where a fast pore pressure build-up with high magnitude and responsive to pressure transients (BH1 and BH4) is recorded. Behavior B where slow pore pressure build-up with lower magnitude and non-responsive to pressure transients (BH2, BH3 and BH5) is observed. An idealized sketch for these behaviors is shown in Fig. 17.

Fig. 17

Idealized sketch of the pore pressure behavior at the instrumentation location

The boreholes with behavior A intersect an open joint in addition to other relatively tight joints. For example, BH1 intersects the single conductive joint (Fig. 5) in addition to foliation joints (Jf) and BH4 intersects the conductive joint set (J2) in addition to joint set (J1). The boreholes with behavior B intersect relatively tighter joints of both foliation joints (Jf) and cross-joints (J1) and have no direct hydraulic connection to the conductive joints. These observations show that pore pressure response of the rock mass is generally dominated by joint systems that are conductive and communicative, which is quite logical.

Pore Pressure Magnitude

It is observed through this instrumentation that the boreholes with behavior A have almost the same pore pressure magnitude. On the other hand, the boreholes with behavior B show varying pore pressure magnitudes. BH2, BH3 and BH5 have pressure magnitudes from highest to lowest (Fig. 12), respectively. This may be explained due to the fact that either the length of flow paths from the tunnel through joint systems to each boreholes are different or the joint systems in the rock mass have varying roughness and infilling conditions, which pose different levels of resistance to flow through the joint system.

Conductivity of rock mass is a phenomenon that describes the movement of a fluid fracture openings and is a function of condition of the discontinuities present in the rock mass, viscosity of the fluid (in this case water) and degree of porosity of the intact rock. Since the viscosity of water and intact rock porosity are constant in this experiment, the conductivity of the joint system mainly governs the extent of borehole response.

The roughness profiles of major joint sets that contribute to the observed behavior were measured using Barton’s comb. Typical roughness profiles from the measurements are shown in Fig. 18 in such a way that it is possible to visualize possible jointing conditions prevailing in the rock mass at the instrumentation area. Panthi (2006) presents a modified description of roughness profiles along with corresponding joint roughness coefficient (JRC) described by Barton and Bandis (1990). The measured roughness profiles are compared to this description to qualitatively describe the roughness conditions and assess the ranges of JRC values.

Fig. 18

Roughness profiles and resulting aperture of major joint system contributing to the pore pressure response at the instrumentation area of the tunnel at Roskrepp

Figure 18 is a simplified version of the jointing condition that reflects the response phenomenon prevalent at the instrumentation area where similar joint stiffness and stress levels exist. In general, the higher undulation in the rock joint walls is linked to larger hydraulic aperture. The undulating joints with higher aperture have relatively less contact between the joint surfaces and thus will cause less tortuosity of flow through them resulting in higher conductivity as well as higher local pore pressure in the joint wall as seen in boreholes with behavior A. Brown (1987) conducted computer simulation to study the effect of surface roughness on flow through joints and concluded that at large separations (aperture) the surface topography has little effect on flow. At small separations, the flow is tortuous, tending to be channeled through high-aperture regions.

It is evident that longer flow paths will pose higher resistance to flow causing higher tortuosity and friction loss which reduces pore pressure in the rock mass. This type of behavior is more pronounced in case of tighter joints. BH2 showed the highest pressure magnitude (almost the same pressure as in the tunnel) among the non-responsive boreholes, which may be linked with the fact that it is close to cross-joint set (J2), which reduces the length of flow path through other joint sets. Moreover, the left wall has more joints exposed at the tunnel wall (Sect. 3.2), which also contributes to more net flow from the tunnel towards the borehole and hence higher pore pressure. In BH3, the nearest high-pressure zone to the borehole is Jf_conductive on the right wall. All other joints intersecting with this joint contribute to the pore pressure registered in this borehole. However, unlike the left wall, the right wall has a smaller number of joints exposed to the tunnel, which may explain its pressure being lower than BH2. BH5 has the least magnitude of pore pressure, which may be linked to the fact that it only intersects tight joints with longer flow paths and have no connection to other conductive joints. This shows that pore pressure is a highly localized phenomenon in unlined pressure tunnels and varies at different tunnel locations depending upon the jointing intensity and jointing conditions present in the rock mass.

Further, both BH1 and BH3 have registered pressure drops while the power plant is not in operation and the tunnel water pressure is either static or increasing. Such pressure drops can be attributed to the seepage that is occurring through interconnected joint network in the rock mass that daylight to the existing construction adit. The adit tunnel wall near the datalogger is seen to be wet due to such seepage from the headrace tunnel (Fig. 10).

Response to Pressure Transients

Assuming very tight joint walls (73 μm) in the rock mass, Helwig (1987) concluded that the changes in rock mass pore pressure due to fast-acting water hammer are limited to a relatively shallow zone of rock mass wall (1.5 m) around the unlined tunnel perimeter, while the slow-acting mass oscillations may cause pore pressure changes deeper into the rock mass.

The observations of this instrumentation show that in case of open joints the water hammer can also travel deep into the rock mass as seen in BH4 (Fig. 13b). However, the amplitude is greatly reduced as compared to BH1. This difference in amplitude is most likely attributed to the difference in length of flow paths along the joints from the tunnel to the respective boreholes. The instrumentation has clearly demonstrated that if the joints are tight, the water hammer has almost no effect on the rock mass pore pressure (BH2, BH3 and BH5).

The current design practice in general, ignores the effect of water hammer in unlined pressure tunnel because the hydraulic stress on the rock block surfaces is acting only for a very short period of time. Dynamic phenomena with very short time period such as seismic waves can have the highest effect on structures and cause failure when they have eigenfrequencies close to the seismic wave frequency. It can be neglected in case of water hammer because the eigenfrequency of rock mass is much slower than water hammer. However, it may still have a significant impact for a hydropower plant where the frequency of water hammer is slower and comparatively closer to the seismic wave frequency. Further, this instrumentation indicates that it is worthwhile to investigate the effect of higher occurrence of such events over a long period of time since the cumulative dynamic impact of frequent pressure pulses may be relevant regarding long-term stability of rock blocks in tunnel periphery.

It is learned from this instrumentation that even slow-acting mass oscillations do not travel into the rock mass if the joints in the rock mass are very tight (BH2, BH3 and BH5). On the contrary, if the joints are open, the effect of mass oscillations is considerable deep into the rock mass as seen in BH4. The BH4 intersects conductive joint J2 at least 8 m away from the tunnel wall. The effect of pressure transients can be seen clearly in this borehole. The length of flow path along an open joint does not seem to significantly affect the pore pressure magnitude in case of open joints, since BH1 and BH4 have almost similar pore pressure magnitude during mass oscillations as summarized in Table 4.

Table 4 Summary of behaviors during pressure transients

From these observations, it can be concluded that joint geometry plays a dominant role regarding the effect of pressure transients as compared to the time period of pressure transients.

Delayed Pore Pressure Response

Out of two responsive boreholes BH1 and BH4, the noticeable delay in pore pressure response has been seen only in BH4. In the case of BH1, the delay occurs for a very short period and later the pore pressure changes almost as fast as the tunnel water pressure and hence does not cause destabilizing pressure gradients in the rock mass during transients. However, this will not be true in case of delayed response as observed in BH4.

Both BH1 and BH4 are located in similar rock mass conditions, intersecting the open joints with similar roughness and aperture but at different lengths from the tunnel contour. Hence, the only parameter that is different between BH1 and BH4 is the distance between tunnel contour and the boreholes along the length of the conductive joint. The borehole intersects the respective conductive joints approximately 1.5 m, 8 m along the length of these joints in case of BH1 and BH4, respectively. Therefore, it can be concluded that the delay in pore pressure response is mainly due to the distance that needs to be traveled by the pressure transient along the joints in the rock mass. This in authors’ opinion is quite logical since the pressure wave requires more time to travel through a longer distance in the joint with a similar void geometry. It is noted here that the pressure gradient during a transient event is only about 0.1 MPa (Fig. 14) which is relatively small compared to the strength of rock joint walls with no clay infilling. However, regular occurrence of such events may ultimately lead to block failure even in relatively fresh joint wall condition as a result of cyclic fatigue over long-term operation of unlined pressure tunnels with frequent start–stop sequences as being experienced in Norwegian hydropower plants.

The observed phenomenon of delayed response during a pressure transient principally has the same effect on rock blocks in the rock mass as in case of a tunnel dewatering. Both events induce seepage forces on block surfaces as a result of hydraulic gradient developed between the rock mass and tunnel. Nevertheless, transients occur much faster and the pressure gradient and its time of application are much less as compared to a dewatering event. Even though they have smaller amplitude acting for a small period of time, they occur more frequently as load changes are occurring almost every day or even every few hours as seen in Fig. 12.

Conclusion

The effect of power plant operation on pore pressure in jointed rock mass of an unlined hydropower tunnel has been studied experimentally in an operating power plant for the first time. Monitoring of leakage from the tunnel during first water filling in unlined pressure tunnels is a standard procedure in Norway and worldwide. However, to the best of authors’ knowledge, field monitoring of pore pressure variation in an unlined headrace tunnel during power plant operation has not been conducted in the past.

The observations confirm the understanding that joint properties dominantly affect the fluid flow through the rock mass. More importantly, the experiment clearly demonstrates that the dominance of one or more sets conductive joints decides the pore pressure response of the rock mass. It is also concluded that around unlined hydropower tunnels, rock mass pore pressure is a highly localized phenomenon and varies in different locations in rock mass surrounding the tunnel depending upon the length of flow path and void geometry (aperture) of the joint systems.

Two main behaviors in pore pressure response against pressure transients have been clearly visualized: (A) responsive and (B) non-responsive condition. It is also concluded that the open joints show similar responsive behaviors, where roughness of joint wall seems less relevant in relation to flow and pore pressure. On the other hand, in the case of tighter joints, roughness influences the flow tortuosity, which results in different pore pressure magnitudes. It is seen through the observation that joint geometry plays a more dominant role regarding the effect of pressure transients as compared to the time period of pressure transients.

A delayed pore pressure response of the rock mass was observed during load changes, which causes a pressure gradient in the rock mass and in the tunnel. As instrumentation results suggest, even though the pressure gradient during a transient event is only about 0.1 MPa which is relatively small compared to the strength of rock joint walls, the regular occurrence of such events may cause block failure as a result of cyclic fatigue over long-term operation of unlined pressure tunnels with frequent start–stop sequences.

Hence, this experiment demonstrates that frequent load changes can affect tunnel stability. The overall effect depends on the pore pressure response in the rock mass, which is mainly governed by the conditions of joint geometry and their properties. The cumulative impact of small but frequent pressure gradients over many years of operation can result in increased instances of block falls and tunnel collapses. The findings of the instrumentation are valuable and will be helpful in developing a methodology using numerical modeling so that it is possible to predict extent of block fall events in unlined water tunnels experiencing different hydrostatic head with frequent start–stop sequences, which the authors are presently focused on.