Abstract
The production of hydrocarbons from unconventional reservoirs, like tight shale plays, increased tremendously over the past decade. Hydraulic fracturing is a commonly applied method to increase the productivity of a well drilled in these reservoirs. Unfortunately, the production rate decreases over time presumably due to fracture closure. The fracture closure rate induced by proppant crushing and embedment depends on mechanical properties of shales and proppants that are influenced by confining pressure (pc), temperature (T), and shale composition. We performed constant strain rate deformation tests at ambient and in situ conditions of a typical shale reservoir (pc ≤ 100 MPa, T ≤ 125 °C) using European shale samples exhibiting variable mineralogy, porosity and maturity. We focused on a comparison of Posidonia shale with Bowland shale, which is believed to be the most prospective shale formation in the United Kingdom. Compression tests were performed perpendicular to bedding orientation. Stress–strain curves show that Bowland shales are relatively strong and brittle compared to Posidonia shale which display semibrittle deformation behavior. Brittleness estimated from elastic properties is in good agreement with the recorded stress–strain behavior but shows no clear relation to composition. Compressive strengths (σUCS = uniaxial compressive strength, σTCS = triaxial compressive strength) and static Young’s moduli, E, reveal a strong confining pressure and mineralogy dependence, whereas temperature and strain rate only have a minor influence on σTCS and E. The coefficient of internal friction for both shales is ≈ 0.42 ± 0.03. With increasing amount of weak minerals (e.g., clay, mica) σUCS, σTCS and E strongly decrease. This may be related to a shift from deformation supported by a load-bearing framework of hard minerals to deformation of interconnected weak minerals at about 25–30 vol% of weak phases. At the applied conditions, the triaxial compressive strength and Young’s moduli of most shales deformed normal to bedding are close to the Reuss bound. To our knowledge, this is the first study, which presents results of experimental investigations carried out to characterize the mechanical behavior of Bowland shale. The observed results are helpful to estimate the potential of the Bowland reservoir with respect to the economical extraction of hydrocarbons.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Providing energy from oil and gas recovered from unconventional hydrocarbon reservoirs, such as shale gas plays, is widely believed to act as bridge technology between conventional and renewable energy resources (Hausfather 2015; Zhang et al. 2016). Typically, these reservoirs exhibit low permeability, which makes an economical exploitation difficult (McGlade et al. 2013). To increase the productivity of a well drilled in these tight reservoir rocks, hydraulic fracturing (HF) is a suggested method to create artificial fractures which are expected to connect to natural fractures present in the reservoir (Li et al. 2015). In particular in North America with its shale formations exhibiting a large geographical extent such as the Haynesville, Marcellus or Bakken shale, HF was used in recent years as the key technique for an economic exploitation of hydrocarbons (McGlade et al. 2013). Europe also shows potential for economical extraction of hydrocarbons from shale reservoirs, e.g., from Posidonia (Germany) and Alum (Denmark) formations. In the United Kingdom, the Bowland–Hodder (England) formation is believed to contain relatively large amounts of hydrocarbons (Andrews 2013).
Several criteria were developed to characterize regions within a formation representing the best potential for an economic hydrocarbon production, often defined as sweet spots, mainly based on geochemistry, petrology, mineralogy and geomechanical properties (Rickman et al. 2008; Sondergeld et al. 2010; Berard et al. 2012). To maintain fractures induced by hydraulic fracturing, proppants (ceramic, bauxite, quartz) are often added to the frac fluid. However, the production rate of a fractured well typically declines over time (Al-Rbeawi 2018; Wang 2016), due to depletion of the reservoir and possibly due to fracture closure processes (Cerasi et al. 2017; Wang 2016). Fracture closure is affected by confining pressure (Niandou et al. 1997; Petley 1999; Naumann et al. 2007; Kuila et al. 2011; Islam and Skalle 2013), temperature (Johnston 1987; Masri et al. 2014), non-isostatic stress conditions (Swan et al. 1989; Chong and Boresi 1990; Ibanez and Kronenberg 1993; Kwon and Kronenberg 1994; Sone and Zoback 2013a; Rybacki et al. 2015, 2017) and petrophysical and mechanical properties such as mineralogy, porosity, permeability and brittleness of the reservoir rocks (Rybacki et al. 2016; Morley et al. 2017; Li et al. 2017; Teixeira et al. 2017; Cerasi et al. 2017). Therefore, knowledge of the geomechanical behavior of shale rocks with respect to the above-mentioned parameters is important to better understand their fracture closure behavior (Morley et al. 2017; Ilgen et al. 2017; Kikumoto et al. 2017; Li et al. 2017; Cerasi et al. 2017).
We performed deformation experiments at constant strain rates and ambient and elevated confining pressures and temperatures up to 100 MPa and 125 °C to investigate the mechanical properties of various, particularly European, shale rocks with different mineralogies, focusing on the comparison between Posidonia shale and Bowland shale. The latter is poorly investigated so far but expected to be a very prospective shale play, (Smith et al. 2010; Imber et al. 2014; Hough et al. 2014). Here we establish empirical relations between mechanical properties (strength, Young’s modulus) and confining pressure, temperature and strain rate, which are important in the petroleum industry (Draege et al. 2006; Farrokhrouz et al. 2014) for assessment of borehole stability and evaluation of stable mud weight windows for drilling or hydraulic fracturing (Warpinski et al. 2009; Britt and Schoeffler 2009; Soliman et al. 2012; Meier et al. 2013, 2015; Gholami et al. 2014). The results are also helpful to correlate with data measured during in situ operations such as wire line well logging (Horsrud 2001; Chang et al. 2006). Constant stress (creep) experiments performed on similar shales at ambient and elevated confining pressures and temperatures will be presented in a companion paper to improve our understanding of the fracture closure behavior of shale rocks.
2 Sample Material
Various black shales mainly from different formations throughout Europe were investigated. Samples include Cambrian Alum (DK) shale (core sample depth z ≈ 17 m), Carboniferous Bowland (UK) shale and Lower Jurassic Posidonia (GER) shale. The latter formation is represented by three different localities (1) Haddessen (HAD, overmature gas shale), (2) Harderode (HAR, peak oil maturity), and Dotternhausen (DOT, immature oil shale). HAD and HAR shales were recovered at shallow depth (z ≈ 58–61 m) from old drill cores of research wells in N-Germany (Gasparik et al. 2014), whereas DOT shale was collected from freshly blasted blocks of a quarry in S-Germany (Rybacki et al. 2015). Alum shale (ALS) is highly overmature and was recovered from fresh cores of the Skelbro-2 well (Ghanizadeh et al. 2014). Mature to overmature Bowland (BOS) shales are divided into Upper (BOS1–7, BOS11–14, BOS_OC) and Lower Bowland shales (BOS8–10) (Yang et al. 2015). Samples BOS1–10 (z ≈ 2076–2719 m) were recovered from drill cores from the Preese Hall 1 well (PH1) drilled in 2010 (Green et al. 2012) and samples BOS11–14 (z ≈ 32–80 m) were derived from the MHD13 well drilled in Marl Hill Moor (MHM). Because of limited availability of Upper Bowland core samples, we collected also Upper Bowland shale samples (BOS_OC) from an outcrop located within the county of Lancashire (NW England). For comparison, we examined an immature and an overmature North American shale (Haynesville, overmature and Marcellus, immature) recovered from unknown depth.
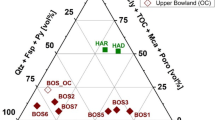
Mineral composition of all samples was determined by X-ray diffraction analysis (XRD) and reveals a mixture of quartz (Qtz), feldspar (Fsp), pyrite (Py), carbonates (Cb), clay (Cly), mica (Mca) and organic matter (TOC). Porosity (incl. micro pores) varies between 1 and 15% (Table 1) and was measured on cylindrical samples (length = 20 mm, diameter = 10 mm) by He-pycnometry, after storing the samples for at least 48 h in an oven at 50 °C. Vitrinite reflectance, calculated from Tmax (Jarvie et al. 2005), accounting for thermal maturity of investigated samples ranges from 0.6 to 3.8% VRr. Bulk density of samples was calculated from the ratio of weight and volume of prepared cylindrical specimens, yielding values between 2.14 and 2.73 g/cm3. Petrophysical data of all investigated samples are listed in Table 1. Note that composition data are presented here in vol% instead of wt%, since only the volumetric fraction and spatial distribution is of interest for mechanical behavior. To convert wt% to vol% the following density, ρ values were assumed: 2.65 g/cm3 for Qtz, 2.6 g/cm3 for Fsp, 5.01 g/cm3 for Py, 2.71 g/cm3 for Cb, 2.5 g/cm3 for Cly, 2.82 g/cm3 for Mca and 1.3 g/cm3 for TOC, respectively (Rybacki et al. 2015). Note that in Table 1, columns 6–12 refer to vol% of individual phases calculated from measured wt%, whereas volume fractions given in columns 13–15 are renormalized taking into account the pore volume. CTMP displays the cumulative amounts of clay, TOC, mica and porosity and QFP represents the sum of quartz, feldspar and pyrite constituents. With respect to the mechanical properties, CTMP and QFP are considered as weak and strong constituents, respectively. Cb constituents are regarded as intermediate strong. Figure 1a reveals that both Posidonia and Alum shale are clay-rich, whereas Bowland shales are either quartz- or carbonate-rich, except for one Upper Bowland sample from the Marl Hill Moor well. The Upper Bowland outcrop sample contains higher fractions of clay than core-derived samples. Unfortunately, no XRD-mineral data of investigated Haynesville and Marcellus shale exists (Fig. 1a). Cylindrical samples (10 mm diameter × 20 mm length) with parallel end surfaces were prepared perpendicular to bedding for triaxial deformation experiments. In addition, for uniaxial tests cuboids with 2 × 2 × 4 mm in size were cut perpendicular to bedding. The sample size was adapted to the uniaxial deformation apparatus. Scanning electron microscopy reveals a very fine-grained matrix (d ≤ 20 µm) of Posidonia (HAR, Fig. 2a) and Upper Boland (BOS_OC, Fig. 2d) shale with preferred alignment of organic matter and phyllosilicates defining the bedding orientation. All specimens were dried at 50 °C for at least 48 h before the deformation experiments were performed.
a Ternary plots displaying mineral composition of investigated samples. Composition is separated into mechanically strong (QFP = Qtz + Fsp + Py), intermediate strong (Cb) and weak (Cly + TOC + Mca + Poro) fractions. Qtz quartz, Fsp feldspar, Py pyrite, Cb carbonate, Cly clay, TOC total organic carbon, Mca mica, Poro porosity. Mineral data are given in vol%, normalized to 100 vol% taking also the sample porosity into account. Alum and Posidonia shales are clay-rich, whereas Bowland shales are either carbonate- or quartz-rich. Outcrop samples of Bowland shale reveal higher amounts of weak material than core-derived samples. Superimposed values are indicating triaxial compressive strength, σTCS, in [MPa] (b) and static Young’s modulus, E, in [GPa] (c). PH1 Preese Hall 1, OC outcrop, MHM Marl Hill Moor
SEM-backscattered (BSE) images (a–c) of low-porosity (≈ 3%) Posidonia shale (HAR) and (d–f) porous (≈ 8%) Bowland shales (OC). a, d Show undeformed samples. The remaining images were taken from samples deformed at pc = 50 MPa, T = 100 °C and \(\dot {\varepsilon }\) = 5 × 10−4 s−1. Bold white arrows indicate the loading direction, which was always perpendicular to bedding. Main mineral constituents of both shales are phyllosicates (Phy), calcite (Cal), dolomite (Dol), quartz (Qtz) and pyrite (Py) in addition to organic matter (Om). Accessory minerals are apatite (Ap) and titanite (Ttn), respectively. Pores and organic matter appear nearly black, quartz is medium gray, phyllosicates and carbonates (Cal + Dol) are light gray and pyrite is almost white. Long black lines are unloading cracks perpendicular to the loading direction. b, c Deformation microstructures in Posidonia shale sample close to the main shear fracture (upper left corner) are crushed and smeared pyrite aggregates, intercrystalline fractures subparallel to the main fracture (b, bold black arrows) and broken calcite grains (c, bold black arrow). With increasing distance from the main fracture no deformation microstructures were observed in Posidonia shale samples. e Deformed Bowland shales show formation of inter—as well as intracrystalline fractures (bold black arrows) close to the main fracture (upper right corner). In addition, framboidal pyrite is squeezed and smeared along and perpendicular to fractures, respectively (open white arrow). f At larger distance from the main fracture in Bowland shale less deformation microstructures are visible, such as intracrystalline fractures within quartz grains (f, bold black arrow)
3 Experimental Technique
Triaxial deformation experiments were performed at elevated confining pressures (pc = 50, 75 and 100 MPa), temperatures (T = 75, 100 and 125 °C) and constant strain rates (\(\dot {\varepsilon }\) = 5 × 10−6, 5 × 10−5 and 5 × 10−4 s−1) using a Paterson-type deformation apparatus (Paterson 1970). Argon gas was used as confining pressure medium. Samples were covered by thin (wall thickness ≈ 0.35 mm) copper jackets to prevent gas intrusion into the specimen. Axial load was recorded by an internal load cell, installed within the pressure vessel. Assuming constant volume deformation, axial stresses calculated from measured forces were corrected for copper jacket strength, determined from previous calibration runs. Axial strain was calculated from recorded displacement and corrected for system compliance. Accuracies of resulting axial peak stresses and strains are ± 4 and ± 6%, respectively.
Uniaxial compression tests were performed at ambient confining pressure (pc = 0.1 MPa) and temperature (T = 20 °C) using a uniaxial creep rig with a modified electro-mechanical actuator (Freund et al. 2004; Götze et al. 2010). Shale samples were uniaxially deformed at strain rates of \(\dot {\varepsilon }\) = 2.5–5 × 10−4 s−1. Axial strain was determined from measured displacement and corrected for the stiffness of the apparatus, resulting in errors of calculated axial strains < 5%.
The Young’s modulus, E, is given here as the tangent modulus measured at ≈ 50% of the peak stress in recorded stress–strain curves. The tangent modulus was used since the secant modulus would ignore effects of pore closure at the beginning of performed experiments, mainly accounting for tests performed at ambient conditions (Fig. 3a). Using instead the secant modulus determined from the slope of the stress–strain curves from the origin to the strain at ~ 50% of the peak stress would result on average in ≈ 20% higher Young’s moduli of triaxially deformed samples.
Stress–strain curves of samples deformed at ambient confining pressure and temperature (a) and empirical cross-correlation between uniaxial compressive strength, σUCS, and static Young’s modulus, E, (b). Loading direction is perpendicular to bedding. U-BOS Upper Bowland shale, POS Posidonia shale, HAR Harderode, OC outcrop, PH1 Preese Hall 1
Due to the relatively high system compliance of both apparatuses, accuracy of E determined at uniaxial and triaxial conditions is ± 13% and ± 20%, respectively.
The post-peak stress–strain deformation behavior of many of the samples could not be measured due to violent specimen failure. The low stiffness of both apparatuses resulted in a large amount of elastic energy stored in the loading frame that is abruptly released at sample failure. Typically, failure occurred at maximum axial strains of ≈ 1–2% for uniaxial and ≈ 1.5–20% for triaxial deformation, depending on applied pc–T, stress conditions and mineral composition. Most experiments were terminated after failure. Only few specimens displayed deformation to a barrel-shaped sample (Figs. 3a, 4a, b).
Representative stress–strain curves of deformed shales (a, b) under triaxial conditions and empirical relation between triaxial compressive strength, σTCS, and static Young’s modulus, E, (c). Deformation conditions are indicated. U-BOS Upper Bowland shale, L-BOS Lower Bowland shale, HSV Haynesville shale, MAS Marcellus shale, ALS Alum shale, POS Posidonia shale, HAR Harderode, DOT Dotternhausen, HAD Haddessen, OC outcrop, PH1 Preese Hall 1, MHM Marl Hill Moor
Detailed microstructural observations were performed on mechanically polished, carbon-coated thin sections using a scanning electron microscope (SEM, Zeiss Ultra 55 Plus), operating at 20 kV in backscatter electron (BSE) mode. Energy dispersive X-ray (EDX) measurements and semi-quantitative geochemical analysis were performed on the samples.
4 Results
In total, we conducted 8 uniaxial compression and 34 triaxial compressions tests (Tables 2, 3, 4). First, we present results of uniaxial experiments obtained at ambient confining pressure and temperature and subsequently data of triaxial tests performed at elevated pc–T conditions. For HAR and BOS_OC samples, additional tests were performed varying either \(\dot {\varepsilon }\), pc or T.
4.1 Mechanical Properties: Uniaxial
Uniaxial compression tests were mainly focused on Upper Bowland shales since their mechanical properties were hardly investigated so far. All tests were performed with loading direction perpendicular to bedding. The stress–strain curves reveal predominantly elastic and minor inelastic deformation prior to reaching peak stresses of up to about 320 MPa. Beyond peak stress, most samples failed abruptly (Fig. 3a). Uniaxial compressive strength, σUCS, of the shale samples range from 75 to 318 MPa, with lower and upper limits represented by Posidonia and Bowland (core) shales, respectively. Commonly, deformed samples failed by forming a single shear fracture or by axial splitting. Bowland shale samples prepared from drill cores are noticeably stronger than samples collected from surface outcrop and both are distinctively stronger than Posidonia shale. This is attributed to the difference in mineralogical composition and porosity between Posidonia and Bowland shales (Fig. 1). Axial strain at peak stress is lower for Bowland samples from cores compared to outcrop samples. The static Young’s modulus, E, derived from the tangent modulus varies between 6 and 34 GPa (Table 2). As shown in Fig. 3b, the uniaxial compressive strength increases almost linearly with increasing static Young’s modulus. The effect of mineralogy on the mechanical properties obtained from stress–strain behavior will be explained in more detail in Sect. 5.1 below.
4.2 Mechanical Properties: Triaxial
Triaxial compression tests were performed at constant strain rates of \(\dot {\varepsilon }\) = 5 × 10−6, 5 × 10−5 and 5 × 10−4 s−1, confining pressures of pc = 50, 75 and 100 MPa and temperatures of T = 75, 100 and 125 °C. One set of experiments performed on European and American shale samples aimed at unraveling the effect of mineral composition and porosity on the mechanical behavior at fixed \(\dot {\varepsilon }\), pc–T conditions. A second series of tests was performed on Bowland outcrop samples and Posidonia shale to study the influence of varying deformation conditions on the mechanical behavior. All tests were performed with loading direction perpendicular to bedding.
4.2.1 Effect of Mineral Composition and Porosity on Mechanical Properties
To investigate the influence of petrophysical properties on the mechanical behavior of the samples, we performed constant strain rate experiments at 50 MPa confining pressure, 100 °C temperature and strain rate of 5 × 10−4 s−1. The tests conditions were chosen to represent in situ conditions at 2–3 km depth.
In uniaxial and triaxial tests, the relative strengths of Bowland and Posidonia shales are similar (Fig. 4a, b, cf., Fig. 3a). The triaxial compressive strength, σTCS, and static Young’s modulus, E, of triaxially deformed samples are about 75 and 40% higher on average compared to measurements at ambient conditions (Table 3). Maximum axial strains reached before failure occurred were also larger by about ≈ 1% at triaxial conditions (Fig. 4a; Tables 2,3).
In general, deformed shales display brittle to semibrittle mechanical behavior. Small inelastic axial strain and hardening followed by abrupt failure indicate brittle deformation. In contrast, semibrittle deformation exhibits pronounced non-linear hardening before peak stress and post-peak stable weakening (Evans et al. 1990; Evans and Kohlstedt 1995). Clay-rich Posidonia (HAD, DOT) and Alum shales with high porosity displayed semibrittle deformation at low triaxial compressive strength (σTCS ~ 160 to 175 MPa) (Fig. 4b). In contrast, also clay-rich but low-porosity Posidonia (HAR) (σTCS = 165 MPa) and Haynesville (σTCS = 188 MPa) shale specimens displayed brittle deformation with predominantly elastic deformation and minor hardening before failure occurred. Marcellus and Bowland shale samples deformed brittle, irrespective of porosity and contents of strong (QFP) and intermediate strong (Cb) minerals. Marcellus and Bowland shales were much stronger (σTCS ≈ 280 to 550 MPa) than the other investigated shale rocks (Fig. 4b; Table 3). In general, static Young’s moduli were larger at elevated pressures and for samples displaying high triaxial compressive strength (Fig. 4c). At failure, a single shear fracture formed in the triaxially deformed shale samples except for sample BOS11. Ductile deformation of specimen BOS11 resulted in a barrel-shaped specimen after deformation. This is likely due to a relatively high porosity and TOC content of sample BOS11. Specimen HAD (Posidonia) was still intact when we stopped the experiment at 19% axial strain (Table 1).
4.2.2 Effect of Confining Pressure on Strength
To characterize the influence of confining pressure on the mechanical properties of Posidonia (HAR) and Upper Bowland outcrop shales (BOS_OC), we performed deformation tests at constant strain rate (\(\dot {\varepsilon }\) = 5 × 10−4 s−1), temperature (T = 100 °C) and confining pressures of pc = 50, 75 and 100 MPa (Table 4). Upper Bowland shale samples for these tests were exclusively prepared from outcrop material as not sufficient core material was available. At elevated confining pressures and increasing maximum axial strain, low-porosity, clay-rich Posidonia shales revealed a change from post-peak strain weakening towards steady-state deformation (Fig. 5a). This transition indicates a switch from brittle to semibrittle deformation with increasing confining pressure as also described by Rybacki et al. (2015) for Posidonia (DOT) shales.
The deformed quartz-rich Bowland shale samples (BOS_OC) failed abruptly along a localized single shear fracture, independent of the applied confining pressure (Fig. 5a). Axial strain at peak stress increased only slightly with confining pressure but deformation remained brittle. The triaxial compressive strength of Posidonia and Bowland shales increased with increasing confining pressure (Fig. 5b; Table 4), also observed by Rybacki et al. (2015) and Ibanez and Kronenberg (1993) for Posidonia (DOT) and Wilcox shales, respectively (for description of microstructures see Sect. 4.3 below). Assuming a lithostatic effective pressure gradient of 25 MPa/km, the observed confining pressure dependence would result in an increase of triaxial compressive strength of Posidonia and Bowland shales of ~ 23 and ~ 40 MPa/km, respectively. The triaxial compressive strength of BOS_OC (ϕ ~ 8%) shale was more sensitive to confining pressure changes compared to Posidonia–HAR (ϕ ~ 3%) shale (Table 1). Maximum axial strains before failure of Posidonia shale samples were more affected by confining pressure compared to Bowland shale. Presumably this is due to a much higher clay content of (HAR) Posidonia shale (32 vol%) than present in Bowland outcrop samples (4 vol%). The static Young’s moduli of Posidonia and Bowland shales remained nearly constant showing no significant change with increasing confining pressure (Table 4). This was also observed by Rybacki et al. (2015) for other Posidonia shales and for US shale rocks (Sone and Zoback 2013a).
4.2.3 Effect of Temperature on Strength
For the same shale types (Posidonia (HAR) and BOS_OC), deformation experiments were also performed at different temperatures (T = 75, 100, 125 °C) while keeping the confining pressure (pc = 50 MPa) and strain rate (\(\dot {\varepsilon }\) = 5 × 10−4 s−1) constant (Table 4; Fig. 6). In general, the influence of temperature on strength was small between 75 and 125 °C (Fig. 6a). The stress–strain curves reveal a small decrease of σTCS and a slightly increasing axial strain at peak stress with increasing temperature, which is more pronounced for Posidonia than for Bowland shale (Fig. 6b; Table 4). This may be related to a relatively high amount of clays in Posidonia shale, which dehydrate at higher temperatures (Mikhail and Guindy 1971) leading to a triaxial compressive strength decrease due to stress corrosion (subcritical crack growth) (Brantut et al. 2014). Samples subjected to elevated temperatures showed formation of an incipient single shear fracture. No significant influence of temperature on static Young’s modulus could be observed (cf., Table 4). Assuming a geothermal gradient of 25 °C/km, the observed temperature sensitivity would result in a decrease of triaxial compressive strength of Posidonia and Bowland shales of ~ 12 and ~ 6 MPa/km depth, respectively. This is considerably lower than the confining pressure-induced triaxial compressive strength increase per km depth, in particular for Bowland shale. Consequently, the confining pressure-induced increase of strength, σTCS, will not be compensated by the observed temperature-induced σTCS reduction, assuming a linear correlation between σTCS and confining pressure and temperature.
4.2.4 Effect of Strain Rate on Strength
At constant confining pressure (pc = 50 MPa) and constant temperature (T = 100 °C), Posidonia and Bowland shales were deformed at varying strain rates of \(\dot {\varepsilon }\) of 5 × 10−6, 5 × 10−5 and 5 × 10−4 s−1, respectively (Table 4). We observed no significant effect of strain rate on the mechanical behavior of the investigated shale samples (Fig. 7a, b; Table 4). For Posidonia shale samples, axial strains at peak stresses slightly increased with decreasing strain rates, likely related to the high fraction of weak phases (Chong et al. 1976, 1980; Rybacki et al. 2015). Also, the static Young’s modulus remained almost constant at varying deformation rates (cf., Table 4).
4.3 Microstructures
All samples, except for one, failed spontaneously along a single shear fracture. The shear fractures are inclined at an angle of \(\varphi\) ≈ 35 ± 2° with respect to the sample axis. This indicates an apparent coefficient of internal friction of µi ≈ 0.7 ± 0.05. Note that sample shape, end effects, length–diameter ratio of the sample and sample jacketing may affect the measurements of the coefficient of internal friction. Only sample BOS11 did not fracture but remained intact and displayed barreling. This sample contained significantly higher porosity, a large fraction of sheet silicates and organic matter.
Microstructures of HAR and BOS_OC samples deformed at pressures of pc = 50 MPa, temperature T = 100 °C and strain rates of \(\dot {\varepsilon }\) = 5 × 10−4 s−1 were investigated using scanning electron microscopy (SEM).
In general, microstructural inspection of deformed samples only showed deformation structures close to the macroscopic single shear fracture. We observed mainly inter- and intracrystalline microcracks, indentation of strong into weaker mineral phases and stretching of framboidal pyrite. In deformed Posidonia samples, the main fracture is surrounded by a damage zone with subparallel intercrystalline microcracks (bold black arrows in Fig. 2b), sheared pyrite minerals and in few cases intracrystalline fracturing of calcite grains (Fig. 2c, bold black arrow). At slightly larger distance from the macro crack, no deformation structures could be identified in the micrographs. Bowland shales reveal formation of inter- and intragranular microcracks close to the main fracture (bold black arrows in Fig. 2e). Pyrite is crushed and smeared along these fractures (open white arrows). With increasing distance from the main fracture, only intracrystalline fractures are found in few quartz grains (bold black arrows in Fig. 2f).
5 Discussion
The shale samples investigated in this study showed mainly brittle to semibrittle deformation behavior at confining pressures and temperatures ranging from 0.1 to 100 MPa and 20 to 125 °C, respectively (Figs. 3a, 4b, 5a, 6a, 7a). Brittle deformation is defined by minor inelastic axial strain and hardening and abrupt failure along a localized shear fracture. Semibrittle deformation shows pronounced non-linear hardening before peak stress is reached, which is followed by weakening. Microstructures of deformed Posidonia (HAR) and Bowland (BOS_OC) shales indicate mostly brittle deformation only close to the macro fracture. Undulose extinction, grain boundary sliding or rotation of grains could not be identified.
Uniaxial and triaxial compressive strength, maximum axial strain at peak stress and static Young’s modulus are affected by mineralogical composition, organic matter content, porosity and the applied experimental conditions (confining pressure, temperature and strain rate) as previously described for other shales (Ibanez and Kronenberg 1993). Following this, we will first discuss the role of material parameters starting with sample composition and then address the effect of loading conditions.
5.1 Sample Composition
Here we attempt to identify possible correlations between sample composition and mechanical properties such as σUCS/σTCS, static Young’s modulus, E, and maximum axial strain before failure, εmax, measured perpendicular to bedding. Sample composition varied significantly between shale types but the main constituents are porosity, \(\phi\), fractions of strong (QFP), intermediate strong (carbonate) and weak (Clay + TOC + Mica) mineral phases.
The influence of strong components (QFP) (Fig. 8a) and carbonates (Fig. 8b) on the uniaxial compressive strength, σUCS, of Posidonia and Upper Bowland shales is minor when measured at ambient conditions (pc = 0.1 MPa, T = 20 °C). This is in good agreement with results of Tan et al. (2014) for shales recovered from the Upper Yangtze Platform (China). For Posidonia shales, Rybacki et al. (2015) found a similar correlation between uniaxial compressive strength measured normal to bedding and the volumetric content of carbonates and QFP. However, Upper Bowland samples were found to be weaker with increasing amounts of weak materials (Fig. 8c). Tan et al. (2014) found a similar relationship for Lower Silurian shale. Sample porosity had no significant influence on the uniaxial compressive strength within error bars (Table 2), in contrast to results published by Rybacki et al. (2015) and Tan et al. (2014). We found a strong correlation between uniaxial compressive strength, σUCS, and Young’s moduli, E, (Fig. 3b). The static Young’s modulus does not correlate with porosity or the fraction of strong and intermediate strong components (Table 3) but clearly decreased with increasing amounts of weak phases (Fig. 8d).
Influence of mineralogy in terms of volumetric fraction of QFP = quartz + feldspar + pyrite (a), carbonate (b), clay + TOC + mica (c) on uniaxial compressive strength, σUCS, and static Young’s moduli, E, (d) of investigated shales. Data were obtained at ambient experimental conditions. The relation between fraction of weak phases and uniaxial compressive strength and Young’s modulus is indicated by a dashed line in (c) and (d), respectively. The corresponding equations are: \({\sigma _{{\text{UCS}}}}\left[ {{\text{MPa}}} \right]=669[{\text{MPa}}] \times {({\text{Clay}}+{\text{TOC}}+{\text{Mca}}+\phi )^{ - 0.53}}\) (R2 = 0.92) and \(E[{\text{GPa}}]=101[{\text{GPa}}] \times {({\text{Clay}}+{\text{TOC}}+{\text{Mca}}+\phi )^{ - 0.72}}\) (R2 = 0.92). HAR Harderode, PH1 Preese Hall 1, OC outcrop
Interestingly, the maximum axial strain before failure at ambient conditions appeared to increase slightly with increasing amounts of strong components (Fig. 9a) and to decrease with increasing carbonate fraction (Fig. 9b). Porosity and the amount of weak components had no effect on maximum axial strain before failure (Table 2).
Effect of volumetric fraction of QFP = quartz + feldspar + pyrite (a, c) and carbonate (b, d) on max. axial strain εmax reached before failure of shale shales. Experiments were performed at ambient conditions (a, b) and elevated (c, d) confining pressures and temperatures. HAR Harderode, PH1 Preese Hall 1, OC outcrop, MHM Marl Hill Moor
Similar to σUCS, the triaxial compressive strength, at 50 MPa confining pressure and 100 °C temperature, was independent of the content of strong (Fig. 10a) and intermediate strong (Fig. 10b) minerals. In contrast, Rybacki et al. (2015) found increasing triaxial compressive strength with increasing fractions of these components. This is likely due to different pc–T conditions of the tests, influencing the strength of individual sample constituents and affecting the correlations between mechanical properties and sample mineralogy. In addition, any differences in microstructure or water content (drying of the samples) are expected to influence the deformation behavior. Water-rich shale rocks are believed to exhibit lower triaxial compressive strength and static Young’s modulus than dried samples, due to swelling of smectite clay minerals occurring within shales (cf., Vales et al. 2004) and due to a reduction of the effective pressure. Examples are given by Rybacki et al. (2015) for Alum shale and by Ibanez and Kronenberg (1993) for Wilcox shale. Therefore, the drying procedure applied to our samples may not represent in situ conditions and our obtained strength and Young’s modulus values overestimate the mechanical properties under natural conditions. However, drying of samples allows a better comparison of shale rocks recovered from different formations or localities.
Influence of volumetric fraction of QFP = quartz + feldspar + pyrite (a), carbonate (b), clay + TOC + mica (c), porosity (d) and density (e) on triaxial compressive strength, σTCS, and static Young’s modulus, E, (f) of investigated shales. Data were obtained at elevated confining pressure and temperature given in (e). The correlation indicated in (c) by the dashed line can be approximated by the following equation: \({\sigma _{{\text{TCS}}}}\left[ {{\text{MPa}}} \right]=899[{\text{MPa}}] \times {({\text{Clay}}+{\text{TOC}}+{\text{Mica}}+\phi )^{ - 0.45}}\) (R2 = 0.88). OC outcrop, PH1 Preese Hall 1, MHM Marl Hill Moor
In this study, the triaxial compressive strength was reduced with fraction of weak phases increasing up to about 30%, above which σTCS is almost constant (Fig. 10c). A threshold of about 30 vol% fraction of (corresponding to ≈ 25 wt%) weak phases possibly separates triaxial compressive strength of samples with load-bearing framework of hard minerals from triaxial compressive strength of aggregates with interconnected layers of weak minerals. A similar threshold value between stronger and softer materials of ≈ 30 wt% clays was suggested by Bourg (2015) for deformation of various shales. Similarly, Crawford et al. (2008) observed a threshold of 20–30 wt% clay for synthetic quartz–clay mixtures experimentally sheared at various confining pressures. They also noted a transition from a strong quartz grain framework to weak clay matrix support if the clay fraction exceeds porosity and the quartz framework is replaced by a high clay particle fraction. Neglecting the clay- and TOC-rich Posidonia and Alum shale, there is also a clear reduction of σTCS with increasing porosity (Fig. 10d), in agreement with (Rybacki et al. 2015). The Young’s modulus E shows no clear correlation with the fraction of QFP and carbonate Cb (Table 3), but decreases with increasing weak mineral fraction and porosity (Fig. 10e; Table 3). Sone and Zoback (2013a) found a similar empirical relation of decreasing Young’s moduli with increasing amounts of weak minerals for Barnett, Haynesville and Eagle Ford shales. In agreement with this study, Rybacki et al. (2015) found that static Young’s modulus is anti-correlated with porosity for several Posidonia shales. In contrast, these authors found no correlation between E and weak mineral phases but with the amount of QFP, again related to different test conditions and sample material. Triaxial compressive strength and static Young’s modulus correlate with sample bulk density, which is mainly affected by TOC and porosity due to their relatively low density compared to the remaining sample constituents (Eseme et al. 2007) (Fig. 10f). Below a source rock density of ρ ≈ 2.5 g/cm3, triaxial compressive strength is almost independent of bulk density (Fig. 10f). Since the density of source rocks can easily be determined in situ by wire line gamma logs, a trend as shown in Fig. 10f may be used to estimate σTCS directly.
The effect of composition on the maximum axial strain before failure is more complex and often visible only for sample subsets of different shale formations. As would be intuitively expected, samples with a high fraction of strong minerals are more brittle and the maximum axial strain before failure is reduced (Fig. 9c). This was found for Upper Bowland (PH1) and Posidonia shales. However, for strongly varying composition within a single formation, the trend is obscured (Table 3). If variation in mineralogy is small, bulk composition is important for the mechanical behavior of the shales (Rybacki et al. 2015). At elevated confining pressures and temperatures, the maximum axial strain before failure of Upper Bowland shales increased slightly with increasing Cb content (Fig. 9d), whereas εmax decreased at increasing QFP fractions (Fig. 9c). This contrasting behavior provides a good example for a possible change of dominant deformation behavior at elevated confining pressure and temperature compared to ambient conditions. In general, εmax increased with higher amount of clay + kerogen, but if restricted to individual formations with relatively small variation of weak phases (e.g., Bowland PH1 or Posidonia), we found no correlation. This also holds for the effect of porosity on maximum axial strain before failure measured at ambient and elevated deformation conditions (Tables 2, 3).
The influence of shale composition on σTCS and E is summarized in Fig. 1b, c. The ternary diagrams show the volumetric fraction of mechanically weak (Cly + TOC + Mca + Poro), intermediate strong (Cb) and strong (QFP) phases of the shales. The triaxial compressive strength (superimposed values in Fig. 1b) and static Young’s modulus (superimposed values in Fig. 1c) are not dependent as much on carbonate and QFP content, but clearly decrease for high amounts of weak phases (Fig. 1b, c). Upper Bowland outcrop samples are distinctively weaker than core samples (Figs. 1b, 4a), due to a higher fraction of weak phases (cf. Table 1; Fig. 1). This confirms that samples retrieved from surface outcrops will not fully represent in situ mechanical properties of shales, as weathering processes may affect mechanical properties. For example, comparing Bowland shale outcrop material with core-derived samples (PH1) shows increased porosity for the outcrop samples. Posidonia shales, containing mainly soft mineral components, are distinctively weaker than outcrop- and core-derived Bowland shales. The static Young’s modulus shows the same behavior with respect to sample mineralogy (Fig. 1c). In summary, any change in fractions of strong (e.g., quartz) or intermediate strong (carbonates) mineral phases did hardly affect the uni- and triaxial compressive strengths and static Young’s moduli of the investigated shales but affected the maximum axial strain before failure of deformed samples. Most strikingly, the uni- and triaxial compressive strengths and Young’s moduli anticorrelate with the fraction of weak components (e.g., clays) (Fig. 10c, f).
5.1.1 Comparing Sample Triaxial Compressive Strength and Young’s Modulus to Predictions from Effective Medium Theories
Effective medium theories allow characterizing mechanical properties of rocks with respect to mineral composition, such as Young’s modulus (Mavko et al. 2009). Typically, the approach relies on volumetric fractions of sample constituents and cannot capture chemical, cementation or structural effects (Rybacki et al. 2015). In applying this approach, we simplified the mineral composition of investigated shales defining two endmembers: relatively weak (TOC, Cly, \(\phi\)) and relatively strong (Qtz, Cb, Mca, Fsp, Py) mineral constituents (Sone and Zoback 2013a).
Ji (2004) suggested a phenomenological approach to predict the mechanical properties (Young’s modulus, triaxial compressive strength) of multiphase materials in terms of volume fractions and component properties. We applied his generalized mixture rule (GMR) to interpret our data. The GMR is defined as:
where M is a specific mechanical property (in our case σTCS, E), f is the volumetric fraction of the component, subscripts i and c represent the ith phase of a composite (c) consisting of N phases, and J is a scaling parameter ranging between − 1 and + 1. Here, the arithmetic (J = + 1) and harmonic (J = − 1) average represent an upper (Voigt) or lower bound (Reuss), respectively. The Voigt–Reuss–Hill average is described as the mean value of Voigt and Reuss bound.
For the upper triaxial compressive strength endmember, we used literature data of Novaculite giving σTCS-Nov = 699 MPa at the same pc–T conditions as applied here (Rybacki et al. 2015). The lower triaxial compressive strength limit is represented here by σTCS of Boom clay extrapolated to 50 MPa confining pressure (Bouazza et al. 1996), where σTCS-Cly = 35.5 MPa.
For the endmember elastic properties, we calculated the weighted average of weak and strong sample constituents, assuming the following elastic moduli and weighting factors, w, (determined from mean composition): ETOC = 6.3 GPa, EClay = 3.2 GPa, Eϕ = 0 GPa, wTOC = 0.29, wClay = 0.42, wϕ = 0.29 for the weak components and EMica = 99.6 GPa, ECb = 82.9 GPa, EQtz = 93.2 GPa, EPy = 309.5 GPa, EFsp = 40.5 GPa, wMica = 0.06, wCb = 0.43, wQtz = 0.49, wPy = 0.01 and wFsp = 0.01 for the strong components (Mavko et al. 2009), resulting in Eweak = 3 GPa and Estrong = 91 GPa, where the subscripts weak and strong represent the endmember values for the lower and upper bound, respectively. To characterize the elastic properties (E) of investigated shales, we also calculated the Hashin–Shtrikman bounds (Mavko et al. 2009):
with:
where subscript HS is Hashin–Shtrikman, ± is either upper (+) or lower (−) bound, K is bulk modulus and µ is shear modulus of simplified sample constituents. Upper bound is given when strong material is K1, µ1 and lower bound when weak material is K1, µ1. Here, we assume Kweak = 1.5 GPa, Kstrong = 37 GPa, µweak = 1.4 GPa, µstrong = 44 GPa, where the strong endmember phase is represented by quartz and the weak endmember by clay (Mavko et al. 2009). Finally, we used an approach predicting the elastic constants of multiphase materials as introduced by Paul (1960):
In general, the triaxial compressive strengths of all investigated shales are within the bounds, mostly plotting closer to the Reuss bound (Fig. 11). σTCS of almost all Bowland shales follow the lower (Reuss) bound, whereas Alum shales plot close to the upper (Voigt) bound (Fig. 11a). σTCS of Posidonia shales plot between the Voigt–Reuss–Hill and lower (Reuss) bound.
Triaxial compressive strength, σTCS, (a) and static Young’s modulus, E, (b) obtained at elevated confining pressures and temperatures plotted against volumetric fractions of weak components. Experimental data is compared to different effective medium theories. Gray symbols display mechanical data of black shales measured by Rybacki et al. (2015) at similar deformation conditions. V and R indicate upper and lower bounds, respectively. Voigt–Reuss–Hill (V–R–H) is the average value of Voigt and Reuss bounds. J represents best fit bound proposed by Ji (2004) for Posidonia [J (POS)] and Bowland shales [J (BOS)]. P displays approach introduced by Paul (1960) and Hashin–Shtrikman (HS) upper (+) and lower (−) bounds as described by Mavko et al. (2009). Deformation conditions are indicated. ALM Alum, POS Posidonia, PH1 Preese Hall 1, OC Outcrop, MHM Marl Hill Moor
The best fit value of the GMR scaling parameter J for σTCS of all Posidonia shales including literature data yields JPosidonia = − 0.13 (Fig. 11a). Ji (2004) suggested a value of J ≈ − 0.25 for rock samples with a weak-phase supported structure (fstrong < 0.5), which is close to our value. A value of J ≈ + 0.25, as supposed by Ji (2004) for aggregates with a strong-phase supported structure (fstrong > 0.7), would not fit our data (JBowland = − 0.38). An average value of J = 0.23 was determined by Rybacki et al. (2015) for black shales (fstrong < 0.3) measured at ambient and elevated pc–T conditions. J = 0.23 is far above the value that we calculated and J ≈ − 0.25 that is suggested by Ji (2004), presumably due to differences in fabric and humidity between shales investigated in previous studies and our samples.
The static Young’s moduli plot between the Reuss bound and the upper Hashin–Shtrikman scheme (HS+) (Fig. 11b). Alum shales fit very well to the Voigt–Reuss–Hill average and Bowland shales plot in general close to the lower (Reuss) bound. The static Young’s modulus of Posidonia shales range between the average for elastic properties of multiphase materials (Paul 1960) and the lower (Reuss) bound. The elastic properties of Posidonia shales also fit to the lower Hashin–Shtrikman bound (HS−) (Fig. 11b). This suggests that Bowland shales may have a stronger degree of anisotropy compared to Posidonia shales although mechanical testing using bedding-parallel samples is necessary to confirm. Fitting the Posidonia and Bowland dataset to the GMR approach yielded best fit values for the scaling parameter JPosidonia of − 0.62 and JBowland = − 0.82, respectively, which are close to the lower (Reuss) bound (J = − 1).
Shales are often known to be very anisotropic and thus a separate trend closer to the Voigt average is expected if measured parallel to bedding.
5.1.2 Brittleness of Shale Rocks
Common practice (used in the Exploration and Production industry) in estimating the potential of a successful hydraulic borehole stimulation is to determine the brittleness, B, of the reservoir rock (Holt et al. 2011). The brittleness of a rock is an empirical rock parameter often normalized to range between 0 (ductile) and 1 (brittle). Typically, ductile rocks are expected to show fast fracture closure, whereas brittle rocks are believed to be easily fractured. Various empirical brittleness indices exist (Rybacki et al. 2016). Here, we first calculated the brittleness of the shales based on their mineral composition (Rybacki et al. 2016):
where Bmin is the brittleness determined from mineralogy, wQFP, wCb, wClyTOC and wϕ are weighting factors ranging from 0 to 1 and fxx is the fraction of mineral xx given in vol%. We set wQFP = wClyTOC = wϕ = 1 and wCb = 0.5 as suggested by Rybacki et al. (2016) for shale rocks.
Second, we calculated the brittleness index based on the Young’s modulus. Rybacki et al. (2016) suggested the following empirical relation between brittleness and E:
where BE is the brittleness determined from E based on a comparison of E with stress–strain behavior at low pc–T conditions and E0 is a normalization factor with [E0] = 1GPa. The resulting Bmin and BE values are shown in Fig. 12 a, b, including Posidonia shales observed by Rybacki et al. (2016). Bowland shales generally give substantial higher brittleness values compared to Posidonia and Alum shales (Fig. 12a, b). Bmin is decreasing with increasing amounts of weak sample constituents, and with increasing fractions of carbonates (Fig. 12a). By definition, increasing amounts of strong components result in higher brittleness indices. Also, BE is decreasing with increasing amounts of weak components but does not significantly dependent on carbonates or strong components (QFP), in line with the trend found for E shown in Fig. 1b (Fig. 12b). BE values are lower on average than Bmin values.
Ternary plots displaying mineral composition of investigated samples. Composition is separated into mechanically strong (Qtz + Fsp + Py), intermediate strong (Cb) and weak (Cly + TOC + Mca + Poro) fractions. Qtz quartz, Fsp feldspar, Py pyrite, Cb carbonate, Cly clay, TOC total organic carbon, Mca mica. Mineral data are given in vol%, normalized to 100 vol% taking also the sample porosity into account. Superimposed values indicate brittleness determined from composition Bmin (a) and static Young’s modulus BE (b) (Rybacki et al. 2016). Maximum axial strain εmax (in %) before failure vs. brittleness determined from composition Bmin (c) and static Young’s modulus BE (d). OC outcrop, PH1 Preese Hall 1, MHM Marl Hill Moor, PH1 Preese Hall 1, OC outcrop, MHM Marl Hill Moor
Samples displaying increasing brittleness values also show decreasing maximum axial strain εmax before failure, when deformed at elevated confining pressures and temperatures (Fig. 12c, d). A brittleness threshold at about BE ~ 0.4 ± 0.1 separates sample deformation in dominantly ductile (BE < 0.4 ± 0.1) or dominantly brittle regimes (BE > 0.4 ± 0.1) as shown by the stress–strain plots (Fig. 4a).
5.2 Effect of Confining Pressure
Several empirical failure criteria exist to describe the confining pressure-dependent triaxial compressive strength of a rock. These are, for example, Mohr–Coulomb, Drucker–Prager, Hoek–Brown, Griffith, Murrell or Fairhurst criteria (Sheorey 1997). To characterize the influence of confining pressure on the triaxial compressive strength of Posidonia and Bowland shales, we used the linear Mohr–Coulomb failure criterion given by
where \(\tau\) is the shear stress, S0 is the cohesion, \({\sigma _{\text{n}}}\) is the normal stress, \({\mu _{\text{i}}}\) is the coefficient of internal friction, pc is the confining pressure, \({\sigma _1}\) = \({\sigma _{{\text{TCS}}}}\)+ pc and n is a constant. The coefficient of internal friction may be determined from the best fit slope n in a σ1–pc diagram (Fig. 13) with \({\mu _{\text{i}}}\) = (n − 1)/(2\(\sqrt n\)), (Zoback 2007). Figure 13 shows the data measured at elevated pc–T conditions on Posidonia (HAR) and Bowland (outcrop) shales (c.f., Table 4; Fig. 5b) yielding \({\mu _{\text{i}}}\) values of 0.42 ± 0.03. This friction coefficient is significantly lower than predicted from the measured angle between the fracture surface and the \({\sigma _1}\) loading direction. This may to some extent be related to boundary effects such as end cap friction. Extrapolation to ambient confining pressure results in higher values of σUCS than were determined in uniaxial compression tests. Note that measured σUCS define an upper limit since they were determined at ambient temperature whereas triaxial experiments were performed at T = 100 °C. It is conceivable that enhanced sample compaction at increasing confining pressure may result in a substantial strength increase that is not captured by a linear fit (Rybacki et al. 2017). The estimated coefficients of internal friction µi of shale rocks from this study are similar to published data on Wilcox shale (µi ≈ 0.3–0.5) (Ibanez and Kronenberg 1993), Opalinus clay (µi ≈ 0.25) (Jordan and Nüesch 1989), Posidonia shales (µi ≈ 0.16–0.32), Alum shales (µi = 0.36–0.55) (Rybacki et al. 2015) and Eagle Ford and Haynesville shales (µi = 0.3–0.5) (Sone and Zoback 2013b) (Fig. 13). Interestingly, published data on Barnett shale reveal relatively high values of µi ≈ 0.7–1.1 (Sone and Zoback 2013b; Rybacki et al. 2015). Sone and Zoback (2013b) also found a slight decrease of \({\mu _{\text{i}}}\) for increased amounts of weak components (clay + TOC). Including data from Rybacki et al. (2015) on shales obtained at similar experimental conditions, we found no clear correlation between \({\mu _{\text{i}}}\) and porosity or the amount of weak material (Table 5).
5.3 Strain Rate and Temperature Effects
A change in strain rate by two orders of magnitude has no significant effect on triaxial compressive strength of Posidonia and Bowland shales at pc of 50 MPa and T of 75–125 °C (Fig. 14). Lajtai et al. (1991) report similar observations for other rocks, such as limestone (brittle) and salt (ductile). A common approach to express the strain rate sensitivity of rocks deforming by dislocation glide is an exponential law of the form:
which was applied by (Chong et al. 1980; Kwon and Kronenberg 1994) for shales from different formations or localities. α is an empirical constant, which is negative for the whole data set of investigated Posidonia and Bowland shales (αPOS = − 0.46, αBOS = − 4.61), determined from regression lines in semi-logarithmic space (Fig. 14a). Restricting the fit to the two measurements obtained at low strain rate (\(\dot {\varepsilon }\) = 5 × 10−6 and 5 × 10−5 s−1) yields α values for Posidonia and Bowland shales of ≈ 0.16 and ≈ 0.57, respectively. This is similar to values reported by Ibanez and Kronenberg (1993) (α ≈ 0.36), Kwon and Kronenberg (1994) (α ≈ 0.27) and Rybacki et al. (2015) (α ≈ 0.33) for other shales.
With increasing temperature, the triaxial compressive strength of investigated shales decreased slightly (Fig. 6b), as also described by Ibanez and Kronenberg (1993) and Masri et al. (2014) for Wilcox and Tounemire shale, respectively. Assuming that dislocation glide in clay minerals is mainly responsible for strain rate and temperature sensitivity, we use the following constitutive relation (Ibanez and Kronenberg 1993)
where A is a material constant, Q is the activation energy, R is the gas constant and Ta is absolute temperature. Note that Eq. (10) may be used only as first-order approximation, since the flow law is valid only at steady-state creep conditions (Rybacki et al. 2015). Using αPOS = 0.16 and αBOS = 0.57 and fitting Eq. (10) to the corresponding Arrhenius plot (Fig. 14b) yields apparent activations energies of QPOS ≈ 98 kJ/mol and QBOS ≈ 140 kJ/mol. Ibanez and Kronenberg (1993) and Rybacki et al. (2015) measured comparable activation energies of Wilcox shale (Q = 87 ± 40 kJ/mol) and Posidonia shale (Q = 167 kJ/mol), respectively, deformed perpendicular to bedding.
6 Conclusions
Deformation experiments performed on black shales originating from different formations and with varying mineralogy and maturity reveal dominantly brittle to semibrittle deformation behavior at the imposed pc–T conditions. For Upper Bowland shale, samples retrieved from surface outcrops are somewhat weaker and less brittle than samples prepared from core material. The triaxial compressive strength and static Young’s moduli are strongly influenced by sample mineralogy and confining pressure conditions, whereas the effects of sample porosity, temperature and strain rate are minor.
σTCS and E of investigated shales clearly decrease with increasing amounts of weak components (Clay + TOC + Mica). However, the effect is small above a threshold of ≈ 25–30 vol% weak mineral constituents in the samples. In general, this trend follows predictions of effective medium approaches, with experimental data mostly plotting close to the lower bound. Brittleness, in particular if calculated from Young’s modulus, shows the same general trend of an existing threshold at BE ~ 0.4.
The obtained results lead us to suggest a substantially lower fracture closure rate of brittle Bowland shales compared to semibrittle Posidonia shales. However, the relatively low hydrocarbon content and low porosity of inspected Upper Bowland core samples, in conjunction with their low maturity, may also limit the prospectivity of these shales compared to Posidonia shale. Considering instead the overmature Lower Bowland shale as target formation for gas extraction may be more successful, since it ranges within the gas window contrasting to the peak oil—mature Upper Bowland shale. In a companion paper we will compare short-term mechanical properties of Posidonia and Bowland shales as described here with long-term creep behavior of shales.
Abbreviations
- ϕ :
-
Porosity
- ρ :
-
Density
- p c :
-
Confining pressure
- T :
-
Temperature
- T a :
-
Absolute temperature
- σ UCS :
-
Uniaxial compressive strength
- σ TCS :
-
Triaxial compressive strength
- E :
-
Static Young’s modulus
- \(\dot {\varepsilon }\) :
-
Strain rate
- ε max :
-
Maximum axial strain before failure of specimen
- µ i :
-
Coefficient of internal friction
- M :
-
Specific mechanical property (e.g., triaxial compressive strength, Young’s modulus)
- f :
-
Volumetric fraction
- J :
-
Scaling parameter
- K :
-
Bulk modulus
- µ :
-
Shear modulus
- B min :
-
Brittleness determined from mineralogy
- B E :
-
Brittleness determined from Young’s modulus
- τ :
-
Shear strength
- S 0 :
-
Cohesion
- σ n :
-
Normal stress
- Q :
-
Activation energy
- R :
-
Gas constant
- n, α, A :
-
Constants
References
Al-Rbeawi S (2018) The optimal reservoir configuration for maximum productivity index of gas reservoirs depleted by horizontal wells under Darcy and non-Darcy flow conditions. J Natural Gas Sci Eng 49:179–193. https://doi.org/10.1016/j.jngse.2017.11.012
Andrews IJ (2013) The carboniferous Bowland shale gas study: geology and resource estimation. British Geological Survey for Department of Energy and Climate Change, London, p 64. https://doi.org/10.1080/10962247.2014.897270
Berard T, Liu Q, Dubost F-X, Jing B (2012) A screening process for shale gas prospecting. In: EAGE annual conference & exhibition, pp 4–7
Bouazza A, Van Impe WF, Haegeman W (1996) Some mechanical properties of reconstituted boom clay. Geotech Geol Eng 14(4):341–352. https://doi.org/10.1007/BF00421948
Bourg IC (2015) Sealing shales versus brittle shales: a sharp threshold in the material properties and energy technology uses of fine-grained sedimentary rocks. Environ Sci Technol Lett 2(10):255–259. https://doi.org/10.1021/acs.estlett.5b00233
Brantut N, Heap MJ, Baud P, Meredith PG (2014) Rate- and strain-dependent brittle deformation of rocks. J Geophys Res Solid Earth 119(3):1818–1836
Britt LK, Schoeffler J (2009) The geomechanics of a shale play: what makes a shale prospective. In: SPE eastern regional meeting, pp 23–25. https://doi.org/10.2118/125525-MS
Cerasi P, Lund E, Kleiven ML, Stroisz A, Pradhan S, Kjøller C, Frykman P, Fjær E (2017) Shale creep as leakage healing mechanism in CO2 sequestration. Energy Proc 114:3096–3112. https://doi.org/10.1016/j.egypro.2017.03.1439
Chang C, Zoback MD, Khaksar A (2006) Empirical relations between rock strength and physical properties in sedimentary rocks. J Petrol Sci Eng 51(3–4):223–237. https://doi.org/10.1016/j.petrol.2006.01.003
Chong K, Boresi AP (1990) Strain rate dependent mechanical properties of new albany reference shale. Int J Rock Mech Min Sci Geomech Abstr 27(3):199–205. https://doi.org/10.1016/0148-9062(90)94328-Q
Chong K, Smith JW, Chang B, Philip MH, Carpenter HC (1976) Characterization of oil shale under uniaxial compression. American Rock Mechanics Association the 17th U. https://www.onepetro.org/conference-paper/ARMA-76-0465
Chong K, Hoyt PM, Smith JW, Paulsen BY (1980) Effects of strain rate on oil shale fracturing. Int J Rock Mech Min Sci Geomech Abstr 17:35–43. https://doi.org/10.1016/0148-9062(80)90004-2
Crawford BR, Faulkner DR, Rutter EH (2008) Strength, porosity, and permeability development during hydrostatic and shear loading of synthetic quartz-clay fault gouge. J Geophys Res Solid Earth 113(3):1–14. https://doi.org/10.1029/2006JB004634
Draege A, Jakobsen M, Johansen TA (2006) Rock physics modelling of shale diagenesis. Petrol Geosci 12(1):49–57. https://doi.org/10.1144/1354-079305-665
Eseme E, Urai JL, Krooss BM, Littke R (2007) Review of mechanical properties of oil shales: implications for exploitation and basin modelling. Oil Shale 24(2):159–174
Evans B, Kohlstedt DL (1995) Rheology of rocks. In: Rock physics and phase relations—a handbook of physical constants. AGU Reference Shelf 3, pp 148–165. https://doi.org/10.1029/RF003p0148
Evans B, Fredrich JT, Wong T-F (1990) The brittle-ductile transition in rocks: recent experimental and theoretical progress. Geophys Monogr Ser. https://doi.org/10.1029/GM056p0001
Farrokhrouz M, Asef MR, Kharrat R (2014) Empirical estimation of uniaxial compressive strength of shale formations. Geophysics 79(4):D227–D233. https://doi.org/10.1190/geo2013-0315.1
Freund D, Wang Z, Rybacki E, Dresen G (2004) High-temperature creep of synthetic calcite aggregates: influence of Mn-content. Earth Planet Sci Lett 226(3–4):433–448. https://doi.org/10.1016/j.epsl.2004.06.020
Gasparik M, Bertier P, Gensterblum Y, Ghanizadeh A, Krooss BM, Littke R (2014) Geological controls on the methane storage capacity in organic-rich shales. Int J Coal Geol 123:34–51. https://doi.org/10.1016/j.coal.2013.06.010
Ghanizadeh A, Gasparik M, Amann-Hildenbrand A, Gensterblum Y, Krooss BM (2014) Experimental study of fluid transport processes in the matrix system of the european organic-rich shales: I. Scandinavian alum shale. Mar Petrol Geol 51:79–99. https://doi.org/10.1016/j.marpetgeo.2013.10.013
Gholami R, Moradzadeh A, Rasouli V, Hanachi J (2014) Practical application of failure criteria in determining safe mud weight windows in drilling operations. J Rock Mech Geotech Eng 6(1):13–25. https://doi.org/10.1016/j.jrmge.2013.11.002
Götze LC, Abart R, Rybacki E, Keller LM, Petrishcheva E, Dresen G (2010) Reaction rim growth in the system MgO-Al2O3-SiO2 under uniaxial stress. Mineral Petrol 99(3–4):263–277. https://doi.org/10.1007/s00710-009-0080-3
Green, Christopher A, Styles P, Brian J, Baptie (2012) Shale gas fracturing review & recommendations for induced seismic migration, p 26. http://www.businessgreen.com/digital_assets/5216/DECC_shale_gas_report.pdf
Hausfather Z (2015) Bounding the climate viability of natural gas as a bridge fuel to displace coal. Energy Policy 86:286–294. https://doi.org/10.1016/j.enpol.2015.07.012
Holt RM, Fjaer E, Nes OM, Alassi HT (2011) A shaly look at brittleness. American Rock Mechanics Association
Horsrud P (2001) Estimating mechanical properties of shale from empirical correlations. Soc Petrol Eng SPE 56017:68–73. https://doi.org/10.2118/56017-PA
Hough E, Vane CH, Nigel JP, Smith, Moss-Hayes VL (2014) The Bowland shale in the Roosecote borehole of the Lancaster fells sub-basin, Craven basin, UK: a potential UK shale gas play? In: SPE/EAGE European unconventional resources conference and exhibition. https://doi.org/10.2118/167696-MS
Ibanez WD, Kronenberg AK (1993) Experimental deformation of shale: mechanical properties and microstructural indicators of mechanisms. Int J Rock Mech Min Sci Geomech Abstr 30(7):723–734. https://doi.org/10.1016/0148-9062(93)90014-5
Ilgen AG, Heath JE, Yucel Akkutlu I, Taras Bryndzia L, Cole DR, Kharaka YK, Kneafsey TJ, Milliken KL, Pyrak-Nolte LJ, Suarez-Rivera R (2017) Shales at all scales: exploring coupled processes in mudrocks. Earth Sci Rev 166:132–152. https://doi.org/10.1016/j.earscirev.2016.12.013
Imber J, Armstrong H, Clancy S, Daniels S, Herringshaw L, McCaffrey K, Rodrigues J, Trabucho-Alexandre J, Warren C (2014) Natural fractures in a United Kingdom shale reservoir analog, Cleveland Basin, Northeast England. AAPG Bull 98(11):2411–2437. https://doi.org/10.1306/07141413144
Islam MA, Skalle P (2013) An experimental investigation of shale mechanical properties through drained and undrained test mechanisms. Rock Mech Rock Eng 46(6):1391–1413. https://doi.org/10.1007/s00603-013-0377-8
Jarvie D, Hill RJ, Pollastro RM (2005) Assessment of the gas potential and yields from shales: the Barnett Shale model. In: Oklahoma Geological Survey circular, vol 110, pp 9–10
Ji S (2004) A generalized mixture rule for estimating the viscosity of solid-liquid suspensions and mechanical properties of polyphase rocks and composite materials. J Geophys Res. https://doi.org/10.1029/2004JB003124
Johnston DH (1987) Physical properties of shale at temperature and pressure. Geophysics 52(10):1391–1401. https://doi.org/10.1190/1.1442251
Jordan P, and Rolf Nüesch (1989) Deformational behavior of shale interlayers in evaporite detachment horizons, Jura Overthrust, Switzerland. J Struct Geol 11(7):859–871. https://doi.org/10.1016/0191-8141(89)90103-X
Kikumoto M, Nguyen VPQ, Yasuhara H, Kishida K (2017) Constitutive model for soft rocks considering structural healing and decay. Comput Geotechn 91:93–103. https://doi.org/10.1016/j.compgeo.2017.07.003
Kuila U, Dewhurst DN, Siggins AF, Raven MD (2011) Stress anisotropy and velocity anisotropy in low porosity shale. Tectonophysics 503(1–2):34–44. https://doi.org/10.1016/j.tecto.2010.09.023
Kwon O, Kronenberg AK (1994) Deformation of Wilcox shale: undrained strengths and effects of strain rate. American Rock Mechanics Association
Lajtai EZ, Scott Duncan EJ, Carter BJ (1991) Technical note—the effect of strain rate on rock strength. Rock Mech Rock Eng 24:99–109. https://doi.org/10.1007/BF01032501
Li Q, Xing H, Liu J, Liu X (2015) A review on hydraulic fracturing of unconventional reservoir. Petroleum 1(1):8–15. https://doi.org/10.1016/j.petlm.2015.03.008
Li Z, Li L, Huang B, Zhang L, Li M, Zuo J, Li A, Yu Q (2017) Numerical investigation on the propagation behavior of hydraulic fractures in shale reservoir based on the DIP technique. J Petrol Sci Eng 154:302–314. https://doi.org/10.1016/j.petrol.2017.04.034
Masri M, Sibai M, Shao JF, Mainguy M (2014) Experimental investigation of the effect of temperature on the mechanical behavior of tournemire shale. Int J Rock Mech Min Sci 70:185–191. https://doi.org/10.1016/j.ijrmms.2014.05.007
Mavko G, Mukerji T, Dvorkin J (2009) The rock physics handbook—tools for seismic analysis of porous media, 2nd edn. Cambridge University Press, Cambridge
McGlade C, Speirs J, Sorrell S (2013) Unconventional gas—a review of regional and global resource estimates. Energy 55:571–584. https://doi.org/10.1016/j.energy.2013.01.048
Meier T, Rybacki E, Reinicke A, Dresen G (2013) Influence of borehole diameter on the formation of borehole breakouts in black shale. Int J Rock Mech Min Sci 62::74–85. https://doi.org/10.1016/j.ijrmms.2013.03.012
Meier T, Rybacki E, Backers T, Dresen G (2015) Influence of bedding angle on borehole stability: a laboratory investigation of transverse isotropic oil shale. Rock Mech Rock Eng 48(4):1535–1546. https://doi.org/10.1007/s00603-014-0654-1
Mikhail R, Guindy N (1971) Rates of low-temperature dehydration of montmorillonite and illite. J Appl Chem Biotechnol 21(4):113–116. https://doi.org/10.1002/jctb.5020210407
Morley CK, von Hagke C, Hansberry RL, Collins AS, Kanitpanyacharoen W, King R (2017) Review of major shale-dominated detachment and thrust characteristics in the diagenetic zone: part I, meso- and macro-scopic scale. Earth Sci Rev 173:168–228. https://doi.org/10.1016/j.earscirev.2017.07.019
Naumann M, Hunsche U, Schulze O (2007) Experimental investigations on anisotropy in dilatancy, failure and creep of Opalinus clay. Phys Chem Earth 32(8–14):889–895. https://doi.org/10.1016/j.pce.2005.04.006
Niandou H, Shao JF, Henry JP, Fourmaintraux D (1997) Laboratory investigation of the mechanical behaviour of Tournemire shale. Int J Rock Mech Min Sci 34(1):3–16. https://doi.org/10.1016/S1365-1609(97)80029-9
Paterson MS (1970) A high-pressure, high-temperature apparatus for rock deformation. Int J Rock Mech Min Sci Geomech Abstr 7(5):517–526. https://doi.org/10.1016/0148-9062(70)90004-5
Paul B (1960) Prediction of elastic constants of multiphase materials. Trans Metall Soc AIME 218:36–41
Petley DN (1999) Failure envelopes of mudrocks at high confining pressures. Geol Soc Lond Spec Publ 158(1):61–71. https://doi.org/10.1144/GSL.SP.1999.158.01.05
Rickman R, Mullen MJ, Petre JE, Grieser WV, Kundert D (2008) A practical use of shale petrophysics for stimulation design optimization: all shale plays are not clones of the Barnett shale. In: SPE Annual Technical Conference and Exhibition, pp 1–11. https://doi.org/10.2118/115258-MS
Rybacki E, Reinicke A, Meier T, Makasi M, Dresen G (2015) What controls the mechanical properties of shale rocks?—part I: strength and Young’s modulus. J Petrol Sci Eng 135:702–722. https://doi.org/10.1016/j.petrol.2016.02.022
Rybacki E, Meier T, Dresen G (2016) What controls the mechanical properties of shale rocks?—part II: brittleness. J Petrol Sci Eng 144:39–58. https://doi.org/10.1016/j.petrol.2016.02.022
Rybacki E, Herrmann J, Wirth R, Dresen G (2017) Creep of Posidonia shale at elevated pressure and temperature. In: Rock mechanics and rock engineering. Springer, Vienna, pp 1–20. https://doi.org/10.1007/s00603-017-1295-y
Sheorey PR (1997) Empirical rock failure criteria. A.A. Balkema, Rotterdam
Smith N, Turner P, Williams G, Survey BG, Centre KD, Hill N, Ng K (2010) UK data and analysis for shale gas prospectivity. Geol Soc Lond Petrol Geol Conf Ser 7:1087–1098. https://doi.org/10.1144/0071087
Soliman MY, Daal J, East L (2012) Fracturing unconventional formations to enhance productivity. J Natural Gas Sci Eng 8:52–67. https://doi.org/10.1016/j.jngse.2012.01.007
Sondergeld CH, Newsham KE, Comisky JT, Rice MC, Rai CS (2010) Petrophysical considerations in evaluating and producing shale gas resources. In: SPE unconventional gas conference. https://doi.org/10.2118/131768-MS
Sone H, Zoback MD (2013a) Mechanical properties of shale-gas reservoir rocks—part 2: ductile creep, brittle strength, and their relation to the elastic modulus. Geophysics 78(5):D393–D402. https://doi.org/10.1190/geo2013-0051.1
Sone H, Zoback MD (2013b) Mechanical properties of shale-gas reservoir rocks—part 1: static and dynamic elastic properties and anisotropy. Geophysics 78(5):D381–D392. https://doi.org/10.1190/geo2013-0050.1
Swan G, Cook J, Bruce S, Meehan R (1989) Strain rate effects in Kimmeridge bay shale. Int J Rock Mech Min Sci Geomech Abstr 26(2):135–149. https://doi.org/10.1016/0148-9062(89)90002-8
Tan J, Horsfield B, Fink R, Krooss B, Schulz HM, Rybacki E, Zhang J, Boreham CJ, Graas GV, Tocher BA (2014) Shale gas potential of the major marine shale formations in the upper Yangtze platform, south China, part III: mineralogical, lithofacial, petrophysical, and rock mechanical properties. Energy Fuels 28(4):2322–2342. https://doi.org/10.1021/ef4022703
Teixeira M, Goulart F, Donzé F, Renard H, Panahi E, Papachristos, Scholtès L (2017) Microfracturing during primary migration in shales. Tectonophysics 694:268–279. https://doi.org/10.1016/j.tecto.2016.11.010
Vales F, Nguyen Minh D, Gharbi H, Rejeb A (2004) Experimental study of the influence of the degree of saturation on physical and mechanical properties in Tournemire Shale (France). Appl Clay Sci 26:(1–4 SPEC. ISS.):197–207. https://doi.org/10.1016/j.clay.2003.12.032
Wang HY (2016) What factors control shale gas production decline trend: a comprehensive analysis and investigation. In: SPE/IAEE hydrocarbon economics and evaluation symposium, p 32. https://doi.org/10.2118/179967-MS
Warpinski NR, Mayerhofer MJ, Vincent MC, Cipolla CL, Lolon ER (2009) Stimulating unconventional reservoirs: maximizing network growth while optimizing fracture conductivity. J Can Petrol Technol 48(10):39–51. https://doi.org/10.2118/114173-PA
Yang S, Horsfield B, Mahlstedt NL, Stephenson MH, Könitzer SF (2015) On the primary and secondary petroleum generating characteristics of the Bowland shale, Northern England. J Geol Soc Lond 173(2):292–305. https://doi.org/10.1144/jgs2015-056
Zhang X, Myhrvold NP, Hausfather Z, Caldeira K (2016) Climate benefits of natural gas as a bridge fuel and potential delay of near-zero energy systems. Appl Energy 167:317–322. https://doi.org/10.1016/j.apenergy.2015.10.016
Zoback MD (2007) Reservoir geomehanics, 1st edn. Cambridge University Press, Cambridge
Acknowledgements
We thank the ShaleXenvironmenT (SXT) research project funded by the European Union’s Horizon 2020 research and innovation programme under Grant Agreement No. 640979, Michael Naumann for assistance with uniaxial and triaxial deformation experiments, Stefan Gehrmann for sample and thin section preparation, Anne-Laure Fauchille for some XRD results, Nils Backeberg for organizing the fieldtrip and Ilona Schäpan for SEM handling.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Herrmann, J., Rybacki, E., Sone, H. et al. Deformation Experiments on Bowland and Posidonia Shale—Part I: Strength and Young’s Modulus at Ambient and In Situ pc–T Conditions. Rock Mech Rock Eng 51, 3645–3666 (2018). https://doi.org/10.1007/s00603-018-1572-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00603-018-1572-4