Abstract
In this article, we investigated the resonant curves of geo-centric satellite due to the rate of change in earth’s equatorial ellipticity parameter \((\dot{\gamma })\), moon’s angular velocity around the earth \((\dot{\vartheta })\), and angular velocity of bary-center \((\dot{\Theta })\) around the sun. We expressed the equations of the motion of the satellite in a spherical coordinate system using the earth’s potential. The system of equations are reduced into a second-order ordinary differential equation and determined its solution. From the solution, it is noted that resonance appears due to the frequencies \(\dot{\delta _{s0 }}\), \(\dot{\gamma }\), \(\dot{\Theta _0}\) and \(\dot{\vartheta _0}\) at ten resonant points \({\dot{\delta }_{s0}}={2\dot{\gamma }}\), \({\dot{\delta }_{s0}}={\dot{\gamma }}\), \({\dot{\delta }_{s0}}={2\dot{\Theta }_0}\), \({\dot{\delta }_{s0}}={\dot{\Theta }_0}\), \({\dot{\delta }_{s0}}=\frac{{2 \dot{\Theta }_0}}{3}\), \({\dot{\delta }_{s0}}=\frac{\dot{\Theta }_0}{2}\), \({\dot{\delta }_{s0}={2\dot{\vartheta _0}}}\), \({\dot{\delta }_{s0}={\dot{\vartheta _0}}}\), \({\dot{\delta }_{s0}=\frac{{2\dot{\vartheta _0}}}{3}}\), and \({\dot{\delta }_{s0}=\frac{{dot{\vartheta _0}}}{2}}\), where \({\dot{\delta }_{s0}}\), \({\dot{\Theta }_0}\) and \({\dot{\vartheta _0}}\) are the steady-state value of \({\dot{\delta }_{s}}\), \({\dot{\Theta }}\) and \({\dot{\vartheta }}\) respectively. We have drawn the resonant curves corresponding to the resonant points. From the graph, it is observed that the effect of earth’s equatorial ellipticity parameter on the resonant curves are very small. Also, we have shown the effect of eccentricity (e) and semi-major axes (a) on the oscillatory amplitudes \((A_i)\), where \(i=1,2,3\ldots 21\). Finally, we have analyzed the phase portrait by using Poincaré section method when the system is free from forces.





















Similar content being viewed by others
Abbreviations
- (X, Y, Z):
-
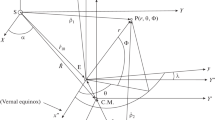
Initial reference coordinate system of the sun and center of sun be its origin (Fig. 1)
- \((X', Y', Z')\) :
-
Initial reference coordinate system of the earth-moon system and the center of mass be its origin (Fig. 1)
- \((X'', Y'', Z'')\) :
-
Initial reference coordinate system of the earth and the center of earth be its origin (Fig. 1)
- (x, y, z):
-
Initial reference coordinate system with origin at the center of the earth and xy-plane in the earth’s equatorial plane (Fig. 1)
- \({{\vec {x}}_1}, \vec {y_1}, \vec {z_1} \) :
-
Unit vectors for the \((X, Y, Z), (X', Y', Z')\) and \((X'', Y'', Z'') \) coordinate systems
- \(a_{r_s}\) :
-
Acceleration component of satellite along the direction \(\vec {r_1}\)
- \(a_{\delta _s}\) :
-
Acceleration component of the satellite along the direction \(\vec {r_2}\)
- \(a_{\varphi _s}\) :
-
Acceleration component of satellite along the direction \(\vec {r_3}\)
- \(a_x, a_y, a_z\) :
-
Direction cosines of \(\vec {r_1}\)
- \(b_x, b_y, b_z\) :
-
Direction cosines of \(\vec {r_2}\)
- \(c_x, c_y, c_z\) :
-
Direction cosines of \(\vec {r}_3\)
- \(\vec {F}_{EM}\) :
-
Earth’s gravitational force on the moon
- \(\vec {F}_{SM}\) :
-
Sun’s gravitational force on the moon
- \(\vec {F}_{SE}\) :
-
Sun’s gravitational force on the earth
- \(\vec {F}_{ME}\) :
-
Moon’s gravitational force on the earth
- \(\vec {F}_{Ss}\) :
-
Sun’s gravitational force on the satellite
- \(\vec {F}_{Es}\) :
-
Earth’s gravitational force on the satellite
- \(\vec {F}_{Ms}\) :
-
Moon’s gravitational force on the satellite
- \(m_s\) :
-
Satellite’s mass
- \(M_M\) :
-
\(7.3476\times 10^{22}\) kg: Moon’s mass
- \(M_E\) :
-
\(5.972\times 10^{24}\) kg: Earth’s mass
- \(M_S\) :
-
\(1.989\times 10^{30}\) kg: Sun’s mass
- \(R_E\) :
-
6371 km: Earth’s radius
- \(R_S\) :
-
696340 km: Sun’s radius
- \(R_M\) :
-
1737.4 km: Moon’s radius
- \(g_E\) = \(9.8 \mathrm{{m/s}}^2\) :
-
Gravitational acceleration on the earth’s surface
- \(g_{S}\) = \(274 \mathrm{{m/s}}^2\) :
-
Gravitational acceleration on the sun’s surface
- \(g_M\) = \(1.62 \mathrm{{m/s}}^2\) :
-
Gravitational acceleration on the moon’s surface
- \(J_2\) = \(+1.08219\times 10^{-3}\) :
-
Earth’s oblateness coefficient
- \(J^{(2)}_2\) = \(-5.35\times 10^{-6}\) :
-
Earth’s equatorial ellipticity coefficient
- \(\gamma =\delta _s-\delta _E\) :
-
Earth’s equatorial ellipticity parameter
- \(\varphi _s\) :
-
Satellite’s latitude
- \(\delta _s\) :
-
Satellite’s longitude
- \(\vec {r_1}\), \(\vec {r_2}\), \(\vec {r}_3\) :
-
Unit vectors along the direction \(r_s, \delta _{s}\), and \(\varphi _s\)
- \(\vec {\rho _{Ss}}\) :
-
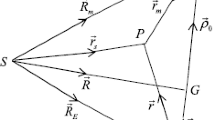
Be a vector from center of sun to the satellite
- \(\vec {\rho _{Ms}}\) :
-
Be a vector from center of moon to the satellite
- \(\vec {r_{SE}}\) :
-
Be a vector from center of sun to the center of earth
- \(\vec {r_{ME}}\) :
-
Be a vector from center of moon to center of the earth
- U :
-
Earth’s potential
- \(\Theta \) :
-
Angle between vector \(\vec {R}\) and \(\vec {x_1}\)
- \(\dot{\Theta }\) :
-
0.01720 rad/solar day = angular velocity of the earth-moon system around the sun
- \(\dot{\Theta _0}\) :
-
Steady-state value of \(\dot{\Theta }\)
- \(\delta _{s0}\) :
-
Steady-state value of \(\delta _s\)
- \(\delta _E\) :
-
Angular position of the minor axis of the earth’s equatorial section
- \(\dot{\delta }_E\) :
-
6.3004 rad/solar day = angular velocity of of earth
- \(\lambda \) :
-
\(23^027'\) = inclination angle of the equatorial plane to the plane of the ecliptic
- \(\mu \) :
-
Mass ratio of the earth-moon system
- \(\vartheta \) :
-
Angle between the vector \(-\vec {r_{ME}}\) and \(\vec {x_1}\)
- \(\dot{\vartheta }\) :
-
0.22998 rad/solar day = angular velocity of moon around the earth
- \(\dot{\vartheta _0}\) :
-
Steady-state value of \(\dot{\vartheta }\)
References
R. Aggarwal, S. Yadav, Resonance in a geo-centric synchronous satellite under the gravitational forces of the sun, the moon and the earth including it’s equatorial ellipticity. Astrophys. Space Sci. 349(2), 727–743 (2014)
G. Alimov, A. Greb, E. Kuznetsov, E. Polyakhova, Approximate analytical theory of satellite orbit prediction presented in spherical coordinates frame. Celest. Mech. Dyn. Astron. 81(3), 219–234 (2001)
E. Andrade-Ines, P. Robutel, Secular dynamics of multiplanetary circumbinary systems: stationary solutions and binary-planet secular resonance. Celest. Mech. Dyn. Astron. 130(1), 1–29 (2018)
A. Celletti, Stability and Chaos in Celestial Mechanics (Springer, Berlin, 2010)
A. Celletti, C. Galeş, A study of the main resonances outside the geostationary ring. Adv. Space Res. 56(3), 388–405 (2015)
M. El-Saftawy, Analytical study of the resonance caused by solar radiation pressure on a spacecraft. Astrophys. Space Sci. 295(3), 407–419 (2005)
J.K.S. Formiga, R.V.D. Moraes, 15: 1 resonance effects on the orbital motion of artificial satellites. J. Aerosp. Technol. Manag. 3, 251–258 (2011)
R. Frick, T. Garber, Perturbations of a synchronous satellite, the rand corporation. Technical report, R-399-NASA (1962)
T. Gallardo, L. Coito, L. Badano, Planetary and satellite three body mean motion resonances. Icarus 274, 83–98 (2016)
N. Harwood, G. Swinerd, Tesseral harmonics of 13th order from the analysis of satellite orbits at resonance. Planet. Space Sci. 44(5), 421–426 (1996)
C. Kaur, B.K. Sharma, S. Yadav, Resonance in the motion of a geocentric satellite due to Poynting–Robertson drag and equatorial ellipticity of the earth. Appl. Appl. Math. 14(1), 29 (2019)
D. King-Hele, A. Winterbottom, Comparison of geopotential harmonics in comprehensive models with those derived from satellite resonance, 1972–1993. Planet. Space Sci. 42(5), 359–365 (1994)
S.J. Kortenkamp, Trapping and dynamical evolution of interplanetary dust particles in earth’s quasi-satellite resonance. Icarus 226(2), 1550–1558 (2013)
J. Luan, P. Goldreich, Classification of satellite resonances in the solar system. Astron. J. 153(1), 17 (2016)
R. Malhotra, Orbital resonances in planetary systems. Encycl. Life Support Syst. UNESCO 6, 55 (2012)
M.-A. Rodríguez-Licea, F.-J. Perez-Pinal, J.-C. Nuñez-Pérez, Y. Sandoval-Ibarra, On the n-dimensional phase portraits. Appl. Sci. 9(5), 872 (2019)
S.W. Shaw, P. Holmes, A periodically forced piecewise linear oscillator. J. Sound Vib. 90(1), 129–155 (1983)
S. Valk, A. Lemaître, F. Deleflie, Semi-analytical theory of mean orbital motion for geosynchronous space debris under gravitational influence. Adv. Space Res. 43(7), 1070–1082 (2009)
I. Wytrzyszczak, S. Breiter, W. Borczyk, Regular and chaotic motion of high altitude satellites. Adv. Space Res. 40(1), 134–142 (2007)
S. Yadav, R. Aggarwal, Resonance in a geo-centric satellite due to earth’s equatorial ellipticity. Astrophys. Space Sci. 347(2), 249–259 (2013)
S. Yadav, R. Aggarwal, Perturbations of a geo-centric synchronous satellite with resonance. Astrophys. Space Sci. 353(2), 417–424 (2014)
S. Yadav, R. Aggarwal, B. Kaur, Resonance in the perturbations of a synchronous satellite due to angular rate of the earth-moon system around the sun and the earth’s rotation rate (2016)
S. Yadav, M. Kumar, V. Kumar, Resonant curve of geo-synchronous satellite including effect of earth’s equatorial ellipticity and resistive force using perturbations technique. New Astron. 86, 101573 (2021)
Acknowledgements
We are thankful to the Center for Fundamental Research in Space Dynamic and Celestial Mechanics (CFRSC) for providing all facilities for this research work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Yadav, S., Kumar, V. & Aggarwal, R. Effect of Earth’s Equatorial Ellipticity on the Resonant Curve and Phase Portrait of Geo-centric Satellite Under the Gravitational Effect of the Earth–Moon–Sun System by Using Unperturbed Solution. Few-Body Syst 63, 41 (2022). https://doi.org/10.1007/s00601-022-01744-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00601-022-01744-2