1 Introduction

It has been found that a kinematic property in the three-body system generates a long range effect in a very low energy region. The effect is called a general particle transfer (GPT) potential, which becomes the Yukawa-type potential for the shorter range but a \(1/r^n\) potential for the longer range [1,2,3,4,5,6]. We will review the GPT formalism in Sect. 2. It was found that the similar property can occur not only at the three-body threshold (3BT) but also at the quasi two-body threshold (Q2T) with two-body bound states in the three-body system. However, the GPT potential has two parameters: a damping range (a) and an index number (n) which shows the degree of the long range. We would like to investigate a relation between the two parameters by utilizing the NN\(\pi \) system, where the familiar one pion exchange potential (OPEP) will be the example. Such a long range potential was first proposed by Efimov [7, 8], which was not given by a single two-body potential but a three-body potential where a nonlinear form or an entangled two-body long range potential was proposed. We would like to generalize the three-body long range Efimov potential by using the GPT potential in Sect. 3. The conclusion and discussion will be given in Sect. 4.

2 The Quasi Two-Body Systems in the AGS Equation

2.1 Fourier Transformation of the One Particle Exchange Potential

For the three-body free energy E and the two-body binding energy \(z=-\epsilon _B\le 0\), we take into account \(E_{cm}\equiv E+\epsilon _B<0\). The off-shell part of the two-body subsystem is written in terms of \({\overline{\mathbf{p}}}_j =(m_i{\overline{\mathbf{q}}}_k-m_k{\overline{\mathbf{q}}}_i)/(m_k+m_i)\), and \({\overline{\mathbf{q}}}_j\) which is the relative momentum between the center of mass of the two-body subsystem and the spectator particle j with the reduced mass \(\mu _j=m_j(m_k+m_i)/(m_i+m_j+m_k)\). The one particle transfer potential, or the AGS [9] Born term in the three-body Faddeev formalism [10, 11], is represented by

$$\begin{aligned}&Z_{in,jm}({\overline{\mathbf{q}}}_i,{\overline{\mathbf{q}}}_j;-|E_{cm}|)\nonumber \\&\quad = \frac{g_{in}({\overline{\mathbf{p}}}_i)g_{jm}({\overline{\mathbf{p}}}_j)(1-\delta _{i,j})}{-|E_{cm}|-{\overline{q}}_j^2/2\mu _j} \end{aligned}$$
(1)
$$\begin{aligned}&=-2\mu _j \frac{g_{in}({\overline{\mathbf{p}}_i})g_{jm}({\overline{\mathbf{p}}_j})(1-\delta _{i,j})}{\sigma ^2+{\overline{q}}_j^2}\nonumber \\&\quad =-\frac{C_{in,jm}({\overline{\mathbf{q}}_i},{\overline{\mathbf{q}}_j})}{\sigma ^2+{\overline{q}}_j^2}, \end{aligned}$$
(2)

where \(\sigma \) and the numerator are defined by

$$\begin{aligned}&\sigma \equiv \sqrt{2\mu _j |E_{cm}|}, \end{aligned}$$
(3)
$$\begin{aligned}&C_{in,jm}({\overline{\mathbf{q}}_i},{\overline{\mathbf{q}}_j}) \equiv 2\mu _j {g_{in}({\overline{\mathbf{p}}_i})g_{jm}({\overline{\mathbf{p}}_j})(1-\delta _{i,j})}. \end{aligned}$$
(4)

It should be remind that \(C_{in_jm}\) \((q_i,q_j)\) includes a re-coupling operator based on the AGS-Born term. Since the degree’s of freedom of the two-body off-shell momentum \(\overline{p_i}\) and \(\overline{p_i}\) vanishes at the Q2T, therefore we adopt simply an "effective potential depth" \(V_o\) for the moment, which could yield binding energies for example,

$$\begin{aligned} -C_{in,jm}({\mathbf{0}},{\mathbf{0}})=-C_{in,jm}=4\pi V_0<0. \end{aligned}$$
(5)

In order to obtain the r-space potential, the Fourier transformation for Eq. (1) near at the Q2T is given by Oryu [1, 2],

$$\begin{aligned} \mathcal{{F}}\{Z_{in,jm}({\overline{\mathbf{q}}}_i,{\overline{\mathbf{q}}}_j;-|E_{cm}|)\}=V_0\frac{e^{-\sigma r}}{r}\equiv V_\sigma (r). \end{aligned}$$
(6)

For \(\sigma =0\), Eq. (6) becomes the Coulomb-like potential (or the gravitational potential), where the AGS equation is essentially the same equation as the Lippmann–Schwinger (LS) equation, therefore it diverges at the Q2T with \(\overline{q}_j=0\). Such a potential has an infinite number of eigenvalues with the quantum number relation of \(1/n^2\). While \(\sigma =m_\pi \) (with \(\hbar =c=1\)) corresponds to the Yukawa potential, where the potential Eq. (6) is energy dependent with respect to \(\sigma \) in r-space. A parameter a indicates a damping range from the singularity at the Q2T which parameterizes the transition from the “Coulomb potential” to the “Yukawa potential”, or interpolates between two energies along \(\sigma \) by a damping factor \(e^{-a\sigma }\) , where it can be shown in terms of the pion mass \(m_\pi \) that

$$\begin{aligned} 0\le \sigma \le m_\pi , \end{aligned}$$
(7)

or the inequality for the inverse argument is given by

$$\begin{aligned} 1/m_\pi \le \sigma ^{-1} <\infty . \end{aligned}$$
(8)

This implies an inequality for the damping range,

$$\begin{aligned} 1/m_\pi \le a<\infty , \end{aligned}$$
(9)

where \(a=1/m_\pi \) and \(a=\infty \) correspond to the Yukawa potential and the Coulomb potential, respectively.

Let us take an energy average with respect to \(\sigma \); we adopt a weight function \(P_\sigma \) with a parameter \(\gamma \), and the damping range a for the moment [1],

$$\begin{aligned} P_\sigma= & {} \frac{\sigma ^{2\gamma +1}e^{-a\sigma }}{\rho (2\gamma +1)}, \end{aligned}$$
(10)
$$\begin{aligned} \rho (2\gamma +1)= & {} \int _0^\infty \sigma ^{2\gamma +1}e^{-a\sigma }d\sigma =\frac{\Gamma (2\gamma +2)}{a^{2\gamma +2}}. \end{aligned}$$
(11)

By using Eqs. (10) and (11), (6) becomes,

$$\begin{aligned}&\mathcal{{F}}\{Z_{in,jm}({\overline{\mathbf{q}}}_i,{\overline{\mathbf{q}}}_j;-|E_{cm}|)\}=\mathcal{L}\Big \{V_\sigma (r)\Big \}\nonumber \\&\quad =\mathcal{L}\Big \{\frac{V_0 e^{-\sigma r}}{r}\Big \} =\frac{V_0 }{\rho (2\gamma +1)}\int _0^\infty \sigma ^{2\gamma +1}e^{-a\sigma }\frac{ e^{-\sigma r}}{r}d\sigma \end{aligned}$$
(12)
$$\begin{aligned}&\quad =V_0 \frac{a^{2\gamma +2}}{r(r+a)^{2\gamma +2}} \end{aligned}$$
(13)
$$\begin{aligned}&\quad =V_0\frac{a^{n-1}}{r(r+a)^{n-1}}\equiv V(n,a;r), \end{aligned}$$
(14)

where we can replace \(\gamma \) by an index number n with

$$\begin{aligned} n=2\gamma +3. \end{aligned}$$
(15)

Equation (12) is the Laplace transformation and is the “Euler integral of the second kind” with respect to Eq. (6).

Therefore, we have

$$\begin{aligned} V(n,a;r)= & {} V_0\frac{a^{n-1}}{r(r+a)^{n-1}} \end{aligned}$$
(16)
$$\begin{aligned}\rightarrow & {} V_0\frac{e^{-(n-1)r/a}}{r}\equiv V_0\frac{e^{-\mu r}}{r}\quad \mathrm{for}\quad r\ll a, \end{aligned}$$
(17)
$$\begin{aligned}\rightarrow & {} V_0\frac{a^{n-1}}{r^{n}}\quad \mathrm{for}\quad a\ll r. \end{aligned}$$
(18)

It is found that in the short range, the GPT potential is a kind of Yukawa-type with the range \(\mu \); therefore, Eq. (17) gives a relation between the damping range and the index number for an exchange particle mass of \(\mu \ne 0\),

$$\begin{aligned} n =a\mu +1. \end{aligned}$$
(19)

For an exchanged particle with mass \(\mu \), the potential V(n, a; r) becomes a Yukawa-type potential for \(r\ll a\), but \(1/r^n\)-type long range potential for \(a\ll r\); see Table 1.

If we choose \(\mu =m_\pi \) in Eq. (17), it becomes the Yukawa potential. Furthermore, the damping parameter could be taken for the Yukawa range: \(a=1/m_\pi \). Then we obtain \(n=am_\pi +1=2\) in Eq. (19). On the other hand in Eq. (18), the GPT potential has a long range property of the form: \(1/r^n\), where if we take \(a=1/m_\pi \) in Eq. (19), then we obtain \(n=\mu a+1=m_\pi a+1=2\) which gives \(1/r^2\). However, in order to obtain the traditional observables, we have to choose an r-dependent (n, a) while maintaining the ratio: \(m_\pi =(n-1)/a=[n(r)-1]/a(r)\).

Table 1 The GPT potential \(V_0a^{n-1}/[r(r+a)^{n-1}]\) is illustrated, which is given by an energy average below the 3BT (\(E=0\), \(\epsilon _B=0\)) and below the Q2T (\(E=-\epsilon _B\), \(\epsilon _B\ne 0\)) with two-parameters a and n.
Full size table

2.2 Mass and the Index Number for the Long Range Potential

In Eq. (17), \(\mu \) is the “general particle” mass of the exchanged particle k in the three-body system for (i,  j,  k) which corresponds to the range of the Yukawa-type potential.

If we consider a one pion exchange (\(i, ~j, ~\pi \)) system, then we can take

$$\begin{aligned} \mu =m_\pi , \end{aligned}$$
(20)

and Eq. (19) becomes

$$\begin{aligned} n= & {} a m_\pi +1. \end{aligned}$$
(21)

In Eq. (9), the damping parameter is given by a value between \(1/m_\pi \) and \(\infty \). Since the Yukawa potential corresponds \(a=1/m_\pi \), then the index number in Eq. (21) becomes

$$\begin{aligned} n=2. \end{aligned}$$
(22)

Alternatively, if we choose \(a=2/m_\pi \), one has \(n=3\).

It should be noted that Eq. (19) is obtained for the case: \(\mu \ne 0\) where \(a\rightarrow \infty \) leads \(n\rightarrow \infty \). However for the case: \(\mu =0\) in Eq. (19), we automatically obtain \(n=0\times a+1=1\). The latter relation is also obtained from the original GPT potential in Eq. (16) which is not the Yukawa-type, but the Coulomb-type,

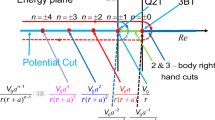
$$\begin{aligned} V(n,a;r)=\lim _{a\rightarrow \infty }V_0\frac{a^{n-1}}{r(r+a)^{n-1}} =V_0\frac{1}{r}. \end{aligned}$$
(23)

As a consequence, the index number is an increasing function with respect to the mass of the exchange particle \(\mu (\ne 0)\) in Eq. (19) which is shown in Fig. 1.

Fig. 1
figure 1

The relation between the mass \(\mu \) of the exchanged particle and the index number n of the long range potential is illustrated where the horizontal line is given in units of the pion mass \(m_\pi \). The red line shows the \(n-\mu \) relation for the damping range \(a=2/m_\pi \), and the blue line is the case for \(a=1/m_\pi \) where the blue line gives \(1/r^2\) potential for one pion exchange, while the red line shows the \(1/r^3\) potential for one pion exchange. Therefore, n becomes larger for the non-zero mass particle exchange

Full size image

2.3 The OPEP and the GPT Potential in the NN\(\pi \) Three-Body System

In order to find a relation between the OPEP and the GPT potential for the non-zero mass case, we choose \(n=2\) for simplicity; it gives

$$\begin{aligned} a(r)=a_\mathrm{opp}(r) =\frac{e^{-m_\pi r} r}{(1-e^{-m_\pi r})}. \end{aligned}$$
(24)

In this case, \(a_{\mathrm{opp}}(r)\) can only be used within the OPEP region; it fails for the full GPT potential region. For the full region, we can use a new damping parameter and an index number n(r), and with very large factor \(\chi \),

$$\begin{aligned} a(r)= & {} \frac{1}{m_\pi }+\chi \Big (\frac{re^{-m_\pi r}}{1-e^{-m_\pi r}} +\frac{(1-e^{-m_\pi r})}{m_\pi }-\frac{1}{m_\pi }\Big ) \end{aligned}$$
(25)
$$\begin{aligned} n(r)= & {} a(r)m_\pi +1 \end{aligned}$$
(26)
$$\begin{aligned} V(r)= & {} V_0\frac{[a(r)]^{n(r)-1}}{r[r+a(r)]^{n(r)-1}}. \end{aligned}$$
(27)

The traditional OPEP is only used to reproduce scattering observables and the deuteron binding energy on the basis of the short range potential. The GPT potential with \(n=2\), for example, gives the infinite scattering length [12].

3 Three-Body Long Range Efimov Potential

Nicholson [12] found that the \(1/r^2\) potential produces an infinite value of the scattering length. The three-body problem with such a potential is compared with the borromean ring problem. In the 3BT, the Efimov effect is given by such a two-body potential. Efimov proposed not the two-body \(1/r^2\) but a three-body long range (3BL) potential which we call the Efimov potential with Efimov [7]

$$\begin{aligned}&V_e(r_i,r_j,r_k)\nonumber \\&\quad =\frac{V_{e0}}{(r_i-r_j)^2+(r_j-r_k)^2+(r_k-r_i)^2},\nonumber \\&\quad \equiv \frac{V_{e0}}{r_{ij}^2+r_{jk}^2+r_{ki}^2}. \end{aligned}$$
(28)

The equation indicates that the two-body long range interaction is the same for the three-different channels: (i, j), (j, k) and (k, i), with the same index number \(n=2\). Therefore, this represents the three identical particle case. However, such a condition is very rare and restricted. One could imagine that such a condition must be general from the view point of the above mentioned GPT potential for the one pion exchange case. Since the hadron-hadron interaction is universally written in terms of a one pion exchange potential, therefore any pair interactions are given by a \(1/r^2\) potential.

We presume that the Efimov formula is one of the nonlinear potentials which are entangled by three-different two-body long range (2BL) potentials with respect to the GPT potential Eq. (18),

$$\begin{aligned} V_{ij}^L=\frac{V_0^{i,j}a_{ij}}{r_{ij}^2}\equiv \frac{1}{a_{ij}{r_{ij}^2}} \end{aligned}$$
(29)
Fig. 2
figure 2

A is one pion (k) exchange in the NN\(\pi \) system, while B represents a nucleon (i) transfer Feynman diagram with a black bold line (N), a black small line \((\pi )\), where the small circles indicate the two-body form factors which also contain a virtual pion exchange with red dashed lines in (A\('\)) and (B\('\)). One can recall that the two-hadron interaction is given not only by the three-body problem, but also by a many-body problem with some virtual pions

Full size image

Generally speaking, the NN\(\pi \) system is well described by the relativistic AGS equation [13,14,15,16,17,18,19,20]. If the one pion exchange potential which is given by (A) for the (ij) pair in Fig. 2, the (jk) and (ki) form factors could also be represented by the AGS equation. Therefore, the NN\(\pi \) system could be described not only by the three-body system but also by many-body systems with an attached pion which is shown by (A\('\)) for (jk) and (ki) pairs in Fig. 2. Such a potential can not be written as a linear equation in terms of the sum of two-body potentials which is described in the Faddeev formalism,

$$\begin{aligned} V_e(r_1,r_2,r_3)=V_{ij}^{L}+V_{jk}^{L}+V_{ki}^{L}. \end{aligned}$$
(30)

Now, let us define a nonlinear three-body long range potential by

$$\begin{aligned} V_e(r_i,r_j,r_k)= & {} \frac{1}{\{V_{ij}^L\}^{-1}+\{V_{jk}^L\}^{-1}+\{V_{ki}^L\}^{-1} } \end{aligned}$$
(31)
$$\begin{aligned}= & {} \Big [\alpha _{ij}{r_{ij}^2}+\alpha _{jk}{r_{jk}^2}+\alpha _{ki}{r_{ki}^2}\Big ]^{-1} \end{aligned}$$
(32)

For the three identical particle system, \(a^{-1}_{ij}=a^{-1}_{jk}=a^{-1}_{ij}=a^{-1}_{ki}\), or \(V^{ij}_{0}a_{ij}=V^{jk}_{0}a_{jk}=V^{ki}_{0}a_{ki}\), \(V_{0}a\)  Eq.(32)

$$\begin{aligned} V_e(r_i,r_j,r_k)=\frac{V_{0}a}{r_{ij}^2+r_{jk}^2+r_{ki}^2}. \end{aligned}$$

Therefore, we obtain the same equation as Eq. (28) except for the depth parameter: \(V_{e0}\) which is given by Efimov, although the origin of the parameter is unclear. However, Eq. (32) diverges at the origin for \(r_{ij}^2=r_{jk}^2=r_{ki}^2=0\).

In order to avoid the singularity at origin, we can easily add a small number \(a_e\) in the denominator, by using \(V_0a=W_0a_e^2\),

$$\begin{aligned}&V_e(r_i,r_j,r_k) =\frac{W_0a_e^2}{r_{ij}^2+r_{jk}^2+r_{ki}^2+a_e^2}. \end{aligned}$$
(33)

However, one of the weakness of this method is that \(a_e\) is an ambiguous parameter, and the second is that Eq. (33) should be continued with the short range potentials at a proper range which is also unclear.

On the other hand, if we subtract the short range component from the GPT potential, then the resultant part is a two-body pure long range (2PLR) potential which is simply given by Eqs. (16) and (17), not by directly using Eq. (18),

$$\begin{aligned} V^{long}(n,a;r)=V_0\Big \{\frac{a^{n-1}}{r(r+a)^{n-1}}-\frac{e^{-(n-1)r/a}}{r}\Big \}. \end{aligned}$$
(34)

It does not include the short range component and satisfies

$$\begin{aligned}&V^{long}(n,a;0)=0, \end{aligned}$$
(35)
$$\begin{aligned}&V^{long}(n,a;r)=V_0\frac{a^{n-1}}{r^{n}} \quad \mathrm{for}~~~a\ll r. \end{aligned}$$
(36)

By using Eqs. (34) and (33) can be rewritten for an entangled three-body pure long range (3PLR) potential,

$$\begin{aligned} V_e(r_i,r_j,r_k)=\frac{1}{\{V_{ij}^{long}\}^{-1}+\{V_{jk}^{long}\}^{-1} +\{V_{ki}^{long}\}^{-1} }, \end{aligned}$$
(37)

with the (ij)-pair 2PLR potential in Eq. (34),

$$\begin{aligned} V^{long}_{ij}(n,a;r)=\frac{\left[ V_0\Big \{\frac{a^{n-1}}{r(r+a)^{n-1}}-\frac{e^{-(n-1)r/a}}{r}\Big \}\right] _{ij}}{\rightarrow \Big [\frac{V_{0}a}{r^2}\Big ]_{ij} \qquad \text{ for }\quad a_{ij}\ll r_{ij}}\equiv V^{long}_{ij} \end{aligned}$$
(38)

In the simplest case of the NN\(\pi \) system, if we adopt \(a=1/m_\pi \), and \(n=\mu /m_\pi +1=2\) with \(\mu =m_\pi \). Our long range three-body potential Eq. (37) can complement the traditional NN\(\pi \) three-body calculation by just adding the term Eq. (37) without the short range component and without ambiguity.

For a three-nuclear cluster system, if a potential tail of two-cluster interaction has a kind of Yukawa-type by a virtual meson exchange with the mass of \(\mu _{ij}\), it will be written by,

$$\begin{aligned} V^{CC}_{ij}(r-R) \rightarrow \Big [V_0\frac{e^{-\mu (r-R)}}{r-R}\Big ]_{ij}. \end{aligned}$$
(39)

with a cluster-cluster range R.

The potential depth: \(V_0^{ij}\) as well as the mass: \(\mu _{ij}\) are important to clarify the interaction. If the mass satisfies \(m_\pi \le \mu _{ij}\), the index number is not always \(n=2\), but given by Eq. (19): \(n=\mu _{ij} a+1\), where if \(a=1/m_\pi \) is chosen, the index number can be found on the blue line in Fig. 1, or if \(a=2/m_\pi \) is selected, it shows the red line in Fig. 1. For any index number, the 2PLR potential is represented by Eq. (38). One can imagine that the potential tail of the nucleus-nucleus interaction is presumably analogous to the OPEP, or the two-pion exchange potential, or a heavy meson exchange potential, where the different parameters could be utilized. It could be inferred that the most effective long range property is given by the one pion exchange long range effect with \(n=2\) in the hadron system. Consequently, our method could be applicable for many two- and three-hadron systems.

4 Conclusion and Discussion

A kinematic property in the three-body system represents a characteristic feature in the potential. The GPT potential is governed by two parameters, the first is the damping range which is a distance from the Q2T singularity, and the second is the index with respect to the long range potential which relates to the exchanged particle mass. The mass dependence of the exchanged particle was investigated, and a formula relating the index and masses was obtained. The traditional OPEP is reproduced by the GPT potential with an r-dependent damping parameter. A new pure three-body long range potential so called 3PLR potential is obtained from the differrent two-body GPT potentials, although the Efinov potential is usually used for the three identical particles systems.

Finally, it should be stressed that the traditional two- and three-hadron equations with short range potentials can be easily compensated by the 2PLR and 3PLR potentials. Since these potentials dominate the pico-meter region, they could affect observables caused by the nuclear and molecular mutual dynamics [6, 21, 22].