1 Introduction

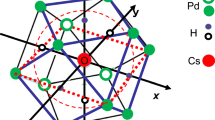
In the traditional nuclear fusion approach, the most important problem is whether the incident energy can penetrate the Coulomb barrier or not, because the reaction is usually started in the free field. Recently we pointed out that the Cs–d penetration in the quasi-molecule which is developed in the Pd-crystal could easily occur [1], since the energy levels of such a quasi-molecule could close to the top of Cs–d Coulomb barrier or over the barrier in the “Pd-cage” which is a repulsive Coulomb barrier between the ions (Cs/D) and outer Pd. Therefore, the penetration problem is resolved in the quasi-molecule: \(\hbox {CsD}_2\) in the \(\hbox {CsD}_2\hbox {Pd}_{{12}}\) system, and \(\hbox {CsD}_4\) in \(\hbox {CsD}_4\hbox {Pd}_{{12}}\), and also \(\hbox {CsD}_6\) in the system \(\hbox {CsD}_6\hbox {Pd}_{{12}}\) which are given by the hydrogen storage in the \(\hbox {Pd}_{{13}}\) cub octahedron/\(\hbox {D}_6\), or Pd-cluster where the central Pd is substituted by Cs which was precisely investigated by Watari et al. [2]. In their paper, the numerical calculation was done with the molecular ADF program, which is based on the linear combination of atomic orbital’s method using density functional theory with all-electron Slater-type basis sets [2]. They found that the external electron configuration of \(\hbox {CsD}_2\hbox {Pd}_{{12}}\) is very similar to that of La [2]. Therefore one could confirm that such a quasi-molecule exists independently from the Pd-cluster. By this reason, we call \(\hbox {CsD}_2\) in the \(\hbox {CsD}_2\hbox {Pd}_{{12}}\) crystal the quasi molecule (see Fig. 1). However, their calculation was done in the region of \(10^{4}~\mathrm{fm}\le r<\infty \), therefore, it is very hard to investigate the nuclear fusion problem which is performed in the region of \(0\le r\le \infty \).

On the other hand, in the nuclear cluster physics, it is known that the highest excited state of the nucleus is the linear chain of the clusters [3,4,5,6,7,8,9], which is very similar to the molecular system in the present case (see Fig. 1). However, such a nuclear energy level is still far from the molecular state. Therefore, one could imagine that the nuclear states with the long range potential, which have predicted in the hadron three-body system [10,11,12,13,14] could interpolate such a region between the nuclear state and the molecular state.

In order to investigate a very shallow nuclear state, we would like to study nuclear d–Cs–d three-body problem by a very accurate three-body variational (HDV) method with 80 to 100 figures based on a usual variational approach [15]. For the nuclear potentials, the WS potential is adopted with the repulsive Coulomb potentials for Cs–D, D–D, and the repulsive Pd-cage, and also we have to take into account the electron effects for the attractive Ze-Cs, Ze-D Coulomb potentials.

The total Hamiltonian of the quasi-molecule D–Cs–D with the Pd-cage and the nuclear d–Cs–d (or D–Cs–D) system is discussed in Sect. 2. In Sect. 3, the quasi molecular low-lying wave function \(\psi _m\) and the nuclear wave function of the highest excited state of La \(\psi _n\) are obtained for the reaction: Cs(2d, \(\gamma \))La. The WFO value between both wave functions: \(\psi _n\), and \(\psi _m\) will be compared for the cases where the two- and three-body long range potentials are included or not. The conclusion and discussion will be given in Sect. 4.

2 Effective Three-Body Hamiltonian In Molecular D–Cs–D and Nuclear d–Cs–d Systems in Pd-Cluster

Since some electrons could be contained between Cs and d nuclei in the molecular system, therefore we use the sign D–Cs–D for the three-ion system, while we take a sign d–Cs–d for the nuclear system where no electron exists between Cs and d. Therefore, hereafter we will frequently use “H” instead of “D and d”, and also use “N” for nucleus or ions {Cs, D or d} without confusion. The two-body Coulomb potentials in the H–Cs–H three-body system are given by the Cs–H potential: \(V_c^{\mathrm{CsH}}\), and the H–H potential: \(V_c^{\mathrm{HH}}\), the sum of the attractive Coulomb potentials between Z-electrons (Zel) and ion: \(V^{M}_{\mathrm{N-Zel}}\) where N stands for {Cs, D} ions, and the electron-electron Coulomb repulsive potential: \(V_{\mathrm{el-el}}^M\) which is the sum of the ith-electron and the jth-electron: \(V_{c}^{\mathrm{e}_i-\mathrm{e}_j}\). For the three-nuclear (hadron) system: d–Cs–d, the two-body nuclear potentials are given by \(V_{\mathrm{3-N}}^{had}\) especially for the Cs–d potential: \(V_N^{\mathrm{Csd}}\), and for the d–d potential: \(V_N^{\mathrm{dd}}\). The two-body Coulomb interactions among three ions: \(V_{\mathrm{3-N}}^C\), especially for Cs–H interaction: \(V_c^{\mathrm{CsH}}\), and also for H–H interaction: \(V_c^{\mathrm{HH}}\), respectively.

Fig. 1
figure 1

\(\hbox {CsD}_2\) quasi-molecule in the \(\hbox {CsD}_2\hbox {Pd}_{{12}}\) cluster which is based on in the \(\hbox {Pd}_{{13}}\) cub octahedron/\(\hbox {D}_6\), where one of the central Pd is substituted by Cs

Full size image

Therefore the total Hamiltonian of H–Cs–H quasi-molecule in the Pd-cluster is given by using the repulsive Coulomb barrier with the one-body potential: \(V_c^{\mathrm{Pd}}\), and by adding three-cluster force to fit the ground state of La: \(V_t\), and also with a two- or three-body long range hadron interaction: \(V_e\) if any,

$$\begin{aligned} H= & {} (K_{\mathrm{3-N}}+V_{\mathrm{3-N}}^{had}+V_{\mathrm{3-N}}^C +V_c^{\mathrm{Pd}}+V_t+V_e) +(K_{\mathrm{Z-el}}+V_{\mathrm{N-Zel}}^M+V_{\mathrm{el-el}}^M)\nonumber \\= & {} H_{had}+h_c^M, \end{aligned}$$
(1)

where \(K_{\mathrm{3-N}}\) and \(K_{\mathrm{Z-el}}\) are the three-hadron kinetic energy, and Z-electron kinetic energy, respectively.

The total Hamiltonian consists of the hadron part and the electron part,

$$\begin{aligned}&\displaystyle H_{had}=K_{\mathrm{3-N}}+V_{\mathrm{3-N}}^{had}+V_{\mathrm{3-N}}^C +V_c^{\mathrm{Pd}}+V_t+V_e \end{aligned}$$
(2)
$$\begin{aligned}&\displaystyle h_c^M=K_{\mathrm{Z-el}}+V_{\mathrm{N-Zel}}^M+V_{\mathrm{el-el}}^M \end{aligned}$$
(3)

where the potentials are defined by using coordinates: \(\mathbf{r}_{ij}=\mathbf{r}_i-\mathbf{r}_j\), for three-different ions \(\mathbf{r}_1\), \(\mathbf{r}_2\) and \(\mathbf{r}_3\),

$$\begin{aligned}&\displaystyle V_{\mathrm{3-N}}^{had}(\mathbf{r}_1,\mathbf{r}_2,\mathbf{r}_3) =\Big [V_{N}^{\mathrm{Csd_1}}(\mathbf{r}_{31}) +V_{N}^{\mathrm{Csd_2}}(\mathbf{r}_{23}) +V_{N}^{\mathrm{d_1d_2}}(\mathbf{r}_{12})\Big ] \end{aligned}$$
(4)
$$\begin{aligned}&\displaystyle V_{\mathrm{3-N}}^{C}(\mathbf{r}_1,\mathbf{r}_2,\mathbf{r}_3) =\Big [V_{c}^{\mathrm{Csd_1}}(\mathbf{r}_{31})+ V_{c}^{\mathrm{Csd_2}}(\mathbf{r}_{23})+ V_{c}^{\mathrm{d_1d_2}}(\mathbf{r}_{12})\Big ] \end{aligned}$$
(5)
$$\begin{aligned}&\displaystyle V_{\mathrm{N-Zel}}^M(\mathbf{r}_1,\mathbf{r}_2,\mathbf{r}_3) =\Big [V_{c}^{\mathrm{ZeD_1}}(\mathbf{r}_{1})+ V_{c}^{\mathrm{ZeD_2}}(\mathbf{r}_{2})+ V_{c}^{\mathrm{ZeCs}}(\mathbf{r}_{3})\Big ] \end{aligned}$$
(6)
$$\begin{aligned}&\displaystyle V_{\mathrm{el-el}}^M=\sum _{i=1}^Z\sum _{j\ne i}V_{c}^{\mathrm{e}_i-\mathrm{e}_j} \end{aligned}$$
(7)
$$\begin{aligned}&\displaystyle V_c^{\mathrm{Pd}}(\mathbf{r}_1,\mathbf{r}_2,\mathbf{r}_3) =V_c^{\mathrm{PdCs}}(\mathbf{r}_3) +V_c^{\mathrm{PdD_1}}(\mathbf{r}_1)+V_c^{\mathrm{PdD_2}}(\mathbf{r}_2). \end{aligned}$$
(8)

\(V_c^{\mathrm{Pd}}(\mathbf{r}_1,\mathbf{r}_2,\mathbf{r}_3)\), \(V_t(\mathbf{r}_1,\mathbf{r}_2,\mathbf{r}_3)\), and \(V_e(\mathbf{r}_1,\mathbf{r}_2,\mathbf{r}_3)\) are a one-body potential of the Pd Coulomb barrier, the three-cluster nuclear potential, and a long range three-body potential if any. Equation (7) is represented only by the operator form which should be given by the different arguments for \((Z+2)\)-electron degrees of freedom.

In Eq. (4), we adopt the WS potential for the ith-N and jth-N nuclear potential: \(V_{N}^{\mathrm{N}_i\mathrm{N}_j}(\mathbf{r}_{ij})\),

$$\begin{aligned} V_{W}^{\mathrm{N}_i\mathrm{N}_j}(r_{ij})=V_{W0}^{\mathrm{N}_i\mathrm{N}_j} \left[ 1+\exp \left( \frac{r_{ij}-R_W^{\mathrm{N}_i\mathrm{N}_j}}{a_W^{\mathrm{N}_i\mathrm{N}_j}}\right) \right] ^{-1} \end{aligned}$$
(9)

with parameters, \(V_{W0}^{\mathrm{Cs}\mathrm{d}}=-\,79.30\) MeV, \(V_{W0}^{\mathrm{d}\mathrm{d}}=-\,27.57\) MeV, \(R_W^{\mathrm{Cs}\mathrm{d}}= 10.21\) fm, \(R_W^{\mathrm{d}\mathrm{d}}= 1.49\) fm, \(a_W^{\mathrm{Cs}\mathrm{d}}= 0.4\) fm, \(a_W^{\mathrm{d}\mathrm{d}}= 0.3\) fm, respectively.

In Eq. (5), we have

$$\begin{aligned} V_{c}^{\mathrm{N}_i\mathrm{N}_j}(r_{ij})= \left\{ \begin{array}{ll} \dfrac{Z_iZ_je^2}{8\pi R} \left[ 3-\left( \dfrac{r_{ij}}{R_c^{\mathrm{N}_i\mathrm{N}_j}}\right) ^2\right] &{}\quad \mathrm{for}\quad {r_{ij}}\le R \\ \dfrac{Z_iZ_je^2}{4\pi r_{ij}}Q&{}\quad \mathrm{for}\quad R< {r_{ij}} \end{array} \right. \end{aligned}$$
(10)

with \(R_c^{\mathrm{CsH}}= 10.21 \mathrm{fm}\), and \(R_c^{\mathrm{H_1H_2}}= 1.49 \mathrm{fm}\).

In Eq. (7), the electron-electron interaction may be attributed to the electron density function that is responsible for the potential in Eq. (6). Therefore, we can omit Eq. (7) in our three-body calculation. Furthermore, the attractive Coulomb potential between the Ze-charged ion and the \(-Z'e\)-charged electron cloud constructs the \(\hbox {CsD}_2\hbox {Pd}_{{12}}\) cluster with the characteristic lattice constants. Therefore, we can also omit the potential Eq. (6) when we take into account our three-cluster system. Although, the potential is formally given by using the electron density function \(\rho (r)\) with the fine structure constant \(\alpha \),

$$\begin{aligned} V_c^{\mathrm{Z'eN}_i}(r_i)= & {} Z_i\hbar c\alpha \Big [ \frac{4\pi }{r_i} \int _0^{r_i}\rho (r')r^{'2}dr' +4\pi \int _{r_i}^{\infty } \rho (r')r'dr'\Big ] \end{aligned}$$
(11)
$$\begin{aligned}= & {} Z_i\hbar c\alpha \Big [ \frac{4\pi }{r_i} \int _0^{{\infty }}\rho (r')r^{'2}dr' -\frac{4\pi }{r_i} \int _{r_i}^{{\infty }}\rho (r')r^{'2}dr' \nonumber \\&\quad +4\pi \int _{r_i}^{\infty } \rho (r')r'dr'\Big ] \end{aligned}$$
(12)
$$\begin{aligned}= & {} -Z_i\hbar c\alpha \Big [\frac{Z'}{r_i} +\frac{4\pi }{r_i}\int _{r_i}^{{\infty }} \rho (r')\{r^{'2}-r'r_i\}dr'\Big ], \end{aligned}$$
(13)

where the electron distribution is given by,

$$\begin{aligned} \rho (r)=\sum _{i=1}^Mc_i\exp \Big [-\Big (\frac{r}{R_i^e}\Big )^2\Big ], \end{aligned}$$
(14)

with

$$\begin{aligned} 4\pi \int _0^{\infty }\rho (r')r^{'2}dr'=-Z', \end{aligned}$$
(15)

where \(Z'\) is variable by the electron supply from Pd-cage.

In Eq. (8), the Pd-\(\hbox {N}_i\) Coulomb barrier is represented by a one-body potential,

$$\begin{aligned} V_c^{\mathrm{PdN}_i}({ r}_i)= & {} V_{c0}^{\mathrm{Pd}}\Big (\frac{r_i}{a_c^{\mathrm{Pd}}}\Big )^{10} \mathrm{exp}\Big \{-\Big (\frac{r_i-a_c^{\mathrm{Pd}}}{b_c^{\mathrm{Pd}}} \Big )^2\Big \} \end{aligned}$$
(16)

with \(V_{c0}^{\mathrm{Pd}}=1.0\times 10^{-4}\) MeV, \(a_c^{\mathrm{Pd}}= 5.0\times 10^5\) fm, and \(b_c^{\mathrm{Pd}}=3.1623\times 10^{5}\) fm, respectively. These parameters for the Pd-cage indicate that the location of Pd is \(1.57\times 10^6\) fm, and 2.73 MeV height, however, these values may vary.

In this paper, we adopt a three-cluster potential as,

$$\begin{aligned}&V_t(r_1,r_2,r_3)=V_{t0} \exp \Big [ -\Big (\frac{r_1-r_2}{a_t} \Big )^2 -\Big (\frac{r_2-r_3}{a_t} \Big )^2 -\Big (\frac{r_3-r_1}{a_t} \Big )^2 \Big ], \end{aligned}$$
(17)

where \(V_{t0}=1800\) MeV and \(a_t=3.0\) fm are used to fit the ground state of La by adding the Coulomb force.

We obtain a very good fit to the experimental ground state energy \({{\mathcal {E}}}_0=-\,32.3\) MeV, the root mean square (rms) radius \(R_0=6.25\) fm, the highest excited energy \({{{\mathcal {E}}}_{max}=-\,3.5134\times 10^2}\) keV for the negative value, and the rms radius \(R_{max}=165.5\) fm, for the usual nuclear potential with the Coulomb plus three-cluster force by the HDV calculation. Therefore, the highest energy level is far from that of the usual molecular state, although the higher partial waves and the non-central part of the WS potential have been omitted for the first time.

On the other hand, in order to obtain shallow energy levels that could be close to the molecular states we adopt a kind of three-body long range potential with \(1/r_{ij}^n\) tail which was proposed as the GPT potential [10,11,12,13,14] with a Lorentz form or given by the modified Efimov type [16,17,18]:

$$\begin{aligned}&V_e(r_1,r_2,r_3)=V_{e0}a_e^n \Big [(r_1-r_2)^n +(r_2-r_3)^n +(r_3-r_1)^n +a_e^n \Big ]^{-1}, \end{aligned}$$
(18)

where we choose \(n=2\) in this paper. Parameters \(V_{e0}=-\,80{,}000\) MeV, and \(a_e=5000\) fm are taken, and also a supplemental \(a_e^n\) is used to avoid divergence. It could be noticed that these parameters seem to be too large to compare to the parameters in the WS potential, however Eq. (18) does not change the usual nuclear potential in the shorter range, because \(V_e\) and \(V_t\) are complementary.

On the kth-particle transfer diagram in the three-body AGS Born term [19], \(V_e\) becomes (A) \(V_e=V_{e0}a_e^2/[r_{ij}^2+a_e^2]\) for (\(r_{ki}=0\) and \(r_{jk}=0\)), \(V_e=V_{e0}a_e^2/[2r_{ij}^2+a_e^2]\) for (\(r_{ki}=0\) or \(r_{jk}=0\)) which are the three-body long range potential between a pair and the spectator particle; and (B) \(V_e=V_{e0}a_e^2/[2r_{kj}^2+a_e^2] =V_{e0}a_e^2/[2r_{ki}^2+a_e^2]\) (for \(r_{ij}=0\)) which indicates the two-body long range potential. (C) While, putting \(\mathbf{r}_k=(\mathbf{r}_i+\mathbf{r}_j)/2\), it gives \(V_e=V_{e0}a_e^2/[3r_{ij}^2/2+a_e^2]\) which is due to the three-body long range potential as well as (A) [10].

Therefore, the D–Cs–D system is given by a wine bottle-type potential which is represented by Eqs. (9), (10), (16), (17), and (18) (see Fig. 2). Figure 2 represents the half of the wine bottle-type potential. The constituents of the quasi molecule \(\hbox {CsD}_2\) align in this potential, where Cs is located in the center of the potential, which are the highly resonated La nucleus d–Cs–d, where the electrons could encircle the \(\hbox {CsD}_2\) and rather stick to the Pd-cage.

Fig. 2
figure 2

The upper figure illustrates the absolute value of the total potential where the vertical line is the energy with MeV unit in the log scale. \(+\) sign is the positive and − sign indicates negative value. The horizontal line is the potential range with the log scale in fm unit. The upper red line (B) is given by the traditional nuclear potential case, while the lower black line (A) is obtained by adding long range potential. The left hand side with + sign is the repulsive three-cluster force potential, the next part with − sign means the attractive WS potential for A and B. The next + sign for A gives the repulsive Coulomb potential, and the next − sign means an attractive potential. Finally, the last enhancement \(+\) indicates the repulsive Pd cage. In the B-line, \(+\) region is continued from the Coulomb repulsive part to the Pd-cage. The lower left figure (A) and the right figure (B) are the calculated energy levels (black points) where the vertical lines give the energy with the absolute value by MeV unit, and the horizontal line means the quantum number n where A and B correspond to the potentials: A and B, respectively. The left parts give the negative energies and the right hand side is the positive energies. Some important values are, in the lower left figure, \(n=5:-1.0391\times 10^6\) eV, \(n=20:-58.975\) eV, \(n=52:+1.4633\times 10^4\) eV, and \(n=55:+7.4047\times 10^4\) eV. In the lower right figure, \(n=5:-3.5134\times 10^5\) eV, \(n=6:+3.3479\) eV, \(n=50:+1.3395\times 10^5\) eV, \(n=53:+2.2726\times 10^5\) eV, respectively

Full size image
Table 1 Some related ions and the shallow spin-parities: \(J^\pi \), and masses by (u) and (MeV) units, where \(1\hbox {u}=931.5019\) MeV is the universal constant
Full size table

3 Numerical Results

The two-cluster potential between Cs and d could be constructed by the three-body reaction: \(\mathrm{Cs}+\mathrm{d}\equiv \mathrm{Cs}+(\hbox {N},\hbox {N}) \rightleftharpoons (\mathrm{Cs},\mathrm{N})+\mathrm{N}\) which gives the general particle transfer (GPT) potential [14] or the AGS Born term [19]. However, in such a way, it is very hard to make the two-cluster form-factors with the core excitation for the three-cluster problem: d–Cs–d. Therefore, we adopt the WS-type Cs–d potential of Eq. (9). By using the WS and the Coulomb potentials, the two-body energy levels are shown in Table 2, where the ground states are well fitted. It is found that the number of the calculated energy levels considering only the central part of the WS potential are rather small. Therefore, additional WS components should be incorporated containing for example spin-orbit and tensor terms for the two-cluster interactions.

Especially, we know the four-nucleon Faddeev-Yakubovsky equations for the deuteron-deuteron interaction [20]. However, our aim in this paper is to obtain the highest three-cluster (or -ion) nuclear level, where the shallow energy levels should be well introduced by the S-wave or even central potential. Furthermore, we obtained the La ground state \(-\,32.3\) MeV (Table 3) for d + Cs + d system by using the central two-cluster Cs–d and d–d potentials, and with the three-cluster force Eq. (17), where we confirmed that the phenomenological method for the La ground state is not very sensitive to the shallow bound and/or resonance states.

Table 2 Calculated two-body binding energies by using the WS potential with the above mentioned parameters and the Coulomb potential, where \(E_1\) values are compared with the 2-body type in Table 3
Full size table
Table 3 Some reaction types of binding energies by the mass relation using Table 1 with (MeV) unit
Full size table
Fig. 3
figure 3

Faddeev calculations [21] for the negative energy levels: (A) indicates the calculation by Eq. (20), and (B) is given by Eq. (19). The most excited state in (A) is \(-\,2.9\) eV which is very close to the molecular levels, however it is not very stable. Therefore, we take the next state: \(-\,44\) eV which is relatively stable with two digits accuracy. In the traditional nuclear potential, since the most shallow state \(-\,14\) keV in (B) is not stable, then we take a stable \(-\,450\) keV which is comparable to HDV result \(-\,351\) keV, and far from the molecular state

Full size image

The traditional nuclear interaction appears in the region of \(0\le r< 10^4\) fm, however, the molecular levels are calculated in the region of 10\(^4 {~\mathrm fm}\le r <10^{7}\) fm. Therefore, the nuclear wave functions and the molecular wave functions do not overlap to give rise to the electro-magnetic (EM) transition. This means that the molecular states are stable and never go down to the nuclear states.

However, the binding energy of \(\hbox {CsD}_2\) in the \(\hbox {Pd}_{{12}}\)-cage is completely different from the free field. We solve the three-ion system in the \(\hbox {Pd}_{{12}}\)-cage for the full region: \(0\le r<\infty \) by the HDV method. In other words, for the nuclear and the molecular systems we can solve the eigen-equation on the basis of a common field in the full region with the 80-100 figures accuracy, however it seems to be very hard for the usual FORTRAN program in this stage. The second promising method is shown in Ref. [1] where the entire wave function could be made by the nuclear state and the molecular state: \(|\varPsi >=|\psi \otimes \psi _M>\). Both energy states could be corrected by the \( {boost ~up ~effect}\) which is shown in Ref. [1], however we do not take this method in this paper.

We compared the calculated results for two potentials,

  1. (1)

    The first one is the three-body calculation for the full potential

    with the traditional short range WS potential,

    $$\begin{aligned} V_{\mathrm{3-N}}^{had}+V_{\mathrm{3-N}}^C+V_c^{\mathrm{Pd}}+V_t. \end{aligned}$$
    (19)
  2. (2)

    The second one is the three-body calculation for the full potential

    with the two- and three-body long range potential \(V_e\):

    $$\begin{aligned} V_{\mathrm{3-N}}^{had}+V_{\mathrm{3-N}}^C+V_c^{\mathrm{Pd}}+V_t+V_e. \end{aligned}$$
    (20)
Table 4 Negative highest excited state of La binding energy (\({{\mathcal {E}}}_{max}\)), and the positive energy (\({{\mathcal {E}}}_{+}\)) which give max-\(W_{nm}\), and the value of max-\(W_{nm}\) (maximum value of WFO)
Full size table

The calculated results by the HDV method show a series of negative binding energy levels which starts from \(-\,32.3\) MeV to the negative highest nuclear level: \({{\mathcal {E}}}_{max}=-\,3.5134\times 10^5\) eV for the short range Eq. (19), and to \({{\mathcal {E}}}_{max}=-\,58.975\) eV for the long range Eq. (20). On the other hand, there is a series of the positive energy states over the Coulomb barrier through to the Pd-cage which is located at \(1.57\times 10^6 \) fm and 2.73 MeV height. Let us call such positive energy states the “quasi molecular states” conventionally.

Therefore, for Eq. (19) the energy gap between the negative nuclear state and the quasi molecular state is very large. However, the calculations with the long range nuclear potential Eq. (20) give a series of discrete negative energy band from \(-\,32.3\) MeV to \(-\,58.975\) eV (HDV-method: see Fig. 2), or \(-\,44\) eV (Faddeev-method: see Fig. 3, where \(-\,2.9\) eV is unstable). Therefore, we can conclude that the three-body Faddeev calculation with the r-space method gives qualitatively similar results with those by the HDV method in the negative energy region, although the Faddeev method [21] is rather hard to reach the Pd-cage. These results show that the energy gap between the negative nuclear state and the quasi molecular state is rather small for the long range nuclear potential.

Finally, in Table 4, the WFO results of max-\(W_{nm}\) with the long range potential are 3.33 times, and of \(W_{n}\) with 12.3 times larger values than those with the usual short range nuclear potential. Therefore, the long range nuclear potential could be favorable to bring about the low energy Cs(2d, \(\gamma \))La reaction.

4 Conclusion and Discussion

This work is based on the assumption that a quasi-molecular system exists in a Pd-cluster. Such a quasi-molecule is almost isolated in the Pd-cage. Therefore, the excited state of the quasi-molecule: \(\hbox {CsD}_2\) does not break-up, because it is not in the free space but restricted in the Pd-cage. Therefore, some excited states could easily penetrate the Coulomb barrier of the Cs–D interaction or even over the top of it. Therefore, they could go into the nuclear quasi-resonance states by means of “stable” states in the Pd-cage. Hence, a quasi-resonance wave packet of \(\hbox {CsD}_2\) could overlap with that of the highest nuclear excited state or the most shallow bound state of La nucleus. In such a case, the WFO has a non zero value, allowing the EM transitions to occur. The possible transition will be started from the E2 or M1 transition, because the E1 transition is forbidden by the same \(J^\pi \) values for Cs and La. Once, the transfer to the nuclear state occurs, then the nuclear transition to the next states is automatically continued. In our present calculations for the ordinary short range nuclear potential, and for the nuclear potential with a long range, we found that the former case gives a small WFO, but the latter case could offer a larger value by an order of magnitude. We mentioned that the WFO value is critical for the occurrence of the Cs(2d, \(\gamma \))La reaction.

Recently, one of the authors (S.O) proposed a new long range nuclear potential of the form: \(1/r^n\) [10,11,12,13,14]. We pointed out why such a long range part in the one pion transfer interaction or the Yukawa potential comes from [14]. Our conclusion was that any particle transfer in the three-body Faddeev theory [19] generates not only the short range, but also the long range interactions which was called the general particle transfer (GPT) potential. Therefore, any two-body nuclear potential in the three-body constituents is constructed by the GPT potential [10,11,12,13,14]. Furthermore, the three-body problem with the GPT potential generates also a GPT potential between the two-body center of mass and the spectator. This idea is concretely represented by the potential form of Eq. (18). If the long range part contains a \(1/r^2\)-type potential, the scattering length will become infinity [16,17,18]. The GPT-potential with the \(1/r^2\)-type gives the three-body bound states near at the three-body threshold which would be very close to the molecular states.

There are some reports of the experimental results about the low temperature nuclear transition (LTNT) [22,23,24,25,26,27,28]. Unfortunately, it seems that a reasonable theoretical description for such reactions has not been given as of yet, since almost all of the traditional theories are based on the short range nuclear forces which could reach as far as 100 fm. Therefore, the nuclear reaction rate is too small for the LTNT, where the Coulomb repulsive force dominates the attractive nuclear force. Our theory may give a hint to the experimental physicists to investigate a mysterious phenomena such as inexplicable thermal generation measured by a special arrangement in the materials, without any usual nuclear reaction phenomena or radioactive substances. One could imagine that such a high energy \(\gamma \)-ray emission does not come from the slow reaction caused by the condensed states, or the \(\gamma \)-ray radiation would be diminished due to the multiple Compton scattering off the electrons in the Pd-cluster, although many nuclear physicists still wonder why some radioactive particles or high energy \(\gamma \)-rays are not observed in the LTNT.

Finally, it should be noticed that the present calculation adopted only the S-wave trial function, and the central nuclear potential. Therefore, we can not give the final conclusion in this paper. However, our results seem to suggest that if the LTNT experiment could be realized, then the long range potential in the nuclear system could be observed.