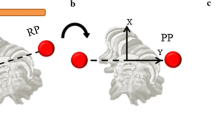
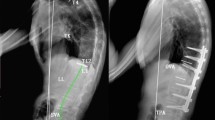
Abstract
Purpose
To predict the sagittal spinal parameters as measured in a 3D model of the spine using the 2D radiographic measurements.
Methods
Bi-planar low-dose stereoradiography images of 73 right thoracic AIS patients were processed to generate 3D models of the spine and pelvis. T1–T12 kyphosis, L1–S1 lordosis, and pelvic rotation were calculated using these 3D models. With the same X-rays, T1–T12 kyphosis, L1–S1 lordosis, thoracic and lumbar frontal curves, and pelvic rotation (calculated from the frontal and sagittal distances between the femoral heads) were manually measured on the X-rays by two independent observers. 3D sagittal parameters were predicted from only 2D sagittal parameters (simple regression) and from 2D sagittal parameters, 2D frontal parameters, and pelvic rotation (multiple regression). The simple and multiple regression models were compared for efficiency and accuracy of prediction.
Results
Comparing single and multiple regression models, multiple regression improved the prediction of the 3D sagittal parameters for kyphosis (R2 = 0.78–0.86) and lordosis (R2 = 0.88–0.92) measurements when compared to simple regression. The impact of pelvic rotation was significant when 2D kyphosis was higher than 40° and thoracic curve was less than 60° or 2D kyphosis was less than 40° and thoracic curve was higher than 60°, p < 0.05. Lordosis of 60° and higher were more prone to measurement error when pelvic rotation was present, p < 0.05.
Conclusions
Both pelvic rotation and frontal deformity affect the accuracy of the 2D sagittal measurements of the scoliotic spine. We suggest the importance of the 3D considerations in sagittal evaluation of AIS.





Similar content being viewed by others

References
Stokes IA (1994) Three-dimensional terminology of spinal deformity. A report presented to the Scoliosis Research Society by the Scoliosis Research Society Working Group on 3-D terminology of spinal deformity. Spine (Phila Pa 1976) 19(2):236–248
Perdriolle R, Le Borgne P, Dansereau J, de Guise J, Labelle H (2001) Idiopathic scoliosis in three dimensions: a succession of two-dimensional deformities? Spine (Phila Pa 1976) 26(24):2719–2726
Pasha S, Flynn JM, Sponseller PD, Orlando G, Newton PO, Cahill PJ, Harms Study Group (2017) Timing of changes in three-dimensional spinal parameters after selective thoracic fusion in Lenke 1 adolescent idiopathic scoliosis: two-year follow-up. Spine Deform 5(6):409–415. https://doi.org/10.1016/j.jspd.2017.04.003
Pasha S, Cahill PJ, Dormans JP, Flynn JM (2016) Characterizing the differences between the 2D and 3D measurements of spine in adolescent idiopathic scoliosis. Eur Spine J 25(10):3137–3145. https://doi.org/10.1007/s00586-016-4582-5
Newton PO, Fujimori T, Doan J, Reighard FG, Bastrom TP, Misaghi A (2015) Defining the “three-dimensional sagittal plane” in thoracic adolescent idiopathic scoliosis. J Bone Joint Surg Am 97(20):1694–1701. https://doi.org/10.2106/JBJS.O.00148
Nault ML, Mac-Thiong JM, Roy-Beaudry M, Turgeon I, Deguise J, Labelle H, Parent S (2014) Three-dimensional spinal morphology can differentiate between progressive and nonprogressive patients with adolescent idiopathic scoliosis at the initial presentation: a prospective study. Spine (Phila Pa 1976) 39(10):E601–E606. https://doi.org/10.1097/brs.0000000000000284
Newton PO, Khandwala Y, Bartley CE, Reighard FG, Bastrom TP, Yaszay B (2016) New EOS imaging protocol allows a substantial reduction in radiation exposure for scoliosis patients. Spine Deform 4(2):138–144. https://doi.org/10.1016/j.jspd.2015.09.002
Ilharreborde B, Dubousset J, Le Huec JC (2014) Use of EOS imaging for the assessment of scoliosis deformities: application to postoperative 3D quantitative analysis of the trunk. Eur Spine J 23(Suppl 4):S397–S405. https://doi.org/10.1007/s00586-014-3334-7
Lechner R, Putzer D, Dammerer D, Liebensteiner M, Bach C, Thaler M (2017) Comparison of two- and three-dimensional measurement of the Cobb angle in scoliosis. Int Orthop 41(5):957–962. https://doi.org/10.1007/s00264-016-3359-0
Humbert L, De Guise JA, Aubert B, Godbout B, Skalli W (2009) 3D reconstruction of the spine from biplanar X-rays using parametric models based on transversal and longitudinal inferences. Med Eng Phys 31(6):681–687. https://doi.org/10.1016/j.medengphy.2009.01.003
Schmid SL, Buck FM, Boni T, Farshad M (2016) Radiographic measurement error of the scoliotic curve angle depending on positioning of the patient and the side of scoliotic curve. Eur Spine J 25(2):379–384. https://doi.org/10.1007/s00586-015-4259-5
Gareen IF, Gatsonis C (2003) Primer on multiple regression models for diagnostic imaging research. Radiology 229(2):305–310. https://doi.org/10.1148/radiol.2292030324
Schneider CA, Rasband WS, Eliceiri KW (2012) NIH Image to ImageJ: 25 years of image analysis. Nat Methods 9(7):671–675
Berry WG, Golder M, Milton D (2012) Improving tests of theories positing interaction. J Politics 74(3):653–671. https://doi.org/10.1017/S0022381612000199
Fox J (2003) Effect displays in R for generalised linear models. J Stat Softw 8:1–27
R Core Team (2015) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria
Ilharreborde B, Steffen JS, Nectoux E, Vital JM, Mazda K, Skalli W, Obeid I (2011) Angle measurement reproducibility using EOS three-dimensional reconstructions in adolescent idiopathic scoliosis treated by posterior instrumentation. Spine (Phila Pa 1976) 36(20):E1306–E1313. https://doi.org/10.1097/brs.0b013e3182293548
Gangnet N, Dumas R, Pomero V, Mitulescu A, Skalli W, Vital JM (2006) Three-dimensional spinal and pelvic alignment in an asymptomatic population. Spine (Phila Pa 1976) 31(15):E507–E512. https://doi.org/10.1097/01.brs.0000224533.19359.89
Hayashi K, Upasani VV, Pawelek JB, Aubin CE, Labelle H, Lenke LG, Jackson R, Newton PO (2009) Three-dimensional analysis of thoracic apical sagittal alignment in adolescent idiopathic scoliosis. Spine (Phila Pa 1976) 34(8):792–797. https://doi.org/10.1097/brs.0b013e31818e2c36
Somoskeoy S, Tunyogi-Csapo M, Bogyo C, Illes T (2012) Clinical validation of coronal and sagittal spinal curve measurements based on three-dimensional vertebra vector parameters. Spine J 12(10):960–968. https://doi.org/10.1016/j.spinee.2012.08.175
Rehm J, Germann T, Akbar M, Pepke W, Kauczor HU, Weber MA, Spira D (2017) 3D-modeling of the spine using EOS imaging system: inter-reader reproducibility and reliability. PLoS ONE 12(2):e0171258. https://doi.org/10.1371/journal.pone.0171258
Parvaresh KC, Osborn EJ, Reighard FG, Doan J, Bastrom TP, Newton PO (2017) Predicting 3D thoracic kyphosis using traditional 2D radiographic measurements in adolescent idiopathic scoliosis. Spine Deform 5(3):159–165. https://doi.org/10.1016/j.jspd.2016.12.002
Stokes IA, Bigalow LC, Moreland MS (1986) Measurement of axial rotation of vertebrae in scoliosis. Spine (Phila Pa 1976) 11(3):213–218
Eijgenraam SM, Boselie TF, Sieben JM, Bastiaenen CH, Willems PC, Arts JJ, Lataster A (2017) Development and assessment of a digital X-ray software tool to determine vertebral rotation in adolescent idiopathic scoliosis. Spine J 17(2):260–265. https://doi.org/10.1016/j.spinee.2015.09.039
Jain D, Berven S (2017) Commentary on development and assessment of a digital X-ray software tool to determine vertebral rotation in adolescent idiopathic scoliosis. Spine J 17(2):266–268. https://doi.org/10.1016/j.spinee.2016.08.027
Sullivan TB, Bastrom T, Reighard F, Jeffords M, Newton PO (2017) A novel method for estimating three-dimensional apical vertebral rotation using two-dimensional coronal cobb angle and thoracic kyphosis. Spine Deform 5(4):244–249. https://doi.org/10.1016/j.jspd.2017.01.012
Sullivan TB, Reighard FG, Osborn EJ, Parvaresh KC, Newton PO (2017) Thoracic idiopathic scoliosis severity is highly correlated with 3D measures of thoracic kyphosis. J Bone Joint Surg Am 99(11):e54. https://doi.org/10.2106/JBJS.16.01324
Faria R, McKenna C, Wade R, Yang H, Woolacott N, Sculpher M (2013) The EOS 2D/3D X-ray imaging system: a cost-effectiveness analysis quantifying the health benefits from reduced radiation exposure. Eur J Radiol 82(8):e342–e349. https://doi.org/10.1016/j.ejrad.2013.02.015
Dietrich TJ, Pfirrmann CW, Schwab A, Pankalla K, Buck FM (2013) Comparison of radiation dose, workflow, patient comfort and financial break-even of standard digital radiography and a novel biplanar low-dose X-ray system for upright full-length lower limb and whole spine radiography. Skeletal Radiol 42(7):959–967. https://doi.org/10.1007/s00256-013-1600-0
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
About this article
Cite this article
Pasha, S., Ecker, M. & Deeney, V. Considerations in sagittal evaluation of the scoliotic spine. Eur J Orthop Surg Traumatol 28, 1039–1045 (2018). https://doi.org/10.1007/s00590-018-2175-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00590-018-2175-1