Introduction

Understanding the spinal alignment and morphology is critical for spinal surgeons to evaluate the pathophysiology of spinal diseases. Various angular or linear radiographic parameters had been introduced to describe the spinopelvic morphology in the sagittal plane [1]. On the other hand, direct categorization of sagittal spinal alignment, rather than measuring the parameters, was also described in both healthy and adolescent idiopathic scoliosis populations [2,3,4].

Artificial intelligence based on deep learning (DL) approaches enabled the automatic recognition of anatomic landmarks and the subsequent estimation of various spinopelvic parameters [5,6,7,8]. Galbusera et al. [5] incorporated the DL approaches and reported a fully automatic system able to locate anatomic landmarks and calculate sagittal spinopelvic parameters with good performances. Korez et al. [7] also developed a two-stage DL model achieving clinically equivalent measurement of sagittal spinopelvic parameters. In addition, Cina et al. [8] trained a 2-step DL model with 10,193 lumbar spine images capable of calculating lumbar radiographic parameters with minimal errors.

Quantitative evaluation of spinal curvature had been widely investigated in both coronal and sagittal planes [9]. Using computerized models, the characteristics of spinal curvatures, such as inflection points (IPs) and apices (APs), could be mathematically defined [10,11,12]. However, these semi-automatic methods still required manual annotation of vertebral landmarks, which was time-consuming and could result in inter- or intra-observer variability. Recent advances of the DL approach have demonstrated a fully automatic annotation of vertebral landmarks with high accuracy and reduced inter- or intra-observer variability [13]. By combining techniques based on DL and numerical methods, this study aimed to develop a fully automatic spinal sagittal curvature analysis system and build a novel formalism to determine the location of IPs and APs in whole-spine lateral radiographs.

Methods

Dataset

From January 2018 to December 2019, 2361 consecutive whole-spine lateral plain radiographs were retrospectively collected under the approval of the institutional review board of our hospital (IRB no. 202100821B0); a waiver for informed consent was granted for this study. A senior radiologist screened the entire image dataset and excluded (1) 149 images of inadequate length that did not include the C2 dens or the bilateral femoral heads, (2) 232 images with anatomic variance in which the vertebral column contained fewer or more than 25 vertebrae, and (3) 180 images with poor contrast that prevented the identification of pelvic anatomic structures. After the exclusion of these images, 1800 images were annotated and randomly divided into (1) a training dataset of 1500 images and (2) a testing dataset of 300 images.

For the annotated 1800 images, the mean age was 37.9 ± 24.9 years (range: 11–96) at the time of radiographic examination. Furthermore, spinal implants were observed in 602 annotated images (33%), with an instrumentation level ranging from C4 to the ilium (average length: 7.9 ± 3.8 levels).

Study design

For each image of the training and testing dataset (1800 images), 25 coordinates of vertebral landmarks (the vertebral centers of C2–C7, T1–T12, L1–L5, anterosuperior corner of S1, and anteroposterior corner of S1) were annotated by four orthopedic residents and verified by an orthopedic surgeon using a customized graphical user interface written in MATLAB.

A detailed illustration of the workflow for data preparation and model evaluation is shown in Fig. 1. The annotated training dataset (1500 images) was used to train a previously developed automatic landmark localizer [13]. During the model testing phase, the trained landmark localizer predicted 25 landmark coordinates in each image of the testing dataset (300 images) (Fig. 2). These 25 coordinates were then fed into a numerical algorithm to generate the whole spinal curvature (Fig. 3), the locations of IPs and APs, and the curvature angles (Fig. 4a) in each image of the testing dataset.

Fig. 1
figure 1

Workflow for data preparation and model evaluation

Full size image
Fig. 2
figure 2

a Whole-spine lateral radiograph. b Twenty-five predicted landmark coordinates (red crosses). c Three predicted landmark coordinates (red crosses) and their corresponding heatmaps

Full size image
Fig. 3
figure 3

a Fitted spinal curve and the determined apices. b First-order derivative of the fitted spinal curve. The four zeros of this curve are the locations of the apices. c Second-order derivative of the fitted spinal curve. The five zeros of this curve are the locations of the inflection points. d Fitted spinal curve and determined inflection points. We highlighted the curve segments as lordosis (green), kyphosis (blue), or a nearly straight line (orange)

Full size image
Fig. 4
figure 4

Angles of thoracic kyphosis (\({\theta }_{\mathrm{TK}}\)) and lumbar lordosis (\({\theta }_{\mathrm{LL}}\)) were measured by a the deep learning model and b a human expert. In a, three lines were determined to measure \({\theta }_{\mathrm{TK}}\) and \({\theta }_{\mathrm{LL}}\): two normal lines (solid yellow), which are normal to the spinal curve and pass through the predicted inflection points (T3 center and L1 center), and one line of the sacral endplate (solid cyan), which was determined by connecting the predicted locations of two sacral landmarks. In b, Cobb angles were measured using lines (solid yellow and solid cyan) that align with the vertebral endplates

Full size image

The landmark localization error, defined as the Euclidean distance between the predicted and human-annotated landmark coordinates, was used to evaluate the performance of the trained landmark localizer. In addition, a senior orthopedic surgeon and a radiologist manually determined the IPs, APs, and Cobb angles (Fig. 4b) in a subset of 50 images (randomly selected from the testing dataset) by using the tools provided by the picture archiving and communication system (PACS) of our hospital. The interrater reliability between the human experts and the DL model was calculated using the intraclass correlation coefficient (ICC).

Automatic localization of vertebral landmarks

A variant of the Cascaded Pyramid Network [13], which is referred to as the landmark localizer throughout this paper, was applied for the automatic localization of 25 vertebral landmarks of a given radiograph (Fig. 2a, b). The coordinates of vertebral landmarks were predicted by estimating the expected values of 25 landmark heatmaps (probability maps). To illustrate this process, three heatmaps and their expected values are presented in Fig. 2c. The heatmaps of the C7 and L3 centers were confined to a small region, indicating that the landmark localizer was certain about the locations of C7 and L3. By contrast, the heatmap of the T9 center was confined within a wide region (from T7 to T11), indicating that the determination of T9 was difficult, and our landmark localizer was less certain about its decision.

Regression of the spinal curves

The predicted vertebral coordinates were used to regress the spinal curve (Fig. 3). In this study, we used a linear combination of one-dimensional functions to model a spinal curve; that is, \(f\left(x\right)={\beta }_{0}+{\beta }_{1}{B}_{1}\left(x\right)+{\beta }_{2}{B}_{2}\left(x\right)+{\dots +\beta }_{N}{B}_{N}\left(x\right)\), where \(x\) is on the vertical axis of the radiograph, \({\{B}_{1}\left(x\right), {B}_{2}\left(x\right), \dots , {B}_{N}\left(x\right)\)} is a set of \(N\) functions, and \({\beta }_{0}, {\beta }_{1}, \dots , {\beta }_{N}\) are parameters for curve fitting.

Polynomials (in the form of \({B}_{k}\left(x\right)={x}^{k}\)) are commonly used to construct a set of functions for curve fitting. However, instead of polynomials, we used B-spline functions [14] in this study. B-spline functions have high flexibility in that they allow the piecewise modeling of the spinal curve. However, this flexibility means that we might use too many B-spline functions for curve fitting, resulting in an unrealistic oscillating spinal curve. In this study, the density of knots (joints of piecewise functions) was configured to be proportional to the density of vertebral landmarks, and the adjusted \({R}^{2}\) was used to select the optimal number of B-spline functions. The optimal number of spline functions was defined as the point at which the adjusted \({R}^{2}\) did not improve (or the adjusted \({R}^{2}>0.9\)) as the number of spline functions increased.

Determination of APs, IPs, and curvature angles

The mathematical formulas for APs and IPs can be determined according to prior illustrations of APs and IPs [12]. Because an apex or inflection point lies on the place where the slope or curvature of the spine is zero, we defined APs and IPs as the roots (locations of zeros) of the first- and second-order derivatives of the spinal curve (as depicted in Fig. 3), respectively. In this work, the derivatives were obtained from the B-spline-represented spinal curve, and the roots were identified iteratively by using the bisection method [15]. After the IPs were determined, the curvature angles between the normal lines of any two adjacent IPs could be measured (Fig. 4a).

Statistical analysis

The landmark localization error was used to evaluate the performance of the trained landmark localizer. Because of the nonnormal distribution characteristics of the localization errors, we illustrated the localization errors of the 25 landmarks using boxenplots (also known as letter-value plots [16]). We used boxenplots to illustrate more detailed information on the tails of error distributions.

Interrater reliability was used to determine the level of agreement between the following three raters:

  • Rater 1 (R1): a senior orthopedic surgeon

  • Rater 2 (R2): a radiologist

  • The proposed DL model (landmark localizer + numerical algorithm)

In this study, the ICC was used to assess inter-rater reliability. We aimed to investigate the extent to which the three raters agreed on certain characteristics of the spinal curve (e.g., the locations of IPs and APs). The ICC estimates and their 95% confidence intervals were calculated using a two-way-random model with absolute agreement. In addition, the ICC scores were evaluated as described by Cicchetti [17].

In addition, the differences in measurements between the proposed DL model and the human experts were evaluated. The measurements of two human experts (R1 and R2) were averaged and compared with the measurements of the DL model using the Wilcoxon signed-rank test. Differences were considered significant if the p-value was less than 0.05.

In this work, all statistical tests and procedures were conducted using SPSS version 25.0 (SPSS Inc, Chicago, IL, USA).

Results

Testing dataset demographic

The testing dataset contained images from 209 females and 91 male patients with a mean age of 39.5 ± 25.7 years (range: 11–90). Spinal implants were observed in 92 (31%) images, with the instrumentation level ranging from T2 to the ilium (average length: 7.8 ± 3.9 levels).

Performance of the landmark localizer

The localization errors of 25 landmarks are visualized using boxenplots in Fig. 5. The landmark localizer performed the best for the cervical landmarks (median error: 1.7–2.0 mm), followed by the lumbosacral landmarks (median error: 1.9–2.8 mm). The thoracic landmarks (median error: 2.7–4.1 mm) had larger localization errors than the cervical and lumbosacral landmarks.

Fig. 5
figure 5

Localization error of 25 vertebral coordinates. The error is represented using quantile boxes. The values of median error are represented by the numbers in the boxes

Full size image

Manual measurement versus DL model predictions

The interrater reliability of spinal curvature characteristics between the two human experts and the proposed DL model is presented in Table 1. The reliability between the senior orthopedic surgeon and the radiologist was excellent in all spinal curvature characteristics (all ICCs > 0.9). Compared with the measurements by human experts, the proposed DL model demonstrated inferior reliability in predicting the cervicothoracic IP, thoracic AP, and thoracic kyphosis but similar reliability in predicting the thoracolumbar IP, cervical and lumbar APs, and lumbar lordosis. Overall, the reliability between the proposed DL model and any of the two experts was good to excellent (all ICCs > 0.85).

Table 1 Interrater reliability between human experts and the deep learning model
Full size table

As shown in Table 2, no significant differences were observed between the measurements of spinal curvature characteristics by the proposed DL model and human experts (all p > 0.05).

Table 2 Spinal curvature characteristic measurements compared between the deep learning model and human experts
Full size table

Predicted spinal curvature characteristics

The predicted spinal curvature characteristics of the testing dataset are presented in Table 3. Of the 300 images, the mean cervicothoracic IP was located at C7/T1, and the mean thoracolumbar IP was located at T12. The mean APs were located at C4/C5 for the cervical spine, T7 for the thoracic spine, and L3/L4 for the lumbar spine. In addition, the predicted thoracic kyphosis and lumbar lordosis were 50.9° ± 15.3° and 47.4° ± 18.6°, respectively.

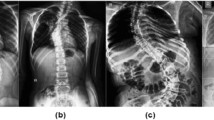
Table 3 Predicted spinal curvature characteristics of the testing dataset
Full size table

Figures 6, 7, and 8 demonstrate three cases of DL model predictions of the postoperative changes in spinal curvature characteristics.

Fig. 6
figure 6

a A 70-year-old female patient with an osteoporotic compression fracture at L2 and L3. b The patient underwent percutaneous vertebroplasty of L2 and L3. The cervicothoracic inflection point, thoracic apex, and lumbar apex shifted as the sagittal balance improved from + 9.7 cm to + 1.7 cm

Full size image
Fig. 7
figure 7

a A 60-year-old male patient with spondylolisthesis with spinal stenosis. b The patient underwent posterior instrumentation and interbody fusion from L2 to S1. The thoracolumbar inflection point, thoracic apex, and lumbar apex shifted as the lumbar lordosis improved from 30.9° to 41.4°

Full size image
Fig. 8
figure 8

a A 70-year-old female patient with an L1 compression fracture nonunion with thoracolumbar kyphosis. b The patient underwent posterior instrumentation and L1 cement augmentation to correct the kyphosis. The thoracic apex, cervicothoracic inflection point, and thoracolumbar inflection point shifted after redistribution of the thoracic kyphosis and the lumbar lordosis

Full size image

Discussion

Several previous studies have characterized lateral spine plain radiographs automatically by using DL techniques. For example, Weng et al. [6] developed a DL model based on ResUNet for automatic SVA measurement, which achieved excellent reliability compared with human experts. The automatic measurement of spinopelvic parameters in whole-spine lateral X-rays was expanded to various parameters, such as PI, sacral slope (SS), and PT, with acceptable error and strong correlations with ground truth values [5, 7]. Yeh et al. [13] reported that the automatic predictions of spinopelvic parameters using a two-stage DL model could match the reliability of human experts in complex spinal diseases.

One of the major advantages of DL applications in medical images is achieving fast, objective, and consistent interpretations. Even with the help of the PACS and other dedicated commercial software such as Surgimap (Nemaris, MA, USA), the manual labeling of IPs and APs still requires a substantial professional workforce and extensive time. Few studies have reported automatic curvature feature analysis in different spine imaging modalities [18, 19]. With annotated vertebral centers, spline-based curve angle measurement achieved higher intrarater and interrater reliability than the traditional manual Cobb angle measurement for anteroposterior spinal X-ray images did [20]. However, these studies have primarily focused on the frontal plane curvature analysis rather than the sagittal plane.

The locations of IPs and APs in the spinal sagittal curvatures have been widely investigated in healthy and diseased individuals [2, 21,22,23]. From a biomechanical standpoint, the IP locations represent reciprocal changes between different sagittal curves, and the AP locations affect lumbar lordotic distributions [24,25,26]. Therefore, proper AP and IP relocation and ideal sagittal profile restoration remain crucial in spinal surgeries. Previous computerized algorithms required manually identified vertebral borders to simulate spinal curvatures [9,10,11,12]. Semi-automatic methods of Cobb angle measurement improved the inter- and intra-rater reliabilities as compared to traditional manual measurement [27, 28]. In the present study, the proposed DL model localized the vertebral centers accurately through the landmark localizer (Fig. 2) and estimated the characteristics of the spinal curve (such as the IPs, APs, and curvature angles) by using the developed numerical algorithm. The numerical algorithm identified the IPs and APs by using a proposed mathematical formula that used the roots of the first- and second-order derivatives of the spinal curve to represent the IPs and APs, respectively (Fig. 3). The accuracy of the landmark localizer was within an acceptable range (median error: 1.7–4.1 mm), and the interrater reliability was good to excellent (all ICCs > 0.85) between the proposed DL model and human experts when measuring the characteristics of spinal curves.

The contribution of this study is twofold. First, we showed that APs and IPs could be determined by the proposed numerical algorithm. Second, by using techniques based on deep learning and numerical methods, we demonstrated that the whole estimation process of APs and IPs could be automatic, accurate, and without human bias. It was shown that the CPN model can be used in the process of spine parameter estimation and can achieve good to excellent consistency as compared with human experts [13]. However, in this study, we observed that high localization errors (> 40 mm) are still possible in some rare cases, as shown in the boxenplot in Fig. 5. The potential causes of the observed error outliers are skip-level and duplicate landmark recognition in the adjacent level. However, the performance improvement in DL-based landmark localizers is beyond the scope of this study. We believe the DL-based landmark localizer could be improved by increasing the size and diversity of the training data or by finetuning the DL model architecture. Although the proposed DL model may save tremendous works of manual labeling, a human review process can be added in the real clinical setting. After adjustment of the deviated vertebral centers, the spinal curve, APs, and IPs can still be predicted accurately by the proposed numerical algorithm.

The present study has several limitations. First, it lacked an external validation dataset. The current dataset contained images from only one medical center. Different image quality and radiographic examination protocols may hinder the performance of the DL model when its application is expanded to a multicenter database. Second, images with anomalous vertebral numbering (greater or fewer than 25 vertebrae) were excluded from the dataset. Therefore, the proposed DL model may not produce accurate predictions for individuals with conditions that lead to anomalous vertebral numbering, such as lumbosacral transitional vertebrae or other congenital vertebral anomalies. Third, the predictions were only based on lateral X-rays. A biplanar scanner, such as an EOS imaging system with possible three-dimensional reconstruction, could be an ideal radiographic modality for assessing patients with spinal deformities. Fourth, the whole spine lateral radiographs were taken due to different spinal conditions, including fractures, deformities, spinal implants, and cement assessment. The performances and accuracy of the DL model may vary in different spinal conditions. Despite these limitations, the proposed DL model was able to characterize and interpret the sagittal spinal curve automatically and consistently. Future applications of the proposed DL model will focus on aiding postoperative follow-up radiographic evaluations, large-scale spinal curvature analysis of a preexisting database, and incorporating advanced imaging modalities, such as biplanar EOS imaging, with DL techniques.

Conclusions

A DL model for automatic spinal curve analysis of whole-spine lateral plain radiographs is developed. The estimated locations of IPs, APs, and curvature angles demonstrated good to excellent reliability compared with human experts (all ICCs > 0.85). Future applications for surgical planning, database analysis, postoperative follow-up, and population-based screening should be explored to validate the system and improve its clinical efficiency.