Abstract
Purpose
Prognostic models play an important clinical role in the clinical management of neck pain disorders. No study has compared the performance of modern machine learning (ML) techniques, against more traditional regression techniques, when developing prognostic models in individuals with neck pain.
Methods
A total of 3001 participants suffering from neck pain were included into a clinical registry database. Three dichotomous outcomes of a clinically meaningful improvement in neck pain, arm pain, and disability at 3 months follow-up were used. There were 26 predictors included, five numeric and 21 categorical. Seven modelling techniques were used (logistic regression, least absolute shrinkage and selection operator [LASSO], gradient boosting [Xgboost], K nearest neighbours [KNN], support vector machine [SVM], random forest [RF], and artificial neural networks [ANN]). The primary measure of model performance was the area under the receiver operator curve (AUC) of the validation set.
Results
The ML algorithm with the greatest AUC for predicting arm pain (AUC = 0.765), neck pain (AUC = 0.726), and disability (AUC = 0.703) was Xgboost. The improvement in classification AUC from stepwise logistic regression to the best performing machine learning algorithms was 0.081, 0.103, and 0.077 for predicting arm pain, neck pain, and disability, respectively.
Conclusion
The improvement in prediction performance between ML and logistic regression methods in the present study, could be due to the potential greater nonlinearity between baseline predictors and clinical outcome. The benefit of machine learning in prognostic modelling may be dependent on factors like sample size, variable type, and disease investigated.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Neck pain (NP) is a highly prevalent condition that results in considerable pain and suffering. Between 1990 and 2017, it has been estimated that the point prevalence of NP per 100 000 population was estimated to be 3551.1, and the years lived with disability from NP per 100 000 population were 352.0 [1]. The economic burden of NP is also considerable. For example in the Netherlands, the total health care cost in 1996 for NP was estimated at €485million [2]. Considering the rising costs of health care, it is plausible that these estimates would be higher today.
The natural history of NP is typically favourable, although up to 50–85% will report pain 1–5 years from onset [3]. For those who go on to have persistent pain, the condition often becomes challenging to treat and costly [4]. Prognostic modelling research [5] has the capacity to optimize clinical decision-making, manage patient expectations, and prioritize clinical efforts to individuals most at risk of poor recovery. Therefore, the development of clinical prognostic models has been recommended as a key research priority [6].
Most prognostic modelling research in NP have used either logistic or linear regression as statistical methods for predicting key clinical outcomes, depending on whether the outcomes are binary or continuous [7,8,9]. The advantages of these traditional statistical methods are that the ensuing clinical models are interpretable and that many free and commercial software is available to conduct such analyses. However, methods such as logistic and linear regression are at a disadvantage when the relationships between the outcome (or logit of outcome) and predictors are nonlinear, and when the number of candidate predictors is high relative to the sample size. Increasingly, however, machine learning (ML) is being employed for prognostic modelling [10, 11]. One of the biggest distinguishing factors between traditional statistics and ML is that the former emphasizes inference (i.e. infer the process of data generation), whereas ML emphasizes prediction. The advantage of ML is that there is a suite of algorithms ranging from those that can model highly nonlinear relationships, with the ensuing model being complex and essentially a “black-box” (e.g. support vector machine [SVM]), to those that simultaneously perform variable selection and produce clinically interpretable solutions (e.g. least absolute shrinkage and selection operator [LASSO]).
ML has been touted to offer superior predictive accuracy compared to traditional statistical methods. However, to date, there are no studies in NP to provide evidence of which modelling approach should be used for prognostic modelling. The primary aim of the present study is to compare the predictive performance of prognostic models developed using traditional logistic regression, and seven ML models. The primary hypothesis was that traditional stepwise logistic regression would result in the lowest performance (i.e. smallest area under the Receiver Operating Characteristic [ROC] curve), compared to ML.
Methods
Design
This was a prospective, observational study where participants were assessed at baseline upon recruitment and 3 months follow-up.
Setting
Forty-seven health care centres were selected by the Spanish Back Pain Research Network to be invited to participate in this study, based on their past involvement in research on neck and low back pain. The centres were located across 11 out of the 17 Administrative regions in the country (Andalucía, Aragón, Asturias, Baleares, Castilla-León, Cataluña, Extremadura, Galicia, Madrid, Murcia, Vascongadas). Fifteen centres belonged to the Spanish National Health Service (SNHS), six to not-for-profit institutions working for the SNHS, and 26 were private. They included eight primary care centres, 18 physical therapy practices, and 21 specialty Services (five in rheumatology, six in rehabilitation, four in neuroreflexotherapy (NRT), and six in orthopaedic surgery). Since this study did not require any changes to standard clinical practice, according to the Spanish law it was not subject to approval by an Institutional Review Board. All procedures followed were in accordance with the ethical standards of the Helsinki Declaration of 1975, as revised in 1983.
Participants
Participant recruitment spanned the period of March 2014 to February 2017. Participants were included in the study if they suffered from NP, with or without arm pain, that was unrelated to trauma or systemic disease were seeking care for NP in a participating unit, and were proficient in Spanish. Participants were excluded if they had any central nervous system disorders (treated or untreated), other causes of referred or radicular arm pain (e.g. peripheral nerve damage) and not having signed the informed consent.
Sample size
In order to analyse the association of up to 40 variables, the sample had to include at least 400 subjects who would not experience improvement [12], following the 1:10 (1 variable per 10 events) rule of thumb. Approximately 80–85% of patients with spinal pain, experience a clinically relevant improvement in pain, referred pain and disability, at 3 months, while losses to follow-up at that period range between 5 and 10% [13, 14]. Therefore, the sample size was established at 2934 subjects. There were no concerns about the sample size being too large, due to the observational nature of the study.
Predictor and outcome variables
The 3 months follow-up period was undertaken, because (a) This study sought to analyse the outcome of a single episode of neck pain rather than relapses, (b) This timeframe implies that all patients who are symptomatic at follow-up, would be chronic; and (c) Existing studies have shown that losses to follow-up remain minimal for periods of up to 3 months [13], rise at 6 months [15], and become increasingly significant thereafter [16].
The registry gathered data from patients and clinicians. Data requested from participants at the first assessment, were: sex, age, duration of the current pain episode (days), the time elapsed since the first episode (years), and employment status (Table 1). On both assessments, patients were asked to report the intensity of their neck and arm pain, and neck-related disability. To this end, they completed two separate 10 cm visual analogue scales (VAS) for NP and arm pain (AP) (0 = no pain and 10 = worst imaginable pain), and a validated Spanish version of the Neck Disability Index (NDI-, 0 = no disability and 100 = worst possible disability) [17] (Table 1). Data requested from recruiting clinicians were: diagnostic procedures prescribed for the current episode, patients’ radiological findings on imaging procedures performed for the current or previous episodes, as reported by radiologists, clinical diagnosis, and treatments undergone by the patient throughout the study, and NRT intervention (Table 1).
Three outcomes were analysed in this study, NP intensity, AP intensity, and NDI, all at the 3rd month follow-up. Reductions in VAS or NDI scores between the baseline and follow-up assessments were considered to reflect improvement only if they were greater than the minimal clinically important change (MCIC). The MCIC for pain and disability has been established as 30% of their baseline scores, with a minimum value of 1.5 for VAS and 7 NDI points for neck pain-related disability [17]. Details of the predictors and outcomes used can be found in the supplementary material.
Pre-processing and missing data handling
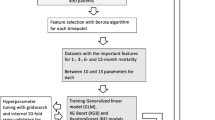
There were 26 predictors included in the study, five numeric and 21 categorical. Exploratory data analysis using the VIM package [18] was used to generate matrices and plots of missing data, to identify patterns of missing-ness. From the complete data (n = 3001), we split the data into a training set (80%, n = 2402) for model development, and testing set (20%, n = 599) for external validation of prediction performance.
Multiple Imputation by Chained Equations method [19] was performed given that we did not detect systematic patterns of missing data. Imputation of the complete data (n = 3001) will result in information from the testing set to be leaked into the training set, resulting in potentially an over-optimistic model. Multiple imputations on the training set were performed on all predictor and outcome variables with missing values, with the ensuing imputation model used to impute the missing data in the testing set.
A total of 21 models were created using seven algorithms and three outcomes. The following common processing steps were undertaken for all models. First, all continuous predictors were scaled (demeaned and divided by its standard deviation [SD]). Second, all categorical variables were transformed into integers using one-hot encoding.
ML algorithms
The codes used for the present study are included in the lead author’s public repository (https://bernard-liew.github.io/spanish_data/index.html). A simplified graphical illustration of the algorithms can be found in the supplementary material.
-
1.
Stepwise logistic regression
The simplest algorithm is the stepwise logistic regression model. Starting from a model with all predictors included, a stepwise selection procedure was used to remove variables based on the Akaike information criterion (AIC). As some removed variables might improve the model once other predictors are removed, the procedure also allows to add back already removed variables. The procedure proceeds in a greedy fashion and stops if neither adding nor removing variables yields to an improvement in the AIC.
-
2.
LASSO regression
The LASSO regression constitutes a penalized linear model that aims to create the best performing parsimonious model [20, 21]. It does so by adding a penalty equal to the absolute value of the magnitude of coefficients. Larger penalties result in coefficient values closer to zero, and some coefficients can become zero and be removed from the model.
-
3.
K nearest neighbours (KNN)
KNN [22] is a distance-based method, whereby the class of the outcome is taken to be the class of the Kth closest training data, based on a predefined distance metric and value K.
-
4.
Gradient boosting machines (GBM)
GBM [23] and one of its variants gradient tree boosting (GTB) is an ensemble procedure that iteratively fits very simple statistical models to the data. GTB uses classification trees as simple statistical models to model the data. Iteratively, GTB evaluates how well the current model performs, and adds another tree to the errors made previously, and updates the model by adding the regression tree to the ensemble. We use Xgboost [24], one of the most popular implementations of GTB which allows for fast computation.
-
5.
SVM
The SVM is an algorithm based on the idea of finding an optimal separating hyperplane between multiple classes. The optimal hyperplane is typically found by (1) Finding the optimal curvature of the hyperplane, and (2) Maximizing the separating distance between the nearest data points from each class [25].
-
6.
Random forest (RF)
Similar to GBT, a Random Forest (RF) [26] is an ensemble technique that combines several classification trees to form a prediction by a majority vote of the single tree. Each constituent tree is fitted onto a random subsample of the data set, using a random sub-selection of the available predictors.
-
7.
Artificial neural networks (ANN)
Inspired by neurons of the human brain [27], ANN is a nonlinear aggregate extension of simpler regression methods. The network transforms all the input information from the predictors, in both a linear nonlinear fashion and passes the result to the next layer. This is repeated until an output layer is reached which forms the prediction of the network [28].
Model tuning and validation
All ML algorithms, apart from stepwise logistic regression, have one or more parameters whose value was used to control the learning process to optimize the predictive accuracy of the model. The hyperparameters that were tuned for each model can be found in Table 2. Hyperparameter tuning was combined with model validation using a nested cross-validation (CV) approach. For model validation, we split the data into 80% for model training and 20% for testing, whilst for hyperparameter tuning, we used a threefold CV. As a tuning strategy to choose the optimal hyperparameter values to optimize the area under the receiver operator curve (AUC), we used a random search with a budget of 2000 trials per algorithm. This means a random selection of 2000 hyperparameter combinations was taken and the performance evaluated using the threefold CV.
The primary measure of model performance was the AUC of the validation set. AUC ranges from 0 to 1, with a value of 1 being when the model can perfectly distinguish between all the improvements and no improvements correctly, 0.5 when the model cannot distinguish the classes, and 0 being when the model is perfectly incorrect in its discrimination. The secondary measures of performance were classification accuracy, precision, sensitivity, specificity, and the F1 score. Accuracy reflects the ratio between the number of correct predictions made by the model to the total number of predictions made—this ranges from 0 (no correct prediction) to 1 (perfect prediction). Precision reflects the ratio of participants predicted to improve relative to those predicted to have improved. Sensitivity reflects the proportion of participants who were predicted to improve relative to those that have improved. Specificity reflects the proportion of participants who were predicted to not have improved relative to those that did not improve. F1 is the weighted harmonic mean of precision and recall, reaching its optimal value at 1 and its worst value at 0.
Results
The descriptive characteristics of participants can be found in Table 3. The optimal hyperparameters for each ML algorithm, for each outcome, can be found in Table 2.
The ML algorithm with the greatest AUC for predicting arm pain (AUC = 0.765), neck pain (AUC = 0.726), and disability (AUC = 0.703) was Xgboost (Fig. 1). Stepwise logistic regression resulted in the lowest AUC for predicting arm pain (AUC 0.684), neck pain (AUC = 0.623), whilst KNN was the poorest performing model for disability (AUC = 0.583) (Fig. 1). The improvement in classification AUC from stepwise logistic regression to the best performing ML algorithms was 0.081, 0.103, and 0.077 for predicting arm pain, neck pain, and disability, respectively.
Performance metrics of seven machine learning algorithms in the prediction of the outcomes of arm pain, neck pain, and disability. Abbreviations. AUC: area under the receiver operating characteristic curve; ACC: accuracy; Precs: precision; F1: F1 score; Sens: sensitivity; Specs: specificity; Knn: K nearest neighbour; Lasso: least absolute shrinkage and selection operator; Xgb: extreme gradient boosting; RF: random forest; Svm: support vector machine; ANN: artificial neural networks
For accuracy, stepwise logistic regression was the best performing algorithm for predicting arm pain (ACC = 0.737), RF for predicting neck pain (ACC = 0.777), and Xgboost for predicting disability (ACC = 0.657) (Fig. 1). Stepwise regression was the most sensitive algorithm for predicting arm pain (Sens = 0.489), Lasso and KNN were equally sensitive for predicting neck pain (Sens = 0.345), and Xgboost and ANN were equally sensitive for predicting disability (Sens = 0.609) (Fig. 1). RF was the most specific algorithm for predicting neck pain (Spec = 0.958) and disability (Spec = 0.729), whilst SVM was the most specific for predicting arm pain (Spec = 0.955) (Fig. 1).
Discussion
ML is increasingly being employed for prognostic modelling in pain research [10, 11], and also in other healthcare fields [29]. We hypothesized that ML would be superior to traditional stepwise logistic regression in predicting recovery status for individuals with neck pain. Our hypothesis was partially supported in that stepwise logistic regression was the poorest performing algorithm for predicting arm pain and neck pain, but KNN was the poorest performing algorithm for disability. Differences in the AUC between stepwise logistic regression and the best performing algorithms were between 0.07 and 0.10.
Our findings contrast with another study that similarly compared different ML algorithms and logistic regression for predicting mortality and unfavourable outcomes in individuals with traumatic brain injury [29]. A previous study reported that the difference in predictive performance (AUC) between the best performing ML algorithm and logistic regression was 0.01 [29]. In addition, a systematic review reported that logistic regression performed similarly to most ML algorithms for prognosis in a heterogeneous set of clinical conditions [30]. Gravesteijn et al. [29] pooled data from 15 studies including a total of 11 022 participants, whilst the systematic review included studies with a median sample size of 1250 (range 72 to > 3 million) [30]. To our knowledge, no studies to date have performed any subgroup analyses to understand if the performance differences between methods could be attributed to variations in sample size.
An often-cited advantage of ML over logistic regression is that it can model complex, nonlinear relationships between the predictors and outcome [29]. The complexity between the predictors and outcome in previous studies [29, 30] may be too low for ML to have a meaningful benefit over logistic regression. A previous study in cervical radiculopathy found nonlinear relationships between baseline self-reported predictors and 12 months clinical outcomes of neck and arm pain and disability [31]. The nonlinear relationship between baseline and outcomes may not be surprising given that previous studies reported different nonlinear rates of recovery in disability with different baseline neck disability scores in individuals with whiplash-associated disorders (WAD) [32]. The potential greater nonlinearity between baseline predictors and clinical outcome in the present study could contribute to the better performance of ML compared to stepwise logistic regression.
ML may further benefit prognostic models when functional predictors are included. The most common predictors used in prognostic modelling in neck pain are self-reported pain and psychological variables [7,8,9]. These variables are discrete, meaning that each observation takes on a single value. Functional variables are typically temporal and/or spatial variables, where each observation for each variable can take on multiple values [33]. The most common example of functional variables would be kinematic and muscle activation data, which are temporal variables [34, 35]. Less common functional variables are cortical activation patterns and radiological images [36, 37]. Given that functional variables lie on a higher-dimensional space, we anticipate that their relationship with clinical outcomes would be more complex, less linear, as compared to discrete variables.
The lack of consideration of functional variables, such as kinematic data is surprising given that neck pain primarily affects movement [38], clinicians always assess movement, and neck pain severity scales with movement impairments [38]. In a cross-sectional study, seven electromyography functional predictors achieved an AUC of 0.90 when classifying individuals with and without low back pain [35]. Whilst the study was limited by a cross-sectional design [35], the result was much better than other cross-sectional low back pain studies which used only self-reported variables and achieved an AUC of 0.71 [39, 40]. Predictors in current prognostic models of neck pain have only included discrete variables, but not functional variables, and this we believe occurs due to several reasons. First, self-reported and psychological data are logistically easiest to collect. However, the growing availability and reduced cost of technologies, such as that of wearable sensors, make objective functional data collection increasingly feasible. Second, traditionally taught statistics like logistic/linear regression can only incorporate discrete variables, and unfamiliarity of alternative ML methods may preclude the latter’s use. Third, more complex ML methods that can model functional variables are typically not available on popular commercial statistical software (e.g. Statistical Package for the Social Sciences [SPSS]), again precluding its more widespread use.
A limitation in the present study was that our models were not calibrated. Calibration refers to the agreement between the distribution of the observed outcomes and predictions, with a well calibrated model resulting in high agreement. Most ML algorithms, unlike logistic regression, are not designed to optimize the agreement between the two distributions. Rather, most ML algorithms necessarily manipulate the agreement, to maximize both the accuracy and consistency of predictions. However, because our primary performance measure was the AUC (a measure of discrimination that is not affected by miscalibration), and that our ML models were optimized for the AUC, the lack of calibration will not influence our primary findings. The same cannot be said for our secondary performance measures, which relies on a well calibrated model. Hence, interpretation of our secondary performance measures should be done with caution. Another limitation was that we did not statistically compare the predictive performance between algorithms. Comparing the performance of different algorithms is challenging, because unless a very large dataset is involved, typical validation procedures (e.g. bootstrapping, k-fold validation) will create correlated subsamples, thereby violating the independence assumption in many statistical inference tests. Although there are statistical tests for comparing different algorithms based on a single test dataset [41], these tests rely on a well-calibrated model to produce realistic class probability values. Hence, we adopted a qualitative comparison in the present study, but this should be verified in a separate validation study. Lastly, the relative importance of each predictor and its relationship with the outcome was not reported. Understanding the predictor-outcome relationships is a focus of prognostic factor research [5], where this study focused on prognostic modelling research. Indeed, a disadvantage of many ML algorithms is that it does not intrinsically calculate the predictor-outcome relationships. However, there is a growing number of “post-hoc” statistical methods that can quantify the relative importance and relationship between each predictor and outcome [42]. Whether an improvement in the AUC between 0.07 and 0.10 is considered a clinically important improvement in model performance is unknown as such thresholds have not been reported in the literature.
Conclusion
Differences in the AUC between stepwise logistic regression and the best performing algorithms were between 0.07 and 0.10. The improvement in prediction performance between ML and logistic regression methods in the present study, and not in prior studies, could be due to the potential greater nonlinearity between baseline predictors and clinical outcome in the former. Given the increasing availability of technologies within the clinics to monitor objective functional variables, ML may play a more prominent role in prognostic modelling. However, we still advocate for caution in the optimism of applying ML in prognostic modelling, and its benefit is likely dependent on factors like sample size, variable type, disease investigated, to name a few.
References
Safiri S, Kolahi A-A, Hoy D, Buchbinder R, Mansournia MA, Bettampadi D et al (2020) Global, regional, and national burden of neck pain in the general population, 1990–2017: systematic analysis of the global burden of disease study 2017. BMJ 368:m791. https://doi.org/10.1136/bmj.m791
Borghouts JAJ, Koes BW, Vondeling H, Bouter LM (1999) Cost-of-illness of neck pain in The Netherlands in 1996. Pain 80:629–636. https://doi.org/10.1016/s0304-3959(98)00268-1
Carroll LJ, Hogg-Johnson S, van der Velde G, Haldeman S, Holm LW, Carragee EJ et al (2008) Course and prognostic factors for neck pain in the general population: results of the bone and joint decade 2000–2010 task force on neck pain and its associated disorders. Spine (Phila Pa 1976) 33:S75-82. https://doi.org/10.1097/BRS.0b013e31816445be
Haldeman S, Carroll LJ, Cassidy JD (2008) The empowerment of people with neck pain: introduction: the bone and joint decade 2000–2010 task force on neck pain and its associated disorders. Spine (Phila Pa 1976) 33:S8–S13. https://doi.org/10.1097/BRS.0b013e3181643f51
Hemingway H, Croft P, Perel P, Hayden JA, Abrams K, Timmis A et al (2013) Prognosis research strategy (PROGRESS) 1: a framework for researching clinical outcomes. BMJ 346:e5595. https://doi.org/10.1136/bmj.e5595
Kelly J, Ritchie C, Sterling M (2017) Clinical prediction rules for prognosis and treatment prescription in neck pain: a systematic review. Musculoskelet Sci Pract 27:155–164. https://doi.org/10.1016/j.math.2016.10.066
Dagfinrud H, Storheim K, Magnussen L, Ødegaard T, Hoftaniska I, Larsen L et al (2013) The predictive validity of the Örebro musculoskeletal pain questionnaire and the clinicians’ prognostic assessment following manual therapy treatment of patients with LBP and neck pain. Man Ther 18:124–129
Schellingerhout JM, Heymans MW, Verhagen AP, Lewis M, de Vet HC, Koes BW (2010) Prognosis of patients with nonspecific neck pain: development and external validation of a prediction rule for persistence of complaints. Spine (Phila Pa 1976) 35:E827–E835
Kovacs FM, Seco-Calvo J, Fernández-Félix BM, Zamora J, Royuela A, Muriel A (2019) Predicting the evolution of neck pain episodes in routine clinical practice. BMC Musculoskelet Disord 20:620. https://doi.org/10.1186/s12891-019-2962-9
Lötsch J, Ultsch A (2018) Machine learning in pain research. Pain 159:623–630. https://doi.org/10.1097/j.pain.0000000000001118
Tagliaferri SD, Angelova M, Zhao X, Owen PJ, Miller CT, Wilkin T et al (2020) Artificial intelligence to improve back pain outcomes and lessons learnt from clinical classification approaches: three systematic reviews. npj Digit Med 3:93. https://doi.org/10.1038/s41746-020-0303-x
Harrell F (2001) Regression modeling strategies with applications to linear models, logistics regression, and survival analysis. Springer
Kovacs FM, Seco J, Royuela A, Melis S, Sánchez C, Díaz-Arribas MJ et al (2015) Patients with neck pain are less likely to improve if they experience poor sleep quality: a prospective study in routine practice. Clin J Pain 31:713–721. https://doi.org/10.1097/ajp.0000000000000147
Royuela A, Kovacs FM, Campillo C, Casamitjana M, Muriel A, Abraira V (2014) Predicting outcomes of neuroreflexotherapy in patients with subacute or chronic neck or low back pain. Spine J 14:1588–1600. https://doi.org/10.1016/j.spinee.2013.09.039
Kovacs FM, Muriel A, Abriaira V, Medina JM, Castillo Sanchez MD, Olabe J (2005) The influence of fear avoidance beliefs on disability and quality of life is sparse in Spanish low back pain patients. Spine (Phila Pa 1976) 30:E676-682. https://doi.org/10.1097/01.brs.0000186468.29359.e4
Kovacs FM, Llobera J, Abraira V, Lázaro P, Pozo F, Kleinbaum D (2002) Effectiveness and cost-effectiveness analysis of neuroreflexotherapy for subacute and chronic low back pain in routine general practice: a cluster randomized, controlled trial. Spine (Phila Pa 1976) 27:1149–1159. https://doi.org/10.1097/00007632-200206010-00004
Kovacs FM, Bagó J, Royuela A, Seco J, Giménez S, Muriel A et al (2008) Psychometric characteristics of the Spanish version of instruments to measure neck pain disability. BMC Musculoskelet Disord 9:42. https://doi.org/10.1186/1471-2474-9-42
Kowarik A, Templ M (2016) Imputation with the R package VIM. J Stat Softw 74:1–16
van Buuren S, Groothuis-Oudshoorn K (2011) Mice: multivariate imputation by chained equations in R. J Stat Softw 45:1–67
Tibshirani R (1996) Regression shrinkage and selection via the lasso. J R Stat Soc Ser B Stat Methodol 58:267–288
Moons KGM, Altman DG, Reitsma JB, Ioannidis JPA, Macaskill P, Steyerberg EW et al (2015) Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD): explanation and elaboration. Ann Intern Med 162:W1–W73. https://doi.org/10.7326/m14-0698
Altman NS (1992) An introduction to kernel and nearest-neighbor nonparametric regression. Am Stat 46:175–185. https://doi.org/10.1080/00031305.1992.10475879
Friedman JH (2001) Greedy function approximation: a gradient boosting machine. Ann Stat 29:1189–1232
Chen T, Guestrin C (2016) XGBoost: a scalable tree boosting system. In: Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining. Association for computing machinery, San Francisco, pp 785–794
Smola AJ, Schölkopf B (2004) A tutorial on support vector regression. Stat Comput 14:199–222. https://doi.org/10.1023/B:STCO.0000035301.49549.88
Breiman L (2001) Random forests. Mach Learn 45:5–32. https://doi.org/10.1023/a:1010933404324
Rosenblatt F (1958) The perceptron: a probabilistic model for information storage and organization in the brain. Psychol Rev 65:386–408. https://doi.org/10.1037/h0042519
Goodfellow I, Bengio Y, Courville A (2016) Deep learning. The MIT Press
Gravesteijn BY, Nieboer D, Ercole A, Lingsma HF, Nelson D, van Calster B et al (2020) Machine learning algorithms performed no better than regression models for prognostication in traumatic brain injury. J Clin Epidemiol 122:95–107. https://doi.org/10.1016/j.jclinepi.2020.03.005
Christodoulou E, Ma J, Collins GS, Steyerberg EW, Verbakel JY, Van Calster B (2019) A systematic review shows no performance benefit of machine learning over logistic regression for clinical prediction models. J Clin Epidemiol 110:12–22. https://doi.org/10.1016/j.jclinepi.2019.02.004
Liew BXW, Peolsson A, Rugamer D, Wibault J, Löfgren H, Dedering A et al (2020) Clinical predictive modelling of post-surgical recovery in individuals with cervical radiculopathy: a machine learning approach. Sci Rep 10:16782. https://doi.org/10.1038/s41598-020-73740-7
Sterling M, Hendrikz J, Kenardy J (2010) Compensation claim lodgement and health outcome developmental trajectories following whiplash injury: a prospective study. Pain 150:22–28. https://doi.org/10.1016/j.pain.2010.02.013
Brockhaus S, Rügamer D, Greven S (2020) Boosting functional regression models with FDboost. J Stat Softw 94(10):1–50. https://doi.org/10.18637/jss.v094.i10
Liew BXW, Rugamer D, Stocker A, De Nunzio AM (2020) Classifying neck pain status using scalar and functional biomechanical variables-development of a method using functional data boosting. Gait Posture 76:146–150. https://doi.org/10.1016/j.gaitpost.2019.12.008
Liew X, Rugamer D, De Nunzio A, Falla D (2020) Interpretable machine learning models for classifying low back pain status using functional physiological variables. Eur Spine J 29:1845–1859
Lamichhane B, Jayasekera D, Jakes R, Glasser MF, Zhang J, Yang C et al (2021) Multi-modal biomarkers of low back pain: a machine learning approach. NeuroImage Clin 29:102530. https://doi.org/10.1016/j.nicl.2020.102530
Hill L, Aboud D, Elliott J, Magnussen J, Sterling M, Steffens D et al (2018) Do findings identified on magnetic resonance imaging predict future neck pain. A systematic review. Spine J 18:880–891. https://doi.org/10.1016/j.spinee.2018.01.025
Sarig Bahat H, Weiss PL, Sprecher E, Krasovsky A, Laufer Y (2014) Do neck kinematics correlate with pain intensity, neck disability or with fear of motion? Man Ther 19:252–258. https://doi.org/10.1016/j.math.2013.10.006
Owari Y, Miyatake N (2019) Prediction of chronic lower back pain using the hierarchical neural network: comparison with logistic regression-a pilot study. Medicina (Kaunas) 55:295. https://doi.org/10.3390/medicina55060259
Parsaeian M, Mohammad K, Mahmoudi M, Zeraati H (2012) Comparison of logistic regression and artificial neural network in low back pain prediction: second national health survey. Iran J Public Health 41:86–92
Dietterich TG (1998) Approximate statistical tests for comparing supervised classification learning algorithms. Neural Comput 10:1895–1923. https://doi.org/10.1162/089976698300017197
Saarela M, Jauhiainen S (2021) Comparison of feature importance measures as explanations for classification models. SN Appl Sci 3:272. https://doi.org/10.1007/s42452-021-04148-9
Acknowledgements
We thank the Spanish Back Pain Research Network (REIDE), a Spanish not-for-profit organization that specializes in neck and back pain research, for providing logistical and administrative support for this study.
Funding
No funds were received in support of this work.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflicts of interest to declare.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liew, B.X.W., Kovacs, F.M., Rügamer, D. et al. Machine learning versus logistic regression for prognostic modelling in individuals with non-specific neck pain. Eur Spine J 31, 2082–2091 (2022). https://doi.org/10.1007/s00586-022-07188-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00586-022-07188-w