A cluster analysis describing spine and torso shape in Lenke type 1 adolescent idiopathic scoliosis

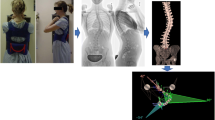
Abstract

Purpose

The purpose of this work is to identify the variability and subtypes of the combined shape of the spine and torso in Lenke type 1 adolescent idiopathic scoliosis (AIS).

Methods

Using ISIS2 surface topography, measures of coronal deformity, kyphosis and skin angulation (as a measure of torso asymmetry) in a series of children with Lenke 1 convex to the right AIS were analyzed using k-means clustering techniques to describe the combined variability of shape in the spine and torso. Following this, a k-nearest neighbor algorithm was used to measure the ability to automatically identify the correct cluster for any particular datum.

Results

There were 1399 ISIS2 images from 691 individuals available for analysis. There were 5 clusters identified in the data representing the variability of the 3 measured parameters which included mild, moderate and marked coronal deformity, mild, moderate and marked asymmetry alongside normal and hypokyphosis. The k-nearest neighbor identification of the correct cluster had an accuracy of 93%.

Conclusion

These clusters represent a new description of Lenke 1 AIS that comprises both coronal and sagittal measures of the spine combined with a measure of torso asymmetry. Automated identification of the clusters is accurate. The ability to identify subtypes of deformity, based on parameters that affect both the spine and the torso in AIS, leads to as better understanding of the totality of the deformity seen.

Introduction

In adolescent idiopathic scoliosis (AIS), the spinal curve in the coronal plane is associated with changes in sagittal shape [1] and axial rotation [2] of the vertebral column. There is often an associated asymmetry of the posterior torso, otherwise known as the rib hump, best observed in the Adams forward bend position. The classification of AIS, has been used to describe and guide management of the condition. Historically, classification has been based on a number of different subtypes of spinal shape [3,4,5]. The King classification used the coronal view of the spine [4]. The Lenke classification [3] makes use of both the coronal and sagittal shape of the spine including the size of the deformity in the coronal plane, the sagittal profile the behavior of the lumbar curve and the anatomical location and flexibility of the curves. The Peking Union Medical College (PUMC) classification also describes a number of spinal shapes in the coronal and sagittal planes.[5]. Further developments in the description of AIS have come with a greater understanding of the three-dimensional (3D) nature of the spinal deformity and how that is best represented and categorized, particularly using the ‘top-down’ or Da Vinci view [6].

The use of statistical methods for the further understanding of the subdivisions of AIS has been reported previously [7,8,9,10,11]. Poncet et al. [9] describe the calculation of geometric torsion, identifying 3 different types of torsion curve pattern in AIS. Pasha et al. [8] use a 3D hierarchal classification to describe 5 different groups of right thoracic curves in a group with AIS. Duong et al. [7], Shen et al. [10] and Stokes et al. [11] use clustering methods to identify subtypes of scoliosis based on a number of parameters seen in AIS. Duong [7] identifies five clusters in a similar fashion to those seen in the King [4] and Lenke [3] classifications, but when using twelve clusters, identify patterns of deformity in 3D. Shen [10] detect eleven subgroups not recognized as part of the King [4] or Lenke [3] classifications. Stokes [11] identifies 4 subgroups based on a number of parameters including the size of the scoliosis and the amount of rotation in the plane of maximal curvature. Consequently it is acknowledged that there are many different curve types within the umbrella term of a Lenke 1 curve.

A description of adolescent scoliosis that encompasses parameters that measure the spine, combined with the torso shape, has not been published, preventing an assessment of torso asymmetry from being part of the greater understanding of the totality of the deformity. The purpose of this study is to examine the different subtypes of AIS using the coronal and sagittal spinal shape in conjunction with the asymmetry of the torso in a cohort of AIS with Lenke 1 curves. This is to examine the subtypes of deformity seen when observed using the parameters that are representative of the three planes of the deformity. Subsequently, a k-nearest neighbor algorithm [12] is used to demonstrate how robust and accurate the future identification of the correct cluster for new individuals is, as previously reported by Ghaneei et al. [13].

Methods

As an ethically approved research project, a review was undertaken of the surface topography pictures taken of adolescents with idiopathic scoliosis from one institution (NRES Committee East Midlands—Northampton 15/EM/0283). All of the images reviewed were taken with the surface topography Integrated Surface Imaging System 2 (ISIS2) system [14] as part of routine care. From these previously collected data, only pre-operative convex to the right thoracic curves were selected (Lenke 1 curves [3]).

The ISIS2 system automatically measures and records a number of parameters that reflect the surface topography of the spine and posterior torso. For this study, the parameters selected for analysis were the measures of lateral asymmetry, kyphosis and skin angle. Lateral asymmetry is the ISIS2 equivalent of the Cobb angle [15] to measure the size of the scoliosis. It is measured from the points of inflection between the vertebra prominence (VP) and the sacrum in the spinal line projected on the coronal plane. The spinal line is estimated from the surface topography data [14]. Kyphosis is measured using the same Cobb technique between the VP and the point of inflection marking the junction between kyphosis and lordosis along the spine line projected in the sagittal plane. The parameter sum skin angle is the sum of the absolute maximum transverse skin angles to the right and to the left that are measured in ISIS2. Skin angle is the ISIS2 parameter that describes the asymmetry of the posterior torso, in a similar way to how a scoliometer can be used to measure the angle of trunk rotation [16]. As standard in ISIS2, the posterior torso is subdivided into 19 transverse levels equally spaced down the spine line. The angle between the left and right sides of the torso relative to the coronal plane through the body is measured for each of these 19 levels over a central section (Fig. 1). By definition, the skin angle is positive if the right side is more prominent and negative if the left is more prominent. The sum skin angle is the sum of the absolute maximum skin angles to the right and to the left (i.e. effectively ignoring the negative sign for the angles to the left, thus summing 2 positive values).

Fig. 1

An ISIS2 image that shows the results of the calculation of skin angle at 19 transverse levels down the back

All analysis was performed using R [17]. Using the parameters of lateral asymmetry, kyphosis and sum skin angle for each individual ISIS2 image, a 3D scatter plot of the data was created using the R rgl package [18]. Further analysis was performed using a k-means clustering algorithm from the R class package [19] to identify patterns of 3D shape within the cohort. The number of clusters was pre-defined using the elbow method [20]. The k-means algorithm is an unsupervised machine learning algorithm where, for a pre-specified number of centroids, all data points are grouped dependent on how close that point is to one of the centroids for the parameters specified. The data points were assigned to the clusters using the k-means clustering technique. The mean and 95% confidence ellipsoids were calculated for the data in each cluster.

A method was then developed using a machine learning tool, the k-nearest neighbor algorithm [12], to allow the identification of an appropriate cluster for a specific individual. This involves the creation of a training set, in this case set at 10% of the data, as a subset of the original data. The algorithm then uses the training set and identifies the best cluster for each individual data point. The k-nearest neighbor algorithm maps a certain number of the closest data points of a particular parameter from a subset of the total data set (the training group), and the remaining data points are then mapped through clustering and classification methods [12] where the nearest neighbor is found through Euclidean geometry. The benefit is that there is no bias is introduced as there are no a priori assumptions made about the data. The accuracy of the identification of the correct cluster when compared to the cluster identified with the k-nearest neighbor algorithm was assessed as a function of the machine learning algorithm.

Results

The database contained 1399 images from 691 individuals (104 males and 587 females) with AIS who had a Lenke 1, convex to the right, curves. Repeat images taken on different dates were available for a number of patients included in the cohort. The numbers of repeat images are shown in Table 1. Table 2 lists the demographics of the cohort. The mean, standard deviation and range of the parameters of the lateral asymmetry, kyphosis and the sum skin angle parameters are given in Table 3. The elbow method identified that the optimum number of clusters for the data was 5. Figure 2 shows the 3D scatter plot of these 5 clusters with their 95% ellipsoids, the 3 axes of the plot being lateral asymmetry, kyphosis and sum skin angle, all measured in degrees.

Table 1 Number of repeat images per individual

Table 2 Demographics of the cohort

Table 3 Variability of the parameters used for the cluster analysis

Fig. 2

A 3D plot showing the clusters with the axes of lateral asymmetry (°), kyphosis (°) and sum skin angle (°). The clusters are the 5 different colored ellipsoids (cluster 1—black, cluster 2—red, cluster 3—green, cluster 4—navy blue and cluster 5—light blue). Individual data points are seen in the color of the cluster that they are associated with

Table 4 describes the 5 clusters numerically (mean and standard deviation) and narratively. Visual representations of the clinical and ISIS2 surface topography images and analysis results for one representative individual from each cluster are shown in Fig. 3a–e.

Table 4 Variability of the parameters in each of the clusters identified

Fig. 3

a ISIS2 image and clinical photograph of an individual identified as part of cluster 1. b ISIS2 image and clinical photograph of an individual identified as part of cluster 2. c ISIS2 image and clinical photograph of an individual identified as part of cluster 3. d ISIS2 image and clinical photograph of an individual identified as part of cluster 4. e ISIS2 image and clinical photograph of an individual identified as part of cluster 5

Using the k-nearest neighbor algorithm, the accuracy of identification of the correct cluster for a subset of the original data set was 93%.

Discussion

AIS is recognized as a 3D deformity of the spine and torso. Previous reports have identified a variability in the 3D shape of the torso in AIS [21]. The variability in spinal shape seen in AIS has been responsible for the development of a number of classification systems reported in the literature [3,4,5] of which the Lenke classification is most widely used.

Further understanding of the 3D nature of AIS combined with a desire to be able to represent this has led to the development of 3D classifications of the shape of the spine [22], most notably as the Da Vinci, or top-down, representation [6, 10].

Furthermore, there is interest in the external shape of the torso in AIS. This is demonstrated by the patient-reported scoring systems that have been developed, such as the Spinal Appearance Questionnaire (SAQ) [23] and the Trunk Appearance Perception Scale (TAPS) [24], which allow the patient to quantify their own deformity through a series of images that depict the whole torso and spine. However, there is no reported description of AIS that identifies subtypes of curves based on a combined assessment of both the spine and the torso shape. This paper explores this issue, and through the use of the 3D data of both the spine and torso shape from a large number of Lenke 1 convex to the right curves, it identifies a number of different types of combined spinal and torso deformity.

Cluster analysis has been previously used in a number of forms within the study of scoliosis [7, 11, 25] where subtypes of curve were described. The benefit of cluster analysis as a technique is that a large number of data points can be grouped, without bias, into subtypes that explain the variability in the data. In this particular case, k-means clustering was the technique used [12]. In this method, the number of centroids is calculated prior to the clustering using the elbow method [20] which showed there were 5 clusters in the data. The clusters are shown in Fig. 2 as a 3D scatter plot with 95% confidence ellipsoids, different colors indicating the different clusters. In narrative terms, the clusters describe mild, moderate and marked scoliosis, normal and hypokyphosis and mild, moderate and marked asymmetry. Of particular interest is cluster 2 where, as shown in Fig. 3b, both the clinical and ISIS2 images demonstrate a convex to the right thoracic curve, but with a greater asymmetry on the left, the concavity of the curve. This demonstrates that the direction of the scoliosis is not always the same as the side of the torso asymmetry. What is apparent from the clusters is that a Lenke 1, convex to the right scoliosis, includes a spectrum of deformities that cover a breath of the size of the scoliosis, the degree of kyphosis and the amount of torso asymmetry. Torso asymmetry is seen with both moderate and marked scoliotic curves and with both normal and hypokyphosis. The description of the different types of curve pattern described in this paper adds to the literature as an assessment of the amount of torso asymmetry is not made in any of the published classifications. Given that, from the point of view of the patient, the amount of asymmetry is a key factor in scoliosis surgery [26], then the assessment of that asymmetry should be part of the assessment of the overall scoliosis.

For the cluster analysis presented here to be useful in the future, a method allowing identification of the cluster to which a new individual belonged is required. This function is performed using the k-nearest neighbor algorithm. In this paper, the k-nearest neighbor algorithm was accurate in 93% of the time in identifying the correct cluster for a particular data point. This gives an assurance of how well future data points would be classified to the correct cluster; however, future validation with an unrelated data set is required.

K-nearest neighbor techniques have been used in the field of scoliosis previously [13]. The paper of Ghaneei et al. [13], which followed on from the previous work of the same group in the identification of a scoliotic curve using a marker-less surface topography and decision trees. Ghaneei used the k-nearest neighbor technique and demonstrated an improvement in the accuracy, sensitivity and specificity of the prediction of the magnitude of the curve and the progression of an identified curve. The k-nearest neighbor technique is not known to have been used previously in the fashion described in this paper.

Future work in this area is required to assess whether the clusters identified would help the surgical team plan the most appropriate operation, focused on the 3D parameters of most interest to both the patient and surgeon. This would take the form of a prospective study that would analyze the pre-operative cluster from the 3 parameters of lateral asymmetry, kyphosis and sum skin angle using the k-nearest neighbor algorithm. With this information and in combination with the surgical technique employed intra-operatively and the post-operative outcome, quantification of the utility of the classification of 3D spine and torso shape described in this paper to achieve the surgical result could be assessed.

Conclusion

This work shows that there are 5 different types of Lenke 1 curve when assessed using the parameters of scoliosis curve size, kyphosis and the amount of torso asymmetry. Using the k-nearest neighbor algorithm, these clusters can be identified with accuracy in an automated fashion. The assessment of a scoliosis requires an appreciation of the shape of both the spine and the torso, and this paper provides the framework to allow for this with future work to develop an understanding of how this information can better guide surgical intervention.