Introduction

During 2000 to 2009, there was an annual publication of 40 RCTs on lumbar pain, using a Patient-Reported Outcome Measure (PROM). The most common measures were the Oswestry Disability Index (ODI—physical function), the Numeric Rating Scale (NRS—pain) and the Euroqol-5-Dimensions (EQ-5D—quality of life) [1].

When a PROM is used repeatedly on the same patient, a measurement error will be present because of natural fluctuations in symptoms, variation in the measurement process, or both. A useful way of presenting the measurement error is the Smallest Detectable Change (SDC). It is described by Polit and Yang as a change in score of sufficient magnitude that the probability of it being the result of random error is low [2]. In trials, where a measurement of change is involved, it is practical to refer to a repeatability parameter such as the SDC, which is in the units of the PROM in question.

The SDC is a measure of the reliability of a PROM, based on the measurement error and repeatability of each instrument. Recently published reviews found that studies exploring such measurement properties were few and of inadequate quality [3,4,5].

A statistically significant change in outcome does not necessarily mean that it is of interest in real life. A person’s opinion about the smallest score change is named the Minimal Important Change (MIC) [6]. For many years, there has been a conceptual confusion around the many measurements of change parameters defining the cut-off in a PROM score that distinguishes a success from failure [7,8,9,10,11,12]. Terwee et al. [13] have emphazised the important link between SDC and MIC.

The aim of this study was to define the SDC in the most commonly used outcome measures in degenerative lumbar spine surgery and compare them to the MIC.

Patients and methods

Outcome variables

The Numeric Rating Scale for back and leg pain, respectively, (NRSBACK/LEG), the Oswestry Disability Index (ODI), version 2.1a, and the European Quality of life questionnaire (EQ-5DINDEX) are well known and described in detail earlier [1].

The Global Assessment of back and leg pain, respectively, (GABACK/LEG) [14] assesses patients’ retrospective perception of treatment effect. The question is worded: “How is your back/leg pain today as compared to before you had your back surgery?” with 6 response options: 0/Had no back/leg pain, 1/Completely pain free, 2/Much Better, 3/Somewhat Better, 4/Unchanged, 5/Worse.

The first question of the Short-Form 36 questionnaire (SF36GH) [15] was added to reveal changes in global health during the retest period. The question is worded: “In general, would you say your health is” with response options: Excellent/Very Good/Good/Fair/Poor.

The MIC population

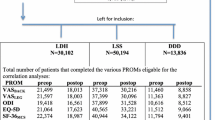
MIC computations were based on the entire Swespine register [16]. Table 1 presents anthropometrics, baseline data and 1-year follow-up of the degenerative lumbar spine population, operated 1998–2017 (n = 98,732). Adults, with either of the three degenerative diagnoses, lumbar disk herniation, lumbar spinal stenosis or degenerative disk disease, were included.

Table 1 Baseline data of the retest and Swespine populations, respectively
Full size table

The retest population

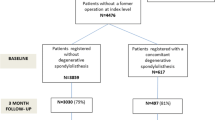
The study participants were collected consecutively at Stockholm Spine Center and Spine Center Göteborg between November 2017 and May 2019. In order to cover as much of the range of each PROM scale as possible, they were collected from both the waiting list (pre-op group) and from those followed up 1 year after surgery (post-op group). At least 30 individuals from each of the three diagnoses groups were obtained.

The pre-op group filled out the first booklet (T1) at the clinic on the day they were listed for surgery. The second booklet (T2) was sent by mail 1 week later, and the respondents were asked to return the form within 5 days. One reminder was sent after 1 week.

In the post-op group, a request for study participation was added to the 1-year Swespine follow-up booklet (T1). One week after the booklet was registered at the Swespine office, the second questionnaire (T2) was sent out by mail, with a request to return the form within 5 days. Inclusion to the pre-op group stopped as the total number of participants exceeded 30 in all three diagnoses. For the analyses, the pre-op and the post-op groups, as well as the diagnoses, were merged.

The time interval between the two points of estimation, T1 and T2, was within 10 to 35 days. The difference in PROM score for each participant between T1 and T2 was plotted against the time interval and correlated in Spearman rank analyses to check whether the number of days between T1 and T2 had an influence on the PROM score or not.

The occurrence of systematic differences between T1 and T2 was examined using the Sign test for categorical data (i.e., GABACK/LEG and SF 36GH) and the Wilcoxon’s sign rank test for continuous data (i.e., NRSBACK/LEG, ODI and EQ-5DINDEX).

A maximum of two missing items was accepted for the ODI and zero missing items for the remaining PROMs, according to published score algorithms [17, 18].

The study was conducted according to the COSMIN checklist, boxes B, C, and J [6].

Descriptive data are presented as means (\(\pm\) SD) or numbers (%).

MIC

The MIC estimates were previously calculated for the diagnosis groups LDH, LSS, and DDD [19] using the anchor-based ROC curve method [20]. In the current study, MIC values without stratification for diagnosis were added. The measure used as gold standard was the GA, which has been shown to have an acceptable correlation to the instruments at issue [14]. Patients’ self-assessments on the GA as either “pain free” or “much better” was considered an important improvement (i.e., equal to, or above the MIC). The ability of each PROM to distinguish between improved and not improved was measured by the Area Under the ROC Curve (AUC), with an acceptable level of 0.70. The cut-off score defining the MIC also represents the level where the sensitivity and specificity of the PROMs are mutually maximized. The probability that a patient reaching the MIC will also express an important improvement on the GA is called the positive predictive value (PPV). The probability that a patient not reaching the MIC will express a non-important improvement on the GA is called the negative predictive value (NPV) [21].

SDC

The reliability of change scores the Smallest Detectable Change (SDC)  \(=\) 1.96 \(\times \sqrt 2 \times\) SEM (Standard Error of Measurement).

SEM

Agreement between T1 and T2 was expressed as the intra-individual standard deviation, also known as the Standard Error of Measurement [13]. The SEM is a standard error in an observed score that obscures the true score and is given in the units of the PROM. The SEM = \(\sqrt {intra\, indiviual\, variance}\) of an ANOVA analysis. The difference between a subject’s PROM score and the true value would be expected to be within \(\pm\) 1.96SEM for 95% of the individuals. The assumption that the score distribution is unrelated to the magnitude of the measurement (heteroscedasticity) was checked by plotting the individual patient’s standard deviations against his or her means.

ICC

The reliability parameter was the Intra-class Correlation Coefficient, ICC. ICC estimates and their 95% CI were calculated using an absolute agreement, two-way random-effects single measures model. Based on the 95% CI of the ICC, estimate values less than 0.40 indicate poor reliability, while estimates between 0.4 and 0.59 indicate fair, 0.6–0.74 good and 0.75–1.00 excellent reliability [22]. The relation of the ICC to the SEM is described as SEM = SD \(\surd\) 1-ICC.

Kappa

The reliability measure weighted kappa was calculated for the categorical variables (i.e., GABACK/LEG and SF36GH). An instrument is reliable when the kappa is above 0.70 [6]. Since these instruments have several ordinal response options, kappa was calculated using the weighting scheme of quadratic weights which is mathematically identical to an ICC of absolute agreement. Further, overall agreement between T1 and T2 as well as the proportion of respondents indicating a better outcome at T1 than at T2 or vice versa were calculated.

IBM SPSS Statistics for Windows, Version 24.0. Armonk, NY: IBM Corp. was used in all the statistical analyses apart from the MIC computations, where JMP®, Version 13.1 SAS Institute Inc., Cary, NC, 1989-2019, was used.

Ethical considerations

Informed consent was obtained from all participants in Swespine, and written consent was acquired from the participants in the retest study. This research project was approved by the regional ethical review board.

Results

Descriptives

In total, 248 participants filled out the booklet at T1. Both questionnaires were returned by 182 (74.6%) participants, 83 from the pre-op group and 99 from the post-op group. Table 1 presents demographics and mean PROM scores at baseline and at the 1-year follow-up for the retest group and for the Swespine population.

Timing of measurements

The time interval between T1 and T2 was 20 \(\pm 8\) days. The number of days between T1 and T2 did not correlate with the PROM scores (Spearman rank correlation coefficient for ODI: − 0.07; NRSBACK: 0.06; NRSLEG: − 0.08; EQ-5DINDEX: − 0.03; GABACK: 0.045; GALEG: − 0.144; Satisfaction: 0.128; SF36GA: − 0.064). Figure 1 visualizes this pattern in a scatter plot, exemplified by the ODI.

Fig. 1
figure 1

Scatter plot illustrating a non-correlation between the time interval and ODI score. The horizontal line is the mean score difference between the two occasions of measurement (T2–T1 = − 0.25), n = 169. The same pattern was seen for NRSBACK/LEG and the EQ-5DINDEX

Full size image

Measurement error and score change reliability

There were no statistically significant systematic differences between T1 and T2 as measured by the Wilcoxon sign rank test (NRS, ODI, EQ-5DINDEX) and the Sign test (GA, Satisfaction, SF-36GH) for any of the PROMs.

The data were not found to be heteroscedastic, meaning that the measurement error appeared to be uniform across scale values. Table 2 presents reliability measures of each PROM demonstrating excellent or good reliability and large SDCs for all prospective PROMs. The influence of random error on the SDCs is illustrated in Fig. 2, with the ODI illustrating the typical pattern.

Table 2 Measurement properties (reliability and measurement error parameters) of four PROMs
Full size table
Fig. 2
figure 2

A Bland–Altman plot of the ODI test–retest scores. The horizontal line close to “0” illustrates the mean difference in score between the test and the retest occasion. The upper dotted line is of interest if the concern is an improvement and the lower line if the research question is about a deterioration. Values within these limits are, with 95% confidence, due to random error, n = 172

Full size image

The MIC calculations were based on the lumbar Swespine register population, stratified for diagnosis [19]. In Table 3, the SDCs are compared to these MIC values. For NRSBACK/LEG and ODI the SDCs exceeded the MICs to some extent. As for the EQ-5D, the difference was more remarkable.

Table 3 Measurement of change parameters (SDC, MIC) for PROMs in three lumbar spine conditions
Full size table

In Table 4, the SDCs are compared to the MIC values that were calculated for the entire lumbar Swespine population. The SDC for both NRS scales exceeded the corresponding MICs, while the SDC and MIC were equal for the ODI. The considerable gap between the SDC and MIC for the EQ-5DINDEX remained. The AUCs were all above 0.70. The ODI had the best ability to correctly classify patients as importantly improved according to GA with a sensitivity of 76%. The specificity was similar for all PROMs. NRSLEG reached the highest specificity (83%), indicating the best ability to correctly classify patients as not importantly improved.

Table 4 The SDC of four PROMs compared to their MIC values based on the entire Swespine lumbar population
Full size table

The weighted kappa for the categorical variables GABACK/LEG and SF-36GH were above the level of acceptance. The percentages of agreement are given in Table 5.

Table 5 Reliability of retrospective single-item questions
Full size table

Discussion

This study found large SDCs, frequently exceeding tough MIC cut-off values, for some of the most commonly used PROMs in spine surgery research. The error was mainly due to a large intra-individual variation between the two test occasions and not to systematic differences. It has important implications.

For instance, consider a trial exploring a possible difference in outcome between two groups undergoing posterolateral fusion with or without interbody fusion, and the outcome variable is NRSBACK. Then—according to the present study—both groups need to reach a change of 3.6 before there is a 95% certainty that the change from baseline is not a mere chance. If—and only if—both groups reach this level of improvement, the research question can be answered.

In other studies on low back pain populations, using the same definition of SDC as in this paper, the SDCs were also rather high: 2.4–4.7 for NRSBACK, 11–16.7 for ODI, and 0.28–0.58 for the EQ-5D [4, 5, 23].

The MIC corresponds to the minimal level of change that makes the efforts of the surgery worthwhile. A statistically detectable change does not reveal any information about its value in real life. That estimation has to be based on opinions of the persons undergoing the treatment. Accepting the opinion-based MIC does however not allow for the exclusion of the SDC!

If we recycle the example above but change the research question to whether there is a clinically important difference between the groups or not, a MIC in NRSBACK of 2.9 must be reached by both groups before the question can be answered. Note that the answer should not be given in terms of a mean difference between the groups, but rather as the percentage in each group reaching the MIC cut-point. However, as the SDC was 3.6, a change of 2.9 may just be a measurement error—no matter the importance of personal opinions.

As long as it can be shown that the MIC estimate exceeds the SDC it can be used separately. But as soon as it is the opposite way, both the SDC and the MIC should be presented in such a manner that the reader can get a clear picture of the true degree of change. This simultaneous usage of both a distribution-based cut-off value and anchor-based estimate has earlier been advocated by Terwee and colleagues [13].

If the SDC by far outreaches the MIC, as was the case for EQ-5D, the use of that PROM should not be accepted, simply because the size of the error is too large to make sound inferences. Why this was the case for EQ-5D in the current study is not clear. Variations in measurement-of-change estimates for this particular PROM stretch from 0.15 to 0.45 [24]. In this study, the SDC was 0.48 and the MIC was 0.10–0.18 depending on which diagnosis group the calculations were based. A possible explanation is that the preference-based summary index systematically divides the population in two, making it difficult to define an SDC, which is based on dispersion.

Based on the large Swespine database, the MIC values in this study may be considered credible. However, it must be remembered that the MIC is anchored to a retrospective single-item transition question, requiring that each patient remembers his or her health state prior to their operation. Also demanded is an honest response about the degree of improvement or deterioration where the patient excludes factors such as disappointment, gratitude, insurance, sick leave or work-related issues. The human nature probably makes sure that recall bias and response shift will always have an impact on the response to these types of questions.

The PPV of 0.88 for NRSLEG indicates the probability that patients with a change exceeding the MIC, also classified themselves as being importantly improved on the anchor. The NPV of 0.64 is the probability that patients with a change less than the MIC self-assessed a non-important improvement on the anchor.

The reliability of the retrospective single-item questions, interpreted by their weighted kappa values, was almost perfect (above 0.8) or substantial (0.75) according to Landis and Koch [25]. A high weighted kappa also indicates that misclassifications mainly occurred between adjacent response options.

Conclusion

A consequence of large measurement errors in PROMs, is the need of considerable change in outcome in order to distinguish a random error from true change.