Abstract
Objectives
To automatically measure the Cobb angle and diagnose scoliosis on chest X-rays, a computer-aided method was proposed and the reliability and accuracy were evaluated.
Methods
Two Mask R-CNN models as the core of a computer-aided method were used to separately detect and segment the spine and all vertebral bodies on chest X-rays, and the Cobb angle of the spinal curve was measured from the output of the Mask R-CNN models. To evaluate the reliability and accuracy of the computer-aided method, the Cobb angles on 248 chest X-rays from lung cancer screening were measured automatically using a computer-aided method, and two experienced radiologists used a manual method to separately measure Cobb angles on the aforementioned chest X-rays.
Results
For manual measurement of the Cobb angle on chest X-rays, the intraclass correlation coefficients (ICC) of intra- and inter-observer reliability analysis was 0.941 and 0.887, respectively, and the mean absolute differences were < 3.5°. The ICC between the computer-aided and manual methods for Cobb angle measurement was 0.854, and the mean absolute difference was 3.32°. These results indicated that the computer-aided method had good reliability for Cobb angle measurement on chest X-rays. Using the mean value of Cobb angles in manual measurements > 10° as a reference standard for scoliosis, the computer-aided method achieved a high level of sensitivity (89.59%) and a relatively low level of specificity (70.37%) for diagnosing scoliosis on chest X-rays.
Conclusion
The computer-aided method has potential for automatic Cobb angle measurement and scoliosis diagnosis on chest X-rays.
Graphic abstract
These slides can be retrieved under Electronic Supplementary Material.

Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
Introduction
Scoliosis is defined as a three-dimensional spinal deformity involving one or more spinal curves with lateral deviation and axial rotation of the vertebrae [1]. Standing coronal radiographs, including the entire spine and iliac crest, is an economical imaging evaluation modality for scoliosis [2]. The diagnosis and treatment of scoliosis rely on the severity of the spinal deformity and the risk of progression [3]. Currently, the Cobb angle is an objective radiographic parameter to quantify the severity of scoliosis on coronal radiographs [4]. A Cobb angle > 10° is considered clinically significant for scoliosis diagnosis [5], whereas the variability of Cobb angle measurements has been reported to range from 3° to 10° in previous studies [6]. In addition, manual measurement is time-consuming, especially in scoliosis screening. To reduce such variability and improve efficiency, computer-aided methods have been introduced.
A few previous studies have been conducted for measuring the Cobb angle. A contour and angle-function based methodology was proposed by Bonanni et al. [7] as an alternative to the classical vertebra endplate method for determining the Cobb angle. The method was less sensitive to noise and image artifacts because of dependence on the overall spine features, rather than endplate surface features. Recently, several studies have attempted to develop computer-aided methods using a deep learning technique. Wu et al. [8] proposed a multi-view correlation network (MVC-Net) that allowed automatic assessment of the spinal curvature on anteroposterior and lateral X-ray views through joint multi-view input feature learning and explicit reinforcement of reciprocal relationships between the spinal landmark and Cobb angle; however, the MVC-Net might not be ideally suited for elderly patients with scoliosis because the spinal landmark located in the four vertices of each vertebral body would be varied with the formation of marginal osteophytes. Zhang et al. [9] developed a computer-aided method using a deep neural network that still requires manual intervention, such as assignment of vertebral patches, and was not reliable to measure Cobb angle for in vivo radiographs.
Scoliosis is a common imaging finding on chest X-rays from lung cancer screening. All of the abnormal findings, including scoliosis on chest X-rays, have to be reported in the clinical workflow and can provide opportunistic screening of thoracic and upper lumbar scoliosis. To measure the Cobb angle and diagnose scoliosis on chest X-rays during lung cancer screening without manual intervention, a computer-aided method is proposed and the reliability and accuracy were evaluated.
Materials and methods
Sample size assessment
The sample size was evaluated using Eq. 1, with an expected sensitivity and specificity of 80%, a confidence interval (CI) of 95%, and a permissible error of 0.075. The calculated sample size was 219.
Subjects
A retrospective analysis of chest X-rays obtained between January and June 2018 and scanned into the electronic medical imaging database of Ruijin Hospital in Shanghai, China, was performed. We acquired all chest X-rays with the following inclusion criteria: posteroanterior chest X-rays from lung cancer screening; and age > 18 years. The chest X-rays with primary or secondary spinal tumors, vertebral fractures, and metal artifacts in the area of the spine were excluded. A total of 4960 chest X-rays were selected and numbered after concealing identifying information. The sample size was 5% of the total, and simple random sampling without replacement was performed using a computer-generated randomization list. Two hundred forty-eight chest X-rays were included to evaluate the reliability and accuracy of the computer-aided method in the current study. All chest X-ray fields in the craniocaudal direction ranged from the suboccipital area to the lower area of the costophrenic angle. The acquisition information of the chest X-rays was a tube voltage of 81 kVp and a tube current–time product of 2.85 mAs. Ethics approval for this study (IRB Number 201872) was obtained from the Health Ethics Research Committee in a local hospital, and informed consent was waived given the retrospective nature of the study.
Computer-aided method
The core of the computer-aided method was the Mask R-CNN models that were introduced by He et al. [10]. Two Mask R-CNN models were used to separately detect and segment spine and vertebral bodies on chest X-rays. The midpoints of the superior and inferior endplates of each vertebral body were determined from the output of the Mask R-CNN models.
Mask R-CNN
Mask R-CNN is a state-of-the-art technique, for instance segmentation tasks, and is an improvement in the Faster R-CNN that was designed for combining object detection and semantic segmentation [10]. Mask R-CNN continued the region proposals network of Faster R-CNN as a feature extractor. Briefly, Mask R-CNN was built on several neural networks with certain orders. First, a backbone neural network was used to process the images and extract the features. A feature pyramid network (FPN) was recommended to be used for accuracy and speed [11]. A lateral connection was used in FPN to merge the bottom-up and top-down pathways [11]. The bottom-up pathway is a forward propagation convolutional network process for feature extraction; the upper part of the layer indicates less spatial resolution and a higher level of structure detection. Moreover, the bottom-up pathway was adopted by Fast R-CNN only using the last layer of the network, which should contain the most abundant semantic values [12]. To utilize the features of the bottom layer, a top-down pathway was adopted in the reconstructed layer of the FPN to include semantic values and high-resolution features. Thus, FPN starts from the top layer with upsampling to enhance the object locations precisely, and the lateral connections merge the reconstructed layers and the corresponding feature maps from the bottom-up pathway [11].
In this study, the FPN based on ResNet-101 was chosen for high-performance feature extraction. Then, the alignment pooling layer was used to automatically detect the regions of interest (ROI). As a regional proposal network, the FPN was designed to select the potential ROI and produce standard-sized feature maps. The alignment pooling was an improvement to Faster R-CNN pooling by increasing the accuracy of the coordinates. Then, each ROI was applied as input for the following two branches: The fully connected layers inherited from the Faster R-CNN to predict boundary boxes and classes, and the fully convolutional network (FCN) was added to predict the segmentation mask.
Computer-aided measurement of the Cobb angle
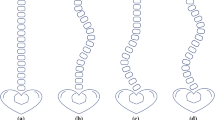
Because scoliotic deformities manifest as deviations of the spine from the natural contour in the coronal planes, the overall structural curve of the spine is a more natural focus for deformities [7]. Computer-aided measurement included two main steps: separate segmentation of the spine and vertebral bodies using two Mask R-CNN models and determination of the maximum angle using designed algorithms for postprocessing from segments of the spine and vertebral bodies. Mask R-CNN models showed a better performance in segmentation of the spine and vertebral bodies if the contrast limited adaptive histogram equalization (CLAHE) method was applied in image preprocessing. The CLAHE function with a set clipLimit of 100 and tileGridSize of (8, 8) was built through openCV-python. Different parameters were tested until optimal parameters that could increase the contrast in the area of the spine were found. Generally, the models with a ResNet-50-FPN backbone require less computational recourse than ResNet-101-FPN, while they sacrifice the performance of models to a greater or lesser extent. To balance both performance and computational load, ResNet-101 with FPN as the backbone was chosen in this study. Pre-trained models in the MSCOCO database (http://cocodataset.org) were applied as the initialized models which were trained in 100 epochs with a learning rate of 0.001, followed by 0.0001 decay in each epoch. Additionally, the learning rate is multiplied by 0.1 in the 40th and 80th epochs. A sample of original images, the results of image preprocessing, and detection and segmentation of the spine and vertebral bodies are shown in Fig. 1. It is worth noticing that the spine and vertebral bodies were trained in two separate, rather than one, Mask R-CNN model. There are two main considerations: if two categories trained in a single model, available data with both spine and vertebral body annotations would be reduced to 235 cases and the remaining data with mere spine annotations would be wasted. The difference in the number of annotations for the two categories is due to the fact that the annotation of vertebral body is more labor intensive than that of spine. Another reason is vertebral bodies located inside of the spine cause non-maximum suppression (NMS) and need additional modification to satisfy the usage. Nearly, all of the vertebral bodies should be filtered by the default NMS algorithm. The training and testing datasets of the Mask R-CNN models are shown in Table 1.
The masks of the spine and vertebral bodies segments were generated as the output of the Mask R-CNN models. First, the central line of the spine boundary was linked by locating the midpoint in each spine mask row. The rows with certain gaps were selected; then, the midpoint of one row was determined by finding the minimum and maximum on the x-axis. The central line of the spine was generated by linking the midpoints found in the rows. The intersection between the central line of the spine and the superior/inferior endplate of each vertebral body was determined and is represented with red and blue dots in Fig. 2. Two intersections in the central line of the spine with the superior and inferior endplates of each vertebral body were viewed as a group, and there were a dozen groups based on the number of vertebrae on the chest X-ray. The longitudinal central line of each vertebral body was defined by linking two intersections in a group. The perpendiculars of the longitudinal central line were drawn through two intersections in a group. The angle between any superior perpendicular of the cranial vertebral body and any inferior perpendicular of the caudal vertebral body was calculated. A set of permutation and combination groups were used to obtain all possible angles, and a maximum angle was determined. The maximum angle was considered as the Cobb angle. The result of computer-aided measurement on a chest X-ray is shown in Fig. 2.
Manual method
The Cobb angles on 248 chest X-rays were measured by computer-aided and manual methods. The computer-aided method was compared with the manual method to evaluate reliability and accuracy for the Cobb angle measurement and scoliosis diagnosis. The manual method was adopted to measure the Cobb angle on digital chest X-rays using picture archiving and communication systems (PACS) rather than on printed radiographs. Manual measurement through PACS was the same as the classic measurement (Fig. 3) [13], except for the automatic calculation of the Cobb angle. If the endplate was not seen clearly after enlargement and contrast adjustment, lines are drawn along the pedicles [14]. The Cobb angles on chest X-rays were measured by two radiologists in the same PACS workstation (RadiForce G20; EIZO Nanao Corporation, Japan) at different times. Two radiologists were involved in the radiology clinic > 10 years and were familiar with the classic measurement. Manual measurement was repeated twice with a 3-week interval. Both radiologists were blinded to the results of the previous and computer-aided measurements.
Statistical analysis
Statistical analysis was performed using SPSS 22.0 software (SPSS, Inc., Chicago, IL, USA). Intraclass correlation coefficients (ICCs) with 95% CIs were used to analyze the reliability; ICC < 0.70, 0.70–0.79, 0.80–0.89, and 0.9–0.99 were considered as poor, fair, good, and excellent reliability, respectively [6]. For variability analysis, the mean absolute difference (MAD) of the two measurements was calculated [9]. Using the mean value of Cobb angles in manual measurements > 10° as a reference standard for scoliosis, the sensitivity, specificity, accuracy, and positive and negative predictive values of the computer-aided method for diagnosing scoliosis were calculated. A p < 0.05 was considered statistically significant.
Result
The subjects were between 22 and 93 years of age with an average age of 48.0 ± 17.3 years, including 107 males and 141 females. There were 234 single and 14 double curves on chest X-rays. The mean value of the Cobb angles was 14.87° ± 5.57° (range, 6.6°–48.3°) in 992 manual measurements (Table 2).
The intra- and inter-observer reliability of the manual method is shown in Table 3. For both radiologists, intra-observer analyses produced an ICC > 0.9 with a 95% CI between 0.895 and 0.964, as well as a MAD < 3°, which showed that the intra-observer reliability was excellent. In the first and second measurements, inter-observer reliability was good with an ICC > 0.85 and a 95% CI between 0.834 and 0.925, as well as a MAD < 3.5°. The overall ICC of intra- and inter-observer reliability analysis was 0.941 and 0.887, and an overall MAD was 2.20° and 2.94°, respectively. Generally, the intra-observer reliability of the manual method was slightly better than the inter-observer reliability.
Compared with the manual method, the reliability of the computer-aided method for the Cobb angle measurement was evaluated and is shown in Table 4. The reliability analyses between the computer-aided and manual measurement produced ICC > 0.8 with 95% CI between 0.723 and 0.902. The MAD between the computer-aided and manual measurement was < 4°. The overall ICC of 0.854 indicated that the computer-aided method has good reliability for the Cobb angle measurement. The overall MAD of 3.32° was < a 5° threshold of measurement variability.
Various diagnostic test evaluation metrics, including sensitivity, specificity, accuracy, and positive and negative predictive values, are summarized in Table 5. The sensitivity and specificity of the computer-aided method for diagnosing scoliosis were 89.59% and 70.37%, respectively. The accuracy of 87.50% demonstrated that the computer-aided method had a good performance for scoliosis diagnosis.
Discussion
The Cobb angle is involved in the diagnosis and therapeutic decisions of scoliosis. Therefore, the reliability and accuracy are crucial with respect to the Cobb angle measurement. Manual measurement on printed radiographs can be easily performed and regarded as the standard for reliability assessment [9, 15]. In some cases, the endplates of vertebral bodies are difficult to recognize on printed chest X-rays. Contrast adjustment and image magnification of PACS can result in relatively clear recognition for endplates. Hence, the manual measurement was performed on digital chest X-rays using PACS in the current study. The intra- and inter-observer variability of manual measurement on digital chest X-rays performed by radiologists was comparable with that on printed radiographs performed by orthopedic surgeons in previous studies [9, 16, 17] (Table 6). Even though radiologists received support from PACS, the variability that was caused by the defect in classic measurement of the Cobb angle still remained [17]. The Cobb angle was measured on the basis of the orientation of endplates in classic measurement [13]. Unlike radiographs of the spine, the endplates located behind the superior mediastinum are usually not apparent on chest X-rays. Additionally, the projection of endplates occasionally appears to be a cup or fusiform shape (Fig. 4). In the case in which the endplates of the end vertebrae occur in the aforementioned condition, the classic measurement would be unreliable and variability prone [17, 18].
In our approach, a computer-aided method was proposed in accordance with the orientation of the overall spinal curve rather than the endplates. The Cobb angle, as measured by the computer-aided method, was the maximum angle between the superior perpendicular of the cranial vertebrae and the inferior perpendicular of the caudal vertebrae at the longitudinal central lines of the vertebral bodies. Generally, the variability of the Cobb angle measurement > 5° can interfere with the diagnosis and treatment of scoliosis [19]. Compared with manual measurements, the variability of computer-aided measurement using our proposed method was 3.32°, implying clinical value. Our result was slightly better than other computer-aided methods without manual intervention [8, 15] (Table 6). The ICC between the computer-aided result with the proposed method and manual measurement was > 0.8, which is considered good reliability. Although our computer-aided method had a slightly theoretical alteration for classical measurement, the results of reliability analysis indicated that it could provide similar clinical validity in the Cobb angle measurement. For diagnosing scoliosis on chest X-rays, our computer-aided method achieved a high level of sensitivity (89.59%) and a relatively low level of specificity (70.37%). The low value of specificity was expected to be compensated in the future by increasing the variability of the vertebral appearance in the learning procedure of the Mask R-CNN model. The accuracy of 87.50% indicated that the computer-aided method had a good performance in diagnosis of scoliosis. This is the first report of the diagnostic accuracy of a computer-aided method for diagnosing scoliosis on chest X-rays.
The computer-aided method was targeted to automatically diagnose scoliosis on chest X-rays from lung cancer screening. Because the number of chest X-rays is enormous, the efficiency is an important parameter to appraise the application value of computer-aided method. Manual intervention was not needed in the computer-aided method, which was an important advantage comparing with the previous studies [6, 9, 16, 20,]. Moreover, the average process time of a chest X-ray was < 15 s and superior to the documented results [6, 15]. It was implied that the computer-aided method could be used in real-time scoliosis diagnosis during lung cancer screening using chest X-rays.
There were a few limitations in the current study. First, the Cobb angle measured by the computer-aided method was the maximum angle between the superior perpendicular of cranial vertebrae and inferior perpendicular of caudal vertebrae at the longitudinal central line of the vertebral body. When the spinal curves were ≥ 3, the computer-aided method might occasionally yield an incorrect result (Fig. 5). Second, the whole spine radiographs were considered as the standard images for scoliosis assessment. The computer-aided method was needed to be trained and tested on the whole spine radiographs. Third, this retrospective study was a preliminary evaluation of the computer-aided method, and a prospective evaluation would be performed in further study.
Conclusion
For Cobb angle measurement on chest X-rays, our computer-aided method showed good reliability and its variability was < the 5° threshold. Additionally, the computer-aided method achieved a high level of sensitivity (89.59%) and a relatively low level of specificity (70.37%) for diagnosing scoliosis. Therefore, the computer-aided method was potential and hopeful for automatic diagnosis of scoliosis on chest X-rays from lung cancer screening.
References
Qiu GX (2017) Scoliosis in China: history and present status. Chin Med J (Engl) 130(21):2521–2523. https://doi.org/10.4103/0366-6999.217081
Kim W, Porrino JA, Hood KA, Chadaz TS, Klauser AS, Taljanovic MS (2018) Clinical evaluation, imaging, and management of adolescent idiopathic and adult degenerative scoliosis. Curr Probl Diagn Radiol. https://doi.org/10.1067/j.cpradiol.2018.08.006
Trobisch P, Suess O, Schwab F (2010) Idiopathic scoliosis. Dtsch Arztebl Int 107(49):875–884. https://doi.org/10.3238/arztebl.2010.0875
Schmid SL, Buck FM, Böni T, Farshad M (2016) Radiographic measurement error of the scoliotic curve angle depending on positioning of the patient and the side of scoliotic curve. Eur Spine J 25(2):379–384. https://doi.org/10.1007/s00586-015-4259-5
Ye X, Lou D, Ding X, Xie C, Gao J, Lou Y, Cen Z, Xiao Y, Miao Q, Xie F, Zheng X, Wu J, Li F, Luo W (2017) A clinical study of the coronal plane deformity in Parkinson disease. Eur Spine J 26(7):1862–1870. https://doi.org/10.1007/s00586-017-5018-6
Zhang J, Lou E, Shi X, Wang Y, Hill DL, Raso JV, Le LH, Lv L (2010) A computer-aided Cobb angle measurement method and its reliability. J Spinal Disord Tech 23(6):383–387. https://doi.org/10.1097/BSD.0b013e3181bb9a3c
Bonanni PG (2017) Contour and Angle-Function Based Scoliosis Monitoring: relaxing the Requirement on Image Quality in the Measurement of Spinal Curvature. Int J Spine Surg 11:22. https://doi.org/10.14444/4022
Wu H, Bailey C, Rasoulinejad P, Li S (2018) Automated comprehensive adolescent idiopathic scoliosis assessment using MVC-Net. Med Image Anal 48:1–11. https://doi.org/10.1016/j.media.2018.05.005
Zhang J, Li H, Lv L, Zhang Y (2017) Computer-aided cobb measurement based on automatic detection of vertebral slopes using deep neural network. Int J Biomed Imaging 2017:9083916. https://doi.org/10.1155/2017/9083916
He K, Gkioxari G, Dollar P, Girshick R (2018) Mask R-CNN. IEEE Trans Pattern Anal Mach Intell. https://doi.org/10.1109/tpami.2018.2844175
Lin T Y, Dollár P, Girshick R, He K, Hariharan B, Belongie S (2017) Feature pyramid networks for object detection. In: The IEEE conference on computer vision and pattern recognition (CVPR), pp 2117–2125. https://doi.org/10.1109/cvpr.2017.106
Ren S, He K, Girshick R, Sun J (2017) Faster R-CNN: towards real-time object detection with region proposal networks. IEEE Trans Pattern Anal Mach Intell 39(6):1137–1149. https://doi.org/10.1109/TPAMI.2016.2577031
Wang J, Zhang J, Xu R, Chen TG, Zhou KS, Zhang HH (2018) Measurement of scoliosis Cobb angle by end vertebra tilt angle method. J Orthop Surg Res 13(1):223. https://doi.org/10.1186/s13018-018-0928-5
Guo J, Deng XC, Ling QJ, Yin ZX, He EX (2017) Reliability analysis of Cobb measurement in degenerative lumbar scoliosis using endplate versus pedicle as bony landmarks. Postgrad Med 129(7):762–767. https://doi.org/10.1080/00325481.2017.1343645
Sardjono TA, Wilkinson MH, Veldhuizen AG, van Ooijen PM, Purnama KE, Verkerke GJ (2013) Automatic Cobb angle determination from radiographic images. Spine (Phila Pa 1976) 38(20):E1256–E1262. https://doi.org/10.1097/brs.0b013e3182a0c7c3
Qiao J, Liu Z, Xu L, Wu T, Zheng X, Zhu Z, Zhu F, Qian B, Qiu Y (2012) Reliability analysis of a smartphone-aided measurement method for the Cobb angle of scoliosis. J Spinal Disord Tech 25(4):E88–E92. https://doi.org/10.1097/BSD.0b013e3182463964
Gstoettner M, Sekyra K, Walochnik N, Winter P, Wachter R, Bach CM (2007) Inter- and intraobserver reliability assessment of the Cobb angle: manual versus digital measurement tools. Eur Spine J 16(10):1587–1592. https://doi.org/10.1007/s00586-007-0401-3
Morrissy RT, Goldsmith GS, Hall EC, Kehl D, Cowie GH (1990) Measurement of the Cobb angle on radiographs of patients who have scoliosis Evaluation of intrinsic error. J Bone Jt Surg Am 72(3):320–327. https://doi.org/10.1016/0020-1383(90)90076-7
Langensiepen S, Semler O, Sobottke R, Fricke O, Franklin J, Schönau E, Eysel P (2013) Measuring procedures to determine the Cobb angle in idiopathic scoliosis: a systematic review. Eur Spine J 22(11):2360–2371. https://doi.org/10.1007/s00586-013-2693-9
Al-Bashir AK, Al-Abed MA, Amari HK, Al-Rousan FM, Bashmaf OMK, Abdulhay EW, Al Abdi RM, Arunkumar N, Tapas Bapu BR, Al-Basheer AK (2018) Computer-based Cobb angle measurement using deflection points in adolescence idiopathic scoliosis from radiographic images. Neural Comput Appl. https://doi.org/10.1007/s00521-018-3614-y
Funding
Funding was provided by “Yanhai-Ruijin Artificial Intelligence Aided Imaging Diagnostic Platform” Special Fund (Grant No. 2018188), Magnetic Resonance (MR)-Dominated Joint Replacement Imaging Evaluation System Research and Clinical Application (Grant No. 17411964900), and Action Plan of Major Diseases Prevention and Treatment (Grant No. 2017ZX01001-S12).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Pan, Y., Chen, Q., Chen, T. et al. Evaluation of a computer-aided method for measuring the Cobb angle on chest X-rays. Eur Spine J 28, 3035–3043 (2019). https://doi.org/10.1007/s00586-019-06115-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00586-019-06115-w