Skip to main content
SpringerLink
Log in

A priori error estimates for upwind finite volume schemes for two-dimensional linear convection diffusion problems

  • Published:
Bulletin of the Brazilian Mathematical Society, New Series Aims and scope Submit manuscript

Abstract

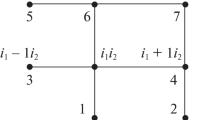
It is still an open problem to prove a priori error estimates for finite volume schemes of higher order MUSCL type, including limiters, on unstructured meshes, which show some improvement compared to first order schemes. In this paper we use these higher order schemes for the discretization of convection dominated elliptic problems in a convex bounded domain Ω in R2 and we can prove such kind of an a priori error estimate. In the part of the estimate, which refers to the discretization of the convective term, we gain h 1/2. Although the original problem is linear, the numerical problem becomes nonlinear, due to MUSCL type reconstruction/limiter technique.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. D. Bouche, J.-M. Ghidaglia and F-P. Pascal. Error estimate for the upwind finite volumemethod for the nonlinear scalar conservation law. J. Comput. Appl. Math., 235(18) (2011), 5394–5410.

    Article  MathSciNet  MATH  Google Scholar 

  2. A. Bradji and J. Fuhrmann. Some abstract error estimates of a finite volume scheme for a nonstationary heat equation on general nonconforming multidimensional spatial meshes. Appl. Math., Praha, 58(1) (2013), 1–38.

    MathSciNet  MATH  Google Scholar 

  3. F. Brezzi, T. J. R. Hughes, L. D. Marini, A. Russo and E. Süli. A priori error analysis of residual-free bubbles for advection-diffusion problems. SIAMJ. Numer. Anal., 36(6) (1999), 1933–1948.

    Article  MathSciNet  MATH  Google Scholar 

  4. C. Chainais-Hillairet. Second-order finite-volume schemes for a nonlinear hyperbolic equation: Error estimate. Math. Methods Appl. Sci., 23(5) (2000), 467–490.

    Article  MathSciNet  MATH  Google Scholar 

  5. B. Cockburn, F. Coquel and P. LeFloch. An error estimate for finite volumemethods for multidimensional conservation laws. Math. Comp., 63(207) (1994), 77–103.

    Article  MathSciNet  MATH  Google Scholar 

  6. B. Cockburn, F. Coquel and P. LeFloch. Convergence of the finite volume method for multidimensional conservation laws. SIAMJ. Numer. Anal., 32 (1995), 687–705.

    Article  MathSciNet  MATH  Google Scholar 

  7. B. Cockburn and P.-A. Gremaud. A priori error estimates for numerical methods for scalar conservation laws. Part I: The general approach. Math. Comp., 65(214) (1996), 533–573.

    Article  MathSciNet  MATH  Google Scholar 

  8. B. Cockburn and C. W. Shu. TVB Runge–Kutta projection discontinuous Galerkin finite element method for conservation laws. II: General framework. Math. Comp., 52 (1989), 411–435.

    MathSciNet  MATH  Google Scholar 

  9. B. Cockburn and W. Zhang. A posteriori error estimates for HDG methods. J. Sci. Comput., 51 (3) (2012), 582–607.

    Article  MathSciNet  MATH  Google Scholar 

  10. L. J. Durlofsky, B. Engquist and S. Osher. Triangle based adaptive stencils for the solution of hyperbolic conservation laws. J. Comput. Phys., 98 (1992), 64–73.

    Article  MATH  Google Scholar 

  11. R. Eymard, T. Gallouët and R. Herbin. Cell centred discretisation of non linear elliptic problems on general multidimensional polyhedral grids. J. Numer. Math., 17 (3) (2009), 173–193.

    Article  MathSciNet  MATH  Google Scholar 

  12. R. Eymard, G. Henry, R. Herbin, F. Hubert and R. Klöfkorn. 3D benchmark on discretization schemes for anisotropic diffusion problems on general grids. In: Fort, Jaroslav (ed.) et al., “Finite volumes for complex applications VI: Problems and perspectives”. FVCA 6, international symposium, Prague, Czech Republic, June 2011, Vol. 1 and 2. Springer Proceedings inMathematics, 4 (2011), 895–930.

    MATH  Google Scholar 

  13. M. Feistauer, J. Felcman and M. Lukácová-Medvidová. On the convergence of a combined finite volume-finite element method for nonlinear convection–diffusion problems. Num. Meth. PDE, 13 (1997), 1–28.

    Article  MathSciNet  MATH  Google Scholar 

  14. B. Heinrich. Finite Difference Methods on Irregular Networks. Birkhäuser, Basel, (1987).

    Book  MATH  Google Scholar 

  15. R. Herbin. An error estimate for a finite volume scheme for a diffusion-convection problem on triangular mesh. Num. Meth. PDE, 11 (1995), 165–173.

    Article  MathSciNet  MATH  Google Scholar 

  16. C. Johnson and A. Szepessy. Convergence of a finite elementmethod for a nonlinear hyperbolic conservation law. Math. Comp., 49 (1987), 427–444.

    Article  MathSciNet  MATH  Google Scholar 

  17. C. Johnson. Numerical solution of partial differential equations by the finite element method. Cambridge University Press, (1994).

    Google Scholar 

  18. D. Kröner, S. Noelle and M. Rokyta. Convergence of higher order upwind finite volume schemes on unstructured grids for scalar conservation laws in two space dimensions. Num. Math., 71 (4) (1995), 527–560.

    Article  MATH  Google Scholar 

  19. D. Kröner and M. Rokyta. Convergence of upwind finite volume schemes for scalar conservation laws in 2D. SIAMJ. Numer. Anal., 31 (2) (1994), 324–343.

    Article  MATH  Google Scholar 

  20. D. Kröner and M. Rokyta. Apriori error estimates for upwind finite volume schemes for two-dimensional linear convection diffusion problems. Preprint, to appear.

  21. G. Lube. Streamline diffusion finite element method for quasilinear elliptic problems. Num. Math., 61 (1992), 335–357.

    Article  MathSciNet  MATH  Google Scholar 

  22. M. Lukácová-Medvidová. Combined finite element-finite volume method (convergence analysis). Comment. Math. Univ. Carolinae, 38(3) (1997), 717–741.

    MathSciNet  MATH  Google Scholar 

  23. C. Rohde. Weakly coupled hyperbolic systems. PhD Thesis, Universität Freiburg, (1996).

    MATH  Google Scholar 

  24. E. Süli. A posteriori error analysis and adaptivity for finite element approximations of hyperbolic problems, in: Kröner, Dietmar (ed. ) et al., “An introduction to recent developments in theory and numerics for conservation laws”. Proceedings of the international school, Freiburg/ Littenweiler, Germany, October 20-24, 1997. Springer. Lect. Notes Comput. Sci. Eng. 5 (1999), 123–194.

    Article  MathSciNet  MATH  Google Scholar 

  25. J.-P. Vila. Convergence and error estimates in finite volume schemes for general multi-dimensional scalar conservationlaws. I:Explicitmonotone schemes. M2AN, 28(3) (1994), 267–295.

    MathSciNet  MATH  Google Scholar 

  26. M. Vlasak, V. Dolejsi and J. Hajek. A priori error estimates of an extrapolated space-time discontinuous Galerkin method for nonlinear convection-diffusion problems. Numer. Methods Partial Differential Equations, 27(6) (2011), 1456–1482.

    Article  MathSciNet  MATH  Google Scholar 

  27. Q. Zhang and C.-W. Shu. Error estimates to smooth solutions of Runge-Kutta discontinuous Galerkin method for scalar conservation laws. SIAM J. Numer. Anal., 42(2) (2004), 641–666.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Universität Freiburg, Institut für AngewandteMathematik, Hermann–Herder–Str. 10, 79104, Freiburg, Germany

    Dietmar Kröner

  2. Charles University, Faculty of Mathematics and Physics, Department of Mathematical Analysis, Sokolovská 83, 186 75, Praha, Czech Republic

    Mirko Rokyta

Authors
  1. Dietmar Kröner
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mirko Rokyta
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dietmar Kröner.

Additional information

M. Rokyta was partially supported by Prvouk P47.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kröner, D., Rokyta, M. A priori error estimates for upwind finite volume schemes for two-dimensional linear convection diffusion problems. Bull Braz Math Soc, New Series 47, 473–488 (2016). https://doi.org/10.1007/s00574-016-0163-9

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00574-016-0163-9

Keywords

Mathematical subject classification

Search

Navigation