1 Introduction

Thanks to the recent development of new magnetic and piezoelectric materials, it is now possible to build sensors for measuring constant magnetic field strength with values from just a few to several hundreds of A/m (Mermelstein 1992; Prieto et al. 1998). The principle of operation of this type of sensor is based on the mechanical effect of the magnetostrictive element (due to the magnetic field) on the piezoelectric associated with it Duc and Huong Giang (2008). This interaction is described in the literature as the magnetoelectric effect (ME). It is based on changes in the dielectric polarisation (P) of the piezoelectric caused by the magnetostrictive deformation of the cooperating magnetic material, after applying the magnetic field (H) to it Dong et al. (2003).

The aim of the paper is to present modeling and measurements of the internal characteristics of the ring-shaped magnetoelectric sensor. This is the original design aimed at overcoming the existing problems with measuring the weak magnetic fields and non-linearity of the characteristics in such devices. Its internal operation is primarily represented by the magnetic hysteresis loop, which should be suppressed if possible. The important part of the work is this loop modelling to accurately represent the actual device, depending on its physical characteristics (such as dimensions or material parameters). Constructing such a function is a regression task, which can be solved with different algorithms. The Multilayered Perceptron (MLP) and Support Vector Machine (SVM) in regression mode were used for this purpose. The accuracy of the heuristic modelling was verified by exploiting the actual sensor.

The structure is as follows. In Sect. 2, the state of the art in the field of magnetoelectric sensors is presented due to stress deficiencies and limitations of existing designs. Section 3 covers the structure of the sensor. In Sect. 4 the theoretical model is described, while in Sect. 5 the heuristic regression algorithms for the output voltage from the sensor characteristics modeling are introduced. Section 6 covers the experimental results. In Sect. 7 conclusions are provided.

2 Magnetoelectric sensors

In the literature numerous examples of magnetoelectric sensor implementations can be found, working mainly in the resonance frequency (Gao et al. 2021; Bichurin et al. 2017, 2021; Dong et al. 2004; Leung et al. 2010). Solutions with an open magnetic circuit (rectangular-type ME laminates) are usually presented, which reduces the output signal by demagnetization (Mermelstein 1992; Prieto et al. 1998; Duc and Huong Giang 2008; Dong et al. 2003, 2004; Gao et al. 2021; Bichurin et al. 2021, 2017; Leung et al. 2010). In Bichurin et al. (2017) the characteristics of a nonresonant current sensor were described, showing that in the operating range of up to 5A, the sensor had a sensitivity of 0.34 V/A and a non-linearity of less than 1%.

For this reason, solutions with a closed magnetic circuit have a greater development potential. In devices presented in Dong et al. (2004), the voltage induced in the transducer at the output of the piezoelectric electrodes (excited by a constant magnetic field) was proportional to the measured alternating magnetic field. Alternatively, current transducers made of ME composites allow for the measurement of alternating or direct current in a conductor by measuring the excited eddy field around it, according to Ampere’s law. The magnetic field’s strength depends on the value of the current I in the conductor and the distance r from it (i.e. H = I/2πr) (Dong et al. 2004). Therefore, ME ring laminates are essential for electrical current sensors. For example, in Leung et al. (2010) a ring electric current sensor is proposed, which reacts to an eddy magnetic field. The design of the device was based on a ring shape consisting of an axially polarised PZT ceramic ring sandwiched between two circumferentially magnetised composite rings composed of an epoxy resin, the Terfenol-D/NdFeB magnet. Such a structure is complex and its operation depends on matching the individual elements. Sensitivity of the electric current sensor was assessed both theoretically and experimentally. The sensor demonstrated a high non-resonant sensitivity of ~ 12.6 mV/A over a narrow frequency range of 1 Hz–30 kHz and a high resonant sensitivity of 92.2 mV/A at a basic resonance of 67 kHz, in addition to a linear relationship between the input electric current and the voltage induced at the output (Leung et al. 2010). This sensor can be used to measure the current flowing in a power line cable.

Another example is the cylindrical layered multiferroic Ni/PZT/Ni heterostructures prepared by the low-voltage deposition method. A thin Ni foil, as the magnetic phase, was deposited on a commercial PZT substrate, which is the piezoelectric phase. Hollow Pb (Zr, Ti) O3 cylinders with dimensions of outer diameter D1 = 13 mm, inner diameter D2 = 11 mm and height h = 20 mm, 25 mm, 30 mm were cut. By controlling the low voltage deposition time, the thicknesses of the outer and inner Ni layers were controlled and measured at 80 ± 2 µm with an optical microscope. After electroless deposition, the cylindrical Ni/PZT/Ni compound is polarised along the radial direction in silicone oil under an electric field of 30 kV/cm (Xie et al. 2014).

In Giang et al. (2020) the eddy magnetic field sensor made of Metglas/piezoelectric (PZT) laminates with open and closed magnetic circuit (OMC and CMC) of various widths, lengths, and diameters was proposed. Among these geometries, CMC laminates show advantages not only in terms of magnetic flux distribution, but also sensitivity and independence from the position of the vortex center. It was found that the ME voltage signal is enhanced by increasing the volume of the magnetostrictive phase. Four layers of Metglas metal ribbon were used to produce a multilayer magnetoelectric current sensor based on a double-ring-shaped CMC with dimensions D × W = 6 × 1.5 mm. With a resonant frequency of 174.4 kHz, this sensor exhibited a sensitivity of 5.426 V/A (Giang et al. 2020).

In Kuczynski (2010), the possibility of making a ring magnetic field sensor was described, where an amorphous ribbon is glued to the outer surface of the ring. Its utility model and preliminary tests were presented in Kuczynski et al. (2020), Kuczynski et al. (2023). A similar design in terms of the usage of the Metglas ribbon and the PZT ring is presented in Chashin and Fetisov (2021). The construction of the sensor shows significant changes in inductance at frequencies of 0.1-10 kHz.

3 Sensor design

The developed sensor is the use of a magnetic element with a closed magnetic circuit. Such a structure reduces the impact of interference on the useful signal and the possibility of determining the return of the measured constant magnetic field strength, which has not been realized so far in sensors with an open magnetic circuit. Thanks to this concept, it is possible to obtain a greater sensitivity of this type of sensors than in the case of sensors with an open magnetic circuit, e.g., stripe core.

The two ring-shaped sensor solution was also created. It detects eddy fields and direct or alternating currents flowing in the conductor. In this case a small area of the piezoelectric subject to deformation from the magnet results in low sensitivity for fields other than vertical ones. To detect both eddy and other magnetic fields, a ring with a height comparable to the diameter should be used. This increases the sensitivity of the sensor and creates new possibilities for field detection.

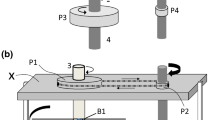
The sensor shown in Fig. 1 consists of a thin-walled ring made of piezoelectric ceramics with a height approximately equal to half the outer diameter. The piezoelectric ceramics are characterized by high values of the dielectric constant, piezoelectric constants and the piezoelectric voltage ratio. On the outer surface of the piezoelectric ring, there is a centrally glued amorphous ribbon with a width twice smaller than the height of the ring. It has a narrow magnetic hysteresis loop, resulting in a small loss of energy needed to remagnetize the material. The amorphous ribbon is connected to the PZT ring using an adhesive used to attach the strain gauges. An excitation winding is wound on the PZT ring joined to ribbon. The control current Is is fed to the winding, which produces a variable control field Hs (marked with an arrow), which activates the sensor. The ribbon stuck to the ring is influenced by a constant, measured magnetic field Hdc, causing a magnetostrictive deformation in the magnetic ribbon, transferred to the piezoelectric ring. As a result of the Hdc + Hs field on the sensor in the electrodes of the PZT ring, a voltage Uout proportional to the value of the Hdc field is generated. The generated output voltage from the sensor's is proportional to the measured magnetic field created around the wire in which the current flows (Kuczynski 2010, 2013).

Fig. 1
figure 1

The diagram of the magnetoelectric sensor prototype (Kuczynski 2013)

Full size image

The sensor prototype was made of the Metglas 2506Co amorphous ribbon and the PZ27 ring. The following catalogue data are available for these materials: elastic compliance at constant electric displacement, piezoelectric constant, dielectric stiffness at constant stress, magnetostriction saturation, and density of the magnetostrictive and piezoelectric materials.

The research results carried out so far have been presented in Kuczynski (2010, 2013), Kuczynski et al. (2020). In Kuczynski et al. (2020, 2023), the preliminary results of magnetic hysteresis loop tests for the amorphous ribbon were presented. In Chashin and Fetisov (2021) the implementation of such a solution was presented and it was shown that changes in the inductance are greatest at frequencies of 0.1–10 kHz.

4 Theoretical model

For magnetoelectric flat sensors, many mathematical models have been developed, especially the ones using equivalent circuits (Bichurin and Petrov 2014; Bichurin et al. 2019). However, since around 2012, researchers have mainly used the Hamiltonian principle to model magnetoelectric ring sensors (Zhang et al. 2012, 2019). This work implements a modified mathematical model presented in 2010 (Guo and Dong 2010). It shows a magnetoelectric sensor composed of piezoelectric and magnetic rings connected in layers. However, in the ring magnetic field sensor built as part of this work, the cylindrical ring is made of a piezoelectric material which is covered with a magnetostrictive layer in the form of an amorphous ribbon glued to the outer surface of the piezoelectric material. We focus on a cylindrical annulus made of a piezoelectric material with the outer surface covered with a thin magnetostrictive ribbon glued to the piezoelectric material.

The advantage of the presented sensor solution is that the tape thickness (amorphous ribbon) is about 40 µm and thus its dimensions limit eddy current losses at higher frequencies, which makes it possible to measure fast-changing current waveforms, where the sensor no longer requires additional excitation.

The inner radius of the annulus is R1, while the outer radius is R2, as depicted in Fig. 2. Assuming that the outer magnetostrictive ribbon is very thin (that is, R2 ≈ R3), an appropriate boundary condition on the outer surface of the piezoelectric can be imposed. In cylindrical polar coordinates, the focus is on the strains Sθ and Sr, and stresses Tθ and Tr, representing the diagonal radial and azimuthal components of the strain and stress tensor, respectively. In the considered design, the magnetic field is expected to have an azimuthal direction, and the resulting electric field to be radial, thus only the electric field Er and electric induction field Dr is considered. The constitutive equations for the piezoelectric material can then be written as Guo and Dong (2010), Ha and Kim (2001):

$${S}_{rr}={s}_{11}{T}_{rr}+{s}_{12}{T}_{\theta \theta }+{g}_{11}{D}_{r}$$
(1)
$${S}_{\theta \theta }={s}_{12}{T}_{rr}+{s}_{11}{T}_{\theta \theta }+{g}_{11}{D}_{r}$$
(2)
$${E}_{r}={-g}_{11}\left({T}_{rr}+{T}_{\theta \theta }\right)+{\beta }_{11}{D}_{r}$$
(3)

where s11, s12 is the elastic compliance at constant electric displacement, g11 is the piezoelectric constant, and β11 denotes dielectric stiffness at constant stress. Due to the special axial symmetry, it is assumed that there is no azimuthal displacement and that the displacement u is radial: u = u(r). All axial displacements (i.e., the ones in the z direction) are omitted. The Kirchhoff hypotheses for thin round plates [for which Hook’s law general (Szeptynski 2020; Murakami 2017) is fulfilled] are applicable here. The middle plane does not experience any elongations or deformations, while plate points normal to the median plane remain also after deformation (the section perpendicular to the undeformed median surface remains rectilinear, nonelongated, and perpendicular to the median surface). Finally, normal stresses perpendicular to the median surface are small compared to other stresses. The strain- displacement relationship takes the form:

Fig. 2
figure 2

Top view of the sensor. The gold-shaded area is a piezoelectric material. The blue outline marks the magnetostricitve metal ribbon

Full size image
$${S}_{rr}=\frac{du\left(r\right)}{dr}, {S}_{\theta \theta }=\frac{u\left(r\right)}{r}$$
(4)

The electrodes in the proposed device are placed on the inner and outer surface of the cylinder. Thus, the voltage V between the electrodes can be found by integrating the electric field across the piezoelectric layer:

$$V=\underset{{R}_{1}}{\overset{{R}_{2}}{\int }}E\left(r\right)dr$$
(5)

The electric induction field is then found as a function of the voltage and used to calculate the total charge in the cylinder as:

$$D\left(r\right)=\frac{V}{\overline{\beta }}-\gamma \left({S}_{rr}+{S}_{\theta \theta }\right)=\frac{V}{\overline{\beta }}-\gamma \left(\frac{du\left(r\right)}{dr}+\frac{u\left(r\right)}{r}\right)$$
(6)
$$Q=\underset{{R}_{1}}{\overset{{R}_{2}}{\int }}D\left(r\right)rdr=\frac{V}{\overline{\beta }}-\gamma \underset{{R}_{1}}{\overset{{R}_{2}}{\int }}\left({S}_{rr}+{S}_{\theta \theta }\right)rdr={C}_{0}V-\gamma {\left.u\left(r\right)\right|}_{{R}_{1}}^{{R}_{2}}$$
(7)

where the following constants are defined Szeptynski (2020), Murakami (2017):

$$\overline{\beta }={\beta }_{11}\left(1+\frac{2{g}_{11}^{2}}{{\beta }_{11}{s}_{11}\left(1-\sigma \right)}\right), \sigma =-\frac{{s}_{12}}{{s}_{11}}, \gamma =-\frac{{g}_{11}}{\overline{\beta }{s}_{11}\left(1-\sigma \right)}$$
(8)

Following a similar derivation to that described in Chashin and Fetisov (2021) and Bichurin and Petrov (2014), the following equation for the radial displacement is obtained as:

$$\frac{{d}^{2}u}{d{r}^{2}}+\frac{1}{r}\frac{du}{dr}-\frac{u}{{r}^{2}}+{\lambda }^{2}u=0$$
(9)

with λ being a function of the angular frequency:

$$\lambda =\frac{\rho }{{s}_{11}d}\omega$$
(10)

Because (9) is a Bessel equation, the family of solutions can be deduced to be Bessel functions of the first and second kind: J1(λr) and Y1(λr), respectively. The coefficients of the solution are determined from boundary conditions. The vectors of the coefficients in this solution are defined by Szeptynski (2020), Murakami (2017):

$${\varvec{A}}=\left({A}_{1},{A}_{2}\right)$$
(11)
$${\varvec{\phi}}=\left({J}_{1}\left(\lambda r\right),{Y}_{1}\left(\lambda r\right)\right)$$
(12)
$${\varvec{u}}={\varvec{\phi}}\cdot {\varvec{A}}$$
(13)

The forces and displacements at the boundary are then given by:

$${\varvec{F}}={{\varvec{B}}}^{F}\cdot {\varvec{A}}+{{\varvec{C}}}^{H}\cdot {{\varvec{H}}}_{0}+{{\varvec{C}}}^{{\varvec{V}}}V$$
(14)
$${\varvec{u}}={{\varvec{B}}}^{{\varvec{u}}}\cdot {\varvec{A}}$$
(15)

The impedance matrix is then formed, for which the velocity vector U and electric current I are used instead of the displacement u and charge Q, respectively. In the harmonic response approach, these are related by:

$${\varvec{U}}=j\omega {\varvec{u}}, {\varvec{I}}=j\omega {\varvec{Q}}$$
(16)

Now, the force on the boundary may be related to the velocity as:

$$\left( {\begin{array}{*{20}c} \varvec{F} \\ { - \varvec{I}} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} \varvec{Z} \\ {sym.} \\ \end{array} \begin{array}{*{20}c} {\varvec{C}^{V} } \\ { - \varvec{Z}_{C}^{{ - 1}} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} \varvec{U} \\ \varvec{V} \\ \end{array} } \right) + \varvec{H}_{0} \left( {\begin{array}{*{20}c} {\varvec{C}^{H} } \\ 0 \\ \end{array} } \right)$$
(17)
$${\varvec{Z}}=\frac{1}{j\omega }{{\varvec{B}}}^{{\varvec{F}}}{\left({{\varvec{B}}}^{{\varvec{u}}}\right)}^{-1}$$
(18)
$${{\varvec{Z}}}_{{\varvec{C}}}=\frac{1}{j\omega }{\left({{\varvec{C}}}_{0}\right)}^{-1}$$
(19)

Exchanging the positions force and velocity vectors, the admittance matrix is constructed:

$$\left( {\begin{array}{*{20}c} \varvec{U} \\ \varvec{I} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} \varvec{Y} \\ {sym.} \\ \end{array} \begin{array}{*{20}c} { - \varvec{Y} \cdot \varvec{C}^{V} } \\ {\varvec{Y}_{E}^{{}} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\varvec{F} - \varvec{H}_{0} \cdot \varvec{C}^{H} } \\ \varvec{V} \\ \end{array} } \right)$$
(20)

with the electrical admittance matrices

$${\varvec{Y}}={\left({\varvec{Z}}\right)}^{-1}$$
(21)
$${{\varvec{Y}}}_{{\varvec{E}}}={\left({{\varvec{C}}}^{{\varvec{V}}}\right)}^{{\varvec{T}}}\cdot {\varvec{Y}}\cdot {{\varvec{C}}}^{{\varvec{V}}}+j\omega {{\varvec{C}}}_{0}$$
(22)

This allows for expressing the voltage between the inner and outer surfaces of the piezoelectric as a ‘linear’ function of the external field.

$$V=-{{\varvec{H}}}_{0}\frac{{\left({{\varvec{C}}}^{{\varvec{V}}}\right)}^{{\varvec{T}}}\cdot {\varvec{Y}}\cdot {{\varvec{C}}}^{{\varvec{H}}}}{j\omega {{\varvec{C}}}_{0}+{\left({{\varvec{C}}}^{{\varvec{V}}}\right)}^{{\varvec{T}}}\cdot {\varvec{Y}}\cdot {{\varvec{C}}}^{{\varvec{V}}}}=f\left(\omega \right){{\varvec{H}}}_{0}$$
(23)

with the response coefficient depending on the properties of the material. This enables to study the frequency dependent response of the system.

5 Heuristic modeling

The advantage of the heuristic regression is the automated construction of the input–output relationship indirectly, i.e. without the accurate description of the internal state of the sensor. Such methods are useful when the mathematical relations are complex and their calculation would be difficult and time consuming. In the experiments presented here, the selected regression methods were used to produce the processing output characteristics which can be compared to the theoretical ones. To use such algorithms, the training data must be used, with the input values of the excitation field Hs and the output values of the voltage from the sensor. This allows for supervised training, where the expected output of the regression machine is known. The training sets were obtained from the prototype of the sensor, containing 1198 observations, each having single input and output values. The modeled characteristics included output voltage from the sensor. Because the training data might be affected by the noise, the applied algorithms should be able to consider it during the function construction.

The heuristics were modeled in Python with the use of scikit-learn module for machine learning. Of multiple available approaches to regression modelling [such as linear regression, M5 tree (Behrooz et al. 2018) or Gaussian process regression (Forsyth 2019)], multilayer perceptron (MLP) (Lopez and Caicedo 2005; Rohani et al. 2017) and support vector machine (SVM) (Behrooz et al. 2018) were selected. The Artificial Neural Network (ANN) is well known in industrial applications, used in tasks where continuous non-linear functions can be modelled. It is often used as a reference Forsyth (2019), Stampfli and Youssef (2020). The network consists of inputs, at least one hidden layer of neurons with nonlinear activation functions (such as hyperbolic tangent or sigmoidal function) and a single linear output neuron. Training the network exploits the error backpropagation technique. Hyperparameters of the ANN include the number of hidden layers and the number of neurons inside each layer. In Zhu et al. (2021), convolutional neural networks (CNN) was used. Presented results show that ANN can be used to predict the magnetoelectric effect. In our experiments, we used MLP and SVM networks in regression mode. For the MLP network, we used activation functions in the form of a hyperbolic tangent.

The SVM-based regression machine (SVR) was selected because it allows for obtaining acceptable results under measurement uncertainty conditions. It is based on the kernel transformation to change the original feature space into the new one, where the regression function has the relative low error (evaluated by one of the popular measures, such as Mean Square Error—MSE, R2, or Root MSE, i.e., RMSE). The SVM has then the single, real-valued output, which produces the desired value. The SVM hyperparameters include the kernel function with its parameters and the regularization coefficient (determining the acceptable regression error on the training data). For the experiments presented here, the RBF function is used. The RBF functions are considered to be the most useful and flexible for a wide range of regression tasks. The effectiveness of these AI models were evaluated with MSE.

6 Experiments

The scope of the presented work is the construction of the theoretical model, which is then confronted against the selected regression-based models, producing the desired sensor characteristics. In the presented work, the most important outcome is the comparison regarding the accuracy between the heuristic and theoretical modelling.

The presented results and experiments conducted here are important part of the authors work on the smart sensor, which will exploit the magnetoelectric effect and will be equipped with the microprocessor part running the characteristics to produce the digital reading of the magnetic field based on the evaluation of the induced current.

Sensor prototype tests were performed using the measurement system shown in Fig. 3. It includes the source of the Hs field controlling the operation of the digital data acquisition system. The sensor’s output signal, which is a function of the measured constant magnetic field Hdc, is processed in a digital measuring system. This system enables visualization of the joint characteristics of Uout.

Fig. 3
figure 3

The scheme of the measurement system

Full size image

Figure 4 shows the waveform of the output voltage obtained experimentally, while Fig. 5 shows the voltage waveform obtained from the mathematical model described in Sect. 5. A distorted sine wave composed of the sin and cos functions with the amplitude resulting from relation (23) was generated. The analytical model created on the basis of the material data and the dimensions of the sensor was verified with the experimental data for this prototype. The standard tool for evaluation of the modeling accuracy is the Mean Square Error (MSE), which allows to determine the distances between the computed and measured voltages:

Fig. 4
figure 4

The output voltage obtained experimentally from the sensor

Full size image
Fig. 5
figure 5

The voltage waveform obtained from the mathematical model

Full size image
$$MSE = \frac{1}{N} \cdot \sum\limits_{{i = 1}}^{N} {\left( {U_{{out}} \left[ i \right] - U_{m} \left[ i \right]} \right)^{2} }$$
(24)

Here, Uout denotes the measured voltage value for the specific magnetic field strength, Um is the modelled value, and N is the number of considered data points. In our system, the MSE value was calculated, which is MSE = 113,3174 mV2.

The experimental measurements show the hysteresis of the magnetic material in the sensor output signal, which is observed in the response of the mathematical model. Yet the values are well-mapped using the mathematical model.

The discrete Fourier transformation of the recorded measurement waveform from Fig. 5 was also performed to determine which harmonics have an influence on the waveform of the output signal from the sensor. Python software was used to create the heuristic model and DFT calculations. Proper results were obtained (Fig. 6), proving that the first 10 harmonics have the greatest influence on the waveform.

Fig. 6
figure 6

DFT for the Uout measurement sequence from Fig. 4

Full size image

The output signal from the sensors was first modeled by a two-layer ANN. Figure 7 shows the result of the operation of a network with the optimal number of 46 neurons in the first hidden layer and 13 neurons in the second, with the MSE error value of 3.3966 mV2.

Fig. 7
figure 7

Modelling of the Uout waveform in Fig. 4 using the MLP network

Full size image

Next, the SVM was applied to the same task. The optimized parameters included the width of the RBF kernel and the regularization coefficient. The optimal results were obtained for the regularisation coefficient of 1 and the kernel width of 100. The number of support vectors was 632 for a dataset of 1198 patterns (Fig. 8). Using SVR, the sensor output voltage (Fig. 8) and the magnetostrictive hysteresis loop (Fig. 9) were obtained. Figure 9 shows a simplification, a negligible magnetostrictive hysteresis loop. The obtained curve maps the measurement data with the magnetostrictive hysteresis loop. Due to the fact that amorphous ribbons have a narrow hysteresis loop, such an approximation was considered sufficient. The MSE was calculated, which was MSE = 4.6411 mV2 for Fig. 8 and MSE = 4.1240 mV2 for Fig. 9.

Fig. 8
figure 8

Modelling the Uout waveform from Fig. 4 using the SVR network

Full size image
Fig. 9
figure 9

Modeling of magnetostrictive hysteresis loop from Fig. 4 using the SVR network

Full size image

The presence of two waveforms in the Figs. 5, 7 and 8 results from the magnetic hysteresis of the amorphous tape (coercive field), which expands as a result of internal stresses created in the production process of the amorphous ribbon (Tumanski 2011). Additional stresses are created by gluing the magnetic tape to the rigid ring of the piezoelectric.

Additional tests were performed on the second prototype of the sensor, where the strip was annealed in the coiled state at a temperature lower than the Curie temperature. This resulted in minimising the width of the magnetic hysteresis loop. The maximum magnetoelectric coefficient of 4.5 mV/cm·Oe was achieved.

The same strip was also tested after annealing, resulting in a decrease in coercivity, which was clearly visible in the tests of the previous prototype (see Figs.  10, 11, 12, 13, 14, 15). Our preliminary studies of magnetic and magnetostrictive hysteresis loops are presented in Kuczynski et al. (2023).

Fig. 10
figure 10

The output voltage obtained experimentally from the second prototype sensor

Full size image
Fig. 11
figure 11

The voltage waveform obtained from the mathematical model for the second prototype sensor

Full size image
Fig. 12
figure 12

DFT for the Uout measurement sequence of the second prototype sensor

Full size image
Fig. 13
figure 13

Modelling of the Uout waveform second prototype sensor in Fig. 10 using the MLP network

Full size image
Fig. 14
figure 14

Modelling the Uout waveform second prototype sensor from Fig. 10 using the SVR network

Full size image
Fig. 15
figure 15

Modeling of magnetostrictive hysteresis loop second prototype sensor from Fig. 10 using the SVR network

Full size image

7 Conclusions

Based on the obtained results and the research methodology, a utility model of a magnetoelectric magnetic field sensor was developed and basic tests of its functional properties were carried out. The use of annealing at a temperature below the Curie temperature resulted in the removal of stresses, which was visible in the reduction of the coercive field. Attention was paid to the presence of the first 10 harmonics in the recorded signal from the prototype sensor. The developed heuristic model can be used in the construction of energy harvesters and powering security devices and data transmission. In the future, automatic AI algorithms based on heuristics allow for hands-off acquisition of parameter values of the sensor models. This, in turn, allows for the identification and modification of sensor parameters.