The initial run-in and long-term drift of the adhesive force between polycrystalline silicon MEMS sidewalls

Abstract

In this paper we measure the evolution of adhesion between two polycrystalline silicon sidewalls of a microelectromechanical adhesion sensor during three million contact cycles. We execute a series of AFM-like contact force measurements with comparable force resolution, but using real MEMS multi-asperity sidewall contacts mimicking conditions in real devices. Adhesion forces are measured with a very high sub-nanonewton resolution using a recently developed optical displacement measurement method. Measurements are performed under well-defined, but different, low relative humidity conditions. We found three regimes in the evolution of the adhesion force. (I) Initial run-in with a large of cycle-to-cycle variability, (II) Stability with low variability, and (III) device-dependent long term drift. The results obtained demonstrate that although a short run-in measurement shows stabilization, this is no guarantee for long-term stable behavior. Devices performing similarly in region II, can drift very differently afterwards. The adhesion force drift during millions of cycles is comparable in magnitude to the adhesion force drift during initial run-in. The boundaries of the drifting adhesion forces are reasonably well described by an empirical model based on random walk statistics. This is useful knowledge when designing polycrystalline silicon MEMS with contacting surfaces.

1 Introduction

The contact mechanics of micro electromechanical systems (MEMS) is a topic of increasing interest. For the major a part of the MEMS devices currently on the market, contact mechanics plays no role, simply because the devices are designed such that no moving components are required to touch each other. However, even in these devices some parts may occasionally come into contact when they are subjected to impact accelerations. For devices like MEMS switches, latches and mirrors, where components are required to come into contact, the study of contact mechanics and in particular the study of adhesion is of primary importance.

The phenomenon of adhesion has been understood and mitigated quite well on the macroscale for a long time and significant advances have been made on atomic scale adhesion (Carpick and Salmeron 1997). However, our understanding of so-called ‘mesoscale’ contact mechanics: the domain where the number of contact points, or asperities between two contacting surfaces is larger that one (atomic scale) but not ‘close to infinity’ (macroscale), is lagging behind.

Much progress has been made in the development of anti-stiction coatings (Maboudian et al. 2002) and novel methods of lubrication have been discovered (Asay et al. 2008). We believe that an important reason why MEMS devices with contacting surfaces are still under-represented, is the lack of fundamental knowledge about what actually goes on at the interface of a mesoscale multi-asperity contact.

The reason for this knowledge gap is threefold. First, it is relatively difficult to create a physical model of a realistic mesoscale multi-asperity contact. This is because the working distances of the mechanisms involved in generating the forces between the contacts, are of the same order of magnitude as the roughness of the contacting surfaces. The behavior of contacting surfaces with exactly the same roughness statistics can differ by orders of magnitude, simply because at the actual contact points, the surfaces are physically different (van Spengen 2015; Zhao et al. 2003).

Second, due to the stochastic nature of mesoscale contact mechanics, highly variable results are found under otherwise equal circumstances, which makes it hard to execute repeatable experiments. In addition, most real MEMS surfaces contain a number of unknown contaminants that will influence the result.

Third, although mesoscale contact forces are large compared to the other forces in a typical microsystem, they are still very small in an absolute sense, and are therefore hard to measure with sufficient precision. Until very recently, atomic force microscopes (AFM) were the only instruments capable of measuring such tiny forces (Carpick and Salmeron 1997), and direct measurements of contact forces in MEMS devices typically suffered from a low signal to noise ratio (van Spengen 2010).

However, our new optical technique based on curve fitting allows displacement measurements with deep subnanometer resolution (Kokorian et al. 2015). The merits of the technique have already been demonstrated by measuring adhesion forces in MEMS devices made entirely out of diamond (Buja et al. 2015). We have also previously presented a single adhesion experiment on silicon MEMS (Kokorian et al. 2015), in which we observed surprising run-in behavior of the adhesion force between two sidewalls that were repeatedly brought into contact.

2 Theory: how to determine the adhesion force from displacement

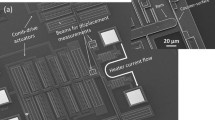
Figure 1 shows a scanning electron microscope (SEM) micrograph of the type of MEMS adhesion sensor that we have used in this chapter. The device consist of a ‘battering ram’ that is suspended by folded-flexure support springs, and can be moved forwards and backwards by comb-drive actuators. When the ram moves forward by ${2}\,{\upmu }\hbox {m}$, it makes contact with a ‘counter-surface’ to which it will temporarily adhere.

Fig. 1

Scanning electron microscope (SEM) micrograph of the MEMS adhesion sensor used in the experiments

Equation (1) shows the force balance of all the forces that act on the adhesion sensor (neglecting air damping),

$$\begin{aligned} F_\mathrm {act} + F_\mathrm {spring} (x) + F_\mathrm {adh} (x) + F_\mathrm {contact} = m\cdot \frac{\mathrm {d}^2 x}{\mathrm {d} t^2} \end{aligned}$$

(1)

where $F_\mathrm {act}$ (positive) is the force generated by the comb-drive, $F_\mathrm {spring}$ (negative) is the restoring spring force exerted by the beam springs in which the ram is suspended, $F_\mathrm {adh}$ (positive) is the adhesion force between the ram and the counter-surface, $F_\mathrm {contact}$ (negative) is the force exerted by the counter-surface on the ram and m is the mass of the ram. This equation is valid at any value of $F_\mathrm {act}$. We can write for $F_\mathrm {spring}$ and $F_\mathrm {contact}$:

$$\begin{aligned} F_\mathrm {spring}&= k_\mathrm {spring} \cdot x_\mathrm {ram} \end{aligned}$$

(2)

$$\begin{aligned} F_\mathrm {contact}&= -k_\mathrm {contact} \cdot d_\mathrm {contact} \quad \text {if } x_\mathrm {ram} \ge y_\mathrm {slider} \end{aligned}$$

(3)

where $d_\mathrm {contact}$ is the elastic deformation of the contact, $x_\mathrm {ram}$ is the position of the head of the ram and $y_\mathrm {slider}$ is the position of the counter-surface.

Fig. 2

The voltage displacement curve of a single contact cycle, zoomed in on the adhesion hysteresis loop. The important points are marked with numbers 1–8 and correspond to the numbers in Fig. 3

Fig. 3

The different phases of a contact cycle. The numbers correspond to the annotations in the graph of Fig. 2. (1) free motion, (2) just before snap-in, (3) snap-in motion, (4) contact right after snap-in, (5) increase contact force, (6) decrease contact force, just before snap-off, (7) snap-off motion, (8) right after snap-off. Note that steps (3) and (7) are not present in Fig. 2, because it only shows stationary positions

The actuator force $F_\mathrm {act}$ is the only variable in Eq. (1) that can be controlled directly, by applying a voltage difference $V_\mathrm {act}$ between the comb-drive actuator fingers.

Figure 3 illustrates the events that occur during a single ‘contact cycle’, by which we mean a forth and back motion of the ram in which it makes and breaks contact with the counter surface.

Before the ram makes contact with the counter surface (1), $F_\mathrm {adh} =0$ and $F_\mathrm {contact} = 0$ and an increase in $F_\mathrm {act}$ will cause the ram to accelerate and displace. At $x=x_\mathrm {eq}$, where the restoring spring force $k_\mathrm {spring} = -F_\mathrm {act}$, the ram will show a damped oscillation around its equilibrium position. When the voltage is increased so much that $x_\mathrm {ram}$ is close to $x_\mathrm {cs}$, the attractive van der Waals, electrostatic and capillary forces between the ram and the counter-surface come into play (2). Their contributions are aggregated in $F_\mathrm {adh}$ . Typically, $F_\mathrm {adh}$ depends strongly on the gap distance $d_\mathrm {gap}$ in a non-linear fashion, so as soon as $F_\mathrm {adh}$ becomes non-zero while the ram approaches the counter-surface, a stable equilibrium position no longer exists and the ram is pulled into the counter-surface (3). At this point, the reaction force $F_\mathrm {contact}$ will become non-zero to compensate the force with which $F_\mathrm {adh}$ pulls the ram to the surface (4). Increasing $F_\mathrm {act}$ even further will not cause a change in $F_\mathrm {adh}$ , but the contact will slightly deform due to the non-zero value of $k_\mathrm {contact}$ (5).

When the voltage is now lowered to the value at which snap-in occurred, the ram will not immediately pull-off from the counter surface, because $F_\mathrm {adh}$ is still non-zero. When further decreasing the voltage, at some point the adhesion force will be exactly compensated by the restoring spring force such that $F_\mathrm {act} + F_\mathrm {adh} = -k_\mathrm {spring} \cdot y_\mathrm {slider}$ and $F_\mathrm {contact} = 0$, but the ram is still touching the counter-surface (6). An infinitesimally small further decrease in $F_\mathrm {act}$ causes $F_\mathrm {adh}$ to become zero, which results in non-zero net force that accelerates the ram back towards its equilibrium position such that ${F_\mathrm {act} =-F_\mathrm {spring} (x_\mathrm {eq})}$ (7). We can now obtain an expression for $F_\mathrm {adh}$ that is independent of $F_\mathrm {act}$.

Just before snap-off:

$$\begin{aligned} F_\mathrm {act} + F_\mathrm {adh}&= -k_\mathrm {spring} \cdot y_\mathrm {slider} \end{aligned}$$

(4)

$$\begin{aligned} F_\mathrm {adh}&= -k_\mathrm {spring} \cdot y_\mathrm {slider}- F_\mathrm {act} \end{aligned}$$

(5)

Right after snap-off

$$\begin{aligned} F_\mathrm {act}&= -k_\mathrm {spring} \cdot x_\mathrm {eq} \end{aligned}$$

(6)

Equating:

$$\begin{aligned} F_\mathrm {adh}&= k_\mathrm {spring} \cdot (y_\mathrm {slider}- x_\mathrm {eq}) \end{aligned}$$

(7)

$$\begin{aligned}&= k_\mathrm {spring} \cdot d_\mathrm {snap-off} \end{aligned}$$

(8)

where $d_\mathrm {snap-off}$ is the snap-off displacement length (8). The spring constant of the moving ram can be found by measuring the resonance frequencies of two devices with the same value of $k_\mathrm {spring}$, but different values for the device’s effective moving mass $m_\mathrm {eff}$. The adhesion force can then be determined from the snap-off displacement by multiplying it with the spring constant. This means that we have successfully shifted the problem of measuring a force to measuring a displacement, for which we have an excellent, high-resolution measurement solution.

3 Experiments

3.1 Adhesion sensor

In all the measurements discussed in this chapter we used a polycrystalline silicon MEMS adhesion sensor as shown in Fig. 1. It was fabricated the PolyMUMMPS™(MEMSCap 2020) multi-user MEMS process by MEMScap inc. Figure 3 shows the gap distance between the ram and the counter-surface as a function of the voltage between the comb-drive actuator fingers. Using standard cantilever beam approximations (Legtenberg et al. 1996), we have analytically calculated the spring constant of the battering ram suspension to be ${k_\mathrm {spring} = ({2.5\pm 0.2}\,\hbox {Nm}^{-1}})$. We measure the displacement of the ram by using an optical displacement measurement technique based on curve-fitting (see Kokorian et al. 2015), and experimentally determine the adhesion forces from the observed snap-off distance, as explained in Sect. 2.

The adhesion sensors were wire bonded to a ceramic dual-in-line package (DIP) after having been stored in a gel-pack for a short period of time. Before the experiments, the devices had been stored for about a year in the package in which they were shipped to us by the foundry.

3.2 Measurement setup

All adhesion experiments were carried out in a measurement setup that was specifically made for conducting these high-precision force measurements with MEMS devices. It consists of an IDS uEye 3370CP CMOS camera in line with a Motic PSM-1000 optical microscope, mounted above a small environmental and vacuum chamber. Inside the chamber, the DIL-packaged MEMS adhesion sensors are placed into a socket which provides electrical connections to the outside world. The chamber can be closed with a lid that contains a glass view port, which allows optical access from the microscope to the sample. The walls of the chamber are temperature controlled, and can be heated to ${110}^\circ$C to perform a dehumidifying ‘bake-out’. The chamber is fitted with gas in- and outlets, and can be evacuated down to ${\sim \,1}\,\hbox {mbar}$ by a oil-free, membrane-type vacuum pump. To create a dry and inert atmosphere it can be flushed with pure Argon after bake-out and pumping. The atmospheric conditions close to the sample are monitored using a Honeywell HIH4000 humidity sensor and a Pt100 temperature sensor, of which the output is logged every second. The entire setup is suspended in bungee cords inside an acoustic isolation booth (Fig. 4). The booth itself is placed on top of an stiff optical table with active pneumatic supports. This construction that we developed ensures maximum mechanical decoupling from the outside world.

Fig. 4

A close-up view of the environmental chamber with a wire bonded adhesion sensor mounted in the socket

3.3 Adhesion measurements

Table 1 Summary of the six adhesion experiments that were carried out, sorted by relative humidity of the atmosphere

The adhesion sensor was illuminated through the microscope objective by a liquid light-guide coupled Sutter HPX-L5 90W LED light source, which has the equivalent light output of a 150W xenon arc lamp. The optical path of the microscope consisted of a long working distance $20\times$ magnification objective with a numerical aperture of 0.5, an additional $2\times$ magnification lens built into the microscope, and an adjustable diaphragm. The internal diaphragm of the microscope was closed to it’s minimum aperture to block any stray light scattered back from the chamber view port. Images were captured with exposure times of around 1 ms per image.

Six adhesion experiments were carried out, under different low-humidity atmospheric conditions. They are summarized in Table 1. Each adhesion experiment has been conducted using the same procedure. The device was placed in the socket inside the chamber. The ram was moved forwards to make contact with the counter-surface and press against it, and then retracted again. This was achieved by sweeping $V_\mathrm {act}$ from 70 V to 85 V and back in 2000 discrete steps. After each step an image of the device support springs was acquired from which the displacement was calculated using the curve-fitting method described in Kokorian et al. (2015).

Three million of these contact cycles were executed in total for every device. However, because an accurate measurement of a complete contact cycle takes $\sim {30}\,\hbox {s}$, recording all three million cycles this way would take about three years. Therefore, only 50 sets of 20 consecutive cycles were actually recorded. The contact cycles in between the measurement sets were executed at a higher rate of 100 Hz with only 10 voltage steps per cycle. The amount of intermediate cycles between measurement sets was increased exponentially in such a way that the total amount of contact cycles was close to three million, and the resulting data points are spaced equidistantly when plotted against the logarithm of the total number of elapsed cycles.

3.4 Environmental conditions

For the experiments carried out in a very dry atmosphere (${0}\%_{\mathrm{RH}}$, ${0}\%_{\mathrm{RH}}$ and ${2}\%_{\mathrm{RH}}$), the chamber was dehydrated by baking it out at ${110}^ \circ$C for about 16 h while it was being evacuated continuously. After the chamber had cooled down and its walls had reached a stable temperature of ${25}^ \circ$C, the vacuum pump was switched off, and the chamber was filled with 99.99% pure argon gas.

For the experiments carried out in a wetter, but still fairly dry atmosphere (${10}\%_{\mathrm{RH}}$, ${10}\%_{\mathrm{RH}}$ and ${26}\%_{\mathrm{RH}}$), the chamber was left to ‘breathe’ for a couple of minutes to equilibrate the chamber atmosphere with the surroundings. The lid was then closed to keep the atmospheric conditions constant throughout the experiment. However, because the chamber temperature was maintained at ${25}^ \circ$C and the laboratory ambient temperature was ${21}^ \circ$C, the temperature of the gas inside the chamber slowly increased to match the chamber wall temperature which caused a corresponding decrease of the relative humidity. In addition, it turned out that the chamber walls acted as a strong ‘getter’ for water, especially after it had been kept at ${0}\%_{\mathrm{RH}}$ for longer stretches of time. The time it took for the relative humidity to become stable turned out to be about a day, much longer than we initially expected. For that reason, the relative humidity was not completely stable in some of the experiments. For the same reason it was not practically possible to obtain high levels of relative humidity with this setup.

4 Results

Each experiment yielded a total number of 1000 contact cycles, which amounts to a total of 6000 contact cycles, each consisting of 2000 pictures. We do not show all the raw results here, but we discuss some peculiar details in Appendix A.

Figure 5 shows the adhesion force against the total number of elapsed contact cycles for all measurements.

Fig. 5

The adhesion force plotted against the total number of contacts for all measured devices. The mean relative humidities during the experiments are indicated in the legend. The colored bands indicate the minimum value, the 25% and 75% percentiles, and the maximum value. The solid line indicates the mean

The width of the region is a measure for the variability of the adhesion force from contact-to-contact. The colored regions in the graph give a qualitative view of the distribution of the measured adhesion forces in the experiment. The darker region represents the 25–75% percentile interval, the dark center line is the mean value, and the lighter colored region indicates the total range of measured adhesion forces. The variability is also shown separately in Fig. 6, where the 25–75% percentile interval of the cycle-to-cycle adhesion force values is plotted against the total number of cycles.

All adhesion trend lines show a slowly varying drift over the total range of 3 million cycles. The lines corresponding to the samples measured under relatively dry conditions: sample J$_\mathrm {c}$, G, H, J$_\mathrm {d}$ and D, show a slight increase in adhesion after $10^{4}$ contact cycles. The trend of sample J$_\mathrm {d}$ shows a gradual decrease in adhesion after $10^{5}$ contact cycles. The sample that was measured under wet conditions, B shows a different trend: the adhesion force decreases almost monotonously.

In all experiments, the cycle-to-cycle variability of the adhesion force is large at the start of the experiment, but decreases rapidly as a function of the number of elapsed contact cycles.

Fig. 6

The variability of the adhesion force within each measurement set of 20 consecutive cycles, plotted against the total number of contacts for all measured devices. In all cases the variability decreases with an increasing number of elapsed contacts

5 Discussion

The most striking feature of this set of experimental data is that device-to-device variation due to surface roughness and differences in local sidewall contamination result in strong differences. So strong in fact, that they preclude the possibility to see any overall quantitative similarity of the adhesion force evolution. However, there are certain trends that occur in every experiment. We observe three regimes (Table 2).

Table 2 Overview of the three regimes of distinct adhesion behavior observed

At the start of each experiment, adhesion forces show a large cycle-to-cycle variability. The measured adhesion forces of each individual sample fall within a range of about ${\pm 10}\,\,\hbox {nN}$ around their mean value, but the adhesion forces from all experiments combined show a spread that is $\sim {5}$ times larger: from 50 to 250nN. As the number of elapsed contact cycles increases, we clearly see that the adhesion variability of each individual device decreases by about a factor 3. This reduction is caused by flattening of the highest asperities. This behavior is characteristic of regime I.

All adhesion curves seem to converge into a narrow range of 65–115nN between ${50\times {10^{3}}\,\, {\mathrm{to}}\,\, 250\times {10^{3}}}$ contact cycles (regime II). This convergence can be the indication of a physical process that makes the sidewall surfaces appear fairly similar after the initial run-in. After ${250\times {10^{3}}}$ cycles the curves start to diverge again (regime III).

Because the adhesion run-in is a process that slows down exponentially as more contact cycles have elapsed, all the graphs that we have shown in the results section have a logarithmic horizontal axis. Figure 7 shows the first half of the data that was shown in Fig. 5 on a linear scale. The details of the initial run-in have become obscured, but the general trend is shown in completely different light: after a run-in of 50,000 cycles, the adhesion force is stable for the next 200,000 cycles (Fig. 8).

Fig. 7

The adhesion force versus the first 250,000 cycles on a linear scale. This shows the first half of the graph in Fig. 5 in a different light. Although the run-in happens logarithmically and does not actually stabilize, an initial run-in of 50,000 cycles stabilizes the adhesion behavior during the next 200,000 cycles

Fig. 8

The adhesion force values in regime III versus the number of elapsed cycles on a linear scale from ${250\times {10^{3}}\,\, {\mathrm{to}}\,\, 3\times {10^{6}}}$ contact cycles. In this regime the curves start to diverge again from the stable values of regime II

6 An empirical model to describe the adhesion force drift

The fact that the measured data are fairly similar for the different humidities proves that if the humidity is low enough not to cause large-scale capillary bridges, its’ effect is not pronounced. In the following we therefore treat the measurement data as a single set with no differences between the devices other than regular statistical variation. We can extrapolate the data in Fig. 5 to predict the expected adhesion drift for longer-term operation of the devices. To obtain reliability predictive power from the measured data we can take several routes. As the MEMS system is too complex for direct physical modeling, a new empirical model is needed. Here we present two of these models, both with their strong points and limitations, as presented below.

6.1 The simple log(n) fit model

For the simplest model, we us the experimentally observed fact that on the semi-logarithmic plot in Fig. 9 the adhesion long-term drift is roughly linear in Region II and III. The corresponding first order model starts by noting that the adhesion $F_\mathrm {adh} (n)$ in a single experiment in such a case can be written according to the following equation:

$$\begin{aligned} F_\mathrm {adh} (n) = F_\mathrm {start} + F_\mathrm {drift} \cdot \log (n) - F_\mathrm {drift} \cdot \log (n_\mathrm {start}) \end{aligned}$$

(9)

In this equation n is the number of cycles that the experiment is running in total, and $n_\mathrm {start}$ = 10,000 cycles: roughly the cycle number from which point most curves plot roughly linear. $F_\mathrm {start}$ is the adhesion measured at $n_\mathrm {start}$ cycles and $F_\mathrm {drift}$ is a fit parameter that defines the average slope of the measured curve in region II and III. Both $F_\mathrm {start}$ and $F_\mathrm {drift}$ can be obtained by curve fitting Eq. (9) to the measured data in region II and III combined. If we perform this curve fitting procedure for all measured curves we can calculate the mean and standard deviation of $F_\mathrm {start}$ and $F_\mathrm {drift}$ of the measurement. For the data of Fig. 5 these are given in Table 3.

Table 3 Determination of the standard deviation of $F_\mathrm {start}$ and $F_\mathrm {drift}$ for the measured data of Fig. 5 in Regions II and III

We define the ${\bar{x}}$ operator as giving the mean of x, and the $\left| x\right|$ operator as giving the average deviation of x. The predicted one standard deviation boundaries on the adhesion force for large n give the predicted adhesion with its most probable drift, for which we use the notation $\left\{ F_\mathrm {adh} (n)\right\}$. For this model we get as the prediction for the average drift adhesion boundaries as a function of the number of cycles:

$$\begin{aligned} \left\{ F_\mathrm {adh} (n)\right\}= & {} {\overline{F_\mathrm {start}}} \, \pm \left( \left| F_\mathrm {start} \right| + {\overline{F_\mathrm {drift}}} \cdot \right. \nonumber \\&\left. \log (n) - {\overline{F_\mathrm {drift}}} \cdot \log (n_\mathrm {start})\right) . \end{aligned}$$

(10)

The prediction of Eq. (10) is that the adhesion drift goes with a comforting $\log (n)$ and will not grow very large with higher numbers of cycles for reasonable values of n. The predictive power of this model of course depends on the underlying validity of Eq. (9). With a second model we show that this assumption need not necessarily be true.

6.2 The random walk model

For the second model the adhesion shown in Fig. 5 in region II and III is interpreted as showing a ‘random walk’ type of behavior. This choice is made because of the erratic drift of $F_\mathrm {adh}$ that sometimes even changes sign. A simple random walk of a variable Z is defined as $Z_n = \sum _{j=1}^{n}Z_j$, with $Z_j=1$ or $Z_j=-1$ with equal probability, and n the number of steps. The expectation value of $Z_n$ itself is zero: the possibilities of the walk are symmetrical around 0. However, the expectation value E of the average deviation from zero of $Z_n$ is $E(|Z_n|) \approx \sqrt{\frac{2n}{\pi }}$ for large n, with the |x| operator again defined as giving the average deviation of x.

For large n the $\sqrt{n}$ factor of the average deviation of the standard random walk has a higher second derivative than the $\log (n)$ relation of Eq. (9). Hence the deviations of $F_\mathrm {adh}$ for high n are expected to be larger in the case of the random walk than those in the $\log (n)$ model of Eq. (9). It is true that as the number of cycles increases, the variation per step is seen to decrease slightly in the measurements (Fig. 6) unlike the step size in the simple random walk described above. However, the change is not quite large enough to cause a significant change in the shape of the $\sqrt{n}$ function behavior; for large n it represents just a scaling factor. Assuming underlying random walk statistics for the adhesion experiment, the equivalent fit function of Eq. (9) becomes:

$$\begin{aligned} F_\mathrm {adh} (n) = F_\mathrm {start} + F_\mathrm {rw} \cdot \sqrt{n} - F_\mathrm {rw} \cdot \sqrt{n_\mathrm {start}}, \end{aligned}$$

(11)

in which the fit parameter $F_\mathrm {rw}$ absorbs the factor $\sqrt{\frac{2}{\pi }}$ and is the random walk equivalent of $F_\mathrm {drift}$ in Eq. (9). The fit parameters are given in Table 3. For the random walk model we get as the prediction for the average adhesion plus drift as a function of the number of cycles:

$$\begin{aligned} \left\{ F_\mathrm {adh} (n)\right\} = {\overline{F_\mathrm {start}}} \pm \left( \Vert F_\mathrm {start} \Vert + {\overline{F_\mathrm {rw}}}\cdot \sqrt{n} - {\overline{F_\mathrm {rw}}} \cdot \sqrt{n_\mathrm {start}} \right) . \end{aligned}$$

(12)

6.3 Discussion

Fig. 9

Measured adhesive forces and predicted average deviation of the adhesive force for the $\log (n)$ model in Eq. (9) and the random walk model in Eq. (12)

In Fig. 9 we show a comparison of the two model predictions and the measured data. Both models describe the measured data quite well. The initial ‘stability’ of the adhesive force in Region II and the subsequent diverging adhesive force in Region III is a prominent feature of the random walk model, but is absent in the $\log (n)$ model. This may favor the random walk model over the $\log (n)$ model.

At the end of Region III the slopes of the curves of the two models differ considerably. If the adhesion drift is dominated by random walk statistics, the expected drift will be much higher than if it is governed by the $\log (n)$ model. A long-term test up to a much higher number of cycles, preferably with more devices, is recommended to experimentally distinguish between the two models. This is important to be able to predict the real-life adhesion drift that can be expected during log-term operation of MEMS devices with contacting surfaces.

7 Conclusion

Thanks to the sub-nanonewton force resolution of our measurement technique, we have been able to observe the adhesion force between polycrystalline silicon MEMS sidewalls with unprecedented detail. The results in this chapter clearly demonstrate the differences in the contact mechanics of devices that are in every way identical, apart from the fact that they are not actually the same device. Small variations in surface roughness and hence in maximum normal contact force and local capillary condensation may play a major role in determining the strength and evolution of the adhesive force in these contacts. More experiments should be conducted in order to shed light on what exactly causes all the different effects that we observe. For the first time however, we actually have obtained a quantitative insight in how MEMS contacts evolve over a large number of contact cycles under low force conditions. Although the cycle-to-cycle variability decreases after $\sim {10^{2}}$ cycles, the gradual change of the adhesion force as a result of run-in does not stabilize, even after 3 million cycles. This drift of the adhesion force during millions of cycles is comparable in magnitude to the initial run-in drift. Silicon MEMS devices that rely on the presence of a stable and repeatable adhesion force will therefore not work reliably over many cycles. However, if the intended lifetime of the device is limited, a stable adhesion force can be achieved by running-in the contacting surfaces for roughly 10% of their intended lifetime, and keeping the total number of cycles under ${260\times {10^{3}}}$.

Appendix A: Gradual pullback and contact deformation

Due to the sub-nanometer resolution of our measurements we have observed some interesting effects that do not affect the main story and conclusion of this chapter, but deserve some publicity nonetheless: inelastic contact deformation (ICD) and gradual pullback.

After the ram is snaps into the counter surface and $F_\mathrm {act}$ (and therefore $F_\mathrm {contact}$) is increased, the contact will always deform somewhat, due to the non-zero compliance of both the contact itself and the counter-surface suspension. In the case of elastic contact deformation, the displacement of the ram is independent of time and history, and the forward and backward voltage-displacement curves will overlap. In the case of inelastic contact deformation, the contact will deform permanently (at least within the time-frame of the measurement) when $F_\mathrm {act}$ is increased, and as a result the forward and backward voltage-displacement curves will not overlap.

Gradual pullback is measured when the ram does not snap-off from the counter surface in one discrete jump, but gradually retracts several nanometers before it snaps-off. In some cases, this ‘gradual pullback length’ appears to match the amount of ICD. Both ICD and gradual pullback can be present after any number of contact cycles, as is shown in Figs. 10 and 11.

Fig. 10

The voltage-displacement curve of the first cycle of experiment G, zoomed in around the voltage region in which contact is made and broken (the maximum voltage in this measurement is 85 V). A small amount of inelastic contact deformation is visible just after snap-off, and an equally small amount of gradual pullback can be discerned just before snap-off

Figure 10 shows the voltage-displacement curve of the first measured cycle in experiment G. It is one of the smoothest curves in all of the experiments, with a displacement noise of only 0.21 nm RMS. However, a tiny small amount of inelastic contact deformation (ICD) and gradual pullback can still be discerned.

Figure 11 shows the voltage displacement curve of the 445th curve of experiment D. In addition some elastic contact deformation, both ICD and gradual pullback are visible. The contact does not deform immediately after the ram makes contact with the counter surface but only after $V_\mathrm {act}$ has been increased by an additional $\sim {7} \,{V}$. In this measurement, ‘gradual’ pullback does not happen gradually, but happens in one discrete jump to the same displacement at which the ram and counter surface first made contact, before the contact was deformed.

This behavior can be explained by the assumption that the initial contacting surfaces have two large asperities that first make contact tip-to-tip, but with a slight misalignment. After a certain increase in force, the asperities start to slide sideways, until they settle into a more stable contact. When $F_\mathrm {act}$ is decreased, the ram will first move back to the initial contact position before snapping off.

Fig. 11

The voltage-displacement curve of the 445th cycle of experiment D, zoomed in on the voltage range in which the ram and counter surface are in contact. The contact remains stable for a while (1) until 81.5 V, where the ram slides a bit further (2) and settles itself into a more stable position (3). The ram snaps-off in two discrete steps. The length of the first jump matches the amount contact deformation

Figure 12 shows the voltage displacement curve of the last cycle of experiment D. Both gradual pullback and ICD are clearly visible, but look very different compared to Fig. 11. The contact deforms at a much lower force than before and gradual pullback happens very smoothly over a distance of $\sim {6}\,\hbox {nm}$, almost twice the amount of inelastic contact deformation.

Fig. 12

The voltage-displacement curve the last cycle of experiment D. While the ram pushes into the counter surface. A significant amount of inelastic contact deformation (ICD) can be seen, as well as a smooth gradual pullback before snap-off

The decrease of the force required to push the ram into it’s favored position (situation (3) in Fig. 11) is likely caused by a smoothing of the sliding asperity, and a decrease of the local friction force. We currently have no solid explanation for the origin of the smooth and long gradual pullback, but we believe it to be caused by the in situ tribo-synthesis of a viscous compound. Crushed together by the contact force, hydrocarbon contaminants may have combined with water and ${{\mathrm{SiO}}_{2}}$ debris, forming a nm-thick silicone-like substance on the surface.

Figure 13 show the gradual pullback length versus the number of elapsed contact cycles for all the experiments discussed in this chapter. The plotted values are the median values of the gradual pullback lengths in each measurement set of consecutive cycles. In experiments D and J$_\mathrm {d}$ the gradual pullback effect appears quite suddenly, after ${10^{2}} {\mathrm{to}} {10^{3}}$ cycles. In experiment G the effect also appears suddenly, but only after $\sim {10^{5}}$ cycles. In experiments H and J$_\mathrm {d}$, the gradual pullback length increases more gradually, but suddenly becomes much higher and somewhat erratic between ${10^{4}} {\mathrm{to}} {10^{6}}$ cycles. Experiment B, with the highest relative humidity of ${26}\%_{\mathrm{RH}}$, shows no gradual pullback across the entire range of contact cycles.

Fig. 13

The gradual pullback length versus the total number of elapsed cycles. The data points represent the median of each set of 20 consecutive measurement cycles

Gradual pullback was notably absent in the experiment with B which was performed at ${26}\%_{\mathrm{RH}}$. The dramatic gradual pullback effect that we observed in previous work (Kokorian et al. 2015) at ${40\pm 10}\%_{\mathrm{RH}}$ was completely absent. Taking into account that the devices used in the experiments of the current chapter were much newer than the devices used in Kokorian et al. (2015) and hence much less contaminated, it appears that the device’s contamination history plays a more important role than relative humidity at these low humidity levels, possibly except in the case of experiment B (${26}\%_{\mathrm{RH}}$).