New architectures for micromechanical coupled beam array filters

Abstract

Coupled resonator filters implemented as microelectromechanical systems (MEMS) offer performance advantages as band-pass filters at MHz frequencies. Here new designs based on resonant cavities for acoustic slow waves are developed to allow alternative frequency responses. Derivation of the lumped element model for coupled beam systems with in-plane motion from Rayleigh–Ritz perturbation theory is first reviewed. Departures from ideal behaviour caused by mechanical and electrostatic detuning are resolved. Slow wave theory is then used to develop linear array topologies with novel responses including band-stop and comb filtering with controlled filter roll-off. A systematic procedure is developed to allow rapid identification of design parameters without the need for lengthy numerical simulation, using the lumped element, stiffness matrix and finite element methods to investigate the layout parameters of initial design concepts, detailed mechanical effects and detailed electrostatic effects, respectively. High performance is demonstrated, with good agreement between the models.

1 Introduction

Microelectromechanical systems (MEMS) have had significant economic impact, with widespread adoption in many industries (Elwenspoek and Jansen 1999; Madou 2011; Beeby et al. 2004; Uttamchandani 2013). Applications exploit the high performance, reliability and repeatability and small size of MEMS to enable new, high-value systems. There is now an increasing drive towards nanoelectromechanical systems (NEMS) (Lyshevski 2002). This paper is concerned with MEMS filters containing nanostructured parts.

Band-pass filters have been used in radio receivers since the invention of the super-heterodyne receiver (Armstrong 1921). The super-het uses an intermediate frequency (IF) and requires IF filters with flat passband and small fractional bandwidth. Due to their high Q-factors, coupled mechanical resonators have long been used for filtering (Hathaway and Babcock 1957; Johnson et al. 1971), and electrostatically driven resonators were among the first MEMS (Tang et al. 1989). Low-frequency filters were constructed from comb-drive actuators with folded springs (Lin et al. 1998; Wang and Nguyen 1999), and high-frequency filters from parallel plate actuators and clamped beams (Bannon et al. 2000). In most cases, coupling is between adjacent beams, with their number determining the filter order, but non-adjacent coupling has been used to increase roll-off (Li et al. 2004). Gas damping, thermoelastic damping and support losses all reduce Q-factor (Zhang and Tang 1994; Yang et al. 2002; Srikar and Senturia 2002), but the first two can be small for single crystal materials at low pressure and the third reduced using free-free beams (Wang et al. 2000).

The coupling must be weak for small fractional bandwidth. Suitable results can be achieved by placing coupling springs near beam roots or coupling via the supports (Ho et al. 2004). Weak springs based on nanowires have also been demonstrated (Galayko et al. 2003; Pourkamali and Ayazi 2005a); however, sidewall patterning (Pourkamali and Ayazi 2005b) may be a simpler way to combine micro- and nano-scale flexures. An alternative is electrostatic coupling (Galayko et al. 2006; Hajhashemi et al. 2012; Lee and Seshia 2009), which allows electrical tuning (Pourkamali et al. 2003; Toan et al. 2014). However, small electrode gaps are needed to reduce matching loads, and parasitic coupling to the substrate must be compensated (Abdolvand et al. 2004). Sub-micron gaps have been obtained using the HARPSS process (Arellano et al. 2008) or movable electrodes (Liu and Syms 2014).

Careful design and appropriate modelling are also essential. Perturbation theory (Dowell 1971; Jacquot and Gibson 1972) can establish the effect of spring- and mass-loading of continuous beams (Bannon et al. 2000; Meng et al. 1993). The results have been used in lumped element models (LEM) of single-mode systems, often based on circuit analogies (Lin et al. 1998; Wang and Nguyen 1999; Bannon et al. 2000). The stiffness matrix method (SMM) (Livesey 1964; McGuire et al. 2000) can highlight the effect of higher modes in any elastic elements that can be described using Euler theory, and the multi-physics tools needed to describe electrostatic actuation have been linked to dynamic nodal analysis (Clark et al. 1998,2000). The finite element method (FEM) (Zienkiewicz et al. 2013) is the most widely used tool for MEMS design (Senturia et al. 1992; Gilbert et al. 1995) and has been used for detailed studies of coupled beam filters (Hammad 2014). However, de-synchronisation effects complicate the search for suitable parameters, and efficient FEM experiment design is required (Hung and Senturia 1999). These difficulties have prevented exploration of alternative filter topologies.

In this paper we develop a systematic approach for designing new filter architectures based on arrays of electrostatically driven, mechanically coupled in-plane MEMS resonators. We begin in Sect. 2 by reviewing the use of perturbation theory to derive a suitable LEM and identify the causes of mechanical and electrostatic detuning. Resolution of these difficulties is key to effective design of complex filters. In Sect. 3 we consider the propagation of acoustic slow waves in infinite and semi-infinite coupled resonator arrays. In Sect. 4, we use the LEM show how these concepts can be used to develop different filter types based on slow-wave resonators, including band-stop and comb filters. In Sect. 5 we use the LEM to present numerical results for promising designs. We then show how the SMM (which improves modelling of complex dynamical systems) and the FEM (which accurately models additional electrostatic effects) can then be used for rapid identification of realistic design parameters without excessive computation. Conclusions are presented in Sect. 6.

2 Lumped element model

In this Section, we follow (Bannon et al. 2000) and use Rayleigh–Ritz perturbation theory to derive a unit cell lumped element model, which is then generalised to arrays.

2.1 Perturbation theory

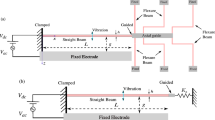
We base the analysis on the unit cell in Fig. 1a, namely a single electrostatically driven beam of length ${L}_{0}$, width ${w}_{o}$ and depth $d$, loaded with weak meander springs. We start with the equation for free vibrations of a uniform, undamped beam:

Fig. 1

a Distributed and b lumped element models of a single electrostatically driven beam with auxiliary springs

$${E}_{0}{I}_{0}\frac{{\partial }^{4}y}{{dx}^{4}}+\rho {A}_{0}\frac{{\partial }^{2}y}{{dt}^{2}}=0$$

(1)

Here $x$ is position, $t$ is time, $y$ is displacement, ${E}_{0}$ and $\rho$ are the Young’s modulus and density, and ${I}_{0}= {w}_{0}^{3}d/12$ and ${A}_{0}={w}_{0}d$ are the second moment of area and cross-sectional area. Assumption of a separated solution $y\left(x,t\right)=\Upsilon\left(x\right)exp\left(j\omega t\right)$ leads to:

$${E}_{0}{I}_{0}{d}^{4}\Upsilon /{dx}^{4}-{\omega }^{2}\rho {A}_{0}\Upsilon=0$$

(2)

The general solution is $\Upsilon=A\mathrm{sin}\left(\beta x\right)+B cos\left(\beta x\right)+C \mathrm{sinh}\left(\beta x\right)+D cosh\left(\beta x\right)$, where ${\beta }^{4}={\omega }^{2}\rho {A}_{0}/{E}_{0}{I}_{0}$. The coefficients A–D are chosen to satisfy the boundary conditions; for a clamped–clamped beam, these are $\Upsilon={\Upsilon}^{^{\prime}}=0$ at $x=0$ and $x={L}_{0}$. Substitution leads to the eigenvalue equation $\mathrm{cos}\left(\beta {L}_{0}\right)\mathrm{cosh}\left(\beta {L}_{0}\right)=1$, which has the discrete solutions ${\beta }_{\nu }$, with ${\beta }_{1}{L}_{0}= \sqrt{22.3733}, {\beta }_{2}{L}_{0}= \sqrt{61.6728},$ and so on. These lead to angular resonant frequencies ${\omega }_{\nu }={\beta }_{\nu }^{2}\sqrt{{E}_{0}{I}_{0}/\rho {A}_{0}}$, with the lowest-order resonance at ${\omega }_{1}=\left(22.3722/{L}_{0}^{2}\right)\sqrt{{E}_{0}{I}_{0}/\rho {A}_{0}}.$ The corresponding mode shapes are:

$${\Upsilon}_{\nu }\left(x\right)=\left(\frac{{\gamma }_{\nu }}{\sqrt{{L}_{0}}}\right)\left\{\frac{sin\left({\beta }_{\nu }x\right)-sinh\left({\beta }_{\nu }x\right)}{sin\left({\beta }_{\nu }{L}_{0}\right)-sinh\left({\beta }_{\nu }{L}_{0}\right)}-\frac{cos\left({\beta }_{\nu }x\right)-cosh\left({\beta }_{\nu }x\right)}{cos\left({\beta }_{\nu }{L}_{0}\right)-cosh\left({\beta }_{\nu }{L}_{0}\right)}\right\}$$

(3)

Here the terms ${\gamma }_{\nu }$ are constants. The modes are orthogonal; if they are also normalised so that $\langle {\Upsilon}_{\nu },{\Upsilon}_{\nu }\rangle ={\int }_{0}^{{L}_{0}}{\Upsilon}_{\nu }^{2}dx=1$, the first such constant has the value ${\gamma }_{1}=56.6369$.

We assume that the springs are formed from elements of length ${L}_{1}$, width ${w}_{1}$, Young’s modulus ${E}_{1}$, depth $d$ and density $\rho$ inclined at 45° angles to give a span $s= {L}_{1}\sqrt{2}$. The equivalent spring constant and mass of each pair are ${k}_{1}=24{E}_{1}{I}_{1}/{L}_{1}^{3}$ and ${m}_{1}=2\rho {A}_{1}{L}_{1}$, where ${I}_{1}= {w}_{1}^{3}d/12$ and ${A}_{1}={w}_{1}d$. Here a different Young’s modulus ${E}_{1}$ has been introduced, to allow a tensor variation in mechanical properties, and the mass ${m}_{1}$ is half the actual mass, to model the reduced motion of the centre of mass of each spring. For a damped, driven beam with damping coefficient $r$ per unit length, loaded at two discrete points ${x}_{i}$ with springs ${k}_{i}$ having associated masses ${m}_{i}$, and with a distributed force $f\left(x,t\right)=\Psi \left(x\right)exp\left(j\omega t\right)$ applied along its length, Eq. (1) modifies to:

$${E}_{0}{I}_{0}{d}^{4}\Upsilon /{dx}^{4}+j\omega r\Upsilon-{\omega }^{2}\rho {A}_{0}\Upsilon+ {\sum }_{i=1}^{2}\left({k}_{i}-{\omega }^{2}{m}_{i}\right)\delta \left(x-{x}_{i}\right)\Upsilon=\Psi $$

(4)

Here $\delta \left(x\right)$ is a delta function at $x=0$. Assuming the result is mainly to excite the lowest mode, the solution can be taken as $\Upsilon\left(x,\omega \right)=a\left(\omega \right){\Upsilon}_{1}\left(x\right)$. Substitution, making use of the eigenvalue equation, taking inner products with ${\Upsilon}_{1}$ and exploiting normalisation yields:

$$\left\{\left({\omega }_{1}^{{^{\prime}}2}-{\omega }^{2}\right)\rho {A}_{0}+j\omega r\right\}a=\langle \Psi ,{\Upsilon}_{1}\rangle $$

(5)

Here ${\omega }_{1}^{^{\prime}}$ is given by ${\omega }_{1}^{{^{\prime}}2}= {\omega }_{1}^{2}+2\left({k}_{1}-{\omega }_{1}^{2}{m}_{1}\right){\Upsilon}_{1}^{2}\left({x}_{1}\right)/\rho {A}_{0}$. The effect of the springs is to increase the resonant frequency, with the change depending on their position as well as their stiffness. The effect of their mass is to lower the resonance; however, when ${\omega }_{1}^{2}{m}_{1}\ll {k}_{1}$, this effect is negligible. The effect of spring damping (omitted) may also be small.

2.2 Lumped element model

The LEM is shown in Fig. 1b. Here a mass $M$ with damping $R$ is suspended on a spring of combined stiffness ${K}_{0}+2{K}_{1}$ and excited by a point force $F$. The equation of motion is:

$$\left\{\left({K}_{0}+2{K}_{1}\right)-M{\omega }^{2}+j\omega R\right\}{Y}_{m}=F$$

(6)

Here ${Y}_{m}=a{\Upsilon}_{1m}$ is the midpoint deflection and ${\Upsilon}_{1m}$ is the maximum of ${\Upsilon}_{1}$. Assuming that the force $\Psi$ is uniform, the correspondence between distributed and lumped systems is:

$$\begin{aligned}M & =\rho {A}_{0}{L}_{0}{\eta }_{2}; {K}_{0}={\omega {^{\prime}}}_{1}^{2}M; R=r{L}_{0}{\eta }_{2} \\ {K}_{1} & =\left({k}_{1}-{\omega }^{2}{m}_{1}\right){{L}_{0}\Upsilon }_{1}^{2}\left({x}_{1}\right){\eta }_{2};F=\Psi {L}_{0}{\eta }_{1}\end{aligned}$$

(7)

Here ${\eta }_{1}=\frac{avg\left({\Upsilon}_{1}\right)}{{\Upsilon}_{1m}}=0.5232$ and ${\eta }_{2}=\frac{avg\left({\Upsilon}_{1}^{2}\right)}{{\Upsilon}_{1m}^{2}}=0.3965$. To simplify modelling of transducer effects, Eq. (6) can be written in terms of the velocity ${S}_{m}=j\omega {Y}_{m}$ as:

$$\left\{\left({K}_{0}+2{K}_{1}\right)-M{\omega }^{2}+j\omega R\right\}{S}_{m}=j\omega F$$

(8)

2.3 Electrostatic transducers

For simplicity, we assume the fixed electrode in Fig. 1a runs the length of the beam; partial electrodes can be modelled in a similar way. For a DC voltage ${V}_{D}$ alone, the distributed force on the beam is $\Psi =\frac{1}{2}{V}_{D}^{2}{C{^{\prime}}}_{p}$, where ${C{^{\prime}}}_{p}$ is the derivative of the per-unit length capacitance ${C}_{p}$ Assuming that the DC deflection approximately follows the mode shape, the effective DC force ${F}_{D}$ can be found by integration as:

$${F}_{D}=\frac{1}{2}{C}^{^{\prime}}{V}_{D}^{2}C{^{\prime}}{\eta }_{1}$$

(9)

Here ${C}^{^{\prime}}$ is the derivative of the total capacitance $C$. If we write${{C}^{^{\prime}}=\varepsilon }_{0}{L}_{0}d/{\left({g}_{0}-{Y}_{mD}\right)}^{2}$, where ${g}_{0}$ is the initial gap$,$ the static mid-point deflection ${Y}_{mD}$ satisfies${F}_{D}={K}_{e0}{Y}_{mD}$, where ${K}_{e0}$ is the effective stiffness. As we show later, it is sufficient to assume that${K}_{e0}={K}_{0}$. This is a standard snap-down problem, and leads to the cubic:

$${y}_{mD}^{3}-2{y}_{mD}^{2}+{y}_{mD}-\gamma =0$$

(10)

Here ${y}_{mD}={Y}_{mD}/{g}_{0}$ is the normalised static deflection and $\gamma ={\varepsilon }_{0}{L}_{0}d{V}_{D}^{2}{\eta }_{1}/\left({2K}_{0}{g}_{0}^{3}\right)$. Solution allows calculation of $C$, ${C}^{^{\prime}}$ and so on. The amplitude of the current $I$ generated from any harmonic motion can then be found by integration as $I= {V}_{D}{C{^{\prime}}}_{p}{\int }_{0}^{L}S dx$, or:

$$I = {V}_{D}C{^{\prime}}{S}_{m}{\eta }_{1}$$

(11)

Greater attention must be paid to nonlinearity in calculating the AC deflection, due to the presence of mixing terms. This time, ${C}^{^{\prime}}$ must be replaced with ${C}^{^{\prime}}{\eta }_{1}+C{^{\prime}}{^{\prime}}{\eta }_{2}{Y}_{m}$, where ${C}^{^{\prime}}{^{\prime}}$ is the second derivative of$C$. Assuming that the voltage $V$ now contains both DC and AC terms of amplitude ${V}_{D}$ and$v$, with $v\ll {V}_{D}$, the amplitude of the time-varying force is:

$$F ={V}_{D}v{C}^{^{\prime}}{\eta }_{1}+\frac{1}{2}{V}_{D}^{2}{C}^{{^{\prime}}{^{\prime}}}{\eta }_{2}{Y}_{m}$$

(12)

If the AC voltage is obtained from a source with voltage ${V}_{A}$ and output impedance ${z}_{L}$, $v= {V}_{A }-I{z}_{L}$. Substituting for ${Y}_{m}$ and $I$ yields:

$$F ={K}_{v}{V}_{A}-{Z}_{L}{S}_{m}+\Delta K{S}_{m}/j\omega $$

(13)

Here the terms ${K}_{v}$, ${Z}_{T}$ and $\Delta K$ are given

$${K}_{v}={V}_{D}{C}^{\mathrm{^{\prime}}}{\eta }_{1},{Z}_{L}= {K}_{v}^{2}{z}_{L}\mathrm{ and \Delta }K=\frac{1}{2}{V}_{D}^{2}{C}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}{\eta }_{2}.$$

(14)

by:

The first term is a driving term, the second is a loading term and the third is the well-known electrostatic stiffness. For the AC terms, the equation of motion is then:

$$\left\{\left({K}_{0}+2{K}_{1}-\Delta K\right)-M{\omega }^{2}+j\omega \left(R+{Z}_{L}\right)\right\}{S}_{m}={j\omega K}_{v}{V}_{A}$$

(15)

The effect of the transformed impedance ${Z}_{L}$ is to increase the damping, and (as we show later) to allow matching. The effect of the term $\Delta K$ is to introduce detuning, so that the effective resonant frequency is now ${\omega {^{\prime}}{^{\prime}}}_{1}$, where ${\omega {^{\prime}}{^{\prime}}}_{1}^{2}=\left({K}_{0}+2{K}_{1}-\Delta K\right)/M$. This equation is the unit cell LEM, which may be generalised to arrays as follows.

2.4 Arrays

Figure 2a and b show distributed and lumped models of an $N$-element coupled beam array. Here connection to electrodes is by bond wires; in practice, multilayer construction would be required. Note that the meander springs are continued to anchor points beyond the array. If this is not done, the mechanically modified frequency ${\omega {^{\prime}}}_{1}$ will differ for the end beams, leading to de-synchronisation when $N>2$. This effect does not appear to have been highlighted, almost certainly due to the focus on small arrays in earlier work. However, since its significance rises as the coupling and bandwidth increase, it is important to eliminate the problem using a simple layout modification.

Fig. 2

a Distributed and b lumped element models of an $\mathrm{N}$-element electrostatically driven coupled beam array

Note also that each beam has a transducer, nominally at the same DC voltage. With no end-springs, this leads to equal static deflection of each beam, and hence to identical electrostatic tuning. Unfortunately, for $N>2$, end-springs cause the deflections to vary and de-synchronise the array. To minimise this effect, ${K}_{v}$ should be small; however, to reduce the load resistance ${z}_{L}$, ${K}_{v}^{2}$ should be large. Fortunately, ${K}_{v}^{2}$ depends on ${C{^{\prime}}}^{2}$, with the latter depending roughly on ${g}_{0}^{-4}$. In contrast, $\Delta K$ depends on $C{^{\prime}}{^{\prime}}$, and hence on ${g}_{0}^{-3}$. Small gaps therefore allow a small ${z}_{L}$ to be combined with a small $\Delta K$. Modification of the voltage applied to the end transducers (not shown) to ${V}_{D1}={V}_{DN}=\beta {V}_{D}$, where $\beta \approx 1+{K}_{1}/2{K}_{0}$, is then sufficient to equalise electrode gaps. Finally, although transducers 1 and $N$ are connected to the source and load here, other port arrangements are clearly possible. Assuming that the beams are synchronous, the LEM for the whole array is:

$$\begin{aligned} \left\{\left({\omega {^{\prime}}{^{\prime}}}_{1}^{2}-{\omega }^{2}\right)M+j\omega \left(R+{Z}_{L}\right)\right\}{S}_{1}-{K}_{1}{S}_{2}={j\omega K}_{v}{V}_{A} \\ & \left\{\left({\omega {^{\prime}}{^{\prime}}}_{1}^{2}-{\omega }^{2}\right)M+j\omega R\right\}{S}_{n}-{K}_{1}\left({S}_{n-1}+{S}_{n+1}\right)=0, 1<n<N\\ & \left\{\left({\omega {^{\prime}}{^{\prime}}}_{1}^{2}-{\omega }^{2}\right)M+j\omega \left(R+{Z}_{L}\right)\right\}{S}_{N}-{K}_{1}{S}_{N-1}=0\end{aligned}$$

(16)

Here we have used the notation ${S}_{n}$ to denote the midpoint velocity in the $n\mathrm{th}$ beam. The equations can clearly be written in the form:

$$\left\{{\varvec{K}}+{\omega }^{2}{\varvec{M}}+j\omega {\varvec{R}}\right\}{\varvec{S}}=j\omega {\varvec{F}}$$

(17)

Here ${\varvec{K}}$, ${\varvec{M}}$ and ${\varvec{R}}$ are $NxN$ stiffness, mass and damping matrices, and ${\varvec{S}}$ and ${\varvec{F}}$ are N-element column vectors. The solution can be found by inversion, assuming that the force vector ${\varvec{F}}$ contains a single element ${F}_{1}$. Reflection and transmission scattering parameters can then be found as ${s}_{11} = 10{\mathrm{log}}_{10}(\rho {\rho }^{*})$ and ${s}_{21}= 10{\mathrm{log}}_{10}(t{t}^{*})$. Here $\rho = 1 - 2{ S}_{1}{Z}_{L}/j\omega {F}_{1}$ is the reflection coefficient, ${S}_{0} = {S}_{1}/ (1 - \rho )$ is the amplitude of the forward acoustic wave and $t={S}_{N}/{S}_{0}$ is the transmission coefficient. Before examining detailed responses, we consider the physics of waves in coupled beam arrays.

3 Acoustic slow waves

In this section, we demonstrate that coupled beam arrays support acoustic slow waves and consider their dispersion, characteristic impedance and conditions for resonance.

3.1 Acoustic slow wave dispersion

We begin with the central recurrence equation in (16), which may be written as:

$$\left\{{{\omega }^{{^{\prime}}{^{\prime}}}}_{1}^{2}/{\omega }^{2}-1+j\left({\omega {^{\prime}}{^{\prime}}}_{1}/\omega \right)/Q\right\}{S}_{n}-\left(\kappa /2\right)\left({\omega {^{\prime}}{^{\prime}}}_{1}^{2}/{\omega }^{2}\right)\left({S}_{n-1}+{S}_{n+1}\right)=0, 1<n<N$$

(18)

Here the quality factor $Q$ and coupling coefficient $\kappa$ are given by:

$$Q={\omega {^{\prime}}{^{\prime}}}_{1}M/R;\kappa =2{K}_{1}/{\omega {^{\prime}}{^{\prime}}}_{1}^{2}M=2{K}_{1}/\left({K}_{0}+2{K}_{1}-\Delta K\right)$$

(19)

Assumption of acoustic wave solutions in the form ${S}_{n}={S}_{0}exp\left(-jka\right)$, where ${S}_{0}$ is an amplitude, $k$ is the propagation constant and $a$ is the beam spacing, yields the dispersion equation for an infinite array:

$${{\omega }^{{^{\prime}}{^{\prime}}}}_{1}^{2}/{\omega }^{2}-1+j\left({{\omega }^{{^{\prime}}{^{\prime}}}}_{1}/\omega Q\right)-\kappa \left({\omega {^{\prime}}{^{\prime}}}_{1}^{2}/{\omega }^{2}\right)cos\left(ka\right)=0$$

(20)

With no loss, the array only supports waves over a finite frequency band, found by noting that $\omega /{\omega {^{\prime}}{^{\prime}}}_{1}= {\left(1-\kappa \right)}^{1/2}$ when $ka=0$ and $\omega /{\omega {^{\prime}}{^{\prime}}}_{1}= {\left(1+\kappa \right)}^{1/2}$ when $ka=\pi$. Making approximations for small $\kappa$, the passband is $1-\kappa /2\le \omega /{\omega {^{\prime}}{^{\prime}}}_{1}\le 1+\kappa /2$ and the fractional bandwidth is $\Delta \omega /{\omega {^{\prime}}{^{\prime}}}_{1}= \kappa$, where $\kappa ={2K}_{1}/{K}_{0}$. A small bandwidth therefore requires weak coupling springs. When $Q$ is finite, $k$ must also be complex. Writing it as $k={k}^{^{\prime}}-j{k}^{{^{\prime}}{^{\prime}}}$, assuming ${k}^{{^{\prime}}{^{\prime}}}a$ is small, and equating real and imaginary parts gives:

$$\begin{aligned} {{\omega }^{{^{\prime}}{^{\prime}}}}_{1}^{2}/{\omega }^{2}-1-\kappa \left({\omega {^{\prime}}{^{\prime}}}_{1}^{2}/{\omega }^{2}\right)cos\left({k}^{^{\prime}}a\right)=0 \\{k}^{{^{\prime}}{^{\prime}}}a=\left(\omega /{\omega {^{\prime}}{^{\prime}}}_{1}\right)/\left(\kappa Q sin\left({k}^{^{\prime}}a\right)\right)\end{aligned}$$

(21)

The upper equation is the lossless dispersion relation and shows that ${k}^{^{\prime}}a$ is almost unaltered by low loss, while the lower equation approximates the true variation of ${k}^{{^{\prime}}{^{\prime}}}a$. Figure 3 shows dispersion diagrams for example parameters of $\kappa =0.1$ and $Q=200$. The full and dashed lines in Fig. 3a show the exact and approximate variations of $\omega /{\omega {^{\prime}}{^{\prime}}}_{1}$ with ${k}^{^{\prime}}a$. The two are clearly similar; however, the effect of loss is to allow out-of-band propagation. The full and dashed lines in Fig. 3b show the exact and approximate variations of ${k}^{{^{\prime}}{^{\prime}}}a$ with $\omega /{\omega {^{\prime}}{^{\prime}}}_{1}$. Losses are minimized when $\omega ={\omega {^{\prime}}{^{\prime}}}_{1}$ and rise rapidly at the band edges. The minimum value of ${k}^{{^{\prime\prime}}{}}a$ is $1/\kappa Q$, so a high Q-factor is needed for low loss if $\kappa$ is small. In contrast to electrical systems, this can be achieved using mechanical resonators, which can have much higher Q’s than assumed here [e.g. 8000 in Bannon et al. (2000)].

Fig. 3

Dispersion diagrams for an array of coupled beam resonators: a $\omega -k$ diagram and b frequency-dependence of loss, assuming $\kappa =0.1$ and $Q=200$. Discrete points indicate resonances for a 4-beam array

3.2 Standing waves and resonance

We now consider the case when a line is terminated without matching, for example at elements $1$ and $N$. The solution is constructed as a sum of forward- and backward-travelling waves, as ${S}_{n} = {S}_{F}{e}^{-jnka} + {S}_{B} {e}^{+jnka}$, with the coefficients chosen to yield ${S}_{n} =0$ at elements 0 and $N+1$. In the lossless case, the result is a standing wave ${S}_{n}={S}_{0}\mathrm{ sin}(nka)$ with $ka=m\pi /\left(N+1\right)$, where ${S}_{0}$ is a constant and $m$ is an integer (the mode number). Thus, a finite line supports longitudinal modes of the form:

$${S}_{nm}={S}_{0} sin\left\{nm\pi /(N+1)\right\} \mathrm{with }m = 1, 2 \dots N$$

(22)

Each mode exists at a frequency found from ${\omega }_{m}^{2}/{\omega {^{\prime}}{^{\prime}}}_{1}^{2}=1-\kappa cos\left\{m\pi /\left(N+1\right)\right\}$ with m = 1, 2 … N. The points in Fig. 3a are the resonant frequencies for an example line with $N=4$. In this case, resonant modes exist when $k{^{\prime}}a=\pi /5, 2\pi /5, 3\pi /5 \,\mathrm{and}\, 4\pi /5$.

3.3 Characteristic impedance and matching

Matching is required to avoid standing wave resonances. Comparison of the last two equations in (16) shows that they will be equivalent if $j\omega {Z}_{L}{S}_{N}=-{K}_{1}{S}_{N+1}$, and hence if ${Z}_{L}$ has the value ${Z}_{0} = -({K}_{1}/j\omega ) {e}^{-jka}$. ${Z}_{0}$ is the characteristic impedance of the slow wave structure. In general, ${Z}_{0}$ is complex, but for lossless systems at resonance it has the real value ${Z}_{0R} ={K}_{1}/{\omega {^{\prime}}{^{\prime}}}_{1}$. Matching can then be achieved by choosing ${Z}_{L}={Z}_{0R}$. This simply requires the load resistance ${z}_{L}$ to be chosen so that ${K}_{v}^{2}{z}_{L}={Z}_{0R}$; however, one well-known issue is that large values of ${z}_{L}$ may be needed if ${K}_{v}$ is small (Bannon et al. 2000; Arellano et al. 2008).

4 Resonant cavity filters

Most researchers have focused on the arrangement in Fig. 4a, where the input and output are taken from transducers $1$ and $N$, with $N$ in the range 2–3. The result is a bandpass filter, whose centre frequency, bandwidth and order are determined by ${\omega {^{\prime}}{^{\prime}}}_{1}$, $\kappa$ and $N$. However, alternative possibilities exist, and can be modelled by altering the port positions. In this Section, we consider filters based on resonant acoustic cavities.

Fig. 4

Device topologies for a band-pass and b band-stop and comb filters

4.1 Coupled cavity filters

Figure 4b shows an array containing $2N$ elements, with the input and output ports at transducers $N$ and $N+1$. This configuration corresponds to a two-element array, with each port additionally coupled to a slow-wave cavity. If the cavities are non-resonant, their effect may be ignored, and the response will be a second-order band-pass. However, there will be a set of resonant frequencies at which energy is coupled into the cavity. Under these conditions, any input will be reflected, inserting stops into the pass band. From Sect. 2, the LEM can simply be written down as:

$$\begin{aligned} & \left\{\left({\omega {^{\prime}}{^{\prime}}}_{1}^{2}-{\omega }^{2}\right)M+j\omega R\right\}{S}_{1}-{K}_{1}{S}_{2}=0 \\ & \left\{\left({\omega {^{\prime}}{^{\prime}}}_{1}^{2}-{\omega }^{2}\right)M+j\omega R\right\}{S}_{n}-{K}_{1}\left({S}_{n-1}+{S}_{n+1}\right)=0; 2\le n\le N-1 \\ & \left\{\left({\omega {^{\prime}}{^{\prime}}}_{1}^{2}-{\omega }^{2}\right)M+j\omega \left(R+{Z}_{L}\right)\right\}{S}_{N}-{K}_{1}\left({S}_{N-1}+{S}_{N+1}\right)={j\omega K}_{v}{V}_{A}\\ & \left\{\left({\omega {^{\prime}}{^{\prime}}}_{1}^{2}-{\omega }^{2}\right)M+j\omega \left(R+{Z}_{L}\right)\right\}{S}_{N+1}-{K}_{1}\left({S}_{N}+{S}_{N+2}\right)=0\\ & \left\{\left({\omega {^{\prime}}{^{\prime}}}_{1}^{2}-{\omega }^{2}\right)M+j\omega R\right\}{S}_{n}-{K}_{1}\left({S}_{n-1}+{S}_{n+1}\right)=0; N+2<n<2N-1\\ & \left\{\left({\omega {^{\prime}}{^{\prime}}}_{1}^{2}-{\omega }^{2}\right)M+j\omega R\right\}{S}_{2N}+{K}_{1}{S}_{2N-1}=0\end{aligned}$$

(23)

These equations may be solved by matrix inversion after writing them in matrix–vector form, and the S-parameters may then be extracted as before. However, an analytic solution that offers greater insight may be found as follows.

4.2 Analytic solution

In the cavity sections, solutions can be taken standing waves, as:

$$\begin{aligned}{S}_{n}& =X sin\left(nka\right), 1\le n\le N\\ {S}_{n}& =Y sin\left(\left[2N+1-n\right]ka\right), N+1\le n\le 2N\end{aligned}$$

(24)

And that remains is then to solve the two central equations, which can be written as:

$$\begin{aligned}G{S}_{N}-{K}_{1}\left({S}_{N-1}+{S}_{N+1}\right)={j\omega K}_{v}{V}_{A} \\ G{S}_{N+1}-{K}_{1}\left({S}_{N}+{S}_{N+2}\right)=0\end{aligned}$$

(25)

With $G=\left({\omega {^{\prime}}{^{\prime}}}_{1}^{2}-{\omega }^{2}\right)M+j\omega \left(R+{Z}_{L}\right)$. Substitution of the cavity solutions gives the two simultaneous equations $AX+BY=E$ ;$CX+DY=F$, with:

$$\begin{aligned} A& =Gsin\left(Nka\right)-{K}_{1}sin\left(\left[N-1\right]ka\right)=D\\B& =-{K}_{1}sin\left(Nka\right)=C;{E=j\omega K}_{v}{V}_{A};F=0\end{aligned}$$

(26)

The solution is $X=DE/\left(AD-BC\right)$ and $Y=-CE/\left(AD-BC\right)$, allowing the amplitudes at the ports to be found as ${S}_{N}=X sin\left(Nka\right)$, ${S}_{N+1}=Y sin\left(Nka\right)$. The variation of S-parameters may then be found as before. However, without solving the equations, it is clear that ${S}_{N}$ and ${S}_{N+1}$ will both be zero whenever $ka=m\pi /N$, with $m=\mathrm{1,2}\dots$., provided $AD-BC$ is finite. At any such point, s₂₁ must be zero, confirming the assume behaviour. If $N=2$, there will be a single stop frequency when $ka=\pi /2$ (i.e., at resonance). A filter of this type may be used as a blocker. For $N>2$ there will be multiple notches and a comb response. These will lie at equal intervals in $k$-space, and hence at slightly unequal intervals in $\omega$-space. However, the frequency spacing will be similar near ${\omega {^{\prime}}{^{\prime}}}_{1}$, and wider deviations may be unimportant.

4.3 Higher order filters

Similar approaches may be used to investigate other coupled cavity filters, simply by writing down the relevant LEM, solving the equations and extracting the S-parameters. We have investigated variants with (a) equal cavity lengths, (b) unequal cavities and (c) non-adjacent ports. Not all display useful responses. Equal cavity lengths perform better than unequal cavities. The most promising designs with non-adjacent ports found to date are formed from equal $N$-element cavities and a total of $4N-1$ coupled beams, and hence have the ports located at transducers $N$ and $3N$. These arrangements also yield comb filters, but with higher order roll-off at the band edges.

5 Numerical results

In this section, we demonstrate typical filter responses using the LEM, and verify these by comparison with the SMM and FEM.

5.1 Lumped element model

The LEM was written in Matlab® (https://www.mathworks.com/products/matlab.html). The analysis of Sect. 2 was first used to determine model coefficients from dimensions and material parameters. The lowest-order resonance ${\omega }_{1}$ was found for an unperturbed beam, and the stiffness ${K}_{0}$ and mass $M$ were estimated from the mode shape. The electrostatic problem was solved to find the snap-down voltage and the electrode gap at the set ${V}_{D}$, and hence calculate the loading and detuning terms ${K}_{v}$ and $\Delta K$ and the electrostatically modified resonance ${\omega {^{\prime}}}_{1}$. The stiffness ${k}_{1}$ and mass ${m}_{1}$ of the coupling springs were then calculated, and the perturbation problem solved with electrostatic detuning described as a reduction in ${E}_{0}$. The results were used to estimate the mechanically modified resonant frequency ${\omega {^{\prime}}{^{\prime}}}_{1}$, stiffness ${K}_{1}$, coupling coefficient $\kappa$ and characteristic impedance ${ Z}_{L}$. The load ${z}_{L}$ was then estimated. The $Q$-factor was the only user-defined parameter; its value is unimportant, provided it is large enough. The analysis of Sects. 3 and 4 was used to select promising designs; the matrix problem was then solved, and the S-parameters were extracted.

5.2 Stiffness matrix model

A 2D SMM was also written in Matlab. SMM solvers model beam networks using a stiffness matrix ${\varvec{K}}$ combining elements from Euler theory with compatibility conditions. ${\varvec{K}}$ was constructed from dimensions and material parameters, with ${E}_{0}$ reduced to model electrostatic detuning. Long beams were subdivided into > 50 segments to ensure accuracy. Axial, transverse and angular displacements at each beam end were found for a vector of applied forces and torques, here taken as a point load on the actuated beam. Dynamic analysis was performed using additional mass and damping matrices. The mass matrix ${\varvec{M}}$ was formed by combining dimensions and densities with standard relations for motions of centres of mass. The damping matrix ${\varvec{C}}$ was modelled using Rayleigh’s method as ${\varvec{R}}=\alpha {\varvec{M}}+\beta {\varvec{K}}$, with $\alpha$ determined from the $Q$-factor and $\beta =0$. Ports were simulated by increasing the damping in the terminal beams, using a damping coefficient determined from ${z}_{L}$. Assuming harmonic forces and displacements, as $\left({\varvec{F}},\boldsymbol{ }{\varvec{U}}\right) {e}^{j\omega t}$, substitution into the governing equation yields $\left({\varvec{K}}-{\omega }^{2}{\varvec{M}}+j\omega {\varvec{R}}\right){\varvec{U}}={\varvec{F}}$. This equation was solved by inversion, and the velocity vector constructed as ${\varvec{S}}=j\omega {\varvec{U}}$. The scattering parameters ${s}_{11}$ and ${s}_{21}$ were then extracted from midpoint velocities. The SMM was used to quantify inaccuracies in the LEM arising from perturbation theory.

5.3 Finite element model

FEM was performed using COMSOL Multiphysics® (https://uk.comsol.com), using three coupled modules: Solid Mechanics, Electrostatics and Electrical Circuit. First, the mechanical layout and constraints were set up, and elastic and inertial constants were defined. Inertial damping was estimated from the $Q$-factor. Electrostatic drives were defined on opposing surfaces of cuboid air volumes between each beam and a fixed electrode. Terminals were added to allow application of DC voltages and connection to AC parts of the circuit. The mechanism and air gaps were meshed using a free triangular mesh, using different mesh sizes to reduce simulation time. A frequency sweep was used to calculate S-parameter variations, from currents or beam velocities. The FEM was then used to correct inaccuracies in the SMM caused by detailed electrostatic effects.

5.4 Parameter selection

Parameters were chosen to model devices operating at 1 MHz with a bandwidth of around 10%. The parameters of an isolated beam with an appropriate resonance were first identified. Spring parameters were then estimated to set the bandwidth, and beam parameters were adjusted to ensure the desired resonance lay within a tuning range set by snap-down. The following parameter values were used: ${d}_{0}=4 \,\mu m$, ${w}_{0}=3 \,\mathrm{\mu m}$, ${L}_{0}=150\, \mathrm{\mu m}$, $Q=5000$, ${E}_{0}=169\times {10}^{9}N/{m}^{2}$, $\alpha ={x}_{1}/{L}_{0}=0.25$, $s=6 \,\mathrm{\mu m}$, ${w}_{1}=0.1 \,\mathrm{\mu m}$, ${E}_{1}=130\times {10}^{9}N/{m}^{2}$, and ${g}_{0}=0.1\, \mathrm{\mu m}$, leading to a snap-down voltage of $\sim 3.5 V$. Values of ${E}_{0}$ and ${E}_{1}$ were chosen to model devices formed in (100) Si with the MEMS and NEMS beams in the < 110 > and < 010 > directions (Hopcroft et al. 2010), and (although unimportant) a Poisson’s ratio of $\nu =0.28$ was assumed in the FEM. ${V}_{D}$ and ${z}_{L}$ were adjusted to achieve tuning and matching, and are identical for all similar devices, whatever their port arrangements.

5.5 Device responses

Figure 5 shows simulated responses obtained using the LEM for second-order notch filters with (a) $N=2$ and (b) $N=4$. The first design has four beams, with ports located at transducers 2 and 3, and yields a bandpass response with a single notch in the frequency variation of ${S}_{21}$, while the second has 8 beams, ports at transducers 4 and 5, and yields a response with three notches. The DC voltage needed to set the resonance was ${V}_{D}=2.83 V$, yielding ${z}_{L}\approx 434 \,\mathrm{k\Omega }$. Three resonance frequencies are marked: ${f}_{00}$ (for an isolated beam), ${f}_{0e}$ (after electrostatic detuning), and ${f}_{0m}$ (after mechanical detuning). The single notch in Fig. 5a corresponds to ${f}_{0m}$, when $ka=\pi /2$, and three notches the frequency variation of ${S}_{21}$ in Fig. 5b lie at frequencies for which $ka=m\pi /4$. In-band transmission is high, and the corresponding reflection is low, confirming that the system is matched. Figure 6 shows similar responses for higher-order notch filters, again with (a) $N=2$ and (b) $N=4$. These designs require 7 and 15 beams; they also yield bandpass responses with 1 and 3 notches, but the roll-off at the band edges is now much steeper.

Fig. 5

Frequency responses of filters with a single and b multiple notches in their pass-bands and second-order roll off, as predicted using the LEM

Fig. 6

Frequency responses of filters with a single and b multiple notches in their pass-bands and high-order roll off, as predicted using the LEM

Figure 7a shows numerical results corresponding to Fig. 5a but obtained using the SMM without changing any parameters except ${V}_{D}$ (now 2.811 V) and ${z}_{L}$ (now 392 $\mathrm{k\Omega }$). The source of the changes needed to the bias voltage and matched load is perturbation theory, which yields a slight overestimate of the effect of mass loading by the coupling springs. For example, Fig. 7b shows the dependence of ${\omega {^{\prime}}}_{1}/{\omega }_{1}$ with ${x}_{1}/{L}_{0}$ as predicted by the LEM (dashed line) and SMM (full line) for the parameters used here. In each case, the variation approximately follows the shape of the lowest order mode, reaching a maximum when the springs are located at the midpoint of the beam. However, the LEM predicts a consistently higher resonance, and hence an over-estimate of the effective stiffness. Providing this effect is small, the only corrections needed are small changes to the tuning and matching conditions.

Fig. 7

a Frequency response of second-order notch filter with N = 2, as predicted using the SMM; b variation of resonant frequency ${\omega {^{\prime}}}_{1}$ with spring position ${x}_{1}$, as predicted using the LEM and SMM

To model designs using the FEM, the voltage ratio $\beta$ introduced in Sect. 2 was first found. Because this value must be known precisely to obtain consistent results, two different methods were used. In the first, $\beta$ was obtained as the value needed to equalize electrode gaps in separate static models of single, isolated beams and similar beams with halved springs connecting to anchors. In the second, electrode gaps were equalised in static models of beam arrays as used here. Equivalent results were obtained for three beam arrays, but the stability of the second solution decreased as the number of beams was raised from 3 to 8. Figure 8a shows the variation of $\beta$ with ${V}_{D}$ found using the first method for the parameters here. The variation is almost constant at around 1.098, until the snap-down voltage ${V}_{S}$ is approached (dotted line). However, away from this point, the value differs slightly from the estimate in Sect. 2 ($1+{K}_{1}/2{K}_{0}\approx 1.027$), presumably due to the use of dynamic rather than static values for ${K}_{1}$ and ${K}_{0}$ in this approximation.

Fig. 8

a Voltage dependence of terminal voltage tuning coefficient $\beta$, and b frequency response of second-order notch filter with N = 2, as predicted using the FEM

Figure 8b shows numerical results corresponding to Figs. 5a and 7a, obtained using the FEM without changing parameters except ${V}_{D}$ (now 3.0085 V) and ${z}_{L}$ (now 390 $\mathrm{k\Omega }$) but introducing the end-transducer voltages ${V}_{D1}$ and ${V}_{DN}$ (both taken as ${\beta V}_{D}$, with the value of $\beta$ obtained from Fig. 8a as $\beta =1.01983$). Excellent agreement is again obtained in the overall response, apart from minor discrepancies in the unimportant nulls in ${S}_{11}$. It was also verified that the notch position could be tuned using ${V}_{D}$ alone. Similar results were obtained for higher-order and comb filters. These results suggest that the complex design concepts proposed here are likely to be realisable in practice, even taking into account the detailed non-linear behaviour of electrostatic transducers.

6 Conclusions

Analysis of MEMS filters based on arrays of coupled resonant beams has been reviewed, and the factors preventing effective operation of large arrays have been identified. Near-ideal results can be obtained, providing synchronisation is retained using correct mechanical design, and desynchronization caused by electrostatic transducers is minimised. Alternative filter characteristics including notch and comb responses have been proposed, based on arrays containing resonant cavities for acoustic slow waves, and the expected responses have been verified. The devices do require an additional tuning voltage, which may be inconvenient. However, in further simulations (not shown here) it has been verified that main effect of using identical tuning voltages on all beams is a slight shift in cavity resonance.

A simple procedure for selection of design parameters has been developed, by using results obtained from a lumped element model to identify basic layout parameters and a stiffness matrix model to improve dynamical modelling. These allow accurate simulation using coupled Multiphysics methods (which offer improved electrostatic modelling) without the need for lengthy design iteration. The results are consistent and suggest that high-performance filters can be constructed. It is also likely that other functionality including three and four port operation can be obtained from coupled beam arrays. However, complex fabrication processes will be required to realise the nanostructured electrode gaps and coupling springs needed for good performance, and to enable simple connection to tuning electrodes internal to the beam array.