Large-amplitude parametric response of fluid-conveying nanotubes due to flow pulsations

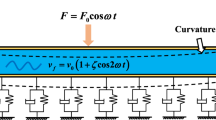
Abstract

In this article, the nonlinear parametric response of viscoelastic nanotubes conveying pulsatile flow is investigated. A two-parameter scale-dependent elasticity-based model is developed within the framework of a nonlocal theory with strain gradient influences. To model the effects of fluid molecules, which slip on the internal nanotube wall, on the parametric response, Karniadakis–Beskok approach is used. Viscoelastic effects are also described via Kelvin–Voigt scheme. Hamilton law, Galerkin and continuation techniques are, respectively, utilized in this analysis for obtaining, discretising and solving nonlinear coupled equations. Both subcritical and supercritical nonlinear parametric responses are examined considering various parameters such as the speed variation amplitude and frequency. The viscoelastic nanotube conveying pulsatile flow exhibits a hardening nonlinearity in the subcritical regime while it displays a softening nonlinearity in the supercritical regime.

Appendix A

To show the accuracy of the obtained results, a reasonable comparison is performed between the presented results and those calculated by Li et al. (2016) in Fig. 12. The strain gradient-to-nonlocal factor and linear critical velocity are given by ${{l_{sg} } \mathord{\left/ {\vphantom {{l_{sg} } {e_{0} a}}} \right. \kern-0pt} {e_{0} a}}$ and $\bar{U} = UL\sqrt {{M \mathord{\left/ {\vphantom {M {EI}}} \right. \kern-0pt} {EI}}}$, respectively. The effects of slip and geometrical nonlinearity are not captured. Geometrical and elastic properties are taken the same as those in the investigation done by Li et al. (2016). From Fig. 12, it is seen that the obtained results perfectly match those available in the literature.

Fig. 12

Linear critical velocity versus the strain gradient-to-nonlocal factor for small-scale tubes (Li et al. 2016)